番禺区2007年九年级数学综合训练(一)

合集下载

2007年广州市数学初中毕业生学业考试

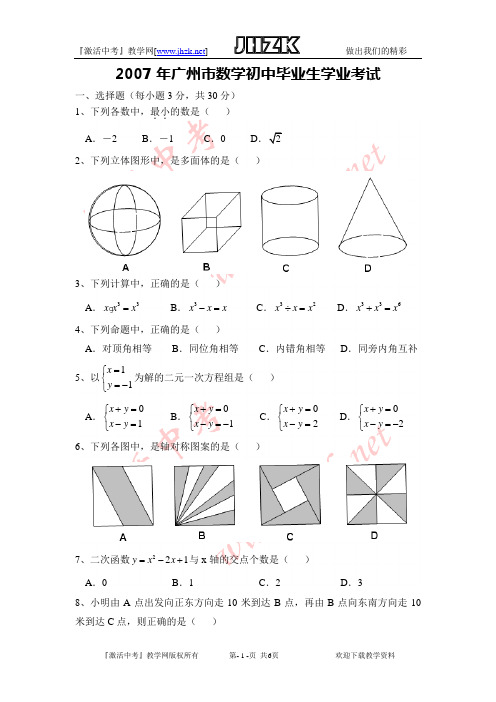
2007年广州市数学初中毕业生学业考试一、选择题（每小题3分，共30分）1、下列各数中，最小．．的数是（）A．－2 B．－1 C．0 D22、下列立体图形中，是多面体的是（）3、下列计算中，正确的是（）A．33x x x=B．3x x x-=C．32x x x÷=D．336x x x+=4、下列命题中，正确的是（）A．对顶角相等B．同位角相等C．内错角相等D．同旁内角互补5、以11xy=⎧⎨=-⎩为解的二元一次方程组是（）A．1x yx y+=⎧⎨-=⎩B．1x yx y+=⎧⎨-=-⎩C．2x yx y+=⎧⎨-=⎩D．2x yx y+=⎧⎨-=-⎩6、下列各图中，是轴对称图案的是（）7、二次函数221y x x=-+与x轴的交点个数是（）A．0 B．1 C．2 D．38、小明由A点出发向正东方向走10米到达B点，再由B点向东南方向走10米到达C点，则正确的是（）A ．∠ABC=22.5°B ．∠ABC=45°C ．∠ABC=67.5°D ．∠ABC=135°9、关于x 的方程20x px q ++=的两根同为负数，则（）A ．0p >且q >0B ．0p >且q <0C ．0p <且q >0D ．0p <且q <010、如图，⊙O 是△ABC 的内切圆，OD ⊥AB 于点D ，交⊙O 于点E ，∠C=60°，如果⊙O 的半径为2，则结论错误的是（）A ．AD DB = B ． AE EB= C ．1OD = D ．3AB =二、填空题（每小题3分，共18分）11、化简2-=12、方程511x =+的解是13、线段AB=4㎝，在线段AB 上截取BC=1㎝，则AC= ㎝143x -有意义，则实数x 的取值范围是15、已知广州市的土地总面积是74342km ，人均占有的土地面积S （单位： 2/km 人），随全市人口n （单位：人）的变化而变化，则S 与n 的函数关系式是16、如图，点D 是AC 的中点，将周长为4㎝的菱形ABCD 沿对角线AC 方向平移AD 长度得到菱形OB ’C ’D ’,则四边形OECF 的周长是㎝三、解答题17、（9分）请以下列三个代数式中任选两个构造一个分式，并化简该分式。

2007年广东省广州市中考数学试卷

2007年广东省广州市中考数学试卷一、选择题（共10小题，每小题3分，满分30分）．．C D．5．（3分）（2007•广州）以为解的二元一次方程组是（）．C D．．C D．2分）（2007•广州）小明由A点出发向正东方向走10米到达B点，再由B点向东南方向走10米到达C点，8．（3210．（3分）（2007•广州）如图，⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，如果⊙O的半径为2，则结论错误的是（）C B=二、填空题（共6小题，每小题3分，满分18分）11．（3分）（2007•广州）计算：|﹣2|=_________．12．（3分）（2007•广州）方程：的解是x=_________．13．（3分）（2007•广州）线段AB=4cm，在线段AB上截取BC=1cm，则AC=_________cm．14．（3分）（2007•广州）若式子有意义，则实数x的取值范围是_________．15．（3分）（2007•广州）已知广州市的土地总面积是7434km2，人均占有的土地面积S（单位：km2/人），随全市人口n（单位：人）的变化而变化，则S与n的函数关系式是_________．16．（3分）（2007•广州）如图，点O是AC的中点，将周长为4cm的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB′C′D′，则四边形OECF的周长是_________cm．三、解答题（共9小题，满分102分）17．（9分）（2007•广州）请以下列三个代数式中任选两个构造一个分式，并化简该分式．a2﹣1；ab﹣b；b+ab．18．（9分）（2007•广州）右图是一个立体图形的三视图，请写出这个立体图形的名称，并计算这个立体图形的体积．（结果保留π）19．（10分）（2007•广州）甲、乙、丙三名学生各自随机选择到A、B两个书店购书，（1）求甲、乙两名学生在不同书店购书的概率；（2）求甲、乙、丙三名学生在同一书店购书的概率．20．（10分）（2007•广州）某校初三（1）班50名学生参加1分钟跳绳体育考试．1分钟跳绳次数与频数经统计后60并且小于70）和扇形统计图．（2）求该班1分钟跳绳成绩在80分以上（含80分）的人数占全班人数的百分比；（3）根据频数分布表估计该班学生1分钟跳绳的平均分大约是多少？并说明理由．21．（12分）（2007•广州）如图，在△ABC中，AB=AC，内切圆O与边BC、AC、AB分别切于D、E、F．（1）求证：BF=CE；（2）若∠C=30°，CE=2，求AC．22．（14分）（2007•广州）二次函数图象过A、C、B三点，点A的坐标为（﹣1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB=OC．（1）求C的坐标；（2）求二次函数的解析式，并求出函数最大值．23．（12分）（2007•广州）某博物馆的门票每张10元，一次购买30张到99张门票按8折优惠，一次购买100张以上（含100张）按7折优惠．甲班有56名学生，乙班有54名学生．（1）若两班学生一起前往参观博物馆，请问购买门票最少共需花费多少元？（2）当两班实际前往该博物馆参观的总人数多于30人且不足100人时，至少要多少人，才能使得按7折优惠购买100张门票比实际人数按8折优惠购买门票更便宜？24．（14分）（2007•广州）一次函数y=kx+k过点（1，4），且分别与x轴、y轴交于A、B点，点P（a，0）在x轴正半轴上运动，点Q（0，b）在y轴正半轴上运动，且PQ⊥AB．（1）求k的值，并在直角坐标系中画出一次函数的图象；（2）求a、b满足的等量关系式；（3）若△APQ是等腰三角形，求△APQ的面积．25．（12分）（2007•广州）已知：在Rt△ABC中，AB=BC，在Rt△ADE中，AD=DE，连接EC，取EC的中点M，连接DM和BM．（1）若点D在边AC上，点E在边AB上且与点B不重合，如图1，探索BM、DM的关系并给予证明；（2）如果将图1中的△ADE绕点A逆时针旋转小于45°的角，如图2，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明．2007年广东省广州市中考数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）．为正数；．C D．5．（3分）（2007•广州）以为解的二元一次方程组是（）．C D．在求解时，可以将代入各个方程组，刚好满足条件．所以答案是．C D．28．（3分）（2007•广州）小明由A点出发向正东方向走10米到达B点，再由B点向东南方向走10米到达C点，210．（3分）（2007•广州）如图，⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，如果⊙O的半径为2，则结论错误的是（）C B==，．二、填空题（共6小题，每小题3分，满分18分）11．（3分）（2007•广州）计算：|﹣2|=2．12．（3分）（2007•广州）方程：的解是x=4．13．（3分）（2007•广州）线段AB=4cm，在线段AB上截取BC=1cm，则AC=3cm．14．（3分）（2007•广州）若式子有意义，则实数x的取值范围是x≥3．15．（3分）（2007•广州）已知广州市的土地总面积是7434km2，人均占有的土地面积S（单位：km2/人），随全市人口n（单位：人）的变化而变化，则S与n的函数关系式是．．S=16．（3分）（2007•广州）如图，点O是AC的中点，将周长为4cm的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB′C′D′，则四边形OECF的周长是2cm．ACAC三、解答题（共9小题，满分102分）17．（9分）（2007•广州）请以下列三个代数式中任选两个构造一个分式，并化简该分式．a2﹣1；ab﹣b；b+ab．=．18．（9分）（2007•广州）右图是一个立体图形的三视图，请写出这个立体图形的名称，并计算这个立体图形的体积．（结果保留π）19．（10分）（2007•广州）甲、乙、丙三名学生各自随机选择到A、B两个书店购书，（1）求甲、乙两名学生在不同书店购书的概率；（2）求甲、乙、丙三名学生在同一书店购书的概率．；=20．（10分）（2007•广州）某校初三（1）班50名学生参加1分钟跳绳体育考试．1分钟跳绳次数与频数经统计后60并且小于70）和扇形统计图．（2）求该班1分钟跳绳成绩在80分以上（含80分）的人数占全班人数的百分比；（3）根据频数分布表估计该班学生1分钟跳绳的平均分大约是多少？并说明理由．，所以由=54% =84%=84%21．（12分）（2007•广州）如图，在△ABC中，AB=AC，内切圆O与边BC、AC、AB分别切于D、E、F．（1）求证：BF=CE；（2）若∠C=30°，CE=2，求AC．，，得22．（14分）（2007•广州）二次函数图象过A、C、B三点，点A的坐标为（﹣1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB=OC．（1）求C的坐标；（2）求二次函数的解析式，并求出函数最大值．﹣+＜﹣有最大值=；，（，x=＜时，=，．23．（12分）（2007•广州）某博物馆的门票每张10元，一次购买30张到99张门票按8折优惠，一次购买100张以上（含100张）按7折优惠．甲班有56名学生，乙班有54名学生．（1）若两班学生一起前往参观博物馆，请问购买门票最少共需花费多少元？（2）当两班实际前往该博物馆参观的总人数多于30人且不足100人时，至少要多少人，才能使得按7折优惠购买100张门票比实际人数按8折优惠购买门票更便宜？24．（14分）（2007•广州）一次函数y=kx+k过点（1，4），且分别与x轴、y轴交于A、B点，点P（a，0）在x 轴正半轴上运动，点Q（0，b）在y轴正半轴上运动，且PQ⊥AB．（1）求k的值，并在直角坐标系中画出一次函数的图象；（2）求a、b满足的等量关系式；（3）若△APQ是等腰三角形，求△APQ的面积．或，×OQ=×（平方单位）1+2b=，此时AP=1+2b=5+2OQ=2+，××5+2=10+，因为点的面积为25．（12分）（2007•广州）已知：在Rt△ABC中，AB=BC，在Rt△ADE中，AD=DE，连接EC，取EC的中点M，连接DM和BM．（1）若点D在边AC上，点E在边AB上且与点B不重合，如图1，探索BM、DM的关系并给予证明；（2）如果将图1中的△ADE绕点A逆时针旋转小于45°的角，如图2，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明．EC=EM=MC DM=。

番禺区2009年九年级数学综合训练试题一答案(印刷)

番禺区2009年九年级数学综合训练试题(一)参考答案与评分说明题号 1 2 3 4 5 6 7 8 9 10 答案 BDBACDDBAC三、17．解：原式2221a a a a =-+--······························································ 6分 31a =-+． ·································································································· 7分当16a =时，原式1316=-⨯+12=． ·································································· 9分三、18．（1）证明：在ABC △和DCB △中，AB DC AC DB BC CB =⎧⎪=⎨⎪=⎩，································································································ 3分 ABC DCB ∴△≌△（SSS ） ············································································ 5分（2）是等腰三角形． ······················································································ 7分ABC DCB ∆≌△，DBC ACB ∴∠=∠, ·························································· 8分 OB OC ∴=,即ΔOBC 是等腰三角形。

2007年初三数学综合测试联考试卷

2007年初三数学综合测试联考试卷(时间：120分钟，满分：150分)一、选择题（本题共10小题，每小题4分，满分40分）在每小题给出的四个选项中，只有一个是符合题意的，把所选项前的标号填在题后的括号内。

1、方程x x =2的根是 [ ]A.1B.0C.0,1D.―12、下列式子正确的是 [ ]A.m n mn D mn a m a n C B ==++=-=--221..1)1.(1)1(3、要调查某校九年级学生周日的睡眠时间，选取调查对象最合适的是 [ ] A.选取一个班级的学生 B.选取50名男生C.随机选取50名九年级学生D.选取50名女生4、已知53=-y y x ，那么能求出值的是 [ ]A.x+yB.x －yC.xyD.y x5、如图，已知MB ＝ND ，∠MBA ＝∠NDC ， [ ]下列条件不能识别△ABM ≌△CDNA.∠M ＝∠NB.AM ＝CNC.AC ＝BDD.AM ∥CN 6、下列命题：①两个全等三角形的周长相等； ②两个全等三角形对应角的平分线相等； ③两个全等三角形的面积相等；④不全等的两个三角形面积不相等，其中真命题的个数有 [ ] A.1个 B.2个 C.3个 D.4个7、某校现有学生1800人，为了增强学生的法律意识，学校组织全体学生进行了一次普法测试，现抽取部分测试成绩（得分取整数）作为样本，进行整理并绘制成频数分布直方图（如图），根据图中信息，下列判断错误的是 [ ] A.样本容量是48B.估计本次测试全校在90分以上的学生约有225人C.样本的中位数落在70.5～80.5这一分数段内D.样本中50.5～70.5这一分数段的频率是0.258、下列一元二次方程中，两实数根的和等于2的方程是 [ ]322.0342.0342.0342.2222=--=+-=--=-+x x D x x C x x B x x A9、如图，在四个均由16个小正方形组成的网格中，各有一个格点三角形，那么与众不同的三角形是 [ ]10、已知⊙O 1与⊙O 2外切，且半径都等于1，则与⊙O 1和⊙O 2都相切且半径为2的圆有 [ ]个 C.4个 D.5个二、填空题 (本题共4小题，每小题5分，满分20分)11、测得某人的一根头发直径约为7.2×10－5米，用小数表示为_____________米。

文档：da2007年广州中考数学试题

2007年广州市初中毕业生学业考试数学题库参考答案一、选择题：本题考查基本知识和基本运算，每小题3分，满分30分. 题号 1 2 3 4 5 6 7 8 9 10 答案ABCACBBDAD二、填空题：本题考查基本知识和基本运算，每小题3分，满分18分.题号 11 12 13 141516 答案2x =433x ≥7434S n=2三、解答题：本大题考查基本知识和基本运算，及数学能力，满分102分. 17．本小题主要考查代数式的基本运算．满分９分. 解：本题共有六种答案，只要给出其中一种答案，均正确.21a ab b --()()()111a a b a +-=-1a b +=. ()()()211111a a a a b ab b a b +---==++. ()()()211111b a ab b ba a a a --==-+-+. ()()1111b a ab b a b ab a b a ---==+++. ()()()211111b a b ab ba a a a ++==-+--. ()()1111b a b ab a ab b b a a +++==---.18.本小题主要考查三视图的概念、圆柱的体积，考查运算能力．满分９分. 解：该立体图形为圆柱.因为圆柱的底面半径5r =，高10h =，所以圆柱的体积22510250V r h πππ==⨯⨯=（立方单位）. 答：所求立体图形的体积为250π立方单位..，BABBAABABBAABBA.，ABBAA19．本小题主要考查等可能性等基本概念，考查简单事件的概率计算．满分10分．解法1：（1）甲、乙两名学生到A、B两个书店购书的所有可能结果有：从树状图可以看出，这两名学生到不同书店购书的可能结果有AB、BA共2种，所以甲、乙两名学生在不同书店购书的概率12142P==.（2）甲、乙、丙三名学生到A、B两个书店购书的所有可能有：从树状图可以看出，这三名学生到同一书店购书的可能结果有AAA、BBB共2种，所以甲、乙、丙三名学生在同一书店购书的概率22184P==.解法2：（1）甲、乙两名学生到A、B两个书店购书的所有可能结果有AA、AB、BA、BB 共4种，其中两人在不同书店购书的可能有AB、BA共2种，所以甲、乙两名学生在不同书店购书的概率12142P==.（2）甲、乙、丙三名学生到A、B两个书店购书的所有可能有AAA、AAB、ABA、ABB、BAA、BAB、BBA、BBB共8种，其中三人在同一书店购书的可能有AAA、BBB 共2种，所以甲、乙、丙三名学生在同一书店购书的概率22184P==.20．本小题主要考查从统计表和统计图中读取有效信息的能力，考查数据分析能力．满分10分.解：（1）由扇形统计图知：初三（1）班1分钟跳绳考试成绩为B等的学生占全班总人数的54％，∴954%50m+=.∴18m=.∵391812250n+++++=，∴6n=.（2）由频数分布表可知：初三（1）班1分钟跳绳成绩在80分以上（含80分）的人数为39181242+++=.∴ 1分钟跳绳成绩在80分以上（含80分）的人数占全班人数的百分比为4284%50=. （3）本题答案和理由不唯一，只要该班学生1分钟跳绳平均分的估计值是85～100分之间的某一个值或某个范围，理由合理，均正确.例如：估计平均分为92分，估计方法为：取每个分数段的中间值分别是115、105、95、85、75、65、30，则该班学生1分钟跳绳的平均分为11531059951885127566523009250x ⨯+⨯+⨯+⨯+⨯+⨯+⨯==（分）.（说明：只要按照在每个分数段中按等距离取值，然后计算加权平均分，均正确.）又如：估计平均分在90～100分之间，理由是：该班有18个人的成绩在90～100分之间，而且30个人的成绩超过90分.21. 本小题主要考查平行线、等腰三角形、特殊直角三角形、直线与圆的位置关系等基础知识，考查运算能力、演绎推理能力和空间观念．满分12分．（1）证明：∵ AE 、AF 是⊙O 的切线， ∴ AE ＝AF ．又∵ AC ＝AB ， ∴ AC -AE ＝AB -AF ． ∴CE ＝BF ，即BF ＝CE ．（2）解法1：连结AO 、OD ，∵ O 是△ABC 的内心， ∴ OA 平分∠BAC ．∵ ⊙O 是△ABC 的内切圆，D 是切点， ∴ OD ⊥BC ．又∵ AC ＝AB ， ∴ AO ⊥BC ．∴ A 、O 、D 三点共线，即AD ⊥BC ． ∵ CD 、CE 是⊙O 的切线， ∴ CD ＝CE =23．图5O FEDCBA图5O FED CB A在Rt △ACD 中，由∠C =30°，CD =23，得234cos303/2CD AC ==＝．解法2：先证 AD ⊥BC ，CD ＝CE =23（方法同解法1）．设AC ＝x ，在Rt △ACD 中，由∠C =30°，得22AC x AD ==． ∵ 222AC AD DC =+, ∴ 222()(23)2xx =+．解之，得4x =（负值舍去）． ∴AC 的长为4．22. 本小题主要考查二次函数、二元一次方程组等基础知识，考查数形结合的数学思想，考查计算能力和推理能力．满分14分．解：（1）∵ A (-1，0)、B (4，0)，∴ AO =1， OB =4，即AB = AO +OB =1+4=5. ∴ OC ＝5，即点C 的坐标为（0，5）.（2）解法1：设图象经过A 、C 、B 三点的二次函数的解析式为 2y ax bx c =++，由于这个函数的图象过点（0，5），可以得到c =5，又由于该图象过点（-1，0）、（4，0），则：50,16450.a b a b -+=⎧⎨++=⎩ 解这个方程组，得5,415.4a b ⎧=-⎪⎪⎨⎪=⎪⎩ ∴ 所求的二次函数解析式为2515544y x x =-++. ∵504a =-<， ∴当1534522()4x =-=⨯-时，y 有最大值225154()5()41254454164()4ac b a ⨯-⨯--==⨯-. 解法2：设图象经过A 、C 、B 三点的二次函数的解析式为(4)(1)y a x x =-+，CO A B xy∵ 点C （0，5）在图象上，∴ 5(04)(01)a =-+，即54a =-．∴ 所求的二次函数解析式为5(4)(1)4y x x =--+． ∵ 点A 、B 的坐标分别为点A (1,0)-、B (4,0)，∴ 线段AB 的中点坐标为3(,0)2，即抛物线的对称轴为直线32x =． ∵ 504a =-<， ∴ 当32x =时，y 有最大值533125(4)(1)42216y =--+=.23．本小题主要考查从文字信息中读取有效信息、数据处理能力，考查分类的数学思想，考查建立不等式（组）模型解决实际问题的能力．满分12分．解：（1）当两个班分别购买门票时，甲班购买门票的费用为56×10×0.8＝448（元）；乙班购买门票的费用为54×10×0.8＝432（元）；甲、乙两班分别购买门票共需花费880元．当两个班一起购买门票时，甲、乙两班共需花费（56＋54）×10×0.7＝770（元）．答：甲、乙两班购买门票最少共需花费770元．（2）当多于30人且不足100人时，设有x 人前往参观，才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜，根据题意，得，30100,0.8101000.710.x x <<⎧⎨⨯>⨯⨯⎩ 解这个不等式组，得87.5100x <<.答：当多于30人且不足100人时，至少有88人前往参观，才能使得按7折优惠购买100张门票比根据实际人数按8折优惠购买门票更便宜.24. 本小题主要考查一次函数、两条直线垂直的性质、三角形相似、等腰三角形、点与坐标等基础知识，考查对数形结合思想的理解，考查分类的数学思想，考查运算和推理能力．满分14分．解：（1）∵ 一次函数y ＝kx +k 的图象经过点（1，4），∴ 4＝k ×1+k ，即k ＝2. ∴ y ＝2x +2.当x ＝0时，y ＝2；当y ＝0时，x ＝－1. 即A （－1，0），B （0，2）.如图，直线AB 是一次函数y ＝2x +2的图象. （2）∵ PQ ⊥AB ，∴ ∠QPO =90°－∠BAO . 又∵∠ABO =90°－∠BAO ， ∴ ∠ABO =∠QPO . ∴ Rt △ABO ∽Rt △QPO .∴ AO OBQO OP=，即12b a =. ∴ a ＝2b . （3）由（2）知a ＝2b . ∴ AP ＝AO +OP ＝1+a ＝1+2b ，22221AQ OA OQ b =+=+，22222222(2)5PQ OP OQ a b b b b =+=+=+=.若AP ＝AQ ，即AP 2＝AQ 2，则22(12)1b b +=+，即0b =或-43，这与0b >矛盾，故舍去；若AQ ＝PQ ，即AQ 2＝PQ 2，则2215b b +=，即1(2b =或-舍去）12，此时，2AP =，12OQ =，111122222APQ S AP OQ =⨯⨯=⨯⨯=△（平方单位）.若AP ＝PQ ，则125b b +=，即25b =+. 此时12525AP b =+=+，25OQ =+.119(525)(25)105222APQ S AP OQ =⨯⨯=⨯+⨯+=+△（平方单位）.∴ △APQ 的面积为12平方单位或（91052+）平方单位.O1 xyAB PQ O1 xyA B25. 本小题主要考查三角形、图形的旋转、平行四边形等基础知识，考查空间观念、演绎推理能力．满分12分．（1）证法1：在Rt △EBC 中，M 是斜边EC 的中点， ∴ 12BM EC =．在Rt △EDC 中，M 是斜边EC 的中点， ∴ 12DM EC =． ∴ BM =DM ，且点B 、C 、D 、E 在以点M 为圆心、BM 为半径的圆上． ∴ ∠BMD =2∠ACB =90°，即BM ⊥DM ．证法2：证明BM =DM 与证法1相同，下面证明BM ⊥DM ． ∵ DM =MC ， ∴ ∠EMD =2∠ECD ． ∵ BM =MC ， ∴ ∠EMB =2∠ECB ．∴ ∠EMD ＋∠EMB =2（∠ECD ＋ECB ）． ∵ ∠ECD ＋∠ECB =∠ACB =45°， ∴ ∠BMD =2∠ACB =90°，即BM ⊥DM ．（2）当△ADE 绕点A 逆时针旋转小于45°的角时，（1）中的结论成立．证明如下：证法1（利用平行四边形和全等三角形）：连结BD ，延长DM 至点F ，使得DM =MF ，连结BF 、FC ，延长ED 交AC 于点H ． ∵ DM =MF ，EM =MC ， ∴ 四边形CDEF 为平行四边形. ∴ DE ∥CF ，ED =CF . ∵ ED = AD , ∴ AD =CF . ∵ DE ∥CF ， ∴ ∠AHE =∠ACF ．MDBACEM DBACEHFMDBACED '∵ 4545(90)45BAD DAH AHE AHE ∠=-∠=--∠=∠-,45BCF ACF ∠=∠-， ∴ ∠BAD =∠BCF . 又∵AB = BC , ∴ △ABD ≌△CBF . ∴ BD =BF ，∠ABD =∠CBF . ∵ ∠ABD +∠DBC =∠CBF +∠DBC ， ∴∠DBF =∠ABC =90°.在Rt △DBF 中，由BD BF =,DM MF =，得BM =DM 且BM ⊥DM ．证法2（利用旋转变换）：连结BD ，将△ABD 绕点B 逆时针旋转90°，点A 旋转到点C ，点D 旋转到点D '，得到△CBD '，则,,,BD BD AD CD BAD BCD '''==∠=∠且90DBD '∠=．连结MD '． ∵CED ∠CEA DEA =∠-∠(180)45180(90)4545ECA EAC ECA BAD ECA BADECB BAD ECB BCD ECD =-∠-∠-=-∠--∠-=-∠+∠=∠+∠'=∠+∠'=∠∴ //DE CD '．又∵DE AD CD '==，∴ 四边形EDCD '为平行四边形． ∴ D 、M 、D '三点共线，且DM MD '=．在Rt △DBD '中，由BD BD '=,DM MD '=，得BM =DM 且BM ⊥DM ．证法3（利用旋转变换）：连结BD ，将△ABD 绕点B 逆时针旋转90°，点A 旋转到点C ，点D 旋转到点D '，得到△CBD '，则,,,BD BD AD CD BAD BCD '''==∠=∠且90DBD '∠=．连结MD '，延长ED 交AC 于点H ．∵ ∠AHD = 90°－∠DAH = 90°－(45°－∠BAD )= 45°＋∠BAD ，45ACD BCD ''∠=+∠，∵BAD BCD '∠=∠，M DBACEHD '∴AHD ACD '∠=∠． ∴ //DE CD '．又∵DE AD CD '==，∴ 四边形EDCD '为平行四边形． ∴ D 、M 、D '三点共线，且DM MD '=．在Rt △DBD '中，由BD BD '=,DM MD '=，得BM =DM 且BM ⊥DM ．。

九年级数学综合训练试题(1)参考答案与评分说明

番禺区2012年九年级数学综合训练试题（一）参考答案与评分说明一、选择题（本大题共10小题，每小题3分，满分30分）第二部分非选择题（共120分）二、填空题（本大题共6小题，每小题3分，满分18分） 11．3-；12．2-；13．60︒；14．25︒，（0~45︒︒均可）；15．3a -；16. 41 三、解答题（本大题共9小题，满分102分）17．解：原式=2221x x x x +++- ……………………6分 =3 ……………………7分当x ==3(1⨯+ ……………………8分=1-+……………………9分18．证明：如图，在□ABCD 中，BC=DA ，C A ∠=∠．……………………4分∵BF=DH ，∴BC －BF=D A －DH, 即FC=HA ． ……………………6分又∵AE=CG ，……………………7分∴AEH △≌CGF △． ……………………9分19．解：（1）∵ 点A (1,)n -在一次函数2y x =-的图象上，∴ 2(1)2n =-⨯-=．… 2分∴ 点A 的坐标为12-（，）．……………………4分∵ 点A 在反比例函数ky x=的图象上，∴ 2k =-．………………5分∴ 反比例函数的解析式为2y x=-．……… 6分（2）点P 的坐标为(2,0)(0,4)-或．………………10分20．解：（１）P （抽到牌面数字４）=13.………………3分（２）游戏规则对双方不公平．………………4分理由如下：【方法一】作数形图如图所示, ………………7分由上述树状图知：所有可能出现的结果共有9种．P （抽到牌面数字相同）=3193=，………………8分 P （抽到牌面数字不相同）=6293=．………………9分∵1233<，∴此游戏不公平，小李赢的可能性大．………………10分【方法二】列表如下, ………………7分【以下同上】21．解:（1）抽测的学生有50人, …2分抽测成绩的众数是5(次)．…4分（2）如图所示； …………7分（3）1614635025250++⨯=（人）． …………10分答：估计该校350名九年级男生中,约有250人左右体能达标．…………12分22．解：如图,设,,CD x AD y ==/次则由题意有50BD y =-．…………1分在Rt △ACD 中，tan37AD yCD x︒==，…………4分则tan37y x =⋅︒，在Rt△BCD 中，50tan 48BD yCD x-︒==，…………7分则50tan48y x =-⋅︒，∴tan3750tan48x x ⋅︒=-⋅︒.…………8分∴505026.82tan37tan480.7536 1.1106x =≈=︒+︒+．…………10分答：小明家所在居民楼与大厦的距离CD 大约是27米．…………………12分 23．（1）证明：连结AE ．…………1分∵ AB 是⊙O 的直径，∴ 90AEB ∠=︒ , ∴ 1290∠+∠=︒．…………2分∵ AB=AC ，∴ 112CAB ∠=∠．又∵ 12CBF CAB ∠=∠，∴ 1CBF ∠=∠． ∴ 290CBF ∠+∠=︒．即∠ABF = 90°．…………3分 ∵ AB 是⊙O 的直径，…………4分 ∴ 直线BF 是⊙O 的切线．…………5分（2）解：过点C 作CG ⊥AB 于点G ．…………6分 ∵sin CBF ∠【过点C 作CG ⊥BF 亦可类似求解】1CBF ∠=∠，∴sin 1∠．…………7分 ∵ 90AEB ∠=︒，AB=5，∴ BE=sin 1AB ⋅∠.又∵ AB=AC ，90AEB ∠=︒， ∴2BC BE ==．在Rt △ABE 中，由勾股定理得 AE=8分∴sin 2∠=，cos 2∠=．在Rt △CBG 中，可求得 4GC =，2GB =．∴ AG=3．∵ GC ∥BF ，∴ △AGC ∽△ABF ．…………10分∴ GC AG BF AB =．∴ 203GC AB BF AG ⋅==．…………12分24．解：（1）GF DF ∴=．…………1分连接EF ，则90EGF D ∠=∠=°，EG AE ED EF EF ===，．题12Rt Rt EGF EDF ∴△≌△．…………2分 GF DF ∴=．…………3分（2）由（1）知，GF DF =．设AB a =，DF b =，则有BC =，CF DC DF a b =-=-，…………4分由对称性有BG AB a ==,BF BG GF a b ∴=+=+．…………5分在Rt BCF △中，222BC CF BF +=，即222)()()a b a b +-=+，…………6分2a b ∴=，…………7分∴2DC aDF b==．…………8分（3）由（1）知，GF DF =．设DF x BC y ==，，则有.GF x AD y ==，DC n DF =·，DC AB BG nx ∴===．…………9分(1)1CF n x BF BG GF n x ∴=-=+=+，（）．…………10分在Rt BCF △中，222BC CF BF +=，即222[1][(1)]y n x n x +-=+（）．…………12分y ∴= …………13分AD y AB nx n ∴==⎝…………14分25. 解：（1）()()()0300A m B m D -，，，，．…………3分（2）设直线ED 的解析式为y kx b =+，将()()300D -，、代入得：图14FA D BC30k b b -+=⎧⎪⎨=⎪⎩，…………4分解得，3k m b ==，． ∴直线ED的解析式为y =+． …………5分将)()3y x m x m =+-化为顶点式：)2y x m =-+． ∴顶点M的坐标为m ⎛⎫⎪ ⎪⎝⎭． …………7分代入3y mx =得：2m m =． 01m m >∴=，．所以，当1m =时，M 点在直线DE 上． (8)连接CD C ，为AB 中点，C 点坐标为()0C m ，．312OD OC CD D ==∴=，，，点在圆上，又222312OE DE OD OE ==+=，， 22222164EC CD CD DE EC ==∴+=，，．90FDC ∴∠=°，∴直线ED 与C ⊙相切．…………10分（3）当03m <<时，()1322AED S AE OD m ==-△· 即：222S m m =-+．…………11分当3m >时，()1322AED S AE OD m m ==-△·，即：222S m m =-．…………12分其图象示意图如图中实线部分．…………【每个区间1分】14分图15。

2007年广州番禺区数学一模

番禺区2007年九年级数学综合训练（一）本试卷分选择题和非选择题两部分，共三大题25小题，满分150分．考试时间为120分钟．注意事项：1.答卷前，考生务必在答题卡第1页上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写考场试室号、座位号，再用2B 铅笔把对应这两个号码的标号涂黑．2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3.非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需要改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4.考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．第一部分选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分．在每小题给出的四个选项中，只有一项是符合题目要求的.）１．3-的结果为（＊）（Ａ）3 （Ｂ）±３（Ｃ）－３（Ｄ）无法确定２．如图，数轴所表示的是一个不等式的解集，则这个不等式为（＊）（Ａ）x ＞２（Ｂ）x ≥２（Ｃ）x ＜２（Ｄ）x ≤２３．下面各整式能直接运用完全平方公式分解因式的为（＊）（Ａ）2x －４（Ｂ）2x ＋６x ＋９（Ｃ）232m m ++ （Ｄ）22x y + ４．计算12(1)π-+-－COS ６０°的结果为（＊）（Ａ）322（Ｃ）－32（Ｄ）１５．如图1，ＢＤ为⊙Ｏ的直径，点Ａ、Ｃ均在⊙Ｏ上，∠ＣＢＤ＝６０°，则∠Ａ的度数为（＊）（Ａ）６０° （Ｂ）３０° （Ｃ）４５° （Ｄ）２０°６．某制衣厂要确定一种衬衫不同号码的生产数量，在做市场调查时，该向商家侧重了解这种衬衫不同号码的销售数量的（＊）（Ａ）平均数（Ｂ）中位数（Ｃ）众数（Ｄ）极差７．对角线互相垂直平分但不相等的四边形是（＊）B1 -2 -32 3 0 -1（Ａ）菱形（Ｂ）矩形（Ｃ）正方形（Ｄ）平行四边形7. 如图2是由一些相同的小正方体堆叠成的几何体的三种视图，则此几何体中的小正方体的个数是（※）（A ） 3 （B ） 4 （C ） 5 （D ） 7９．在平面直角坐标系中，若点Ｐ（x －２，x ＋４）在第二象限，则x 的取值范围为（＊）（Ａ）x ＜２（Ｂ）x ＞－４（Ｃ）x ＞４（Ｄ）－４＜x ＜２10. 正比例函数y x =与反比例函数(0)m y m x=>A 、C 两点，AB x⊥轴于B ，C D x ⊥轴于D （如图3），则四边形A B C D 的面积为（） (A) 2m(B) 2 (C) m(D) 1第二部分非选择题（共120分）二、填空题（本大题共6小题，每小题3分，满分18分．）１１．当x ＝５时，的值为．１２．解一元二次方程2320x x ++=，得x １＝，x ２＝．1 3. 图4、图5是根据某地近两年10月上旬日平均气温情况绘制的折线统计图，通过观察图表，可以判断这两年10月上旬气温比较稳定的年份是___________．１４．已知两圆的半径分别为６㎝和２㎝，圆心距为４㎝，则这两个圆的位置关系为．１５．已知点Ａ（２，０）、Ｂ（０，２）、Ｃ（－１，m ）在同一条直线上，则m 的值为．（图2）俯视图左视图主视图图4 2005年10月上旬图5 2006年10月上旬1 6.如图6，在等腰梯形ABCD 中，AD ∥BC ，AB ＝5，AD ＝6，BC ＝12，点E 在AD 边上，且AE ：ED ＝1：2，点P 是AB 边上的一个动点，（P 不与A ，B 重合）过点P 作PQ ∥CE 交BC 于点Q ，设AP x =，CQ y =，则y 与x 之间的函数关系是_________________.三、解答题（本大题共9小题，满分102分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分9分）分解因式：228x -１８．（本小题满分９分）如图，点Ａ、Ｅ、Ｂ、Ｄ在一条直线上，ＡＥ＝ＤＢ，ＡＣ＝ＤＦ，ＡＣ∥ＤＦ．求证：ＢＣ//ＥＦ１９．（本小题满分１０分）为了保护环境，某校环保小组成员小明收集废电池，第一天收集１号电池４节，５号电池５节，总重量为４５０克，第二天收集１号电池２节，５号电池３节，总重量为２４０克．（１）试求１号电池和５号电池每节分别重多少克？（２）学校环保小组为估算四月份收集废电池的总重量，他们随意抽取了该月某５天每天收集废电池的数量，如下表：分别计算两种废电池的样本平均数；并由此估算该月环保小组收集废电池的总重量是多少千克？２０．（本小题满分１２分）如图，⊙Ｏ的直径ＡＢ垂直于弦ＣＤ，垂足为Ｅ，ＡＢ＝１０，∠ＣＯＤ＝６０°，求：（１）弦ＣＤ的长；（２）∠ＣＯＥ的度数；（３）线段ＢＥ的长（结果用根号表示）．２１．（本小题满分１０分）在形状、大小和质量完全相同且背面图案也一样的六张卡片中，每张卡片的正面画有一个几何图形，分别为：任意四边形（每组对边都不平行）、不等腰梯形、平行四边形、矩形、菱形、正方形．现把它们洗匀后背面朝上放在桌面上．（１）随机地抽取一张，求正好是中心对称图形的概率；（图 6）EDCOBA（２）随机地抽取两张，请分别列出两张都是轴对称图形的所有情况，并求出两张都是轴对称图形的概率．２２．（本小题满分１４分）在直角坐标系中，点Ａ的坐标是（３，０），点Ｐ在第一象限内的直线y ＝－x ＋４上．设点Ｐ的坐标为（x ，y ）．（１）在所给的坐标系中画出直线y ＝－x ＋４；（２）求⊿ＰＯＡ的面积Ｓ与变量x 的函数关系式，并写出自变量x 的取值范围；（３）当Ｓ＝92时，求点Ｐ的坐标，画出此时的⊿ＰＯＡ，并用尺规作图法，作出其外接圆（保留作图痕迹，不写作法）．２3．（本小题满分１２分）据报道，今年４月中旬后，广深铁路高速列车将再提速25％，提速后乘客从广州坐火车到深圳将缩短15分钟，广州、深圳两市距离１５０千米．求提速前、后的列车速度．２4．（本小题满分１２分）如图所示，把一个直角三角尺ＡＢＣ绕着６０°角的顶点Ｂ顺时针旋转，使得点Ｃ与ＡＢ的延长线上的点Ｄ重合．（１）三角尺旋转了多少度？（２）连结ＣＤ，试判断A C D ∆的形状，对结论加以证明；（３）连结ＣＥ，试猜想线段ＡＣ与ＣＥ的大小关系，并予以证明，求出CE 的长．25．（本小题满分14分）已知抛物线的解析式为2224y x m x m =-++-.（1）求证：不论m 取何值，此抛物线与x 轴必有两个交点，且两交点A 、B 之间的距离为定值；（2）设点P 为此抛物线上一点，若P A B ∆的面积为8,求符合条件的所有点P 的坐标（可用含m 的代数式表示）（3）若（2）中P A B ∆的面积为(0)s s >，试根据面积s 值的变化情况，确定符合条件的点P 的个数．ＤＥＡ2007年番禺区数学综合练习（一）参考答案一选择题二填空题三解答题１７．（本小题满分９分）解：22282(4)x x -=- ………………………………………………………… 4分 =2(2)(2)x x +- ……………………………………………………………………… 9分１８．（本小题满分９分）证明：∵ＡＥ＝ＤＢ，∴ＡＥ＋ＥＢ＝ＤＢ＋ＥＢ …………………………… 1分即ＡＢ＝ＤＥ． ………………………………………………………………………… 2分 ∵ＡＣ∥ＤＦ ∴∠Ａ＝∠Ｄ ………………………………………………………… 4分在∆ＡＢＣ和∆ＤＥＦ中，∵ ＡＣ＝ＤＦ，∠Ａ＝∠Ｄ，ＡＢ＝ＤＥ∴ ∆ＡＢＣ≌∆ＤＥＦ ……………………………………………………………… ７分 ∴ A B C D E F ∠=∠ ………………………………………………………………… 8分 ∴ＢＣ//ＥＦ（全等三角形的对应边相等）． ……………………………………… ９分１９．（本小题满分１０分）解：（１）设每节１号电池重x 克，每节５号电池重y 克， ………………………… 1分由题意可得4545023240x y x y +=⎧⎨+=⎩， …………………………………………………………… 3分解此方程组得 x ＝７５，y ＝３０． …………………… 4分 ∴１号电池和５号电池每节的重量分别为７５克、３０克； ……………………… ５分（２）129303228315x ++++=＝３０（节）， ……………………… ６分 551534749505x ++++=＝５０（节）， ………………………… ７分∴该环保小组每天收集的电池总重为：30³75＋30³50＝３７５０（克），………… ８分以该月30天计算，环保小组可收集废旧电池总重量约为：３７５０³３０＝１１２５００（克）【写成112.5千克也可】 ……………… 9分答：（略） ……………… 10分２０．（本小题满分１0分）解：（１）∵半径ＯＣ＝ＯＤ，即∆ＯＣＤ为等腰三角形， …………………… １分又∵∠ＣＯＤ＝６０°，∴∆ＯＣＤ为等边三角形， …………………………… ２分 ∴ＣＤ＝ＯＣ＝12ＡＢ＝５； ……………………………………………………… ３分（２）∵直径ＡＢ垂直于弦ＣＤ于Ｅ，∴ＣＥ＝ＥＤ， ………………………… ４分又∵ＯＣ＝ＯＤ，即ＯＥ为等腰△ＯＣＤ的底边ＣＤ上的高，∴ＯＥ平分∠ＣＯＤ（三线合一）， ……………………………………………… 5分由∠ＣＯＤ＝６０°，得∠ＣＯＥ＝３０°； …………………………………… 6分（３）在Ｒt △ＯＣＥ中，∵O E O C＝COS ∠ＣＯＥ，∴ＯＥ＝ＯＣ²COS ∠ＣＯＥ【用其它三角函数或勾股定理类似给分】……… 8分＝５²COS ３０°＝５²2＝2， ………………………………………… 9分2 0２１．（本小题满分１2分）解：（1）∵在6张卡片中，中心对称图形有：平行四边形、矩形、菱形、正方形4种，…4分∴随机抽取，则抽一张为菱形的概率为4263= . …………………… 6分【若学生回答中心对称有遗漏，概率计算方法正确可酌情给1分】（3）在6张卡片中，轴对称图形有矩形、菱形、正方形,分别记为a 、b 、c ，其余三张记为A 、B 、C,随机抽取两张，各种可能情况可列表表示如下：………………… 9分2³3=6种，……………………………………………………………………… 10分 ∴两张都是轴对称图形的概率为Ｐ＝61305=. ……………………………… 12分【若一一列出15种组合（不含先后顺序），概率计算正确，给满分】２２．（本小题满分１2分）解：（１）画图（略）； ………………………………………………………… 3分（２）∵点Ｐ在第一象限，∴点Ｐ的纵坐标y 的绝对值y 就是△ＰＯＡ的边ＯＡ上高的值， ∴Ｓ＝12·ＯＡ·y ＝32y ，即Ｓ＝32y ， …………………………………… 4分而点Ｐ为线段BC 上一点，故y ＝－x ＋４， ∴Ｓ＝32（－x ＋４）＝－32x ＋６， ……………………………………… 5分又而点Ｐ在线段BC 上, 自变量x 的取值范围为：０＜x ＜４ ……………… 6分即所求Ｓ与变量x 的函数关系式为：Ｓ＝－32x ＋６(04)x <<， ………………………………………………… 7分（３）若Ｓ＝92，则有92＝32y ，y ＝３，代入y ＝－x ＋４，得x ＝１，∴点Ｐ的坐标为（１，３）， ……………… 9分用尺规分别作出△ＰＯＡ的ＯＡ、ＯＰ（或ＡＰ）边的垂直平分线， ……………………… １1分以两线交点为圆心、圆心到任一顶点为半径，作圆， ……………………… １2分即为△ＰＯＡ的外接圆（图形略）．【以图形为准给分，不必写作法】２3．（本小题满分１2分）解：设列车提速前的速度为(/)x km h ，15分钟共计14小时 ………………… 2分则由题意有：1501501(125%)4xx -=+ ……………………………………… 6分【若所列方程有错误，但运行时间的表达式正确，可酌情每个时间项1-2分】去分母得：15041504 1.25x ⨯-⨯=解之得：120(/)x km h =经检验120x =是原方程的根. ……………………………………… 9分∴提速后的列车速度为120(125%)150(/)km h +=. ………………………… 11分答：列车提速前、后的速度为120(/)km h 、150(/)km h . …………………… 12分２4．（本小题满分１4分）解：（1）三角尺旋转了00018060120-=； …………………………………… 2分（2）△A C D 为等腰三角形． …………………………………………… 3分设B E 、C D 相交于F ，由题设三角尺ABC 为R t ∆，0060,60ABC A ∠=∠=，BD E ∆ 由B C A ∆旋转0120而得，由旋转的特征知，B C B D =，060DBE ∠=, …………………………………………… 5分0001206060CBE ∴∠=-=. …………………………………………… 6分 BF ∴为等腰三角形顶角的平分线, 即BF C D ⊥于F .009030BDC DBE ∴∠=-∠=, …………………………………………… 7分 030CAD CDA ∠=∠=.即△A C D 为等腰三角形． ……………………… 9分（3）A C C E =. …………………………………………………………… 10分由（2）知，B E 垂直平分C D ，D E C E ∴=， ……………………… 12分【证明B C E B D E ∆≅∆，或说明四边形B D E C 为轴对称图形，B E 为其对称轴等等，可比照给分】又BD E ∆ 由B C A ∆绕B 旋转而得，A B C ∴∆≌EBD ∆D E A C ∴=.… 1３分 A C C E ∴=, 即两条线段长度相等. …………………………………………14分【若用勾股定理和锐角三角函数分别计算出A C 、C E 的长度，再判断相等可比照给分，但若没有交代每一步计算的依据，或说明不清析则减半扣去该步得分】２5．（本小题满分１4分）解：（1） 22(2)4(1)(4)160m m ∆=-⨯--=>，∴不论m 取何值，此抛物线与x 轴必有两个交点． ……………………2分设12(,0),(,0)A x B x ，则12||||||22x x aaa-==4==。

广州市2007年初中毕业生考试数学试题附答案

2007年广州市初中毕业生学业考试数学试题本试卷分选择题和非选择题两部分，共三大题25小题，满分150分．考试时间120分钟．第一部分选择题(共30分)一、选择题（每小题3分，共30分） 1、下列各数中，最小．．的数是（）A ．－2B ．－1C ．0D 2、下列立体图形中，是多面体的是（）3、下列计算中，正确的是（）A ．33x x x =B ．3x x x -=C ．32x x x ÷=D ．336x x x += 4、下列命题中，正确的是（）A ．对顶角相等B ．同位角相等C ．内错角相等D ．同旁内角互补 5、以11x y =⎧⎨=-⎩为解的二元一次方程组是（）A ．01x y x y +=⎧⎨-=⎩ B ．01x y x y +=⎧⎨-=-⎩ C ．02x y x y +=⎧⎨-=⎩ D ．02x y x y +=⎧⎨-=-⎩6、下列各图中，是轴对称图案的是（）7、二次函数221y x x =-+与x 轴的交点个数是（）A ．0B ．1C ．2D ．38、小明由A 点出发向正东方向走10米到达B 点，再由B 点向东南方向走10米到达C 点，则正确的是（）A ．∠ABC=22.5°B ．∠ABC=45°C ．∠ABC=67.5°D ．∠ABC=135°9、关于x 的方程20x px q ++=的两根同为负数，则（） A ．0p >且q >0 B ．0p >且q <0 C ．0p <且q >0 D ．0p <且q <010、如图，⊙O 是△ABC 的内切圆，OD ⊥AB 于点D ，交⊙O 于点E ，∠C=60°，如果⊙O 的半径为2，则结论错误的是（）A ．AD DB = B ．AE EB =C ．1OD = D ．3AB =第二部分选择题(共120分)二、填空题（每小题3分，共18分） 11、化简2-= .12、方程511x =+的解是 . 13、线段AB=4㎝，在线段AB 上截取BC=1㎝，则AC= ㎝. 14、若代数式3x -x 的取值范围是15、已知广州市的土地总面积是74342km ，人均占有的土地面积S （单位：2/km 人），随全市人口n （单位：人）的变化而变化，则S 与n 的函数关系式是 . 16、如图，点D 是AC 的中点，将周长为4㎝的菱形ABCD 沿对角线AC 方向平移AD 长度得到菱形OB ’C ’D ’,则四边形OECF 的周长是㎝三、解答题17、（9分）请以下列三个代数式中任选两个构造一个分式，并化简该分式。

2007年广州市初中毕业生学业考试数学试题

2007年广州市初中毕业生学业考试数学试题本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分．考试时间120分钟．注意事项：1．答卷前，考生务必在答题卡第1面、第3面上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名；填写座位号，再用2B 铅笔把对应号码的标号涂黑．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题同的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．一、选择题（每小题3分，共30分）1、下列各数中，最小．．的数是（）A ．－2B ．－1C ．0D 2、下列立体图形中，是多面体的是（）3、下列计算中，正确的是（）A ．33x x x =B ．3x x x -=C ．32x x x ÷=D ．336x x x +=4、下列命题中，正确的是（）A ．对顶角相等B ．同位角相等C ．内错角相等D ．同旁内角互补5、以11x y =⎧⎨=-⎩为解的二元一次方程组是（）A ．01x y x y +=⎧⎨-=⎩B ．01x y x y +=⎧⎨-=-⎩C ．02x y x y +=⎧⎨-=⎩D ．02x y x y +=⎧⎨-=-⎩ 6、下列各图中，是轴对称图案的是（）7、二次函数221y x x =-+与x 轴的交点个数是（）A ．0B ．1C ．2D ．38、小明由A 点出发向正东方向走10米到达B 点，再由B 点向东南方向走10米到达C 点，则正确的是（）A ．∠ABC=22.5°B ．∠ABC=45°C ．∠ABC=67.5°D ．∠ABC=135°9、关于x 的方程20x px q ++=的两根同为负数，则（）A ．0p >且q >0B ．0p >且q <0C ．0p <且q >0D ．0p <且q <010、如图，⊙O 是△ABC 的内切圆，OD ⊥AB 于点D ，交⊙O 于点E ，∠C=60°，如果⊙O 的半径为2，则结论错误的是（）A ．AD DB = B ． AE EB=C ．1OD = D ．AB =二、填空题（每小题3分，共18分）11、化简2-= .12、方程511x =+的解是 . 13、线段AB=4㎝，在线段AB 上截取BC=1㎝，则AC= ㎝.14x 的取值范围是15、已知广州市的土地总面积是74342km ，人均占有的土地面积S （单位：2/km 人），随全市人口n （单位：人）的变化而变化，则S 与n 的函数关系式是 .16、如图，点D是AC的中点，将周长为4㎝的菱形ABCD沿对角线AC方向平移AD长度得到菱形OB’C’D’,则四边形OECF的周长是㎝三、解答题17、（9分）请以下列三个代数式中任选两个构造一个分式，并化简该分式。

2007广东省九年级数学中考

2007年广东省初中毕业生学业考试数学试卷一、选择题(本大题共5小题，每小题3分，共15分)1.2006年广东省国税系统完成税收收入人民币3.45065×1011元，连续12年居全国首位，也就是收入了( ) A．345.065亿元B．3450.65亿元C．34506.5亿元D．345065亿元2．在三个数0.5、、∣－∣中，最大的数是( ) A．0.5 B．C．∣－∣D．不能确定3．下列各式中，能用平方差公式分解因式的是 ( ) A．x2+4y2B．x2—2 y2 +l C．一x2+4y2D．一x2一4y2 4．袋中有同样大小的4个小球，其中3个红色，1个白色．从袋中任意地同时摸出两个球，这两个球颜色相同的概率是 ( ) A．B．C．D．5．到三角形三条边的距离都相等的点是这个三角形的 ( )A．三条中线的交点B．三条高的交点C．三条边的垂直平分线的交点D．三条角平分线的交点二、填空题(本大题共5小题，每小题4分，共20分)6．由2点15分到2点30分，时钟的分针转过的角度是．7．如图，在不等边△ABC中，DE∥BC，∠ADE=60°，图中等于60°的角还有8．池塘中放养了鲤鱼8000条，鲢鱼若干．在几次随机捕捞中，共抓到鲤鱼320条，鲢鱼400条．估计池塘中原来放养了鲢鱼条．9．已知a、b互为相反数，并且3a一2b=5，则a2+b2== ．10．如图，菱形ABCD的对角线AC=24，BD=10，则菱形的周长L=三、解答题（一）（本大题5小题。

每小题6分，共30分)11．计算：（－）°－4sin45°tan45°+（－）－1×12．已知不等式x +8>4x+m (m是常数)的解集是x <3，求m．13．如图，在直角坐标系中，已知矩形OABC的两个顶点坐标A(3，0)，B(3，2)，对角线AC所在直线为l，求直线l 对应的函数解析式．14．如图，Rt△ABC的斜边AB=5，cosA=，⑴用尺规作图作线段AC的垂直平分线l(保留作图痕迹，不要求写作法、证明)；⑵若直线l与AB、AC分别相交于D、E两点，求DE的长．15．如图，已知⊙O的直径AB垂直弦CD于点E，连结CO并延长交AD于点F，若CF⊥AD，AB=2，求CD的长．四、解答题（二）(本大题共4小题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。