九年级数学圆综合训练2

合集下载

初三数学二模试题分类汇编——圆的综合综合及答案

初三数学二模试题分类汇编——圆的综合综合及答案一、圆的综合1．如图，点A、B、C分别是⊙O上的点， CD是⊙O的直径，P是CD延长线上的一点，AP=AC．（1）若∠B=60°，求证：AP是⊙O的切线；（2）若点B是弧CD的中点，AB交CD于点E，CD=4，求BE·AB的值．【答案】（1）证明见解析；（2）8．【解析】（1）求出∠ADC的度数，求出∠P、∠ACO、∠OAC度数，求出∠OAP=90°，根据切线判定推出即可；（2）求出BD长，求出△DBE和△ABD相似，得出比例式，代入即可求出答案．试题解析：连接AD，OA，∵∠ADC=∠B，∠B=60°，∴∠ADC=60°，∵CD是直径，∴∠DAC=90°，∴∠ACO=180°-90°-60°=30°，∵AP=AC，OA=OC，∴∠OAC=∠ACD=30°，∠P=∠ACD=30°，∴∠OAP=180°-30°-30°-30°=90°，即OA⊥AP，∵OA为半径，∴AP是⊙O切线．（2）连接AD，BD，∵CD 是直径，∴∠DBC=90°，∵CD=4，B 为弧CD 中点，∴BD=BC=，∴∠BDC=∠BCD=45°，∴∠DAB=∠DCB=45°，即∠BDE=∠DAB ，∵∠DBE=∠DBA ，∴△DBE ∽△ABD ， ∴，∴BE•AB=BD•BD=．考点：1．切线的判定；2．相似三角形的判定与性质．2．在⊙O 中，点C 是AB u u u r上的一个动点(不与点A ，B 重合)，∠ACB=120°，点I 是∠ABC 的内心，CI 的延长线交⊙O 于点D ，连结AD,BD ．（1）求证：AD=BD ．（2）猜想线段AB 与DI 的数量关系，并说明理由．（3）若⊙O 的半径为2，点E ，F 是»AB 的三等分点，当点C 从点E 运动到点F 时，求点I 随之运动形成的路径长．【答案】（1）证明见解析；（2）AB=DI ，理由见解析（323 【解析】分析：（1）根据内心的定义可得CI 平分∠ACB ，可得出角相等，再根据圆周角定理，可证得结论；（2）根据∠ACB=120°，∠ACD=∠BCD，可求出∠BAD的度数，再根据AD=BD，可证得△ABD是等边三角形，再根据内心的定义及三角形的外角性质，证明∠BID=∠IBD，得出ID=BD，再根据AB=BD，即可证得结论；（3）连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧，根据已知及圆周角定理、解直角三角形，可求出AD的长，再根据点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，可证得∠DAI1=∠AI1D，然后利用弧长的公式可求出点I 随之运动形成的路径长.详解：（1）证明：∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD（2）AB=DI理由：∵∠ACB=120°，∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形，∴AB=BD，∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI，∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI（3）解：如图，连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧∵∠ACB=120°，弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2，DE 是直径∴DE=4，∠EAD=90°∴AD=sin ∠AED×DE=×4=2∵点E ，F 是弧AB ⌢的三等分点，△ABD 是等边三角形，∴∠ADB=60°∴弧AB 的度数为120°，∴弧AM 、弧BF 的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI 1=∠FAB+∠DAB=80°∴∠AI 1D=180°-∠ADM-∠DAI 1=180°-20°-80°=80°∴∠DAI 1=∠AI 1D∴AD=I 1D=2∴弧I 1I 2的长为：点睛：此题是一道圆的综合题，有一定的难度，熟记圆的相关性质与定理，并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键，注意数形结合思想的渗透.3．如图，CD 为⊙O 的直径，点B 在⊙O 上，连接BC 、BD ，过点B 的切线AE 与CD 的延长线交于点A ，AEO C =∠∠，OE 交BC 于点F .（1）求证：OE ∥BD ；（2）当⊙O 的半径为5，2sin 5DBA ∠=时，求EF 的长.【答案】（1）证明见解析；（2）EF 的长为212 【解析】试题分析：（1）连接OB ，利用已知条件和切线的性质证明；（2）根据锐角三角函数和相似三角形的性质，直接求解即可.试题解析：（1）连接OB ， ∵CD 为⊙O 的直径， ∴ 90CBD CBO OBD ∠=∠+∠=︒. ∵AE 是⊙O 的切线，∴ 90ABO ABD OBD ∠=∠+∠=︒. ∴ ABD CBO ∠=∠. ∵OB 、OC 是⊙O 的半径，∴OB=OC . ∴C CBO ∠=∠. ∴C ABD ∠=∠.∵E C ∠=∠，∴E ABD ∠=∠. ∴ OE ∥BD .（2）由（1）可得sin ∠C = ∠DBA= 25，在Rt △OBE 中, sin ∠C =25BD CD =,OC =5， 4BD =∴90CBD EBO ∠=∠=︒∵E C ∠=∠，∴△CBD ∽△EBO .∴BD CD BO EO= ∴252EO =. ∵OE ∥BD ，CO =OD ，∴CF =FB .∴122OF BD ==. ∴212EF OE OF =-=4．如图，已知AB 是⊙O 的直径，点C ，D 在⊙O 上，BC=6cm,AC=8cm,∠BAD=45°．点E 在⊙O 外，做直线AE ，且∠EAC=∠D ．（1）求证：直线AE 是⊙O 的切线．（2）求图中阴影部分的面积.【答案】(1)见解析;(2) 25-504π. 【解析】分析：（1）根据圆周角定理及推论证得∠BAE=90°，即可得到AE 是⊙O 的切线；（2）连接OD ，用扇形ODA 的面积减去△AOD 的面积即可.详解：证明：（1） ∵AB 是⊙O 的直径，∴∠ACB=90°，即∠BAC+∠ABC=90°，∵∠EAC=∠ADC ，∠ADC=∠ABC ，∴∠EAC=∠ABC∴∠BAC+∠EAC =90°，即∠BAE= 90°∴直线AE 是⊙O 的切线；（2）连接OD∵ BC=6 AC=8∴ 226810AB =+=∴ OA = 5又∵ OD = OA∴∠ADO =∠BAD = 45°∴∠AOD = 90°∴AOD ODA S S S ∆-阴影扇形＝=90155553602π⨯⨯-⨯⨯ 25504π-= （2cm ）点睛：此题主要考查了圆周角定理和圆的切线的判定与性质，关键是利用圆周角定理和切线的判定与性质，结合勾股定理的和弓形的面积的求法求解，注意数形结合思想的应用.5．如图，在以点O 为圆心的两个同心圆中，小圆直径AE 的延长线与大圆交于点B ，点D 在大圆上，BD 与小圆相切于点F ，AF 的延长线与大圆相交于点C ，且CE ⊥BD ．找出图中相等的线段并证明．【答案】见解析【解析】试题分析：由AE是小⊙O的直径，可得OA=OE，连接OF，根据切线的性质，可得OF⊥BD，然后由垂径定理，可证得DF=BF，易证得OF∥CE，根据平行线分线段成比例定理，可证得AF=CF，继而可得四边形ABCD是平行四边形，则可得AD=BC，AB=CD．然后连接OD、OC，可证得△AOD≌△EOC，则可得BC=AD=CE=AE．试题解析：图中相等的线段有：OA=OE，DF=BF，AF=CF，AB=CD，BC=AD=CE=AE．证明如下：∵AE是小⊙O的直径，∴OA=OE．连接OF，∵BD与小⊙O相切于点F，∴OF⊥BD．∵BD是大圆O的弦，∴DF=BF．∵CE⊥BD，∴CE∥OF，∴AF=CF．∴四边形ABCD是平行四边形．∴AD=BC，AB=CD．∵CE：AE=OF：AO，OF=AO，∴AE=EC．连接OD、OC，∵OD=OC，∴∠ODC=∠OCD．∵∠AOD=∠ODC，∠EOC=∠OEC，∴∠AOC=∠EOC，∴△AOD≌△EOC，∴AD=CE．∴BC=AD=CE=AE．【点睛】考查了切线的性质，垂径定理，平行线分线段成比例定理，平行四边形的判定与性质以及全等三角形的判定与性质等知识．此题综合性很强解题的关键是注意数形结合思想的应用，注意辅助线的作法，小心不要漏解．6．阅读：圆是最完美的图形，它具有一些特殊的性质：同弧或等弧所对的圆周角相等，一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”，再利用圆的性质将问题进行转化，往往能化隐为显、化难为易。

九年级数学圆几何综合单元测试卷(解析版)

九年级数学圆几何综合单元测试卷（解析版）一、初三数学圆易错题压轴题（难）1．已知圆O 的半径长为2，点A 、B 、C 为圆O 上三点，弦BC=AO ，点D 为BC 的中点，(1)如图，连接AC 、OD ，设∠OAC=α，请用α表示∠AOD ； (2)如图，当点B 为AC 的中点时，求点A 、D 之间的距离：(3)如果AD 的延长线与圆O 交于点E ，以O 为圆心，AD 为半径的圆与以BC 为直径的圆相切，求弦AE 的长．【答案】（1）1502AOD α∠=︒-；（2）7AD =3）33133122or【解析】【分析】（1）连接OB 、OC ，可证△OBC 是等边三角形，根据垂径定理可得∠DOC 等于30°，OA=OC 可得∠ACO=∠CAO=α，利用三角形的内角和定理即可表示出∠AOD 的值. （2）连接OB 、OC ，可证△OBC 是等边三角形，根据垂径定理可得∠DOB 等于30°，因为点D 为BC 的中点，则∠AOB=∠BOC=60°，所以∠AOD 等于90°，根据OA=OB=2,在直角三角形中用三角函数及勾股定理即可求得OD 、AD 的长.（3）分两种情况讨论：两圆外切，两圆内切.先根据两圆相切时圆心距与两圆半径的关系，求出AD 的长，再过O 点作AE 的垂线，利用勾股定理列出方程即可求解. 【详解】(1)如图1：连接OB 、OC. ∵BC=AO ∴OB=OC=BC∴△OBC 是等边三角形 ∴∠BOC=60° ∵点D 是BC 的中点 ∴∠BOD=1302BOC ∠=︒ ∵OA=OC∴OAC OCA ∠=∠=α ∴∠AOD=180°-α-α-30︒=150°-2α(2)如图2：连接OB、OC、OD.由（1）可得：△OBC是等边三角形，∠BOD=130 2BOC∠=︒∵OB=2，∴OD=OB∙cos30︒=3∵B为AC的中点，∴∠AOB=∠BOC=60°∴∠AOD=90°根据勾股定理得：AD=227AO OD+=（3）①如图3.圆O与圆D相内切时：连接OB、OC，过O点作OF⊥AE∵BC是直径，D是BC的中点∴以BC为直径的圆的圆心为D点由（2）可得：3D的半径为1∴31设AF=x在Rt △AFO 和Rt △DOF 中，2222OA AF OD DF -=-即()2222331x x -=-+-解得：331x 4+=∴AE=3312AF +=②如图4.圆O 与圆D 相外切时：连接OB 、OC ，过O 点作OF ⊥AE ∵BC 是直径，D 是BC 的中点 ∴以BC 为直径的圆的圆心为D 点由（2）可得：3D 的半径为1 ∴31 在Rt △AFO 和Rt △DOF 中，2222OA AF OD DF -=-即()2222331x x -=- 解得：331x 4-=∴AE=3312AF -=【点睛】本题主要考查圆的相关知识：垂径定理，圆与圆相切的条件，关键是能灵活运用垂径定理和勾股定理相结合思考问题，另外需注意圆相切要分内切与外切两种情况.2．已知：在△ABC中，AB=6，BC=8，AC=10，O为AB边上的一点，以O为圆心，OA长为半径作圆交AC于D点，过D作⊙O的切线交BC于E.（1）若O为AB的中点(如图1)，则ED与EC的大小关系为：ED EC（填“”“”或“”）（2）若OA<3时（如图2），（1）中的关系是否还成立？为什么？（3）当⊙O过BC中点时（如图3），求CE长.【答案】（1）ED=EC；（2）成立；（3）3【解析】试题分析：（1）连接OD，根据切线的性质可得∠ODE=90°，则∠CDE+∠ADO=90°，由AB=6，BC=8，AC=10根据勾股定理的逆定理可证得∠ABC=90°，则∠A+∠C=90°，根据圆的基本性质可得∠A=∠ADO，即可得到∠CDE=∠C，从而证得结论；（2）证法同（1）；（3）根据直角三角形的性质结合圆的基本性质求解即可.（1）连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6，BC=8，AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC；（2）连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6，BC=8，AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC；（3）CE=3.考点：圆的综合题点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．3．选做题：从甲乙两题中选作一题，如果两题都做，只以甲题计分题甲：已知矩形两邻边的长、是方程的两根.（1）求的取值范围；（2）当矩形的对角线长为时，求的值；（3）当为何值时，矩形变为正方形？题乙：如图，是直径，于点，交于点，且．（1）判断直线和的位置关系，并给出证明；（2）当，时，求的面积．【答案】题甲（1）（2）（3）题乙：（1）BD是切线；证明所以OB⊥BD，BD是切线（2）S=【解析】试题分析：题甲：（1）、是方程的两根，则其；由得（2）矩形两邻边的长、，矩形的对角线的平方=；矩形两邻边的长、是方程的两根，则；因为，所以；解得由得（3）矩形变为正方形，则a=b；、是方程的两根，所以方程有两个相等的实数根，即，由得题乙：（1）BD是切线；如图所示，是弧AC所对的圆周角，；因为，所以；于点，，所以，，在三角形OBD中，所以OB⊥BD；BD是切线（2），AB是圆的直径，所以OB=5；于点，交于点，F是BC的中点；，BF=4；在直角三角形OBF中由勾股定理得OF=；根据题意，，则，所以，从而，解得DF=，的面积=考点：直线与圆相切，相似三角形点评：本题考查直线与圆相切，相似三角形；解本题的关键是会判断直线与圆是否相切，能判定两个三角形相似4．如图，在平面直角坐标系中，O为坐标原点，△ABC的边BC在y轴的正半轴上，点A在x轴的正半轴上，点C的坐标为（0，8），将△ABC沿直线AB折叠，点C落在x轴的负半轴D（−4，0）处．（1）求直线AB的解析式；（2）点P从点A出发以每秒45个单位长度的速度沿射线AB方向运动，过点P作PQ⊥AB，交x轴于点Q，PR∥AC交x轴于点R，设点P运动时间为t（秒），线段QR长为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，点N是射线AB上一点，以点N为圆心，同时经过R、Q两点作⊙N，⊙N交y轴于点E，F．是否存在t，使得EF=RQ？若存在，求出t的值，并求出圆心N的坐标；若不存在，说明理由．【答案】（1）132y x=-+（2）d=5t （3）故当 t=85，或815，时，QR=EF，N（-6，6）或（2，2）．【解析】试题分析：（1）由C（0，8），D（-4，0），可求得OC，OD的长，然后设OB=a，则BC=8-a，在Rt△BOD中，由勾股定理可得方程：（8-a）2=a2+42,解此方程即可求得B的坐标，然后由三角函数的求得点A的坐标，再利用待定系数法求得直线AB的解析式；（2）在Rt△AOB 中，由勾股定理可求得AB 的长，继而求得∠BAO 的正切与余弦，由PR//AC 与折叠的性质，易证得RQ=AR ，则可求得d 与t 的函数关系式；（3）首先过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ，易证得四边形NTOS 是正方形，然后分别从点N 在第二象限与点N 在第一象限去分析求解即可求解; 试题解析：（1）∵C （0，8），D （-4，0）， ∴OC=8，OD=4，设OB=a ，则BC=8-a ，由折叠的性质可得：BD=BC=8-a ，在Rt △BOD 中，∠BOD=90°，DB 2=OB 2+OD 2，则（8-a ）2=a 2+42，解得：a=3，则OB=3，则B （0，3）， tan ∠ODB=34OB OD = ，在Rt △AOC 中，∠AOC=90°，tan ∠ACB=34OA OC = ，则OA=6，则A （6，0），设直线AB 的解析式为：y=kx+b ，则60{3k b b +== ，解得：1{23k b =-= ，故直线AB 的解析式为：y=-12x +3；（2）如图所示：在Rt △AOB 中，∠AOB=90°，OB=3，OA=6，则22135,tan 2OB OB OA BAO OA +=∠== ，255OAcos BAO AB∠==，在Rt △PQA 中，905APQ AP t ∠=︒=，则AQ=10cos APt BAO=∠ ,∵PR ∥AC ， ∴∠APR=∠CAB ，由折叠的性质得：∠BAO=∠CAB ， ∴∠BAO=∠APR ， ∴PR=AR ，∵∠RAP+∠PQA=∠APR+∠QPR=90°， ∴∠PQA=∠QPR ， ∴RP=RQ ， ∴RQ=AR ，∴QR=12 AQ=5t, 即d=5t;（3）过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ， ∵EF=QR ， ∴NS=NT ，∴四边形NTOS 是正方形，则TQ=TR=1522QR t = ， ∴1115151022224NT AT AQ TQ t t t ==-=-=（）（），分两种情况，若点N 在第二象限，则设N （n ，-n ），点N 在直线132y x =-+ 上，则132n n -=-+ ，解得：n=-6，故N （-6，6），NT=6，即1564t = ，解得：85t = ;若点N 在第一象限，设N （N ，N ），可得：132n n =-+ , 解得：n=2，故N （2，2），NT=2，即1524t =, 解得：t=815∴当 t =85，或815，时，QR =EF ，N （-6，6）或（2，2）。

北师版九年级数学下册第二章圆综合练习题

（ 2）AC+AD=BC. 理由如下：
如图，连接 OD . ∵ AC 切小圆 O 于点 A ， BC 切小圆 O 于点 E ， ∴ CE CA .
∵ 在 Rt△OAD 与 Rt△OEB 中， OA OE， OD OB， OAD ∴ Rt△OAD ≌ Rt△OEB ，∴ EB AD . ∵ BC CE EB ，∴ BC AC AD . （ 3）∵ BAC 90o， AB=8 cm, BC=10 cm, ∴ AC 6 cm.
∵ ∠ ACD= 25o , ∴ ∠ AOD= 50o, ∴ ∠ BOD=50o.
第 4 题答图
解析：如图，连接 OB， ∵ AB与⊙ O相切，∴ OB⊥ AB，∴ ∠ ABO=90°． ∵ ∠ A=30°，∴ ∠ AOB=60°，∴ ∠ C= 1 ∠ DOB=30°.
2 6. Ｄ解析：由题意得，扇形 DAB的弧长等于正方形 ABCD中边 BC与 CD的和，所以扇形
又∵为直径，∴ ∠ = ，∴∠
∵ ，∴ ，∴
23. 解：（ 1） BC 所在直线与小圆相切
如图，过圆心 O 作 OE BC ，垂足为点 E . ∵ AC 是小圆的切线， AB 经过圆心 O ，∴ OA AC .
又∵ CO 平分 ACB， OE BC , ∴ OE OA . ∴ BC 所在直线是小圆的切线 .
Ｃ，如果∠ ABO＝20°，则∠ C的度数是 ( )
°
°
°
°
3. 在一个圆中，给出下列命题，其中正确的是（
）
Ａ . 若圆心到两条直线的距离都等于圆的半径，则这两条直线不可能垂直Ｂ . 若圆心到两条直线的距离都小于圆的半径，则这两条直线与圆一定有４个公共点Ｃ . 若两条弦所在直线不平行，则这两条弦可能在圆内有公共点Ｄ . 若两条弦平行，则这两条弦之间的距离一定小于圆的半径

九年级数学二模试题分类汇编——圆的综合综合

九年级数学二模试题分类汇编——圆的综合综合一、圆的综合1．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA=6，BC=2，∴AH=0A﹣OH=OA﹣BC=6﹣2=4．∵∠BHA=90°，∠BAO=45°，∴tan∠BAH=BHHA=1，∴BH=HA=4，∴OC=BH=4．故答案为4．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2）．由（1）得：OH =2，BH =4．∵OC 与⊙M 相切于N ，∴MN ⊥OC ．设圆的半径为r ，则MN =MB =MD =r ．∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ．∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2．解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ．∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ．∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2，∴（2﹣x 2=（）2﹣（x ）2．解得：x =5，∴BR 2=OB 2﹣OR 2=（2﹣（5）2=365，∴BR =5．在Rt △ORB 中，sin ∠BOR =BR OB35．故答案为35．（3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ．则有2t =2．解得：t =1．则OP =CD =DB =1．∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2， ∴点E 的坐标为（1，2）．②当∠BED =90°时，如图3．∵∠DBE =OBC ，∠DEB =∠BCO =90°，∴△DBE ∽△OBC ，∴BEBC =2DB BE OB ∴，∴BE =5t ． ∵PE ∥OC ，∴∠OEP =∠BOC ．∵∠OPE =∠BCO =90°，∴△OPE ∽△BCO ，∴OEOB =25OPBC∴，=2t，∴OE=5t．∵OE+BE=OB=255，∴t+5t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=2，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．2．如图，AB 为O e 的直径，弦//CD AB ，E 是AB 延长线上一点，CDB ADE ∠=∠． ()1DE 是O e 的切线吗？请说明理由；()2求证：2AC CD BE =⋅．【答案】（1）结论：DE 是O e 的切线，理由见解析；（2）证明见解析.【解析】【分析】（1）连接OD ，只要证明OD DE ⊥即可；（2）只要证明：AC BD =，CDB DBE V V ∽即可解决问题.【详解】()1解：结论：DE 是O e 的切线．理由：连接OD ．CDB ADE ∠=∠Q ，ADC EDB ∴∠=∠，//CD AB Q ，CDA DAB ∴∠=∠，OA OD =Q ，OAD ODA ∴∠=∠，ADO EDB ∴∠=∠，AB Q 是直径，90ADB ∴∠=o ，90ADB ODE ∴∠=∠=o ，DE OD ∴⊥，DE ∴是O e 的切线．()2//Q，CD AB∠=∠，∴∠=∠，CDB DBEADC DABn n，AC BD∴=∴=，AC BDQ，EDB DAB∠=∠DCB DAB∠=∠，∴∠=∠，EDB DCB∴V∽DBECDBV，CD DB∴=，BD BE2∴=⋅，BD CD BE2∴=⋅．AC CD BE【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识，解题的关键是学会添加常用辅助线，准确寻找相似三角形解决问题，属于中考常考题型.3．如图AB是△ABC的外接圆⊙O的直径，过点C作⊙O的切线CM，延长BC到点D，使CD=BC，连接AD交CM于点E，若⊙OD半径为3，AE=5，（1）求证：CM⊥AD；（2）求线段CE的长.【答案】（1）见解析；（2）5【解析】分析：（1）连接OC，根据切线的性质和圆周角定理证得AC垂直平分BD，然后根据平行线的判定与性质证得结论；（2）根据相似三角形的判定与性质证明求解即可.详解：证明：（1）连接OC∵CM切⊙O于点C，∴∠OCE=90°，∵AB是⊙O的直径，∴∠ACB=90°，∵CD=BC，∴AC垂直平分BD，∴AB=AD，∴∠B=∠D∵∠B=∠OCB∴∠D=∠OCB∴OC∥AD∴∠CED=∠OCE=90°∴CM⊥AD.（2）∵OA=OB，BC=CD∴OC=12AD∴AD=6∴DE=AD-AE=1易证△CDE～△ACE∴CE DEAE CE∴CE2=AE×DE∴点睛：此题主要考查了切线的性质和相似三角形的判定与性质的应用，灵活判断边角之间的关系是解题关键，是中档题.4．如图，已知AB是⊙O的直径，点C为圆上一点，点D在OC的延长线上，连接DA，交BC的延长线于点E，使得∠DAC=∠B．（1）求证：DA是⊙O切线；（2）求证：△CED∽△ACD；（3）若OA=1，sinD=13，求AE的长．【答案】（1）证明见解析；（22【解析】分析：（1）由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线；（2）由∠DAC=∠DCE，∠D=∠D可知△DEC∽△DCA；（3）由题意可知AO=1，OD=3，DC=2，由勾股定理可知AD=2，故此可得到DC2=DE•AD，故此可求得DE的长，于是可求得AE的长．详解：（1）∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB+∠B=90°．∵∠DAC=∠B，∴∠CAB+∠DAC=90°，∴AD⊥AB．∵OA是⊙O半径，∴DA为⊙O的切线；（2）∵OB=OC，∴∠OCB=∠B．∵∠DCE=∠OCB，∴∠DCE=∠B．∵∠DAC=∠B，∴∠DAC=∠DCE．∵∠D=∠D，∴△CED∽△ACD；（3）在Rt△AOD中，OA=1，sin D=13，∴OD=OAsinD=3，∴CD=OD﹣OC=2．∵AD22OD OA-2又∵△CED∽△ACD，∴AD CDCD DE=，∴DE=2CDAD2，∴AE=AD﹣DE222．点睛：本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定，证得△DEC∽△DCA是解题的关键．5．如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于D，连结DC、DA、OA、OC，四边形OADC为平行四边形．（1）求证：△BOC≌△CDA．（2）若AB=2，求阴影部分的面积．【答案】（1）证明见解析；（2）433π-.【解析】分析: （1）根据内心性质得∠1=∠2，∠3=∠4，则AD=CD，于是可判断四边形OADC为菱形，则BD垂直平分AC，∠4=∠5=∠6，易得OA=OC，∠2=∠3，所以OB=OC，可判断点O 为△ABC的外心，则可判断△ABC为等边三角形，所以∠AOB=∠BOC=∠AOC=120°，BC=AC，再根据平行四边形的性质得∠ADC=∠AOC=120°，AD=OC，CD=OA=OB，则根据“SAS”证明△BOC≌△CDA；（2）作OH⊥AB于H，如图，根据等腰三角形的性质和三角形内角和定理得到∠BOH=30°，根据垂径定理得到BH=AH=12AB=1，再利用含30度的直角三角形三边的关系得到OH=3BH=3，OB=2OH=23，然后根据三角形面积公式和扇形面积公式，利用S阴影部分=S扇形AOB-S△AOB进行计算即可.详解:（1）证明：∵O是△ABC的内心，∴∠2=∠3，∠5=∠6，∵∠1=∠2，∴∠1=∠3，由AD∥CO,AD=CO，∴∠4=∠6，∴△BOC≌△CDA（AAS）(2)由（1）得，BC=AC,∠3=∠4=∠6，∴∠ABC=∠ACB∴AB=AC∴△ABC是等边三角形∴O是△ABC的内心也是外心∴OA =OB =OC设E 为BD 与AC 的交点，BE 垂直平分AC .在Rt △OCE 中，CE=12AC=12AB=1，∠OCE=30°， ∴OA=OB=OC=233∵∠AOC=120°，∴=AOB AOB S S S -V 阴影扇 =21202313()23602π-⨯⨯ =4339π- 点睛: 本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了等边三角形的判定与性质和扇形面积的计算.6．矩形ABCD 中，点C （3，8），E 、F 为AB 、CD 边上的中点，如图1，点A 在原点处，点B 在y 轴正半轴上，点C 在第一象限，若点A 从原点出发，沿x 轴向右以每秒1个单位长度的速度运动，点B 随之沿y 轴下滑，并带动矩形ABCD 在平面内滑动，如图2，设运动时间表示为t 秒，当点B 到达原点时停止运动．（1）当t =0时，点F 的坐标为；（2）当t =4时，求OE 的长及点B 下滑的距离；（3）求运动过程中，点F 到点O 的最大距离；（4）当以点F 为圆心，FA 为半径的圆与坐标轴相切时，求t 的值．【答案】（1）F （3，4）；（2）8-33）7；（4）t 的值为245或325. 【解析】试题分析：（1）先确定出DF ，进而得出点F 的坐标；（2）利用直角三角形的性质得出∠ABO =30°，即可得出结论；（3）当O 、E 、F 三点共线时，点F 到点O 的距离最大，即可得出结论；（4）分两种情况，利用相似三角形的性质建立方程求解即可．试题解析：解：（1）当t =0时．∵AB =CD =8，F 为CD 中点，∴DF =4，∴F （3，4）；（2）当t =4时，OA =4．在Rt △ABO 中，AB =8，∠AOB =90°，∴∠ABO =30°，点E 是AB 的中点，OE =12AB =4，BO =43，∴点B 下滑的距离为843-．（3）当O 、E 、F 三点共线时，点F 到点O 的距离最大，∴FO=OE+EF=7．（4）在Rt △ADF 中，FD 2+AD 2=AF 2，∴AF 22FD AD +，①设AO =t 1时，⊙F 与x 轴相切，点A 为切点，∴FA ⊥OA ，∴∠OAB +∠FAB =90°．∵∠FAD +∠FAB =90°，∴∠BAO =∠FAD ．∵∠BOA =∠D =90°，∴Rt △FAE ∽Rt △ABO ，∴AB AO FA FE =，∴1853t =，∴t 1=245，②设AO =t 2时，⊙F 与y 轴相切，B 为切点，同理可得，t 2=325．综上所述：当以点F 为圆心，FA 为半径的圆与坐标轴相切时，t 的值为245或325．点睛：本题是圆的综合题，主要考查了矩形的性质，直角三角形的性质，中点的意义，勾股定理，相似三角形的判定和性质，切线的性质，解（2）的关键是得出∠ABO =30°，解（3）的关键是判断出当O 、E 、F 三点共线时，点F 到点O 的距离最大，解（4）的关键是判断出Rt △FAE ∽Rt △ABD ，是一道中等难度的中考常考题．7．如图，AB 是半圆O 的直径，半径OC ⊥AB ，OB ＝4，D 是OB 的中点，点E 是弧BC 上的动点，连接AE ，DE ．（1）当点E 是弧BC 的中点时，求△ADE 的面积；（2）若3tan 2AED ∠= ，求AE 的长；（3）点F 是半径OC 上一动点，设点E 到直线OC 的距离为m ，当△DEF 是等腰直角三角形时，求m 的值.【答案】（1）62ADE S =；（2）1655AE =；（3）23m = ，22m =，71m =-.【解析】【分析】（1）作EH ⊥AB ，连接OE ，EB ，设DH ＝a ，则HB ＝2﹣a ，OH ＝2+a ，则EH ＝OH ＝2+a ，根据Rt △AEB 中，EH 2＝AH•BH ，即可求出a 的值，即可求出S △ADE 的值；（2）作DF ⊥AE ，垂足为F ，连接BE ，设EF ＝2x ，DF ＝3x ，根据DF ∥BE 故AF ADEF BD=，得出AF ＝6x ，再利用Rt △AFD 中，AF 2+DF 2＝AD 2，即可求出x ，进而求出AE 的长；（3）根据等腰直角三角形的不同顶点进行分类讨论，分别求出m 的值. 【详解】解：（1）如图，作EH ⊥AB ，连接OE ，EB ，设DH ＝a ，则HB ＝2﹣a ，OH ＝2+a ， ∵点E 是弧BC 中点， ∴∠COE ＝∠EOH ＝45°， ∴EH ＝OH ＝2+a ，在Rt △AEB 中，EH 2＝AH•BH ，（2+a ）2＝（6+a ）（2﹣a ），解得a ＝222±-， ∴a ＝222-， EH=22，S △ADE ＝1622AD EH =n n ;（2）如图，作DF ⊥AE ，垂足为F ，连接BE设EF ＝2x ，DF ＝3x ∵DF ∥BE∴AF ADEF BD = ∴622AF x ==3 ∴AF ＝6x在Rt △AFD 中，AF 2+DF 2＝AD 2 （6x ）2+（3x ）2＝（6）2 解得x ＝255 AE ＝8x ＝1655（3）当点D 为等腰直角三角形直角顶点时，如图设DH ＝a由DF=DE,∠DOF=∠EHD=90°，∠FDO+∠DFO=∠FDO+∠EDH ， ∴∠DFO=∠EDH ∴△ODF ≌△HED ∴OD ＝EH ＝2在Rt △ABE 中，EH 2＝AH•BH （2）2＝（6+a ）•（2﹣a ）解得a ＝±232- m ＝23当点E 为等腰直角三角形直角顶点时，如图同理得△EFG ≌△DEH设DH＝a，则GE＝a，EH＝FG＝2+a在Rt△ABE中，EH2＝AH•BH（2+a）2＝（6+a）（2﹣a）解得a＝222±-∴m＝22当点F为等腰直角三角形直角顶点时，如图同理得△EFM≌△FDO设OF＝a，则ME＝a，MF＝OD＝2∴EH＝a+2在Rt△ABE中，EH2＝AH•BH（a+2）2＝（4+a）•（4﹣a）解得a＝71m71【点睛】此题主要考查圆内综合问题，解题的关键是熟知全等三角形、等腰三角形、相似三角形的判定与性质.8．如图1，等边△ABC的边长为3，分别以顶点B、A、C为圆心，BA长为半径作¶AC、¶CB、¶BA，我们把这三条弧所组成的图形称作莱洛三角形，显然莱洛三角形仍然是轴对称图形，设点l为对称轴的交点．（1）如图2，将这个图形的顶点A与线段MN作无滑动的滚动，当它滚动一周后点A与端点N重合，则线段MN的长为；（2）如图3，将这个图形的顶点A与等边△DEF的顶点D重合，且AB⊥DE，DE=2π，将它沿等边△DEF的边作无滑动的滚动当它第一次回到起始位置时，求这个图形在运动过程中所扫过的区域的面积；（3）如图4，将这个图形的顶点B与⊙O的圆心O重合，⊙O的半径为3，将它沿⊙O的圆周作无滑动的滚动，当它第n次回到起始位置时，点I所经过的路径长为（请用含n的式子表示）【答案】（1）3π；（2）27π；（3）23nπ．【解析】试题分析：（1）先求出¶AC 的弧长，继而得出莱洛三角形的周长为3π，即可得出结论；（2）先判断出莱洛三角形等边△DEF 绕一周扫过的面积如图所示，利用矩形的面积和扇形的面积之和即可；（3）先判断出莱洛三角形的一个顶点和O 重合旋转一周点I 的路径，再用圆的周长公式即可得出．试题解析：解：（1）∵等边△ABC 的边长为3，∴∠ABC =∠ACB =∠BAC =60°，¶¶¶AC BC AB ==，∴¶¶AC BCl l ==¶AB l =603180π⨯=π，∴线段MN 的长为¶¶¶AC BC ABl l l ++=3π．故答案为3π；（2）如图1．∵等边△DEF 的边长为2π，等边△ABC 的边长为3，∴S 矩形AGHF =2π×3=6π，由题意知，AB ⊥DE ，AG ⊥AF ，∴∠BAG =120°，∴S 扇形BAG =21203360π⨯=3π，∴图形在运动过程中所扫过的区域的面积为3（S 矩形AGHF +S 扇形BAG ）=3（6π+3π）=27π；（3）如图2，连接BI 并延长交AC 于D ．∵I 是△ABC 的重心也是内心，∴∠DAI =30°，AD =12AC =32，∴OI =AI =3230AD cos DAI cos ∠=︒=3，∴当它第1次回到起始位置时，点I所经过的路径是以O 为圆心，OI 为半径的圆周，∴当它第n 次回到起始位置时，点I 所经过的路径长为n •2π•3=23n π．故答案为23n π．点睛：本题是圆的综合题，主要考查了弧长公式，莱洛三角形的周长，矩形，扇形面积公式，解（1）的关键是求出¶AC的弧长，解（2）的关键是判断出莱洛三角形绕等边△DEF 扫过的图形，解（3）的关键是得出点I第一次回到起点时，I的路径，是一道中等难度的题目．9．在平面直角坐标系中，已知点A（2，0），点B（0，），点O（0，0）．△AOB绕着O顺时针旋转，得△A'OB'，点A、B旋转后的对应点为A'，B'，记旋转角为α．（Ⅰ）如图1，A'B'恰好经过点A时，求此时旋转角α的度数，并求出点B'的坐标；（Ⅱ）如图2，若0°＜α＜90°，设直线AA'和直线BB'交于点P，求证：AA'⊥BB'；（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．【答案】（Ⅰ）α＝60°，B'（3，）；（Ⅱ）见解析；（Ⅲ）点P纵坐标的最小值为﹣2．【解析】【分析】（Ⅰ）作辅助线,先根据点A（2,0）,点B（0,）,确定∠ABO＝30°,证明△AOA'是等边三角形,得旋转角α＝60°,证明△COB'是30°的直角三角形,可得B'的坐标;（Ⅱ）依据旋转的性质可得∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',即可得出∠OBB'＝∠OA'A ＝（180°﹣α）,再根据∠BOA'＝90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'＝90°,即AA'⊥BB';（Ⅲ）作AB的中点M（1,）,连接MP,依据点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解：（Ⅰ）如图1，过B'作B'C⊥x轴于C,∵OA ＝2,OB＝2,∠AOB＝90°,∴∠ABO＝30°,∠BAO＝60°,由旋转得：OA＝OA',∠A'＝∠BAO＝60°,∴△OAA'是等边三角形,∴α＝∠AOA'＝60°,∵OB＝OB'＝2,∠COB'＝90°﹣60°＝30°,∴B'C＝OB’＝,∴OC＝3,∴B'（3,）,（Ⅱ）证明：如图2,∵∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',∴∠OBB'＝∠OA'A＝（180°﹣α）,∵∠BOA'＝90°+α,四边形OBPA'的内角和为360°,∴∠BPA'＝360°﹣（180°﹣α）﹣（90°+α）＝90°,即AA'⊥BB';（Ⅲ）点P纵坐标的最小值为-2．理由是：如图，作AB的中点M（1,）,连接MP,∵∠APB ＝90°,∴点P 的轨迹为以点M 为圆心,以MP ＝AB ＝2为半径的圆,除去点（2,2）,∴当PM ⊥x 轴时,点P 纵坐标的最小值为﹣2．【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P 的轨迹为以点M 为圆心,以MP 为半径的圆．10．如图，过⊙O 外一点P 作⊙O 的切线PA 切⊙O 于点A ，连接PO 并延长，与⊙O 交于C 、D 两点，M 是半圆CD 的中点，连接AM 交CD 于点N ，连接AC 、CM ．（1）求证：CM 2=MN.MA ；（2）若∠P=30°，PC=2，求CM 的长．【答案】（1）见解析；（2）2 【解析】【分析】（1）由··CMDM =知CAM DCM ∠=∠，根∠CMA=∠NMC 据证ΔAMC ∽ΔCMN 即可得；（2）连接OA 、DM ，由直角三角形PAO 中∠P=30°知()1122OA PO PC CO ==+，据此求得OA=OC=2，再证三角形CMD 是等腰直角三角形得CM 的长．【详解】（1）O Q e 中，M 点是半圆CD 的中点，∴ ··CMDM =， CAM DCM ∴∠=∠，又CMA NMC ∠=∠Q ， AMC CMN ∽∴∆∆， ∴ CM AM MN CM=，即2·CM MN MA =；（2）连接OA 、DM ，PA Q 是O e 的切线，90PAO ∴∠=︒，又30P ∠=︒Q ，()1122OA PO PC CO ∴==+，设O e 的半径为r ，2PC =Q ，()122r r ∴=+，解得：2r =，又CD Q 是直径， 90CMD ∴∠=︒， CM DM =Q ，CMD ∴∆是等腰直角三角形，∴在Rt CMD ∆中，由勾股定理得222CM DM CD +=，即()222216CM r ==，则28CM =，22CM ∴=．【点睛】本题主要考查切线的判定和性质，解题的关键是掌握切线的性质、圆周角定理、相似三角形的判定和性质等知识点11．在中，，，，分别是边，的中点，若等腰绕点逆时针旋转，得到等腰，设旋转角为，记直线与的交点为.（1）问题发现如图1，当时，线段的长等于_________，线段的长等于_________.（2）探究证明如图2，当时，求证：，且.（3）问题解决求点到所在直线的距离的最大值.（直接写出结果）【答案】（1）；；（2）详见解析；（3）【解析】【分析】（1）利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和CE1的长；（2）根据旋转的性质得出，∠D1AB=∠E1AC=135°，进而求出△D1AB≌△E1AC（SAS），即可得出答案；（3）首先作PG⊥AB，交AB所在直线于点G，则D1，E1在以A为圆心，AD为半径的圆上，当BD1所在直线与⊙A相切时，直线BD1与CE1的交点P到直线AB的距离最大，此时四边形AD1PE1是正方形，进而求出PG的长．【详解】（1）解：∵∠A=90°，AC=AB=4，D，E分别是边AB，AC的中点，∴AE=AD=2，∵等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0＜α≤180°），∴当α=90°时，AE1=2，∠E1AE=90°，∴BD1=；故答案为：；；（2）证明：由题意可知，，，∵是由绕点逆时针旋转得到，∴，，在和中，，∴，∴，.∵，∴，∴，∴，且.（3）点的运动轨迹是在的上半圆周，点的运动轨迹是在的弧段.即当与相切时，有最大值.点到所在直线的距离的最大值为.【点睛】此题主要考查了几何变换以及等腰腰直角三角形的性质和勾股定理以及切线的性质等知识，根据题意得出PG的最长时P点的位置是解题关键．12．如图，AB是⊙O的直径，AD是⊙O的弦，点F是DA延长线上的一点，过⊙O上一点C作⊙O的切线交DF于点E，CE⊥DF．(1)求证：AC平分∠FAB；(2)若AE＝1，CE＝2，求⊙O的半径．【答案】（1）证明见解析；（2）5 2【解析】试题分析：（1）连接OC，根据切线的性质和圆周角定理，得出∠OCA=∠OAC与∠CAE=∠OCA，然后根据角平分线的定义可证明；（2）由圆周角定理得到∠BCA=90°，由垂直的定义，可求出∠CEA=90°，从而根据两角对应相等的两三角形相似可证明△ACB∽△AEC，再根据相似三角形的对应边成比例求得AB的长，从而得到圆的半径.试题解析：(1)证明：连接OC.∵CE是⊙O的切线，∴∠OCE =90°∵CE⊥DF，∴∠CEA=90°，∴∠ACE+∠CAE=∠ACE+∠OCA=90°，∴∠CAE=∠OCA ∵OC＝OA，∴∠OCA=∠OAC.∴∠CAE=∠OAC，即AC平分∠FAB(2)连接BC.∵AB是⊙O的直径，∴∠ACB =∠AEC =90°.又∵∠CAE=∠OAC，∴△ACB∽△AEC,∴AB AC AC AE=.∵AE＝1，CE＝2，∠AEC =90°，∴2222125AC AE CE=+=+=∴()22551ACABAE===，∴⊙O的半径为52．13．如图1，D是⊙O的直径BC上的一点，过D作DE⊥BC交⊙O于E、N，F是⊙O上的一点，过F的直线分别与CB、DE的延长线相交于A、P，连结CF交PD于M，∠C＝12∠P．（1）求证：PA是⊙O的切线；（2）若∠A＝30°，⊙O的半径为4，DM＝1，求PM的长；（3）如图2，在（2）的条件下，连结BF、BM；在线段DN上有一点H，并且以H、D、C 为顶点的三角形与△BFM相似，求DH的长度．【答案】（1）证明见解析；（2）PM＝32；（3）满足条件的DH的值为632-或12311+【解析】【分析】（1）如图1中，作PH⊥FM于H．想办法证明∠PFH=∠PMH，∠C=∠OFC，再根据等角的余角相等即可解决问题；（2）解直角三角形求出AD，PD即可解决问题；（3）分两种情形①当△CDH∽△BFM时，DH CD FM BF=．②当△CDH∽△MFB时，DH CDFB MF=，分别构建方程即可解决问题；【详解】（1）证明：如图1中，作PH⊥FM于H．∵PD⊥AC，∴∠PHM＝∠CDM＝90°，∵∠PMH＝∠DMC，∴∠C＝∠MPH，∵∠C＝12∠FPM，∴∠HPF＝∠HPM，∵∠HFP+∠HPF＝90°，∠HMP+∠HPM＝90°，∴∠PFH＝∠PMH，∵OF＝OC，∴∠C＝∠OFC，∵∠C+∠CMD＝∠C+∠PMF＝∠C+∠PFH＝90°，∴∠OFC+∠PFC＝90°，∴∠OFP＝90°，∴直线PA是⊙O的切线．（2）解：如图1中，∵∠A＝30°，∠AFO＝90°，∴∠AOF＝60°，∵∠AOF＝∠OFC+∠OCF，∠OFC＝∠OCF，∴∠C＝30°，∵⊙O的半径为4，DM＝1，∴OA＝2OF＝8，CD33，∴OD＝OC﹣CD＝43，∴AD＝OA+OD＝8+43＝123，在Rt△ADP中，DP＝AD•tan30°＝（123）3＝3﹣1，∴PM＝PD﹣DM＝3﹣2．（3）如图2中，由（2）可知：BF ＝12BC ＝4，FM ＝3BF ＝43 ，CM ＝2DM ＝2，CD ＝3 ， ∴FM ＝FC ﹣CM ＝43﹣2，①当△CDH ∽△BFM 时，DH CD FM BF = ， ∴ 34432=- ，∴DH ＝632- ②当△CDH ∽△MFB 时，DH CD FB MF =， ∴34432DH =- ，∴DH ＝1223+ ， ∵DN ＝()22443833--=- ，∴DH ＜DN ，符合题意，综上所述，满足条件的DH 的值为63- 或1223+．【点睛】本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题.14．如图1，⊙O 的直径AB =12，P 是弦BC 上一动点（与点B ，C 不重合），∠ABC =30°，过点P 作PD ⊥OP 交⊙O 于点D ．（1）如图2，当PD ∥AB 时，求PD 的长；（2）如图3，当弧DC=弧AC时，延长AB至点E，使BE=12AB，连接DE．①求证：DE是⊙O的切线；②求PC的长．【答案】（1）26；（2）①证明见解析；②33﹣3．【解析】试题分析：（1）根据题意首先得出半径长，再利用锐角三角三角函数关系得出OP，PD的长；（2）①首先得出△OBD是等边三角形，进而得出∠ODE=∠OFB=90°，求出答案即可；②首先求出CF的长，进而利用直角三角形的性质得出PF的长，进而得出答案．试题解析：（1）如图2，连接OD，∵OP⊥PD，PD∥AB，∴∠POB=90°，∵⊙O的直径AB=12，∴OB=OD=6，在Rt△POB中，∠ABC=30°，∴OP=OB•tan30°=6×=2，在Rt△POD中，PD===；（2）①如图3，连接OD，交CB于点F，连接BD，∵，∴∠DBC=∠ABC=30°，∴∠ABD=60°，∵OB=OD，∴△OBD是等边三角形，∴OD⊥FB，∵BE=AB，∴OB=BE，∴BF∥ED，∴∠ODE=∠OFB=90°，∴DE是⊙O的切线；②由①知，OD⊥BC，∴CF=FB=OB•cos30°=6×=3，在Rt△POD中，OF=DF，∴PF=DO=3（直角三角形斜边上的中线，等于斜边的一半），∴CP=CF﹣PF=3﹣3．考点：圆的综合题15．如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF=∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG．（1）求证：DF是⊙O的切线；（2）若AD=DP，OB=3，求»BD的长度；（3）若DE=4，AE=8，求线段EG的长．【答案】（1）证明见解析（2）π（3）13【解析】试题分析：（1）连接OD，由等腰三角形的性质得出∠DAB=∠ADO，再由已知条件得出∠ADO=∠DAF，证出OD∥AF，由已知DF⊥AF，得出DF⊥OD，即可得出结论；（2）易得∠BOD=60°，再由弧长公式求解即可；（3）连接DG，由垂径定理得出DE=CE=4，得出CD=8，由勾股定理求出DG，再由勾股定理求出EG即可．试题解析：（1）证明：连接OD，如图1所示：∵OA=OD，∴∠DAB=∠ADO，∵∠DAF=∠DAB，∴∠ADO=∠DAF，∴OD∥AF，又∵DF⊥AF，∴DF⊥OD，∴DF是⊙O的切线；（2）∵AD=DP∴∠P=∠DAF=∠DAB =x0∴∠P+∠DAF+∠DAB =3x o=90O∴x0=300∴∠BOD=60°，∴»BD的长度=π（3）解：连接DG，如图2所示：∵AB⊥CD，∴DE=CE=4，∴CD=DE+CE=8，设OD=OA=x，则OE=8﹣x，在Rt△ODE中，由勾股定理得：OE2+DE2=OD2，即（8﹣x）2+42=x2，解得：x=5，∴CG=2OA=10，∵CG是⊙O的直径，∴∠CDG=90°，∴DG=2222-=-=6，108CG CD∴EG=2222+=+=213.64DG DE。

2020年九年级中考数学复习专题训练：《圆的综合》(含答案)

2020年九年级中考数学复习专题训练：《圆的综合》1．如图，在Rt△ACB中，∠ACB＝90°，以AC为直径作⊙O，交AB于点D．（1）若AB＝8，∠ABC＝30°，求⊙O的半径；（2）若点E是边BC的中点，连结DE，求证：直线DE是⊙O的切线；（3）在（1）的条件下，保持Rt△ACB不动，将⊙O沿直线BC向右平移m个单位长度后得到⊙O′，当⊙O′与直线AB相切时，m＝．2．如图，矩形ABCD中，AB＝13，AD＝6．点E是CD上的动点，以AE为直径的⊙O与AB交于点F，过点F作FG⊥BE于点G．（1）当E是CD的中点时：tan∠EAB的值为；（2）在（1）的条件下，证明：FG是⊙O的切线；（3）试探究：BE能否与⊙O相切？若能，求出此时BE的长；若不能，请说明理由．3．如图，已知正方形ABCD 的边长为1，正方形BEFG 中，点E 在AB 的延长线上，点G 在BC 上，点O 在线段AB 上，且AO ≥BO ．以OF 为半径的⊙O 与直线AB 交于点M ，N ．（1）如图1，若点O 为AB 中点，且点D ，点C 都在⊙O 上，求正方形BEFG 的边长．（2）如图2，若点C 在⊙O 上，求证：以线段OE 和EF 为邻边的矩形的面积为定值，并求出这个定值．（3）如图3，若点D 在⊙O 上，求证：DO ⊥FO ．4．如图，四边形ABCD 内接于⊙O ，AC 为直径，AC 和BD 交于点E ，AB ＝BC ．（1）求∠ADB 的度数；（2）过B 作AD 的平行线，交AC 于F ，试判断线段EA ，CF ，EF 之间满足的等量关系，并说明理由；（3）在（2）条件下过E ，F 分别作AB ，BC 的垂线，垂足分别为G ，H ，连接GH ，交BO 于M ，若AG ＝3，S 四边形AGMO ：S 四边形CHMO ＝8：9，求⊙O 的半径．5．定义：当点P在射线OA上时，把的的值叫做点P在射线OA上的射影值；当点P不在射线OA上时，把射线OA上与点P最近点的射影值，叫做点P在射线OA上的射影值．例如：如图1，△OAB三个顶点均在格点上，BP是OA边上的高，则点P和点B在射线OA 上的射影值均为＝．（1）在△OAB中，①点B在射线OA上的射影值小于1时，则△OAB是锐角三角形；②点B在射线OA上的射影值等于1时，则△OAB是直角三角形；③点B在射线OA上的射影值大于1时，则△OAB是钝角三角形．其中真命题有．A．①②B．①③C．②③D．①②③（2）已知：点C是射线OA上一点，CA＝OA＝1，以〇为圆心，OA为半径画圆，点B是⊙O 上任意点．①如图2，若点B在射线OA上的射影值为．求证：直线BC是⊙O的切线；②如图3，已知D为线段BC的中点，设点D在射线OA上的射影值为x，点D在射线OB上的射影值为y，直接写出y与x之间的函数关系式为．6．问题发现：（1）如图1，△ABC内接于半径为4的⊙O，若∠C＝60°，则AB＝；问题探究：（2）如图2，四边形ABCD内接于半径为6的⊙O，若∠B＝120°，求四边形ABCD的面积最大值；解决问题：（3）如图3，一块空地由三条直路（线段AD、AB、BC）和一条弧形道路围成，点M 是AB道路上的一个地铁站口，已知AD＝BM＝1千米，AM＝BC＝2千米，∠A＝∠B＝60°，的半径为1千米，市政府准备将这块空地规划为一个公园，主入口在点M处，另外三个入口分别在点C、D、P处，其中点P在上，并在公园中修四条慢跑道，即图中的线段DM、MC、CP、PD，是否存在一种规划方案，使得四条慢跑道总长度（即四边形DMCP 的周长）最大？若存在，求其最大值；若不存在，说明理由．7．如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点（点P不与A，B两点重合），连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP，AE．（1）求证：直线PQ为⊙O的切线；（2）若直径AB的长为4．①当PE＝时，四边形BOPQ为正方形；②当PE＝时，四边形AEOP为菱形．8．已知AB是⊙O的直径，DA为⊙O的切线，切点为A，过⊙O上的点C作CD∥AB交AD于点D，连接BC、AC．（1）如图①，若DC为⊙O的切线，切点为C，求∠ACD和∠DAC的大小．（2）如图②，当CD为⊙O的割线且与⊙O交于点E时，连接AE，若∠EAD＝30°，求∠ACD和∠DAC的大小．9．已知AB为⊙O的直径，点C为⊙O上一点，点D为AB延长线一点，连接AC．（Ⅰ）如图①，OB＝BD，若DC与⊙O相切，求∠D和∠A的大小；（Ⅱ）如图②，CD与⊙O交于点E，AF⊥CD于点F连接AE，若∠EAB＝18°，求∠FAC的大小．10．如图，AB为⊙O的直径，点P为AB延长线上的一点，过点P作⊙O的切线PE，切点为M，过A、B两点分别作PE的垂线AC，BD，垂足分别为C，D，连接AM．（1）求证：AM平分∠CAB；（2）若AB＝4，∠APE＝30°，求的长．11．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于E，过点A作AF⊥AC于F，交⊙O于D，连接DE，BE，BD（1）求证：∠C＝∠BED；（2）若AB＝12，tan∠BED＝，求CF的长．12．已知，点A为⊙O外一点，过A作⊙O的切线与⊙O相切于点P，连接PO并延长至圆上一点B连接AB交⊙O于点C，连接OA交⊙O于点D连接DP且∠OAP＝∠DPA．（1）求证：PO＝PD；（2）若AC＝，求⊙O的半径．13．如图，AB是⊙O的直径，C为⊙O上一点，P是半径OB上一动点（不与O，B重合），过点P作射线l⊥AB，分别交弦BC，于D，E两点，过点C的切线交射线1于点F．（1）求证：FC＝FD．（2）当E是的中点时，①若∠BAC＝60°，判断以O，B，E，C为顶点的四边形是什么特殊四边形，并说明理由；②若＝，且AB＝30，则OP＝．14．如图，在∠DAM内部做Rt△ABC，AB平分∠DAM，∠ACB＝90°，AB＝10，AC＝8，点N 为BC的中点，动点E由A点出发，沿AB运动，速度为每秒5个单位，动点F由A点出发，沿AM运动，速度为每秒8个单位，当点E到达点B时，两点同时停止运动，过A、E、F作⊙O．（1）判断△AEF的形状为，并判断AD与⊙O的位置关系为；（2）求t为何值时，EN与⊙O相切？求出此时⊙O的半径，并比较半径与劣弧长度的大小；（3）直接写出△AEF的内心运动的路径长为；（注：当A、E、F重合时，内心就是A点）（4）直接写出线段EN与⊙O有两个公共点时，t的取值范围为．（参考数据：sin37°＝，tan37°＝，tan74°≈，sin74°≈，cos74°≈）15．如图1，CD是⊙O的直径，且CD过弦AB的中点H，连接BC，过弧AD上一点E作EF∥BC，交BA的延长线于点F，连接CE，其中CE交AB于点G，且FE＝FG．（1）求证：EF是⊙O的切线；（2）如图2，连接BE，求证：BE2＝BG•BF；（3）如图3，若CD的延长线与FE的延长线交于点M，tan F＝，BC＝5，求DM的值．16．如图，在Rt△ABC中，AB⊥BC，以AB为直径的圆交AC于点D，E是BC的中点，连接DE．（1）求证：DE是⊙O的切线；（2）设⊙O的半径为r，证明r2＝AD•OE；（3）若DE＝4，sin C＝，求AD之长．17．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到该边所对顶点连线的平方，则称这个点为三角形该边的“好点”．如图1，△ABC中，点D是BC 边上一点，连结AD，若AD2＝BD•CD，则称点D是△ABC中BC边上的“好点”．（1）如图2，△ABC的顶点是4×3网格图的格点，请仅用直尺画出AB边上的一个“好点”．（2）△ABC中，BC＝9，tan B＝，tan C＝，点D是BC边上的“好点”，求线段BD的长．（3）如图3，△ABC是⊙O的内接三角形，OH⊥AB于点H，连结CH并延长交⊙O于点D．①求证：点H是△BCD中CD边上的“好点”．②若⊙O的半径为9，∠ABD＝90°，OH＝6，请直接写出的值．18．如图，在等腰三角形ABC中，AB＝AC，以AC为直径的⊙O分别交AB、BC于点M、N，过点C作⊙O的切线交AB的延长线于点P．（1）求证：∠CAB＝2∠BCP；（2）若⊙O的直径为5，sin∠BCP＝，求△ABC内切圆的半径；（3）在（2）的条件下，求△ACP的周长．19．已知四边形ABCD为⊙O的内接四边形，直径AC与对角线BD相交于点E，作CH⊥BD于H，CH与过A点的直线相交于点F，∠FAD＝∠ABD．（1）求证：AF为⊙O的切线；（2）若BD平分∠ABC，求证：DA＝DC；（3）在（2）的条件下，N为AF的中点，连接EN，若∠AED+∠AEN＝135°，⊙O的半径为2，求EN的长．20．如图，在Rt△ABC中，∠ACB＝90°，O是线段BC上一点，以O为圆心，OC为半径作⊙O，AB与⊙O相切于点F，直线AO交⊙O于点E，D．（1）求证：AO是△CAB的角平分线；（2）若tan∠D＝，求的值；（3）如图2，在（2）条件下，连接CF交AD于点G，⊙O的半径为3，求CF的长．参考答案1．解：（1）在Rt△ABC中，∵AB＝8，∠ABC＝30°，∴AC＝AB sin∠ABC＝8sin30°＝4，∴⊙O的半径为2；（2）证明：连接OD，CD，∵AC为⊙O的直径，∴CD⊥AB，∴∠CDB＝90°，∵点E是边BC的中点，∴DE＝CE＝CB，∴∠DCE＝∠CDE，∵OC＝OD，∴∠OCD＝∠ODC，∴∠ACE＝∠ACD+∠DCE＝90°，∴∠ODE＝∠ODC+∠CDE＝90°，∴OD⊥DE，∴直线DE是⊙O的切线；（3）连接OO′交AB于F，设⊙O′与AB相切于G，连接O′G，则∠O′GF＝90°，∵将⊙O沿直线BC向右平移m个单位长度后得到⊙O′，∴OO′∥BC，AO＝O′G，∴∠AOF＝∠ACB＝90°，∵∠AFO＝∠O′FG，∴△AOF≌△O′GF（AAS），∴O′F＝AF，∵在Rt△AOF中，∵∠A＝60°，AO＝2，∴AF＝4，OF＝2，∴O′F＝AF＝4，∴OO′＝4+2，∴m＝4+2．故答案为：4+2．2．（1）解：∵四边形ABCD是矩形，∴∠D＝90°，CD∥AB，CD＝AB＝13，∴∠EAB＝∠DEA，∵E是CD的中点，∴DE＝CD＝，∴tan∠DEA＝＝＝．故答案为：．（2）证明：连接OF，在矩形ABCD中，AD＝BC，∠ADE＝∠BCE＝90°，又CE＝DE，∴△ADE≌△BCE（SAS），∴AE＝BE，∴∠EAB＝∠EBA．∵OF＝OA，∴∠OAF＝∠OFA，∴∠OFA＝∠EBA．∴OF∥EB．∵FG⊥BE，∴FG⊥OF，∴FG是⊙O的切线．（3）解：若BE能与⊙O相切，由AE是⊙O的直径，则AE⊥BE，∠AEB＝90°．设DE＝x，则EC＝13﹣x．由勾股定理得：AE2+EB2＝AB2，即（36+x2）+[（13﹣x）2+36]＝132，整理得x2﹣13x+36＝0，解得：x1＝4，x2＝9，∴DE＝4或9，当DE＝4时，CE＝9，BE＝＝＝3，当DE＝9时，CE＝4，BE＝＝＝2，∴BE能与⊙O相切，此时BE＝2或3．3．解：（1）如图1，连接OC，∵四边形ABCD和四边形BEFG为正方形，∴AB＝BC＝1，BE＝EF，∠OEF＝∠ABC＝90°，∵点O为AB中点，∴OB＝AB＝，设BE＝EF＝x，则OE＝x+，在Rt△OEF中，∵OE2+EF2＝OF2，∴，在Rt△OBC中，∵OB2+BC2＝OC2，∴＝OC2，∵OC，OF为⊙O的半径，∴OC＝OF，∴，解得：x＝，∴正方形BEFG的边长为；（2）证明：如图2，连接OC，设OB＝y，BE＝EF＝x，同（1）可得，OE2+EF2＝OF2，OB2+BC2＝OC2，∴OF2＝x2+（x+y）2，OC2＝y2+12∵OC，OF为⊙O的半径，∴OC＝OF，∴x2+（x+y）2＝y2+12，∴2x2+2xy＝1，∴x2+xy＝，即x（x+y）＝，∴EF×OE＝，∴以线段OE和EF为邻边的矩形的面积为定值，这个定值为．（3）证明：连接OD，设OA＝a，BE＝EF＝b，则OB＝1﹣a，则OE＝1﹣a+b，∵∠DAO＝∠OEF＝90°，∴DA2+OA2＝OD2，OE2+EF2＝OF2，∴12+a2＝OD2，（1﹣a+b）2+b2＝OF2，∵OD＝OF，∴12+a2＝（1﹣a+b）2+b2，∴（b+1）（a﹣b）＝0，∵b+1≠0，∴a﹣b＝0，∴a＝b，∴OA＝EF，在Rt△AOD和Rt△EFO中，，∴Rt△AOD≌Rt△EFO（HL），∴∠FOE＝∠ODA，∵∠DAO＝90°，∴∠ODA+∠AOD＝90°，∴∠FOE+∠AOD＝90°，∴∠DOF＝90°，∴DO⊥FO．4．解：（1）如图1，∵AC为直径，∴∠ABC＝90°，∴∠ACB+∠BAC＝90°，∵AB＝BC，∴∠ACB＝∠BAC＝45°，∴∠ADB＝∠ACB＝45°；（2）线段EA，CF，EF之间满足的等量关系为：EA2+CF2＝EF2．理由如下：如图2，设∠ABE＝α，∠CBF＝β，∵AD∥BF，∴∠EBF＝∠ADB＝45°，又∠ABC＝90°，∴α+β＝45°，过B作BN⊥BE，使BN＝BE，连接NC，∵AB＝CB，∠ABE＝∠CBN，BE＝BN，∴△AEB≌△CNB（SAS），∴AE＝CN，∠BCN＝∠BAE＝45°，∴∠FCN＝90°．∵∠FBN＝α+β＝∠FBE，BE＝BN，BF＝BF，∴△BFE≌△BFN（SAS），∴EF＝FN，∵在Rt△NFC中，CF2+CN2＝NF2，∴EA2+CF2＝EF2；（3）如图3，延长GE，HF交于K，由（2）知EA 2+CF 2＝EF 2， ∴EA 2+CF 2＝EF 2，∴S △AGE +S △CFH ＝S △EFK ，∴S △AGE +S △CFH +S 五边形BGEFH ＝S △EFK +S 五边形BGEFH ，即S △ABC ＝S 矩形BGKH ， ∴S △ABC ＝S 矩形BGKH ，∴S △GBH ＝S △ABO ＝S △CBO ，∴S △BGM ＝S 四边形COMH ，S △BMH ＝S 四边形AGMO ，∵S 四边形AGMO ：S 四边形CHMO ＝8：9，∴S △BMH ：S △BGM ＝8：9，∵BM 平分∠GBH ，∴BG ：BH ＝9：8，设BG ＝9k ，BH ＝8k ，∴CH ＝3+k ，∵AG ＝3，∴AE ＝3， ∴CF ＝（k +3），EF ＝（8k ﹣3），∵EA 2+CF 2＝EF 2， ∴+＝，整理得：7k 2﹣6k ﹣1＝0，解得：k 1＝﹣（舍去），k 2＝1．∴AB ＝12，∴AO ＝AB ＝6，∴⊙O的半径为6．5．解：（1）①错误．点B在射线OA上的射影值小于1时，∠OBA可以是钝角，故△OAB 不一定是锐角三角形；②正确．点B在射线OA上的射影值等于1时，AB⊥OA，∠OAB＝90°，△OAB是直角三角形；③正确．点B在射线OA上的射影值大于1时，∠OAB是钝角，故△OAB是钝角三角形；故答案为：B．（2）①如图2，作BH⊥OC于点H，∵点B在射线OA上的射影值为，∴＝，＝，CA＝OA＝OB＝1，∴＝，又∵∠BOH＝∠COB，∴△BOH∽△COB，∴∠BHO＝∠CBO＝90°，∴BC⊥OB，∴直线BC是⊙O的切线；②图形是上下对称的，只考虑B在直线OC上及OC上方部分的情形．过点D作DM⊥OC，作DN⊥OB，当∠DOB＜90°时，设DM＝h，∵D为线段BC的中点，∴S△OBD ＝S△ODC，∴OB×DN＝OC×DM，∴DN＝2h，∵在Rt△DON和Rt△DOM中，OD2＝DN2+ON2＝DM2+OM2，∴4h2+y2＝h2+x2，∴3h2＝x2﹣y2①，∵BD2＝CD2，∴4h2+（1﹣y）2＝h2+（2﹣x）2②，①②消去h得：y＝2x﹣．如图，当∠BOD＝90°时，过点D作DM⊥OC于点M，∵D为线段BC的中点，∴S△OBD ＝S△ODC，∴OB×DO＝OC×DM，∵CA＝OA＝OB＝1，∴OD＝2DM，∴sin∠DOM＝，∴∠DOM＝30°，设DM＝h，则OD＝2h，OM＝h，∴h2+＝1+4h2，∴h＝，∴OM＝，当点B在OC上时，OD＝，综上所述，当≤x≤时，y＝0；当＜x≤时，y＝2x﹣．故答案为：y＝0（≤x≤）或y＝2x﹣（＜x≤）．6．解：（1）如图1，连接OA、OB，过点O作OH⊥AB于点H，∵∠C＝60°，∴∠AOB＝120°，∵OA＝OB，∴△OAB为等腰三角形，∵OH⊥AB，∴∠AOH＝∠BOH＝60°，∴AH＝OA sin∠AOH＝4×＝2，则AB＝2AH＝4；故答案为4；（2）如图2，连接AC，过点D作DE⊥AC于点E，过点B作BF⊥AC于点F，∵四边形ABCD的面积S＝AC×DE AC×BF＝AC×（DE+BF），∴当D、E、F、B四点共线且为直径时，四边形ABCD的面积S最大；∵∠ABC＝120°，∴∠ADC＝60°，∴∠AOC＝120°，在△AOC中，由（1）知，AC＝2×OA sin60°＝2×6×＝6，∴四边形ABCD的面积S的最大值为：×AC×BD＝6×12＝36，故四边形ABCD的面积的最大值为36；（3）如图3，过点D作DK⊥AB于点K，连接CD，在△ADM中，DK＝AD•sin A＝1×＝，同理AK＝，则KM＝AM﹣AK＝2﹣＝，则tan∠DMK＝＝∴∠DMK＝30°，故△ADM为直角三角形，同理△CMB为直角三角形，在Rt△ADM中，DM＝＝＝，∴∠DMC＝180°﹣∠DMA﹣∠CMB＝60°∵AD＝BM，AM＝BC，∠A＝∠B＝60°，∴Rt△ADM≌Rt△BMC（SAS），∴DM＝CM，∴△CDM为等边三角形；设所在的圆的圆心为R，连接DR、CR、MR，∵DM＝CM，RM＝RM，DR＝CR，∴△DRM≌△CRM（SSS），∴∠DMR＝∠CMR＝∠DMC＝30°，在△DMR中，DR＝1，∠DMR＝30°，DM＝＝CM，过点R作RH⊥DM于点H，则RM＝＝＝1＝RD，故D、P、C、M四点共圆，∴∠DPC＝120°，如图4，连接MP，在PM上取PP′＝PC，∵△CDM为等边三角形，∴∠CDM＝60°＝∠CPM，∴△P′PC为等边三角形，则PP′＝P′C＝PC，∵∠PMC＝∠PDC，∠CP′M＝180°﹣∠PP′C＝120°＝∠DPC，CD＝CM，∴△PDC≌△P′MC（AAS），∴PD＝P′M，∴PD+PC＝PP′+PD＝PP′+P′M＝PM，故当PM是直径时，PD+PC最大值为2；∵四边形DMCP的周长＝DM+CM+PC+PD＝2+PD+PC，而PD+PC最大值为2；故四边形DMCP的周长的最大值为：2+2，即四条慢跑道总长度（即四边形DMCP的周长）最大为2+2．7．（1）证明：∵OQ∥AP，∴∠EOC＝∠OAP，∠POQ＝∠APO，又∵OP＝OA，∴∠APO＝∠OAP，又∵∠BOQ＝∠EOA＝∠OAP，∴∠POQ＝∠BOQ，在△BOQ与△POQ中，，∴△POQ≌△BOQ（SAS），∴∠OPQ＝∠OBQ＝90°，∵点P在⊙O上，∴PQ是⊙O的切线；（2）解：①∵△POQ≌△BOQ，∴∠OBQ＝∠OPQ＝90°，当∠BOP＝90°，四边形OPQB为矩形，而OB＝OP，则四边形OPQB为正方形，此时点C、点E与点O重合，PE＝PO＝AB＝2；②∵PE⊥AB，∴当OC＝AC，PC＝EC，四边形AEOP为菱形，∵OC＝OA＝1，∴PC＝＝＝，∴PE＝2PC＝2．故答案为：2；2．8．解：（1）∵AB是⊙O的直径，DA为⊙O的切线，切点为A，∴DA⊥AB，∴∠DAB＝90°，∵DC为⊙O的切线，切点为C，∴DC＝DA，∵CD∥AB，∴∠D+∠DAB＝180°，∴∠D＝90°，∴∠ACD＝∠DAC＝45°；（2）∵AB是⊙O的直径，DA为⊙O的切线，切点为A，∴DA⊥AB，∴∠DAB＝90°，∠DEA＝∠EAB，∴∠ADC＝90°，∵∠EAD＝30°，∴∠DEA＝60°，∴∠EAB＝60°，∴∠BCE＝120°，∵AB是⊙O的直径，∴∠BCA＝90°，∴∠ACD＝30°，∴∠DAC＝60°．9．解：（Ⅰ）如图①，连接OC，BC，∵AB为⊙O的直径，∴∠ACB＝90°，∵DC与⊙O相切，∴∠OCD＝90°，∵OB＝BD，∴BC＝OD＝OB＝BD，∴BC＝OB＝OC，∴△OBC是等边三角形，∴∠OBC＝∠OCB＝∠COB＝60°，∴∠BCD＝∠OCA＝30°，∴∠D＝∠A＝30°；（Ⅱ）如图②，连接BE，∵AB为⊙O的直径，∴∠AEB＝90°，∵AF⊥CD，∴∠AFC＝90°，∵∠ACF是圆内接四边形ACEB的外角，∴∠ACF＝∠ABE，∴∠FAC＝∠EAB＝18°，答：∠FAC的大小为18°．10．解：（1）连接OM，∵PE为⊙O的切线，∴OM⊥PC，∵AC⊥PC，∴OM∥AC，∴∠CAM＝∠AMO，∵OA＝OM，∠OAM＝∠AMO，∴∠CAM＝∠OAM，即AM平分∠CAB；（2）∵∠APE＝30°，∴∠MOP＝∠OMP﹣∠APE＝90°﹣30°＝60°，∵AB＝4，∴OB＝2，∴的长为＝．11．（1）证明：∵AB是⊙O的直径，CA切⊙O于A，∴∠C+∠AOC＝90°；又∵OC⊥AD，∴∠OFA＝90°，∴∠AOC+∠BAD＝90°，∴∠C＝∠BAD．又∵∠BED＝∠BAD，∴∠C＝∠BED．（2）解：由（1）知∠C＝∠BAD，tan∠BED＝，∴tan∠C＝，∴tan∠C＝＝，且OA＝AB＝6，∴，解得AC＝8，∴＝10，∵OC•AF＝OA•AC，∴．∴＝＝．12．（1）证明：∵PA与⊙O相切于点P，∴BP⊥AP∴∠OPD+∠DPA＝90°，∠OAP+∠AOP＝90°∵∠OAP＝∠DPA．∴∠OPD＝∠AOP∴OD＝PD∵PO＝OD∴PO＝PD．（2）连接PC，∵PB为⊙O的直径∴∠BCP＝90°∵PO＝PD＝OD∴∠AOP＝60°设⊙O的半径为x，则PB＝2x，＝tan60°∴PA＝x∴AB＝＝x∵∠BPA＝∠BCP＝90°，∠B＝∠B∴△BAP∽△BPC∴＝∵AC＝∴＝∴7x﹣＝4x∴x＝∴⊙O的半径为．13．证明：（1）连接OC，（1）证明：连接OC∵CF是⊙O的切线，∴OC⊥CF，∴∠OCF＝90°，∴∠OCB+∠DCF＝90°，∵OC＝OB，∴∠OCB＝∠OBC，∵PD⊥AB，∴∠BPD＝90°，∴∠OBC+∠BDP＝90°，∴∠BDP＝∠DCF，∵∠BDP＝∠CDF，∴∠DCF＝∠CDF，∴FC＝FD；（2）如图2，连接OC，OE，BE，CE，①以O，B，E，C为顶点的四边形是菱形．理由如下：∵AB是直径，∴∠ACB＝90°，∵∠BAC＝60°，∴∠BOC＝120°，∵点E是的中点，∴∠BOE＝∠COE＝60°，∵OB＝OE＝OC，∴△BOE，△OCE均为等边三角形，∴OB＝BE＝CE＝OC∴四边形BOCE是菱形；②∵，∴设AC＝3k，BC＝4k（k＞0），由勾股定理得AC2+BC2＝AB2，即（3k）2+（4k）2＝302，解得k＝6，∴AC＝18，BC＝24，∵点E是的中点，∴OE⊥BC，BH＝CH＝12，＝OE×BH＝OB×PE，即15×12＝15PE，解得：PE＝12，∴S△OBE由勾股定理得OP＝＝＝9．故答案为：9．14．解：（1）过点E作EH⊥AF于H，连接OA、OE、OH，如图1所示：∵∠ACB＝90°，AB＝10，AC＝8，∴BC＝＝＝6，设运动时间为t，则AE＝5t，AF＝8t，∵∠AHE＝∠ACB＝90°，∠EAH＝∠BAC，∴△EAH∽△BAC，∴＝，即：＝，∴AH＝4t，∴FH＝AF﹣AH＝8t﹣4t＝4t，∴AH＝FH，∵EH⊥AF，∴△AEF是等腰三角形，∴E为的中点，∠EAF＝∠EFA，∵AH＝FH，∴OH⊥AC，∴E、H、O三点共线，∴∠OAF+∠AOE＝90°，∵AB平分∠DAM，∴∠DAE＝∠EAF＝∠EFA，∵∠AOE＝2∠EFA，∴∠AOE＝∠DAE+∠EAF＝∠DAF，∴∠DAF+∠OAF＝90°＝∠DAO，即OA⊥AD，∵OA为⊙O的半径，∴AD与⊙O相切；故答案为：等腰三角形，相切；（2）连接OA、OF、OE，OE于AC交于H，如图2所示：由（1）知：EH⊥AC，∵EN与⊙O相切，∴∠OEN＝90°，∵∠ACB＝90°，∴四边形EHCN为矩形，∴EH＝NC，在Rt△AHE中，EH＝＝＝3t，∴NC＝3t，∵点N为BC的中点，∴BC＝2NC＝6t，∵BC＝6，∴6t＝6，∴t＝1，∴AH＝4，EH＝3，设⊙O的半径为x，则OH＝x﹣3，在Rt△AOH中，由勾股定理得：OA2＝OH2+AH2，即x2＝（x﹣3）2+42，解得：x＝，∴⊙O的半径为，∴OH＝，∴tan∠AOH＝＝，∴∠AOH＝74°，∵∠AOH＝60°时，△AOE是等边三角形，AE＝OA，74°＞60°，∴AE＞OA，∴劣弧长度的大于半径；（3）当点E运动到B点时，t＝10÷5＝2，∴AF＝2×8＝16，AE＝EF＝AB＝10，此时△AEF的内心记为G，当A、E、F重合时，内心为A点，∴△AEF的内心运动的路径长为AG，作GP⊥AE于P，GQ⊥EF于Q，连接AG、GF，则CG＝PG＝NQ，如图3所示：S△AEF＝AF•BC＝×16×6＝48，设CG＝PG＝NQ＝a，则S△AEF ＝S△AGF+S△AEB+S△FEG＝AF•CG+AE•PG+EF•NQ＝×（16+10+10）a＝48，解得：a＝，在Rt△AGC中，AC2+CG2＝AG2，即82+（）2＝AG，∴AG＝，故答案为：；（4）分别讨论两种极限位置，①当EN与⊙O相切时，由（2）知，t＝1；②当N在⊙O上，即ON为⊙O的半径，连接OA、ON、OE，OE交AC于H，过点O作OK⊥BC于K，如图4所示：则四边形OKCH为矩形，OA＝OE＝ON，∴OH＝CK，AH＝4t，EH＝3t，设⊙O的半径为x，则在Rt△AOH中，AH2+OH2＝OA2，即（4t）2+（x﹣3t）2＝x2，解得：x＝t，∴OH＝CK＝t﹣3t＝t，在Rt△OKN中，OK2+KN2＝ON2，即（8﹣4t）2+（3+t）2＝（t）2，解得：t＝，∴线段EN与⊙O有两个公共点时，t的取值范围为：1＜t≤，故答案为：1＜t≤．15．解：（1）连接OE，则∠OCE＝∠OEC＝α，∵FE＝FG，∴∠FGE＝∠FEG＝β，∵H是AB的中点，∴CH⊥AB，∴∠GCH+∠CGH＝α+β＝90°，∴∠FEO＝∠FEG+∠CEO＝α+β＝90°，∴EF是⊙O的切线；（2）∵CH⊥AB，∴＝∴∠CBA＝∠CEB，∵EF∥BC，∴∠CBA＝∠F，故∠F＝∠CEB，∴∠FBE＝∠GBE，∴△FEB∽△EGB，∴BE2＝BG•BF；（3）如图2，过点F作FR⊥CE于点R，设∠CBA＝∠CEB＝∠GFE＝γ，则tanγ＝，∵EF∥BC，∴∠FEC＝∠BCG＝β，故△BCG为等腰三角形，则BG＝BC＝5，在Rt△BCH中，BC＝5，tan∠CBH＝tanγ＝，则sinγ＝，cosγ＝，CH＝BC sinγ＝5×＝3，同理HB＝4；设圆的半径为r，则OB2＝OH2+BH2，即r2＝（r﹣3）2+（4）2，解得：r＝；GH＝BG﹣BH＝5﹣4＝，tan∠GCH＝＝＝，则cos∠GCH＝，则tan∠CGH＝3＝tanβ，则cosβ＝，连接DE，则∠CED＝90°，在Rt△CDE中cos∠GCH＝＝＝，解得：CE＝，在△FEG中，cosβ＝＝＝，解得：FG＝；∵FH＝FG+GH＝，∴HM＝FH tan∠F＝×＝；∵CM＝HM+CH＝，∴MD＝CM﹣CD＝CM﹣2r＝．16．（1）证明：连接OD、BD，∵AB为圆O的直径，∴∠BDA＝90°，∴∠BDC＝180°﹣90°＝90°，∵E为BC的中点，∴DE＝BC＝BE，∴∠EBD＝∠EDB，∵OD＝OB，∴∠OBD＝∠ODB，∵∠EBD+∠DBO＝90°，∴∠EDB+∠ODB＝90°，∴∠ODE＝90°，∴DE是圆O的切线．（2）证明：如图，连接BD．由（1）知，∠ODE＝∠ADB＝90°，BD⊥AC．∵E是BC的中点，O是AB的中点，∴OE是△ABC的中位线，∴OE∥AC，∴OE⊥BD．∴OE∥AC，∴∠1＝∠2．又∵∠1＝∠A，∴∠A＝∠2．即在△ADB与△ODE中，∠ADB＝∠ODE，∠A＝∠2，∴△ADB∽△ODE．∴＝，即＝．∴r2＝AD•OE；（3）∵AB为⊙O的直径，∴∠ADB＝∠BDC＝90°，∵点E为BC的中点，∴BC＝2DE＝8，∵sin C＝，∴设AB＝3x，AC＝5x，根据勾股定理得：（3x）2+82＝（5x）2，解得x＝2．则AC＝10．由切割线定理可知：82＝（10﹣AD）×10，解得，AD＝3.6．17．解：（1）如答图1，当CD⊥AB或点D是AB的中点是，CD2＝AD•BD；（2）作AE⊥BC于点E，由，可设AE＝4x，则BE＝3x，CE＝6x，∴BC＝9x＝9，∴x＝1，∴BE＝3，CE＝6，AE＝4，设DE＝a，①如答图2，若点D在点E左侧，由点D是BC边上的“好点”知，AD2＝BD•CD，∴a2+42＝（3﹣a）（6+a），即2a2+3a﹣2＝0，解得，a＝﹣2（舍去），2∴．②如答图3，若点D在点E右侧，由点D是BC边上的“好点”知，AD2＝BD•CD，∴a2+42＝（3+a）（6﹣a），即2a2﹣3a﹣2＝0，＝2，（舍去）解得a1∴BD＝3+a＝3+2＝5．∴或5．（5）①∵∠CHA＝∠BHD，∠ACH＝∠DBH∴△AHC∽△DHB，∴，即AH•BH＝CH•DH，∵OH⊥AB，∴AH＝BH，∴BH2＝CH•DH∴点H是△BCD中CD边上的“好点”．②．理由如下：如答图4，连接AD，BD，∵∠ABD＝90°，∴AD是直径，∴AD＝18．又∵OH⊥AB，∴OH∥BD．∵点O是线段AD的中点，∴OH是△ABD的中位线，∴BD＝2OH＝12．在直角△ABD中，由勾股定理知：AB＝＝＝6．∴由垂径定理得到：BH＝AB＝3．在直角△BDH中，由勾股定理知：DH＝＝＝3．又由①知，BH2＝CH•DH，即45＝3CH，则CH＝．∴＝＝，即．18．解：（1）如图，连接AN，∵AC为直径，∴AN⊥BC，∵AB＝AC，∴AN平分∠BAC，∵PC是圆的切线，∴∠ACP＝90°，∵∠NAC+∠ACB＝∠PCB+∠ACB＝90°，∴∠NAC＝∠BCP，即∠BAC＝2∠BCP；（2）由（1）知，AN平分∠BAC，则∠NAC＝∠BCP，故sin∠NAC＝sin∠BCP＝，则tan∠NAC＝，在Rt△NAC中，AC＝5，NC＝AC•sin∠NAC＝5×＝，同理AN＝2，则BC＝2NC＝2；S＝×BC•AN＝2×2＝10，△ABC设△ABC内切圆的半径为r，则S＝（AB+AC+BC）•r＝×（5+5+2）＝10，△ABC解得：r＝；故△ABC内切圆的半径为；（3）在△ABC中，设AC边长的高为h，则S＝AC•h＝×5×h＝10，解得：h＝4，△ABCsin∠BAC＝＝，在Rt△ACP中，∵sin∠BAC＝＝，设PC＝4m，则AP＝5m，则AC＝3m＝5，解得m＝，△ACP的周长＝3m+4m+5m＝12m＝20．19．（1）证明：如图1，∵AC为⊙O的直径，∴∠ADC＝90°，∴∠DAC+∠DCA＝90°．∵＝，∴∠ABD＝∠DCA，∵∠FAD＝∠ABD，∴∠FAD＝∠DCA，∴∠FAD+∠DCA＝90°，∴CA⊥AF，∴AF为⊙O的切线．（2）证明：如图2，连接OD，∵＝，∴∠ABD＝∠AOD，∵＝，∴∠DBC＝∠DOC，∵BD平分∠ABC，∴∠ABD＝∠DBC，∴∠DOA＝∠DOC，∴DA＝DC．（3）如图3，连接OD交CF于M，作EP⊥AD于P，∵AC为⊙O的直径，∴∠ADC＝90°．∵DA＝DC，∴DO⊥AC，∴∠FAC＝∠DOC＝90°，∴AF∥OM，∵AO＝OC，∴OM＝AF．∵∠ODE+∠DEO＝90°，∠OCM+∠DEO＝90°．∴∠ODE＝∠OCM．∵∠DOE＝∠COM，OD＝OC，∴∴△ODE≌△OCM，∴OE＝OM，设OM＝m，∴AE＝2﹣m，AP＝PE＝2﹣m，DP＝2+m，∵∠AED+∠AEN＝135°，∠AED+∠ADE＝135°，∴∠AEN＝∠ADE，∵∠EAN＝∠DPE，∴△EAN∽△DPE，∴＝，∴＝，∴m＝，∴AN＝，AE＝，∴勾股定理得NE＝．20．（1）证明：连接OF，∵AB与⊙O相切于点F，∴OF⊥AB，∵∠ACB＝90°，OC＝OF，∴∠OAF＝∠OAC，即AO是△ABC的角平分线；（2）如图2，连接CE，∵ED是⊙O的直径，∴∠ECD＝90°，∴∠ECO+∠OCD＝90°，∵∠ACB＝90°，∴∠ACE+∠ECO＝90°，∴∠ACE＝∠OCD，∵OC＝OD，∴∠OCD＝∠ODC，∴∠ACE＝∠ODC，∵∠CAE＝∠CAE，∴△ACE∽△ADC，∴，∵tan∠D＝，∴，∴；（3）由（2）可知：＝，∴设AE＝x，AC＝2x，∵△ACE∽△ADC，∴，∴AC2＝AE•AD，∴（2x）2＝x（x+6），解得：x＝2或x＝0（不合题意，舍去），∴AE＝2，AC＝4，∴AO＝AE+OE＝2+3＝5，如图3，连接CF交AD于点G，∵AC，AF是⊙O的切线，∴AC＝AF，∠CAO＝∠OAF，∴CF⊥AO，∴∠ACO＝∠CGO＝90°，∵∠COG＝∠AOC，∴△CGO∽△ACO，∴，∴OC2＝OG•OA，∴OG＝，∴CG＝＝＝，∴CF＝2CG＝．。

九年级数学二模试题分类汇编——圆的综合综合含详细答案

九年级数学二模试题分类汇编——圆的综合综合含详细答案一、圆的综合1．如图，点P是正方形ABCD内的一点，连接PA，PB，PC．将△PAB绕点B顺时针旋转90°到△P'CB的位置.(1)设AB的长为a，PB的长为b(b<a)，求△PAB旋转到△P'CB的过程中边PA所扫过区域(图中阴影部分)的面积；(2)若PA=2，PB=4，∠APB=135°，求PC的长.【答案】(1) S阴影=(a2-b2)；(2)PC=6.【解析】试题分析：（1）依题意，将△P′CB逆时针旋转90°可与△PAB重合，此时阴影部分面积=扇形BAC的面积-扇形BPP'的面积，根据旋转的性质可知，两个扇形的中心角都是90°，可据此求出阴影部分的面积．（2）连接PP'，根据旋转的性质可知：BP=BP'，旋转角∠PBP'=90°，则△PBP'是等腰直角三角形，∠BP'C=∠BPA=135°，∠PP'C=∠BP'C-∠BP'P=135°-45°=90°，可推出△PP'C是直角三角形，进而可根据勾股定理求出PC的长．试题解析：（1）∵将△PAB绕点B顺时针旋转90°到△P′CB的位置，∴△PAB≌△P'CB，∴S△PAB=S△P'CB，S阴影=S扇形BAC-S扇形BPP′=（a2-b2）；（2）连接PP′，根据旋转的性质可知：△APB≌△CP′B，∴BP=BP′=4，P′C=PA=2，∠PBP′=90°，∴△PBP'是等腰直角三角形，P'P2=PB2+P'B2=32；又∵∠BP′C=∠BPA=135°，∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°，即△PP′C是直角三角形．PC==6．考点：1.扇形面积的计算；2.正方形的性质；3.旋转的性质．2．如图，已知⊙O 的半径为1，PQ 是⊙O 的直径，n 个相同的正三角形沿PQ 排成一列，所有正三角形都关于PQ 对称，其中第一个△A 1B 1C 1的顶点A 1与点P 重合，第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点，…，最后一个△A n B n C n 的顶点B n 、C n 在圆上．如图1，当n=1时，正三角形的边长a 1=_____；如图2，当n=2时，正三角形的边长a 2=_____；如图3，正三角形的边长a n =_____（用含n 的代数式表示）．3831343n 【解析】分析：（1）设PQ 与11B C 交于点D ，连接1B O ，得出OD=1A D -O 1A ，用含1a 的代数式表示OD ，在△O 1B D 中，根据勾股定理求出正三角形的边长1a ；（2）设PQ 与2B 2C 交于点E ，连接2B O ，得出OE=1A E-O 1A ，用含2a 的代数式表示OE ，在△O 2B E 中，根据勾股定理求出正三角形的边长2a ；（3）设PQ 与n B n C 交于点F ，连接n B O ，得出OF=1A F-O 1A ，用含an 的代数式表示OF ，在△O n B F 中，根据勾股定理求出正三角形的边长an ．本题解析：(1)易知△A 1B 1C 1的高为323 ∴a 13.(2)设△A 1B 1C 1的高为h ，则A 2O ＝1－h ，连结B 2O ，设B 2C 2与PQ 交于点F ，则有OF ＝2h －1.∵B 2O 2＝OF 2＋B 2F 2，∴1＝(2h －1)2＋2212a ⎛⎫ ⎪⎝⎭. ∵h ＝32a 2，∴1＝32－1)2＋14a 22，解得a 283. (3)同(2)，连结B n O ，设B n C n 与PQ 交于点F ，则有B n O 2＝OF 2＋B n F 2，即1＝(nh －1)2＋212n a ⎛⎫ ⎪⎝⎭.∵h ＝32 a n ，∴1＝14a n 2＋231n na ⎛⎫- ⎪ ⎪⎝⎭，解得a n ＝24331nn + .3．如图，在RtΔABC 中，∠ABC=90°，AB=CB ，以AB 为直径的⊙O 交AC 于点D ，点E 是AB 边上一点（点E 不与点A 、B 重合），DE 的延长线交⊙O 于点G ，DF ⊥DG ，且交BC 于点F.（1）求证：AE=BF ；（2）连接EF ，求证：∠FEB=∠GDA ；（3）连接GF,若AE=2，EB=4，求ΔGFD 的面积.【答案】（1）（2）见解析；（3）9 【解析】分析：（1）连接BD ，由三角形ABC 为等腰直角三角形，求出∠A 与∠C 的度数，根据AB 为圆的直径，利用圆周角定理得到∠ADB 为直角，即BD 垂直于AC ，利用直角三角形斜边上的中线等于斜边的一半，得到AD =DC =BD =12AC ，进而确定出∠A =∠FBD ，再利用同角的余角相等得到一对角相等，利用ASA 得到三角形AED 与三角形BFD 全等，利用全等三角形对应边相等即可得证；（2）连接EF ，BG ，由三角形AED 与三角形BFD 全等，得到ED =FD ，进而得到三角形DEF 为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行，再根据平行线的性质和同弧所对的圆周角相等，即可得出结论；（3）由全等三角形对应边相等得到AE =BF =1，在直角三角形BEF 中，利用勾股定理求出EF 的长，利用锐角三角形函数定义求出DE 的长，利用两对角相等的三角形相似得到三角形AED 与三角形GEB 相似，由相似得比例，求出GE 的长，由GE +ED 求出GD 的长，根据三角形的面积公式计算即可．详解：（1）连接BD ．在Rt △ABC 中，∠ABC =90°，AB =BC ，∴∠A =∠C =45°． ∵AB 为圆O 的直径，∴∠ADB =90°，即BD ⊥AC ，∴AD =DC =BD =12AC ，∠CBD =∠C =45°，∴∠A=∠FBD．∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°．∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB．在△AED和△BFD中，A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AED≌△BFD（ASA），∴AE=BF；（2）连接EF，BG．∵△AED≌△BFD，∴DE=DF．∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°．∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF，∴∠FEB=∠GBA．∵∠GBA=∠GDA，∴∠FEB=∠GDA；（3）∵AE=BF，AE=2，∴BF=2．在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF2=EB2+BF2．∵EB=4，BF=2，∴EF=2242+=25．∵△DEF为等腰直角三角形，∠EDF=90°，∴cos∠DEF=DEEF．∵EF=25，∴DE=25×2=10．∵∠G=∠A，∠GEB=∠AED，∴△GEB∽△AED，∴GEAE=EBED，即GE•ED=AE•EB，∴10•GE=8，即GE=410，则GD=GE+ED=910．∴1191011092252S GD DF GD DE=⨯⨯=⨯⨯=⨯⨯=．点睛：本题属于圆综合题，涉及的知识有：全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，圆周角定理，以及平行线的判定与性质，熟练掌握判定与性质是解答本题的关键．4．如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC 交AC于点E，交PC于点F，连结AF．(1)判断AF与⊙O的位置关系并说明理由；(2)若AC ＝24，AF ＝15，求sin B ．【答案】(1) AF 与⊙O 相切理由见解析；（2）35【解析】试题分析：（1）连接OC ，先证∠OCF =90°，再证明△OAF ≌△OCF ，得出∠OAF =∠OCF =90°即可；（2）先求出AE 、EF ，再证明△OAE ∽△AFE ，得出比例式OA AEAF EF=，可求出半径，进而求出直径，由三角函数的定义即可得出结论．试题解析：解：（1）AF 与⊙O 相切．理由如下：连接OC ．如图所示．∵PC 是⊙O 的切线，∴OC ⊥PC ，∴∠OCF =90°．∵OF ∥BC ，∴∠B =∠AOF ，∠OCB =∠COF ．∵OB =OC ，∴∠B =∠OCB ，∴∠AOF =∠COF ．在△OAF 和△OCF 中，∵OA =OC ，∠AOF =∠COF ，OF =OF ，∴△OAF ≌△OCF （SAS ），∴∠OAF =∠OCF =90°，∴AF 与⊙O 相切；（2）∵△OAF ≌△OCF ，∴∠OAE =∠COE ，∴OE ⊥AC ，AE =12AC =12，∴EF =2215129-=．∵∠OAF =90°，∴△OAE ∽△AFE ，∴OA AE AF EF =，即12159OA =，∴OA =20，∴AB =40，sin B =243405AC AB ==．点睛：本题考查了切线的性质与判定和全等三角形的判定与性质以及相似三角形的判定与性质；熟练掌握切线的证法和三角形相似是解题的关键．5．阅读下列材料：如图1，⊙O 1和⊙O 2外切于点C ，AB 是⊙O 1和⊙O 2外公切线，A 、B 为切点，求证：AC ⊥BC证明：过点C 作⊙O 1和⊙O 2的内公切线交AB 于D ， ∵DA 、DC 是⊙O 1的切线 ∴DA=DC ． ∴∠DAC=∠DCA ．同理∠DCB=∠DBC ．又∵∠DAC+∠DCA+∠DCB+∠DBC=180°， ∴∠DCA+∠DCB=90°．即AC ⊥BC ．根据上述材料，解答下列问题：（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；（2）以AB 所在直线为x 轴，过点C 且垂直于AB 的直线为y 轴建立直角坐标系（如图2），已知A 、B 两点的坐标为（﹣4，0），（1，0），求经过A 、B 、C 三点的抛物线y=ax 2+bx+c 的函数解析式；（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O 1O 2上，并说明理由．【答案】（1）见解析；（2）213222y x x =+- ；（3）见解析【解析】试题分析：（1）由切线长相等可知用了切线长定理；由三角形的内角和是180°，可知用了三角形内角和定理；（2）先根据勾股定理求出C 点坐标，再用待定系数法即可求出经过、、A B C 三点的抛物线的函数解析式；（3）过C 作两圆的公切线，交AB 于点D ，由切线长定理可求出D 点坐标，根据,C D 两点的坐标可求出过,C D 两点直线的解析式，根据过一点且互相垂直的两条直线解析式的关系可求出过两圆圆心的直线解析式，再把抛物线的顶点坐标代入直线的解析式看是否适合即可．试题解析：(1)DA 、DC 是1O e 的切线， ∴DA =DC .应用的是切线长定理；180DAC DCA DCB DBC ∠+∠+∠+∠=o ，应用的是三角形内角和定理.(2)设C 点坐标为(0,y ),则222AB AC BC =+，即()()222224141y y --=-+++，即225172y =+,解得y =2(舍去)或y =−2.故C 点坐标为(0,−2)，设经过、、A B C 三点的抛物线的函数解析式为2y ax bx c ，=++则16402,a b ca b cc-+=⎧⎪++=⎨⎪=-⎩解得12322abc⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩，故所求二次函数的解析式为2132.22y x x=+-(3)过C作两圆的公切线CD交AB于D,则AD=BD=CD,由A(−4,0),B(1,0)可知3(,0)2D-，设过CD两点的直线为y=kx+b,则322k bb⎧-+=⎪⎨⎪=-⎩，解得432kb⎧=-⎪⎨⎪=-⎩，故此一次函数的解析式为423y x=--，∵过12,O O的直线必过C点且与直线423y x=--垂直，故过12,O O的直线的解析式为324y x=-，由(2)中所求抛物线的解析式可知抛物线的顶点坐标为325(,)28--，代入直线解析式得33252,428⎛⎫⨯--=-⎪⎝⎭故这条抛物线的顶点落在两圆的连心12O O上.6．如图，正三角形ABC内接于⊙O，P是BC上的一点，且PB＜PC，PA交BC于E，点F 是PC延长线上的点，CF=PB，13PA=4．（1）求证：△ABP≌△ACF；（2）求证：AC2=PA•AE；（3）求PB和PC的长．【答案】（1）证明见解析；（2）证明见解析；（3）PB=1，PC=3．【解析】试题分析：（1）先根据等边三角形的性质得到AB=AC ，再利用圆的内接四边形的性质得∠ACF=∠ABP ，于是可根据“SAS”判断△ABP ≌△ACF ；（2）先根据等边三角形的性质得到∠ABC=∠ACB=60°，再根据圆周角定理得∠APC=∠ABB=60°，加上∠CAE=∠PAC ，于是可判断△ACE ∽△APC ，然后利用相似比即可得到结论；（3）先利用AC 2=PA•AE 计算出AE=134 ，则PE=AP-AE=34，再证△APF 为等边三角形，得到PF=PA=4，则有PC+PB=4，接着证明△ABP ∽△CEP ，得到PB•PC=PE•A=3，然后根据根与系数的关系，可把PB 和PC 看作方程x 2-4x+3=0的两实数解，再解此方程即可得到PB 和PC 的长．试题解析：（1）∵∠ACP+∠ABP=180°，又∠ACP+∠ACF=180°， ∴∠ABP=∠ACF 在ABP ∆和ACF ∆中，∵AB=AC ，∠ABP=∠ACF ， CF PB = ∴ABP ∆≌ACF ∆． (2)在AEC ∆和ACP ∆中， ∵∠APC=∠ABC ，而ABC ∆是等边三角形，故∠ACB=∠ABC=60º， ∴∠ACE =∠APC . 又∠CAE =∠PAC ， ∴AEC ∆∽ACP ∆ ∴AC AEAP AC=,即2AC PA AE =⋅. 由（1）知ABP ∆≌ACF ∆， ∴∠BAP=∠CAF ， CF PB = ∴∠BAP+∠PAC=∠CAF+∠PAC∴∠PAF=∠BAC=60°，又∠APC ＝∠ABC ＝60°. ∴APF ∆是等边三角形 ∴AP=PF∴4PB PC PC CF PF PA +=+=== 在PAB ∆与CEP ∆中，又∠APB=∠EPC=60°， ∴PAB ∆∽CEP ∆ ∴PB PAPE PC=,即PB PC PA PE ⋅=⋅ 由（2）2AC PA AE =⋅，∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+= ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴()2222224133PB PC PA AC PA AB ⋅=-=-=-=因此PB 和PC 的长是方程2430x x --=的解．解这个方程，得11x =， 23x =． ∵PB<PB ，∴PB=11x =，PC=23x =， ∴PB 和PC 的长分别是1和3。

九年级数学上册圆几何综合综合测试卷(word含答案)

九年级数学上册圆几何综合综合测试卷（word 含答案）一、初三数学圆易错题压轴题（难）1．如图，在直角体系中,直线AB 交x 轴于点A(5,0),交y 轴于点B,AO 是⊙M 的直径,其半圆交AB 于点C,且AC=3.取BO 的中点D,连接CD 、MD 和OC ．（1）求证：CD 是⊙M 的切线；（2）二次函数的图象经过点D 、M 、A,其对称轴上有一动点P,连接PD 、PM,求△PDM 的周长最小时点P 的坐标；（3）在（2）的条件下,当△PDM 的周长最小时,抛物线上是否存在点Q ，使S △PDM =6S △QAM ？若存在，求出点Q 的坐标；若不存在，请说明理由.【答案】解：（1）证明：连接CM ，∵OA 为⊙M 直径，∴∠OCA=90°．∴∠OCB=90°． ∵D 为OB 中点，∴DC=DO ．∴∠DCO=∠DOC ． ∵MO=MC ，∴∠MCO=∠MOC ． ∴．又∵点C 在⊙M 上，∴DC 是⊙M 的切线．（2）∵A 点坐标（5，0），AC=3 ∴在Rt △ACO 中，．∴545(x )x 5)12152-=--（，∴，解得10OD 3=．又∵D 为OB 中点，∴15524+∴D 点坐标为（0，154)．连接AD ，设直线AD 的解析式为y=kx+b ，则有解得．∴直线AD 为．∵二次函数的图象过M （56，0)、A(5，0)， ∴抛物线对称轴x=154． ∵点M 、A 关于直线x=154对称，设直线AD 与直线x=154交于点P ， ∴PD+PM 为最小．又∵DM 为定长，∴满足条件的点P 为直线AD 与直线x=154的交点．当x=154时，45y (x )x 5)152=--（． ∴P 点的坐标为（154，56）．（3）存在． ∵，5y a(x )x 5)2=--（又由（2）知D （0，154)，P （154，56）， ∴由，得，解得y Q =±103．∵二次函数的图像过M(0，56)、A(5，0）， ∴设二次函数解析式为，又∵该图象过点D （0，154)，∴，解得a=512． ∴二次函数解析式为．又∵Q 点在抛物线上，且y Q =±103． ∴当y Q =103时，，解得x=1552-或x=1552+；当y Q =512-时，，解得x=154．∴点Q 的坐标为（15524-，103)，或（15524+，103)，或（154，512-）．【解析】试题分析：（1）连接CM ，可以得出CM=OM ，就有∠MOC=∠MCO ，由OA 为直径，就有∠ACO=90°，D 为OB 的中点，就有CD=OD ，∠DOC=∠DCO ，由∠DOC+∠MOC=90°就可以得出∠DCO+∠MCO=90°而得出结论．（2）根据条件可以得出2222OC OA AC 534=-=-=和OC OBtan OAC AC OA∠==，从而求出OB 的值，根据D 是OB 的中点就可以求出D 的坐标，由待定系数法就可以求出抛物线的解析式，求出对称轴，根据轴对称的性质连接AD 交对称轴于P ，先求出AD 的解析式就可以求出P 的坐标．（3）根据PDM DAM PAM S S S ∆∆∆=-，求出Q 的纵坐标，求出二次函数解析式即可求得横坐标．2．如图，以A （0，3）为圆心的圆与x 轴相切于坐标原点O ，与y 轴相交于点B ，弦BD 的延长线交x 轴的负半轴于点E ，且∠BEO ＝60°，AD 的延长线交x 轴于点C ．（1）分别求点E 、C 的坐标；（2）求经过A 、C 两点，且以过E 而平行于y 轴的直线为对称轴的抛物线的函数解析式；（3）设抛物线的对称轴与AC 的交点为M ，试判断以M 点为圆心，ME 为半径的圆与⊙A 的位置关系，并说明理由．【答案】（1）点C 的坐标为（－3，0）（2）2343333y x x =++3）⊙M 与⊙A 外切【解析】试题分析：（1）已知了A 点的坐标，即可得出圆的半径和直径，可在直角三角形BOE 中，根据∠BEO 和OB 的长求出OE 的长进而可求出E 点的坐标，同理可在直角三角形OAC 中求出C 点的坐标；（2）已知了对称轴的解析式，可据此求出C 点关于对称轴对称的点的坐标，然后根据此点坐标以及C ，A 的坐标用待定系数法即可求出抛物线的解析式；（3）两圆应该外切，由于直线DE ∥OB ，因此∠MED=∠ABD ，由于AB=AD ，那么∠ADB=∠ABD ，将相等的角进行置换后可得出∠MED=∠MDE ，即ME=MD ，因此两圆的圆心距AM=ME+AD ，即两圆的半径和，因此两圆外切.试题解析：（1）在Rt△EOB 中，3cot60232EO OB =⋅︒=⨯=， ∴点E 的坐标为（－2，0）．在Rt△COA 中，tan tan60333OC OA CAO OA =⋅∠=⋅︒=⨯=， ∴点C 的坐标为（－3，0）．（2）∵点C 关于对称轴2x =-对称的点的坐标为F （－1，0），点C 与点F （－1，0）都在抛物线上．设()()13y a x x =++，用()03A ，代入得()()30103a =++，∴33a =． ∴()()313y x x =++，即 2343333y x x =++．（3）⊙M 与⊙A 外切，证明如下： ∵ME ∥y 轴，∴MED B ∠=∠．∵B BDA MDE ∠=∠=∠， ∴MED MDE ∠=∠． ∴ME MD =．∵MA MD AD ME AD =+=+， ∴⊙M 与⊙A 外切．3．如图，已知直线AB 经过⊙O 上的点C ，并且OA ＝OB ，CA ＝CB ，（1）求证：直线AB 是⊙O 的切线；（2）OA ，OB 分别交⊙O 于点D ，E ，AO 的延长线交⊙O 于点F ，若AB ＝4AD ，求sin ∠CFE 的值．【答案】（1）见解析；（25 【解析】【分析】（1）根据等腰三角形性质得出OC⊥AB，根据切线的判定得出即可；（2）连接OC、DC，证△ADC∽△ACF，求出AF=4x，CF=2DC，根据勾股定理求出DC=355x，DF=3x，解直角三角形求出sin∠AFC，即可求出答案．【详解】（1）证明：连接OC，如图1，∵OA＝OB，AC＝BC，∴OC⊥AB，∵OC过O，∴直线AB是⊙O的切线；（2）解：连接OC、DC，如图2，∵AB＝4AD，∴设AD＝x，则AB＝4x，AC＝BC＝2x，∵DF为直径，∴∠DCF＝90°，∵OC⊥AB，∴∠ACO＝∠DCF＝90°，∴∠OCF＝∠ACD＝90°﹣∠DCO，∵OF＝OC，∴∠AFC＝∠OCF，∴∠ACD＝∠AFC，∵∠A＝∠A，∴△ADC∽△ACF，∴122 AC AD DC xAF AC CF x====，∴AF＝2AC＝4x，FC＝2DC，∵AD＝x，∴DF ＝4x ﹣x＝3x ，在Rt △DCF 中，（3x ）2＝DC 2+（2DC ）2，解得：DC ＝355x ， ∵OA ＝OB ，AC ＝BC ， ∴∠AOC ＝∠BOC ， ∴DC EC =， ∴∠CFE ＝∠AFC ，∴sin ∠CFE ＝sin ∠AFC ＝DC DF＝355535x x =．【点睛】本题考查了等腰三角形的性质，切线的判定，解直角三角形，圆心角、弧、弦之间的关系，相似三角形的性质和判定的应用，能综合运用知识点进行推理和计算是解此题的关键，难度偏大．4．如图，在△ABC 中，∠C=90°，∠CAB=30°，AB=10，点D 在线段AB 上，AD=2．点P ，Q 以相同的速度从D 点同时出发，点P 沿DB 方向运动，点Q 沿DA 方向到点A 后立刻以原速返回向点B 运动．以PQ 为直径构造⊙O ，过点P 作⊙O 的切线交折线AC ﹣CB 于点E ，将线段EP 绕点E 顺时针旋转60°得到EF ，过F 作FG ⊥EP 于G ，当P 运动到点B 时，Q 也停止运动，设DP=m ．（1）当2＜m≤8时，AP=，AQ=．（用m 的代数式表示）（2）当线段FG 长度达到最大时，求m 的值；（3）在点P ，Q 整个运动过程中，①当m 为何值时，⊙O 与△ABC 的一边相切？ ②直接写出点F 所经过的路径长是．（结果保留根号）【答案】（1）2+m ，m ﹣2;（2）m=5.5;（3）①当m=1或4或10433与△ABC 的边相切．②点F 1136572【解析】试题分析：（1）根据题意可得AP =2+m ，AQ =m −2.（2）如图1中在Rt △EFG 中, 30,90EFG A EGF ∠=∠=∠=，推出3cos30cos302FG EF PE EP =⋅=⋅=，所以当点E 与点C 重合时，PE 的值最大，求出此时EP 的长即可解决问题．（3）①当02t <≤ (Q 在往A 运动)时，如图2中，设O 切AC 于H ，连接OH .当28m <≤(Q 从A 向B 运动)时,则PQ =(2+m )−(m −2)=4，如图3中，设O 切AC 于H .连接OH .如图4中，设O 切BC 于N ，连接ON .分别求解即可．②如图5中,点F 的运动轨迹是F 1→F 2→B .分别求出122F F F B ，即可解决问题．试题解析：(1)当28m <≤时，AP =2+m ，AQ =m −2. 故答案为2+m ，m −2. (2)如图1中，在Rt △EFG 中, 30,90EFG A EGF ∠=∠=∠=，3cos30cos302FG EF PE EP ∴=⋅=⋅=， ∴当点E 与点C 重合时，PE 的值最大，易知此时53553AC BC EP AB ⨯⨯=== 3tan30(2)EP AP m =⋅=+ 533(2)23m ∴=+⋅ ∴m =5.5(3)①当02t <≤ (Q 在往A 运动)时，如图2中，设O 切AC 于H ，连接OH .则有AD =2DH =2， ∴DH =DQ =1，即m =1.当28m <≤(Q 从A 向B 运动)时,则PQ =(2+m )−(m −2)=4，如图3中，设O 切AC 于H .连接OH .则AO =2OH =4，AP =4+2=6， ∴2+m =6， ∴m =4. 如图4中，设O 切BC 于N ，连接ON .在Rt △OBN 中, 43sin60OB ON ==4310AO ∴=- 4312AP ∴=-432123m ∴+=-， 4310m ∴=-，综上所述,当m =1或4或4310-时，O 与△ABC 的边相切。

2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)

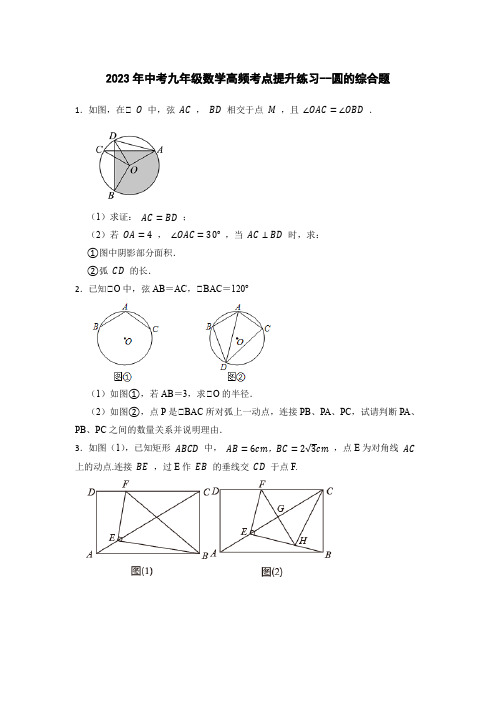
2023年中考九年级数学高频考点提升练习--圆的综合题1．如图，在⊙ O中，弦AC，BD相交于点M，且∠OAC=∠OBD．（1）求证：AC=BD；（2）若OA=4，∠OAC=30°，当AC⊥BD时，求：①图中阴影部分面积．②弧CD的长．2．已知⊙O中，弦AB＝AC，⊙BAC＝120°（1）如图①，若AB＝3，求⊙O的半径．（2）如图②，点P是⊙BAC所对弧上一动点，连接PB、PA、PC，试请判断PA、PB、PC之间的数量关系并说明理由．3．如图（1），已知矩形ABCD中，AB=6cm，BC=2√3cm，点E为对角线AC 上的动点.连接BE，过E作EB的垂线交CD于点F.（1）探索BE与EF的数量关系，并说明理由.（2）如图（2），过F作AC垂线交AC于点G，交EB于点H，连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动，设E的运动时间为ts.①是否存在t，使得H与B重合？若存在，求出t的值；若不存在，说明理由；②t为何值时，△CFH是等腰三角形；③当CG=GH时，求△CGH的面积.4．如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD＝CB，延长CD交BA的延长线于点E.（1）求证：CD是⊙O的切线；（2）求证：⊙C＝2⊙DBE.（3）若EA＝AO＝2，求图中阴影部分的面积.（结果保留π）5．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到该边所对顶点连线的平方，则称这个点为三角形该边的“好点”.如图1，⊙ABC中，点D 是BC边上一点，连结AD，若AD2=BD⋅CD，则称点D是⊙ABC中BC边上的“好点”.（1）如图2，⊙ABC的顶点是4×3网格图的格点，请仅用直尺画出AB边上的一个“好点”.（2）⊙ABC中，BC=9，tanB=43，tanC=23，点D是BC边上的“好点”，求线段BD的长.（3）如图3，⊙ABC是⊙O的内接三角形，OH⊙AB于点H，连结CH并延长交⊙O于点D.①求证：点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9，⊙ABD=90°，OH=6，请直接写出CHDH的值.6．如图，⊙O为等边⊙ABC的外接圆，半径为2，点D在劣弧上运动（不与点A，B 重合），连接DA，DB，DC.（1）求证：DC是⊙ADB的平分线；（2）设四边形ADBC的面积为S，线段DC的长为x，试用含x的代数式表示S；（3）若点M，N分别在线段CA，CB上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置，⊙DMN的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值.7．在⊙ABC中，D，E分别是⊙ABC两边的中点，如果弧DE（可以是劣弧、优弧或半圆）上的所有点都在⊙ABC的内部或边上，则称弧DE为⊙ABC的中内弧．例如，图1中弧DE是⊙ABC其中的某一条中内弧．（1）如图2，在边长为4 √3的等边⊙ABC中，D，E分别是AB，AC的中点．画出⊙ABC的最长的中内弧DE，并直接写出此时弧DE的长；（2）在平面直角坐标系中，已知点A（2 √3，6），B（0，0），C（t，0），在⊙ABC中，D，E分别是AB，AC的中点．①若t＝2 √3，求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围；②请写出一个t的值，使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值．8．如图，⊙O是⊙ABC的外接圆，AC是直径，过点O作OD⊙AB于点D，延长DO 交⊙O于点P，过点P作PE⊙AC于点E，作射线DE交BC的延长线于F点，连接PF．（1）若⊙POC=60°，AC=12，求劣弧PC的长；（结果保留π）（2）求证：OD=OE；（3）求证：PF是⊙O的切线．9．如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O.点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E.在射线CD上取点F，使DF=32CD，以DE，DF为邻边作矩形DEGF.设AQ=3x.（1）用关于x的代数式表示BQ=，DF=.（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长.（3）当点P在点A右侧时，作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长.10．如图，⊙ABC中，⊙ACB=90°，D是边AB上一点，且⊙A=2⊙DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．（1）求证：AB是⊙O的切线；（2）若CD的弦心距为1，BE=EO，求BD的长．11．已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM 在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持⊙ABP=90°不变，BP边与直线l相交于点P．（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；（2）请利用如图1所示的情形，求证：ABPB=OMBM；（3）若AO=2 √6，且当MO=2PO时，请直接写出AB和PB的长．12．（问题情境）如图①，小区A、B位于一条笔直的道路l的同侧，为了方便A，B两个小区居民投放垃圾，现在l上建一个垃圾分类站C，使得C与A，B的距离之比为2：1.（1）（初步研究）在线段AB上作出点C，使CACB=2.如图，做法如下：第一步：过点A作射线AM，以A为圆心，任意长为半径画弧，交AM于点P1；以P1为圆心，AP1长为半径画弧，交AM于点P2；以P2为圆心，AP1长为半径画弧，交AM于点P3.第二步：连接BP3，作∠AP2C=∠AP3B，交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.（2）（深入思考）如图，点C在线段AB上，点D在直线AB外，且DADB=CACB=2.求证：DC是∠ADB的平分线.（3）（问题解决）如图，已知点A，B和直线l，点C在线段AB上，且CACB=2.用直尺和圆规完成下列作图.（保留作图痕迹，不写作法）（⊙）在直线AB上作出点E（异于点C），使EAEB=2；（⊙）在直线l上作出点F，使FAFB=2.13．在矩形ABCD中，BC=2AB，点E是对角线AC上任意一点，过点E作AD的垂线分别交AD，BC于点F，G，作FH平行AC交CD于点H．（1）证明：EF=CH．（2）连结GH交AC于点K，若AE：CK=3，求AE：EK的值．（3）作⊙FGH的外接圆⊙O，且AB=1．①若⊙O与矩形的边相切时，求CH的长．②作点E关于GH的对称点E'，当E'落在⊙O上时，直接写出⊙FGH的面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

圆24.1.1—1.4综合训练
山东省东营市利津县虎滩中学马新华
一、选择题（本题共10小题，每题4分，共40分） 1．（改编）下列命题中，正确的个数是
⑴直径是弦，但弦不一定是直径 ⑵半圆是弧，但弧不一定是半圆
⑶圆周角等于圆心角的一半 ⑷一条弦把圆分成的两段弧中，至少有一段是优弧。

A ．1个
B ．2个
C ．3个
D ．4个
2． ⊙O 中，∠AOB ＝∠84°，则弦AB 所对的圆周角的度数为（）
A ．42°
B ．138°
C ．69°
D ．42°或138°
3．(原创)如图，⊙O 的直径CD 垂直于弦EF ，垂足为G ，若∠EOD=40°,则∠CDF 等于（）
A ．80°
B ． 70°
C ． 40°
D ． 20°
4．．(08长春中考试题)如图,AB 是⊙O 的直径,弦CD ⊥AB,垂足为E,如果AB=20,CD=16, 那么线
段OE 的长为（）
A 、10
B 、8
C 、6
D 、4
5．已知O 的半径为5cm ,弦AB ∥CD ,且6AB cm =，8CD cm =,则弦AB,CD 间的距离
为（）.
A ．1cm
B ．7cm
C ．5cm
D ．7cm 或1cm
6．如图24—A —4，AB 为⊙O 的直径，点C 在⊙O 上，若∠B=60°，则∠A 等
于（）
A ．80°
B ．50°
C ．40°
D ．30°
7．如图24—A —5，P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B ，CD 切⊙O
于点E ，分别交PA 、PB 于点C 、D ，若PA=5，则△PCD 的周长为（）
A ．5
B ．7
C ．8
D ．10
8．若粮仓顶部是圆锥形，且这个圆锥的底面直径为4m ，母线长为3m ，为防雨
需在粮仓顶部铺上油毡，则这块油毡的面积是（）
A．2
6m
B．2
6m
πC．2
12m D．2
12m
π
9．如图24—A—6，两个同心圆，大圆的弦AB与小圆相切于点P，
大圆的弦CD经过点P，且CD=13，PC=4，则两圆组成的圆环的面
积是（）
A．16πB．36πC．52πD．81π
10．已知在△ABC中，AB=AC=13，BC=10，那么△ABC的内切圆的半径为（）
A．
3
10
B．
5
12
C．2 D．3
11．如图24—A—7，两个半径都是4cm的圆外切于点C，一只蚂蚁由
点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长
度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006π
cm后才停下来，则蚂蚁停的那一个点为（）
A．D点 B．E点 C．F点 D．G点
二、填空题
12．如图24—A—8，在⊙O中，弦AB等于⊙O的半径，OC⊥AB交⊙O于点C，
则∠AOC= 。

13．如图24—A—9，AB、AC与⊙O相切于点B、C，∠A=50゜，P为⊙O上
异于B、C的一个动点，则∠BPC的度数为。

14．已知⊙O的半径为2，点P为⊙O外一点，OP长为3，那么以P为圆心且与
⊙O相切的圆的半径为。

15．一个圆锥的底面半径为3，高为4，则圆锥的侧面积是。

16．扇形的弧长为20πcm，面积为240πcm2，则扇形的半径为 cm。

17．如图24—A—10，半径为2的圆形纸片，沿半径OA、OB裁成1：3两部分，
用得到的扇形围成圆锥的侧面，则圆锥的底面半径分别为。

18．在Rt△ABC中，∠C=90゜，AC=5，BC=12，以C为圆心，R为半径作圆
与斜边AB相切，则R的值为。

19．已知等腰△ABC的三个顶点都在半径为5的⊙O上，如果底边BC的长为8，
那么BC边上的高为。

20．已知扇形的周长为20cm，面积为16cm2，那么扇形的半径为。

21．如图24—A—11，AB为半圆直径，O 为圆心，C为半圆上一点，
E是弧AC的中点，OE交弦AC于点D。

若AC=8cm，DE=2cm，则
OD的长为cm。

图24—A—6
图24—A—7
图24—A—8 图24—A—9 图24—A—10
图24—A—11
三、解答题本题共8小题，共48分）
22、（5分）如图，已知：AB交圆O于C、D，且AC＝BD.你认为OA＝OB吗？为什
么？
23．（5分）如图，AD、BC是⊙O的两条弦，且AD=BC，
求证：AB=CD。

6．（5分）如图，已知：⊙O的半径为5，弦AB长为8，弦BC∥OA，求AC长
7．（5分）（2008黄冈市）如图是“明清影视城”的圆弧形门，黄红同学到影视城游玩，很想知道这扇门的相关数据，于是她从景点管理人员处打听到：这个圆弧形门所在的圆与水平地面是相切的，AB=CD=20 cm，且AB，CD与水平地面都是垂直的．根据以上数据，请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少？
8．（6分）如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C
．若AB是⊙O的直径，D是BC的中点．
（1）试判断AB、AC之间的大小关系，并给出证明;
（2）在上述题设条件下，ΔABC还需满足什么条件，点E才一定是AC的中点？（直接
写出结论）
9．（6分）如图.某货船以20海里∕时的速度将一批重要物资由A处运往正西方向的B 处，经16h的航行达到，达到后必须立即卸货。

此时接到气象部门的通知，一台风中心正
以40海里∕时的速度由
A向北偏西60的方向移动，距台风中心200海里的圆形区域
（包括边界）均回受到影响。

问：
(1）.B处是否回受到台风的影响？请说明理由：
(2）.为避免受到台风的影响，该船应在多少小时内卸完货物？(供选用数据：
2 1.4,
3 1.7
≈≈）
10．（8分）如图，⊙O是△ABC的外接圆，AB为直径，
⌒
AC＝
⌒
CF，CD⊥AB于D，且交⊙O于G，AF交CD于E．
(1）求∠ACB的度数；
(2）求证：AE＝CE；
11．（改编）（8分）如图，ABC
△是⊙O的内接三角形，AC BC
=，D为⊙O中⌒AB上一点，延长DA至点E，使CE CD
=．
(1）求证：AE BD
=；
(2）若2
AD BD CD
+=，求证：AC BC
⊥．
A
B D C
E
O。