专题05:常用逻辑用语知识点和典型例题(解析版)-2022年高考数学一轮复习
集合与常用逻辑用语高考考点梳理及真题分类解析(2022年高考备考版)
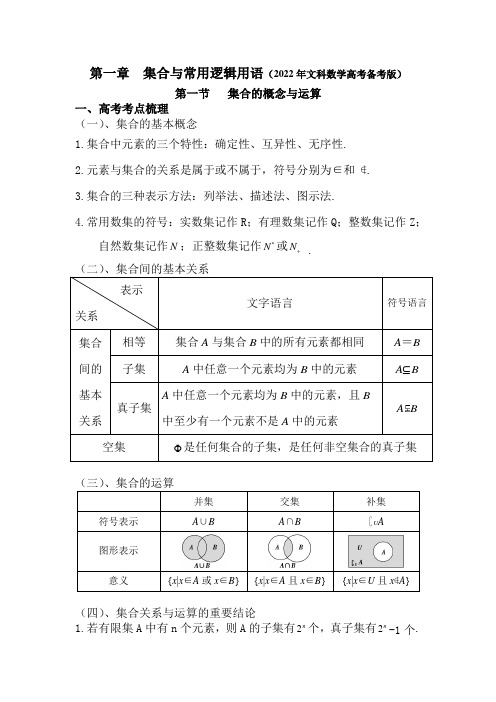
第一章集合与常用逻辑用语(2022年文科数学高考备考版)第一节集合的概念与运算一、高考考点梳理(一)、集合的基本概念1.集合中元素的三个特性:确定性、互异性、无序性.2.元素与集合的关系是属于或不属于,符号分别为∈和∉.3.集合的三种表示方法:列举法、描述法、图示法.4.常用数集的符号:实数集记作R;有理数集记作Q;整数集记作Z;自然数集记作N;正整数集记作*N或N .+A B(四)、集合关系与运算的重要结论1.若有限集A中有n个元素,则A的子集有个,真子集有-1个.n2n22.传递性:A ⊆B ,B ⊆C ,则A ⊆C .3.A ∪B =A ⇔B ⊆A ; A ∩B =A ⇔A ⊆B .4.∁U (A ∪B )=(∁U A )∩(∁U B );∁U (A ∩B )=(∁U A )∪(∁U B ) . 二、历年高考真题题型分类突破题型一 集合的基本概念【例1】(2021全国甲卷) 设集合{}{}1,3,5,7,9,27M N x x ==>,则MN =( )A. {}7,9B. {}5,7,9C. {}3,5,7,9D. {}1,3,5,7,9解析:∵7,2N ⎛⎫=+∞ ⎪⎝⎭,∴MN ={}5,7,9,故选:B .【例2】(2020全国Ⅰ卷)已知合集{}2340A x x x =--<,{}4,1,3,5B =-,则A B =( )A.{}4,1-B. {}1,5C. {}3,5D. {}1,3解析:∵{}2340A x x x =--<={ x |-1< x <4},∴A ∩B ={1,3},故选D . 【例3】(2013全国Ⅰ卷)已知集合A ={1,2,3,4},},|{2A n n x x B ∈==, 则=B A ( ).A .}4,1{B .}3,2{C .}16,9{D .}2,1{ 解析:∵B ={x |x =n 2,n ∈A }={1,4,9,16},∴A ∩B ={1,4},故选A .题型二 集合间的关系【例4】(2021全国乙卷) 已知全集{}1,2,3,4,5U =,集合{}{}1,2,3,4M N ==,则∁U (M ∪N ) =( ) A. {}5B. {}1,2C. {}3,4D. {}1,2,3,4解析:由题意可得:{}1,2,3,4MN =,则∁U (M ∪N ) ={}5. 故选:A .【例5】(2020全国Ⅲ卷) 已知集合{}1,2,3,5,7,11A =,{}|315B x x =<<,则A B中元素的个数为( )A. 2B. 3C. 4D. 5解析:根据题意,得A ∩B ={5,7,11},故选B .【例6】(2017全国Ⅰ卷)已知集合A ={}|2x x <,B ={}|320x x ->,则( ).A .AB =3|2x x ⎧⎫<⎨⎬⎩⎭ B .A B =∅ C .AB 3|2x x ⎧⎫=<⎨⎬⎩⎭D .AB=R解析:由B ={}|320x x ->,得B 3|2x x ⎧⎫=<⎨⎬⎩⎭,因为A ={}|2x x <,所以A B =3|2x x ⎧⎫<⎨⎬⎩⎭,故选A .题型三 集合的运算【例7】(2020全国Ⅱ卷)已知集合A={}3,x x x Z <∈,B={}1,x x x Z >∈,则A B =( )A. ∅B. {}3,2,2,3--C. {}2,0,2-D. {}2,2-解析:由以知,得A ={x |-3< x <3,x ∈Z},B ={x |x <-1或x >1,x ∈Z}, 所以A ∩B ={-2,2},故选D .【例8】(2019全国Ⅰ卷)已知集合U ={1,2,3,4,5,6,7},A ={2,3,4,5},B ={2,3,6,7},则B ∩∁U A =( ).A .{1,6}B .{1,7}C .{6,7}D .{1,6,7}解析:∵U ={1,2,3,4,5,6,7},A ={2,3,4,5},B ={2,3,6,7}, ∴∁U A ={1,6,7},则B ∩∁U A ={6,7},故选C .第二节 命题及其关系、充分条件与必要条件一、高考考点梳理 (一)、命题的定义可以判断真假用文字或符号表述的语句叫做命题。
常用逻辑用语讲义-高考数学一轮复习

常用逻辑用语充分条件与必要条件1、判断:当命题“若p则q”为真时,可表示为p⇒q,称p为q的充分条件,q是p的必要条件.事实上,与“p ⇒q”等价的逆否命题是“¬q⇒¬p”.它的意义是:若q不成立,则p一定不成立.这就是说,q对于p是必不可少的,所以说q是p的必要条件.例如:p:x>2;q:x>0.显然x∈p,则x∈q.等价于x∉q,则x∉p一定成立.2、充要条件:如果既有“p⇒q”,又有“q⇒p”,则称条件p是q成立的充要条件,或称条件q是p成立的充要条件,记作“p⇔q”.p与q互为充要条件.【练习】1.“x>1”是“x>2”的()A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2.已知a是实数,则“a<﹣1”是“”的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件3.若x,y∈R,则“x>y”的一个充分不必要条件可以是()A.|x|>|y| B.x2>y2C.D.2x﹣y>24.设x∈R,则“”是“x>3”的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件5.设a,b∈R,则“”是“a>1且b>1”的()A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件6.“x>1”是“x≥1”的()A.充分非必要条件 B.必要非充分条件C.充要条件 D.既非充分又非必要条件全称量词与特称量词、全称命题与特称命题【全称量词】:短语“对所有的”“对任意一个”在逻辑中通常叫做全称量词.符号:∀全称量词:对应日常语言中的“一切”、“任意的”、“所有的”、“凡是”、“任给”、“对每一个”等词,用符号“∀”表示.【全称命题】含有全称量词的命题.“对任意一个x∈M,有p(x)成立”简记成“∀x∈M,p(x)”.同一个全称命题、特称命题,由于自然语言的不同,可以有不同的表述方法,现列表如下命题全称命题∀x∈M,p(x)特称命题∃x0∈M,p(x0)表述方法①所有的x∈M,使p(x)成立①存在x0∈M,使p(x0)成立②对一切x∈M,使p(x)成立②至少有一个x0∈M,使p(x0)成立③对每一个x∈M,使p(x)成立③某些x∈M,使p(x)成立④对任给一个x∈M,使p(x)成立④存在某一个x0∈M,使p(x0)成立⑤若x∈M,则p(x)成立⑤有一个x0∈M,使p(x0)成立【存在量词】:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词.符号:∃特称命题:含有存在量词的命题.符号:“∃”.存在量词:对应日常语言中的“存在一个”、“至少有一个”、“有个”、“某个”、“有些”、“有的”等词,用符号“∃”表示.【特称命题】含有存在量词的命题.“∃x∈M,有p(x0)成立”简记成“∃x0∈M,p(x0)”.“存在一个”,“至少有一个”叫做存在量词.命题全称命题∀x∈M,p(x)特称命题∃x0∈M,p(x0)表述方法①所有的x∈M,使p(x)成立①存在x0∈M,使p(x0)成立②对一切x∈M,使p(x)成立②至少有一个x0∈M,使p(x0)成立③对每一个x∈M,使p(x)成立③某些x∈M,使p(x)成立④对任给一个x∈M,使p(x)成立④存在某一个x0∈M,使p(x0)成立⑤若x∈M,则p(x)成立⑤有一个x0∈M,使p(x0)成立【练习】1.下列语句不是全称量词命题的是()A.任何一个实数乘以零都等于零 B.自然数都是正整数C.高一(1)班绝大多数同学是团员 D.每一个实数都有大小2.下列命题含有全称量词的是()A.某些函数图象不过原点 B.实数的平方为正数C.方程x2+2x+5=0有实数解 D.素数中只有一个偶数3.已知命题“∀x∈[1,2],2x+x﹣a>0”为假命题,则实数a的取值范围是()A.x≤5 B.x≥6 C.x≤3 D.x≥34.若命题“∀x∈[﹣1,2],x2+1≥m”是真命题,则实数m的取值范围是()A.x≤0 B.x≤1 C.x≤2 D.x≤55.命题“∀x∈R,mx2﹣2mx+1>0”是假命题,则实数m的取值范围为()A.0≤m<1 B.m<0或m≥1 C.m≤0或m≥1 D.0<m<16.已知命题p:“∃x∈R,x2﹣ax+1<0”为假命题,则实数a的取值范围为()A.x≤2 B.2<x<2C.x≤2或x≥2 D.2≤x≤27.已知命题p:∃x∈R,使得ax2+2x+1<0成立为真命题,则实数a的取值范围是()A.(﹣∞,0] B.(﹣∞,1)C.[0,1)D.(0,1]命题的否定全称命题的否定一般地,对于含有一个量词的全称命题的否定,有下面的结论:全称命题p:∀x∈M,p(x)它的否命题¬p:∃x0∈M,¬p(x0).写全称命题的否定的方法:(1)更换量词,将全称量词换为存在量词,即将“任意”改为“存在”;(2)将结论否定,比如将“>”改为“≤”.值得注意的是,全称命题的否定的特称命题.特称命题的否定一般地,对于含有一个量词的特称命题的否定,有下面的结论:特称命题p:∃x0∈M,p(x0)它的否命题¬p:∀x∈M,¬p(x).写特称命题的否定的方法:(1)更换量词,将存在量词换为全称量词,即将“存在”改为“任意”;(2)将结论否定,比如将“>”改为“≤”.值得注意的是,特称命题的否定的全称命题.【练习】1.命题p:∃n∈N,n2≥2n,则命题p的否定为()A.∀n∈N,n2≤2n B.∃n∈N,n2≤2n C.∀n∈N,n2<2n D.∃n∈N,n2<2n2.命题“∀x>1,x2﹣x>0”的否定是()A.∃x0≤1,B.∀x>1,x2﹣x≤0C.∃x0>1,D.∀x≤1,x2﹣x>03.命题“∃x0∈R,使得”的否定为()A.B.∃x0∈R,使得C.D.∃x0∈R,使得4.命题“∀x∈R,x2>1﹣2x”的否定是()A.∀x∈R,x2<1﹣2x B.∀x∈R,x2≤1﹣2xC.∃x∈R,x2≤1﹣2x D.∃x∈R,x2<1﹣2x5.命题“∃a∈R,ax2+1=0有实数解”的否定是()A.∀a∈R,ax2+1≠0有实数解B.∃a∈R,ax2+1=0无实数解C.∀a∈R,ax2+1=0无实数解D.∃a∈R,ax2+1≠0有实数解四种命题(原命题、否命题、逆命题、逆否命题)常见词语的否定如下表所示:词语是一定是都是大于小于词语的否定不是一定不是不都是小于或等于大于或等于词语且必有一个至少有n个至多有一个所有x成立词语的否定或一个也没有至多有n﹣1个至少有两个存在一个x不成立【练习】1.下列语句是命题的是()A.0是偶数吗?B.这个数学问题真难啊!C.你好烦,出去!D.关于x的方程x2=1无解2.下列语句是命题的是()A.空集是任何集合的子集B.指数函数是增函数吗?C.x>15 D.2x﹣1<03.设m∈R,命题“若m≥0,则方程x2=m有实根”的逆否命题是()A.若方程x2=m有实根,则m≥0 B.若方程x2=m有实根,则m<0C.若方程x2=m没有实根,则m≥0 D.若方程x2=m没有实根,则m<04.命题“若x2+y2>2,则|x|>1或|y|>1”的否命题是()A.若x2+y2>2,则|x|≤1且|y|≤1 B.若x2+y2≤2,则|x|≤1或|y|≤1C.若x2+y2≤2,则|x|≤1且|y|≤1 D.若x2+y2>2,则|x|≤1或|y|≤15.“红豆生南国,春来发几枝?愿君多采撷,此物最相思!”这首《相思》是唐代山水田园诗人王维的作品,王维字摩诘,号摩诘居士.苏轼有云:“味摩诘之诗,诗中有画;观摩诘之画,画中有诗.”这首《相思》中,在当时的条件下,其中可以作为命题的诗句是()A.红豆生南国B.春来发几枝C.愿君多采撷D.此物最相思6.在原命题及其逆命题、否命题、逆否命题中,真命题的个数可以是()A.1或2或3或4 B.0或2或4 C.1或3 D.07.命题“若x=﹣3,则x2+2x﹣3=0”的逆否命题是()A.若x≠﹣3,则x2+2x﹣3≠0 B.若x=﹣3,则x2+2x﹣3≠0C.若x2+2x﹣3≠0,则x≠﹣3 D.若x2+2x﹣3≠0,则x=﹣38.已知原命题“若a=1,则(a﹣1)(a﹣2)=0”,那么原命题与其逆命题的真假情况是()A.原命题为真,逆命题为假 B.原命题为假,逆命题为真C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题9.若命题p的否命题为r,命题r的逆命题为s,p的逆命题为t,则s是t的()A.逆否命题B.逆命题C.否命题D.原命题逻辑联结词“或”、“且”、“非”【或】一般地,用连接词“或”把命题和命题连接起来,就得到一个新命题,记作pⅤq,读作“p或q”.规定:当p,q两个命题中有一个命题是真命题时,pⅤq是真命题;当p,q两个命题都是假命题时,pⅤq是假命题.【且】一般地,用连接词“且”把命题p和命题q连接起来,就得到一个新命题,记作p∧q读作“p且q”.规定:当p,q都是真命题时,p∧q是真命题;当p,q两个命题中有一个命题是假命题时,p∧q是假命题.“且”作为逻辑连接词,与生活用语中“既…”相同,表示两者都要满足的意思,在日常生活中经常用“和”,“与”代替.【非】一般地,对一个命题p全盘否定,就得到一个新命题,记作¬p,读作“非p”或“p的否定.规定:若p是真命题,则¬p必是假命题;若p是假命题,则¬p必是真命题.“非p”形式复合命题的真假与p的真假相反;“非p”形式复合命题的真假可以用下表表示:p¬p真假假真“非”是否定的意思,必须是只否定结论.“p或q”、“p且q”的否定分别是“非p且非q”和“非p或非q”,“都”的否定是“不都”.“等于”的否定是“不等于”,“大(小)于”的否定是“不大(小)于”,“所有”的否定是“某些”,“任意”的否定是“某个”,“至多有一个”的否定是“至少有两个”等等.必须注意与否命题的区别.【复合命题及其真假】若原命题P为真,则¬P必定为假,但否命题可真可假,与原命题的真假无关,否命题与逆命题是等价命题,同真同假.【练习】1.在一次跳伞训练中,甲.乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“两位学员都没有降落在指定范围”可表示为()A.(¬p)∨(¬q)B.p∨(¬q)C.p∨q D.(¬p)∧(¬q)2.命题“12既是4的倍数,又是3的倍数”的形式是()A.p∨q B.p∧q C.¬p D.简单命题3.设p:4是素数,q:4是偶数,则“4既不是素数,也不是偶数”可符号化为()A.¬p∨¬q B.p∧q C.¬p∧¬q D.¬p→¬q4.对于命题p,q,若p∧q是假命题,p∨¬q是假命题,则下列判断正确的是()A.p,q都是真命题B.p,q都是假命题C.p是真命题,q是假命题D.p是假命题,q是真命题5.已知是无理数,命题q:∃x∈R,x2<0,则为真命题的是()A.p∧q B.p∧¬q C.¬p∨q D.¬(p∨q)6.已知命题p:“若b<a,则”;命题q:“a=x2﹣x,b=x﹣2,则a>b”.则下列命题是真命题的是()A.p∧q B.(¬p)∧(¬q) C.p∨(¬q)D.(¬p)∨q7.已知p:∀x>0,x2+3x>0;q:∃x∈R,x2+1=0.则下列命题中,真命题是()A.¬p∧q B.¬p∨q C.p∧¬q D.p∧q8.已知p:﹣2<a<2,q:关于x的方程x2﹣x+a=0有实数根.(1)若q为真命题,求实数a的取值范围;(2)若p∨q为真命题,¬q为真命题,求实数a的取值范围.9.设p:(3﹣k)(1+k2)>0;q:关于x的方程x2﹣2kx+k=0无实根.(1)若q为真命题,求实数k的取值范围;(2)若p∧q是假命题,且p∨q是真命题,求实数k的取值范围.10.命题p:∀x∈R,x2﹣2ax+3a>0;命题q:∃x∈R,x2﹣2x+a<0.(1)若命题p为真命题,求实数a的取值范围;(2)若命题p,q至少有一个为真命题,求实数a的取值范围.。
常用逻辑用语+讲义-2023届高三数学一轮复习

常用逻辑用语考点1 命题及其关系1.命题“若4πα=,则1tan =α”的逆否命题是( ) A .若4πα≠,则1tan ≠α B .若4πα=,则1tan ≠αC .若1tan ≠α,则4πα≠ D .若1tan ≠α,则4πα=2.已知a ,b ,c ∈R ,命题“若a +b +c =3,则a 2+b 2+c 2≥3”的否命题是( )A .若a +b +c ≠3,则a 2+b 2+c 2<3B .若a +b +c =3,则a 2+b 2+c 2<3C .若a +b +c ≠3,则a 2+b 2+c 2≥3D .若a 2+b 2+c 2≥3,则a +b +c =33.给定下列命题:①若k >0,则方程x 2+2x -k =0有实数根; ②“若a >b ,则a +c >b +c ”的否命题;③“矩形的对角线相等”的逆命题;④“若xy =0,则x ,y 中至少有一个为0”的否命题.其中是真命题的序号是___________.4.【2020•新课标Ⅲ理16,5】关于函数f (x )=sin x +有如下四个命题:Ⅲf (x )的图象关于y 轴对称.Ⅲf (x )的图象关于原点对称.Ⅲf (x )的图象关于直线x =对称.Ⅲf (x )的最小值为2.其中所有真命题的序号是 .考点2 简单逻辑联结词1.若p 是真命题,q 是假命题,则( )A .p ∧q 是真命题B .p ∨q 是假命题C .p 是真命题D .q 是真命题2.下列选项正确的是( )A .若p ∨q 为真命题,则p ∧q 为真命题B .“x =5”是“x 2-4x -5=0”的充分不必要条件C .命题“若x <-1,则x 2-2x -3>0”的否定为:“若x ≥-1,则x 2-3x +2≤0”D .已知命题p :∃x ∈R ,使得x 2+x -1<0,则p :∃x ∈R ,使得x 2+x -1≥03.设命题p :函数y =sin2x 的最小正周期为π2,命题q :函数y =cos x 的图象关于直线x =π2对称.则下列判断正确的是( )A .p 为真B .q 为假C .p ∧q 为假D .p ∨q 为真 4.【2021乙卷】已知命题:,sin 1p x x ∃∈<R ﹔命题:q x ∀∈R ﹐||e 1x ≥,则下列命题中为真命题的是( )A .p q ∧B .p q ⌝∧C .p q ∧⌝D .()p q ⌝∨ 5.【2020全国Ⅱ卷文理16】设有下列四个命题:1p :两两相交且不过同一点的三条直线必在同一平面内.2p :过空间中任意三点有且仅有一个平面.3p :若空间两条直线不相交,则这两条直线平行.4p :若直线⊂l 平面α,直线⊥m 平面α,则l m ⊥. 则下述命题中所有真命题的序号是 .①41p p ∧ ②21p p ∧ ③32p p ∨⌝ ④ 43p p ⌝∨⌝考点3 全称量词与特称量词1.设命题p :n N ∃∈,22n n >,则p ⌝为( )A .2,2n n N n ∀∈>B .2,2n n N n ∃∈≤C .2,2n n N n ∀∈≤D .2,2n n N n ∃∈= 2.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p :(,),22x y D x y ∀∈+≥-,2p :(,),22x y D x y ∃∈+≥,3P :(,),23x y D x y ∀∈+≤,4p :(,),21x y D x y ∃∈+≤-.其中真命题是( ) A .2p ,3P B .1p ,4p C .1p ,2p D .1p ,3P3.命题“[)30,.0x x x ∀∈+∞+≥”的否定是( ) A .()30,.0x x x ∀∈+∞+< B .()3,0.0x x x ∀∈-∞+≥ C .[)30000,.0x x x ∃∈+∞+< D .[)30000,.0x x x ∃∈+∞+≥ 4.【2021乙卷】已知命题:,sin 1p x x ∃∈<R ﹔命题:q x ∀∈R ﹐||e 1x ≥,则下列命题中为真命题的是( )A .p q ∧B .p q ⌝∧C .p q ∧⌝D .()p q ⌝∨5.已知命题p :“∀x ∈[0,1],a ≥e x ”,命题q: “∃x ∈R ,x 2+4x +a =0”,若命题“p ∧q ” 是真命题,则实数a 的取值范围是( )A .(4,+∞)B .[1,4]C .[e ,4]D .(-∞,1]考点4 充分条件与必要条件1.设α,β为两个平面,则αⅢβ的充要条件是( )A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面2.已知空间中不过同一点的三条直线,,m n l ,则“,,m n l 在同一平面”是“,,m n l 两两相交”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.设a ∈R ,则“1a >”是“2a a >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.设x ∈R ,则“250x x -<”是“|1|1x -<”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.已知αβ∈R ,,则“存在k ∈Z ,使得π(1)k k αβ=+-”是“βαsin sin =”的() A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6.函数()f x 在0=x x 处导数存在,若()00p f x '=:,0:q x x =是()f x 的极值点,则()A .p 是q 的充分必要条件B .p 是q 的充分条件,但不是q 的必要条件C .p 是q 的必要条件,但不是q 的充分条件D .p 既不是q 的充分条件,也不是q 的必要条件7.下列命题中,真命题是( )A .∃x 0∈R ,0x e ≤0B .∀x ∈R,2x >x 2C .a +b =0的充要条件是a b =-1D .a >1,b >1是ab >1的充分条件8.下列说法正确的是( )A .函数f (x )=1x 在其定义域上是减函数B .两个三角形全等是这两个三角形面积相等的必要条件C .命题“∃x ∈R ,x 2+x +1>0”的否定是“∀x ∈R ,x 2+x +1<0”D .给定命题p ,q ,若p ∧q 是真命题,则p 是假命题。
高考数学一轮专项复习ppt课件(新高考用)-常用逻辑用语

故选:B
题型突破·考法探究
题型三:全称量词命题与存在量词命题的真假
【典例3-2】(2024·高三·北京通州·期中)下列命题中的假命题是(
A.∀ ∈ ,
1
2
)
1
2
B.∃ ∈ , >
>0
C.∀ ∈ ,2|| > 1
D.∃ ∈ ,tan > 1
【答案】C
则此时方程 2 + 2 + 1 = 0有两个负根,符合题意.
综上所述,为真命题时,的取值范围是 −∞, 1 .
若为真命题的一个必要不充分条件为 ≤ + 1,则 + 1 > 1, > 0.
题型突破·考法探究
题型二:根据充分必要条件求参数的取值范围
【变式2-2】已知集合 =
若“ ∈ ”是“ ∈ ”的必要非充分条件,则集合B是集合A的真子集,
− 1 ≥ −2
则
,且等号不能同时成立,解得−1 ≤ ≤ 3,
+1≤4
所以实数a的取值范围是 | − 1 ≤ ≤ 3 .
题型突破·考法探究
题型三:全称量词命题与存在量词命题的真假
【典例3-1】下列正确命题的个数为(
2 −2
≤ 3 + 2;解得 ≥ 3,符合题意;
、把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集
1
.
合之间的关系列出关于参数的不等式求解
在充分必要条件求解参数取值范围
③“ ∈ ”是“ ∈ ”的必要不充分条件时,当 = ∅,2 − > 3 + 2,得 < 3;
时,要注意端点能否能取到,容易出错.
高考数学一轮专项复习ppt课件-常用逻辑用语(通用版)

高考一轮总复习•数学
充分、必要条件的两种判断方法 (1)定义法:根据 p⇒q,q⇒p 进行判断. (2)集合法:根据 p,q 成立时对应的集合之间的包含关系进行判断.
第22页
高考一轮总复习•数学
第23页
对点练 2(2023·全国甲卷,理)“sin2α+sin2β=1”是“sin α+cos β=0”的( )
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
高考一轮总复习•数学
第19页
解析:方法一:甲:{an}为等差数列,设其首项为 a1,公差为 d, 则 Sn=na1+nn2-1d,Snn=a1+n-2 1d=d2n+a1-d2,nS+n+11-Snn=d2, 因此Snn为等差数列,则甲是乙的充分条件; 反之,乙:Snn为等差数列,即nS+n+11-Snn=nSn+n1-n+n+11Sn=nnann++1-1Sn为常数,设为 t, 即nnann++1-1Sn=t,则 Sn=nan+1-t·n(n+1),有 Sn-1=(n-1)an-t·n(n-1),n≥2, 此推导过程略显繁琐,等差数列的本质可从各个方面体现出来.(1)通项公式为一次函 数型. (2)前 n 项和为 n 的二次函数型且无常数项.
高考一轮总复习•数学
第26页
(2) 若 “x ∈ P” 是 “x ∈ S” 的 充 分 不 必 要 条 件 , 则
P
S
,
∴
1-m≤-2, 1+m>10
或
1-m<-2, 1+m≥10,
∴m≥9,则 m 的取值范围为[9,+∞).故答案为[9,+∞).
数形结合:S 理解为以 1 为中心,到 1 的距离小于或等于 m(m≥0 )的闭区间,只有当 m≥9
高考一轮总复习•数学
2024年高考数学一轮复习(新高考版) 第1章《常用逻辑用语》

第
二 部 分
探究核心题型
题型一 充分、必要条件的判定
例1
(1)(2023·淮北模拟)
“a>b>0”是“
a b
>1”的
A.充要条件
√B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
由 a>b>0,得ab>1,反之不成立, 如 a=-2,b=-1,满足ab>1,但是不满足 a>b>0, 故“a>b>0”是“ab>1”的充分不必要条件.
题型三 全称量词与存在量词
命题点1 含量词命题的否定 例3 (2022·漳州模拟)命题“∀a∈R,x2-ax+1=0有实数解”的否定是 A.∀a∈R,x2-ax+1=0无实数解
√B.∃a∈R,x2-ax+1=0无实数解
C.∀a∈R,x2-ax+1≠0有实数解 D.∃a∈R,x2-ax+1≠0有实数解
1 A.2
B.-12
3 C. 2
√D.-
3 2
因为“∃x∈-π3,π3,sin x<m”是假命题,
所以“∀x∈-π3,π3,m≤sin x”是真命题, 即 m≤sin x 对于∀x∈-π3,π3恒成立,所以 m≤(sin x)min,
因为 y=sin x 在-π3,π3上单调递增, 所以 x=-π3时,y=sin x 最小,其最小值为 y=sin-π3=-sin π3=- 23,
课时精练
第
一 部 分
落实主干知识
知识梳理
1.充分条件、必要条件与充要条件的概念
若p⇒q,则p是q的 充分 条件,q是p的 必要 条件
p是q的 充分不必要 条件
p⇒q且q⇏p
p是q的 必要不充分 条件
2022年高考数学(文)一轮复习文档:高考零距离1集合与常用逻辑用语 Word版含答案

集合与常用规律用语年份卷别具体考查内容及命题位置2022 甲卷集合的表示、集合的交集运算、一元二次不等式的解法·T1 乙卷集合的表示、集合的交集运算、一元二次不等式的解法·T1丙卷集合的表示、集合的补集运算·T12021 Ⅰ卷集合的表示、集合的交集运算·T1Ⅱ卷集合的表示、集合的并集运算、一元二次不等式的解法·T12022 Ⅰ卷集合的表示、集合的交集运算·T1Ⅱ卷集合的表示、集合的交集运算、一元二次方程的解法·T11.集合作为高考必考内容,多年来命题较稳定,多以选择题的形式在前3题的位置进行考查,难度较小,命题的热点照旧会集中在集合的运算上,常与简洁的一元二次不等式结合命题.2.高考对常用规律用语考查的频率较低,且命题点分散,其中含有量词的命题的否定、充分必要条件的推断需要关注,多结合函数、平面对量、三角函数、不等式、数列等学问命题.题示参数真题呈现考题溯源题示对比(2021·高考全国卷Ⅱ,T1)已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B=( )A.(-1,3) B.(-1,0)C.(0,2) D.(2,3)(2022·高考全国卷丙,T1)设集合A={0,2,4,6,8,10},B={4,8},则∁A B=( )A.{4,8} B.{0,2,6}C.{0,2,6,10} D.{0,2,4,6,8,10}(2022·高考全国卷乙,T1)设集合A={x|x2-4x+3<0},B={x|2x-3>0},则A∩B=( )A.⎝⎛⎭⎪⎫-3,-32B.⎝⎛⎭⎪⎫-3,32C.⎝⎛⎭⎪⎫1,32D.⎝⎛⎭⎪⎫32,3(2021·高考全国卷Ⅰ,T3)设命题p:∃n∈N,n2>2n,则¬p为( )A.∀n∈N,n2>2n B.∃n∈N,n2≤2nC.∀n∈N,n2≤2n D.∃n∈N,n2=2n题溯源(必修1 P8例5)设集合A={x|-1<x<2},集合B={x|1<x<3},求A∪B.题溯源(必修1 P11例8)设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求∁U A,∁U B.题溯源(1)(必修1 P11习题1.1A组T5(1))已知集合A={x|2x-3<3x},则有-3________A.(2)(必修5 P80习题3.2A组T4)已知集合A={x|x2-16<0},B={x|x2-4x+3>0},求A∪B.题溯源(选修11P26习题1.4A组T3(1))写出下列命题的否定:∀x∈N,x3>x2.题材评说(1)集合的考题多数源于教材,将教材中的问题用恰当的集合形式表示出来,依据交、并、补或子集的概念设置选项,从而将教材的原问题用美丽和谐的选择题呈现出来(2)特称命题或全称命题的否定,教材的例题和习题均可变为选择题作为考题,主要留意两个方面:第一,特定的否定形式;其次,四个选项的恰当设置1.(必修1 P11练习T4改编)已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则(∁U A)∩B=( )A.{1,3,5,6,7} B.{1,3,7}C .{5}D .{3,5,7} B (∁U A )∩B ={1,3,6,7}∩{1,3,5,7}={1,3,7},选B.2.(必修1 P12习题1.1A 组T4(3)改编)设A ={x ∈Z |-3<2x -1≤3},B ={x |3x ≥4-2x },则A ∩B =( ) A .{1,2} B .{2} C .{x |45≤x ≤2}D .{0,1}A A ={x ∈Z |-1<x ≤2}={0,1,2},B ={x |x ≥45},所以A ∩B ={1,2},选A.3.(必修1 P11练习T2改编)设A ={x |x 2-4x -5<0},B ={x |x 2<4},则A ∪B =( ) A .(-1,2) B .(-2,5) C .(2,5)D .(-2,-1)B A ={x |-1<x <5},B ={x |-2<x <2}, 所以A ∪B ={x |-2<x <5}.选B.4.(必修1 P83复习参考题B 组T1改编)设集合A ={y |y =log 2(|sin x |+1),x ∈R },B ={y |y =2cos x,x ∈R },则A ∩B =( )A .B .C .D .[12,1]D 由于|sin x |+1∈,所以A ={y |y =log 2(|sin x |+1),x ∈R }={y |0≤y ≤1}, 又cos x ∈,所以B ={y |y =2cos x,x ∈R }={y |12≤y ≤2},所以A ∩B =∩⎣⎢⎡⎦⎥⎤12,2=⎣⎢⎡⎦⎥⎤12,1,选D. 5.(选修11 P25例4(1)改编)对于命题p :∃x 0∈R ,x 20+2x 0+2≤0,则下列说法正确的是( ) A .¬p :∀x ∈R ,x 2+2x +2≤0是假命题 B .¬p :∀x ∈R ,x 2+2x +2>0是真命题 C .¬p :∃x 0∈R ,x 20+2x 0+2>0是真命题 D .¬p :∀x ∈R ,x 2+2x +2>0是假命题B ¬p :∀x ∈R ,x 2+2x +2>0,由于x 2+2x +2=(x +1)2+1>0对于一切x ∈R ,恒成立,故选B. 6.(选修11 P12练习T2(2)改编)已知条件p :x -3>0,条件q :(x -3)(x -4)≥0,则( ) A .p 是q 的充分条件 B .p 是¬q 的必要条件 C .¬p 是¬q 的充分条件 D .p 是q 的必要条件B 将命题p 、q 转化为用集合表示:p :A ={x |x -3>0}={x |x >3}.¬p :B ={x |x -3≤0}={x |x ≤3}.q :C ={x |(x -3)(x -4)≥0}={x |x ≤3或x ≥4},¬q :D ={x |(x -3)(x -4)<0}={x |3<x <4}. 明显,A 不是C 的子集,故A 错.D ⊆A ,即p 是¬q 的必要条件,故B 正确.B 不是D 的子集,故C 错,C 不是A 的子集,故D 错,所以选B.。
高考数学一轮复习常用逻辑用语

A .(-∞,-1]
B .[1,+∞)
C .[2,+∞)
D .(2,+∞)
[解析] (1)p:x2+x-6=0,即 x=2 或 x=-3,q:∵a≠0,∴x=1a, 由题意知 p 是 q 的必要不充分条件,则1a=2 或1a=-3,解得 a=12或 a= -13,故选 D .
(2)由x+3 1< 1,得xx- +21> 0,即(x+1)(x-2)> 0,解得 x< -1 或 x> 2.由 题意可得{x|x> k} {x|x< -1 或 x> 2},所以 k≥2,因此,实数 k 的取值范
第二节
常用逻辑用语
01
课前 自主、全面地落实基础
02
课堂 精细、多维地研习考法题点
第二节 常用逻辑用语
1.理解充分条件、必要条件、充要条件的意义. 2.理解判定定理与充分条件的关系,性质定理与必要条件的关系,
理解数学定义与充要条件的关系. 3.理解全称量词命题与存在量词命题的意义,能正确对两种命题进
“x>y”的
()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:C
2.(苏教版必修①P 31·例 1 改编)在△ABC 中,“sin A=21”是“A=π6”的 ()
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
答案:C 3.(苏教版必修①P47·T10改编)若命题“∀x∈R,x2+1>m”是真命题,
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
[解析] (1)由 sin x=1,得 x=2kπ+π2(k∈Z ),则 cos2kπ+π2=cosπ2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题5:常用逻辑用语知识点和典型例题(解析版)一.知识点回顾:1、命题:可以判断真假的语句叫命题;逻辑联结词:“或”“且”“非”这些词就叫做逻辑联结词;简单命题:不含逻辑联结词的命题;复合命题:由简单命题与逻辑联结词构成的命题.常用小写的拉丁字母p ,q ,r ,s ,……表示命题.1.给出下列语句:①二次函数是偶函数吗?②2>2;③sin2 =1;④x 2-4x +4=0.其中是命题的有( )A .1个B .2个C .3个D .4个 【答案】B【分析】利用命题的定义判断即可【详解】解:只有②和③是命题,语句①是疑问句,语句④含有变量x ,不能判断真假. 故选:B .2.“红豆生南国,春来发几枝?愿君多采撷,此物最相思!”这首《相思》是唐代山水田田园诗人王维的作品,王维字摩诘,号摩诘居士,苏轼有云:“味摩诘之诗,诗中有画?观摩诘之画,画中有诗,”这首诗中,在当时的条件下,可以作为命题的是( ) A .红豆生常国B .春来发几枝C .愿君多采撷?D .此物最相思【答案】A【分析】根据命题的定义判断可得出结论.【详解】对于A 选项,“红豆生南国”是陈述句,所述事件在唐代是事实,所以,本句是命题; 对于B 选项,“春来发几支”是疑问句,不是命题;对于C 选项,“愿君多采撷”是祈使句,不是命题;对于D 选项,“此物最相思”是感叹句,不是命题.故选:A.2、四种命题及其相互关系四种命题的真假性之间的关系:⑴ 两个命题互为逆否命题,它们有相同的真假性;⑵两个命题为互逆命题或互否命题,它们的真假性没有关系.3.在命题“若4a π=,则tan 1α=”的原命题、逆命题、否命题、逆否命题中,正确命题的个数是( )A .2B .0C .3D .4 【答案】A【分析】根据原命题与其逆否命题同真假,逆命题与否命题同真假可得答案.【详解】原命题:若4a π=,则tan 1α=,正确;所以其逆否命题也正确;逆命题:若tan 1α=,则4a π=,不正确,因为由tan 1α=也可能推出54πα=.故否命题也不正确. 故在原命题、逆命题、否命题、逆否命题中,正确命题的个数是2个.故选:A4.下列四个命题①若()f x 是余弦函数,则()f x 是周期函数;②若()f x 不是余弦函数,则()f x 不是周期函数;③若()f x 是周期函数,则()f x 是余弦函数:④若()f x 不是周期函数,则()f x 不是余弦函数.其中真命题是( )A .①④B .①③C .②③D .③④【答案】A【分析】先利用三角函数的周期性,判断①②;再利用原命题与逆否命题具有相同的真假性判断即可.【详解】周期函数有正弦函数,余弦函数,正切函数等,所以①正确,②不正确;③为②的逆否命题,所以③不正确;④为①的逆否命题,所以④正确;故选:A.5.命题“若a >﹣3,则a >﹣6”以及它的逆命题、否命题、逆否命题中,假命题的个数为( )A .1B .2C .3D .4 【答案】B【分析】根据四种命题的关系即可判断.【详解】在命题的四种形式中原命题和逆否命题互为逆否命题,同真同假,否命题和逆命题互为逆否题同真同假.∵命题“若3a >-,则6a >-”为真命题;∴命题的逆否命题为真命题,逆命题: “若6a >-,则3a >-”是假命题,∴命题的否命题为假命题,故选:B.6.命题“若0m >,则方程20x x m +-=有实根”及它的逆命题、否命题、逆否命题中,真命题的个数为( )A .0B .1C .2D .4【答案】C【分析】利用原命题与其逆否命题同真同假可判断真命题的个数.【详解】当0m >时,140m ∆=+>,故方程20x x m +-=有实根,故原命题为真命题, 所以逆否命题也为真命题.逆命题为:若方程20x x m +-=有实根,则0m >. 取14m =-,则20x x m +-=有实根12-,当104m =-<,故逆命题为假命题, 所以否命题为假命题,故答案为:C.7.证明若222x y +=,则2x y +≤时,可以转化为证明( )A .若2x y +≤,则222x y +=B .若2x y +>,则222x y +≠C .若222x y +≠,则2x y +>D .若2x y +≤,则222x y +≤【答案】B【分析】根据原命题与逆否命题的真假性相同即可得正确答案.【详解】命题若222x y +=,则2x y +≤的逆否命题为若2x y +>,则222x y +≠,所以证明若222x y +=,则2x y +≤时,可以转化为证明若2x y +>,则222x y +≠, 故选:B8.命题“若x +2y =9,则x =3且y =3”及其逆命题、否命题和逆否命题中,真命题的个数为( )A .1B .2C .3D .4 【答案】B【分析】先求出其逆命题,再分别判断原命题与逆命题的真假,逆命题与否命题同真同假,原命题与逆否命题同真同假,即可得出结果.【详解】逆命题为“若x =3且y =3,则x +2y =9”,它为真命题,所以否命题也为真命题;原命题“若x +2y =9,则x =3且y =3”,其中x =1且y =4,也满足题意,故为假命题,所以它的逆否命题也为假命题,真命题的个数为2,故答案为:B.【点睛】本题考查四种命题之间的关系,属于基础题.3、复合命题⑴复合命题有三种形式:p 或q (p q ∨);p 且q (p q ∧);非p (p ⌝).⑵复合命题的真假判断“p 或q ”形式复合命题的真假判断方法:全假为假;“p 且q ”形式复合命题的真假判断方法:全真为真;“非p ”形式复合命题的真假判断方法:真假相对.9.对命题p :A ∅=∅,命题q :A A ⋃∅=,下列说法正确的是( ) A .p 且q 为真B .p 或q 为假C .非p 为真D .非q 为真【答案】A【分析】先判断p ,q 的真假,再判断有逻辑连接词或且非的命题的真假.【详解】 p 真,q 真,p 且q 为真.故选A.【点睛】或:有真则真;且:有假则假;非:真假相反.10.有两个命题:命题p :正方形的四个角相等,命题q :正方形的四条边相等.则下列判断错误的是( )A .新命题“p 且q ”是真命题B .新命题“p 或q ”是真命题C .新命题“非p ”是假命题D .新命题“p 或q ”是假命题【答案】D【分析】先判断两命题的真假,再由且或非命题真假的定义,即可得出结果.【详解】因为命题p :正方形的四个角相等;是真命题,所以非p 是假命题;命题q :正方形的四条边相等;是真命题,所以非q 是假命题;所以“p 且q ”是真命题,“p 或q ”是真命题,即ABC 都正确,D 错.故选:D.11.已知命题“p q ∨”为真命题,“p ⌝”为真命题,则( )A .p 为假命题,q 为真命题B .p 为真命题,q 为真命题C .p 为真命题,q 为假命题D .p 为假命题,q 为假命题 【答案】A【分析】根据复合命题的真假表即可得出结果.【详解】若“p ⌝”为真命题,则p 为假命题,又“p q ∨”为真命题,则,p q 至少有一个是真命题,所以q 为真命题,即p 为假命题,q 为真命题.故选:A12.设命题p :若21x =,则1x =;命题q :若x y =,则sin sin x y =,判断命题“p ⌝”、“p q ∧”、“p q ∨”为假命题的个数为( )A .0B .1C .2D .3【答案】B【分析】先判断命题p 与命题q 的真假,然后判断“p ⌝”、“p q ∧”、“p q ∨”的真假.【详解】命题p :若21x =,则1x =±,故p 为假命题,p ⌝为真;命题q :若x y =,则sin sin x y =成立,故q 为真命题,所以p q ∧为假命题,p q ∨为真命题.故选:B.4、全称量词与存在量词⑴全称量词与全称命题短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“∀”表示.含有全称量词的命题,叫做全称命题.⑵存在量词与特称命题短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“∃”表示.含有存在量词的命题,叫做特称命题.⑶全称命题与特称命题的符号表示及否定①全称命题p :,()x p x ∀∈M ,它的否定p ⌝:00,().x p x ∃∈M ⌝全称命题的否定是特称命题.②特称命题p :00,(),x p x ∃∈M ,它的否定p ⌝:,().x p x ∀∈M ⌝特称命题的否定是全称命题.13.已知命题:p x R ∀∈,2104x x -+,则p ⌝( )A .21,04x x x ∃∈-+R B .21,04x x x ∃∈-+>R C .21,04x x x ∀∈-+>R D .21,04x x x ∀∈-+<R 【答案】B【分析】 根据全称命题的否定直接写出答案.【详解】命题p 为全称命题,根据全称命题的否定为特称命题,可得:p ⌝: 21,04x x x ∃∈-+>R 故选:B【点睛】全称量词命题的否定是特称(存在)量词命题,特称(存在)量词命题的否定是全称量词命题.14.命题“3200010x R x x ∃∈-+>,”的否定是( )A .3210x R x ∀∈-+≤,xB .3210x R x x ∀∈-+>,C .3200010x R x x ∃∈-+≤,D .不存在3200010x R x x ∈-+≤, 【答案】A【分析】根据命题的否定的定义判断.【详解】特称命题的否定是全称命题.命题“3200010x R x x ∃∈-+>,”的否定是:3210x R x ∀∈-+≤,x .故选:A .15.下列命题是特称命题的是( )①有一个实数a ,a 不能取对数;②所有不等式的解集A ,都有A ⊆R ;③有些向量方向不定;④矩形都是平行四边形.A .①③B .②④C .①②D .③④ 【答案】A【分析】找出命题中含有的量词,根据量词的特征即可判断.【详解】①中含有存在量词“有一个”;②中含有全称量词“所有”;③中含有存在量词“有些”;④中含有存在量词“都是”.故①③是特称命题.故选:A.16.命题“2,0∈≥∀x R x ”的否定是( )A .2,0x R x ∃∈≥B .2,0x R x ∀∈<C .2,0x R x ∃∈<D .2,0x R x ∃∈≤【答案】C【分析】利用全称命题的否定分析解答.【详解】因为全称命题的否定是特称命题,所以命题:x R ∀∈,20x ≥的否定是:x R ∃∈,20x <.故选:C5、充分条件、必要条件与充要条件⑴、一般地,如果已知p q ⇒,那么就说:p 是q 的充分条件,q 是p 的必要条件; 若p q ⇔,则p 是q 的充分必要条件,简称充要条件.⑵、充分条件,必要条件与充要条件主要用来区分命题的条件p 与结论q 之间的关系: Ⅰ、从逻辑推理关系上看:①若p q ⇒,则p 是q 充分条件,q 是p 的必要条件;②若p q ⇒,但q p ,则p 是q 充分而不必要条件;③若p q ,但q p ⇒,则p 是q 必要而不充分条件;④若p q ⇒且q p ⇒,则p 是q 的充要条件;⑤若p q 且q p ,则p 是q 的既不充分也不必要条件. Ⅱ、从集合与集合之间的关系上看:已知{A x x =满足条件}p ,{B x x =满足条件}q : A B ⊆,则p 是q 充分条件; ②若B A ⊆,则p 是q 必要条件;③若A B ,则p 是q 充分而不必要条件;④若B A ,则p 是q 必要而不充分条件;⑤若A B =,则p 是q 的充要条件;⑥若A B ⊄且B A ⊄,则p 是q 的既不充分也不必要条件.17.1943年19岁的曹火星在平西根据地进行抗日宣传工作,他以切身经历创作了歌曲《没有共产党就没有中国》,后毛泽东主席将歌曲改名为《没有共产党就没有新中国》.2021年是中国共产党建党100周年,仅从逻辑学角度来看,“没有共产党就没有新中国”这句歌词中体现了“有共产党”是“有新中国”的( )A .充分条件B .必要条件C .充要条件D .既不充分也不必要条件 【答案】B【分析】改写为逆否命题,可得结论.【详解】从逻辑学角度,命题“没有共产党就没有新中国”的逆否命题是“有了新中国就有了共产党”,因此“有共产党”是“有新中国”的必要条件,故选:B .18.ABC 中,A ,B ,C 是ABC 的内角,则“3A π=”是“1cos 2A =”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】C【分析】根据充要条件的定义分析可得答案.【详解】若3A π=,则1cos 2A =成立,所以“3A π=”是“1cos 2A =”的充分条件,若1cos 2A =,因为(0,)A π∈,所以3A π=,所以“3A π=”是“1cos 2A =”的必要条件, 所以“3A π=”是“1cos 2A =”的充分必要条件, 故选:C .19.设,,αβγ为三个不同的平面,若αβ⊥,则“//γβ是“αγ⊥”的( ) A .充分不必要条件B .充要条件C .必要不充分条件D .既不充分也不必要条件 【答案】A【分析】利用充分条件和必要条件的定义判断,即可得正确答案.【详解】因为αβ⊥,//γβ,则αγ⊥,所以由αβ⊥,//γβ可以得出αγ⊥,若αβ⊥,αγ⊥,则γ与β可能相交或平行,所以αβ⊥,αγ⊥,得不出//γβ,所以若αβ⊥,则“//γβ是“αγ⊥”的充分不必要条件,故选:A20.若,a b ∈R ,使||||6a b +>成立的一个充分不必要条件是( ) A .6a b +≥B .6a ≥C .6b <-D .||3a ≥且3b ≥ 【答案】C【分析】利用不等式的性质以及充分条件、必要条件的定义逐一判断即可.【详解】A ,3+36≥,不满足6a b +> ;B ,660a b =≥=,,不满足6a b +> ;C ,由6b <-可得6a b +>,反之,6a b +>,得不到6b <-,如2,5a b ==-.D ,33≥,33≥,不满足6a b +>.故选:C21.伟人毛泽东的《清平乐•六盘山》传颂至今,“天高云淡,望断南飞雁.不到长城非好汉,屈指行程二万,六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?”现在许多人前往长城游玩时,经常会用“不到长城非好汉”来勉励自己,由此推断,“到长城”是“为好汉”的( )A .充分条件B .必要条件C .充要条件D .既不充分也不必要条件【答案】B【分析】根据充分条件和必要条件的定义进行判断即可.【详解】解:设p ⌝为不到长城,推出q ⌝非好汉,即p q ⌝⇒⌝,则q p ⇒,即好汉⇒到长城,故“到长城”是“好汉”的必要条件,故选:B .22.2020年2月11日,世界卫生组织将新型冠状病毒感染的肺炎命名为COVID -19(新冠肺炎)新冠肺炎,患者症状是发热、干咳、浑身乏力等外部表征.“新冠肺炎患者”是“患者表现为发热、干咳、浑身乏力”的( )已知该患者不是无症状感染者.............A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】A【分析】根据充分必要条件的定义判断.【详解】新冠肺炎患者症状是发热、干咳、浑身乏力等外部表征,充分的同,但有发热、干咳、浑身乏力等外部表征的不一定是新冠肺炎患者,不必要,即为充分不必要条件.故选:A .。
