两个同方向同频率简谐运动合成
合集下载
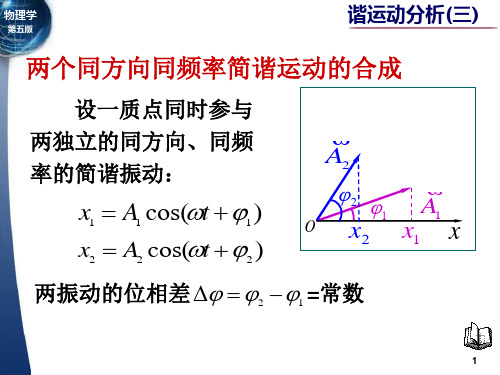
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
(2)相位差 (2k 1) π(k 0,1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
(1)相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0,1, ) 加强
(2)相位差
2
1
(2k 1) π
(k 0,1, )
A A A
1
2
减弱
(3)一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气(室温为 20C)中来 回摆动. 摆线长l 1.0 m,摆锤是半径r 5.0103 m 的铅球.求(1)摆动周期;(2)振幅减小 10%所需的时间;(3)能量减小10%所需 的时间;(4)从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
第4章-振动合成

两个频率比为1:2的简谐运动的合成
x1 A1 cos( t 1 )
x x1 x2 A1 ( t 1 ) A2 cos(2 t 2 )
x
x1
2T
x2
T
x
t
谐振分析*
x = 4A (sinω t
x
T
A
π
t
+
1 3sin3ω t
+
1 5 sin5ω
t)
x
合成后
x
A2 x y= A1
合振动振幅为 合振动为谐振动
A = A1 + A
2
2 2
r
A A cos t
2 1 2 2
2. 2 1 或 2k 1 2 2 x A1 cos( t 1 )
y
y A2 cos( t 2 ) A2 sin( t 1 )
2
F0 k , 2 , f 0 m m m
d x dx 2 2 0 x f 0 cos t dt dt 2
方程的解:
2
2 x A0 e t cos 0 2 t 0 A cost
稳定后的振动表达式:
x A cost
A
C
N
A AN
R
2
A1
A2
A3
N A 2 R sin 2 a 2 R sin 2 N a sin 2 A
sin
( N 1)
2
N 1 2
x A cos(t )
例1 . 两个同方向的简谐振动曲线(如图所示) 1、求合振动的振幅。 x x (t ) 2、求合振动的振动方程。 A1 1 解: A
简谐振动的合成

0 < ∆ϕ < π
质点沿顺时针方向运动
π < ∆ϕ < 2π 质点沿逆时针方向运动
说明:任何一个直线简谐振动, 说明:任何一个直线简谐振动,椭圆运动或匀速 圆周运动都可分解为两个相互垂直的简谐振动. 圆周运动都可分解为两个相互垂直的简谐振动
上页 下页 返回 结束
第九章 振 动
用旋转矢量描绘振动合成图
(1) ϕ2 − ϕ1 = 0或2π
A2 y= x A1
y
A2
o
A1
x
时刻t 质点离开平衡位置的位移(合振动) 时刻 质点离开平衡位置的位移(合振动)
2 r = x2 + y 2 = A12 + A2 cos(ωt + ϕ )
2 2 A = A1 + A2
——合振动也是谐振动 合振动也是谐振动
上页 下页 返回 结束
上页 下页 返回 结束
第九章 振 动
Acosϕ = A1 cosϕ1 + A2 cosϕ2
令
Asinϕ = A1 sinϕ1 + A2 sinϕ2
A = A12 + A22 + 2A1 A2 cos( 2 −ϕ1 ) ϕ
A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
上页
下页
返回
结束
第九章 振 动
两相 互垂直同 频率不同 相位差简 谐运动的 合成图
上页
下页
返回
结束
第九章 振 动பைடு நூலகம்
§9.4.4 互相垂直不同频率简谐振动的合成·李萨如图形 互相垂直不同频率简谐振动的合成 李萨如图形
92简谐运动的叠加

/ 2
第七章 振动与波动
24
物理学
利用旋转矢量合成
/2
y
7
8
6
y
7
6
8
5
5
1
4
4
2 3
1x
2 3
4
3 2
5
1x
6
8
7
第七章 振动与波动
25
物理学
用旋转矢量描绘振动合成图
第七章 振动与波动
26
物理学 (3) π
4y
8
1
7
6 2
5
3 4
y
8
7
1
6 5
2
x
3 4
4
3 2
5
1x
6
8
合振动轨迹方程
x A1
2
y A2
2
2xy
cos(2
A1 A2
1
)
sin
2 (2
1
)
物理学
作 业: 9-17
第七章 振动与波动
35
x x1 x2
x A1 cos(t 1) A2 cos(t 2 )
采用旋转矢量图解法合成合振动
第七章 振动与波动
3
物理学
设一质点同步参加 两独立旳同方向、同频 率旳简谐振动:
x1
A1
cos(t
1
)
x A cos(t )
2
2
2
A2
2 1
O x2
A1
x1 x
两振动旳位相差
2
且方向相同步为t = 0,将该方向定为x轴正
向):
A2
A w1
ω2t
第七章 振动与波动
24
物理学
利用旋转矢量合成
/2
y
7
8
6
y
7
6
8
5
5
1
4
4
2 3
1x
2 3
4
3 2
5
1x
6
8
7
第七章 振动与波动
25
物理学
用旋转矢量描绘振动合成图
第七章 振动与波动
26
物理学 (3) π
4y
8
1
7
6 2
5
3 4
y
8
7
1
6 5
2
x
3 4
4
3 2
5
1x
6
8
合振动轨迹方程
x A1
2
y A2
2
2xy
cos(2
A1 A2
1
)
sin
2 (2
1
)
物理学
作 业: 9-17
第七章 振动与波动
35
x x1 x2
x A1 cos(t 1) A2 cos(t 2 )
采用旋转矢量图解法合成合振动
第七章 振动与波动
3
物理学
设一质点同步参加 两独立旳同方向、同频 率旳简谐振动:
x1
A1
cos(t
1
)
x A cos(t )
2
2
2
A2
2 1
O x2
A1
x1 x
两振动旳位相差
2
且方向相同步为t = 0,将该方向定为x轴正
向):
A2
A w1
ω2t
Ch6-2 简谐运动的合成
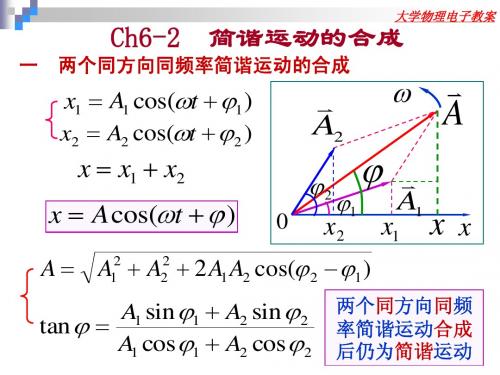
A = A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 )
A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
两个同方向同 两个同方向同频 率简谐运动合成 率简谐运动合成 后仍为简谐 简谐运动 后仍为简谐运动
大学物理电子教案
A = A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) ± ± 1)相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0 , 1, 2,L)
大学物理电子教案
x1 = A1 cos ω1t = A1 cos 2π ν 1t x2 = A2 cos ω 2t = A2 cos 2π ν 2t
讨论
x = x1 + x2
A1 = A2 , ν 2 − ν 1 << ν 1 + ν 2 的情况
方法一
x = x1 + x 2 = A1 cos 2π ν 1t + A2 cos 2π ν 2 t
π y = A2 cos(ωt + ) 2
A2 y
x = A1 cos ωt
o
A1
x
大学物理电子教案
用 旋 转 矢 量 描 绘 振 动 合 成 图
大学物理电子教案
两 相 互 垂 直 同 频 率 不 同 相 位 差
简 谐 运 动 的 合 成 图
大学物理电子教案
五
两相互垂直不同频率的简谐运动的合成 李 萨 如 图
讨论
2 1 2 2
x
o ϕ A
x
o
T
A = A1 + A2 x = ( A1 + A2 ) cos( ω t + ϕ ) ϕ = ϕ 2 = ϕ1 + 2 k π
6-2简谐振动的叠加

5
讨论:1. 2 1 2kπ k 0,1,2,
A A1 A2
A
A1
A2
合振幅最大,振动加强
2.
2 1 (2k 1)π k 0,1,2, A2 A A1 A2 A1 A 合振幅减小,振动减弱
3. 一般情况 为任意值
§7-2 简谐振动的叠加
一、同一直线上两个同频率简谐振动的合成 设有两个同频率的简谐振动 x1 A1 cos( t 1 ) x2 A2 cos( t 2 )
合振动 x x1 x2 A1 cos( t 1 ) A2 cos( t 2 )
A1 sin 1 A2 sin 2 合振动的初相位为: arctan A1 cos 1 A2 cos 2
。
3 0.05sin 0.06sin 5 5 arctan 3 0.05cos 0.06 cos 5 5 6812' 或 24812'
248°12′位于第三象限不合题意, 故知合振动的初相位
(1)
(2)
18
x cost cos sin t sin 改写为 A y cos t cos sint sin B
(3) (4)
以cos 乘以(3)式,cos 乘以(4)式,后相减得
x y cos cos sin t sin( ) A B
x1 a cost x2 a cos(t 0 ) x3 a cos(t 20 ) xN a cos[t ( N 1)0 ]
求它们的合振动的振幅和初相。 解:采用旋转矢量法可使问题得到简化,从而避开繁 琐的三角函数运算。 根据矢量合成法则,N个简谐振动对应的旋转矢量 的合成如下图所示:
8-5简谐运动的合成
(1)相位差 2k π (k 0,1,)
A A1 A2
相互加强
(2)相位差 (2k 1) π (k 0,1,)
A A1 A2
(3)一般情况
相互削弱
A1 A2 A A1 A2
第八章 机械振5 动
8-5 简谐运动的合成
思考
例 图中所画的是两个简谐振动的振动曲线. 若这 两个简谐振动可叠加,则合成的余弦振动的初相为
arctan11rad
第八章 机械振8 动
O A1
O
A2
A
T t
A A1 A2
2 1 2kπ
x ( A1 A2 ) cos(t )
第八章 机械振3 动
8-5 简谐运动的合成
A A12 A22 2A1A2 cos(2 1)
(2)相位差 2 1 (2k 1)π (k 0,1, )
tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
第八章 机械振2 动
8-5 简谐运动的合成
讨论 A A12 A22 2A1A2 cos(2 1) (1)相位差 2 1 2kπ (k 0,1, 2,)
xx
8-5 简谐运动的合成
两个同方向同频率简 当 t 0时
谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )
x x1 x2
A2
2 1
O x20
A1
x10
A x Acos(t )
两个同方向、同频率 简谐运动的合振动仍是简 谐运动,其频率与分振动
(A)3π / 2
大学物理第五章5-4 一维简谐运动的合成 拍现象
x A cos(t )
O
1 A1
2
3 A2
x
多个同方向同频率简谐运动合成仍为简谐运动
第五章 机械振动
xN A0 cos[t ( N 1) ]
讨 论
(1) 2kπ
x1 A0 cost x2 A0 cos(t ) x3 A0 cos(t 2 )
x1 A1 cost x ( A2 A1 ) cos( t π) x2 A2 cos( t π )
x
x
O
2
A1
O
A A1 A2 2
T
t
A2
第五章 机械振动
A
5 – 4 一维简谐运动的合成 拍现象
物理学教程 (第二版)
A
A A 2 A1 A2 cos( 2 1 )
第五章 机械振动
5 – 4 一维简谐运动的合成 拍现象 方法二 旋转矢量合成法
物理学教程 (第二版)
(2 1 )t (2 1 )
1 A1
2t 2
A2 2
A
2 1
1t 1
2 1
x
O
2 2
x2
x1
x
1 2 0
2 π ( 2 1 )t
第五章 机械振动
5 – 4 一维简谐运动的合成 拍现象 * 二 多个同方向同频率简谐运动的合成
物理学教程 (第二版)
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
xn An cos(t n )
A A 3
x x1 x2 xn
O
1 A1
2
3 A2
x
多个同方向同频率简谐运动合成仍为简谐运动
第五章 机械振动
xN A0 cos[t ( N 1) ]
讨 论
(1) 2kπ
x1 A0 cost x2 A0 cos(t ) x3 A0 cos(t 2 )
x1 A1 cost x ( A2 A1 ) cos( t π) x2 A2 cos( t π )
x
x
O
2
A1
O
A A1 A2 2
T
t
A2
第五章 机械振动
A
5 – 4 一维简谐运动的合成 拍现象
物理学教程 (第二版)
A
A A 2 A1 A2 cos( 2 1 )
第五章 机械振动
5 – 4 一维简谐运动的合成 拍现象 方法二 旋转矢量合成法
物理学教程 (第二版)
(2 1 )t (2 1 )
1 A1
2t 2
A2 2
A
2 1
1t 1
2 1
x
O
2 2
x2
x1
x
1 2 0
2 π ( 2 1 )t
第五章 机械振动
5 – 4 一维简谐运动的合成 拍现象 * 二 多个同方向同频率简谐运动的合成
物理学教程 (第二版)
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
xn An cos(t n )
A A 3
x x1 x2 xn
谐振动分析(三)两个同方向同频率简谐运动的合成共36页文档
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
谐振动分析(三)两个同方向同频率简 谐运动的合成
6
、
露
凝
无
游
氛
,天Βιβλιοθήκη 高风景澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
36
4-2 两个同方向同频率简谐运动的合成
A2 2
A
1
A1
X
10
2
6
例 求两个同方向同频率的简谐振动的合振幅
电 子 工 程 学 院 杨 小
π π π 2 1 ( ) 3 6 2 2 A A12 A2 2 A1 A2 cos( 2 1 ) A2
x1 (3 10 m) cos(t π 6) 2 x2 (4 10 m) cos(t π 3)
A 2 A1
A A1 A2 合振幅最大。 A1 A2 时,
2 1 (2k 1) k 0,1,2, 电讨论二: A 子 A | A1 A2 | 合振幅最小。 工 A0 当 A1 A2时, 程 学 A2 k 讨论三: 一般情况为 2 1 院
两个同方向同频 率简谐运动合成 后仍为简谐运动
A1 sin 1 A2 sin 2 tan 杨 A1 cos 1 A2 cos 2
3
2 A A12 A2 2 A1 A2 cos( 2 1 )
讨论一: 2 1 2k
当
k 0,1,2,
2
( SI)
电 子 工 程 学 院 杨 小
A2
Hale Waihona Puke A1X5
例 两个同方向同频率的简谐振动,其合振动的振幅 为 20cm,与第一个简谐振动的相位差为 1 / 6 若第一个简谐振动的振幅为 10 3cm 17.3cm ,则第 二个简谐振动的振幅为______________ cm ,第一、二 两个简谐振动的相位差 1 2 为____________. 电 子 工 程 学 院 杨 小
杨 小
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合振动频率
振动频率 (1 2 ) 2
振幅
A
2 A1 cos2 π 2
1
2
t
Amax 2A1 Amin 0
第九章 振 动
16
物理学
第五版
9-5 简谐运动的合成
方法二:旋转矢量合成法
(2 1)t (2 1)
2t 2
2 A2
1t 1 o
x2
N
0
(1) 2kπ
讨 (k 0,1,2,)
论 (2) N 2k ' π
(k ' kN, k ' 1,2,)
i A4 A5
O A6
A0
A3
A2
A1
x
第九章 振 动
12
物理学
第五版 一般情况下
x x1 x2 xn
后仍为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5 简谐运动的合成
(1)相位差
2
1
2k π
(k
0,1, 2,)
x
x
o
o
A1
A2
A
T
t
A A1 A2 x (A1 A2 )cos(t )
合成结果为相互加强
第九章 振 动
3
物理学
第五版
9-5 简谐运动的合成
简谐运动
第九章 振 动
11
例 物理学 第五版
9-5 简谐运动的合成
x A cost
1
0
x A cos(t )
2
0
x3 A0cos(t 2)
o
A1
A2
A3
A4
A5
A
x
A Ai NA0
x A cos[t (N 1)]
x x1 x2
讨论
A1
A2
,
2
1
1
2
的情况
第九章 振 动
15
物理学
第五版
9-5 简谐运动的合成
方法一
x x1 x2 A1 cos2 π1t A2 cos2 π2t
x (2A1 cos2 π
2
2
1 t)cos2 π
2
2
1t
振幅部分
y2 A22
1
x A cost
y
1
A
cos(t
π)
2
2
y
A2
o A1 x
第九章 振 动
8
物理学
第五版
9-5 简谐运动的合成
用旋转矢量描绘振动合成图
第九章 振 动
9
物理学
第五版
两相 互垂直同 频率不同 相位差简 谐运动的 合成图
9-5 简谐运动的合成
第九章 振 动
10
物理学
第五版
9-5 简谐运动的合成
A2
o
x
A1
1
x2 x1
x
1t 2t 2 1
cost x1 x2
A
1 2
2
第九章 振 动
18
质点运动轨迹 (椭圆方程)
x2 A12
y2 A22
2xy A1 A2
cos(2
1 )
sin2 (2
1 )
第九章 振 动
6
物理学
第五版
9-5 简谐运动的合成
讨 论
x2 A12
y2 A22
2xy A1 A2
cos(2
1 )
sin2 (2
y
1 )
(1)2 1 0或 2π
y A2 x A1
(2)2
1
π
y A2 x A
1
A2 A1
ox
y
A2
o A1 x
第九章 振 动
7
物理学
第五版
9-5 简谐运动的合成
讨 论
x2 A12
y2 A22
2xy A1 A2
cos(2
1 )
sin2 (2
1 )
(3)2
1
π
2
x2 A12
第五版
9-5 简谐运动的合成
x A cos(t )
A
A2 1
A2 2
2A1 A2
cos(2
1 )
x x1 x2
A
x tan
A1
sin
1
A2
sin2
A1 cos1 A2 cos2
A2
2
1
A1
O x2 x1 x
两个同方向同频率简谐运动合成
A A A
1
2
加强
(2)相位差
2
1
(2k 1) π
(k 0,1,)
A A A
1
2
减弱
(3)一般情况
A A A A A
1
2
1
2
第九章 振 动
5
物理学
第五版
9-5 简谐运动的合成
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
y A2 cos(t 2 )
x Acos(t )
A Ax2 Ay2 arctg Ay
Ax
9-5 简谐运动的合成
A
A3
3
A2 2
o 1 A1
x
Ax A1 cos1 A2 cos2 ...... An cosn
Ay A1 sin 1 A2 sin 2 ...... An sin n
*三 多个同方向同频率简谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )
xn
An
cos(t
n
)
x x1 x2 xn
x Acos(t )
A
A3 3 Nhomakorabea
A2 2
o 1 A1
x
多个同方向同频率简谐运动合成仍为
物理学
第五版
9-5 简谐运动的合成
一 两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动:
x1
A1
cos(t
1
)
x2
A2
cos(t
2
)
A2
2 1
A1
O x2 x1 x
合位移 x x1 x2 可用旋转矢量法求出
第九章 振 动
1
物理学
(2)相位差
2
1
(2k
1)
π(k
0 , 1,
)
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A A )cos(t )
2
1
合成结果为相互减弱
第九章 振 动
4
物理学
第五版
9-5 简谐运动的合成
小结
(1)相位差 2 1 2k π (k 0,1,)
1 2 0
A
1
A1
x1
2 1
x
x
2 π(2 1)t
第九章 振 动
17
物理学
第五版
9-5 简谐运动的合成
振幅 A A1 2(1 cos)
2 A1 cos( 2
1
2
t)
拍频 2 1
振动圆频率
(2 1)t
2
A
第九章 振 动
13
物理学
第五版
四
的合成
9-5 简谐运动的合成
两个同方向不同频率简谐运动
第九章 振 动
14
物理学
第五版
9-5 简谐运动的合成
频率较大而频率之差很小的两个同方 向简谐运动的合成,其合振动的振幅时而 加强时而减弱的现象叫拍.
x1 A1 cos1t A1 cos2π1t x2 A2 cos2t A2 cos2π2t
