材料力学第七章弯曲剪应力
合集下载
材料力学弯曲剪应力
,max
S
* z ,max
Izd
FS,max
Iz S*
z ,max
d
75103 N 47.73 102m 12.5 103m
12.6 106 Pa 12.6 MPa
第15页/共68页
例题 4-13
2. 求ta ta
其中:
FS
,max
S
* za
Izd
S
* za
166
mm
21
mm
560 mm 2
思考题: 试通过分析说明,图a中
所示上、下翼缘左半部分 和右半部分横截面上与腹 板横截面上的切应力指向 是正确的,即它们构成了 “切应力流”。
第12页/共68页
例题 4-13
由56a号工字钢制成的简支梁如图a所示,试求
梁的横截面上的最大切应力tmax和同一横截面上腹 板上a点处(图b)的切应力t a 。不计梁的自重。
3 2
FS bh
第4页/共68页
2. 工字形截面梁 (1) 腹板上的切应力
t
FS
S
* z
Izd
其中
Sz*
b
h 2
2
h 2
y d
h 2
y
y
2
b
2
h
d 2
h 2
2
y
2
第5页/共68页
可见腹板上的切应力在与中性轴z垂直的方向 按二次抛物线规律变化。
第6页/共68页
(2) 在腹板与翼缘交界处:
第10页/共68页
F* N2
自由边 t1 t1
A* F* dx
N1
u
根据 d FS t可1 得d x出
材料力学-第七章弯曲剪应力
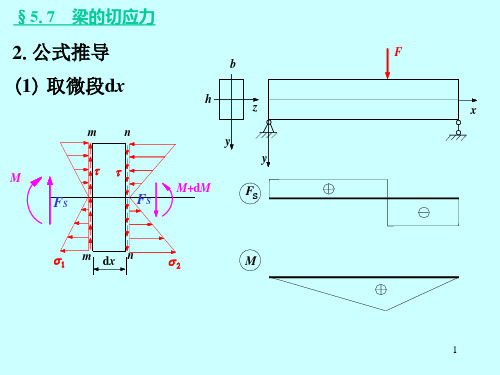
§5.7 梁的切应力
2.公式推导 (1) 取微段dx
mn
M
tt
FS
FS
b
h
z
y y
M+dM
FS
s1 m dx n
s2
M
F x
1
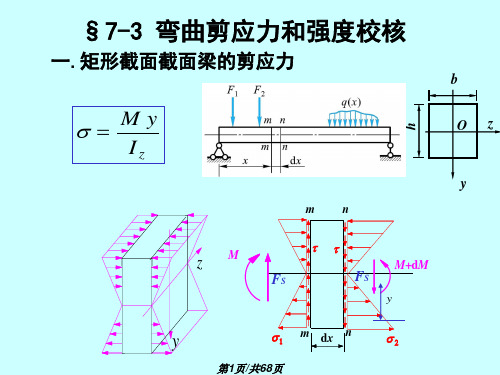
§7-3 弯曲剪应力和强度校核
一.矩形截面截面梁的剪应力
b
s My
Iz
mn
h
Oz y
zM
y
tt
M+dM
FS
FS
y
s1 m dx n
s2
2
假设
在hb的情况下
1.t的方向都与 FS 平行 2.t 沿宽度均布。
8.6106 Pa 8.6 MPa
17
例题 4-13
腹板上切应力沿高度的变化规律如图所示。
tmax
18
3. 薄壁环形截面梁 薄壁环形截面梁在竖直平面
内弯曲时,其横截面上切应力 的特征如图a所示:
(1) 由于d <<r0,故认为切应
力t 的大小和方向沿壁厚 无变
化; (2) 由于梁的内、外壁上无切
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
4
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS ( h 2 y 2 )
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A
*
2.公式推导 (1) 取微段dx
mn
M
tt
FS
FS
b
h
z
y y
M+dM
FS
s1 m dx n
s2
M
F x
1
§7-3 弯曲剪应力和强度校核
一.矩形截面截面梁的剪应力
b
s My
Iz
mn
h
Oz y
zM
y
tt
M+dM
FS
FS
y
s1 m dx n
s2
2
假设
在hb的情况下
1.t的方向都与 FS 平行 2.t 沿宽度均布。
8.6106 Pa 8.6 MPa
17
例题 4-13
腹板上切应力沿高度的变化规律如图所示。
tmax
18
3. 薄壁环形截面梁 薄壁环形截面梁在竖直平面
内弯曲时,其横截面上切应力 的特征如图a所示:
(1) 由于d <<r0,故认为切应
力t 的大小和方向沿壁厚 无变
化; (2) 由于梁的内、外壁上无切
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
4
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS ( h 2 y 2 )
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A
*
《弯曲剪应力》课件

研究方法:目前,弯曲剪应力的研究方法主要包括理论分析、实验研究和数值模拟等。
研究趋势:未来,弯曲剪应力的研究将更加注重多学科交叉、多尺度研究,以及与工程实 践的结合。
应用前景:弯曲剪应力的研究在工程领域具有广泛的应用前景,如结构设计、材料选择、 疲劳寿命预测等。
弯曲剪应力研究的重要成果与突破
添加项标题
弯曲剪应力的应用:弯曲剪应力在工程设计中具有重要意义,如 桥梁、建筑等结构设计中需要考虑弯曲剪应力的影响。
03
弯曲剪应力的作用
弯曲剪应力对材料的影响
弯曲剪应力会导致材料产生变形和断裂 弯曲剪应力的大小和方向会影响材料的强度和刚度 弯曲剪应力对材料的疲劳寿命有重要影响 弯曲剪应力对材料的塑性变形和弹性变形有影响
单击此处添加副标题
弯曲剪应力
汇报人:
目录
01 02 03 04 05 06
添加目录项标题 弯曲剪应力的概念 弯曲剪应力的作用 弯曲剪应力的应用 弯曲剪应力的研究进展 弯曲剪应力的未来展望
01
添加目录项标题
02
弯曲剪应力的概念
剪应力的定义
剪应力:物体在受到剪切力作 用时,在剪切面上产生的应力
剪切力:作用在物体表面上的 力,使物体产生剪切变形
添加标题
添加标题
添加标题
添加标题
20世纪初,英国科学家泰勒对弯 曲剪应力进行了深入研究,提出 了泰勒公式
21世纪初,中国科学家钱伟长对 弯曲剪应力进行了深入研究,提 出了钱伟长公式
弯曲剪应力研究的现状与趋势
研究现状:弯曲剪应力的研究已经取得了一定的成果,包括理论分析、实验研究和数值模 拟等方面。
弯曲剪应力在智能结构中的应用: 提高结构的稳定性和可靠性,降 低维护成本
研究趋势:未来,弯曲剪应力的研究将更加注重多学科交叉、多尺度研究,以及与工程实 践的结合。
应用前景:弯曲剪应力的研究在工程领域具有广泛的应用前景,如结构设计、材料选择、 疲劳寿命预测等。
弯曲剪应力研究的重要成果与突破
添加项标题
弯曲剪应力的应用:弯曲剪应力在工程设计中具有重要意义,如 桥梁、建筑等结构设计中需要考虑弯曲剪应力的影响。
03
弯曲剪应力的作用
弯曲剪应力对材料的影响
弯曲剪应力会导致材料产生变形和断裂 弯曲剪应力的大小和方向会影响材料的强度和刚度 弯曲剪应力对材料的疲劳寿命有重要影响 弯曲剪应力对材料的塑性变形和弹性变形有影响
单击此处添加副标题
弯曲剪应力
汇报人:
目录
01 02 03 04 05 06
添加目录项标题 弯曲剪应力的概念 弯曲剪应力的作用 弯曲剪应力的应用 弯曲剪应力的研究进展 弯曲剪应力的未来展望
01
添加目录项标题
02
弯曲剪应力的概念
剪应力的定义
剪应力:物体在受到剪切力作 用时,在剪切面上产生的应力
剪切力:作用在物体表面上的 力,使物体产生剪切变形
添加标题
添加标题
添加标题
添加标题
20世纪初,英国科学家泰勒对弯 曲剪应力进行了深入研究,提出 了泰勒公式
21世纪初,中国科学家钱伟长对 弯曲剪应力进行了深入研究,提 出了钱伟长公式
弯曲剪应力研究的现状与趋势
研究现状:弯曲剪应力的研究已经取得了一定的成果,包括理论分析、实验研究和数值模 拟等方面。
弯曲剪应力在智能结构中的应用: 提高结构的稳定性和可靠性,降 低维护成本
工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析,都需要求出应力的极值, 无论是强度分析还是刚度分析,都需要求出应力的极值,为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向, 到构件内最大应力的位置和方向,需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合,称为一点的 受力构件内一点处所有方位截面上应力的集合,称为一点的 研究一点的应力状态时, 应力状态 。研究一点的应力状态时,往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定: 主应力符号按代数值的大小规定:
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0
材料力学第七章弯曲剪应力
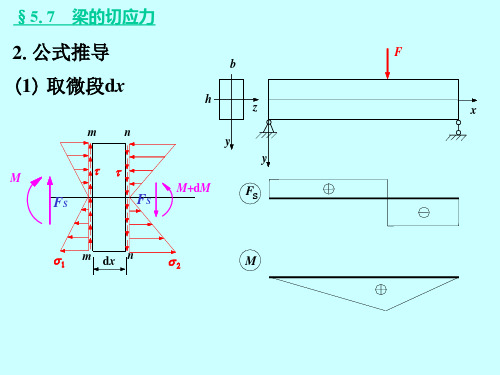
腹板负担了截面上的绝大部分剪力,翼缘负担了 截面上的大部分弯矩。
对于标准工字钢梁:
t max
*
F SS zmax Izb
FS
b
Iz
/
S* Z max
在翼板上:
FN I
A* sⅠdA
My dA
I A* z
FN
M Iz
ydA
A*
M Iz
Sz*
FN II
A* (s Ⅱ)dA
(M dM )
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS
h2 (
y2)
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A*
y* C
b
h
y
y
h 2
y
2
2
b 2
h2 4
y2
用剪应力为[τ],求螺栓的最小直径?
解:叠梁承载时,每
F
梁都有自己的中性层
L
FS
F
-FL
M
h 2
1.梁的最大正应力:
h 2
b
s max
1 2
M
max
W
其中:
W
b( h )2 2
bh2
6 24
s max
M max 2W
12FL bh2
对于标准工字钢梁:
t max
*
F SS zmax Izb
FS
b
Iz
/
S* Z max
在翼板上:
FN I
A* sⅠdA
My dA
I A* z
FN
M Iz
ydA
A*
M Iz
Sz*
FN II
A* (s Ⅱ)dA
(M dM )
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS
h2 (
y2)
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A*
y* C
b
h
y
y
h 2
y
2
2
b 2
h2 4
y2
用剪应力为[τ],求螺栓的最小直径?
解:叠梁承载时,每
F
梁都有自己的中性层
L
FS
F
-FL
M
h 2
1.梁的最大正应力:
h 2
b
s max
1 2
M
max
W
其中:
W
b( h )2 2
bh2
6 24
s max
M max 2W
12FL bh2
材料力学第七章 应力状态

主平面的方位:
tan
2a0
2 xy x
y
主应力与主平面的对应关系: max 与切应力的交点同象限
例题:一点处的平面应力状态如图所示。
已知 x 60MPa, xy 30MPa, y 40MPa, a 30。
试求(1)a 斜面上的应力; (2)主应力、主平面; (3)绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解:(1)a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下,任意两个垂直面上,其σ的和为一常数。
在二向应力状态下,任意两个垂直面上,其σ 的和为
一常数。
证明: a
x y
弯曲应力(剪应力6月9日)(1)
[1 12
16
283
16
28
(14
13)2 ]
[1 12
8 103
18 10
(19
13)2 ]
26200cm4
Wz
Iz ym a x
26200 (28 13)
1748cm3
(3)正应力校核
max
M Wz
1.2 105 1748 106
1.0 1.04 1.12 1.57 2.30
(四)切应力强度条件
max
(
FQ Sz,max
I z
)max
[
]
对于等宽度截面, m ax发生在中性轴上;对于宽度变化的截面,
m ax不一定发生在中性轴上。
在进行梁的强度计算时,需注意以下问题: (1)对于细长梁的弯曲变形,正应力的强度条件是主要的,剪应
S
* z
:y以外面积对中性轴的静矩
I z :整个截面对中性轴的惯性矩
b:y处的宽度
c
yc
y
z h
b
对于矩形:
S* z
A*
yc
b(h 2
y) [ y
h 2
2
y
]
b (h2 24
y2)
弯曲应力/弯曲时的剪应力
而
Iz
1 bh3 12
6FQ bh3
( h2 4
y2)
力的强度条件是次要的。但对于较粗短的梁,当集中力较大 时,截面上的剪力较大而弯矩较小,或是薄壁截面梁时,也 需要较核剪应力强度。
弯曲应力-材料力学
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
另外,根据不同的弯曲形式和受力情 况,还可以采用其他计算公式来求解 弯曲应力,如均布载荷下的简支梁、 集中载荷下的悬臂梁等。
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
弯曲应力可能导致材料发生弯曲变形,影响结构的稳定性和精度。
弯曲应力对材料刚度的影响
弯曲应力对材料的刚度有影响,材料的刚度随着弯曲应力的增大而 减小。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
弯曲应力
材料的韧性和强度都会影响其弯曲应力的大小和分布。韧性好的材料能够更好地分散和 吸收弯曲应力,而高强度的材料则能够承受更大的弯曲应力而不发生断裂。
材料韧性、强度与弯曲应力的关系
韧性
是指材料在受到外力作用时吸收能量的能力。韧性好的材料能够吸收更多的能量,从而 减少因弯曲应力而产生的脆性断裂。
强度
剪切应力的分布
剪切应力在材料截面的边缘最大,向中性轴方向 逐渐减小。
3
剪切应力和弯曲应力的关系
剪切应力和弯曲应力共同作用,影响梁的承载能 力和稳定性,在设计时需要考虑两者的相互作用。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
材料力学第07章应力状态与应变状态分析
以上由单元体公式
应力圆(原变换)
下面寻求: 由应力圆
单元体公式(逆变换)
只有这样,应力圆才能与公式等价
换句话,单元体与应力圆是否有一一对应关系?
为什么说有这种对应关系?
DE R sin[180o ( 2 20 )] R sin( 2 20 )
( R cos 20 ) sin 2 ( R cos 20 )cos 2
2
cos2
xy
sin 2
同理:
x
y
2
sin 2
xy
cos2
n
Ox
图2
二、极值应力
令:d
d
0
x
y
sin202 xycos200
由此得两个驻点:
01、(
01
2
)和两个极值:
tg20
2 xy x
y
y
mm
ax in
x
y ±(x
2
y
2
)2
2 xy
0 0极值正应力就是主应力 !
y
O
x
七、主单元体、主平面、主应力:
y
y
主单元体(Principal bidy):
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
A
材料力学教程-7.弯曲变形
数据处理
根据需要,对数据进行计算、 绘图等处理,以便更好地理解 和分析实验结果。
结果分析
结合实验数据和理论分析,评 估材料的弯曲性能,并探讨影 响材料弯曲性能的因素。
结论总结
总结实验结果,得出结论,并 提出改进和优化材料弯曲性能
的建议。
04
弯曲变形的工程应用实例
桥梁的弯曲变形分析
总结词
桥梁的弯曲变形分析是确保桥梁安全的重要环节,通过分析桥梁在不同载荷下的弯曲变形程度,可以评估桥梁的 承载能力和安全性。
转角
梁在弯曲变形后,其横截 面绕其中性轴旋转的角度 称为转角。转角是衡量梁 横截面旋转程度的量。
弯曲变形的物理关系
弯矩
由于外力作用在梁上,使梁产生弯曲变形的力矩 称为弯矩。弯矩是引起梁弯曲变形的力。
剪力
在梁弯曲变形过程中,垂直于轴线的横向剪切力 称为剪力。剪力使梁产生剪切变形。
扭矩
当外力作用在梁的某一侧时,会使梁产生扭转变 形,这种使梁产生扭转变形的力矩称为扭矩。
详细描述
高层建筑由于其高度和规模,对风载和地震等外部载荷非常敏感。因此,在高层建筑设 计阶段,需要进行详细的弯曲变形分析。这包括对建筑物的整体结构和各个楼层在不同 载荷下的弯曲变形进行模拟和分析,以确保建筑物在各种外部载荷下的安全性和稳定性。
机械零件的弯曲变形分析
要点一
总结词
机械零件的弯曲变形分析是确保机械系统正常运行的关键 环节。通过对机械零件在不同工作载荷下的弯曲变形进行 分析,可以优化零件的设计和加工工艺,提高其工作性能 和寿命。
通过实例分析和习题练习,学生可以加深对弯曲 变形的理解,提高解决实际问题的能力。
弯曲变形的未来研究方向
弯曲变形的非线性行为
根据需要,对数据进行计算、 绘图等处理,以便更好地理解 和分析实验结果。
结果分析
结合实验数据和理论分析,评 估材料的弯曲性能,并探讨影 响材料弯曲性能的因素。
结论总结
总结实验结果,得出结论,并 提出改进和优化材料弯曲性能
的建议。
04
弯曲变形的工程应用实例
桥梁的弯曲变形分析
总结词
桥梁的弯曲变形分析是确保桥梁安全的重要环节,通过分析桥梁在不同载荷下的弯曲变形程度,可以评估桥梁的 承载能力和安全性。
转角
梁在弯曲变形后,其横截 面绕其中性轴旋转的角度 称为转角。转角是衡量梁 横截面旋转程度的量。
弯曲变形的物理关系
弯矩
由于外力作用在梁上,使梁产生弯曲变形的力矩 称为弯矩。弯矩是引起梁弯曲变形的力。
剪力
在梁弯曲变形过程中,垂直于轴线的横向剪切力 称为剪力。剪力使梁产生剪切变形。
扭矩
当外力作用在梁的某一侧时,会使梁产生扭转变 形,这种使梁产生扭转变形的力矩称为扭矩。
详细描述
高层建筑由于其高度和规模,对风载和地震等外部载荷非常敏感。因此,在高层建筑设 计阶段,需要进行详细的弯曲变形分析。这包括对建筑物的整体结构和各个楼层在不同 载荷下的弯曲变形进行模拟和分析,以确保建筑物在各种外部载荷下的安全性和稳定性。
机械零件的弯曲变形分析
要点一
总结词
机械零件的弯曲变形分析是确保机械系统正常运行的关键 环节。通过对机械零件在不同工作载荷下的弯曲变形进行 分析,可以优化零件的设计和加工工艺,提高其工作性能 和寿命。
通过实例分析和习题练习,学生可以加深对弯曲 变形的理解,提高解决实际问题的能力。
弯曲变形的未来研究方向
弯曲变形的非线性行为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图a所示:认为离中性轴z为
任意距离y的水平直线kk'上各
点处的切应力均汇交于k点和
k'点处切线的交点O ',且这些
切应力沿y方向的分量ty相等。
因此可先利用公式
ty
FS Sz* I z bkk
求出kk'上各点的切应
力竖向分量ty ,然后求出各点处各自的切应力。
圆截面梁横截面上的
最大切应力tmax在中性轴z
即:M
dM Iz
S
* z
M Iz
S
* z
tbdx
t
S
* z
dM
Izb dx
结论:
t
FS
S
* z
Izb
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS
h2 (
y2)
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A*
y* C
b
h
y
y
h 2
y
2
2
b 2
h2 4
y2
Iz S*
z ,max
d
75103 N 47.73 102m 12.5 103m
12.6 106 Pa 12.6 MPa
例题 4-13
2. 求ta ta
其中:
FS
,max
S
* za
Izd
S
* za
166
mm
21
mm
560 mm 2
21
mm 2
940 103 mm3
于是有:
ta
F* N2
自由边 t1 t1
A* F* dx
N1
u
但是,如果从长为dx的梁段 中用铅垂的纵截面在翼缘上截取如 图所示包含翼缘自由边在内的分离 体就会发现,由于横力弯曲情况下 梁的相邻横截面上的弯矩不相等, 故所示分离体前后两个同样大小的 部分横截面上弯曲正应力构成的合 力FN*1 FN*2
和 不相等,因而铅垂的纵截
面上必有由切d F应S 力 Ft1N*′2构成FN的*1 合力。
F* N2
自由边 t1 t1
A* F* dx
N1
u
根据 d FS t可1 得d x出
t1
FS
S
* z
I z
FS
I z
u
h 2
2
FS uh
2Iz
从而由切应力互等定理可
知,翼缘横截面上距自由边为u
处有平行于翼缘横截面边长的
切应力t1,而且它是随u按线性
§5.7 梁的切应力
2.公式推导 (1) 取微段dx
mn
M
tt
FS
FS
b
h
z
y y
M+dM
FS
s1 m dx n
s2
M
F x
§7-3 弯曲剪应力和强度校核
一.矩形截面截面梁的剪应力
b
s My
Iz
mn
h
Oz y
zM
y
tt
M+dM
FS
FS
y
s1 m dx n
s2
假设
在hb的情况下
1.t的方向都与 FS 平行 2.t 沿宽度均布。
75 103 N 940 106 m3 65586 108 m4 12.5 103 m
8.6106 Pa 8.6 MPa
例题 4-13
腹板上切应力沿高度的变化规律如图所示。
tmax
3. 薄壁环形截面梁 薄壁环形截面梁在竖直平面
内弯曲时,其横截面上切应力 的特征如图a所示:
(1) 由于d <<r0,故认为切应
规律变化的。
思考题: 试通过分析说明,图a中
所示上、下翼缘左半部分 和右半部分横截面上与腹 板横截面上的切应力指向 是正确的,即它们构成了 “切应力流”。
例题 4-13
由56a号工字钢制成的简支梁如图a所示,试求
梁的横截面上的最大切应力tmax和同一横截面上腹 板上a点处(图b)的切应力t a 。不计梁的自重。
Iz
bh3 12
b
F
S
h y
t
y
z
t max
t
t max
3 2
FS bh
2. 工字形截面梁 (1) 腹板上的切应力
t
FS
S
* z
Izd
其中
Sz*
b
h 2
2
h 2
y d
h 2
y
y
2
b
2
Байду номын сангаас
h
d 2
h 2
2
y
2
可见腹板上的切应力在与中性轴z垂直的方向 按二次抛物线规律变化。
(2) 在腹板与翼缘交界处:
力t 的大小和方向沿壁厚 无变
化; (2) 由于梁的内、外壁上无切
应力,故根据切应力互等定理 知,横截面上切应力的方向与 圆周相切;
(3) 根据与y轴的对称关系 可知:
(a) 横截面上与y轴相交的 各点处切应力为零;
(b) y轴两侧各点处的切应 力其大小及指向均与y轴对 称。
薄壁环形截面梁横截面上的最大切应力tmax
例题 4-13
解: 1. 求tmax
梁的剪力图如图c所示,由图可见FS,max=75kN。 由型钢表查得56a号工字钢截面的尺寸如图b所示,
Iz=65 586 cm4和Iz/S * z,max=47.73cm。d=12.5mm
例题 4-13
tmax
FS
,max
S
* z ,max
Izd
FS,max
t min
FS Izd
b
2
h
在中性轴处:
t max
FS
S
* z ,max
Izd
FS Izd
b
2
h
d 2
h 2
2
对于轧制的工字钢,上式中的 Iz就是型钢表 中给出的比值 ,此I值x 已把工字钢截S面z*,ma的x 翼缘厚 度变化和圆角等考虑S在x 内。
(3) 翼缘上的切应力
翼缘横截面上平行于 剪力FS的切应力在其上、 下边缘处为零(因为翼缘的 上、下表面无切应力),可 见翼缘横截面上其它各处 平行于FS的切应力不可能 大,故不予考虑。分析表 明,工字形截面梁的腹板 承担了整个横截面上剪力 FS的90%以上。
A
y2 z2 d A
y2 d A
A
z2 d A
A
Iz Iy 2Iz
得出:
Iz
1 2
Ip
π
r03
从而有
t max
FS
S
* z
Iz 2
FS 2r02 π r03 2
FS 2 FS
r0 π
A
式中, A=2pr0 为整个环形截面的面积。
(4) 圆截面梁 圆截面梁在竖直平面内弯曲
时,其横截面上切应力的特征
t
t
y
FNⅠ
FNII
z
y
A*
y
y A*
dFS
FNⅠ
y A*
FNII
FNI A* sⅠdA
A*
M y1 dA Iz
M Iz
A*
y1 dA
M Iz
Sz*
FNⅡ A* (s Ⅱ)dA
A*
(M
dM ) y1 dA Iz
M
dM Iz
A*
y1 dA
M
dM Iz
S* z
FN II FN I t bdx
处,其计算公式为
t max
FS
S
* z
Izd
FS
1 2
πd 4
在中性轴z上,半个环形截面的面积A*=pr0,其
形心离中性轴的距离(图b)为2r0 ,故求tmax时有
S
* z
π
r0
2r0 π
π
2r02
整个环形截面对于中性 轴z的惯性矩Iz可利用整个截 面对于圆心O的极惯性矩得 到,如下:
Ip
2
A
d
A
2π
r0
r02
2π
r03
及
Ip
2d A
A
