河北省石家庄市2019年中考数学总复习第四章三角形第三节全等三角形同步训练

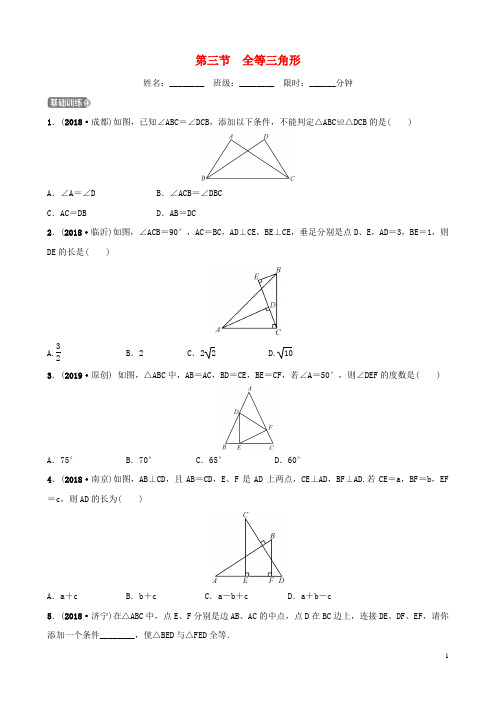
第三节全等三角形
姓名：________ 班级：________ 限时：______分钟
1．(2018·成都)如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB的是( )
A．∠A＝∠D B．∠ACB＝∠DBC
C．AC＝DB D．AB＝DC
2．(2018·临沂)如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别是点D、E，AD＝3，BE＝1，则DE的长是( )
A.3
2
B．2 C．2 2 D.10
3．(2019·原创)如图，△ABC中，AB＝AC，BD＝CE，BE＝CF，若∠A＝50°，则∠DEF的度数是( )
A．75° B．70° C．65° D．60°
4．(2018·南京)如图，AB⊥CD，且AB＝CD，E、F是AD上两点，CE⊥AD，BF⊥AD.若CE＝a，BF＝b，EF ＝c，则AD的长为( )
A．a＋c B．b＋c C．a－b＋c D．a＋b－c
5．(2018·济宁)在△ABC中，点E、F分别是边AB、AC的中点，点D在BC边上，连接DE、DF、EF，请你添加一个条件________，使△BED与△FED全等．
6．(2018·保定一模)已知：如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点E在BC 边上．
(1)求证：△ACD≌△ABE；
(2)若∠CDE＝60°，求∠AEB的度数．
7．(2018·陕西)如图，AB∥CD，E、F分别为AB、CD上的点，且EC∥BF，连接AD，分别与EC、BF相交于点G、H.若AB＝CD，求证：AG＝DH.
8．(2017·恩施州)如图，△ABC、△CDE均为等边三角形，连接BD、AE交于点O，BC与AE交于点P.
求证：∠AOB＝60°.
9．(2018·镇江)如图，△ABC中，AB＝AC，点E，F在边BC上，BE＝CF，点D在AF的延长线上，AD＝AC.
(1)求证：△ABE≌△ACF；
(2)若∠BAE＝30°，则∠ADC＝________°.
10．(2019·原创)如图，已知等腰三角形ABC中，AB＝AC，点D、E分别在边AB、AC上，且AD＝AE，连接BE、CD交于点F.
(1)求证：∠ABE＝∠ACD；
(2)求证：过点A、F的直线垂直平分线段BC.
1．(2019·原创)如图，∠ACB＝90°，AC＝BC，∠DCE＝45°，若AD＝3，BE＝4，则BC的长是( )
A．5 B．5 2
C．6 2 D．7
2．(2018·保定二模)如图，菱形ABCD中，∠ABC＝60°.将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F.
(1)求证：△ABE≌△ACF；
(2)判断△AEF是哪一种特殊三角形，并说明理由．
3．(2018·石家庄长安区模拟)如图①，在等边△ABC和等边△ADP中，AB＝2，点P在△ABC的高CE上(点P与点C不重合)，点D在点P的左侧，连接BD，ED.
(1)求证：BD＝CP；
(2)当点P与点E重合时，延长CE交BD于点F，请你在图②中作出图形，并求出BF的长．
4．(2018·滨州)已知，在△ABC中，∠A＝90°，AB＝AC，点D为BC的中点．
(1)如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE＝AF；
(2)若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE＝AF吗？请利用图②说明理由．
参考答案
【基础训练】
1．C 2.B 3.C 4.D
5．BD＝EF答案不唯一，如BD＝CD或DF∥AB或DE∥AC或∠BED＝∠EDF等．
6．(1)证明：∵∠BAC＝∠DAE＝90°，
∴∠BAC－∠CAE＝∠DAE－∠CAE，
即∠DAC＝∠EAB.
⎩⎪AC ＝AB ∴△ACD≌△ABE(S A S )．
(2)解：在Rt △ADE 中，AD ＝AE ，∠DAE＝90°， ∴∠ADE＝∠AED＝45°.
∵△ACD≌△ABE，∴∠ADC＝∠AEB，
∴∠AEB＝∠ADE＋∠CDE＝45°＋60°＝105°. 7．证明：∵AB∥CD，∴∠A＝∠D. 又∵CE∥BF，∴∠AHB＝∠DGC. 在△ABH 和△DCG 中，⎩⎪⎨⎪
⎧∠A＝∠D ∠AHB＝∠DGC AB ＝CD ，
∴△ABH≌△DCG.∴AH＝DG. 又∵AH＝AG ＋GH ，DG ＝DH ＋GH ， ∴AG＝HD.
8．证明：∵△ABC，△CDE 均为等边三角形， ∴∠ACB＝∠ECD＝60°， ∴∠ACE＝∠BCD.
在△ACE 与△BCD 中，⎩⎪⎨⎪
⎧AC ＝BC ∠ACE＝∠BCD CE ＝CD ，
∴△ACE≌△BCD(S A S )， ∴∠CAE＝∠CBD.
∵∠AOB＋∠CBD＋∠BPO＝180°， ∠BCA＋∠CAE＋∠APC＝180°， 且∠BPO＝∠APC， ∴∠AOB＝∠BCA＝60°. 9．(1)证明：∵AB＝AC ， ∴∠B＝∠ACF.
⎩⎪BE＝CF
∴△ABE≌△ACF.
(2)75.
10．证明：(1)∵AB＝AC，∠BAE＝∠CAD，AE＝AD，
∴△ABE≌△ACD(S A S)，
∴∠ABE＝∠ACD.
(2)∵AB＝AC，
∴∠ABC＝∠ACB.
由(1)可知∠ABE＝∠ACD，
∴∠FBC＝∠FCB，
∴FB＝FC.
又∵AB＝AC，∴点A，F均在线段BC的垂直平分线上，即过点A，F的直线垂直平分线段BC.
【拔高训练】
1．C
2．(1)证明：∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD，
∵∠B＝60°，∴△ABC是等边三角形，
∴∠ACB＝60°，AC＝AB，
同理△ACD是等边三角形，∴∠ACD＝60°.
∵∠BAC＝∠EAF＝60°，
∴∠BAE＝∠CAF，
∴△BAE≌△CAF.
(2)解：△AEF是等边三角形，理由如下：
∵△BAE≌△CAF，∴AE＝AF，
∵∠EAF＝60°，
∴△AEF是等边三角形．
3．(1)证明：∵△ABC是等边三角形，
∴AB＝AC，∠BAC＝60°.
∵△ADP 是等边三角形， ∴AD＝AP ，∠PAD＝60°，
∴∠DAB＋∠PAB＝60°＝∠PAC＋∠PAB， ∴∠DAB＝∠PAC，∴△DAB≌△PAC. ∴BD＝CP.
(2)解：作图如解图所示． ∵△ADP 是等边三角形，
∴当点P 与点E 重合时，有AE ＝DE ，∠AED＝60°. ∵CE⊥AB，
∴AE＝BE ＝DE ，∠BCE＝1
2∠ACB＝30°.
∴∠EBD＝30°，∴∠DBC＝90°. 在Rt △BCF 中，∵BC＝2，tan ∠BCE＝BF
BC ，
吧∴BF＝2tan 30°＝23
3
.
4．(1)证明：连接AD ，如解图①所示. ∵∠BAC＝90°，AB ＝AC ，
∴△ABC 为等腰直角三角形， 图① ∠EBD＝45°. ∵点D 为BC 的中点， ∴AD＝1
2
BC ＝BD ，∠FAD＝45°.
∵∠BDE＋∠EDA＝90°，∠EDA＋∠ADF＝90°， ∴∠BDE＝∠ADF.
在△BDE 和△ADF 中，⎩⎪⎨⎪
⎧∠EBD＝∠FAD BD ＝AD ∠BDE＝∠ADF ，
∴△BDE≌△ADF(A S A)，∴BE＝AF. (2)解：BE ＝AF ，理由如下： 连接AD ，如解图②所示. ∵∠ABD＝∠BAD＝45°， ∴∠EBD＝∠FAD＝135°. 图②
∵∠EDB＋∠BDF＝90°，
∠BDF＋∠FDA＝90°， ∴∠EDB＝∠FDA. 在△EDB 和△FDA 中， ⎩⎪⎨⎪
⎧∠EBD＝∠FAD BD ＝AD
∠EDB＝∠FDA
， ∴△EDB≌△FDA(A S A)， ∴BE＝AF.。