精品解析：江苏省无锡市2018年中考数学试题(原卷版)

合集下载

精品解析：2024年吉林省长春市中考数学试题(解析版)

2024年长春市初中学业水平考试数学本试卷包括三道大题，共6页．全卷满分为120分，考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回．注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试卷上答题无效．一、选择题：本题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 根据有理数加法法则，计算()23+−过程正确的是（）A. ()32++B. ()32+−C. ()32−+D. ()32−−【答案】D 【解析】【分析】本题主要考查了有理数的加法，掌握“将两个数的绝对值相减,结果的符号与绝对值较大的数的符号相同”成为解题的关键．根据将两个数的绝对值相减,结果的符号与绝对值较大的数的符号相同即可解答．【详解】解：()()2332+−−−=．故选D ．2. 南湖公园是长春市著名旅游景点之一，图①是公园中“四角亭”景观的照片，图②是其航拍照片，则图③是“四角亭”景观的（）．A. 主视图B. 俯视图C. 左视图D. 右视图【答案】B 【解析】【分析】本题主要考查了几何体的三视图，熟练掌握三视图的定义是解决本题的关键．根据三视图主视图、俯视图、左视图的定义即可解答．【详解】解：由题意可知图③是从“四角亭”上方看到的，即为俯视图．故选B ．3. 在剪纸活动中，小花同学想用一张矩形纸片剪出一个正五边形，其中正五边形的一条边与矩形的边重合，如图所示，则α∠的大小为（）A. 54oB. 60C. 70D. 72【答案】D 【解析】【分析】本题考查了多边形内角与外角，正多边形的内角和，熟练掌握正多边形的内角和公式是解题的关键．根据正五边形的内角和公式和邻补角的性质即可得到结论．【详解】解：(52)180180725α−⨯︒∠=︒−=︒，故选：D ．4. 下列运算一定正确的是（） A. 236a a a ⋅= B. 236a a a ⋅=C. ()222ab a b =D. ()235a a =【答案】C 【解析】【分析】本题考查了单项式乘单项式、同底数幂的乘法以及幂的乘方与积的乘方，掌握相关运算法则是解答本题的关键．根据单项式乘单项式的运算法则计算并判断A ；根据同底数幂的乘法法则计算并判断B ；根据积的乘方运算法则计算并判断C ；根据幂的乘方运算法则计算并判断D ．【详解】解：A ．2236a a a ⋅=，故本选项不符合题意； B ．235a a a ⋅=，故本选项不符合题意；C ．()222ab a b =，故本选项符合题意；D ．()236a a =，故本选项不符合题意；故选：C ．5. 不等关系在生活中广泛存在．如图，a 、b 分别表示两位同学的身高，c 表示台阶的高度．图中两人的对话体现的数学原理是（）A. 若a b >，则a c b c +>+B. 若a b >，b c >，则a c >C. 若a b >，0c >，则ac bc >D. 若a b >，0c >，则a b c c> 【答案】A 【解析】【分析】本题主要考查不等式的性质，熟记不等式性质是解决问题的关键．根据不等式的性质即可解答．【详解】解：由作图可知：a b >，由右图可知：a c b c +>+，即A 选项符合题意．故选：A ．6. 2024年5月29日16时12分，“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射．当火箭上升到点A 时，位于海平面R 处的雷达测得点R 到点A 的距离为a 千米，仰角为θ，则此时火箭距海平面的高度AL 为（）A. sin a θ千米B.sin aθ千米 C. cos a θ千米D.cos aθ千米【答案】A 【解析】【分析】本题考查解直角三角形，熟记锐角三角函数的定义是解题关键，根据锐角的正弦函数的定义即可求解【详解】解：由题意得：sin AL ALAR aθ== ∴sin AL a θ=千米故选：A7. 如图，在ABC 中，O 是边AB 的中点．按下列要求作图：①以点B 为圆心、适当长为半径画弧，交线段BO 于点D ，交BC 于点E ； ②以点O 为圆心、BD 长为半径画弧，交线段OA 于点F ； ③以点F圆心、DE 长为半径画弧，交前一条弧于点G ，点G 与点C 在直线AB 同侧；④作直线OG ，交AC 于点M ．下列结论不一定成立的是（）A. AOM B ∠=∠B. 180OMC C ∠+∠=C. AM CM =D. 12OM AB =【答案】D 【解析】【分析】本题主要考查了作一个角等于已知角，平行线的性质和判定，平行线分线段成比例定理，解题的关键是熟练掌握相关的性质，先根据作图得出AOM B ∠=∠，根据平行线的判定得出OM BC ∥，根据平行线的性质得出180OMC C ∠+∠=，根据平行线分线段成比例得出1AM AOCM OB==，即可得出AM CM =．【详解】解：A ．根据作图可知：AOM B ∠=∠一定成立，故A 不符合题意； B ．∵AOM B ∠=∠， ∴OM BC ∥，∴180OMC C ∠+∠=一定成立，故B 不符合题意； C ．∵O 是边AB 的中点， ∴AO BO =， ∵OM BC ∥，为∴1AM AOCM OB==， ∴AM CM =一定成立，故C 不符合题意； D ．12OM AB =不一定成立，故D 符合题意． 8. 如图，在平面直角坐标系中，点O 是坐标原点，点()4,2A 在函数()0,0ky k x x=>>的图象上．将直线OA 沿y 轴向上平移，平移后的直线与y 轴交于点B ，与函数()0,0ky k x x=>>的图象交于点C ．若BC =B 的坐标是（）A. (B. ()0,3C. ()0,4D. (【答案】B 【解析】【分析】本题主要考查反比例函数、解直角三角形、平移的性质等知识点，掌握数形结合思想成为解题的关键．如图：过点A 作x 轴的垂线交x 轴于点E ，过点C 作y 轴的垂线交y 轴于点D ，先根据点A 坐标计算出sin OAE ∠、k 值，再根据平移、平行线的性质证明DBC OAE ∠=∠，进而根据sin sin CDDBC OAE BC∠==∠求出CD ，最后代入反比例函数解析式取得点C 的坐标，进而确定2CD =,4OD =，再运用勾股定理求得BD ，进而求得OB 即可解答．【详解】解：如图，过点A 作x 轴的垂线交x 轴于点E ，过点C 作y 轴的垂线交y 轴于点D ，则AE y ∥轴，∵()4,2A ，∴4OE =，OA =∴sinOE OAE OA ∠===． ∵()4,2A 在反比例函数的图象上， ∴428k =⨯=．∴将直线OA 向上平移若干个单位长度后得到直线BC ， ∴OA BC ∥， ∴OAE BOA ∠=∠， ∵AE y ∥轴， ∴DBC BOA ∠=∠， ∴DBC OAE ∠=∠，∴sin si n CD DBC OAE BC ∠===∠=2CD =，即点C 的横坐标为2，将2x =代入8y x=，得4y =， ∴C 点的坐标为()2,4， ∴2CD =,4OD =，∴1BD ==，∴413OB OD BD =−=−=, ∴()0,3B 故选：B ．二、填空题：本题共6小题，每小题3分，共18分．9. 单项式22a b −的次数是_____．【答案】3 【解析】【分析】此题考查单项式有关概念，根据单项式次数的定义来求解，解题的关键是需灵活掌握单项式的系数和次数的定义，单项式中数字因数叫做单项式的系数，所有字母的指数和叫做这个单项式的次数．【详解】单项式22a b −的次数是：213+=，故答案为：3．10.=____．【解析】【分析】利用二次根式的性质化简，再相减．==【点睛】本题考查了二次根式的减法，解题的关键是掌握二次根式的化简及性质． 11. 若抛物线2y x x c =−+（c 是常数）与x 轴没有交点，则c 的取值范围是________．【答案】14c > 【解析】【分析】本题主要考查了抛物线2y ax bx c =++与x 轴的交点问题，掌握抛物线2y ax bx c =++与x 轴没有交点与20x x c −+=没有实数根是解题的关键．由抛物线与x 轴没有交点，运用根的判别式列出关于c 的一元一次不等式求解即可．【详解】解：∵抛物线2y x x c =−+与x 轴没有交点， ∴20x x c −+=没有实数根，∴2141140c c ∆=−⨯⨯=−<，14c >．故答案为：14c >． 12. 已知直线y kx b =+（k 、b 是常数）经过点()1,1，且y 随x 的增大而减小，则b 的值可以是________．（写出一个即可）【答案】2（答案不唯一）【解析】【分析】本题考查了一次函数图象上点的坐标特征以及一次函数的性质，牢记“0k >，y 随x 的增大而增大；0k <，y 随x 的增大而减小”是解题的关键．利用一次函数图象上点的坐标特征，可得出1k b =+，由y 随x 的增大而减小，利用一次函数的性质，可得出0k <，若代入1k =−，求出b 值即可．【详解】解：∵直线y kx b =+（k 、b 是常数）经过点()1,1， ∴1k b =+．∵y 随x 的增大而减小， ∴0k <，当1k =−时，11b =−+，解得：2b =， ∴b 的值可以是2．故答案为：2（答案不唯一）13. 一块含30︒角的直角三角板ABC 按如图所示的方式摆放，边AB 与直线l 重合，12cm AB =．现将该三角板绕点B 顺时针旋转，使点C 的对应点C '落在直线l 上，则点A 经过的路径长至少为________cm ．（结果保留π）【答案】203π【解析】【分析】本题主要考查了旋转的性质、弧长公式等知识点，掌握弧长公式成为解题的关键．由旋转的性质可得60ABC A BC '∠=∠=︒,即120A BA '∠=︒，再根据点A 经过的路径长至少为以B 为圆心，以AB 为半径的圆弧的长即可解答．【详解】解：∵将该三角板绕点B 顺时针旋转，使点C 的对应点C '落在直线l 上， ∴60ABC A BC '∠=∠=︒,即120A BA '∠=︒， ∴点A 经过的路径长至少为12010201803ππ︒⋅⋅=︒．故答案为：203π． 14. 如图，AB 是半圆的直径，AC 是一条弦，D 是AC 的中点，DE AB ⊥于点E ，交AC 于点F ，DB 交AC 于点G ，连结AD ．给出下面四个结论：①ABD DAC ∠=∠； ②AF FG =；③当2DG =，3GB =时，2FG =；④当2BD AD =，6AB =时，DFG 上述结论中，正确结论的序号有________．【答案】①②③ 【解析】【分析】如图：连接DC ，由圆周角定理可判定①；先说明BDE AGD ∠=∠、ADE DAC ∠=∠可得DF FG =、AF FD =，即AF FG =可判定②；先证明∽ADG BDA 可得AD GDBD AD=,即AD GDDG BG AD=+,代入数据可得AD =，然后运用勾股定理可得AG =AF FG =即可判定③；如图：假设半圆的圆心为O ，连接,,OD CO CD ，易得60AOD DOC ∠=∠=︒，从而证明,AOD ODC 是等边三角形，即ADCO 是菱形，然后得到30DAC OAC ∠=∠=︒，再解直角三角形可得DG =ADGS =④．【详解】解：如图：连接DC ，∵D 是AC 的中点， ∴AD DC =,∴ABD DAC ∠=∠，即①正确； ∵AB 是直径， ∴90ADB ∠=︒，∴90DAC AGD ∠+∠=︒， ∵DE AB ⊥ ∴90BDE ABD??,∵ABD DAC ∠=∠， ∴BDE AGD ∠=∠， ∴DF FG =， ∵90BDE ABD??，90BDE ADE ∠+∠=︒,∴ADE ABD ∠=∠， ∵ABD DAC ∠=∠， ∴ADE DAC ∠=∠， ∴AFFD =，∴AF FG =,即②正确；在ADG △和BDA △,90ADG BDA DAG DBA ∠=∠=︒⎧⎨∠=∠⎩， ∴∽ADG BDA ， ∴AD GD BD AD =,即AD GDDG BG AD=+,∴223AD AD=+，即AD =∴AG ==∵AF FG =，∴122FG AG ==，即③正确；如图：假设半圆的圆心为O ，连接,,OD CO CD ， ∵2BD AD =，6AB =，D 是AC 的中点， ∴1,3AD DC AB ==∴60AOD DOC ∠=∠=︒， ∵OA OD OC ==，∴,AOD ODC 是等边三角形，∴6OA AD CD OC OD =====，即ADCO 是菱形， ∴1302DAC OAC DAO ∠=∠=∠=︒， ∵90ADB ∠=︒，∴tan tan 30DG DAC AD ∠=︒=，即36DG=，解得：DG =∴11622ADGSAD DG =⋅=⨯⨯= ∵AF FG = ∴1332DFGADGSS ==故答案为：①②③．【点睛】本题主要考查了圆周角定理、解直角三角形、相似三角形的判定与性质、勾股定理、菱形的判定与性质、等腰三角形的判定与性质等知识点，灵活运用相关知识成为解题的关键．三、解答题：本题共10小题，共78分．15. 先化简，再求值：32222x xx x−−−，其中x=【答案】2x，2【解析】【分析】本题考查了分式的化简求值问题，先算分式的减法运算，再代入求值即可．【详解】解：原式()23222222x xx xx x x−−===−−∵x=，∴原式2=16. 2021年吉林省普通高中开始施行新高考选科模式，此模式有若干种学科组合，每位高中生可根据自己的实际情况选择一种．一对双胞胎姐妹考入同一所高中且选择了相同组合，该校要将所有选报这种组合的学生分成A、B、C三个班，其中每位学生被分到这三个班的机会均等．用画树状图（或列表）的方法，求这对双胞胎姐妹被分到同一个班的概率．【答案】1 3【解析】【分析】本题主要考查列表法与树状图法、概率公式等知识点，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．先列表确定出所有等可能的结果数以及这对双胞胎姐妹被分到同一个班的结果数，然后再利用概率公式计算即可．【详解】解：列表如下：共有9种等可能的结果，其中这对双胞胎姐妹被分到同一个班的结果有3种，所以这对双胞胎姐妹被分到同一个班的概率为31 93 =．17. 《九章算术》被历代数学家尊为“算经之首”．下面是其卷中记载的关于“盈不足”的一个问题：今有共买金，人出四百，盈三千四百；人出三百，盈一百．问人数、金价各几何？这段话的意思是：今有人合伙买金，每人出400钱，会剩余3400钱；每人出300钱，会剩余100钱．合伙人数、金价各是多少？请解决上述问题．【答案】共33人合伙买金，金价为9800钱【解析】【分析】设共x 人合伙买金，金价为y 钱，根据“每人出400钱，会剩余3400钱；每人出300钱，会剩余100钱”，即可得出关于x ，y 的二元一次方程组，解之即可得出结论．【详解】解：设共x 人合伙买金，金价为y 钱，依题意得：4003400300100x yx y −=⎧⎨−=⎩，解得：339800x y =⎧⎨=⎩．答：共33人合伙买金，金价为9800钱．【点睛】本题考查了二元-次方程组的应用以及数学常识，找准等量关系，正确列出二元一次方程组是解题的关键．18. 如图，在四边形ABCD 中，90A B ∠=∠=︒，O 是边AB 的中点，AOD BOC ∠=∠．求证：四边形ABCD 是矩形．【答案】证明见解析．【解析】【分析】本题考查全等三角形的判定与性质、平行四边形的判定及矩形的判定，熟练掌握判定定理是解题关键．利用SAS 可证明AOD BOC ≌△△，得出AD BC =，根据90A B ∠=∠=︒得出AD BC ∥，即可证明四边形ABCD 是平行四边形，进而根据有一个角是直角的平行四边形是矩形即可证明四边形ABCD 是矩形．【详解】证明：∵O 是边AB 的中点， ∴OA OB =，在AOD △和BOC 中，90A B OA OB AOD BOC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，∴AOD BOC ≌△△， ∴AD BC =， ∵90A B ∠=∠=︒， ∴AD BC ∥，∴四边形ABCD 是平行四边形， ∵90A B ∠=∠=︒， ∴四边形ABCD 是矩形．19. 某校为调研学生对本校食堂的满意度，从初中部和高中部各随机抽取20名学生对食堂进行满意度评分（满分10分），将收集到的评分数据进行整理、描述和分析．下面给出了部分信息：a ．高中部20名学生所评分数频数分布直方图如下图：（数据分成4组：67x ≤<，78x ≤<，89x ≤<，910x ≤≤）b ．高中部20名学生所评分数在89x ≤<这一组的是：8.0 8.1 8.2 8.2 8.4 8.5 8.6 8.7 8.8c ．初中部、高中部各20名学生所评分数的平均数、中位数如下：根据以上信息，回答下列问题：的（1）表中m 的值为________；（2）根据调查前制定的满意度等级划分标准，评分不低于8.5分为“非常满意”．①在被调查的学生中，设初中部、高中部对食堂“非常满意”的人数分别为a 、b ，则a ________b ；（填“>”“<”或“=”）②高中部共有800名学生在食堂就餐，估计其中对食堂“非常满意”的学生人数．【答案】（1）8.3（2）①>；②估计其中对食堂“非常满意”的学生人数为360人【解析】【分析】（1）由题意知，高中部评分的中位数为第1011，位数的平均数，即8.28.42m +=，计算求解即可；（1）①利用中位数进行决策即可；②根据4580020+⨯，计算求解即可．【小问1详解】解：由题意知，高中部评分的中位数为第1011，位数的平均数，即8.28.48.32m +==，故答案为：8.3；【小问2详解】①解：由题意知，初中部评分的中位数为8.5，高中部评分的中位数为8.3， ∴a b >，故答案为：>； ②解：∵4580036020+⨯=， ∴估计其中对食堂“非常满意”的学生人数为360人．【点睛】本题考查了条形统计图，中位数，利用中位数进行决策，用样本估计总体．熟练掌握条形统计图，中位数，利用中位数进行决策，用样本估计总体是解题的关键．20. 图①、图②、图③均是33⨯的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点．点A 、B 均在格点上，只用无刻度的直尺，分别在给定的网格中按下列要求作四边形ABCD ，使其是轴对称图形且点C 、D 均在格点上．（1）在图①中，四边形ABCD面积为2；（2）在图②中，四边形ABCD面积为3；（3）在图③中，四边形ABCD面积为4．【答案】（1）见解析（2）见解析（3）见解析【解析】【分析】本题考查网格作图、设计图案、轴对称的性质、平移的性质等知识点，根据轴对称的性质、平移的性质作图是解题的关键．（1）根据轴对称的性质、平移的性质作出面积为2四边形ABCD即可．（2）根据轴对称的性质、平移的性质作出面积为3四边形ABCD即可．（3）根据轴对称的性质、平移的性质作出面积为4四边形ABCD即可．【小问1详解】解：如图①：四边形ABCD即为所求；（不唯一）．【小问2详解】解：如图②：四边形ABCD即为所求；（不唯一）．【小问3详解】解：如图③：四边形ABCD 即为所求；（不唯一）．21. 区间测速是指在某一路段前后设置两个监控点，根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度．小春驾驶一辆小型汽车在高速公路上行驶，其间经过一段长度为20千米的区间测速路段，从该路段起点开始，他先匀速行驶112小时，再立即减速以另一速度匀速行驶（减速时间忽略不计），当他到达该路段终点时，测速装置测得该辆汽车在整个路段行驶的平均速度为100千米/时．汽车在区间测速路段行驶的路程y （千米）与在此路段行驶的时间x （时）之间的函数图象如图所示．（1）a 的值为________；（2）当112x a ≤≤时，求y 与x 之间的函数关系式；（3）通过计算说明在此区间测速路段内，该辆汽车减速前是否超速．（此路段要求小型汽车行驶速度不得超过120千米/时）【答案】（1）15（2）11902125y x x ⎛⎫=+≤≤ ⎪⎝⎭（3）没有超速【解析】【分析】本题考查了一次函数的应用、一次函数的图像、求函数解析式等知识点，掌握待定系数法求函数关系式是解题的关键．（1）由题意可得：当以平均时速为100/千米时行驶时，a 小时路程为20千米，据此即可解答；（2）利用待定系数法求解即可；（3）求出先匀速行驶112小时的速度，据此即可解答．【小问1详解】解：由题意可得：10020a =，解得：15a =．故答案为：15．【小问2详解】解：设当11125x ≤≤时，y 与x 之间函数关系式为()0y kx b k =+≠，则：11761205k b k b ⎧+=⎪⎪⎨⎪+=⎪⎩，解得：902k b =⎧⎨=⎩，∴11902125y x x ⎛⎫=+≤≤⎪⎝⎭．【小问3详解】解：当112x =时，19029.512y =⨯+=， ∴先匀速行驶112小时的速度为：19.5114/12÷=（千米时）， ∵114120＜，∴辆汽车减速前没有超速． 22. 【问题呈现】小明在数学兴趣小组活动时遇到一个几何问题：如图①，在等边ABC 中，3AB =，点M 、N 分别在边AC 、BC 上，且AM CN =，试探究线段MN 长度的最小值．的【问题分析】小明通过构造平行四边形，将双动点问题转化为单动点问题，再通过定角发现这个动点的运动路径，进而解决上述几何问题．【问题解决】如图②，过点C 、M 分别作MN 、BC 的平行线，并交于点P ，作射线AP ．在【问题呈现】的条件下，完成下列问题：（1）证明：AM MP =；（2）CAP ∠的大小为度，线段MN 长度的最小值为________．【方法应用】某种简易房屋在整体运输前需用钢丝绳进行加固处理，如图③．小明收集了该房屋的相关数据，并画出了示意图，如图④，ABC 是等腰三角形，四边形BCDE 是矩形，2AB AC CD ===米，30ACB ∠=︒．MN 是一条两端点位置和长度均可调节的钢丝绳，点M 在AC 上，点N 在DE 上．在调整钢丝绳端点位置时，其长度也随之改变，但需始终保持AM DN =．钢丝绳MN 长度的最小值为多少米．【答案】问题解决：（1）见解析（2）30，32；方法应用：线段MN 长度的最小值为2米【解析】【分析】（1）过点C 、M 分别作MN 、BC 的平行线，并交于点P ，作射线AP ，根据平行四边形性质证明结论即可；（2）先证明30CAPMPA ??，根据垂线段最短求出最小值；（3）过点D 、M 分别作MN 、ED 的平行线，并交于点H ，作射线AH ，连接AD ，求出15MAH ?，进而得45DAH ∠=︒，利用垂线段最短求出即可．【详解】解：问题解决：（1）证明：过点C 、M 分别作MN 、BC 的平行线，并交于点P ，作射线AP ，∴四边形MNCP 是平行四边形，NC MP MN PC \==，AM NC =AM MP ∴=；（2）在等边ABC 中，60ACB ∠=︒，MP CN ∥60PMC ACB \???AM MP =30CAP MPA \???；当CP AP ⊥时，CP 最小，此时MN 最小，在Rt ACP 中，3,30AC CAP=??13322CP \=?， ∴线段MN 长度的最小值为32；方法应用：过点D 、M 分别作MN 、ED 的平行线，并交于点H ，作射线AH ，连接AD ，∴四边形MNDH 是平行四边形，,ND MH MN DH MH ED \==，∥AM ND =AM MH ∴=，四边形BCDE 是矩形，,90BC ED BCD \??∥ BC MH \∥ 30ACB CMH\???AM MH = 15MAH \??3m,120AC CD ACD ACB BCD ==????30DAC ∴∠=︒45DAH ∴∠=︒∴当DH AH ⊥时，DH 最小，此时MN 最小，作CR AD ⊥于点R ，在Rt ACR 中，3,30AC CAR =??13322CR \=?，2AR \=2AD AR \==在Rt ADH中，45AD DAH=??2DH AH \==∴线段MN【点睛】本题考查了平行四边形判定与性质、等腰三角形的判定与性质、三角形外角的性质，垂线段最短及矩形性质，熟练掌握相关性质是解题关键．23. 如图，在ABC 中，5AB AC ==，6BC =．点D 是边BC 上的一点（点D 不与点B 、C 重合），作射线AD ，在射线AD 上取点P ，使AP BD =，以AP 为边作正方形APMN ，使点M 和点C 在直线AD 同侧．的（1）当点D 是边BC 的中点时，求AD 的长；（2）当4BD =时，点D 到直线AC 的距离为________；（3）连结PN ，当PN AC ⊥时，求正方形APMN 的边长；（4）若点N 到直线AC 的距离是点M 到直线AC 距离的3倍，则CD 的长为________．（写出一个即可）【答案】（1）4 （2）85（3）177（4）256或259 【解析】【分析】本题考查等腰三角形性质，勾股定理，锐角三角函数，熟练掌握面积法是解题的关键；（1）根据等腰三角形三线合一性质，利用勾股定理即可求解；（2）利用面积法三角形面积相等即可；（3）设AP x =，则BD x =，6CD x =−，过点D 作DHAC ⊥于Q，根据AQ CQ AC +=，建立方程；即可求解；（4）第一种情况，M ，N 在AC 异侧时，设MQ m =，3NQ m =，则4AN m =，证明CDE ANQ ∽，得到CE CDNQ AQ=，即可求解；第二种情况，当M ，N 在AC 同侧，设CD x =，则35CH x =，45DH x =，3425AH x =⨯，求得3345525x x +⨯=，解方程即可求解；【小问1详解】解：根据题意可知：5AB AC ==，ABC ∴为等腰三角形，故点D 是边BC 的中点时，AD BC ⊥；在Rt ADC 中，4AD ====；【小问2详解】根据题意作DH AC ⊥，如图所示；当4BD =时，则2CD =，设点D 到直线AC 的距离为DH h =，1124522ACDSh =⨯⨯=⨯⨯，解得：85h =；【小问3详解】如图，当NP AC ⊥时，点M 落在AC 上，设AP x =，则BD x =，6CD x =−，过点D 作DH AC ⊥于Q 则()33655CQ CD x ==−，()44655DQ CD x ==− ()44655AQ DQ CD x ===−，AQ CQ AC +=，()()3466555x x ∴−+−= 解得：177x = 故177=AP ，所以正方形APMN 的边长为177；【小问4详解】如图，M ，N 在AC 异侧时；设MQ m =，3NQ m =，则4AN m =ANQ ∴三边的比值为3:4:5，AQN C ∴∠=∠，CAD C ∴∠=∠，∴CDE ANQ ∽CE CDNQ AQ= ∴5525326CD =⨯= 当M ，N 在AC 同侧设MQ m =，则3AN AP m ==，2PQ m =，APO ∴三边比为，AQD ∴三边比为设CD x =，则35CH x =，45DH x =，3425AH x =⨯3345525x x ∴+⨯= 解得：259CD x ==综上所述：CD 的长为256或259 24. 在平面直角坐标系中，点O 是坐标原点，抛物线22y x x c =++（c 是常数）经过点()2,2−−．点A 、B 是该抛物线上不重合的两点，横坐标分别为m 、m −，点C 的横坐标为5m −，点C 的纵坐标与点A 的纵坐标相同，连结AB 、AC ．（1）求该抛物线对应的函数表达式；（2）求证：当m 取不为零的任意实数时，tan CAB ∠的值始终为2；（3）作AC 的垂直平分线交直线AB 于点D ，以AD 为边、AC 为对角线作菱形ADCE ，连结DE ． ①当DE 与此抛物线的对称轴重合时，求菱形ADCE 的面积；②当此抛物线在菱形ADCE 内部的点的纵坐标y 随x 的增大而增大时，直接写出m 的取值范围．【答案】（1）222y x x =+−（2）见详解（3）①9ADCE S =菱形；②3m ≤−或10m −≤<或04m <≤ 【解析】【分析】（1）将()2,2−−代入22y x x c =++，解方程即可；（2）过点B 作BH AC ⊥于点H ，由题意得()()22,22,,22A m m m B m m m +−−−−，则4A B BH y y m =−=，2A B AH x x m =−=，因此tan 2BHCAB AH∠==；（3）①记,AC DE 交于点M ， ()25,22C m m m −+−，而对称轴为直线=1x −，则512m m−+=−，解得：12m =，则32AM =，3AC =，由tan 232DM DMCAB AM∠===，得3DM =，则6DE =，因此9ADCE S =菱形；②分类讨论，数形结合，记抛物线顶点为点F ，则()1,3F −−，故菱形中只包含在对称轴右侧的抛物线，当0m >时，符合题意；当m 继续变大，直至当直线CD 经过点F 时，符合题意，过点F 作FQ AC ⊥于点Q ，由CAD FCQ ∠=∠，得到()()2223215m m m +−−−=−−−，解得：4m =4m =+（舍），故04m <≤，当4m >时，发现此时菱形包含了对称轴左侧的抛物线，不符合题意；当0m <时，符合题意：当m 继续变小，直至点A 与点F 重合，此时1m =−，故10m −≤<；当m 继续变小，直线AE 经过点F 时，也符合题意，过点F 作FQ AC ⊥于点Q ，同上可得，()222321m m m+−−−=−−，解得：3m =−或1m =−（舍），当m 继续变小时，仍符合题意，因此3m ≤−，故m 的取值范围为：3m ≤−或10m −≤<或04m <≤．【小问1详解】解：将()2,2−−代入22y x x c =++，得：442c −+=−，解得：2x =−，∴抛物线表达式为：222y x x =+−；【小问2详解】解：过点B 作BH AC ⊥于点H ，则90AHB ∠=︒，由题意得：()()22,22,,22A m m m B m m m +−−−−，∴4A B BH y y m =−=，2A B AH x x m =−=， ∴在Rt AHB △中，4tan 22mBH CAB AH m∠===；【小问3详解】解：①如图，记,AC DE 交于点M ，由题意得，()25,22C m m m −+−，由2122b a −=−=−，得：对称轴为直线：=1x − ∵四边形ADCE 是菱形，∴点A 、C 关于DE 对称，2,2AC AM DE DM ==， ∵DE 与此抛物线的对称轴重合， ∴512m m−+=−，解得：12m =， ∴12A x =， ∴()13122AM =−−=∴3AC =， ∵tan 232DM DMCAB AM∠===， ∴3DM =，则6DE =， ∴192ADCE S DE AC =⨯=菱形； ②记抛物线顶点为点F ，把=1x −代入222y x x =+−，得：=3y −，∴()1,3F −−，∵抛物线在菱形ADCE 内部的点的纵坐标y 随x 的增大而增大， ∴菱形中只包含在对称轴右侧的抛物线，当0m >时，如图，符合题意，当m 继续变大，直至当直线CD 经过点F 时，符合题意，如图：过点F 作FQ AC ⊥于点Q ， ∵四边形ADCE 是菱形， ∴DA DC =， ∴CAD FCQ ∠=∠， ∴tan tan 2FQFCQ CAD CQ∠=∠==， ∴()()2223215m m m +−−−=−−−，解得：4m =4m =+（舍），∴04m <≤，当4m >当0m <时，如图，符合题意：当m 继续变小，直至点A 与点F 重合，此时1m =−，符合题意，如图：∴10m −≤<；当m 继续变小，直至直线AE 经过点F 时，也符合题意，如图：过点F 作FQ AC ⊥于点Q ，同上可得，tan 2FQFAQ AQ∠==， ∴()222321m m m+−−−=−−，解得：3m =−或1m =−（舍），当m 继续变小时，仍符合题意，如图：∴3m ≤−，综上所述，m 的取值范围为：3m ≤−或10m −≤<或04m <≤．【点睛】本题考查了抛物线与几何的综合，菱形的性质，待定系数法求函数解析式，求锐角的正切值，正确理解题意，利用数形结合的思想，找出临界状态是解决本题的关键．。

2018年全国中考数学真题分类线段垂直平分线、角平分线、中位线解析版(精品文档)

2018年全国中考数学真题分类线段垂直平分线、角平分线、中位线（一）一、选择题1. （2018四川泸州，7题，3分）如图2，ABCD 的对角线AC ，BD 相交于点O ，E 是AB 中点，且AE+EO=4，则ABCD 的周长为（）A.20B. 16C. 12D.8第7题图【答案】B 【解析】ABCD 的对角线AC ，BD 相交于点O ，所以O 为AC 的中点，又因为E 是AB 中点，所以EO是△ABC 的中位线，AE=21AB ，EO=21BC ，因为AE+EO=4，所以AB+BC=2(AE+EO)=8，ABCD 中AD=BC ，AB=CD ，所以周长为2(AB+BC)=16【知识点】平行四边形的性质，三角形中位线2. （2018四川省南充市，第8题，3分）如图，在Rt ABC ∆中，90ACB ∠=，30A ∠=，D ，E ，F 分别为AB ，AC ，AD 的中点，若2BC =，则EF 的长度为（）A ．12B ．1C ．32D【答案】B【思路分析】1.由∠ACB =90°，∠A =30°，BC 的长度，可求得AB 的长度，2.利用直角三角形斜边D的中线等于斜边第一半，求得CD 的长度；3.利用中位线定理，即可求得EF 的长.【解题过程】解：在Rt △ABC 中，∠ACB =90°，∠A =30°，BC =2，，∴AB =4，CD =12AB ，∴CD =12×4=2，∵E ，F 分别为AC ，AD 的中点，∴EF =12CD =12×2=1，故选B.【知识点】30°所对直角边是斜边的一半；直角三角形斜边的中线等于斜边第一半；中位线定理3. （2018四川省达州市，8，3分） △ABC 的周长为19，点D 、E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为N ，∠ACB 的平分线垂直于AD ，垂足为M ．若BC ＝7，则MN 的长为（）． A ．32 B ．2 C ．52D ．3第8题图【答案】C ，【解析】∵△ABC 的周长为19，BC ＝7， ∴AB ＋AC ＝12．∵∠ABC 的平分线垂直于AE ，垂足为N ，∴BA ＝BE ，N 是AE 的中点． ∵∠ACB 的平分线垂直于AD ，垂足为M ，∴AC ＝DC ，M 是AD 的中点． ∴DE ＝AB ＋AC －BC ＝5． ∵MN 是△ADE 的中位线， ∴MN ＝12DE ＝52．故选C.【知识点】三角形的中位线4. （2018浙江杭州， 10，3分）如图，在△ABC 中，点D 在AB 边上，DE//BC ，与边AC 交于点E ，连接BE ，记△ADE ，△BCE 的面积分别为S 1，S 2,（）A. 若2AD>AB ，则3S 1>2S 2B. 若2AD>AB ，则3S 1<2S 2C. 若2AD<AB ，则3S 1>2S 2D. 若2AD<AB ，则3S 1<2S 2【答案】D【思路分析】首先考虑极点位置，当2AD=AB 即AD=BD 时S 1，S 2的关系，然后再考虑AD>BD 时S 1，S 2的变化情况。

精品解析：2024年广东省深圳市中考数学试题(解析版)

2024 年深圳市初中学业水平测试
数学学科试卷
说明：
1．答题前，请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在答题卡定的位置
上，并将条形码粘贴好．
2．全卷共 6 页．考试时间 90 分钟，满分 100 分．
3．作答选择题 1-8，选出每题答案后，用 2B 铅笔把答题卡上对应题目答案标号的信息点框
涂黑．如需改动，用橡皮擦干净后，再选涂其它答案．作答非选择题 9—20，用黑色字迹的
钢笔或签字笔将答案（含作辅助线）写在答题卡指定区域内．写在本试卷或草稿纸上，其答
案一律无效．
4．考试结束后，请将答题卡交回．
第一部分选择题
.一、选择题（本大题共 8 小题，每小题 3 分，共 24 分，每小题有四个选项，其中只有一个是
B、 m2n m = m3n ，故该选项符合题意； C、 3mn − m 3n ，故该选项不符合题意；
D、 (m −1)2 = m2 − 2m +1 m2 −1，故该选项不符合题意；
故选：B． 4. 二十四节气，它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律，二十四个节气分别为：春季（立春、雨水、惊蛰、春分、清明、谷雨），夏季（立夏、小满、芒种、夏至、小暑、大暑），秋季（立秋、处暑、白露、秋分、寒露、霜降），冬季（立冬、小雪、大雪、冬至、小寒、大寒），若从二十四个节气中选一个节气，则抽到的节气在夏季的概率为（）
∴扇形 EOF 的面积为 90 42 = 4 ， 360
故答案为： 4 ．
12. 如图，在平面直角坐标系中，四边形 AOCB 为菱形，tan AOC = 4 ，且点 A 落在反比例函数 y = 3 上，
3
x
点 B 落在反比例函数 y = k (k 0) 上，则 k = ________．

2018年江苏省无锡市中考数学试卷(附参考解析)

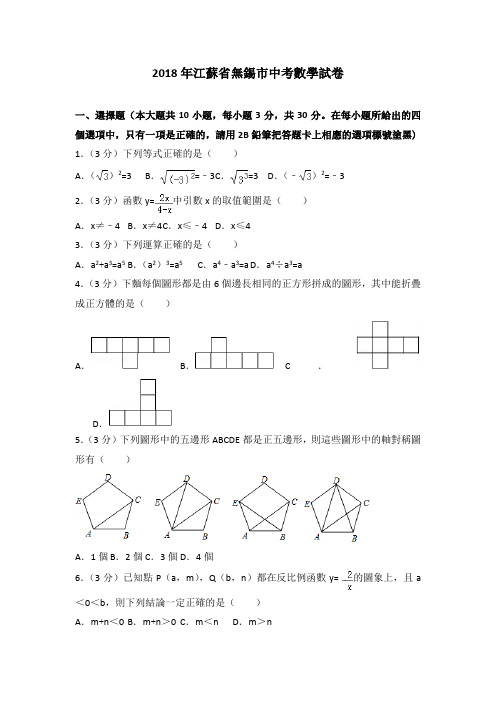
2018年江蘇省無錫市中考數學試卷一、選擇題（本大題共10小題，每小題3分，共30分。

在每小題所給出的四個選項中，只有一項是正確的，請用2B鉛筆把答題卡上相應的選項標號塗黑) 1．（3分）下列等式正確的是（）A．（）2=3 B．=﹣3 C．=3 D．（﹣）2=﹣32．（3分）函數y=中引數x的取值範圍是（）A．x≠﹣4 B．x≠4 C．x≤﹣4 D．x≤43．（3分）下列運算正確的是（）A．a2+a3=a5 B．（a2）3=a5C．a4﹣a3=a D．a4÷a3=a4．（3分）下麵每個圖形都是由6個邊長相同的正方形拼成的圖形，其中能折疊成正方體的是（）A．B．C．D．5．（3分）下列圖形中的五邊形ABCDE都是正五邊形，則這些圖形中的軸對稱圖形有（）A．1個 B．2個 C．3個 D．4個6．（3分）已知點P（a，m），Q（b，n）都在反比例函數y=的圖象上，且a ＜0＜b，則下列結論一定正確的是（）A．m+n＜0 B．m+n＞0 C．m＜n D．m＞n7．（3分）某商場為了解產品A的銷售情況，在上個月的銷售記錄中，隨機抽取了5天A產品的銷售記錄，其售價x（元/件）與對應銷量y（件）的全部數據如下表：9095100105110售價x（元/件）銷量y（件）110100806050則這5天中，A產品平均每件的售價為（）A．100元B．95元C．98元D．97.5元8．（3分）如圖，矩形ABCD中，G是BC的中點，過A、D、G三點的圓O與邊AB、CD分別交於點E、點F，給出下列說法：（1）AC與BD的交點是圓O的圓心；（2）AF與DE的交點是圓O的圓心；（3）BC與圓O相切，其中正確說法的個數是（）A．0 B．1 C．2 D．39．（3分）如圖，已知點E是矩形ABCD的對角線AC上的一動點，正方形EFGH 的頂點G、H都在邊AD上，若AB=3，BC=4，則tan∠AFE的值（）A ．等於B ．等於C ．等於D．隨點E位置的變化而變化10．（3分）如圖是一個沿3×3正方形方格紙的對角線AB剪下的圖形，一質點P由A點出發，沿格點線每次向右或向上運動1個單位長度，則點P由A點運動到B點的不同路徑共有（）A．4條 B．5條 C．6條 D．7條二、填空題（本大題共8小題，每小題2分，共16分。

精品解析：2024年河北省中考数学试题(原卷版)

2024年河北省初中毕业生升学文化课考试数学试卷一、选择题（本大题共16个小题，共38分．1~6小题各3分，7~16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）1.如图显示了某地连续5天的日最低气温，则能表示这5天日最低气温变化情况的是（）A. B. C.D.2.下列运算正确的是（）A.734a a a -= B.222326a a a ⋅= C.33(2)8a a -=- D.44a a a÷=3.如图，AD 与BC 交于点O ，ABO 和CDO 关于直线PQ 对称，点A ，B 的对称点分别是点C ，D ．下列不一定正确的是（）A.AD BC⊥ B.AC PQ⊥ C.ABO CDO△≌△ D.AC BD∥4.下列数中，能使不等式516x -<成立的x 的值为（）A.1B.2C.3D.45.观察图中尺规作图的痕迹，可得线段BD 一定是ABC 的（）A.角平分线B.高线C.中位线D.中线6.如图是由11个大小相同的正方体搭成的几何体，它的左视图是（）A. B. C. D.7.节能环保已成为人们的共识．淇淇家计划购买500度电，若平均每天用电x 度，则能使用y 天．下列说法错误的是（）A .若5x =，则100y = B.若125y =，则4x =C.若x 减小，则y 也减小D.若x 减小一半，则y 增大一倍8.若a ，b 是正整数，且满足8282222222a ba a ab b b ++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯ 个相加个相乘，则a 与b 的关系正确的是（）A.38a b +=B.38a b= C.83a b += D.38a b=+9.淇淇在计算正数a 的平方时，误算成a 与2的积，求得的答案比正确答案小1，则=a （）A.1B.C.1 D.11+10.下面是嘉嘉作业本上的一道习题及解答过程：已知：如图，ABC 中，AB AC =，AE 平分ABC 的外角CAN ∠，点M 是AC 的中点，连接BM 并延长交AE 于点D ，连接CD ．求证：四边形ABCD 是平行四边形．证明：∵AB AC =，∴3ABC ∠=∠．∵3CAN ABC ∠=∠+∠，12CAN ∠=∠+∠，12∠=∠，∴①______．又∵45∠=∠，MA MC =，∴MAD MCB △≌△（②______）．∴MD MB =．∴四边形ABCD 是平行四边形．若以上解答过程正确，①，②应分别为（）A.13∠=∠，AASB.13∠=∠，ASAC.23∠∠=，AAS D.23∠∠=，ASA11.直线l 与正六边形ABCDEF 的边,AB EF 分别相交于点M ，N ，如图所示，则a β+=（）A.115︒B.120︒C.135︒D.144︒12.在平面直角坐标系中，我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”．如图，矩形ABCD 位于第一象限，其四条边分别与坐标轴平行，则该矩形四个顶点中“特征值”最小的是（）A.点AB.点BC.点CD.点D 13.已知A 为整式，若计算22A yxy y x xy -++的结果为x y xy-，则A =（）A.xB.yC.x y+ D.x y-14.扇文化是中华优秀传统文化的组成部分，在我国有着深厚的底蕴．如图，某折扇张开的角度为120︒时，扇面面积为S 、该折扇张开的角度为n ︒时，扇面面积为n S ，若nm SS =，则m 与n 关系的图象大致是（）A. B. C. D.15.“铺地锦”是我国古代一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法运算．淇淇受其启发，设计了如图1所示的“表格算法”，图1表示13223⨯，运算结果为3036．图2表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（）A.“20”左边的数是16B.“20”右边的“□”表示5C.运算结果小于6000D.运算结果可以表示为41001025a +16.平面直角坐标系中，我们把横、纵坐标都是整数，且横、纵坐标之和大于0的点称为“和点”．将某“和点”平移，每次平移的方向取决于该点横、纵坐标之和除以3所得的余数（当余数为0时，向右平移；当余数为1时，向上平移；当余数为2时，向左平移），每次平移1个单位长度．例：“和点”()2,1P 按上述规则连续平移3次后，到达点()32,2P ，其平移过程如下：若“和点”Q 按上述规则连续平移16次后，到达点()161,9Q -，则点Q 的坐标为（）A.()6,1或()7,1 B.()15,7-或()8,0 C.()6,0或()8,0 D.()5,1或()7,1二、填空题（本大题共3个小题，共10分．17小题2分，18~19小题各4分，每空2分）17.某校生物小组的9名同学各用100粒种子做发芽实验，几天后观察并记录种子的发芽数分别为：89，73，90，86，75，86，89，95，89，以上数据的众数为______．18.已知a ，b ，n 均为正整数．（1）若1n n <<+，则n =______；（2）若1,1n n n n -<<<+，则满足条件的a 的个数总比b 的个数少______个．19.如图，ABC 的面积为2，AD 为BC 边上的中线，点A ，1C ，2C ，3C 是线段4CC 的五等分点，点A ，1D ，2D 是线段3DD 的四等分点，点A 是线段1BB 的中点．（1）11AC D △的面积为______；（2）143B C D △的面积为______．三、解答题（本大题共7个小题，共72分．解答应写出文字说明、证明过程或演算步骤）20.如图，有甲、乙两条数轴．甲数轴上的三点A ，B ，C 所对应的数依次为4-，2，32，乙数轴上的三点D ，E ，F 所对应的数依次为0，x ，12．（1）计算A ，B ，C 三点所对应的数的和，并求ABAC的值；（2）当点A 与点D 上下对齐时，点B ，C 恰好分别与点E ，F 上下对齐，求x 的值．21.甲、乙、丙三张卡片正面分别写有,2,a b a b a b ++-，除正面的代数式不同外，其余均相同．a b +2a b +a b-a b +22a b+2a2a b+a b-2a（1）将三张卡片背面向上并洗匀，从中随机抽取一张，当1,2a b ==-时，求取出的卡片上代数式的值为负数的概率；（2）将三张卡片背面向上并洗匀，从中随机抽取一张，放回后重新洗匀，再随机抽取一张．请在表格中补全两次取出的卡片上代数式之和的所有可能结果（化为最简），并求出和为单项式的概率．22.中国的探月工程激发了同学们对太空的兴趣．某晚，淇淇在家透过窗户的最高点P 恰好看到一颗星星，此时淇淇距窗户的水平距离4m BQ =，仰角为α；淇淇向前走了3m 后到达点D ，透过点P 恰好看到月亮，仰角为β，如图是示意图．已知，淇淇的眼睛与水平地面BQ 的距离 1.6m ==AB CD ，点P 到BQ 的距离 2.6m PQ =，AC 的延长线交PQ 于点E ．（注：图中所有点均在同一平面）（1）求β的大小及tan α的值；（2）求CP 的长及sin APC ∠的值．23.情境图1是由正方形纸片去掉一个以中心O 为顶点的等腰直角三角形后得到的．该纸片通过裁剪，可拼接为图2所示的钻石型五边形，数据如图所示．（说明：纸片不折叠，拼接不重叠无缝隙无剩余）操作嘉嘉将图1所示的纸片通过裁剪，拼成了钻石型五边形．如图3，嘉嘉沿虚线EF ，GH 裁剪，将该纸片剪成①，②，③三块，再按照图4所示进行拼接．根据嘉嘉的剪拼过程，解答问题：（1）直接写出线段EF 的长；（2）直接写出图3中所有与线段BE 相等的线段，并计算BE 的长．探究淇淇说：将图1所示纸片沿直线裁剪，剪成两块，就可以拼成钻石型五边形．请你按照淇淇的说法设计一种方案：在图5所示纸片的BC 边上找一点P （可以借助刻度尺或圆规），画出裁剪线（线段PQ ）的位置，并直接写出BP 的长．24.某公司为提高员工的专业能力，定期对员工进行技能测试，考虑多种因素影响，需将测试的原始成绩x （分）换算为报告成绩y （分）．已知原始成绩满分150分，报告成绩满分100分、换算规则如下：当0x p ≤<时，80xy p=；当150p x ≤≤时，()2080150x p y p-=+-．（其中p 是小于150的常数，是原始成绩的合格分数线，80是报告成绩的合格分数线）公司规定报告成绩为80分及80分以上（即原始成绩为p 及p 以上）为合格．（1）甲、乙的原始成绩分别为95分和130分，若100p =，求甲、乙的报告成绩；（2）丙、丁的报告成绩分别为92分和64分，若丙的原始成绩比丁的原始成绩高40分，请推算p 的值：（3）下表是该公司100名员工某次测试的原始成绩统计表：原始成绩（分）95100105110115120125130135140145150人数1225810716201595①直接写出这100名员工原始成绩的中位数；②若①中的中位数换算成报告成绩为90分，直接写出该公司此次测试的合格率．25.已知O 的半径为3，弦MN =，ABC 中，90,3,ABC AB BC ∠=︒==．在平面上，先将ABC 和O 按图1位置摆放（点B 与点N 重合，点A 在O 上，点C 在O 内），随后移动ABC ，使点B 在弦MN 上移动，点A 始终在O 上随之移动，设BN x =．（1）当点B 与点N 重合时，求劣弧 AN 的长；（2）当OA MN ∥时，如图2，求点B 到OA 的距离，并求此时x 的值；（3）设点O 到BC 的距离为d ．①当点A 在劣弧 MN上，且过点A AC 垂直时，求d 的值；②直接写出d 的最小值．26.如图，抛物线21:2C y ax x =-过点(4,0)，顶点为Q ．抛物线22211:()222C y x t t =--+-（其中t 为常数，且2t >），顶点为P ．（1）直接写出a 的值和点Q 的坐标．（2）嘉嘉说：无论t 为何值，将1C 的顶点Q 向左平移2个单位长度后一定落在2C 上．淇淇说：无论t 为何值，2C 总经过一个定点．请选择其中一人的说法进行说理．（3）当4t =时，①求直线PQ 的解析式；②作直线l PQ ∥，当l 与2C 的交点到x 轴的距离恰为6时，求l 与x 轴交点的横坐标．（4）设1C 与2C 的交点A ，B 的横坐标分别为,A B x x ，且A B x x <．点M 在1C 上，横坐标为()2B m m x ≤≤．点N 在2C 上，横坐标为()A n x n t ≤≤．若点M 是到直线PQ 的距离最大的点，最大距离为d ，点N 到直线PQ 的距离恰好也为d ，直接用含t 和m 的式子表示n ．。

【精品】2018年苏教版小升初数学试卷(逐题解析版)

2018年苏教版小升初数学试卷一、计算．（56分）1．（5分）直接写得数．0.36+4=0×= 5.7﹣0.5÷0.25=4×÷4×=0.9=0.22=÷80%=+=81×=（﹣）×12=2．（18分）解方程．（1）9x÷2=54（2）3（x+0.6）÷4=1.2（3）5x﹣2.4=12.6（4）0.4：12=x ：（5）2（x﹣0.8）×3=2.4（6）：x=40．3．（21分）递等式计算，能简算的要简算．×12+0.25×48 9.63÷2.5÷49.6+0.4×（3﹣2.75）19.82﹣6.57﹣3.43 8.37﹣ 3.25﹣（1.37+1.75）4.6×22+46×7.84．（12分）列式计算．（1）一个数的比它的多1.8，这个数是多少？（2）两个12相乘的积比一个数的4倍少24，这个数是多少？（3）比10个多的数是多少？（4）与的和乘它的差是多少？二、概念部分．填空．（18分）5．（5分）9.4cm2=m25t7kg=t1.75时=分6吨=吨千克．6．（2分）北京举办的第29届奥运会，奥运会主场建筑面积为二百五十八万零三百平方米，写作平方米，改写成用“万”作单位的数为万平方米．7．（1分）一本书一共有m页，小胖每天看8页，看了a天，还剩页没看．8．（2分）16和24的最大公因数是；30和25的最小公倍数是．9．（1分）把2.4：3.8化成最简整数比是．三、选择题16．（1分）下列说法中正确的是（）A．14是7的因数B．91是一个质数C．2.5与0.4互为倒数D．2和10是互为质数17．（1分）在数轴上，离开原点5个单位长度的点表示的数是（）A．+5 B．﹣5 C．+5和﹣5 D．018．（1分）如果a是奇数，b是偶数，那么下列各项中是奇数的式子是（）A．a﹣b B．2a﹣b C．2a+b D．2（a+b）19．（1分）某养值场养鸭38只，比养的鸡的2倍多6只，养值场养鸡多少只？（）A．38×2+6 B．38÷2+6 C．（38+6）÷2 D．（38﹣6）÷220．（1分）下列图形中，对称轴最少的是（）A．长方形B．正方形C．等腰三角形D．圆21．（1分）在1千克水中加入20克盐，这时盐占盐水的（）A．B．C．D．22．（1分）一种花生仁的出油率是38%，1000千克花生仁可榨油（）A．380 B．1380 C．约238123．（1分）要统计一袋牛奶里的营养成分所占百分比情况，你会选用（）A．条形统计图B．折线统计图C．扇形统计图三、解答题（共1小题，满分5分）10．（5分）几何部分．求图1和图2的体积（各边单位长度为cm）四、解决问题（20分）11．（4分）一条路全长480米，第一天修了这条路的，第二天修了这条路的，还剩这条路的几分之几没有修？12．（4分）已知梯形的面积是60平方厘米，高是12厘米，下底是4厘米，求上底是多少厘米？13．（4分）某钢厂三月份用电480千瓦时，比二月份节约了25%．节约了多少千瓦时？14．（4分）一个工厂由于采用了新工艺，现在每件产品的成本是37.4元，比原来降低了15%，原来每件成本是多少元？15．（4分）某厂生产一批水泥，原计划每天生产150吨，可以按时完成任务．实际每天增产30吨，结果只用25天就完成了任务．原计划完成生产任务需要多少天？2018年苏教版小升初数学试卷答案与解析一、计算．（56分）1．（5分）直接写得数．0.36+4=0×= 5.7﹣0.9=0.5÷0.25=4×÷4×=0.22=÷80%=+=81×=（﹣）×12=【分析】根据小数和分数四则运算的计算法则以及混合运算的运算顺序计算即可，其中（﹣）×12根据乘法的分配律简算即可．【解答】解：0.36+4=4.360×=0 5.7﹣0.9=4.80.5÷0.25=24×÷4×=0.22=0.04÷80%=1+=81×=（﹣）×12=1【点评】本题属于基本的计算，在平时注意积累经验，逐步提高运算的速度和准确性．关键是熟练掌握计算法则．2．（18分）解方程．（1）9x÷2=54（2）3（x+0.6）÷4=1.2（3）5x﹣2.4=12.6（4）0.4：12=x ：（5）2（x﹣0.8）×3=2.4（6）：x=40．【分析】（1）根据等式的性质，在方程两边同时乘2，再同时除以9得解；（2）根据等式的性质，在方程两边同时乘4，再把方程化简成3x+1.8=4.8，在方程两边同时除以减去1.8，再同时除以3得解；（3）根据等式的性质，在方程两边同时加上2.4，再同时除以5得解；（4）根据比例的基本性质，先把比例式转化成等式12x=0.4×，再根据等式的性质，在方程两边同时除以12得解；（5）根据等式的性质，在方程两边同时除以3，再把方程化简成2x﹣1.6=0.8，在方程两边同时除以加上1.6，再同时除以2得解；（6）求比的后项，就用比的前项除以比值得解．【解答】解：（1）9x÷2=549x÷2×2=54×29x÷9=108÷9x=12（2）3（x+0.6）÷4=1.23（x+0.6）÷4×4=1.2×43x+1.8=4.83x+1.8﹣1.8=4.8﹣1.83x÷3=3÷3x=1（3）5x﹣2.4=12.65x﹣2.4+2.4=12.6+2.45x÷5=15÷5x=3（4）0.4：12=x：12x=0.4×12x÷12=÷12x=（5）2（x﹣0.8）×3=2.42（x﹣0.8）×3÷3=2.4÷32x﹣1.6=0.82x﹣1.6+1.6=0.8+1.62x÷2=2.4÷2x=1.2（6）：x=40x=÷40x=．【点评】本题主要考查了学生根据比例的性质解比例以及利用等式的性质解方程的能力；解答过程中要注意把等号要对齐．3．（21分）递等式计算，能简算的要简算．×12+0.25×48 9.63÷2.5÷419.82﹣6.57﹣3.43 8.37﹣ 3.25﹣9.6+0.4×（3﹣2.75）（1.37+1.75）4.6×22+46×7.8【分析】（1）（7）根据乘法的分配律简算即可．（2）根据乘法的结合律简算即可．（3）根据除法的性质简算即可．（4）（5）根据减法的性质简算即可．（6）先算小括号里的减法，再算外面的乘法，最后算加法．【解答】解：（1）×12+=×（12+1）=×13=66（2）0.25×48=0.25×4×12=1×12=12（3）9.63÷2.5÷4=9.63÷（2.5×4）=9.63÷10=0.963（4）19.82﹣6.57﹣3.43=19.82﹣（6.57+3.43）=19.82﹣10=9.82（5）8.37﹣3.25﹣（1.37+1.75）=8.37﹣3.25﹣1.37﹣1.75=（8.37﹣1.37）﹣（3.25+1.75）=7﹣5=2（6）9.6+0.4×（3﹣2.75）=9.6+0.4×0.25=9.6+0.1=9.7（7）4.6×22+46×7.8=4.6×（22+78）=4.6×100=460【点评】此题是考查四则混合运算，要仔细观察算式的特点，灵活运用一些定律进行简便计算．4．（12分）列式计算．（1）一个数的比它的多1.8，这个数是多少？（2）两个12相乘的积比一个数的4倍少24，这个数是多少？（3）比10个多的数是多少？（4）与的和乘它的差是多少？【分析】（1）把这个数看作单位“1”，它的（﹣）是1.8，求这个数是多少用除法计算．（2）先求出这个数的4倍是12×12+24，然后再除以4就是这个数．（3）用10乘得到的积，再加上即可．（4）分别求与的和与差，然后用得到的和乘差即可．【解答】解：（1）1.8÷（﹣）=1.8÷=10.8答：这个数是10.8．（2）（12×12+24）÷4=168÷4=42答：这个数是42．（3）10×+=2+=2答：比10个多的数是2．（4）（+）×（﹣）=×=答：积是．【点评】本题关键是要分清楚数量之间的关系，先求什么再求什么，找清列式的顺序，列出算式．二、概念部分．填空．（18分）5．（5分）9.4cm2=0.00094m25t7kg= 5.007t1.75时=105分6吨=6吨800千克．【分析】（1）低级单位平方厘米化高级单位平方米除以进率10000．（2）把7千克除以进率1000化成0.007吨再与5吨相加．（3）高级单位时化低级单位分乘进率60．（4）6吨看作6吨与吨之和，把吨乘进率1000化成800千克．【解答】解：（1）9.4cm2=0.00094m2；（2）5t7kg=5.007t；（3）1.75时=105分；（4）645吨=6吨800千克．故答案为：0.00094，5.007，105，6，800．【点评】本题是考查质量、面积、时间的单位换算．单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位，其次记住单位间的进率．6．（2分）北京举办的第29届奥运会，奥运会主场建筑面积为二百五十八万零三百平方米，写作258 0300平方米，改写成用“万”作单位的数为258.03万平方米．【分析】（1）根据整数的写法：从高位到低位，一级一级地写，哪一个数位上一个计数单位也没有，就在那个数位上写0，据此写出．（2）改成用万作单位的数，是把万位后面的4个“0”去掉，或者在万位数的右下角点上小数点，然后把小数末尾的0去掉，再在数的后面写上“万”字，据此改写．【解答】解：二百五十八万零三百平方米，写作：258 0300平方米，改写成用“万”作单位的数为：258.03万平方米．故答案为：258 0300，258.03．【点评】本题主要考查了求大数的近似数，注意：（1）改写和求近似数不同，改写数的大小不变；求近似数数的大小变了；（2）不论是改写还是求近似数，都要带计数单位“亿”字或“万”字．7．（1分）一本书一共有m页，小胖每天看8页，看了a天，还剩m﹣8a页没看．【分析】根据题意，先求出小胖a天看了多少页，进而用总页数减去看了的页数得解．【解答】解：m﹣8×a=m﹣8a（页）．故答案为：m﹣8a．【点评】此题考查用字母表示数，关键是把给出的字母当做已知数，再根据基本的数量关系列式即可．8．（2分）16和24的最大公因数是8；30和25的最小公倍数是150．【分析】根据求两个数最大公约数也就是这两个数的公有质因数的连乘积，最小公倍数是公有质因数与独有质因数的连乘积求解．【解答】解：（1）16=2×2×2×224=2×2×2×3所以16和24的最大公因数是2×2×2=8．（2）25=5×530=2×3×5所以25和30的最小公倍数是5×5×2×3=150；故答案为：8，150．【点评】考查了求几个数的最大公因数的方法与最小公倍数的方法：两个数的公有质因数连乘积是最大公约数；两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数；数字大的可以用短除法解答．9．（1分）把2.4：3.8化成最简整数比是12：19．【分析】根据比的基本性质，即比的前项和后项同时乘或除以一个相同的数（0除外）比值不变，进而把比化成最简比．【解答】解：2.4：3.8=（2.4×5）：（3.8×5）=12：19．故答案为：12：19．【点评】此题考查化简比的方法，要注意化简比的结果仍是一个比．三、选择题16．（1分）下列说法中正确的是（）A．14是7的因数B．91是一个质数C．2.5与0.4互为倒数D．2和10是互为质数【分析】根据题意，对各题进行依次分析、进而得出结论．【解答】解：A、14是7的倍数，所以14是7的因数，说法错误；B、91是一个质数，说法错误，91的因数有1、7、13、91，是合数；C、2.5×0.4=1，所以2.5与0.4互为倒数，说法正确；D、2和10是互为质数，说法错误；故选：C．【点评】此题涉及的知识点较多，但都比较简单，属于基础题，只要认真，容易完成，注意平时基础知识的积累．17．（1分）在数轴上，离开原点5个单位长度的点表示的数是（）A．+5 B．﹣5 C．+5和﹣5 D．0【分析】在数轴上，到原点5个单位长度的点分在原点的左边或右边两种情况，依此即可求解．【解答】解：在数轴上，到原点5个单位长度的点表示的数是+5和﹣5．【点评】考查了数轴的认识，注意本题有两种情况，不要漏解．18．（1分）如果a是奇数，b是偶数，那么下列各项中是奇数的式子是（）A．a﹣b B．2a﹣b C．2a+b D．2（a+b）【分析】此题可以用排除法来选，根据各选项的式子逐一判断其奇偶性．【解答】解：A、a是奇数，b是偶数，奇数﹣偶数=奇数，符合题意；B、因为2a是偶数，b也是偶数，偶数﹣偶数=偶数，不符合题意；C、因为2a是偶数，b也是偶数，偶数+偶数=偶数，不符合题意；D、根据偶数的定义可得：2（a+b）一定是偶数，所以不符合题意．故选：A．【点评】此题考查的目的是理解掌握偶数、奇数的意义以及偶数与奇数的性质．19．（1分）某养值场养鸭38只，比养的鸡的2倍多6只，养值场养鸡多少只？（）A．38×2+6 B．38÷2+6 C．（38+6）÷2 D．（38﹣6）÷2【分析】根据题意可得到等量关系式：养鸡的只数×2+6=养鸭的只数，那么养鸡的只数=（养鸭的只数﹣6）÷2，由此将数据代入等量关系式进行解答即可．【解答】解：（38﹣6）÷2=32÷2=16（只）答：养值场养鸡16只．故选：D．【点评】关键是根据题意得出数量关系式：养鸡的只数×2+=养鸭的只数，由此解答．20．（1分）下列图形中，对称轴最少的是（）A．长方形B．正方形C．等腰三角形D．圆【分析】依据轴对称图形的定义即可作答．【解答】解：据轴对称图形的特点和定义可知：正方形有四条对称轴，长方形有两条对称轴，等腰三角形有一条对称轴，圆形有无数条对称轴；答：对称轴最少的图形是等腰三角形．【点评】此题主要考查如何确定轴对称图形的对称轴条数及位置．21．（1分）在1千克水中加入20克盐，这时盐占盐水的（）A．B．C．D．【分析】在1千克水即1000克中加入20克盐，则盐水重1000+20克，根据分数的意义，此时盐占盐水的20÷（1000+20）．【解答】解：1千克=1000克20÷（1000+20）=20÷1020=即盐占盐水的．故选：C．【点评】求一个数是另一个数的几分之几，用除法．22．（1分）一种花生仁的出油率是38%，1000千克花生仁可榨油（）A．380 B．1380 C．约2381【分析】出油率是指出油量占花生仁总质量的百分比，计算方法是：出油率=×100%，知道其中的两个量就可求出第三个量．【解答】解：1000×38%=380（千克）；答：1000千克花生仁可榨油380千克．故选：A．【点评】此题属于百分率问题，要看清已知的数量与未知数量之间的关系，选择合适的解法．23．（1分）要统计一袋牛奶里的营养成分所占百分比情况，你会选用（）A．条形统计图B．折线统计图C．扇形统计图【分析】扇形统计图是用整个圆表示总数（单位“1”），用圆内各个扇形的大小表示各部分数量占总数的百分之几．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系；由此来解决这个问题．【解答】解：根据扇形统计图的特点和作用，要统计一袋牛奶里的营养成分所占百分比情况，你会选用扇形统计图．故选：C．【点评】此题主要考查扇形统计图的特点和作用，能够根据它的特点和主要解决有关的实际问题．三、解答题（共1小题，满分5分）10．（5分）几何部分．求图1和图2的体积（各边单位长度为cm）【分析】（1）根据圆锥的体积公式：V=sh，正方体的体积公式：V=a3，把数据分别代入公式求出它们的体积和即可．（2）将图形分割为两个长方体，根据长方体的体积公式：V=abh，把数据代入公式求出两个长方体的体积和即可．【解答】解：（1） 3.14×（2÷2）2×3+2×2×2= 3.14×1×3+8=3.14+8=11.14（立方厘米）；答：它的体积是11.14立方厘米．（2）45×10×5+10×5×（20﹣5）=2250+50×15=2250+750=3000（立方厘米）；答：它的体积是3000立方厘米．【点评】解答求组合图形的体积，关键是观察分析图形是由哪几部分组成的是求各部分的体积和、还是求各部分的体积差，再根据相应的体积公式解答．四、解决问题（20分）11．（4分）一条路全长480米，第一天修了这条路的，第二天修了这条路的，还剩这条路的几分之几没有修？【分析】把这条路的总长度看成单位“1”，用总长度“1”减去第一天修的分率，再减去第二天修的分率，就是剩下的占总长度的几分之几没修．【解答】解：1﹣﹣=﹣=答：还剩这条路的没有修．【点评】本题考查了分数减法应用题，关键是确定单位“1”，然后根据分数减法的意义计算．12．（4分）已知梯形的面积是60平方厘米，高是12厘米，下底是4厘米，求上底是多少厘米？【分析】因为梯形面积=（上底+下底）×高÷2，已知面积、高和下底，求上底，用面积乘2除以高，再减去下底即可．【解答】解：60×2÷12﹣4=120÷12﹣4=10﹣4=6（厘米）答：上底是6厘米．【点评】此题考查了学生对梯形面积公式的掌握与运用情况．13．（4分）某钢厂三月份用电480千瓦时，比二月份节约了25%．节约了多少千瓦时？【分析】把二月份的用电量看成单位“1”，三月份的用电量比二月份少25%，那么三月份的用电量就是二月份的1﹣25%，用三月份的用电量除以这个分率就是三月份用电量，然后再乘25%即可求出节约了多少千瓦时．【解答】解：480÷（1﹣25%）×25%=480÷0.75×0.25=160（千瓦时）答：节约了160千瓦时．【点评】本题考查了百分数除法应用题，关键是确定单位“1”，找到具体数量对应的分率；解答依据是：已知一个数的百分之几是多少，求这个数用除法计算．求一个数的百分之几是多少用乘法计算．14．（4分）一个工厂由于采用了新工艺，现在每件产品的成本是37.4元，比原来降低了15%，原来每件成本是多少元？【分析】原来的成本是单位“1”，现在的成本就是原来成本的（1﹣15%），求单位“1”用除法解答，即37.4除以（1﹣15%）即可．【解答】解：37.4÷（1﹣15%）=37.4÷85%=44（元）；答：原来每件成本是44元．【点评】本题先找出单位“1”，已知一个数的百分之几是多少，求这个数用除法求解．15．（4分）某厂生产一批水泥，原计划每天生产150吨，可以按时完成任务．实际每天增产30吨，结果只用25天就完成了任务．原计划完成生产任务需要多少天？【分析】先求出实际每天生产多少吨水泥，再求这批水泥一共有多少吨，再用总吨数除以计划的每天生产的吨数求出计划的天数．【解答】解：（150+30）×25=180×25=4500（吨）4500÷150=30（天）．答：原计划完成生产任务需要30天．【点评】解答此题的关键是先根据工作量=工作效率×工作时间求得总量，再由不变的总量求得单一量．。

精品解析：2024年福建省中考真题数学试题(解析版)

数学试题一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合要求的．1.下列实数中，无理数是（）A.3-B.0C.23D.【答案】D 【解析】【分析】无理数就是无限不循环小数，理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数，由此即可判定选择项．本题主要考查了无理数的定义，其中初中范围内学习的无理数有：,2ππ等；开方开不尽的数；以及像0.1010010001....，等数．故选：D ．2.据《人民日报》3月12日电，世界知识产权组织近日公布数据显示，2023年，全球PCT （《专利合作条约》）国际专利申请总量为27.26万件，中国申请量为69610件，是申请量最大的来源国．数据69610用科学记数法表示为（）A.696110⨯B.2696.110⨯ C.46.96110⨯ D.50.696110⨯【答案】C 【解析】【分析】根据科学记数法的定义解答，科学记数法的表示形式为10n a ⨯的形式，其中110,a n ≤<∣∣为整数，确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值1>时，n 是正数；当原数的绝对值1<时，n 是负数．本题考查了科学记数法，熟悉科学记数法概念是解题的关键．【详解】469610 6.96110=⨯故选：C ．3.如图是由长方体和圆柱组成的几何体，其俯视图是（）A. B.C. D.【答案】C 【解析】【分析】本题考查了简单组合体的三视图，根据从上边看得到的图形是俯视图，可得答案．【详解】解：这个立体图形的俯视图是一个圆形，圆形内部中间是一个矩形．故选：C ．4.在同一平面内，将直尺、含30︒角的三角尺和木工角尺（CD ⊥DE ）按如图方式摆放，若AB CD ，则1∠的大小为（）A.30︒B.45︒C.60︒D.75︒【答案】A 【解析】【分析】本题考查了平行线的性质，由AB CD ，可得60CDB ∠=︒，即可求解．【详解】∵AB CD ，∴60CDB ∠=︒，∵CD ⊥DE ，则90CDE ∠=︒，∴118030CDB CDE ∠=︒-∠-∠=︒，故选：A ．5.下列运算正确的是（）A.339a a a ⋅=B.422a a a ÷= C.()235a a = D.2222a a -=【答案】B 【解析】【分析】本题考查了同底数幂的乘法，同底数幂的除法，幂的乘方，合并同类项，解题的关键是掌握同底数幂的乘法，同底数幂的除法，幂的乘方，合并同类项运算法则．利用同底数幂的乘法，同底数幂的除法，幂的乘方，合并同类项计算后判断正误．【详解】解：336a a a ⋅=，A 选项错误；422a a a ÷=，B 选项正确；()236a a =，C 选项错误；2222a a a -=，D 选项错误；故选：B ．6.哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想，我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．在质数2，3，5中，随机选取两个不同的数，其和是偶数的概率是（）A.14B.13C.12D.23【答案】B 【解析】【分析】此题考查了树状图或列表法求概率，根据题意画出树状图，求和后利用概率公式计算即可．【详解】解：画树状图如下：由树状图可知，共有6种不同情况，和是偶数的共有2种情况，故和是偶数的概率是2163=，故选：B7.如图，已知点,A B 在O 上，72AOB ∠=︒，直线MN 与O 相切，切点为C ，且C 为 AB 的中点，则ACM ∠等于（）A.18︒B.30︒C.36︒D.72︒【答案】A 【解析】【分析】本题考查了切线的性质，三角形内角和以及等腰三角形的性质，根据C 为AB的中点，三角形内角和可求出1(18036)722OCA ∠=⨯︒-︒=︒，再根据切线的性质即可求解．【详解】∵72AOB ∠=︒，C 为 AB 的中点，∴36AOC ∠=︒∵OA OC =∴1(18036)722OCA ∠=⨯︒-︒=︒∵直线MN 与O 相切，∴90OCM ∠=︒，∴18ACM OCM OCA ∠=∠-∠=︒故选：A ．8.今年我国国民经济开局良好，市场销售稳定增长，社会消费增长较快，第一季度社会消费品零售总额120327亿元，比去年第一季度增长4.7%，求去年第一季度社会消费品零售总额．若将去年第一季度社会消费品零售总额设为x 亿元，则符合题意的方程是（）A.()1 4.7%120327x += B.()1 4.7%120327x -=C.1203271 4.7%x=+ D.1203271 4.7%x=-【答案】A 【解析】【分析】本题主要考查了列一元一次方程，解题的关键是理解题意，找出等量关系，根据今年第一季度社会消费品零售总额120327亿元，比去年第一季度增长4.7%，列出方程即可．【详解】解：将去年第一季度社会消费品零售总额设为x 亿元，根据题意得：()1 4.7%120327x +=，故选：A ．9.小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案．如图，其中OAB 与ODC 都是等腰三角形，且它们关于直线l 对称，点E ，F 分别是底边AB ，CD 的中点，OE OF ⊥．下列推断错误的是（）A.OB OD ⊥B.BOC AOB ∠=∠C.OE OF =D.180BOC AOD ∠+∠=︒【答案】B 【解析】【分析】本题考查了对称的性质，等腰三角形的性质等；A.由对称的性质得AOB DOC ∠=∠，由等腰三角形的性质得12BOE AOB ∠=∠，12DOF DOC ∠=∠，即可判断；B.BOC ∠不一定等于AOB ∠，即可判断；C.由对称的性质得OAB ODC ≌，由全等三角形的性质即可判断；D.过O 作GM OH ⊥，可得GOD BOH ∠=∠，由对称性质得BOH COH ∠∠=同理可证AOM AOH ∠=∠，即可判断；掌握性质是解题的关键．【详解】解：A. OE OF ⊥，90BOE BOF ∴∠+∠=︒，由对称得AOB DOC ∠=∠，点E ，F 分别是底边AB ，CD 的中点，OAB 与ODC 都是等腰三角形，12BOE AOB ∴∠=∠，12DOF DOC ∠=∠，90BOF DOF ∴∠+∠=︒，OB OD ∴⊥，结论正确，故不符合题意；B.BOC ∠不一定等于AOB ∠，结论错误，故符合题意；C.由对称得OAB ODC ≌，OE OF ∴=，结论正确，故不符合题意；D.过O 作GM OH ⊥，90GOD DOH ∴∠+∠=︒，90BOH DOH ∠+∠=︒ ，GOD BOH ∴∠=∠，由对称得BOH COH ∠∠=，GOD COH ∴∠=∠，同理可证AOM AOH ∴∠=∠，AOD BOC ∠∠∴+AOD AOM DOG =∠+∠+∠180=︒，结论正确，故不符合题意；故选：B ．10.已知二次函数()220y x ax a a =-+≠的图象经过1,2a A y ⎛⎫⎪⎝⎭，()23,B a y 两点，则下列判断正确的是（）A.可以找到一个实数a ，使得1y a >B.无论实数a 取什么值，都有1y a >C.可以找到一个实数a ，使得20y <D.无论实数a 取什么值，都有20y <【答案】C 【解析】【分析】本题考查二次函数的图象和性质，根据题意得到二次函数开口向上，且对称轴为22ax a -=-=，顶点坐标为()2,a a a-，再分情况讨论，当0a >时，当a<0时，1y ，2y 的大小情况，即可解题．【详解】解：二次函数解析式为()220y x ax a a =-+≠，∴二次函数开口向上，且对称轴为22ax a -=-=，顶点坐标为()2,a a a -，当0a >时，02aa <<，∴21a y a a >>-，当a<0时，02aa <<，∴21a a y a -<<，故A 、B 错误，不符合题意；当0a >时，023a a a <<<，由二次函数对称性可知，20y a >>，当a<0时，320a a a <<<，由二次函数对称性可知，2y a >，不一定大于0，故C 正确符合题意；D 错误，不符合题意；故选：C ．二、填空题：本题共6小题，每小题4分，共24分．11.因式分解：x 2+x =_____．【答案】()1x x +【解析】【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式，若有公因式，则把它提取出来，之后再观察是否是完全平方公式或平方差公式，若是就考虑用公式法继续分解因式．因此，直接提取公因式x 即可．【详解】解：()21x x x x +=+12.不等式321x -<的解集是______．【答案】1x <【解析】【分析】本题考查的是解一元一次不等式，通过移项，未知数系数化为1，求解即可解．【详解】解：321x -<，33x <，1x <，故答案为：1x <．13.学校为了解学生的安全防范意识，随机抽取了12名学生进行相关知识测试，将测试成绩整理得到如图所示的条形统计图，则这12名学生测试成绩的中位数是______．（单位：分）【答案】90【解析】【分析】本题考查了中位数的知识，解题的关键是了解中位数的求法，难度不大．根据中位数的定义（数据个数为偶数时，排序后，位于中间位置的数为中位数），结合图中的数据进行计算即可；【详解】解：∵共有12个数，∴中位数是第6和7个数的平均数，∴中位数是(9090)290+÷=；故答案为：90．14.如图，正方形ABCD 的面积为4，点E ，F ，G ，H 分别为边AB ，BC ，CD ，AD 的中点，则四边形EFGH 的面积为______．【答案】2【解析】【分析】本题考查正方形性质，线段中点的性质，根据正方形性质和线段中点的性质得到1HD DG ==，进而得到 DGH S ，同理可得12AHE EFB CGF S S S === ，最后利用四边形EFGH 的面积=正方形ABCD 的面积4-个小三角形面积求解，即可解题．【详解】解：正方形ABCD 的面积为4，2AB BC CD AD ∴====，90D Ð=°，点E ，F ，G ，H 分别为边AB ，BC ，CD ，AD 的中点，1HD DG ∴==，111122DGH S ∴=⨯⨯= ，同理可得12AHE EFB CGF S S S === ，∴四边形EFGH 的面积为1111422222----=．故答案为：2．15.如图，在平面直角坐标系xOy 中，反比例函数ky x=的图象与O 交于,A B 两点，且点,A B 都在第一象限．若()1,2A ，则点B 的坐标为______．【答案】()2,1【解析】【分析】本题考查了反比例函数的性质以及勾股定理，完全平方公式的应用，先根据()1,2A 得出2k =，设()B n m ，，则2nm k ==，结合完全平方公式的变形与应用得出()()22332120m m m m m m+=-+=--=，，结合()1,2A ，则()21B ，，即可作答．【详解】解：如图：连接OA OB，∵反比例函数ky x=的图象与O 交于,A B 两点，且()1,2A ∴221kk ==，设()B n m ，，则2nm k ==∵OB OA ==∴2225m n +==则()2222549m n m n mn +=++=+=∵点B 在第一象限∴3m n +=把2nm k ==代入得()()22332120m m m m m m+=-+=--=，∴1212m m ==，经检验：1212m m ==，都是原方程的解∵()1,2A ∴()21B ，故答案为：()21，16.无动力帆船是借助风力前行的．下图是帆船借助风力航行的平面示意图，已知帆船航行方向与风向所在直线的夹角PDA ∠为70︒，帆与航行方向的夹角PDQ ∠为30︒，风对帆的作用力F 为400N ．根据物理知识，F 可以分解为两个力1F 与2F ，其中与帆平行的力1F 不起作用，与帆垂直的力2F 仪可以分解为两个力1f 与21,f f 与航行方向垂直，被舵的阻力抵消；2f 与航行方向一致，是真正推动帆船前行的动力．在物理学上常用线段的长度表示力的大小，据此，建立数学模型：400F AD ==，则2f CD ==______．（单位：N ）（参考数据：sin400.64,cos400.77︒=︒=）【答案】128【解析】【分析】此题考查了解直角三角形的应用，求出40ADQ ∠=︒，130PDQ ∠=∠=︒，由AB QD ∥得到40BAD ADQ ∠=∠=︒，求出2sin 256F BD AD BAD ==⋅∠=，求出90160BDC ∠=︒-∠=︒在Rt BCD 中，根据2cos f CD BD BDC ==⋅∠即可求出答案．【详解】解：如图，∵帆船航行方向与风向所在直线的夹角PDA ∠为70︒，帆与航行方向的夹角PDQ ∠为30︒，∴703040ADQ PDA PDQ ∠=∠-∠=︒-︒=︒，130PDQ ∠=∠=︒，∵AB QD ∥，∴40BAD ADQ ∠=∠=︒，在Rt △ABD 中，400F AD ==，90ABD Ð=°，∴2sin 400sin 404000.64256F BD AD BAD ==⋅∠=⨯︒=⨯=，由题意可知，BD DQ ⊥，∴190BDC ∠+∠=︒，∴90160BDC ∠=︒-∠=︒在Rt BCD 中，256,90BD BCD =∠=︒，∴21cos 256cos 602561282f CD BD BDC ==⋅∠=⨯︒=⨯=，故答案为：128三、解答题：本题共9小题，共86分。

精品解析：2024年北京高考数学真题(原卷版)(合并)

绝密★本科目考试启用前2024年普通高等学校招生全国统一考试（北京卷）数学本试卷共12页，150分.考试时长120分钟.考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回.第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项．1.已知集合{|31}M x x =-<<，{|14}N x x =-≤<，则M N ⋃=（）A.{}11x x -≤< B.{}3x x >-C.{}|34x x -<< D.{}4x x <2.已知1i iz=--，则z =（）．A.1i --B.1i -+C.1i- D.1i+3.圆22260x y x y +-+=的圆心到直线20x y -+=的距离为（）A. B.2 C.3 D.4.在(4x -的展开式中，3x 的系数为（）A .6B.6- C.12D.12-5.设a ，b 是向量，则“()()·0a b a b +-= ”是“a b =- 或a b = ”的（）．A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.设函数()()sin 0f x x ωω=>.已知()11f x =-，()21f x =，且12x x -的最小值为π2，则ω=（）A.1B.2C.3D.47.生物丰富度指数1ln S d N-=是河流水质的一个评价指标，其中,S N 分别表示河流中的生物种类数与生物个体总数.生物丰富度指数d 越大，水质越好．如果某河流治理前后的生物种类数S 没有变化，生物个体总数由1N 变为2N ，生物丰富度指数由2.1提高到3.15，则（）A.2132N N =B.2123N N =C.2321N N = D.3221N N =8.如图，在四棱锥P ABCD -中，底面ABCD 是边长为4的正方形，4PA PB ==，PC PD ==该棱锥的高为（）.A.1B.2C.D.9.已知()11,x y ，()22,x y 是函数2x y =的图象上两个不同的点，则（）A.12122log 22y y x x ++< B.12122log 22y y x x ++>C.12212log 2y y x x +<+ D.12212log 2y y x x +>+10.已知()(){}2,|,12,01M x y y x t xx x t ==+-≤≤≤≤是平面直角坐标系中的点集.设d 是M 中两点间距离的最大值，S 是M 表示的图形的面积，则（）A.3d =，1S <B.3d =，1S >C.d =，1S < D.d =，1S >第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11.抛物线216y x =的焦点坐标为________．12.在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于原点对称.若ππ,63α⎡⎤∈⎢⎥⎣⎦，则cos β的最大值为________．13.若直线()3y k x =-与双曲线2214x y -=只有一个公共点，则k 的一个取值为________．14.汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器，其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列，底面直径依次为65mm,325mm,325mm ，且斛量器的高为230mm ，则斗量器的高为______mm ，升量器的高为________mm ．15.设与是两个不同的无穷数列，且都不是常数列.记集合{}*|,N k k M k a b k ==∈，给出下列4个结论：①若与均为等差数列，则M 中最多有1个元素；②若与均为等比数列，则M 中最多有2个元素；③若为等差数列，为等比数列，则M 中最多有3个元素；④若为递增数列，为递减数列，则M 中最多有1个元素.其中正确结论的序号是______.三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.16.在ABC V 中，内角,,A B C 的对边分别为,,a b c ，A ∠为钝角，7a =，sin 2cos 7B b B =．（1）求A ∠；（2）从条件①、条件②、条件③这三个条件中选择一个作为已知，使得ABC V 存在，求ABC V 的面积．条件①：7b =；条件②：13cos 14B =；条件③：sin c A =注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．17.如图，在四棱锥P ABCD -中，//BC AD ，1AB BC ==，3AD =,点E 在AD 上，且PE AD ⊥，2PE DE ==．（1）若F 为线段PE 中点，求证：//BF 平面PCD ．（2）若AB ⊥平面PAD ，求平面PAB 与平面PCD 夹角的余弦值．18.某保险公司为了了解该公司某种保险产品的索赔情况，从合同险期限届满的保单中随机抽取1000份，记录并整理这些保单的索赔情况，获得数据如下表：赔偿次数01234单数800100603010假设：一份保单的保费为0.4万元；前3次索赔时，保险公司每次赔偿0.8万元；第四次索赔时，保险公司赔偿0.6万元.假设不同保单的索赔次数相互独立.用频率估计概率.（1）估计一份保单索赔次数不少于2的概率；（2）一份保单的毛利润定义为这份保单的保费与赔偿总金额之差.（i ）记X 为一份保单的毛利润，估计X 的数学期望()E X ；（ⅱ）如果无索赔的保单的保费减少4%，有索赔的保单的保费增加20%，试比较这种情况下一份保单毛利润的数学期望估计值与（i ）中()E X 估计值的大小．（结论不要求证明）19.已知椭圆E ：()222210+=>>x y a b a b，以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点()(0,t t >且斜率存在的直线与椭圆E 交于不同的两点,A B ，过点A 和()0,1C 的直线AC 与椭圆E 的另一个交点为D ．（1）求椭圆E 的方程及离心率；（2）若直线BD 的斜率为0，求t 的值．20.设函数()()()ln 10f x x k x k =++≠，直线l 是曲线()y f x =在点()()(),0t f t t >处的切线．（1）当1k =-时，求()f x 的单调区间.（2）求证：l 不经过点()0,0.（3）当1k =时，设点()()(),0A t f t t >，()()0,C f t ，()0,0O ，B 为l 与y 轴的交点，ACO S 与ABOS 分别表示ACO △与ABO 的面积．是否存在点A 使得215ACO ABO S S =△△成立？若存在，这样的点A 有几个？（参考数据：1.09ln31.10<<，1.60ln51.61<<，1.94ln71.95<<）21.已知集合(){}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数．给定数列128:,,,A a a a ，和序列12:,,s T T T Ω ，其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ，对数列A 进行如下变换：将A 的第1111,,,i j k w 项均加1，其余项不变，得到的数列记作()1T A ；将()1T A 的第2222,,,i j k w 项均加1，其余项不变，得到数列记作()21T T A ；……；以此类推，得到()21s T T T A ，简记为()A Ω．（1）给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω，写出()A Ω；（2）是否存在序列Ω，使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++，若存在，写出一个符合条件的Ω；若不存在，请说明理由；（3）若数列A 的各项均为正整数，且1357a a a a +++为偶数，求证：“存在序列Ω，使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”．绝密★本科目考试启用前2024年普通高等学校招生全国统一考试（北京卷）数学本试卷共12页，150分.考试时长120分钟.考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回.第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项．1.已知集合{|31}M x x =-<<，{|14}N x x =-≤<，则M N ⋃=（）A.{}11x x -≤< B.{}3x x >-C.{}|34x x -<< D.{}4x x <【答案】C 【解析】【分析】直接根据并集含义即可得到答案.【详解】由题意得{}|34M x x N ⋃=-<<.故选：C.2.已知1i iz=--，则z =（）．A.1i --B.1i-+ C.1i- D.1i+【答案】C 【解析】【分析】直接根据复数乘法即可得到答案.【详解】由题意得()i 1i i 1z =--=-.故选：C.3.圆22260x y x y +-+=的圆心到直线20x y -+=的距离为（）A.B.2C.3D.【答案】D 【解析】【分析】求出圆心坐标，再利用点到直线距离公式即可.【详解】由题意得22260x y x y +-+=，即()()221310x y -++=，则其圆心坐标为()1,3-，则圆心到直线20x y -+==故选：D.4.在(4x -的展开式中，3x 的系数为（）A.6B.6- C.12D.12-【答案】A 【解析】【分析】写出二项展开式，令432r-=，解出r 然后回代入二项展开式系数即可得解.【详解】(4x 的二项展开式为(()()442144C C 1,0,1,2,3,4r rrr rr r T xxr --+==-=，令432r-=，解得2r =，故所求即为()224C 16-=.故选：A.5.设a ，b 是向量，则“()()·0a b a b +-=”是“a b =- 或a b = ”的（）．A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据向量数量积分析可知()()0a b a b +⋅-= 等价于a b =，结合充分、必要条件分析判断.【详解】因为()()220a b a b a b +⋅-=-= ，可得22a b = ，即a b = ，可知()()0a b a b +⋅-= 等价于a b = ，若a b = 或a b =- ，可得a b =，即()()0a b a b +⋅-= ，可知必要性成立；若()()0a b a b +⋅-= ，即a b =，无法得出a b = 或a b =- ，例如()()1,0,0,1a b ==，满足a b = ，但a b ≠ 且a b ≠- ，可知充分性不成立；综上所述，“()()0a b a b +⋅-=”是“a b ≠ 且a b ≠- ”的必要不充分条件.故选：B.6.设函数()()sin 0f x x ωω=>.已知()11f x =-，()21f x =，且12x x -的最小值为π2，则ω=（）A .1B.2C.3D.4【答案】B 【解析】【分析】根据三角函数最值分析周期性，结合三角函数最小正周期公式运算求解.【详解】由题意可知：1x 为()f x 的最小值点，2x 为()f x 的最大值点，则12minπ22T x x -==，即πT =，且0ω>，所以2π2Tω==.故选：B.7.生物丰富度指数1ln S d N-=是河流水质的一个评价指标，其中,S N 分别表示河流中的生物种类数与生物个体总数.生物丰富度指数d 越大，水质越好．如果某河流治理前后的生物种类数S 没有变化，生物个体总数由1N 变为2N ，生物丰富度指数由2.1提高到3.15，则（）A.2132N N =B.2123N N =C.2321N N = D.3221N N =【答案】D 【解析】【分析】根据题意分析可得12112.1,3.15ln ln S S N N --==，消去S 即可求解.【详解】由题意得12112.1, 3.15ln ln S S N N --==，则122.1ln 3.15ln N N =，即122ln 3ln N N =，所以3221N N =.故选：D.8.如图，在四棱锥P ABCD -中，底面ABCD 是边长为4的正方形，4PA PB ==，PC PD ==该棱锥的高为（）.A.1B.2C.D.【答案】D 【解析】【分析】取点作辅助线，根据题意分析可知平面PEF ⊥平面ABCD ，可知⊥PO 平面ABCD ，利用等体积法求点到面的距离.【详解】如图，底面ABCD 为正方形，当相邻的棱长相等时，不妨设4,PA PB AB PC PD =====，分别取,AB CD 的中点,E F ，连接,,PF EF ，则,PE AB EF AB ⊥⊥，且PE EF E ⋂=，,PE EF ⊂平面PEF ，可知AB ⊥平面PEF ，且AB ⊂平面ABCD ，所以平面PEF ⊥平面ABCD ，过P 作EF 的垂线，垂足为O ，即PO EF ⊥，由平面PEF 平面ABCD EF =，PO ⊂平面PEF ，所以⊥PO 平面ABCD ，由题意可得：2,4PE PF EF ===，则222PE PF EF +=，即PE PF ⊥，则1122PE PF PO EF ⋅=⋅，可得PE PF PO EF⋅==，当相对的棱长相等时，不妨设4PA PC ==，PB PD ==，因为BD PB PD ==+，此时不能形成三角形PBD ，与题意不符，这样情况不存在.故选：D.9.已知()11,x y ，()22,x y 是函数2x y =的图象上两个不同的点，则（）A.12122log 22y y x x ++< B.12122log 22y y x x ++>C.12212log 2y y x x +<+ D.12212log 2y y x x +>+【答案】B 【解析】【分析】根据指数函数和对数函数的单调性结合基本不等式分析判断AB ；举例判断CD 即可.【详解】由题意不妨设12x x <，因为函数2x y =是增函数，所以12022x x <<，即120y y <<，对于选项AB ：可得121222222x x x x ++>=，即12122202x x y y ++>>，根据函数2log y x =是增函数，所以121212222log log 222x x y y x x+++>=，故B 正确，A 错误；对于选项D ：例如120,1x x ==，则121,2y y ==，可得()12223log log 0,122y y +=∈，即12212log 12y y x x +<=+，故D 错误；对于选项C ：例如121,x x =-=-，则1211,24y y ==，可得()122223log log log 332,128y y +==-∈--，即12212log 32y y x x +>-=+，故C 错误，故选：B.10.已知()(){}2,|,12,01M x y y x t xx x t ==+-≤≤≤≤是平面直角坐标系中的点集.设d 是M 中两点间距离的最大值，S 是M 表示的图形的面积，则（）A.3d =，1S <B.3d =，1S >C.d =，1S <D.d =，1S >【答案】C 【解析】【分析】先以t 为变量，分析可知所求集合表示的图形即为平面区域212y x y x x ⎧≤⎪≥⎨⎪≤≤⎩，结合图形分析求解即可.【详解】对任意给定[]1,2x ∈，则()210xx x x -=-≥，且[]0,1t ∈，可知()222x x t x x x x x x ≤+-≤+-=，即2x y x ≤≤，再结合x 的任意性，所以所求集合表示的图形即为平面区域212y x y x x ⎧≤⎪≥⎨⎪≤≤⎩，如图阴影部分所示，其中()()()1,1,2,2,2,4A B C，可知任意两点间距离最大值d AC ==；阴影部分面积11212ABC S S <=⨯⨯△.故选：C.【点睛】方法点睛：数形结合的重点是“以形助数”，在解题时要注意培养这种思想意识，做到心中有图，见数想图，以开拓自己的思维．使用数形结合法的前提是题目中的条件有明确的几何意义，解题时要准确把握条件、结论与几何图形的对应关系，准确利用几何图形中的相关结论求解．第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11.抛物线216y x =的焦点坐标为________．【答案】()4,0【解析】【分析】形如()22,0y px p =≠的抛物线的焦点坐标为,02p ⎛⎫⎪⎝⎭，由此即可得解.【详解】由题意抛物线的标准方程为216y x =，所以其焦点坐标为()4,0.故答案为：()4,0.12.在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于原点对称.若ππ,63α⎡⎤∈⎢⎥⎣⎦，则cos β的最大值为________．【答案】12-##0.5-【解析】【分析】首先得出π2π,Z k k βα=++∈，结合三角函数单调性即可求解最值.【详解】由题意π2π,Z k k βα=++∈，从而()cos cos π2πcos k βαα=++=-，因为ππ,63α⎡⎤∈⎢⎥⎣⎦，所以cos α的取值范围是1,22⎡⎢⎣⎦，cos β的取值范围是1,22⎡⎤--⎢⎥⎣⎦，当且仅当π3α=，即4π2π,Z 3k k β=+∈时，cos β取得最大值，且最大值为12-.故答案为：12-.13.若直线()3y k x =-与双曲线2214x y -=只有一个公共点，则k 的一个取值为________．【答案】12（或12-，答案不唯一）【解析】【分析】联立直线方程与双曲线方程，根据交点个数与方程根的情况列式即可求解.【详解】联立()22143x y y k x ⎧-=⎪⎨⎪=-⎩，化简并整理得：()222214243640k x k x k -+--=，由题意得2140k -=或()()()2222Δ244364140k k k =++-=，解得12k =±或无解，即12k =±，经检验，符合题意.故答案为：12（或12-，答案不唯一）.14.汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器，其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列，底面直径依次为65mm,325mm,325mm ，且斛量器的高为230mm ，则斗量器的高为______mm ，升量器的高为________mm ．【答案】①.23②.57.5##1152【解析】【分析】根据体积为公比为10的等比数列可得关于高度的方程组，求出其解后可得前两个圆柱的高度.【详解】设升量器的高为1h ，斗量器的高为2h （单位都是mm ），则2222212325325ππ230221065325ππ22h h h ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭==⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，故223mm h =，1115mm 2h =.故答案为：11523mm,mm 2.15.设与是两个不同的无穷数列，且都不是常数列.记集合{}*|,N k k M k a b k ==∈，给出下列4个结论：①若与均为等差数列，则M 中最多有1个元素；②若与均为等比数列，则中最多有2个元素；③若为等差数列，为等比数列，则M 中最多有3个元素；④若为递增数列，为递减数列，则M 中最多有1个元素.其中正确结论的序号是______.【答案】①③④【解析】【分析】利用两类数列的散点图的特征可判断①④的正误，利用反例可判断②的正误，结合通项公式的特征及反证法可判断③的正误.【详解】对于①，因为{}{},n n a b 均为等差数列，故它们的散点图分布在直线上，而两条直线至多有一个公共点，故M 中至多一个元素，故①正确.对于②，取()112,2,n n n n a b --==--则{}{},n n a b 均为等比数列，但当n 为偶数时，有()1122n n n n a b --===--，此时M 中有无穷多个元素，故②错误.对于③，设()0,1nn b AqAq q =≠≠±，()0n a kn b k =+≠，若M 中至少四个元素，则关于n 的方程n Aq kn b =+至少有4个不同的正数解，若0,1q q >≠，则由n y Aq =和y kn b =+的散点图可得关于n 的方程n Aq kn b =+至多有两个不同的解，矛盾；若0,1q q <≠±，考虑关于n 的方程n Aq kn b =+奇数解的个数和偶数解的个数，当n Aq kn b =+有偶数解，此方程即为nA q kn b =+，方程至多有两个偶数解，且有两个偶数解时ln 0Ak q >，否则ln 0Ak q <，因,ny A q y kn b ==+单调性相反，方程nA q kn b =+至多一个偶数解，当n Aq kn b =+有奇数解，此方程即为nA q kn b -=+，方程至多有两个奇数解，且有两个奇数解时ln 0Ak q ->即ln 0Ak q <否则ln 0Ak q >，因,ny A q y kn b =-=+单调性相反，方程nA q kn b =+至多一个奇数解，因为ln 0Ak q >，ln 0Ak q <不可能同时成立，故n Aq kn b =+不可能有4个不同的整数解，即M 中最多有3个元素，故③正确.对于④，因为{}n a 为递增数列，{}n b 为递减数列，前者散点图呈上升趋势，后者的散点图呈下降趋势，两者至多一个交点，故④正确.故答案为：①③④.【点睛】思路点睛：对于等差数列和等比数列的性质的讨论，可以利用两者散点图的特征来分析，注意讨论两者性质关系时，等比数列的公比可能为负，此时要注意合理转化.三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.16.在ABC V 中，内角,,A B C 的对边分别为,,a b c ，A ∠为钝角，7a =，sin 2cos 7B b B =．（1）求A ∠；（2）从条件①、条件②、条件③这三个条件中选择一个作为已知，使得ABC V 存在，求ABC V 的面积．条件①：7b =；条件②：13cos 14B =；条件③：sin c A =注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．【答案】（1）2π3A =；（2）选择①无解；选择②和③△ABC 面积均为1534.【解析】【分析】（1）利用正弦定理即可求出答案；（2）选择①，利用正弦定理得3B π=，结合（1）问答案即可排除；选择②，首先求出33sin 14B =，再代入式子得3b =，再利用两角和的正弦公式即可求出sinC ，最后利用三角形面积公式即可；选择③，首先得到5c =，再利用正弦定理得到sin 14C =，再利用两角和的正弦公式即可求出sin B ，最后利用三角形面积公式即可；【小问1详解】由题意得32sin cos cos 7B B B =，因为A 为钝角，则cos 0B ≠，则32sin 7B b =，则7sin sin sin 37b a BA A ===，解得3sin 2A =，因为A 为钝角，则2π3A =.【小问2详解】选择①7b =，则sin 714142B b ==⨯=，因为2π3A =，则B 为锐角，则3B π=，此时πA B +=，不合题意，舍弃；选择②13cos 14B =，因为B为三角形内角，则33sin 14B ==，则代入32sin 7B b =得3332147b ⨯=，解得3b =，()2π2π2πsin sin sin sin cos cos sin 333C A B B B B⎛⎫=+=+=+ ⎪⎝⎭13121421414⎛⎫=⨯+-⨯=⎪⎝⎭,则11sin 7322144ABC S ab C ==⨯⨯⨯=.选择③sin c A =2c ⨯=，解得5c =，则由正弦定理得sin sin a c A C =5sin 32C =，解得53sin 14C =，因为C 为三角形内角，则11cos 14C ==，则()2π2π2πsin sin sin sin cos cos sin 333B A C C C C ⎛⎫=+=+=+ ⎪⎝⎭3111533321421414⎛⎫=⨯+-⨯=⎪⎝⎭，则11sin 7522144ABC S ac B ==⨯⨯=△17.如图，在四棱锥P ABCD -中，//BC AD ，1AB BC ==，3AD =,点E 在AD 上，且PE AD ⊥，2PE DE ==．（1）若F 为线段PE 中点，求证：//BF 平面PCD ．（2）若AB ⊥平面PAD ，求平面PAB 与平面PCD 夹角的余弦值．【答案】（1）证明见解析（2）3030【解析】【分析】（1）取PD 的中点为S ，接,SF SC ，可证四边形SFBC 为平行四边形，由线面平行的判定定理可得//BF 平面PCD .（2）建立如图所示的空间直角坐标系，求出平面APB 和平面PCD 的法向量后可求夹角的余弦值.【小问1详解】取PD 的中点为S ，接,SF SC ，则1//,12SF ED SF ED ==，而//,2ED BC ED BC =，故//,SF BC SF BC =，故四边形SFBC 为平行四边形，故//BF SC ，而BF ⊄平面PCD ，SC ⊂平面PCD ，所以//BF 平面PCD .【小问2详解】因为2ED =，故1AE =，故//,=AE BC AE BC ，故四边形AECB 为平行四边形，故//CE AB ，所以CE ⊥平面PAD ，而,PE ED ⊂平面PAD ，故,CE PE CE ED ⊥⊥，而PE ED ⊥，故建立如图所示的空间直角坐标系，则()()()()()0,1,0,1,1,0,1,0,0,0,2,0,0,0,2A B C D P --，则()()()()0,1,2,1,1,2,1,0,2,0,2,2,PA PB PC PD =--=--=-=-设平面PAB 的法向量为(),,m x y z =，则由0m PA m PB ⎧⋅=⎪⎨⋅=⎪⎩可得2020y z x y z --=⎧⎨--=⎩，取()0,2,1m =- ，设平面PCD 的法向量为(),,n a b c =，则由0n PC n PD ⎧⋅=⎪⎨⋅=⎪⎩可得20220a b b c -=⎧⎨-=⎩，取()2,1,1n = ，故cos ,30m n ==-，故平面PAB 与平面PCD 夹角的余弦值为303018.某保险公司为了了解该公司某种保险产品的索赔情况，从合同险期限届满的保单中随机抽取1000份，记录并整理这些保单的索赔情况，获得数据如下表：赔偿次数01234单数800100603010假设：一份保单的保费为0.4万元；前3次索赔时，保险公司每次赔偿0.8万元；第四次索赔时，保险公司赔偿0.6万元.假设不同保单的索赔次数相互独立.用频率估计概率.（1）估计一份保单索赔次数不少于2的概率；（2）一份保单的毛利润定义为这份保单的保费与赔偿总金额之差.（i ）记X 为一份保单的毛利润，估计X 的数学期望()E X ；（ⅱ）如果无索赔的保单的保费减少，有索赔的保单的保费增加20%，试比较这种情况下一份保单毛利润的数学期望估计值与（i ）中()E X 估计值的大小．（结论不要求证明）【答案】（1）110（2）(i)0.122万元；(ii)这种情况下一份保单毛利润的数学期望估计值大于（i ）中()E X 估计值【解析】【分析】（1）根据题设中的数据可求赔偿次数不少2的概率;（2）（ⅰ）设ξ为赔付金额，则ξ可取0,0.8,0.1.6,2.4,3，用频率估计概率后可求ξ的分布列及数学期望，从而可求()E X .（ⅱ）先算出下一期保费的变化情况，结合（1）的结果可求()E Y ，从而即可比较大小得解.【小问1详解】设A 为“随机抽取一单，赔偿不少于2次”，由题设中的统计数据可得()603010180010060301010P A ++==++++.【小问2详解】（ⅰ）设ξ为赔付金额，则ξ可取0,0.8,1.6,2.4,3，由题设中的统计数据可得()()800410010,0.810005100010P P ξξ======，603( 1.6)100050P ξ===，303( 2.4)1000100P ξ===，101(3)1000100P ξ===，故()4133100.8 1.6 2.430.27851050100100E ξ=⨯+⨯+⨯+⨯+⨯=故()0.40.2780.122E X =-=（万元）.（ⅱ）由题设保费的变化为410.496%0.4 1.20.403255⨯⨯+⨯⨯=，故()0.1220.40320.40.1252E Y =+-=（万元），从而()()E X E Y <.19.已知椭圆E ：()222210+=>>x y a b a b，以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点()(0,t t >且斜率存在的直线与椭圆E 交于不同的两点,A B ，过点A 和()0,1C 的直线AC 与椭圆E 的另一个交点为D ．（1）求椭圆E 的方程及离心率；（2）若直线BD 的斜率为0，求t 的值．【答案】（1）221,422x y e +==（2）2t =【解析】【分析】（1）由题意得b c ==，进一步得a ，由此即可得解；（2）设(:,0,AB y kx t k t =+≠>，()()1122,,,A x y B x y ，联立椭圆方程，由韦达定理有2121222424,1221kt t x x x x k k --+==++，而()121112:y y AD y x x y x x -=-++，令0x =，即可得解.【小问1详解】由题意b c ===，从而2a ==，所以椭圆方程为22142x y +=，离心率为2e =；【小问2详解】直线AB 斜率不为0，否则直线AB与椭圆无交点，矛盾，从而设(:,0,AB y kx t k t =+≠>，()()1122,,,A x y B x y ，联立22142x y y kx t ⎧+=⎪⎨⎪=+⎩，化简并整理得()222124240k x ktx t +++-=，由题意()()()222222Δ1682128420k t k t k t=-+-=+->，即,k t 应满足22420kt +->，所以2121222424,1221kt t x x x x k k --+==++，若直线BD 斜率为0，由椭圆的对称性可设()22,D x y -，所以()121112:y y AD y x x y x x -=-++，在直线AD 方程中令0x =，得()()()()2122112121221121212422214C k t x kx t x kx t kx x t x x x y x y y t x x x x x x kt t-++++++====+==+++-，所以2t =，此时k 应满足222424200k t k k ⎧+-=->⎨≠⎩，即k 应满足22k <-或22k >，综上所述，2t =满足题意，此时22k <-或22k >.20.设函数()()()ln 10f x x k x k =++≠，直线l 是曲线()y f x =在点()()(),0t f t t >处的切线．（1）当1k =-时，求()f x 的单调区间.（2）求证：l 不经过点()0,0.（3）当1k =时，设点()()(),0A t f t t >，()()0,C f t ，()0,0O ，B 为l 与y 轴的交点，ACO S 与ABOS 分别表示ACO △与ABO 的面积．是否存在点A 使得215ACO ABO S S =△△成立？若存在，这样的点A 有几个？（参考数据：1.09ln31.10<<，1.60ln51.61<<，1.94ln71.95<<）【答案】（1）单调递减区间为(1,0)-，单调递增区间为(0,)+∞.（2）证明见解析（3）2【解析】【分析】（1）直接代入1k =-，再利用导数研究其单调性即可；（2）写出切线方程()1()(0)1k y f t x t t t ⎛⎫-=+-> ⎪+⎝⎭，将(0,0)代入再设新函数()ln(1)1tF t t t=+-+，利用导数研究其零点即可；（3）分别写出面积表达式，代入215ACO ABO S S = 得到13ln(1)21501tt t t+--=+，再设新函数15()13ln(1)2(0)1th t t t t t=+-->+研究其零点即可.【小问1详解】1()ln(1),()1(1)11x f x x x f x x x x'=-+=-=>-++，当()1,0x ∈-时，′<0；当∈0,+∞，′>0；()f x ∴在(1,0)-上单调递减，在(0,)+∞上单调递增.则()f x 的单调递减区间为(1,0)-，单调递增区间为(0,)+∞.【小问2详解】()11k f x x '=++，切线l 的斜率为11k t++，则切线方程为()1()(0)1k y f t x t t t ⎛⎫-=+-> ⎪+⎝⎭，将(0,0)代入则()1,()111k k f t t f t t t t ⎛⎫⎛⎫-=-+=+ ⎪ ⎪++⎝⎭⎝⎭，即ln(1)1k t k t t tt ++=++，则ln(1)1t t t +=+，ln(1)01tt t +-=+，令()ln(1)1tF t t t=+-+，假设l 过(0,0)，则()F t 在(0,)t ∈+∞存在零点.2211()01(1)(1)t t t F t t t t +-'=-=>+++，()F t ∴在(0,)+∞上单调递增，()(0)0F t F >=，()F t ∴在(0,)+∞无零点，∴与假设矛盾，故直线l 不过(0,0).【小问3详解】1k =时，12()ln(1),()1011x f x x x f x x x+'=++=+=>++.1()2ACO S tf t = ，设l 与y 轴交点B 为(0,)q ，0t >时，若0q <，则此时l 与()f x 必有交点，与切线定义矛盾.由（2）知0q ≠.所以0q >，则切线l 的方程为()()1ln 111y t t x t t ⎛⎫--+=+- ⎪+⎝⎭，令0x =，则ln(1)1t y q y t t ===+-+.215ACO ABO S S = ，则2()15ln(1)1t tf t t t t ⎡⎤=+-⎢⎥+⎣⎦，13ln(1)21501t t t t ∴+--=+，记15()13ln(1)2(0)1th t t t t t=+-->+，∴满足条件的A 有几个即()h t 有几个零点.()()()()()()()()2222221313221152141315294211111t t t t t t t h t t t t t t +-++--+--+-=--=++'==+++，当10,2t ⎛⎫∈ ⎪⎝⎭时，()0h t '<，此时()h t 单调递减；当1,42t ⎛⎫∈⎪⎝⎭时，()0h t '>，此时()h t 单调递增；当()4,t ∞∈+时，()0h t '<，此时()h t 单调递减；因为1(0)0,0,(4)13ln 520131.6200.802h h h ⎛⎫==-⨯-=> ⎪⎝⎭，15247272(24)13ln 254826ln 548261.614820.5402555h ⨯=--=--<⨯--=-<，所以由零点存在性定理及()h t 的单调性，()h t 在1,42⎛⎫⎪⎝⎭上必有一个零点，在(4,24)上必有一个零点，综上所述，()h t 有两个零点，即满足215ACO ABO S S =的A 有两个.【点睛】关键点点睛：本题第二问的关键是采用的是反证法，转化为研究函数零点问题.21.已知集合()}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数．给定数列128:,,,A a a a ，和序列12:,,s T T T Ω ，其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ，对数列A 进行如下变换：将A 的第1111,,,i j k w 项均加1，其余项不变，得到的数列记作()1T A ；将()1T A 的第2222,,,i j k w 项均加1，其余项不变，得到数列记作()21T T A ；……；以此类推，得到()21s T T T A ，简记为()A Ω．（1）给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω，写出()A Ω；（2）是否存在序列Ω，使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++，若存在，写出一个符合条件的Ω；若不存在，请说明理由；（3）若数列A 的各项均为正整数，且1357a a a a +++为偶数，求证：“存在序列Ω，使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”．【答案】（1）():3,4,4,5,8,4,3,10A Ω（2）不存在符合条件的Ω，理由见解析（3）证明见解析【解析】【分析】（1）直接按照()ΩA 的定义写出()ΩA 即可；（2）解法一：利用反证法，假设存在符合条件的Ω，由此列出方程组，进一步说明方程组无解即可；解法二：对于任意序列，所得数列之和比原数列之和多4，可知序列Ω共有8项，可知：()()2122128,1,2,3,4n n n n b b a a n --+-+==，检验即可；（3）解法一：分充分性和必要性两方面论证；解法二：若12345678a a a a a a a a +=+=+=+，分类讨论1357,,,a a a a 相等得个数，结合题意证明即可；若存在序列Ω，使得()ΩA 为常数列，结合定义分析证明即可.【小问1详解】因为数列:1,3,2,4,6,3,1,9A ，由序列()11,3,5,7T 可得()1:2,3,3,4,7,3,2,9T A ；由序列()22,4,6,8T 可得()21:2,4,3,5,7,4,2,10T T A ；由序列()31,3,5,7T 可得(321:3,4,4,5,8,4,3,10T T T A ；所以()Ω:3,4,4,5,8,4,3,10A .【小问2详解】解法一：假设存在符合条件的Ω，可知()ΩA 的第1,2项之和为12a a s ++，第3,4项之和为34a a s ++，则()()()()121234342642a a a a sa a a a s⎧+++=++⎪⎨+++=++⎪⎩，而该方程组无解，故假设不成立，故不存在符合条件的Ω；解法二：由题意可知：对于任意序列，所得数列之和比原数列之和多4，假设存在符合条件的Ω，且()128Ω:,,,A b b b ⋅⋅⋅，因为2642824484+++++++=，即序列Ω共有8项，由题意可知：()()2122128,1,2,3,4n n n n b b a a n --+-+==，检验可知：当2,3n =时，上式不成立，即假设不成立，所以不存在符合条件的Ω.【小问3详解】解法一：我们设序列()21...s T T T A 为{}(),18s n a n ≤≤，特别规定()0,18nn aa n =≤≤.必要性：若存在序列12:,,s T T T Ω ，使得()ΩA 的各项都相等.则,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a =======，所以,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+.根据()21...s T T T A 的定义，显然有,21,21,211,21s j s j s j s j a a a a ----+=++，这里1,2,3,4j =，1,2,...s =.所以不断使用该式就得到12345678,1,2s s a a a a a a a a a a s +=+=+=+=+-，必要性得证.充分性：若12345678a a a a a a a a +=+=+=+.由已知，1357a a a a +++为偶数，而12345678a a a a a a a a +=+=+=+，所以()()24681213574a a a a a a a a a a +++=+-+++也是偶数.我们设()21...s T T T A 是通过合法的序列Ω的变换能得到的所有可能的数列()ΩA 中，使得,1,2,3,4,5,7,8s s s s s s s s a a a a a a a a -+-+--最小的一个.上面已经说明,21,21,211,21s j s j s j s j a a a a ----+=++，这里1,2,3,4j =，1,2,...s =.从而由12345678a a a a a a a a +=+=+=+可得,1,2,3,4,5,6,7,812s s s s s s s s a a a a a a a a a a s +=+=+=+=++.同时，由于t t t t i j k w +++总是偶数，所以,1,3,5,7t t t t a a a a +++和,2,4,6,8t t t t a a a a +++的奇偶性保持不变，从而,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数.下面证明不存在1,2,3,4j =使得,21,22s j s j a a --≥.假设存在，根据对称性，不妨设1j =，,21,22s j s j a a --≥，即,1,22s s a a -≥.情况1：若,3,4,5,6,7,80s s s s s s a a a a a a -+-+-=，则由,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数，知,1,24s s a a -≥.对该数列连续作四次变换()()()()2,3,5,8,2,4,6,8,2,3,6,7,2,4,5,7后，新的4,14,24,34,44,54,64,74,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-减少4，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾；情况2：若,3,4,5,6,7,80s s s s s s a a a a a a -+-+->，不妨设,3,40s s a a ->.情况2-1：如果,3,41s s a a -≥，则对该数列连续作两次变换()()2,4,5,7,2,4,6,8后，新的2,12,22,32,42,52,62,72,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-至少减少2，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾；情况2-2：如果,4,31s s a a -≥，则对该数列连续作两次变换()()2,3,5,8,2,3,6,7后，新的2,12,22,32,42,52,62,72,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-至少减少2，这与,1,2,3,4,5,7,8s s s s s s s s a a a a a a a a -+-+--的最小性矛盾.这就说明无论如何都会导致矛盾，所以对任意的1,2,3,4j =都有,21,21s j s j a a --≤.假设存在1,2,3,4j =使得,21,21s j s j a a --=，则,21,2s j s j a a -+是奇数，所以,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+都是奇数，设为21N +.则此时对任意1,2,3,4j =，由,21,21s j s j a a --≤可知必有{}{},21,2,,1s j s j a a N N -=+.而,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数，故集合{},s m m a N =中的四个元素,,,i j k w 之和为偶数，对该数列进行一次变换(),,,i j k w ，则该数列成为常数列，新的1,11,21,31,41,51,61,71,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-等于零，比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-更小，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾.综上，只可能(),21,201,2,3,4s j s j a a j --==，而,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+，故{}(),Ωs na A =是常数列，充分性得证.解法二：由题意可知：Ω中序列的顺序不影响()ΩA 的结果，且()()()()12345678,,,,,,,a a a a a a a a 相对于序列也是无序的，（ⅰ）若12345678a a a a a a a a +=+=+=+，不妨设1357a a a a ≤≤≤，则2468a a a a ≥≥≥，①当1357a a a a ===，则8642a a a a ===，分别执行1a 个序列()2,4,6,8、2a 个序列()1,3,5,7，可得1212121212121212,,,,,,,a a a a a a a a a a a a a a a a ++++++++，为常数列，符合题意；②当1357,,,a a a a 中有且仅有三个数相等，不妨设135a a a ==，则246a a a ==，即12121278,,,,,,,a a a a a a a a ，分别执行2a 个序列()1,3,5,7、7a 个序列()2,4,6,8可得122712212272778,,,,,,,a a a a a a a a a a a a a a a a ++++++++，即1227122712272712,,,,,,,a a a a a a a a a a a a a a a a ++++++++，因为1357a a a a +++为偶数，即173a a +为偶数，可知17,a a 的奇偶性相同，则*712a a -∈N ，分别执行712a a -个序列()1,3,5,7，()1,3,6,8，()2,3,5,8，()1,4,5,8，可得72172172172172172172173232323232323232,,,,,,,22222222a a a a a a a a a a a a a a a a a a a a a a a+-+-+-+-+-+-+-+，为常数列，符合题意；③若1357a a a a =<=，则2468a a a a =>=，即12125656,,,,,,,a a a a a a a a ，分别执行5a 个()1,3,6,8、1a 个()2,4,5,7，可得1512151215561556,,,,,,,a a a a a a a a a a a a a a a a ++++++++，因为1256a a a a +=+，可得1512151215121512,,,,,,,a a a a a a a a a a a a a a a a ++++++++，即转为①，可知符合题意；④当1357,,,a a a a 中有且仅有两个数相等，不妨设13a a =，则24a a =，即12125678,,,,,,,a a a a a a a a ，分别执行1a 个()2,4,5,7、5a 个()1,3,6,8，可得1512151215561758,,,,,,,a a a a a a a a a a a a a a a a ++++++++，且1256a a a a +=+，可得1512151215121758,,,,,,,a a a a a a a a a a a a a a a a ++++++++，因为13571572a a a a a a a +++=++为偶数，可知57,a a 的奇偶性相同，则()()()()1515151715743a a a a a a a a a a a +++++++=++为偶数，且15151517a a a a a a a a +=+=+<+，即转为②，可知符合题意；⑤若1357a a a a <<<，则2468a a a a >>>，即12345678,,,,,,,a a a a a a a a ，分别执行1a 个()2,3,5,8、3a 个()1,4,6,7，可得1312133415363718,,,,,,,a a a a a a a a a a a a a a a a ++++++++，且1234a a a a +=+，可得1312131215363718,,,,,,,a a a a a a a a a a a a a a a a ++++++++，因为1357a a a a +++为偶数，则()()()()()()131315371313572a a a a a a a a a a a a a a +++++++=+++++为偶数，且13131537a a a a a a a a +=+<+<+，即转为④，可知符合题意；综上所述：若12345678a a a a a a a a +=+=+=+，则存在序列Ω，使得()ΩA 为常数列；（ⅱ）若存在序列Ω，使得()ΩA 为常数列，因为对任意()128Ω:,,,A b b b ⋅⋅⋅，均有()()()()12123434b b a a b b a a +-+=+-+()()()()56567878b b a a b b a a =+-+=+-+成立，若()ΩA 为常数列，则12345678b b b b b b b b +=+=+=+，所以12345678a a a a a a a a +=+=+=+；综上所述：“存在序列Ω，使得()ΩA 为常数列”的充要条件为“12345678a a a a a a a a +=+=+=+”.【点睛】关键点点睛：本题第三问的关键在于对新定义的理解，以及对其本质的分析.。

(中考精品卷)江苏省常州市中考数学真题(解析版)

常州市2022年初中学业水平考试数学试题一、选择题1. 2022的相反数是（）A. 2022B. 2022-C. 12022D. 12022- 【答案】B【解析】【分析】根据相反数的定义直接求解．【详解】解：实数2022的相反数是2022-，故选：B ．【点睛】本题主要考查相反数的定义，解题的关键是熟练掌握相反数的定义．2. x 的取值范围是（）A. 1≥xB. 1x >C. 0x ≥D. 0x >【答案】A【解析】0)…进行计算即可．【详解】解：由题意得： 10x -…，1x ∴…，故选：A ．0)…是解题的关键． 3. 下列图形中，为圆柱的侧面展开图的是（）A. B.C. D.【答案】D【解析】【分析】根据题意，注意其按圆柱的侧面沿它的一条母线剪开，分析得到图形的性质，易得答案．【详解】解：根据题意，把圆柱的侧面沿它的一条母线剪开展在一个平面上，得到其侧面展开图是对边平行且相等的四边形；又有母线垂直于上下底面，故可得是矩形．故选：D ．【点睛】本题考查的是圆柱的展开图，解题的关键是需要对圆柱有充分的理解；难度不大．4. 如图，在△ABC 中，D ，E 分别是AB ，AC 边的中点，若DE ＝2，则BC 的长度是（）A. 6B. 5C. 4D. 3 【答案】C【解析】【分析】直接利用三角形中位线定理得出答案．【详解】∵在△ABC 中，D ，E 分别是AB ，AC 边的中点，∴DE 是△ABC 的中位线，∵DE ＝2，∴BC 的长度是：4．故选：C ．【点睛】此题主要考查了三角形的中位线，正确把握三角形中位线定理是解题关键． 5. 某城市市区人口x 万人，市区绿地面积50万平方米，平均每人拥有绿地y 平方米，则y 与x 之间的函数表达式为（）A. 50y x =+B. 50y x =C. 50y x =D.50=x y 【答案】C【解析】【分析】根据：平均每人拥有绿地y =总面积总人数，列式求解．【详解】解：依题意，得：平均每人拥有绿地50y x=．故选：C 【点睛】本题考查了反比例函数，解题的关键是掌握题目中数量之间的相互关系． 6. 如图，斑马线作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是（）A. 垂线段最短B. 两点确定一条直线C. 过一点有且只有一条直线与已知直线垂直D. 过直线外一点有且只有一条直线与已知直线平行【答案】A【解析】【分析】根据垂线段最短解答即可．【详解】解：行人沿垂直马路的方向走过斑马线，体现的数学依据是垂线段最短，故选：A ．【点睛】本题考查垂线段最短，熟知垂线段最短是解答的关键．7. 在平面直角坐标系xOy 中，点A 与点1A 关于x 轴对称，点A 与点2A 关于y 轴对称．已知点1(1,2)A ，则点2A 的坐标是（）A. (2,1)-B. (2,1)--C. (1,2)-D.(1,2)-- 【答案】D【解析】的A点坐标，即可得出答案．【分析】直接利用关于x，y轴对称点的性质分别得出A，2【详解】解：∵点1A的坐标为（1，2），点A与点1A关于x轴对称，∴点A的坐标为（1，-2），A关于y轴对称，∵点A与点2A的坐标是（-1，﹣2）．∴点2故选：D．【点睛】此题主要考查了关于x，y轴对称点的坐标，正确掌握关于坐标轴对称点的性质是解题关键．km的加速时间和满电续航里程8. 某汽车评测机构对市面上多款新能源汽车的0~100/h进行了性能评测，评测结果绘制如下，每个点都对应一款新能源汽车的评测数据．已知km的加速时间的中位数是s m，满电续航里程的中位数是nkm，相应的直线将0~100/h平面分成了①、②、③、④四个区域（直线不属于任何区域）．欲将最新上市的两款新能源汽车的评测数据对应的点绘制到平面内，若以上两组数据的中位数均保持不变，则这两个点可能分别落在（）A. 区域①、②B. 区域①、③C. 区域①、④D. 区域③、④【答案】B【解析】【分析】根据中位数的性质即可作答．【详解】在添加了两款新能源汽车的测评数据之后，0~100km/h的加速时间的中位数m s，满电续航里程的中位数n km，这两组中位数的值不变，即可知这两款新能源汽车的0~100km/h的加速时间的数值分别处于直线m的上方和下方，满电续航里程的数值分别位于直线n的左侧和右侧，据此逐项判断即可：A项，两款车的0~100km/h的加速时间均在直线m下方，不符合要求，故A项错误；B项，可知这两款新能源汽车的0~100km/h的加速时间的数值分别处于直线m的上方和下方，满电续航里程的数值分别位于直线n的左侧和右侧，符合要求；C 项，两款车的满电续航里程的数值均在直线n 的左侧，不符合要求，故C 项错误；D 项，两款车的0~100km/h 的加速时间均在直线m 上方，不符合要求，故D 项错误；故选：B ．【点睛】本题考查了中位数的概念，根据中位数的值不变可知新添加的一组数据分别处在中位数的左右两侧或刚好都等于该中位数，理解这一点是解答本题的关键．二、填空题9. ___．【答案】2【解析】【分析】根据立方根的定义进行计算．【详解】解：∵23=8，，故答案为：2．10. 计算：42÷=m m _______．【答案】2m【解析】【分析】根据同底数幂的除法运算法则即可求出．【详解】解：422m m m ÷=．故答案为：2m ．【点睛】本题主要考查同底数幂的除法，掌握同底数幂的除法法则是解题的关键． 11. 分解因式：22x y xy +=______．【答案】xy (x +y )【解析】【分析】利用提公因式法即可求解．【详解】22()x y y y xy x x =++，故答案为：()xy x y +．【点睛】本题考查了用提公因式法分解因式的知识，掌握提公因式法是解答本题的关键．12. 2022年5月22日，中国科学院生物多样性委员会发布《中国生物物种名录》2022版，共收录物种及种下单元约138000个．数据138000用科学记数法表示为______．【答案】1.38×105【解析】【分析】科学记数法的表示形式为a ×10n 的形式，其中1≤|a |＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同，当原数绝对值≥10时，n 是正整数数．【详解】解：由题意可知：138000=1.38×105，故答案为：1.38×105【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a ×10n 的形式，其中1≤|a |＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．13. 如图，数轴上的点A 、B 分别表示实数a 、b ，则1a ______1b ．（填“>”、“=”或“<”）【答案】>【解析】【分析】由图可得：1a b <<，再根据不等式的性质即可判断．【详解】解：由图可得：1a b <<，由不等式的性质得：11a b>，故答案为：>．【点睛】本题考查了数轴，不等式的性质，解题的关键是掌握不等式的性质．14. 如图，在ABC 中，E 是中线AD 的中点．若AEC △的面积是1，则ABD △的面积是______．【答案】2【解析】【分析】根据ACE ∆的面积DCE =∆的面积，ABD ∆的面积ACD =∆的面积计算出各部分三角形的面积．【详解】解：AD 是BC 边上的中线，E 为AD 的中点，根据等底同高可知，ACE ∆的面积DCE =∆的面积1=，ABD ∆的面积ACD =∆的面积2AEC =∆的面积2=，故答案为：2．【点睛】本题考查了三角形的面积，解题的关键是利用三角形的中线平分三角形面积进行计算．15. 如图，将一个边长为20cm 的正方形活动框架（边框粗细忽略不计）扭动成四边形ABCD ，对角线是两根橡皮筋，其拉伸长度达到36cm 时才会断裂．若60BAD ∠=︒，则橡皮筋AC _____断裂（填“会”或“不会” 1.732≈）．【答案】不会【解析】【分析】设扭动后对角线的交点为O ，根据正方形的性质，得出扭动后的四边形为菱形，利用菱形的性质及条件，得出ABD △为等边三角形，利用勾股定理算出AO =而得到AC ，再比较即可判断．【详解】解：设扭动后对角线的交点为O ，如下图：60BAD ∠=︒ ，根据正方形的性质得，得出扭动后的四边形四边相等为菱形，20AD AB ==，ABD ∴ 为等边三角形，20BD ∴=，1102BO BD ∴==，AO ∴==根据菱形的对角线的性质：234.64AC AO ==≈，34.6436< ，AC ∴不会断裂，故答案为：不会．【点睛】本题考查了正方形的性质、菱形的判定及性质、等边三角形、勾股定理，解题的关键是要掌握菱形的判定及性质．16. 如图，ABC 是O 的内接三角形．若45ABC ∠=︒，AC =O 的半径是______．【答案】1【解析】【分析】连接OA 、OC ，根据圆周角定理得到90AOC ∠=︒，根据勾股定理计算即可．详解】解：连接OA 、OC ，45ABC ∠=︒ ，290AOC ABC ∴∠=∠=︒，222OA OC AC ∴+=，即222OA =，解得：1OA =，故答案为：1．【点睛】本题考查的是三角形的外接圆与外心，掌握圆周角定理、勾股定理是解题的关键．17. 如图，在四边形ABCD 中，90A ABC ∠=∠=︒，DB 平分ADC ∠．若1AD =，3CD =，则sin ABD ∠=______．【【解析】△为等腰三角【分析】过点D作BC的垂线交于E，证明出四边形ABED为矩形，BCD形，由勾股定理算出DE=BD=，即可求解．【详解】解：过点D作BC的垂线交于E，∴∠=︒DEB90，∠=∠=︒A ABC90∴四边形ABED为矩形，//,1∴==，DE AB AD BE∴∠=∠，ABD BDE∠，Q平分ADCBD∴∠=∠，ADB CDB，AD BE//∴∠=∠，ADB CBD∴∠CDB=∠CBDCD CB∴==，3，==AD BE1∴，CE=2∴===DEBD ∴===sin BE BDE BD ∴∠===sin ABD ∴∠=【点睛】本题考查了锐角三角函数、矩形、等腰三角形形、勾股定理、平行线的性质，解题的关键是构造直角三角形求解．18. 如图，在Rt ABC △中，90C ∠=︒，9AC =，12BC =．在Rt DEF 中，90F ∠=︒，3DF =，4EF =．用一条始终绷直的弹性染色线连接CF ，Rt DEF 从起始位置（点D 与点B 重合）平移至终止位置（点E 与点A 重合），且斜边DE 始终在线段AB 上，则Rt ABC △的外部被染色的区域面积是______．【答案】28【解析】【分析】过点F 作AB 的垂线交于G ，同时在图上标出,,M N F '如图，需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形，所以需要利用勾股定理，相似三角形、平行四边形的判定及性质，求出相应边长，即可求解．【详解】解：过点F 作AB 的垂线交于G ，同时在图上标出,,M N F '如下图：90C ∠=︒ ，9AC =，12BC =，15AB ∴==，在Rt DEF 中，90F ∠=︒，3DF =，4EF =．5DE ∴==，15510AE AB DE =-=-= ，//,EF AF EF AF ''= ，∴四边形AEFF '为平行四边形，10AE FF '∴==，11622DEF S DF EF DE GF =⋅=⋅= ，解得：125GF =， //DF AC ，,DFM ACM FDM CAM ∴∠=∠∠=∠，DFM ACM ∴ ∽，13DM DF AM AC ∴==， 1115344DM AM AB ∴===， //BC AF ' ，同理可证：ANF DNC ' ∽，13AF AN BC DN '∴==， 345344DN AN AB ∴===， 451530444MN DN DM ∴=-=-=， Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形，故答案为：28．【点睛】本题考查了直角三角形，相似三角形的判定及性质、勾股定理、平行四边形的判定及性质，解题的关键是把问题转化为求梯形的面积．三、解答题19. 计算：（1）201(3)3---+π；（2）2(1)(1)(1)+--+x x x ．【答案】（1）43（2）2x +2【解析】【分析】（1）利用负指数公式化简，零指数公式化简，平方根定义化简，合并后即可求出值；（2）利用完全平方，以及平方差计算，再合并即可求出值．【小问1详解】201(3)3---+π＝2﹣1+13＝43；【小问2详解】2(1)(1)(1)+--+x x x＝22211x x x ++-+＝2x +2．【点睛】此题考查了乘法公式，以及实数的运算，实数的运算涉及的知识有：零指数公式，负指数公式，绝对值的代数意义，以及平方根的定义．20. 解不等式组510032x x x -≤⎧⎨+>-⎩，并把解集在数轴上表示出来．【答案】12x -<≤；解集表示见解析【解析】【分析】先求出每个不等式的解集，然后求出不等式组的解集，并在数轴上表示出来即可．【详解】解：原不等式组为510032x x x -≤⎧⎨+>-⎩①②，解不等式①，得2x ≤；解不等式②，得1x >-．∴原不等式组的解集为12x -<≤ ，将不等式组的解集表示在数轴上如下：【点睛】本题主要考查解一元一次不等式组，掌握解一元一次不等式组的方法是解题的关键．21. 为减少传统塑料袋对生态环境的破坏，国家提倡使用可以在自然环境下（特定微生物、温度、湿度）较快完成降解的环保塑料袋．调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查，使用情况为A（不使用）、B（1~3个）、C（4~6个）、D（7个及以上），以下是根据调查结果绘制的统计图的一部分．（1）本次调查的样本容量是_____，请补全条形统计图；（2）已知该小区有1500户家庭，调查小组估计：该小区1周内使用7个及以上环保塑料袋的家庭约有225户．调查小组的估计是否合理？请说明理由．【答案】（1）100，图见解析（2）合理，理由见解析【解析】【分析】（1）利用频数除以频率即可得出，结合条形统计图及扇形统计图，求出,B C涉及的户数再画图即可；（2）利用样本估计总体的思想来解释即可．【小问1详解】解：本次调查的样本容量为：201000.2=（户），C∴使用情况的户数为：10025%25⨯=，D占的比例为：1515% 100=，B∴的比例为：125%20%15%40%---=，B∴使用情况的户数为：10040%40⨯=，补全条形统计图如下：故答案为：100．【小问2详解】解：合理，理由如下：利用样本估计总体：D占的比例为：1515% 100=，150015%225∴⨯=（户），∴调查小组的估计是合理的．【点睛】本题考查了形统计图及扇形统计图，样本估计总体，解题的关键是通过数形结合对数据进行分析．22. 在5张相同的小纸条上，分别写有语句：①函数表达式为y x=；②函数表达式为2y x=；③函数的图像关于原点对称；④函数的图像关于y轴对称；⑤函数值y随自变量x增大而增大．将这5张小纸条做成5支签，①、②放在不透明的盒子A中搅匀，③、④、⑤放在不透明的盒子B中搅匀．（1）从盒子A中任意抽出1支签，抽到①概率是______；（2）先从盒子A中任意抽出1支签，再从盒子B中任意抽出1支签．求抽到的2张小纸条上的语句对函数的描述相符合的概率．【答案】（1）12（2）12【解析】【分析】（1）直接由概率公式求解即可；（2）画出树状图，再由概率计算公式求解即可．【小问1详解】解：从盒子A中任意抽出1支签，抽到①的概率是12；故答案为：12；的【小问2详解】解：画出树状图：共有6种结果，抽到的2张小纸条上的语句对函数的描述相符合的有①、③和①、⑤和②、④共3种，∴抽到的2张小纸条上的语句对函数的描述相符合的概率为3162=．【点睛】本题主要考查了列表法或树状图求概率，一次函数与二次函数的性质，解题的关键是会列出表或树状图以及一次函数与二次函数的性质．23. 如图，在平面直角坐标系xOy 中，一次函数2y x b =+的图象分别与x 轴、y 轴交于点A 、B ，与反比例函数(0)k y x x=>的图象交于点C ，连接OC ．已知点(0,4)B ，BOC 的面积是2．（1）求b 、k 的值；（2）求AOC △的面积．【答案】（1）4；6（2）6【解析】【分析】（1）由点B （0，4）在一次函数y =2x +b 的图象上，代入求得b =4，由△BOC 的面积是2得出C 的横坐标为1，代入直线关系式即可求出C 的坐标，从而求出k 的值；（2）根据一次函数的解析式求得A 的坐标，然后根据三角形的面积公式代入计算即可．【小问1详解】解：∵一次函数2y x b =+的图象y 轴交于点(0,4)B ，∴4b =，OB =4，∴一次函数解析式为24y x =+，设点C （m ，n ），∵BOC 的面积是2． ∴1422m ⨯=，解得：m =1， ∵点C 在一次函数图象上，∴246n =+=，∴点C （1，6），把点C （1，6）代入(0)k y x x =>得：k =6；【小问2详解】当y =0时，024x =+，解得：x =-2，∴点A （-2，0），∴OA =2， ∴12662AOC S ∆=⨯⨯=．【点睛】本题是一次函数与反比例函数的交点问题，考查了待定系数法求函数的解析式，一次函数图象上点的坐标特征，三角形的面积，求出C 的坐标是解题的关键． 24. 如图，点A 在射线OX 上，OA a =．如果OA 绕点O 按逆时针方向旋转(0360)<≤︒n n 到OA '，那么点A '的位置可以用(),︒a n 表示．（1）按上述表示方法，若3a =，37n =，则点A '的位置可以表示为______；（2）在（1）的条件下，已知点B 的位置用()3,74︒表示，连接A A '、A B '．求证：A A A B ''=．【答案】（1）(3,37°)（2）见解析【解析】【分析】（1）根据点的位置定义，即可得出答案；（2）画出图形，证明△AOA ′≌△BOA ′（SAS ），即可由全等三角形的性质，得出结论．【小问1详解】解：由题意，得A ′(a ,n °)，∵a=3,n=37，∴A′(3,37°)，故答案为：(3,37°)；【小问2详解】证明：如图，∵()3,37A '︒，B (3,74°)，∴∠AOA ′=37°，∠AOB =74°，OA = OB =3，∴∠A ′OB =∠AOB -∠AOA ′=74°-37°=37°，∵OA ′=OA ′，∴△AOA ′≌△BOA ′（SAS ），∴A ′A =A ′B ．【点睛】本题考查全等三角形的判定与性质，新定义，旋转的性质，熟练掌握全等三角形的判定与性质是解题的关键．25. 第十四届国际数学教育大会（ICME -14）会徽的主题图案有着丰富的数学元素，展现了我国古代数学的文化魅力，其右下方的“卦”是用我国古代的计数符号写出的八进制数3745．八进制是以8作为进位基数的数字系统，有0~7共8个基本数字．八进制数3745换算成十进制数是3210387848582021⨯+⨯+⨯+⨯=，表示ICME -14的举办年份．（1）八进制数3746换算成十进制数是_______；（2）小华设计了一个n 进制数143，换算成十进制数是120，求n 的值．【答案】（1）2022（2）9【解析】【分析】（1）根据八进制换算成十进制的方法即可作答；（2）根据n 进制换算成十进制的方法可列出关于n 的一元二次方程，解方程即可求解．【小问1详解】3210387848682022⨯+⨯+⨯+⨯=，故答案为：2022；【小问2详解】根据题意有：313233143120n n n ---⨯+⨯+⨯=，整理得：244121n n ++=，解得n =9，（负值舍去），故n 的值为9．【点睛】本题考查了有理数的运算以及一元二次方程的应用等知识，根据题意列出关于n 的一元二次方程是解答本题的关键．26. 在四边形ABCD 中，O 是边BC 上的一点．若OAB OCD V V ≌，则点O 叫做该四边形的“等形点”．（1）正方形_______“等形点”（填“存在”或“不存在”）；（2）如图，在四边形ABCD 中，边BC 上的点O 是四边形ABCD 的“等形点”．已知CD =，5OA =，12BC =，连接AC ，求AC 的长；（3）在四边形EFGH 中，EH //FG ．若边FG 上点O 是四边形EFGH 的“等形点”，求OF OG的值．【答案】（1）不存在，理由见详解（2（3）1【解析】【分析】（1）根据“等形点”的概念，采用反证法即可判断；（2）过A 点作AM ⊥BC 于点M ，根据“等形点”的性质可得AB =CD=OA =OC =5，OB =7=OD ，设MO =a ，则BM =BO -MO =7-a ，在Rt △ABM 和Rt △AOM中，利的用勾股定理即可求出AM，则在Rt△AMC中利用勾股定理即可求出AC；（3）根据“等形点”的性质可得OF=OH，OE=OG，∠EOF=∠GOH，再根据∥，可得∠EOF=∠OEH，∠GOH=∠EHO，即有∠OEH=∠OHE，进而有EH FGOE=OH，可得OF=OG，则问题得解．【小问1详解】不存在，理由如下：假设正方形ABCD存在“等形点”点O，即存在△OAB≌△OCD，∵在正方形ABCD中，点O在边BC上，∴∠ABO=90°，∵△OAB≌△OCD，∴∠ABO=∠CDO=90°，∴CD⊥DO，∵CD⊥BC，∥，∴DO BC∵O点在BC上，∴DO与BC交于点O，∴假设不成立，故正方形不存在“等形点”；【小问2详解】如图，过A点作AM⊥BC于点M，如图，∵O点是四边形ABCD的“等形点”，∴△OAB≌△OCD，∴AB=CD，OA=OC，OB=OD，∠AOB=∠COD，∵CD ，OA=5，BC=12，∴AB=CD=OA=OC=5，∴OB=BC-OC=12-5=7=OD，∵AM⊥BC，∴∠AMO=90°=∠AMB，∴设MO =a ，则BM =BO -MO =7-a ，∴在Rt △ABM 和Rt △AOM 中，22222AM AB BM AO MO =-=-，∴2222AB BM AO MO -=-，即2222(7)5a a --=-，解得：207a =，即207MO =，∴MC =MO +OC =2055577+=，AM ===∴在Rt △AMC 中，AC ===即AC ；【小问3详解】如图，∵O 点是四边形EFGH 的“等形点”，∴△OEF ≌△OGH ，∴OF =OH ，OE =OG ，∠EOF =∠GOH ，∵EH FG ∥，∴∠EOF =∠OEH ，∠GOH =∠EHO ，∴根据∠EOF =∠GOH 有∠OEH =∠OHE ，∴OE =OH ，∵OF =OH ，OE =OG ，∴OF =OG ， ∴1OF OG=．【点睛】本题考查了全等三角形的性质、勾股定理、正方形的性质、平行的性质等知识，充分利用全等三角形的性质是解答本题的关键．27. 已知二次函数23y ax bx =++的自变量x 的部分取值和对应函数值y 如下表： x … 1- 0 1 2 3 …y… 4 3 0 5- 12- …（1）求二次函数23y ax bx =++的表达式；（2）将二次函数23y ax bx =++的图像向右平移(0)k k >个单位，得到二次函数2=++y mx nx q 的图像，使得当13x -<<时，y 随x 增大而增大；当45x <<时，y 随x 增大而减小，请写出一个符合条件的二次函数2=++y mx nx q 的表达式y =______，实数k 的取值范围是_______；（3）A 、B 、C 是二次函数23y ax bx =++的图像上互不重合的三点．已知点A 、B 的横坐标分别是m 、1m +，点C 与点A 关于该函数图像的对称轴对称，求ACB ∠的度数．【答案】（1）223y x x =--+（2）()234y x -=-+（答案不唯一），45k ≤≤（3）∠ACB =45°或135°【解析】【分析】（1）利用待定系数法求解即可；（2）先求出平移后的二次函数对称轴为直线1=-x k ，然后根据二次函数的增减性求出45k ≤≤，即可得到答案；（3）先分别求出A 、B 、C 三点的坐标，然后求出23B C x x m -=+，23B C y y m -=--，然后分四种情况讨论求解即可得到答案．【小问1详解】解：由题意得：403a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得12a b =-⎧⎨=-⎩， ∴二次函数解析式为223y x x =--+；【小问2详解】解：∵原二次函数解析式为()222314y x x x =--+=-++由题意得平移后的二次函数解析式为()214y x k =-+-+，∴平移后的二次函数对称轴为直线1=-x k ，∵二次函数2=++y mx nx q 的图像，使得当13x -<<时，y 随x 增大而增大；当45x <<时，y 随x 增大而减小，且二次函数2=++y mx nx q 的开口向下， ∴314k ≤-≤，∴45k ≤≤，∴符合题意的二次函数解析式可以为()()2214434y x x =-+-+=--+；故答案为：()234y x -=-+（答案不唯一），45k ≤≤；【小问3详解】解：∵二次函数解析式为()222314y x x x =--+=-++，∴二次函数223y x x =--+的对称轴为直线1x =-，∵A 、C 关于对称轴对称，点A 的横坐标为m ，∴C 的横坐标为2m --，∴点A 的坐标为（m ，223m m --+），点C 的坐标为（2m --，223m m --+）， ∵点B 的横坐标为m +1，∴点B 的坐标为（m +1，24m m --），∴23B C x x m -=+，23B C y y m -=--，如图1所示，当A 、B 同时在对称轴左侧时，过点B 作BE ⊥x 轴于E ，交AC 于D ，连接BC ，∵A 、C 关于对称轴对称，∴AC x ∥轴，∴BE AC ⊥，∵23B C x x m -=+，23B C y y m -=--，∴23CD m BD =--=，∴△BDC 是等腰直角三角形，∴∠ACB =45°，同理当AB 同时在对称轴右侧时，也可求得∠ACB =45°，如图2所示，当A 在对称轴左侧，B 在对称轴右侧时，过点B 作直线BD 垂直于直线AC 交直线AC 于D ，同理可证△BDC 为等腰直角三角形，∴∠BCD =45°，∴∠ACB =135°，同理当A 在对称轴右侧，B 在对称轴左侧也可求得∠ACB =135°，综上所述，∠ACB =45°或135°【点睛】本题主要考查了二次函数综合，二次函数的平移，二次函数的增减性，待定系数法求函数解析式等等，熟知二次函数的相关知识是解题的关键．28. （现有若干张相同的半圆形纸片，点O是圆心，直径AB的长是12cm，C是半圆弧上的一点（点C与点A、B不重合），连接AC、BC．（1）沿AC 、BC 剪下ABC ，则ABC 是______三角形（填“锐角”、“直角”或“钝角”）；（2）分别取半圆弧上的点E 、F 和直径AB 上的点G 、H ．已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm 的菱形．请用直尺和圆规在图中作出一个符合条件的菱形（保留作图痕迹，不要求写作法）；（3）经过数次探索，小明猜想，对于半圆弧上的任意一点C ，一定存在线段AC 上的点M 、线段BC 上的点N 和直径AB 上的点P 、Q ，使得由这四个点顺次连接构成的四边形是一个边长为4cm 的菱形．小明的猜想是否正确？请说明理由．【答案】（1）直角（2）见详解（3）小明的猜想错误，理由见详解【解析】【分析】（1）AB 是圆的直径，根据圆周角定理可知∠ACB =90°，即可作答；（2）以A 为圆心，AO 为半径画弧交⊙O 于点E ，再以E 为圆心，EO 为半径画弧交于⊙O 点F 连接EF 、FO 、EA ，G 、H 点分别与A 、O 点重合，即可；（3）过C 点作CG NQ ∥，交AB 于点G ，连接CO ，根据MN PQ ∥，可得MN CN AB BC =，即有13CN BC =，则可求得23BN BC =，依据CG NQ ∥，NQ =4，可得GC =OC =6，即可判断．【小问1详解】如图，∵AB 是⊙O 的直径，∴∠ACB =90°，∴∠ACB 直角，即△ABC 是直角三角形，故答案为：直角，【小问2详解】以A 为圆心，AO 为半径画弧交⊙O 于点E ，再以E 为圆心，EO 为半径画弧交于⊙O 点F 连接EF 、FO 、EA ，G 、H 点分别与A 、O 点重合，即可，作图如下：是由作图可知AE =EF =FH =HG =OA =12AB =6，即四边形EFHG 是边长为6cm 的菱形；【小问3详解】小明的猜想错误，理由如下：如图，菱形MNQP 的边长为4，过C 点作CG NQ ∥，交AB 于点G ，连接CO ，在菱形MNQP 中MN =QN =4，MN PQ ∥，∵MN PQ ∥，∴~CMN CAB ， ∴MN CN AB BC=， ∵AB =12，MN =4， ∴41123MN CN AB BC ===， ∵BN =BC -CN ， ∴23BN BC =， ∵CG NQ ∥，NQ =4，~BQN BGC ，∴243NQ BN GC BC GC===， ∴GC =6，∵AB =12，∴OC =6，∴OC =GC ，显然若C点靠近A点时，要满足GC=OC=6，此时的G点必在BA的延长线上，∵P点在线段AB上，∥相矛盾，∴直线GC必与直线PM相交，这与CG PM故小明的猜想错误．【点睛】本题考查了圆周角定理、尺规作图、菱形的性质、平行的性质等知识，掌握菱形的性质以及平行的性质求得GC=OC是解答本题的关键。

精品解析：2024年广西中考数学试题(解析版)

2024年广西初中学业水平考试数学（全卷满分120分，考试时间120分钟）注意事项：1.答题前，考生务必将姓名、准考证号填写在试卷和答题卡上．2.考生作答时，请在答题卡上作答（答题注意事项见答题卡），在本试卷、草稿纸上作答无效．3.不能使用计算器．4.考试结束后，将本试卷和答题卡一并交回．一、单项选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B 铅笔把答题卡上对应题目的答案标号涂黑．）1. 下列选项记录了我国四个直辖市某年一月份的平均气温，其中气温最低的是（）A. B. C. D.【答案】A 【解析】【分析】本题考查了温度的比较以及正负数的概念，熟悉掌握概念是解决本题的关键．0℃以下记为负数，0℃以上记为正数，温度都小于0℃时，绝对值最大的，温度最低．【详解】解：∵ 4.6 4.6−=， 3.2 3.2−=，4.6 3.2>， ∴ 4.6 3.2 5.88.1−<−<<， ∴气温最低的是北京．故选：A ．2. 端午节是中国传统节日，下列与端午节有关的文创图案中，成轴对称的是（）A. B. C. D.【答案】B 【解析】【分析】本题主要考查成轴对称的定义，掌握成轴对称的定义是解题的关键．把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫作对称轴，折叠后重合的点是对应点，叫作对称点．根据两个图形成轴对称的定义，逐一判断选项即可．【详解】A ．不是轴对称图形，故不符合题意； B ．是轴对称图形，故符合题意； C ．不是轴对称图形，故不符合题意； D ．不是轴对称图形，故不符合题意；故你：B ．3. 广西壮族自治区统计局发布的数据显示，2023年全区累计接待国内游客8.49亿人次．将849000000用科学记数法表示为（） A. 90.84910⨯ B. 88.4910⨯C. 784.910⨯D. 684910⨯【答案】B 【解析】【分析】本题考查科学记数法，根据科学记数法的表示方法：()10110,n a a n ⨯≤<为整数，进行表示即可．【详解】解：88490000008.4910=⨯；故选B ．4. 榫卯是我国传统建筑及家具的基本构件．燕尾榫是“万榫之母”，为了防止受拉力时脱开，榫头成梯台形，形似燕尾，如图是燕尾榫正面的带头部分，它的主视图是（）A. B. C. D.【答案】A 【解析】【分析】本题考查三视图，根据主视图是从前往后看，得到的图形，进行判断即可．【详解】解：由图可知：几何体的主视图为：故选A ．5. 不透明袋子中装有白球2个，红球1个，这些球除了颜色外无其他差别．从袋子中随机取出1个球，取出白球的概率是（）A. 1B.13C.12D.23【答案】D 【解析】【分析】本题考查求概率，直接利用概率公式进行计算即可．【详解】解：从袋子中随机取出1个球，有213+=种等可能的结果，其中取出白球的情况有2种， ∴23P =；故选D ．6. 如图，2时整，钟表的时针和分针所成的锐角为（）A. 20︒B. 40︒C. 60︒D. 80︒【答案】C 【解析】【分析】本题考查了钟面角，用30︒乘以两针相距的份数是解题关键．根据钟面的特点，钟面平均分成12份，每份是30︒，根据时针与分针相距的份数，可得答案．【详解】解：2时整，钟表的时针和分针所成的锐角是30260︒⨯=︒，故选：C ．7. 如图，在平面直角坐标系中，点O 为坐标原点，点P 的坐标为()2,1，则点Q 的坐标为（）A. ()3,0B. ()0,2C. ()3,2D. ()1,2【答案】C 【解析】【分析】本题主要考查点的坐标，理解点的坐标意义是关键．根据点P 的坐标可得出横、纵轴上一格代表一格单位长度，然后观察坐标系即可得出答案．【详解】解：∵点P 的坐标为()2,1， ∴点Q 坐标为()3,2，故选：C ．8. 激光测距仪L 发出的激光束以5310km ⨯的速度射向目标M ，s t 后测距仪L 收到M 反射回的激光束．则L 到M 的距离dkm 与时间s t 的关系式为（）A. 53102d t ⨯=B. 5310d t =⨯C. 52310d t =⨯⨯D. 6310d t =⨯【答案】A 【解析】【分析】本题考查列函数关系式，熟练掌握路程＝速度×时间是解题的关键．根据路程＝速度×时间列式即可．【详解】解：55131031022d t t =⨯⨯=⨯⋅，故选：A ．9. 已知点()11,M x y ，()22,N x y 在反比例函数2y x=的图象上，若120x x <<，则有（） A. 120y y << B. 210y y <<C. 120y y <<D. 120y y <<【答案】A 【解析】【分析】本题考查了反比例函数的图象，熟练掌握反比例函数图象上点的坐标特征是解题的关键．根据点()11,M x y ，()22,N x y 在反比例函数图象上，则满足关系式2y x=，横纵坐标的积等于2，结合120x x <<即可得出答案．【详解】解：点()11,M x y ，()22,N x y 在反比例函数2y x=的图象上， ∴ 112x y =，222x y =，120x x <<，∴ 10y <，20y >，的∴ 120y y <<．故选：A ．10. 如果3a b +=，1ab =，那么32232a b a b ab ++的值为（） A. 0 B. 1 C. 4 D. 9【答案】D 【解析】【分析】本题考查因式分解，代数式求值，先将多项式进行因式分解，利用整体代入法，求值即可．【详解】解：∵3a b +=，1ab =，∴()32232222a b a b ab ab a ab b ++=++()2ab a b =+213=⨯9=；故选D ．11. 《九章算术》是我国古代重要的数学著作，其中记载了一个问题，大致意思为：现有田出租，第一年3亩1钱，第二年4亩1钱，第三年5亩1钱．三年共得100钱．问：出租的田有多少亩？设出租的田有x 亩，可列方程为（） A.1345x x x++= B.100345x x x++= C. 3451x x x ++= D. 345100x x x ++=【答案】B 【解析】【分析】本题考查了一元一次方程的应用，根据“第一年3亩1钱，第二年4亩1钱，第三年5亩1钱．三年共得100钱”列方程即可．【详解】解：根据题意，得100345x x x++=，故选：B ．12. 如图，边长为5的正方形ABCD ，E ，F ，G ，H 分别为各边中点，连接AG ，BH ，CE ，DF ，交点分别为M ，N ，P ，Q ，那么四边形MNPQ 的面积为（）A. 1B. 2C. 5D. 10【答案】C 【解析】【分析】先证明四边形AECG 是平行四边形，得出AG CE ∥，同理AF BH ∥，则可证四边形MNPQ 是平行四边形，利用平行线分线段成比例可得出DQ PQ =，AM QM =，证明()SAS ADG BAH ≌得出DAG ABH ∠=∠，则可得出90QMN AMB ∠=∠=︒，同理90AQD ∠=︒，得出平行四边形MNPQ 是矩形，证明()AAS ADQ BAM ≌，得出DQ AM =，进而得出DQ AM PQ QM ===，得出矩形MNPQ 是正方形，在Rt ADQ △中，利用勾股定理求出25QM =，然后利用正方形的面积公式求解即可．【详解】解：∵四边形ABCD 是正方形，∴AB BC CD DA ===，AB CD ∥，AD BC ∥，90DAB ABC BCD CDA ∠=∠=∠=∠=︒， ∵E ，F ，G ，H 分别为各边中点， ∴12CG DG CD AH ===，12AE AB =，∴DG CG AE ==，∴四边形AECG 是平行四边形， ∴AG CE ∥，同理DFBH ，∴四边形MNPQ 是平行四边形， ∵AG CE ∥， ∴1DQ DGPQ CG==， ∴DQ PQ =，同理AM QM =，∵DG AH =，90ADG BAH ∠=∠=︒，AD BA =，∴()SAS ADG BAH ≌， ∴DAG ABH ∠=∠， ∵90DAG GAB ∠+∠=︒， ∴90ABH GAB ∠+∠=︒，∴90QMN AMB ∠=∠=︒，同理90AQD ∠=︒， ∴平行四边形MNPQ 是矩形，∵90AQD AMB ∠=∠=︒，DAG ABH ∠=∠，AD BA =， ∴()AAS ADQ BAM ≌， ∴DQ AM =，又DQ PQ =，AM QM =， ∴DQ AM PQ QM ===， ∴矩形MNPQ 是正方形，在Rt ADQ △中，222AD DQ AQ =+，∴()22252QM QM =+，∴25QM =，∴正方形MNPQ 的面积为5，故选：C ．【点睛】本题考查了正方形的判定与性质，全等三角形判定与性质，平行线分线段成比例，勾股定理等知识，明确题意，灵活运用相关知识求解是解题的关键．二、填空题（本大题共6小题，每小题2分，共12分．）13. 已知1∠与2∠为对顶角，135∠=︒，则2∠=______°．【答案】35 【解析】【分析】本题主要考查了对顶角性质，根据对顶角相等，得出答案即可．【详解】解：∵1∠与2∠为对顶角，135∠=︒， ∴2135∠=∠=︒．故答案为：35．14.__．【答案】2(答案不唯一) 【解析】【分析】本题考查实数大小比较，估算无理数的大小是解题的关键．大小，再找出符合条件的整数即可．【详解】解：134<<，12∴<<，∴符合条件的数可以是：2(答案不唯一)．故答案为：2．15. 八桂大地孕育了丰富的药用植物．某县药材站把当地药市交易的400种药用植物按“草本、藤本、灌木、乔木”分为四类，绘制成如图所示的统计图，则藤本类有______种．【答案】80 【解析】【分析】本题考查了扇形统计图，用400乘以藤本类的百分比即可求解，看懂统计图是解题的关键．【详解】解：由扇形统计图可得，藤本类有40020%80⨯=种，故答案为：80．16. 不等式7551x x +<+的解集为______．【答案】<2x − 【解析】【分析】本题考查了解一元一次不等式，根据解一元一次不等式的步骤解答即可求解，掌握解一元一次不等式的步骤是解题的关键．【详解】解：移项得，7515x x −<−，合并同类项得，24x <−，系数化为1得，<2x −，故答案为：<2x −．17. 如图，两张宽度均为3cm 的纸条交叉叠放在一起，交叉形成的锐角为60︒，则重合部分构成的四边形的ABCD 的周长为______cm ．【答案】【解析】【分析】本题考查了平行四边形的判定，菱形的判定和性质，菱形的周长，过点A 作AM BC ⊥于M ，AN CD ⊥于N ，由题意易得四边形ABCD 是平行四边形，进而由平行四边形的面积可得AM AN =，即可得到四边形ABCD 是菱形，再解Rt ADN △可得sin 60ANAD ==︒，即可求解，得出四边形ABCD 是菱形是解题的关键．【详解】解：过点A 作AM BC ⊥于M ，AN CD ⊥于N ，则90AND ∠=︒， ∵两张纸条的对边平行， ∴AB CD ∥，AD BC ∥， ∴四边形ABCD 是平行四边形，又∵两张纸条的宽度相等， ∴AM AN =， ∵··ABCDSBC AM CD AN ==，∴BC CD =，∴四边形ABCD 是菱形，在Rt ADN △中，60ADN ∠=︒，3cm AN =，∴sin 60AN AD ===︒， ∴四边形ABCD的周长为4=，故答案为：18. 如图，壮壮同学投掷实心球，出手（点P 处）的高度OP 是7m 4，出手后实心球沿一段抛物线运行，到达最高点时，水平距离是5m ，高度是4m ．若实心球落地点为M ，则OM =______m ．【答案】353【解析】【分析】本题考查的是二次函数的实际应用，设抛物线为()254y a x =−+，把点70,4⎛⎫ ⎪⎝⎭，代入即可求出解析式；当0y =时，求得x 的值，即为实心球被推出的水平距离OM ．【详解】解：以点O 为坐标原点，射线OM 方向为x 轴正半轴，射线OP 方向为y 轴正半轴，建立平面直角坐标系，∵出手后实心球沿一段抛物线运行，到达最高点时，水平距离是5m ，高度是4m ．设抛物线解析式为：()254y a x =−+，把点70,4⎛⎫ ⎪⎝⎭代入得：72544a +=，解得：9100a =−， ∴抛物线解析式为：()2954100y x =−−+；当0y =时，()29540100x −−+=，解得，153x =−（舍去），2353x =，即此次实心球被推出的水平距离OM 为35m 3．故答案为：353三、解答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤．）19. 计算：()()2342−⨯+−【答案】8− 【解析】【分析】本题主要考查了有理数的混合运算．先算乘法和乘方，再算加法即可．【详解】解：原式124=-+8=−．20. 解方程组：2321x y x y +=⎧⎨−=⎩【答案】212x y =⎧⎪⎨=⎪⎩【解析】【分析】本题考查的是二元一次方程组的解法，直接利用加减消元法解方程组即可．【详解】解：2321x y x y +=⎧⎨−=⎩①②，+①②得：24=x ，解得：2x =，把2x =代入①得：12y =， ∴方程组的解为：212x y =⎧⎪⎨=⎪⎩.21. 某中学为了解七年级女同学定点投篮水平，从中随机抽取20名女同学进行测试，每人定点投篮5次，进球数统计如下表：（1）求被抽取的20名女同学进球数的众数、中位数、平均数；（2）若进球数为3以上（含3）为“优秀”，七年级共有200名女同学，请估计七年级女同学中定点投篮水平为“优秀”的人数．【答案】（1）众数为1、中位数为2、平均数为1.9 （2）估计为“优秀”等级的女生约为50人【解析】【分析】（1）根据平均数、中位数、众数的定义求解即可；（2）算出样本的优秀率，再估计总体的优秀人数．【小问1详解】解：女生进球数的平均数为()1011826334151 1.920⨯⨯+⨯+⨯+⨯+⨯+⨯=（个），女生进球数的中位数是第10个和第11个成绩的平均数，即2222+=（个），女生进球个数为1个人最多，故众数是1个；【小问2详解】解：3112005020++⨯=（人），答：估计为“优秀”等级的女生约为50人．【点睛】本题考查了中位数，众数，平均数，用样本件估计总体，掌握中位数，平均数、众数的定义以及优秀率的求法是解题的关键．22. 如图，在ABC 中，45A ∠=︒，AC BC >．（1）尺规作图：作线段AB 的垂直平分线l ，分别交AB ，AC 于点D ，E ：（要求：保留作图痕迹，不写作法，标明字母）（2）在（1）所作的图中，连接BE ，若8AB =，求BE 的长．【答案】（1）见详解（2）【解析】【分析】（1）分别以A 、B 为圆心，大于12AB 为半径画弧，分别交AB ，AC 于点D ，E ，作直线DE ，则的直线l 即为所求．（2）连接BE ，由线段垂直平分线的性质可得出BE AE =，由等边对等角可得出45EBA A ∠=∠=︒，由三角形内角和得出90BEA ∠=︒，则得出ABE 为等腰直角三角形，再根据正弦的定义即可求出BE 的长．小问1详解】解：如下直线l 即为所求．【小问2详解】连接BE 如下图：∵DE 为线段AB 的垂直平分线，∴BE AE =， ∴45EBA A ∠=∠=︒，∴90BEA ∠=︒， ∴ABE 为等腰直角三角形，∴sin 2BE A AB ==，∴822BE AB =⋅=⨯=【点睛】本题主要考查了作线段的垂线平分线，线段的垂线平分线的性质，等腰三角形的性质，三角形内角和定理以及正弦的定义．掌握线段的垂直平分线的性质是解题的关键． 23. 综合与实践在综合与实践课上，数学兴趣小组通过洗一套夏季校服，探索清洗衣物的节约用水策略．【【洗衣过程】步骤一：将校服放进清水中，加入洗衣液，充分浸泡揉搓后拧干；步骤二：将拧干后的校服放进清水中，充分漂洗后拧干．重复操作步骤二，直至校服上残留洗衣液浓度达到洗衣目标．假设第一次漂洗前校服上残留洗衣液浓度为0.2%，每次拧干后校服上都残留0.5kg 水．浓度关系式：0.50.5d d w=+前后．其中d 前、d 后分别为单次漂洗前、后校服上残留洗衣液浓度；w 为单次漂洗所加清水量（单位：kg ）【洗衣目标】经过漂洗使校服上残留洗衣液浓度不高于0.01% 【动手操作】请按要求完成下列任务：（1）如果只经过一次漂洗，使校服上残留洗衣液浓度降为0.01%，需要多少清水？（2）如果把4kg 清水均分，进行两次漂洗，是否能达到洗衣目标？（3）比较（1）和（2）的漂洗结果，从洗衣用水策略方面，说说你的想法．【答案】（1）只经过一次漂洗，使校服上残留洗衣液浓度降为0.01%，需要9.5kg 清水．（2）进行两次漂洗，能达到洗衣目标；（3）两次漂洗的方法值得推广学习【解析】【分析】本题考查的是分式方程的实际应用，求解代数式的值，理解题意是关键；（1）把0.01%d =后，0.2%d =前代入0.50.5d d w=+前后，再解方程即可；（2）分别计算两次漂洗后的残留洗衣液浓度，即可得到答案；（3）根据（1）（2）的结果得出结论即可．【小问1详解】解：把0.01%d =后，0.2%d =前代入0.50.5d d w=+前后得.0.50.2%0.01%05w=+⨯，解得9.5w =．经检验符合题意；∴只经过一次漂洗，使校服上残留洗衣液浓度降为0.01%，需要9.5kg 清水．【小问2详解】解：第一次漂洗：把2kg w =，0.2%d =前代入0.50.5d d w=+前后，∴0.50.2%0.04%0.52d ⨯==+后，第二次漂洗：把2kg w =，0.04%d =前代入0.50.5d d w=+前后，∴0.50.04%0.008%0.52d ⨯==+后，而0.008%0.01%<，∴进行两次漂洗，能达到洗衣目标；【小问3详解】解：由（1）（2）的计算结果发现：经过两次漂洗既能达到洗衣目标，还能大幅度节约用水， ∴从洗衣用水策略方面来讲，采用两次漂洗的方法值得推广学习． 24. 如图，已知O 是ABC 的外接圆，AB AC =．点D ，E 分别是BC ，AC 的中点，连接DE 并延长至点F ，使DE EF =，连接AF ．（1）求证：四边形ABDF 是平行四边形；（2）求证：AF 与O 相切；（3）若3tan 4BAC ∠=，12BC =，求O 的半径．【答案】（1）证明见解析（2）证明见解析（3）10 【解析】【分析】（1）先证明BD CD =，DE EF =，再证明AEF CED △≌△，可得AF CD =，F EDC ∠=∠，再进一步解答即可；（2）如图，连接AD ，证明AD BC ⊥，可得AD 过圆心，结合∥AF BD ，证明AF AD ⊥，从而可得结论；（3）如图，过B 作BQ AC ⊥于Q ，连接OB ，设BQ 3x =，则4AQ x =，可得CQ AC AQ x =−=，求解5x ==，可得5AB x ==18AD ==，设O 半径为r ，可得18OD r =−，再利用勾股定理求解即可．【小问1详解】证明：∵点D ，E 分别是BC ，AC 的中点， ∴BD CD =，AE CE =，又∵AEF CED ∠=∠，DE EF =， ∴AEF CED △≌△， ∴AF CD =，F EDC ∠=∠， ∴AF BD =，∥AF BD ，∴四边形ABDF 是平行四边形；【小问2详解】证明：如图，连接AD ， ∵AB AC =，D 为BC 中点， ∴AD BC ⊥，∴AD 过圆心， ∵∥AF BD ，∴AF AD ⊥，而OA 为半径， ∴AF 为O 的切线；【小问3详解】解：如图，过B 作BQ AC ⊥于Q ，连接OB ，∵3tan 4BAC ∠=， ∴34BQ AQ =，设BQ 3x =，则4AQ x =，∴5AC AB x ===，∴CQ AC AQ x =−=，∴BC ==，12=，∴5x ==，∴5AB x ==∵AB AC =，12BC =，AD BC ⊥， ∴6BD CD ==，∴18AD ==，设O 半径为r ，∴18OD r =−，∴()222186r r =−+，解得：10r =， ∴O 的半径为10．【点睛】本题考查的是全等三角形的判定与性质，等腰三角形的性质，勾股定理的应用，平行四边形的判定与性质，切线的判定，垂径定理的应用，做出合适的辅助线是解本题的关键．25. 课堂上，数学老师组织同学们围绕关于x 的二次函数223y x ax a =++−的最值问题展开探究．【经典回顾】二次函数求最值的方法．（1）老师给出4a =−，求二次函数223y x ax a =++−的最小值． ①请你写出对应的函数解析式；②求当x 取何值时，函数y 有最小值，并写出此时的y 值；【举一反三】老师给出更多a 的值，同学们即求出对应的函数在x 取何值时，y 的最小值．记录结果，并整理成下表：注：*为②的计算结果．【探究发现】老师：“请同学们结合学过的函数知识，观察表格，谈谈你的发现．” 甲同学：“我发现，老师给了a 值后，我们只要取x a =−，就能得到y 的最小值．”乙同学：“我发现，y 的最小值随a 值的变化而变化，当a 由小变大时，y 的最小值先增大后减小，所以我猜想y 的最小值中存在最大值．”（2）请结合函数解析式223y x ax a =++−，解释甲同学的说法是否合理？（3）你认为乙同学的猜想是否正确？若正确，请求出此最大值；若不正确，说明理由．【答案】（1）①287y x x =−−；②当4x =时，y 有最小值为23−（2）见解析（3）正确，114− 【解析】【分析】本题考查二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解题的关键：（1）①把4a =−代入解析式，写出函数解析式即可；②将一般式转化为顶点式，进行求解即可；（2）将一般式转化为顶点式，根据二次函数的性质进行解释即可；（3）将一般式转化为顶点式，表示出y 的最大值，再利用二次函数求最值即可．【详解】解：（1）①把4a =−代入223y x ax a =++−，得：()()22244387y x x x x =+⋅−+−−=−−；∴287y x x =−−；②∵()2287423y x x x =−−=−−，∴当4x =时，y 有最小值为23−；（2）∵()222233y x ax a x a a a =+−+−=++−，∵抛物线的开口向上， ∴当x a =−时，y 有最小值； ∴甲的说法合理；（3）正确；∵()222233y x ax a x a a a =+−+−=++−，∴当x a =−时，y 有最小值为23a a −+−，即：22min111324y a a a ⎛⎫=−+−=−−− ⎪⎝⎭，∴当12a =时，min y 有最大值，114−． 26. 如图1，ABC 中，90B ??，6AB =．AC 的垂直平分线分别交AC ，AB 于点M ，O ，CO 平分ACB ∠．（1）求证：ABC CBO △∽△；（2）如图2，将AOC 绕点O 逆时针旋转得到A OC ''△，旋转角为()0360a α︒<<︒．连接A M '，C M '①求A MC ''△面积的最大值及此时旋转角α的度数，并说明理由； ②当A MC ''△是直角三角形时，请直接写出旋转角α的度数．【答案】（1）见解析（2）①180α=︒；②120︒或240︒为【解析】【分析】（1）利用线段垂直平分线的性质得出OA OC =，利用等边对等角得出A ACO ∠=∠，结合角平分线定义可得出A ACO OCB ∠=∠=∠，最后根据相似三角形的判定即可得证；（2）先求出30A ACO OCB ∠=∠=∠=︒，然后利用含30︒的直角三角形性质求出2BO =，4AO =，2MO =，利用勾股定理求出AM =AC =A C ''中点M '，连接OM '，MM '，作MN A C ''⊥于N ，由旋转的性质知AOC A OC ''≌，OM '为OM 旋转α所得线段，则OM A C '''⊥，A C AC ''==，2OM OM '==，根据点到直线的距离，垂线段最短知MN MM '≤，三角形三边关系得出MN OM OM '≤+，故当M 、O 、M '三点共线，且点O 在线段MM '时，MN 取最大值，最大值为224+=，此时180α=︒，最后根据三角形面积公式求解即可；②先利用三角形三边关系判断出MC A C '''<，MA A C '''<，则当A MC ''△为直角三角形时，只有90A MC ''∠=︒，然后分A 和C '重合，A '和C 重合，两种情况讨论即可．【小问1详解】证明：∵MO 垂直平分AC ， ∴OA OC =， ∴A ACO ∠=∠， ∵CO 平分ACB ∠ ∴ACO OCB ∠=∠， ∴A OCB ∠=∠，又B B ∠=∠； ∴ABC CBO △∽△；【小问2详解】解：①∵90B??，∴90A ACO OCB ∠+∠+∠=︒， ∴30A ACO OCB ∠=∠=∠=︒，∴1122BO CO AO ==，又6AB AO BO =+=， ∴2BO =，4AO =， ∵MO 垂直平分AC ， ∴122OM AO ==，2AC AM =，∴AM ==∴AC =取A C ''中点M '，连接OM '，MM '，作MN A C ''⊥于N ，由旋转的性质知AOC A OC ''≌，OM '为OM 旋转α所得线段，∴OM A C '''⊥，A C AC ''==，2OM OM '==，根据垂线段最短知MN MM '≤，又MM OM OM ≤'+'，∴当M 、O 、M '三点共线，且点O 在线段MM '时，MN 取最大值，最大值为224+=，此时180α=︒，∴A MC ''△面积的最大值为142⨯=；②∵246MC MO OC ''≤+=+=，A C ''=，∴MC A C '''<，同理MA A C '''<∴A MC ''△为直角三角形时，只有90A MC ''∠=︒，当A 和C '重合时，如图，∵AOC A OA '≌∴30A CAO '∠=∠=︒，30OAA OCA '∠=∠=︒，∴120A OA '∠=︒，∵90AMO ∠=︒，∴60AOM ∠=︒，∴180A OA AOM '∠+∠=︒，∴A '、O 、M 三点共线，∴A MC ''△为直角三角形，此时旋转角120A OA α'=∠=︒；当A '和C 重合时，如图，同理30OCC CAO '∠=∠=︒，30C OCA '∠=∠=︒，∴120COC '∠=︒，∵AO CO =，60AOM ∠=︒∴60COM AOM ∠=∠=︒，∴180COM COC '∠+∠=︒，∴C '、O 、M 三点共线，又90AMO ∠=︒∴A MC ''△为直角三角形，此时旋转角360240A OA α'=︒−∠=︒；综上，旋转角α的度数为120︒或240︒时，A MC ''△为直角三角形．【点睛】本题考查了线段垂直平分线的性质，含30︒的直角三角形的性质，勾股定理，旋转的性质等知识，明确题意，正确画出图形，添加辅助线，合理分类讨论是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018年江苏省无锡市中考数学试卷
一、选择题
1.下列等式正确的是（）
A. （）2=3
B. =﹣3
C. =3
D. （﹣）2=﹣3
2.函数y=中自变量x的取值范围是（）
A. x≠﹣4
B. x≠4
C. x≤﹣4
D. x≤4
3.下列运算正确是（）
A. a2+a3=a5
B. （a2）3=a5
C. a4﹣a3=a
D. a4÷a3=a
4.下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（）
A. B. C. D.
5.下列图形中的五边形ABCDE都是正五边形，则这些图形中的轴对称图形有（）
A. 1个
B. 2个
C. 3个
D. 4个
6.已知点P（a，m），Q（b，n）都在反比例函数y=的图象上，且a＜0＜b，则下列结论一定正确的是
（）
A. m+n＜0
B. m+n＞0
C. m＜n
D. m＞n
7.某商场为了解产品A的销售情况，在上个月的销售记录中，随机抽取了5天A产品的销售记录，其售价x （元/件）与对应销量y（件）的全部数据如下表：
售价x（元/件）90 95 100 105 110
销量y（件）110 100 80 60 50
则这5天中，A产品平均每件的售价为（）
A. 100元
B. 95元
C. 98元
D. 97.5元
8.如图，矩形ABCD中，G是BC的中点，过A、D、G三点的圆O与边AB、CD分别交于点E、点F，给出下列说法：（1）AC与BD的交点是圆O的圆心；（2）AF与DE的交点是圆O的圆心；（3）BC与圆O 相切，其中正确说法的个数是（）
A0 B. 1 C. 2 D. 3
9.如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（）
A. 等于
B. 等于
C. 等于
D. 随点E位置的变化而变化
10.如图是一个沿3×3正方形方格纸对角线AB剪下的图形，一质点P由A点出发，沿格点线每次向右或向上运动1个单位长度，则点P由A点运动到B点的不同路径共有（）
A. 4条
B. 5条
C. 6条
D. 7条
二、填空题
11.﹣2的相反数的值等于_____．
12.今年“五一”节日期间，我市四个旅游景区共接待游客约303000多人次，这个数据用科学记数法可记为_____．
13.方程=的解是_____．
14.方程组的解是_____．
15.命题“四边相等四边形是菱形”的逆命题是_____．
16.如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA=AB，则∠ABC=_____．
17.已知△ABC中，AB=10，AC=2，∠B=30°，则△ABC的面积等于_____．
18.如图，已知∠XOY=60°，点A在边OX上，OA=2．过点A作AC⊥OY于点C，以AC为一边在∠XOY 内作等边三角形ABC，点P是△ABC围成的区域（包括各边）内的一点，过点P作PD∥OY交OX于点D，作PE∥OX交OY于点E．设OD=a，OE=b，则a+2b的取值范围是_____．
三、解答题
19.计算：（1）（﹣2）2×|﹣3|﹣（）0；（2）（x+1）2﹣（x2﹣x）
20.（1）分解因式：3x3﹣27x；（2）解不等式组：
21.如图，平行四边形ABCD中，E、F分别是边BC、AD的中点，求证：∠ABF=∠CDE．
22.某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．
请根据以上信息，解答下列问题：
（1）该汽车交易市场去年共交易二手轿车辆．
（2）把这幅条形统计图补充完整．（画图后请标注相应的数据）
（3）在扇形统计图中，D类二手轿车交易辆数所对应扇形圆心角为度．
23.某校组织一项公益知识竞赛，比赛规定：每个班级由2名男生、2名女生及1名班主任老师组成代表队．但参赛时，每班只能有3名队员上场参赛，班主任老师必须参加，另外2名队员分别在2名男生和2名女生中各随机抽出1名．初三（1）班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队，求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率．（请用“画树状图”或“列表”或“列举”等方法给出分析过程）
24.如图，四边形ABCD内接于⊙O，AB=17，CD=10，∠A=90°，cosB=，求AD的长．
25.一水果店是A酒店某种水果的唯一供货商，水果店根据该酒店以往每月的需求情况，本月初专门为他们准备了2600kg的这种水果．已知水果店每售出1kg该水果可获利润10元，未售出的部分每1kg将亏损6元，以x（单位：kg，2000≤x≤3000）表示A酒店本月对这种水果的需求量，y（元）表示水果店销售这批水果所获得的利润．
（1）求y关于x的函数表达式；
（2）问：当A酒店本月对这种水果的需求量如何时，该水果店销售这批水果所获的利润不少于22000元？
26.如图，平面直角坐标系中，已知点B的坐标为（6，4）．
（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）
（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．
27.如图，矩形ABCD中，AB=m，BC=n，将此矩形绕点B顺时针方向旋转θ（0°＜θ＜90°）得到矩形A1BC1D1，点A1在边CD上．
（1）若m=2，n=1，求在旋转过程中，点D到点D1所经过路径的长度；
（2）将矩形A1BC1D1继续绕点B顺时针方向旋转得到矩形A2BC2D2，点D2在BC的延长线上，设边A2B 与CD交于点E，若=﹣1，求的值．
28.已知：如图，一次函数y=kx﹣1的图象经过点A（3，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．
（1）求这个一次函数的表达式；
（2）已知一开口向下、以直线CD为对称轴的抛物线经过点A，它的顶点为P，若过点P且垂直于AP的直线与x轴的交点为Q（﹣，0），求这条抛物线的函数表达式．。