和差倍问题:和差倍综合练习及答案
角的和差倍分专项训练题1(含答案)
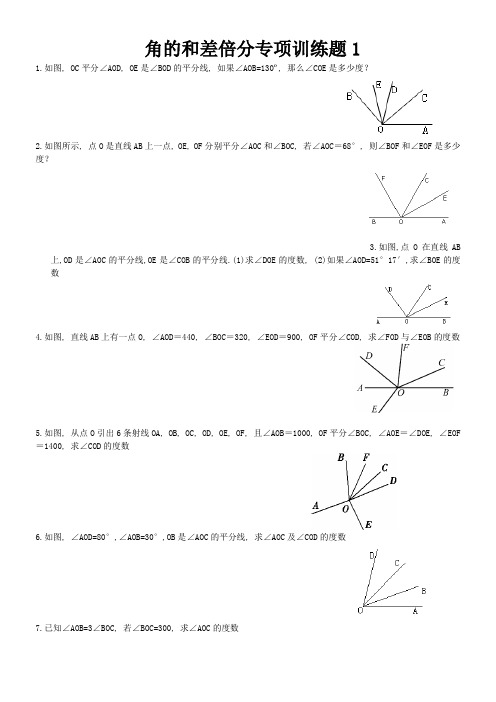
角的和差倍分专项训练题11.如图, OC平分∠AOD, OE是∠BOD的平分线, 如果∠AOB=130º, 那么∠COE是多少度?2.如图所示, 点O是直线AB上一点, OE, OF分别平分∠AOC和∠BOC, 若∠AOC=68°, 则∠BOF和∠EOF是多少度?3.如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线.(1)求∠DOE的度数, (2)如果∠AOD=51°17′,求∠BOE的度数4.如图, 直线AB上有一点O, ∠AOD=440, ∠BOC=320, ∠EOD=900, OF平分∠COD, 求∠FOD与∠EOB的度数5.如图, 从点O引出6条射线OA, OB, OC, OD, OE, OF, 且∠AOB=1000, OF平分∠BOC, ∠AOE=∠DOE, ∠EOF =1400, 求∠COD的度数6.如图, ∠AOD=80°,∠AOB=30°,OB是∠AOC的平分线, 求∠AOC及∠COD的度数7.已知∠AOB=3∠BOC, 若∠BOC=300, 求∠AOC的度数8.如图, ∠BAE =750, ∠DAE= 150, AC是∠BAD的平分线, 求∠CAD的度数9.如图, BD平分∠ABC, BE分∠ABC为2: 5两部分, ∠DBE=240, 求∠ABE的度数10.如图, ∠AOC+∠AOB=1800, OM、ON分别是∠BOC.∠AOB的平分线, ∠MON=600, 求∠AOC和∠AOB的度数11.已知∠AOB, 过O点作射线OC, 若∠AOC=0.5∠AOB, 且∠AOC=220, 求∠BOC的度数12.已知∠AOB=600, ∠BOC=1200, OD平分∠AOB, OE是∠BOC的一条三等分线, 求∠DOE的度数13.如图, 已知∠AOC=900, ∠DOC比∠DOA大280, OB是∠AOC的平分线, 求∠BOD的度数14.如图, 已知∠AOC=1500, OB是∠AOC的平分线, OE, OF分别是∠AOB, ∠BOC的平分线, 求∠EOF的度数15.直线AB.CD相交于点O, OE平分∠AOD, ∠FOC=900, ∠1=400, 求∠2与∠3的度数角的和差倍分专项训练题1参考答案1.分析: 直接利用角平分线的定义进而得出∠AOC=∠DOC, ∠BOE=∠EOD, 即可得出答案解:OC 平分∠AOD, 0E 是∠BOD 的平分线, ∴∠AOC=∠DOC, ∠BOE=∠DOE, ∴∠COE=∠COD+∠DOE=∠AOC+∠BOE=21∠AOB=21×1300=650. 2.分析: 由角平分线的定义, 结合平角的定义, 易求∠BOF 和∠EOF 的度数,解: 点O 是直线AB 上一点, 则∠AOB=180°.若∠AOC=68°, 则∠BOC=∠AOB-∠AOC=180°-68°= 112°, ∵OF 平分∠BOC, ∴∠BOF= ∠BOC= ×112°=56°;又∵OE 平分∠AOC, ∴∠EOF= ∠AOC+ ∠BOC=34°+56°=90, 故∠BOF 和∠EOF 分别是56°和90°.3.分析: (1)由∠AOC+∠COB=180°, 又知OD 是∠AOC 的平分线, OE 是∠COB 的平分线, 故知∠DOE=∠DOC+∠COE= (∠AOC+∠COB)=90°.(2)∵∠A0D+∠BOE=90°和∠AOD=51°17′,可以得到∠BOE 的度数.解: (1)∵∠AOC+∠COB=180°, 已知OD 是∠AOC 的平分线, OE 是∠COB 的平分线∴∠DOC= ∠AOC,∠COE= ∠COB, ∴∠DOE=∠DOC+∠COE= (∠AOC+∠COB)=90°.(2)∵∠AOD+∠BOE=90°,∠AOD=51°17′, ∴∠BOE=90°-∠A0D=38°43′, 故答案为90°, 38°, 43′.4.分析: 根据平角的定义及互补的性质, 解答出即可解:∵∠AOD=44°,∠BOC=32°, ∴∠C0D=104°.∵OF 平分∠COD, ∴∠FOD=52°, 又∵∠EOD=90°, ∴∠EOA=90°-44°=46°, ∴∠BOE=134°.5.分析: 设∠BOF=∠COF=x °, ∠AOE=∠DOE=y °, ∠COD=z °, 根据角的和差列出方程即可求解. 解: 设∠BOF=∠COF=x °,∠AOE=∠DOE=y °,∠COD=z °, 根据题意可得:100+140+x+y=360°, x+y+z=140°, 两式相减得:z=20, 即∠COD=20°.6.分析: 根据角平分线定义求出∠AOC, 代入∠COD=∠AOD-∠AOC 求出即可.解:∵OB 是∠AOC 的平分线,∠AOB=30°, ∴∠AOC=2∠AOB=60°, ∵∠AOD=80°, ∴∠COD=∠AOD-∠AOC=20°.7.分析: 此题需要分类讨论 , 共两种情况, 可以作图后计算.解:∵∠BOC=30°, ∠AOB=3∠BOC,∴∠AOB=3×30°=90°.当OC 在∠AOB 的外侧时, ∠AOC=∠AOB+∠BOC=90°+30°=120°, 当OC 在∠AOB 的内侧时, ∠AOC=∠AOB+∠BOC=90°-30°=60°, 所以 ∠AOC=120°或60°.8.分析:先利用∠BAD=∠BAE-∠DAE 求出∠BAD 的度数, 然后根据角平分线的定义计算∠CAD 的度数.解:∵∠BAE=75°,∠DAE=15°,∴∠BAD=∠BAE-∠DAE=60°,∵AC 是∠BAD 的平分线, ∴∠CAD= 21∠BAD=30°. 9.分析;由角平分线的定义, 则∠CBD=∠DBA, 根据BE 分∠ABC 为2:5两部分这一关系列出方程求解:设∠CBE=2x °,得2x+24=5x-24,解得x=16, ∴∠ABE=5x=5×16°=80°.10.分析: 由OM 、ON 分别是∠AOB 与∠AOC 的平分线, 得出∠AOM=∠BOM= ∠AOB, ∠AOM= ∠AOC ;再由∠AOB 与∠AOC 互补, 得出∠AOB+∠AOC=180°, 得出∠AOM+∠AON=90°, 再进一步结台∠MON=∠AON-∠AOM=40°, 求得∠AOM, 进一步求得结论.解: ∵OM 、ON 分别是∠AOB 与∠AOC 的平分线, ∴∠AOM=∠BOM= ∠AOB,∠AON= ∠AOC ;∵∠AOB +∠AOC=180°, ∴∠AOM+∠AON=90°, ∵∠MON=∠AON-∠AOM=40°, ∴∠AOM=25°∴∠AOB=50°,∠AOC=130°.11.分析: 此题需要分类讨论 , 分两种情况计算.解: 当OC 在∠AOB 的内部时, 根据∠AOC=0.5∠AOB, ∠AOC=220, 可以得出∠BOC=∠AOC=220;当OC在∠AOB的外部时, 根据∠AOC=0.5∠AOB, ∠AOC=220, 可以得出∠BOC=∠AOC+∠AOB=660. 12.分析: 此题需要分类讨论 , 分四种情况计算.(1)如图1, 当∠AOB+∠AOB=180°, 即∠AOC为平角时,OE为靠近OB的一条三等分线.∵∠AOB=60°, OD平分∠AOB, ∴∠DOB=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°, ∴∠BOE=40°∴∠OOE=∠DOB+∠BOE=30°+40°=70°;(2)如图2, 当∠AOB+∠AOB=180°, 即∠AOC为平角时,OE为靠近OC的一条三等分线.∵∠AOB= 60°, OD平分∠AOB, ∴∠DOB=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°, ∴∠BOE= 80°, ∴∠OOE=∠DOB+∠BOE=30°+80°=110°;(3)如图3, 当∠AOB 与∠BOC有公共边OB, ∠AOB的另一边OA在∠BOC内部时, OE为∠BOC内靠近OC边的一条三等分线.∵∠AOB=60°, ∠BOC=60°, ∴OA为∠BOC平分线上, ∵OD平分∠AOB,∴∠DOB=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°∴∠BOE=80°, ∴∠DOE=∠BOE-∠DOB=80°-30°=50°;(4)如图4, 当∠AOB 与∠BOC有公共边OB, ∠AOB的另一边OA在∠BOC内部时, OE为∠BOC内靠近OB边一条三等分线且更靠近∠AOB的平分线OD.∵∠AOB=60°, OD平分∠AOB, ∴∠DOA=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°, ∴∠BOE=40°∴∠DOE=∠BOE+∠AOD-∠AOB=40°+ 30°-60°=10°.13.分析: 先由∠COD﹣∠DOA=28°, ∠COD+∠DOA=90°, 解方程求出∠COD与∠DOA的度数, 再由OB是∠AOC的平分线, 得出∠AOB=∠AOC=45°, 则∠BOD=∠AOB﹣∠DOA, 求出结果. 解: ∵∠COD比∠DOA大28°, ∴∠COD=∠DOA+28°, ∵∠AOC=90°, ∴∠COD+∠DOA=90°, ∴∠DOA+28°+∠DOA=90°, 2∠DOA=62°, 所以∠DOA=31°, ∵OB是∠AOC的平分线, ∴∠AOB =∠BOC=∠AOC=45°, ∴∠BOD=∠AOB﹣∠DOA=45°﹣31°=14°. 故答案为14°.14.分析: 根据角平分线定义得到∠AOB=∠BOC= ∠AOC, ∠AOE =∠BOE= ∠AOB, ∠BOF=∠COF= ∠BOC, 则有∠EOF=∠EOB+∠BOF=∠AOC=75°.解: ∵OB是∠AOC的角平分线, ∴∠AOB=∠BOC= ∠AOC, ∵OE、OF分别是∠AOB.∠COB的角平分线, ∴∠AOE =∠BOE= ∠AOB, ∠BOF=∠COF= ∠BOC, ∴∠EOF=∠EOB+∠BOF=∠AOB+ ∠BOC=(∠AOB+∠BOC)=∠AOC= ×150°=75°.规律: 从一个角的内部任意引一条射线, 这条射线把这个角分成的两个角的角平分线组成的角的度数等于这个角的一半.15.分析:根据平角为180度可得∠2=180°﹣∠1﹣∠FOC, 根据∠AOD=∠BOC可得∠AOD的度数, 再根据角平分线定义进行计算可得∠3.解:∵∠AOB=180°, ∴∠1+∠2+∠COF=180°, ∵∠FOC=90°, ∠1=40°, ∴∠2=180°﹣∠1﹣∠FOC=50°, ∠BOC=∠1+∠FOC=130°, ∴∠AOD=∠BOC=130°, ∵OE平分∠AOD, ∴∠3=∠AOD=65°.。
和倍差倍问题和差问题问题讲义及练习测试参考答案优质的

精心整理(本第一讲和倍问题和倍问题是已知大小两个数的和与它们的倍数关系,求大小两个数的应用题为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
例甲班和乙班共有图书本甲班的图书本数是乙班的倍,甲班和乙班各有图书多少 本?分析设乙班的图书本数为份,则甲班图书为乙班的倍,那么甲班和乙班图书本数的和相当于乙班图书本数的倍还可以理解为份的数量是本,求出份的数量也就求出了乙班的图书本数,然后再求甲班的图书本数用下图表示它们的关系:解:乙班:-F ()(本) 甲班:X (本) 或(本)答:甲班有图书本,乙班有图书本。
这道应用题解答完了,怎样验算呢?可把求出的甲班本数和乙班本数相加,看和是不是本;再把甲班的本数除以乙班本数,看是不是等于倍如果与条件相符,表明这题作对了注意验算决不是把原式再算一遍。
验算:+(本)F (倍)。
例甲班有图书本,乙班有图书本,甲班给乙班多少本,甲班的图书是乙班图书的 倍?分析解这题的关键是找出哪个量是变量,哪个量是不变量从已知条件中得出,不管甲班给乙班多少本书,还是乙班从甲班得到多少本书,甲、乙两班图书总和是不变的量最后要求甲班图书是乙班图书的倍,那么甲、乙两班图书总和相当于乙班现有图书的倍依据解和倍问题的方法,先求出乙班现有图书多少本,再与原有图书本数相比较,可以求出甲班给乙班多少本书(见上图)。
解:①甲、乙两班共有图书的本数是: +(本)② 甲班给乙班若干本图书后,甲、乙两班共有的倍数是: +二(倍)③ 乙班现有的图书本数是:F④甲班给乙班图书本数是:(本)综合算式:(+)4-()(本)(本)答:甲班给乙班本图书后,甲班图书是乙班图书的倍。
验算:()4()=(倍)()()=(本)。
例光明小学有学生人,其中男生比女生的倍少人,男、女生各有多少人?分析把女生人数看作一份,由于男生人数比女生人数的倍还少人,如果用男、女生人数总和人再加上人,就等于女生人数的倍(见下图)。
三年级和差倍问题及答案

三年级和差倍问题及答案1、妈妈的年龄是茵苗的6倍,妈妈和茵苗一共42岁,妈妈和茵苗各几岁?2、茵苗去文具店购买文具,自动铅笔每支2元,钢笔的价格是自动铅笔的8倍,买一支钢笔和铅笔一共花了18元,钢笔和自动铅笔各多少钱?3、茵苗的故事书是小敏的7倍,茵苗和小敏一共有96本故事书,茵苗和小敏各有多少本故事书?4、李步青和小敏一起剪花,李步青剪的花是小敏的4倍,小敏和李步青一共剪了100朵,小敏和李步青各剪了多少朵?5、小敏和茵苗比赛看书,茵苗看书的速度是小敏的5倍,小敏和茵苗一共看了120页,茵苗和小敏各看了多少页?6、有两袋米,大袋的米是小袋的米的3倍,大袋的米比小袋的米重50千克,大袋和小袋的米各有多少千克?7、甲乙各有一些书,甲比乙多60本,甲乙送给幼儿园的小朋友同样多后,甲是乙的3倍,现在甲乙各有多少本书?8、茵苗购买了一本故事书和科技书,故事书的价格是科技书的4倍,茵苗总共花了50元,故事书和科技书各是多少元?参考答案:1、妈妈的年龄是茵苗的6倍,妈妈和茵苗一共42岁,妈妈和茵苗各几岁?2、茵苗去文具店购买文具,自动铅笔每支2元,钢笔的价格是自动铅笔的8倍,买一支钢笔和铅笔一共花了18元,钢笔和自动铅笔各多少钱?1+8=918÷9=2(元) 2x8=16(元)3、茵苗的故事书是小敏的7倍,茵苗和小敏一共有96本故事书,茵苗和小敏各有多少本故事书?7+1=896÷8=12(本)96-12=84(本)4、李步青和小敏一起剪花,李步青剪的花是小敏的4倍,小敏和李步青一共剪了100朵,小敏和李步青各煎了多少朵?4+1=5100÷5=20(朵)20x4=80(朵)2、小敏和茵苗比赛看书,茵苗看书的速度是小敏的5倍,小敏和茵苗一共看了120页,茵苗和小敏各看了多少页?5+1=6120÷6=20(页) 20x5=100(页)5、有两袋米,大袋的米是小袋的米的3倍,大袋的米比小袋的米重50千克,大袋和小牮的米各有多少千克?3-1=2 50÷2=25(千克)25x3=75(千克)6、甲乙各有一些书,甲比乙多60本,甲乙送给幼儿园的小朋友同样多后,甲是乙的3倍,现在甲乙各有多少本书?3-1=260÷2=30 (本) 30x3=90(本)7、茵苗购买了一本故事书和科技书,故事书的价格是科技书的4倍,茵苗总共花了50元,故事书和科技书各是多少元?。
小学奥数和差问题、和倍问题、差倍问题专项练习附答案

小学奥数和差问题、和倍问题、差倍问题专项练习附答案(1)学校去年有12人参加体育兴趣小组,今年是去年的2倍少3人,今年体育兴趣小组有多少人?(2)小红和小明共有零花钱9元,小红的钱数是小明的2倍,小红和小明分别有零花钱多少元?(3)小英和小林共有15个果冻布丁,其中小林的个数比小英少3个。
小英和小林各有多少个果冻布丁?(4)一根电线长22米,剪掉一半后,是另一根电线的5倍少4米,那么另一根电线长多少米?(5)期中考试王平和李杨语文成绩的总和是188分,李杨比王平少4分,两人各考了多少分?(6)两筐水果共重124千克,第一筐比第二筐多8千克,两筐水果各重多少千克?(7)明明家有课外书20本,亮亮家的课外书是明明家的3倍,两人共有课外书多少本?(8)明明和亮亮共有课外书33本,亮亮的课外书是明明的2倍,两人各有课外书多少本?(9)学校苗圃中有月季花和菊花共30棵,其中月季花的棵数比菊花多6棵。
学校的月季花和菊花各有多少棵?(10)甲有19元钱,是乙的3倍少5元,乙有多少钱?(11)幼儿园大班共有14个小朋友,男孩比女孩多2个。
则男孩女孩各有多少人?(12)甲、乙两人年龄的和是35岁,甲比乙小5岁。
问甲、乙各多少岁?(13)甲班和乙班共有图书160本。
甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?(14)一次画展中,人物画和风景画共20幅,其中人物画比风景画少2幅。
风景画有多少幅?(15)小红和妈妈的年龄加在一起是40岁,妈妈年龄是小红年龄的4倍,小红和妈妈各几岁?(16)小红有15颗星,亮亮的颗数是小红的3倍还少4颗,亮亮有多少颗星?(17)小茜和小敏两人今年的年龄和是23岁,4年后,小茜将比小敏大3岁,问小茜和小敏今年各多少岁?(18)小明的邮票比小红多15张,小明的张数是小红的4倍,两人各几张?(19)甲乙两数之和是341,甲数的最后一位数字是0,如果把0去掉,就与乙数相同,问甲乙两数各是多少?(20)两笼鸡蛋共19只,若甲笼再放入4只,乙笼中取出两只,这时乙笼比甲笼鸡蛋还多1只。
和差、和倍、差倍问题综合练习题

差倍问题应用和差问题:大数=(和+差)÷2 小数=(和-差)÷2和倍问题:小数=和÷(倍数+1)。
大数=和-小数,或大数=小数×倍数。
差倍问题:小数=差÷(倍数-1) 大数=小数×倍数(或大数=小数+差)1、植树节的时候,四年级和五年级一同去植树。
四的级比五的级少植120棵,五的级植的是四年级的3倍。
两个的级各植树多少棵?2、长方形的长比宽多18厘米,长是宽的4倍,这个长方形的长和宽各是多少厘米?3、某工地上存放的沙子比水泥多3500吨,沙子的数量比水泥的3倍多500吨。
水泥有多少吨?沙子有多少吨?4、冰清和玉洁各有钱若干元,若冰清给玉洁24元,二人钱数就相等;如果玉洁给冰清30元,则冰清的钱数就是玉洁的3倍,冰清和玉洁原来各有钱多少元?5、一个数的小数点向左移动一位,比原来的数小了2.25。
原数是多少?6、甲和已的钱一样多,甲给已30元,则乙所有的钱是甲的5倍。
你知道甲和已原来各有多少钱吗?.7、姐姐有连环画38本,妹妹有连环画52本,姐姐要给妹妹多少本连环画,才能使妹妹的本数是姐姐的2倍?8、两箱茶叶共176千克,从甲箱取出30千克放乙箱,乙箱的千克数就是甲箱的3倍。
两箱原有茶叶多少千克?9、甲数是乙数的3倍,丙数是乙数的4倍,丁数是丙数的一半,四个数的和是1040,丁数是多少?10、把一个减法算式的被减数、减数、差加起来和是180,已知减数比差大26,被减数、减数和差各是多少?11、一次期末考试中,小华的语数共得分190分,如果他的语文多得6分,那么他的语文和数学的得分就相等。
小分的语文数学各得了多少分?12、两篮鸡蛋,共计200个,如果从甲篮中取出5个放入乙篮中,那么这两篮鸡蛋数相等。
问这两篮中原来各有多少个鸡蛋?13、爸爸一月工资3200元,他取出一部分,其余的留存银行,已知他如果再多取500元,那么留存的和取出的一样多,问爸爸实际取出了多少元?14、妈妈给小花买了一件裙子和一双凉鞋,共用去65元,已知凉鞋比裙子便宜7元,问买凉鞋和裙子各用去多少元?综合练习:1、一个数乘8后比原数多了84,原来的数是多少?2、学校图书馆有科技书和故事书共320本,其中故事书的本数是科技书的3倍,故事书有多少本?3、在一个数的末尾减少上一个“0”以后,得到的数比原来的数减少36。
和倍、差倍、和差问题及答案

和倍、差倍、和差问题及答案数学特长生试题(1)1、两个数的和是682,其中一个加数的个位是X,若把X去掉,则与另一个加数相同,这两个数各是多少?解题思路:设其中一个加数为a,另一个加数为b,根据题意可得:a +b = 682a - X +b = b + b化简可得:a = 2b - X将a代入第一个等式中,得到:3b - X = 682因为X是个位数,所以X只能是2或7,代入方程可得:b = 228,a = 454 或 b = 227,a = 455所以答案为:454和228,或者455和227.2、甲、乙两个车间共生产机床664台,甲车间的产量是乙车间的3倍,两个车间各生产机床多少台?解题思路:设乙车间生产的机床数为x,则甲车间生产的机床数为3x。
根据题意可得:3x + x = 664化简可得:x = 166,所以乙车间生产的机床数为166,甲车间生产的机床数为498.3、某印刷厂第一季度共印书册,二月份印的册数是一月份的2倍,三月份印的册数是一月份的3倍,一、二、三月份各印书多少册?解题思路:设一月份印的书数为x,则二月份印的书数为2x,三月份印的书数为3x。
根据题意可得:x + 2x + 3x =化简可得:x = ,所以一月份印的书数为,二月份印的书数为,三月份印的书数为.4、___一、二月份共生产电机400台,二月份生产的台数比一月份生产的台数的5倍还少68台,两个月各生产多少台?解题思路:设一月份生产的电机数为x,则二月份生产的电机数为5x - 68.根据题意可得:x + 5x - 68 = 400化简可得:x = 94,所以一月份生产的电机数为94,二月份生产的电机数为462.5、甲库存粮108吨,乙库存粮140吨,要使甲库存粮是乙库的3倍,必须从乙库运出多少吨放入甲库?解题思路:设从乙库运出的粮食重量为x,则甲库存粮为3乙库存粮。
根据题意可得:3乙 - 108 = 乙 + x - x化简可得:x = 224,所以从乙库运出224吨放入甲库。
和倍差倍应用题及答案

和倍差倍应用题及答案题目:甲乙两人共同完成一项工作,甲单独完成需要12天,乙单独完成需要18天。
现在甲乙合作,甲先工作了3天后,乙加入,两人一起工作了2天,然后甲离开,乙单独完成了剩余的工作。
问乙单独完成剩余工作需要多少天?答案:首先,我们需要计算甲乙两人的工作效率。
1. 甲的工作效率:甲单独完成需要12天,所以甲的工作效率为\( \frac{1}{12} \)。
2. 乙的工作效率:乙单独完成需要18天,所以乙的工作效率为\( \frac{1}{18} \)。
接下来,我们计算甲乙合作的效率。
3. 甲乙合作的效率:甲乙两人的工作效率之和为 \( \frac{1}{12} + \frac{1}{18} = \frac{3}{36} + \frac{2}{36} = \frac{5}{36} \)。
现在,我们计算甲乙合作2天完成的工作量。
4. 甲乙合作2天完成的工作量: \( \frac{5}{36} \times 2 =\frac{10}{36} \)。
接着,我们计算甲单独工作3天完成的工作量。
5. 甲单独工作3天完成的工作量: \( \frac{1}{12} \times 3 = \frac{3}{12} = \frac{1}{4} \)。
然后,我们计算甲乙合作和甲单独工作后剩余的工作量。
6. 剩余工作量: \( 1 - \frac{1}{4} - \frac{10}{36} =\frac{36}{36} - \frac{9}{36} - \frac{10}{36} = \frac{17}{36} \)。
最后,我们计算乙单独完成剩余工作需要的天数。
7. 乙单独完成剩余工作需要的天数: \( \frac{17}{36} \div\frac{1}{18} = \frac{17}{36} \times 18 = \frac{17 \times 18}{36} = \frac{306}{36} = 8.5 \)。
博识和差倍问题综合(含答案)

和差倍问题一、和倍问题1)和倍例1、纺织厂有职工480人,其中女职工人数是男职工人数的3倍.请问:男、女职工各几人?例2、一个长方形,周长是300厘米,长是宽的2倍,求这个长方形的面积.(☆)例3、甲班和乙班一共有60人,如果从甲班调6个人到乙班,那么甲班的人数就是乙班人数的2倍.求甲、乙两班原来的人数.例4、在一个减法算式里,被减数、减数与差的和是240,减数是差的5倍,则减数是多少?(★★)例5、动物园有5座猴山,其中3座住着金丝猴,2座住着猕猴.这5座猴山上猴子的数量分别为:10,15,30,35,70.已知金丝猴的总数是猕猴的3倍,问:哪两座山上住着猕猴?(★★★)练习题:1、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?(☆)2、甲水库有43亿立方米水,乙水库有37亿立方米水.试问:需要从甲水库调多少亿立方米水到乙水库,才能使乙水库的水比甲水库多两倍?(★★)3、甲班有图书120本,乙班有图书30本,甲班给乙班多少本,甲班的图书是乙班图书的2倍?.2)和倍多例6、甲、乙两堆货物一共有160件,已知甲堆货物比乙堆的3倍还多40件.甲、乙两堆各有多少件货物?(★★)例7、两个自然数相除,商是4,余数是1.如果被除数、除数、商以及余数的和是56,那么被除数等于多少?(★★★)练习题:1、某交通协管员七月份开出78张罚单.这些罚单分为两种:一种是违章停车,另一种是闯红灯.违章停车的罚单较多,比闯红灯罚单数量的4倍还多3张.违章停车的罚单有多少张?(★★)2、果园里一共种340棵桃树和杏树,其中桃树的棵数比杏树的3倍多20棵,两种树各种了多少棵?(☆☆)3)和倍少例8、书架上放着一些童话小说和科幻小说,一共有47本.童话小说的数量比科幻小说数量的4倍少3本.书架上放着多少本科幻小说?(★★)练习题:1、果园中梨树和苹果树共有67棵,梨树比苹果树的2倍少2棵,苹果树有多少棵?(★★)2、光明小学有学生760人,其中男生比女生的3倍少40人,男、女生各有多少人?(☆☆)4)和倍综合例9、三堆糖果共有105颗,其中第一堆糖果的数量是第二堆的3倍,而第三堆糖果的数量又比第二堆的2倍少3颗.第三堆糖果有多少颗?(★★★)例10、甲、乙、丙三个粮仓一共存有109吨粮食.其中甲粮仓的粮食总量比乙粮仓的3倍多1吨,而乙粮仓的粮食总量则是丙粮仓的2倍.问:甲粮仓比丙粮仓多存粮多少吨?(★★★)例11、549是甲、乙、丙、丁4个数的和.如果甲数加上2,乙数减少2,丙数乘以2,丁数除以2以后,则4个数相等.求4个数各是多少?(☆☆☆☆)练习:1、有3条绳子,共长95米,第一条比第二条长7米,第二条比第三条长8米,问3条绳子各长多少米?(☆☆☆)2、果园里有桃树、梨树、苹果树共552棵.桃树比梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、梨树和苹果树各有多少棵?(☆☆☆)3、某驻军有三个坦克连,共有115辆坦克,一连坦克数量比二连的2倍多2,而二连的坦克数量比三连的3倍多1.请问:一连比三连多几辆坦克?(★★★)二、差倍问题1)差倍例12、小陈为找工作准备了中、英文两份简历.中文简历的字数是英文简历字数的3倍,而且中文简历比英文简历多220个字.请问:中文简历的字数是多少?(★★)例13、甲、乙两位学生原计划每周做同样数量的练习,实际上甲每周多做了18道题,而乙偷懒每周少做了14道题,结果乙三周的做题量只相当于甲一周的数量.请问:他们原计划每周做几道题?(★★)例14、甲房地产公司有资金100亿元,乙房地产公司有资金40亿元,两公司联合投资一块地皮,用去同样多的资金后,甲公司剩下的资金是乙公司的5倍.请问:两公司投资这块地皮共用去多少亿元?(★★)例15、有两根同样长的绳子,第一根截去12米,第二根接上14米,这时第二根长度是第一根长的3倍,两根绳子原来各长多少米?(☆☆☆)例16、亚洲杯决赛中,中国记者的数量是外国记者数量的3倍.比赛结束后中国记者有180人离场,外国记者有40人离场,剩下的中、外记者数量相等.原来中、外记者各有多少人?(★★★)例17、甲、乙两个数,如果甲数加上320就等于乙数了.如果乙数加上460就等于甲数的3倍,两个数各是多少?(☆☆☆)练习:1、学校合唱团成员中,女生人数是男生的3倍,而且女生比男生多80人.合唱团里男生和女生各有多少人?(★★)2、一只大象的体重比一头牛重4500千克,又知大象的重量是一头牛的10倍,一只大象和一头牛的重量各是多少千克?(☆☆)3、果园里的桃树比杏树多90棵,桃树的棵数是杏树的3倍,桃树和杏树各有多少棵?(☆☆)4、有两块布,第一块长74米,第二块长50米,两块布各剪去同样长的一块布后,剩下的第一块米数是第二块的3倍,问每块布各剪去多少米?(☆☆)5、三(1)班与三(2)班原有图书数一样多.后来,三(1)班又买来新书74本,三(2)班从本班原书中拿出96本送给一年级小同学,这时,三(1)班图书是三(2)班的3倍,求两班原有图书各多少本?(☆☆☆)6、两块同样长的花布,第一块卖出31米,第二块卖出19米后,第二块是第一块的4倍,求每块花布原有多少米?(☆☆☆)7、甲、乙两校教师的人数相等,由于工作需要,从甲校调30人到乙校去,这时乙校教师人数正好是甲校教师人数的3倍,求甲、乙两校原有教师各多少人?(☆☆☆)8、两筐重量相同的苹果,从甲筐取出7千克,乙筐加入19千克,这时乙筐是甲筐苹果的3倍,问两筐原有苹果多少千克?(☆☆☆)9、有两块同样长的布,第一块卖出25米,第二块卖出14米,剩下的布第二块是第一块的2倍,求每块布原有多少米?(☆☆☆)10、菜站运来的白菜是萝卜的3倍,卖出白菜1800千克,萝卜300千克,剩下的两种蔬菜的重量相等,菜站运来的白菜和萝卜各是多少千克?(☆☆☆)2)差倍多例18、小悦和阿奇在操场上练习跑步.一段时间过后,阿奇跑的距离比小悦跑的3倍还多80米.如果小悦比阿奇少跑了500米,那么小悦和阿奇分别跑了多少米?(★★)例19、阿奇家有两根绳子,长的那根有163米,短的只有97米.他把两根绳子剪去同样长的一段,结果长绳所剩长度比短绳所剩长度的7倍还多6米.那么两根绳子都剪去了多少米?(★★)例20、有两个炮兵营参加军事演习,它们各准备了若干枚炮弹.开始一营比二营多准备了5枚炮弹.后来因为演习需要,一营给了二营20枚炮弹.这时二营炮弹数量就比一营的3倍还多3枚.一营最开始准备了几枚炮弹?(★★★)练习:有两款数码相机,一款是高档专业相机,一款是普通家用相机.家用相机价格较低,比专业相机便宜了4600元.买1台专业相机的钱足够买4台家用相机,而且还能剩下100元.请问:专业相机的价格是多少钱?(★★★)3)差倍少例21、小悦和阿奇在操场上练习跑步.一段时间过后,阿奇跑的距离比小悦跑的3倍少80米.如果小悦比阿奇少跑了500米,那么小悦和阿奇分别跑了多少米?(★★)练习:1、原先《花城日报》和《鹏城晚报》有同样数目的版面.后来《花城日报》扩充版面,增加了10版,这样《花城日报》的版面比《鹏城晚报》的4倍少2版.两种报纸现在各有多少版?(★★)2、甲、乙两筐苹果重量相等.现在从甲筐拿12千克苹果放入乙筐,结果乙筐苹果的重量就比甲筐的3倍少2千克.两筐苹果原来各有多少千克?(★★★)三、和差问题1)和差例22、冬冬在玩具店看中了两件汽车模型.如果两件都买,一共需要400元.已知较贵的模型比便宜的模型贵60元,这两件模型各要多少钱?(★)练习:1、张先生投资股票,2006年和2007年一共盈利40万元,其中2006年比2007年少盈利14万元.张先生2007年盈利多少万元?(★)2、甲、乙两位火炬手负责把火炬从A地传递到B地.先由甲从A地出发,并在途中将火炬传递给乙;乙接过火炬后继续慢跑前往B地.已知A,B两地相距2400米,并且甲比乙多跑了600米.请问:甲跑了多少米?(★)3、两筐水果共重150千克,第一筐比第二筐多8千克,两筐水果各多少千克?(☆)4、果园里有桃树和梨树共150棵,桃树比梨树多20棵,两种果树各有多少棵?(☆)5、用锡和铝制成500千克的合金,铝的重量比锡多100千克,锡和铝各是多少千克?(☆)2)和差问题综合例23、登月行动地面控制室的成员由两组专家组成,两组共有专家125人.原来第一组人数较多,所以从第一组调了20人到第二组,即使这样第一组人数仍比第二组多5人.原来第一组有多少名专家?(★★)例24、一辆公共汽车出发时有48人,到达第一站时有若干人下车,而且下车的比留下的多8人.到达第二站时,又有人下车,这次下车的比留下的少8人.请问:最后有几个人留在了车上?(注:每个车站都无人上车)(★★)例25、小悦和冬冬玩游戏,每玩一局,输的就要给赢的1枚棋子.一开始小悦有18枚棋子,冬冬则有22枚.玩了若干局之后,小悦反而比冬冬多了10枚棋子.请问:此时小悦有多少枚棋子?(★★)例26、今年小强7岁,爸爸35岁,当两人年龄和是58岁时,两人年龄各多少岁?(☆☆)例27、小明期末考试时语文和数学的平均分数是94分,数学比语文多8分,问语文和数学各得了几分?(☆☆)例28、甲、乙两桶油共重30千克,如果把甲桶中6千克油倒入乙桶,那么两桶油重量相等,问甲、乙两桶原有多少油?(☆☆☆)例29、三个物体平均重量是31千克,甲物体比乙、丙两个物体重量之和轻1千克,乙物体比丙物体重量的2倍还重2千克,三个物体各重多少千克?(☆☆☆)例30、公园里柳树和杨树共43棵,松树和柏树共42棵,并且杨树比松树多2棵,比柳树少7棵,那么公园里有柏树多少棵?(★★★)练习:1、甲、乙两个学校共有学生1245人,如果从甲校调20人去乙校后,甲校比乙校还多5人,两校原有学生各多少人?(☆☆)2、甲、乙两个工程队共有1980人,甲队为了支援乙队,抽出285人加入乙队,这时乙队人数还比甲队少24人,求甲、乙两队原有工人多少人?(☆☆)3、甲乙两校共有学生864人,为了照顾学生就近入学,从甲校调入乙校32名同学,这样甲校学生还比乙校多48人,问甲、乙两校原来各有学生多少人?(☆☆)4、某工厂去年与今年的平均产值为96万元,今年比去年多10万元,今年与去年的产值各是多少万元?(☆☆)四、和差倍综合练习1、费叔叔买来三箱水果,总重100千克.其中前两箱重量相差11千克,且前两箱的总重量是第三箱的3倍.请问:这三箱水果中最重的那箱重多少千克?(★★)2、甲、乙、丙三个物体的总重量是93千克,甲物体比乙、丙两个物体的重量之和轻1千克,乙物体比丙物体重量的2倍还重2千克,那么甲、乙、丙各重多少千克?(★★★)3、四年级有3个班,如果把甲班的1名学生调整到乙班,两班人数相等;如果把乙班1名学生调到丙班,丙班比乙班多2人,问甲班和丙班哪班人数多?多几人?(☆☆☆)4、育才小学三年级有3个班,一共有学生126人.如果一班比二班多4人,二班比三班多4人,那么这三个班分别有多少人?(★★)5、三国时期,魏国、蜀国、吴国三国交战.已知吴国军队比蜀国军队多20万人;魏国军队人数是吴国的2倍,又是蜀国的3倍.魏国军队有多少人?(★★★)6、甲、乙两个人一起去商店买东西,两人一共带了80元钱.甲用自己带的钱的一半买了一本漫画书,乙花10元钱买了一盘磁带.这时甲的钱恰好是乙的3倍.开始时乙带了多少元钱?(★★★)7、姐妹俩一起做数学、语文两科作业.姐姐花在数学作业上的时间比妹妹多10分钟;而妹妹花在语文作业上的时间比姐姐多4分钟.已知姐姐一共花了88分钟做完作业,妹妹做数学作业的时间比语文作业少12分钟.请问:妹妹做语文作业花了多少分钟?(★★★)8、游泳池里男生的人数比女生的6倍少11人,比女生的4倍多13人,那么男生有多少人?(★★★)9、红旗小学三年级有甲、乙、丙三个班,一共有学生162人.如果从甲班转出2个人到乙班,则甲、乙两班人数相同.如果这时再从丙班转出3个人到乙班,则乙、丙两班人数相同.请问:甲班原来有多少人?(★★★)答案一、和倍问题1)和倍例1、纺织厂有职工480人,其中女职工人数是男职工人数的3倍.请问:男、女职工各几人?(★)答案:120,360.例2、一个长方形,周长是300厘米,长是宽的2倍,求这个长方形的面积.(☆)答案:5000平方厘米.例3、甲班和乙班一共有60人,如果从甲班调6个人到乙班,那么甲班的人数就是乙班人数的2倍.求甲、乙两班原来的人数.(★★)答案:46,14.例4、在一个减法算式里,被减数、减数与差的和是240,减数是差的5倍,则减数是多少?(★★)答案:100.例5、动物园有5座猴山,其中3座住着金丝猴,2座住着猕猴.这5座猴山上猴子的数量分别为:10,15,30,35,70.已知金丝猴的总数是猕猴的3倍,问:哪两座山上住着猕猴?(★★★)答案:有10只和有30只猴子的山上住着猕猴.练习题:1、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?(☆)答案:120本,40本.2、甲水库有43亿立方米水,乙水库有37亿立方米水.试问:需要从甲水库调多少亿立方米水到乙水库,才能使乙水库的水比甲水库多两倍?(★★)答案:23.3、甲班有图书120本,乙班有图书30本,甲班给乙班多少本,甲班的图书是乙班图书的2倍?(☆☆)答案:20本.2)和倍多例6、甲、乙两堆货物一共有160件,已知甲堆货物比乙堆的3倍还多40件.甲、乙两堆各有多少件货物?(★★)答案:130,30.例7、两个自然数相除,商是4,余数是1.如果被除数、除数、商以及余数的和是56,那么被除数等于多少?(★★★)答案:41.练习题:1、某交通协管员七月份开出78张罚单.这些罚单分为两种:一种是违章停车,另一种是闯红灯.违章停车的罚单较多,比闯红灯罚单数量的4倍还多3张.违章停车的罚单有多少张?(★★)答案:63.2、果园里一共种340棵桃树和杏树,其中桃树的棵数比杏树的3倍多20棵,两种树各种了多少棵?(☆☆)答案:杏树80棵,桃树260棵.3)和倍少例8、书架上放着一些童话小说和科幻小说,一共有47本.童话小说的数量比科幻小说数量的4倍少3本.书架上放着多少本科幻小说?(★★)答案:10.练习题:1、果园中梨树和苹果树共有67棵,梨树比苹果树的2倍少2棵,苹果树有多少棵?(★★)答案:23.2、光明小学有学生760人,其中男生比女生的3倍少40人,男、女生各有多少人?(☆☆)答案:女生200人,男生560人.4)和倍综合例9、三堆糖果共有105颗,其中第一堆糖果的数量是第二堆的3倍,而第三堆糖果的数量又比第二堆的2倍少3颗.第三堆糖果有多少颗?(★★★)答案:33.例10、甲、乙、丙三个粮仓一共存有109吨粮食.其中甲粮仓的粮食总量比乙粮仓的3倍多1吨,而乙粮仓的粮食总量则是丙粮仓的2倍.问:甲粮仓比丙粮仓多存粮多少吨?(★★★)答案:61.例11、549是甲、乙、丙、丁4个数的和.如果甲数加上2,乙数减少2,丙数乘以2,丁数除以2以后,则4个数相等.求4个数各是多少?(☆☆☆☆)答案:甲、乙、丙、丁分别是120、124、61、244.练习:1、有3条绳子,共长95米,第一条比第二条长7米,第二条比第三条长8米,问3条绳子各长多少米?(☆☆☆)答案:39米,32米,24米.2、果园里有桃树、梨树、苹果树共552棵.桃树比梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、梨树和苹果树各有多少棵?(☆☆☆)答案:桃树、梨树、苹果树分别是292棵、140棵和120棵.3、某驻军有三个坦克连,共有115辆坦克,一连坦克数量比二连的2倍多2,而二连的坦克数量比三连的3倍多1.请问:一连比三连多几辆坦克?(★★★)答案:59.二、差倍问题1)差倍例12、小陈为找工作准备了中、英文两份简历.中文简历的字数是英文简历字数的3倍,而且中文简历比英文简历多220个字.请问:中文简历的字数是多少?(★★)答案:330.例13、甲、乙两位学生原计划每周做同样数量的练习,实际上甲每周多做了18道题,而乙偷懒每周少做了14道题,结果乙三周的做题量只相当于甲一周的数量.请问:他们原计划每周做几道题?(★★)答案:30.例14、甲房地产公司有资金100亿元,乙房地产公司有资金40亿元,两公司联合投资一块地皮,用去同样多的资金后,甲公司剩下的资金是乙公司的5倍.请问:两公司投资这块地皮共用去多少亿元?(★★)答案:50.例15、有两根同样长的绳子,第一根截去12米,第二根接上14米,这时第二根长度是第一根长的3倍,两根绳子原来各长多少米?(☆☆☆)答案:25.例16、亚洲杯决赛中,中国记者的数量是外国记者数量的3倍.比赛结束后中国记者有180人离场,外国记者有40人离场,剩下的中、外记者数量相等.原来中、外记者各有多少人?(★★★)答案:210,70.例17、甲、乙两个数,如果甲数加上320就等于乙数了.如果乙数加上460就等于甲数的3倍,两个数各是多少?(☆☆☆)答案:390,710.练习:1、学校合唱团成员中,女生人数是男生的3倍,而且女生比男生多80人.合唱团里男生和女生各有多少人?(★★)答案:40,1202、一只大象的体重比一头牛重4500千克,又知大象的重量是一头牛的10倍,一只大象和一头牛的重量各是多少千克?(☆☆)答案:5000,500.3、果园里的桃树比杏树多90棵,桃树的棵数是杏树的3倍,桃树和杏树各有多少棵?(☆☆)答案:135,45.4、有两块布,第一块长74米,第二块长50米,两块布各剪去同样长的一块布后,剩下的第一块米数是第二块的3倍,问每块布各剪去多少米?(☆☆)答案:38.5、三(1)班与三(2)班原有图书数一样多.后来,三(1)班又买来新书74本,三(2)班从本班原书中拿出96本送给一年级小同学,这时,三(1)班图书是三(2)班的3倍,求两班原有图书各多少本?(☆☆☆)答案:181.6、两块同样长的花布,第一块卖出31米,第二块卖出19米后,第二块是第一块的4倍,求每块花布原有多少米?(☆☆☆)答案:35.7、甲、乙两校教师的人数相等,由于工作需要,从甲校调30人到乙校去,这时乙校教师人数正好是甲校教师人数的3倍,求甲、乙两校原有教师各多少人?(☆☆☆)答案:60.8、两筐重量相同的苹果,从甲筐取出7千克,乙筐加入19千克,这时乙筐是甲筐苹果的3倍,问两筐原有苹果多少千克?(☆☆☆)答案:20.9、有两块同样长的布,第一块卖出25米,第二块卖出14米,剩下的布第二块是第一块的2倍,求每块布原有多少米?(☆☆☆)答案:36.10、菜站运来的白菜是萝卜的3倍,卖出白菜1800千克,萝卜300千克,剩下的两种蔬菜的重量相等,菜站运来的白菜和萝卜各是多少千克?(☆☆☆)答案:菜站运来白菜2250千克,萝卜750千克.2)差倍多例18、小悦和阿奇在操场上练习跑步.一段时间过后,阿奇跑的距离比小悦跑的3倍还多80米.如果小悦比阿奇少跑了500米,那么小悦和阿奇分别跑了多少米?(★★)答案:920.例19、阿奇家有两根绳子,长的那根有163米,短的只有97米.他把两根绳子剪去同样长的一段,结果长绳所剩长度比短绳所剩长度的7倍还多6米.那么两根绳子都剪去了多少米?(★★)答案:87.例20、有两个炮兵营参加军事演习,它们各准备了若干枚炮弹.开始一营比二营多准备了5枚炮弹.后来因为演习需要,一营给了二营20枚炮弹.这时二营炮弹数量就比一营的3倍还多3枚.一营最开始准备了几枚炮弹?(★★★)答案:36.练习:有两款数码相机,一款是高档专业相机,一款是普通家用相机.家用相机价格较低,比专业相机便宜了4600元.买1台专业相机的钱足够买4台家用相机,而且还能剩下100元.请问:专业相机的价格是多少钱?(★★★)答案:6100.3)差倍少例21、小悦和阿奇在操场上练习跑步.一段时间过后,阿奇跑的距离比小悦跑的3倍少80米.如果小悦比阿奇少跑了500米,那么小悦和阿奇分别跑了多少米?(★★)答案:290,790.练习:1、原先《花城日报》和《鹏城晚报》有同样数目的版面.后来《花城日报》扩充版面,增加了10版,这样《花城日报》的版面比《鹏城晚报》的4倍少2版.两种报纸现在各有多少版?(★★)答案:4,14.2、甲、乙两筐苹果重量相等.现在从甲筐拿12千克苹果放入乙筐,结果乙筐苹果的重量就比甲筐的3倍少2千克.两筐苹果原来各有多少千克?(★★★)答案:25.三、和差问题1)和差例22、冬冬在玩具店看中了两件汽车模型.如果两件都买,一共需要400元.已知较贵的模型比便宜的模型贵60元,这两件模型各要多少钱?(★)答案:230,170.练习:1、张先生投资股票,2006年和2007年一共盈利40万元,其中2006年比2007年少盈利14万元.张先生2007年盈利多少万元?(★)答案:27.2、甲、乙两位火炬手负责把火炬从A地传递到B地.先由甲从A地出发,并在途中将火炬传递给乙;乙接过火炬后继续慢跑前往B地.已知A,B两地相距2400米,并且甲比乙多跑了600米.请问:甲跑了多少米?(★)答案:1500.3、两筐水果共重150千克,第一筐比第二筐多8千克,两筐水果各多少千克?(☆)答案:79,71.4、果园里有桃树和梨树共150棵,桃树比梨树多20棵,两种果树各有多少棵?(☆)答案:85,65.5、用锡和铝制成500千克的合金,铝的重量比锡多100千克,锡和铝各是多少千克?(☆)答案:300,200.2)和差问题综合例23、登月行动地面控制室的成员由两组专家组成,两组共有专家125人.原来第一组人数较多,所以从第一组调了20人到第二组,即使这样第一组人数仍比第二组多5人.原来第一组有多少名专家?(★★)答案:85.例24、一辆公共汽车出发时有48人,到达第一站时有若干人下车,而且下车的比留下的多8人.到达第二站时,又有人下车,这次下车的比留下的少8人.请问:最后有几个人留在了车上?(注:每个车站都无人上车)(★★)答案:14.例25、小悦和冬冬玩游戏,每玩一局,输的就要给赢的1枚棋子.一开始小悦有18枚棋子,冬冬则有22枚.玩了若干局之后,小悦反而比冬冬多了10枚棋子.请问:此时小悦有多少枚棋子?(★★)答案:25.例26、今年小强7岁,爸爸35岁,当两人年龄和是58岁时,两人年龄各多少岁?(☆☆)答案:15,43.三年级和差倍强化训练刘静老师整理9 / 10 aoshu_liulaoshi@例27、小明期末考试时语文和数学的平均分数是94分,数学比语文多8分,问语文和数学各得了几分?(☆☆)答案:90,98.例28、甲、乙两桶油共重30千克,如果把甲桶中6千克油倒入乙桶,那么两桶油重量相等,问甲、乙两桶原有多少油?(☆☆☆)答案:21,9.例29、三个物体平均重量是31千克,甲物体比乙、丙两个物体重量之和轻1千克,乙物体比丙物体重量的2倍还重2千克,三个物体各重多少千克?(☆☆☆)答案:甲、乙、丙三个物体的重量分别为46千克、32千克、15千克.例30、公园里柳树和杨树共43棵,松树和柏树共42棵,并且杨树比松树多2棵,比柳树少7棵,那么公园里有柏树多少棵?(★★★)答案:26.练习:1、甲、乙两个学校共有学生1245人,如果从甲校调20人去乙校后,甲校比乙校还多5人,两校原有学生各多少人?(☆☆)答案:甲校原有学生645人,乙校原有学生600人.2、甲、乙两个工程队共有1980人,甲队为了支援乙队,抽出285人加入乙队,这时乙队人数还比甲队少24人,求甲、乙两队原有工人多少人?(☆☆)答案:甲队原有1287人,乙队原有693人.3、甲乙两校共有学生864人,为了照顾学生就近入学,从甲校调入乙校32名同学,这样甲校学生还比乙校多48人,问甲、乙两校原来各有学生多少人?(☆☆)答案:甲校原有学生488人,乙校原有学生376人.4、某工厂去年与今年的平均产值为96万元,今年比去年多10万元,今年与去年的产值各是多少万元?(☆☆)答案:今年的产值是101万元,去年的产值是91万元.四、和差倍综合练习1、费叔叔买来三箱水果,总重100千克.其中前两箱重量相差11千克,且前两箱的总重量是第三箱的3倍.请问:这三箱水果中最重的那箱重多少千克?(★★)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和差倍问题:和差倍综合练习及答案
1.XXX买了三箱水果,总重100千克。
前两箱的重量相
差11千克,且前两箱的总重量是第三箱的3倍。
问最重的一
箱水果重多少千克?
2.甲、乙、丙三个物体的总重量是93千克。
甲物体比乙、丙两个物体的重量之和轻1千克,乙物体比丙物体重量的2倍还重2千克。
问甲、乙、丙各重多少千克?
3.四年级有3个班,如果把甲班的1名学生调整到乙班,
两班人数相等。
如果把乙班1名学生调到丙班,丙班比乙班多
2人。
问甲班和丙班哪班人数多?多几人?
4.XXX三年级有3个班,一共有126名学生。
如果一班
比二班多4人,二班比三班多4人。
问这三个班分别有多少人?
5.三国时期,魏国、蜀国、吴国三国交战。
已知吴国军队
比蜀国军队多20万人;魏国军队人数是吴国的2倍,又是蜀
国的3倍。
问魏国军队有多少人?
6.甲、乙两个人一起去商店买东西,两人一共带了80元钱。
甲用自己带的钱的一半买了一本漫画书,乙花10元钱买了一盘磁带。
这时甲的钱恰好是乙的3倍。
开始时乙带了多少元钱?
7.姐妹俩一起做数学、语文两科作业。
姐姐花在数学作业上的时间比妹妹多10分钟,而妹妹花在语文作业上的时间比姐姐多4分钟。
已知姐姐一共花了88分钟做完作业,妹妹做数学作业的时间比语文作业少12分钟。
问妹妹做语文作业花了多少分钟?
8.游泳池里男生的人数比女生的6倍少11人,比女生的4倍多13人。
问男生有多少人?。
