高斯消去法的理论总结与应用——课程设计 精品
高斯消元法(完整)

高斯消元法解线性方程组在工程技术和工程管理中有许多问题经常可以归结为线性方程组类型的数学模型,这些模型中方程和未知量个数常常有多个,而且方程个数与未知量个数也不一定相同。
那么这样的线性方程组是否有解呢?如果有解,解是否唯一?若解不唯一,解的结构如何呢?这就是下面要讨论的问题。
一、线性方程组设含有n 个未知量、有m 个方程式组成的方程组(3.1) 其中系数,常数都是已知数,是未知量(也称为未知数)。
当右端常数项, , …, 不全为0时,称方程组(3.1)为非齐次线性方程组;当== … == 0时,即(3.2) 称为齐次线性方程组。
由n 个数, , …, 组成的一个有序数组(, , …, ),如果将它们依次代入方程组(3.1)中的, , …, 后,(3.1)中的每个方程都变成恒等式,则称这个有序数组(, , …, )为方程组(3.1)的一个解。
显然由=0,=0, …, =0组成的有序数组(0, 0, …, 0)是齐次线性方程组(3.2)的一个解,称之为齐次线性方程组(3.2)的零解,而当齐次线性方程组的未知量取值不全为零时,称之为非零解。
(利用矩阵来讨论线性方程组的解的情况或求线性方程组的解是很方便的。
因此,我们先给出线性方程组的矩阵表示形式。
)非齐次线性方程组(3.1)的矩阵表示形式为:AX = B其中A = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡mn m m n n a a a a a a a a a 212222111211,X = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n x x x 21,B = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n b b b 21 称A 为方程组(3.1)的系数矩阵,X 为未知矩阵,B 为常数矩阵。
将系数矩阵A 和常数矩阵B 放在一起构成的矩阵][B A =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡m mn m m n n b b b a a a a a a a a a 21212222111211 称为方程组(3.1)的增广矩阵。
高斯消元法完整

高斯消元法(完整)高斯消元法解线性方程组在工程技术和工程管理中有许多问题经常可以归结为线性方程组类型的数学模型,这些模型中方程和未知量个数常常有多个,而且方程个数与未知量个数也不一定相同。
那么这样的线性方程组是否有解呢?如果有解,解是否唯一?若解不唯一,解的结构如何呢?这就是下面要讨论的问题。
一、线性方程组设含有n 个未知量、有m 个方程式组成的方程组a x a x a xb a x a x a x b a x a x a x b n n n n m m mn n m11112211211222221122+++=+++=+++=⎧⎨⎪⎪⎩⎪⎪ (3.1) 其中系数a ij ,常数b j 都是已知数,x i 是未知量(也称为未知数)。
当右端常数项b 1,b 2, …, b m 不全为0时,称方程组(3.1)为非齐次线性方程组;当b 1=b 2= … =b m = 0时,即a x a x a x a x a x a x a x a x a x n n n n m m mn n 111122121122221122000+++=+++=+++=⎧⎨⎪⎪⎩⎪⎪ (3.2) 称为齐次线性方程组。
由n 个数k 1, k 2, …, k n 组成的一个有序数组(k 1, k 2, …, k n ),如果将它们依次代入方程组(3.1)中的x 1, x 2, …, x n 后,(3.1)中的每个方程都变成恒等式,则称这个有序数组(k 1, k 2, …, k n )为方程组(3.1)的一个解。
显然由x 1=0,x 2=0, …, x n =0组成的有序数组(0, 0, …, 0)是齐次线性方程组(3.2)的一个解,称之为齐次线性方程组(3.2)的零解,而当齐次线性方程组的未知量取值不全为零时,称之为非零解。
(利用矩阵来讨论线性方程组的解的情况或求线性方程组的解是很方便的。
因此,我们先给出线性方程组的矩阵表示形式。
高斯消去法高斯塞德尔迭代法

数值计算高斯消去法和高斯-塞德尔迭代法摘要虽然已学过加减消元法、代入消元法、矩阵变换法和Cramer 法则等,但是无法满足实际计算需要,故在此讨论在计算机上实现的有效而实用的解法。
线性方程组的解法大致分2类:直接法(高斯消去法)和迭代法(高斯-赛德尔迭代法),在此对着此类算法进行比较分析。
一、算法设计当计算线性方程组如下时,11112211211222221122n n n n n n nn n na x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ (1-1)为方便起见,常将线性方程组表示成矩阵形式Ax b=其中1111n n nn a a A a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1n x x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1n b b b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦并始终假定A 是非奇异的,即方程组的解存在且唯一。
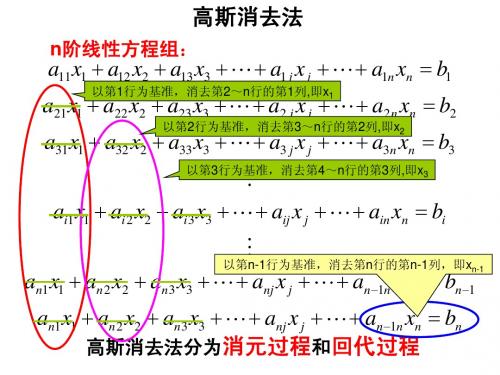
1.1高斯消去法消去法就是按特定顺序进行的矩阵初等变换法,当消元按自然顺序进行时,称为高斯顺序消去法。
一般情况下的高斯顺序消去法的计算机算法如下,现将方程组(1-1)的增广矩阵记作(0)(0)(0)11111(0)(0)(0)11n n n nn nn a a a a a a ++⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦假设经k-1步消元后,增广矩阵化为(0)(0)(0)(0)1112111(1)(1)(1)22221(1)(1)(1)1(1)(1)(1)1nn nn k k k kk knkn k k k nk nnnn a a a a a a a a a a a a a ++---+---+⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其中()s ij a 的上标表示是由s 步消元得到的植。
第k 步消元:设(1)0k kk a -≠,以第k 行为基础,将以后各行中的(1)k ik a -化为0,为此先计算(1)(1)/k k ik ik kk l a a --=然后以第i 行减去第k 行乘以ik l ,即以()(1)(1)k k k ij ij ik kj a a l a --=-()()1,,11,,j k n i k n =++=+于是得(0)(0)(0)11111(1)(1)(1)(1)11()()()11111()()()11n n k k k k kkkk knkn k k k k k k nk n k k k k nnnnn a a a a a a a a a a a a a +----+++++++++⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦经n-1步消元后,增广矩阵化为(0)(0)(0)11111(1)(1)(1)1(1)(1)1n n k k k kk knkn n n nn nn a a a a a a a a +---+--+⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦自下往上逐步回代即可求得其解(1)(1)1(1)(1)(1)11/()/(1,2,,1)n n n nn nnnk k k k kn kj j kk j k x a a x aax a k n n --+---+=+==-=--∑由行列式的初等变换和矩阵初等变换的关系可知,顺序消元法的每一步系数行列式之值不变,因此原方程组之系数行列式的值为(0)(2)(1)1122n nn a a a - ,可在求解过程中逐步累乘求得。
高斯消去法
x1 b1 (a12 x2 a1 j x j a1n xn )
编程注意事项:
1、源代码分为:main()和gauss(),其中 main()的功 能是输入n阶线性方程组的系数以及输出高斯求解的结 果, gauss()的主要功能是计算方程组的解。 不能将gauss()的代码直接写在main()中!!! 2、对于输入和输出要有提示性语言,例 printf(" your input the data is:\n");
a11 x1 a12 x2 a13 x3 a1 j x j a1n xn b1 a21 a21 a21 a21 a21 (a22 a12 ) x2 (a23 a13 ) x3 (a2 j a1 j ) x j (a2 n a1n ) xn b2 b1 a11 a11 a11 a11 a11 a31 a31 a31 a31 a21 (a32 a12 ) x2 (a33 a13 ) x3 (a3 j a1 j ) x j (a3n a1n ) xn b3 b1 a11 a11 a11 a11 a11 ai1 ai1 ai1 ai1 a21 (ai 2 a12 ) x2 (ai3 a13 ) x3 (aij a1 j ) x j (ain a1n ) xn bi b1 a11 a11 a11 a11 a11 an1 an1 an1 an1 a21 (an 2 a12 ) x2 (an3 a13 ) x3 (anj a1 j ) x j (ann a1n ) xn bn b1 a11 a11 a11 a11 a11
a1n xn b1 a2 n xn b2 a3n xn b3
高斯消元法详解

高斯消元法详解高斯消元法是一种线性代数中用于解决线性方程组的方法。
它的基本思想是通过一系列的行变换将一个线性方程组转化为一个上三角矩阵,然后通过回带求解出未知数的值。
高斯消元法的基本步骤如下:1. 将待求解的线性方程组写成增广矩阵形式,即将系数矩阵和常数向量合并成一个矩阵。
2. 选取第一行第一列元素不为零的行作为主元行,通过初等行变换将该行化为主元,即使该行第一列元素为1,其余元素为0。
3. 对于每个未被选中的行,将其第一列元素通过初等行变换化为0。
具体做法是将该行乘以主元所在行第一列的相反数,并加到主元所在行上。
4. 重复步骤2和3直到所有未被选中的行都被化为0或者无法选取主元。
5. 回带求解出未知数的值。
从最后一行开始,依次代入已经求出来的未知数值并计算出当前未知数值。
需要注意的是,在进行高斯消元法时需要注意以下几点:1. 当选择主元时应尽量避免选取小数作为主元,因为小数的精度有限,可能会导致计算误差。
2. 当系数矩阵中存在多个相同的行时,需要将它们合并成一个行,以减少计算量。
3. 在进行回带求解时,应注意未知数的顺序和求解的顺序应该一致。
高斯消元法可以用于求解任意大小的线性方程组,但是当方程组的规模很大时,计算量会非常大。
此外,在某些情况下高斯消元法可能会出现无法选取主元或者主元为0的情况,此时需要采用其他方法进行求解。
总之,高斯消元法是一种简单而有效的线性方程组求解方法,在实际应用中得到了广泛的应用。
熟练掌握高斯消元法可以提高我们在科学计算和工程设计中的能力和水平。
高斯消元法与线性方程组

高斯消元法与线性方程组引言:线性方程组是数学中最基础的问题之一,它在各个领域都有广泛的应用。
解决线性方程组的方法有很多种,其中一种常用且高效的方法是高斯消元法。
本文将介绍高斯消元法的原理和应用,并探讨其在实际问题中的一些限制和改进。
一、高斯消元法的原理高斯消元法是一种基于矩阵运算的方法,用于求解线性方程组。
其基本思想是通过一系列的行变换将线性方程组转化为简化的行阶梯形式,从而得到方程组的解。
具体的步骤如下:1. 构造增广矩阵给定一个线性方程组,我们将其系数矩阵与常数向量合并成一个增广矩阵。
例如,对于一个包含n个未知数的线性方程组,其增广矩阵的大小为n×(n+1)。
2. 主元选取从第一行开始,选择一个非零的元素作为主元素,并将其所在列的其他元素都变为0。
这样可以将主元素所在的行化为行阶梯形式。
主元素的选取可以根据一定的策略进行,常见的方法有部分主元选取和完全主元选取。
3. 行变换通过一系列的行变换操作,将每一行的主元素所在列的其他元素都变为0。
行变换操作包括交换两行、将某一行的倍数加到另一行上等。
4. 回代求解将增广矩阵化为行阶梯形式后,可以通过回代的方式求解线性方程组。
从最后一行开始,依次求解每个未知数的值。
二、高斯消元法的应用高斯消元法在科学和工程领域有广泛的应用。
以下是一些常见的应用场景:1. 电路分析在电路分析中,线性方程组常常用于描述电路中的电流和电压关系。
通过高斯消元法,可以求解电路中各个节点的电压值,从而帮助工程师进行电路设计和故障排除。
2. 机器学习在机器学习中,线性回归模型可以表示为一个线性方程组。
高斯消元法可以用于求解最优的模型参数,从而使得模型在给定数据集上的拟合效果最好。
3. 金融风险评估金融领域中,高斯消元法可以用于评估投资组合的风险。
通过建立一个包含各种金融资产的线性方程组,可以计算不同资产的权重,从而实现风险的分散和控制。
4. 图像处理在图像处理中,高斯消元法可以用于图像去噪和边缘检测。
数值分析实验报告---高斯消去法 LU分解法
数值分析实验报告---高斯消去法 LU分解法实验一:高斯消去法一、实验目的1. 掌握高斯消去法的原理2. 用高斯消去法解线性方程组3. 分析误差二、实验原理高斯消去法(又称为高斯-约旦消去法)是一种利用矩阵消元的方法,将线性方程组化为改进的阶梯形式,从而解出线性方程组的解的方法。
具体而言,高斯消去法将线性方程组的系数矩阵化为一个上三角矩阵,再利用回带法求解线性方程组的解。
三、实验内容1.1、用高斯消去法解线性方程组在具体实验中,我们将使用高斯消去法来解决下述的线性方程组。
5x+2y+z=102x+6y+2z=14x-y+10z=25为了使用高斯消去法来解这个方程组,首先需要将系数矩阵A进行变换,消除A矩阵中第一列中的下角元素,如下所示:1, 2/5, 1/50, 28/5, 18/50, 0, 49/28接着使用回代法来计算该方程组的解。
回代法的过程是从下往上进行的,具体步骤如下:第三个方程的解:z=49/28;第二个方程的解: y=(14-2z-2x)/6;第一个方程的解: x=(10-2y-z)/5。
1.2、分析误差在使用高斯消去法求解线性方程组时,一般会出现截断误差,导致得到的解与真实解之间存在一些误差。
截断误差的大小和矩阵的维数有关。
为了估计截断误差,我们使用矩阵B来生成误差,在具体实验中,我们将使用下面的矩阵:我们来计算该矩阵的行列式,如果方程组有唯一解,则行列性不为0。
本例中,行列式的值是 -1,因此方程组有唯一解。
然后我们计算真实解和高斯消去法得到的解之间的误差,具体公式如下所示:误差 = 真实解的范数 - 高斯消去法得到的解的范数其中,范数的定义如下:||x||1=max{|xi|}; ||x||2=sqrt{(|x1|^2 + |x2|^2 + ... + |xn|^2)}四、实验步骤1、将高斯消去法的每一个步骤翻译成代码,并保存为一个独立的函数。
2、将代码上传至 Python 交互式环境,并使用高斯消去法来解线性方程组。
高斯消去实验报告分析
一、实验背景高斯消去法(Gaussian Elimination)是线性代数中解决线性方程组的重要方法之一。
它通过初等行变换将系数矩阵化为行阶梯形矩阵,从而求解线性方程组。
本实验旨在通过编写程序实现顺序高斯消去法和列主元高斯消去法,并对比分析两种方法的计算效率和精度。
二、实验目的1. 理解高斯消去法的原理和步骤。
2. 编写程序实现顺序高斯消去法和列主元高斯消去法。
3. 比较两种方法的计算效率和精度。
4. 分析高斯消去法的适用范围和局限性。
三、实验内容1. 顺序高斯消去法- 实现顺序高斯消去法,将系数矩阵化为行阶梯形矩阵。
- 求解线性方程组,得到未知数的解。
2. 列主元高斯消去法- 实现列主元高斯消去法,将系数矩阵化为行阶梯形矩阵。
- 求解线性方程组,得到未知数的解。
3. 比较两种方法- 对比两种方法的计算效率和精度。
- 分析两种方法的优缺点。
四、实验步骤1. 编写程序- 使用C/C++、Python等编程语言编写顺序高斯消去法和列主元高斯消去法程序。
- 程序应包含以下功能:- 输入线性方程组的系数矩阵和常数项。
- 实现顺序高斯消去法和列主元高斯消去法。
- 输出求解结果。
2. 测试程序- 使用一组已知线性方程组测试程序的正确性。
- 验证求解结果与精确解是否一致。
3. 比较分析- 使用不同的线性方程组测试两种方法的计算效率和精度。
- 比较两种方法的运行时间、解的精度和误差。
五、实验结果与分析1. 顺序高斯消去法- 计算效率:顺序高斯消去法的时间复杂度为O(n^3),其中n为方程组中未知数的个数。
- 精度:顺序高斯消去法可能会受到舍入误差的影响,导致求解结果与精确解存在一定的误差。
2. 列主元高斯消去法- 计算效率:列主元高斯消去法的时间复杂度同样为O(n^3),但通过选择主元,可以减少舍入误差,提高求解精度。
- 精度:列主元高斯消去法具有更高的精度,求解结果与精确解更接近。
3. 比较分析- 顺序高斯消去法和列主元高斯消去法在计算效率上基本相同,但列主元高斯消去法具有更高的精度。
高斯消元法详解
高斯消元法详解介绍高斯消元法(Gaussian Elimination)是一种线性代数中常用的求解线性方程组的方法。
它的基本思想是通过一系列的行变换将线性方程组转化为上三角形矩阵,再通过回代求解得到方程组的解。
高斯消元法广泛应用于各个领域,包括数学、工程、计算机科学等。
基本原理高斯消元法的基本原理是利用矩阵的初等行变换,将线性方程组转化为上三角形的矩阵形式。
具体步骤如下:1.构造增广矩阵将线性方程组的系数矩阵与常数矩阵合并,构造增广矩阵。
增广矩阵按照方程组的顺序排列,每个行向量表示一个方程。
2.主元选取选择每一列的主元,使得主元所在的列(称为主元所在列)其他元素都为零。
主元可以是行首非零元素或者经过行交换后的非零元素。
3.消元过程从第一行开始,对每一行进行消元。
通过初等行变换,将主元所在列的其他元素变为零。
消元过程分为两种情况:–主元为零:需要进行行交换,将非零元素调整为主元。
–主元不为零:通过乘以一个系数,将主元下方的元素消为零。
4.回代求解将转化后的增广矩阵转化为上三角形矩阵后,从最后一行开始向上回代求解。
通过求解当前方程的未知数,计算出前面的未知数的值,最终得到方程组的解。
算法实现高斯消元法可以用算法描述如下:1.输入: 线性方程组的增广矩阵A。
2.输出:线性方程组的解X。
3.n = A的行数4.for i = 1 to n-1:1. a = A(i,i)(主元)2.for j = i+1 to n:1. b = A(j,i)2.for k = i to n+1:1.A(j,k) = A(j,k) - (b/a) * A(i,k)5.for i = n to 1:1.sum = 02.for j = i+1 to n:1.sum = sum + A(i,j) * X(j)3.X(i) = (A(i,n+1) - sum) / A(i,i)6.输出X示例假设有如下的线性方程组:2x + 3y - z = 14x + 2y + z = -2-2x + y + 2z = 5我们可以将其转化为增广矩阵:[2 3 -1 | 1][4 2 1 | -2][-2 1 2 | 5]按照高斯消元法的步骤,首先选取第一列的主元为2,然后通过消元将主元下方的元素变为零:[2 3 -1 | 1][0 -2 3 | -4][0 4 3 | 7]然后选取第二列的主元为-2,再进行消元:[2 3 -1 | 1][0 4 3 | 7][0 0 15 | -15]最后,进行回代求解,得到解为x=1,y=2,z=-1。
高斯列主元消元说法明书
数学与计算机学院课程设计说明书课程名称:面向对象程序设计-课程设计课程代码: 8404101 题目: 高斯列主元消元法解线性方程组年级/专业/班:学生姓名:学号:开始时间:2010 年月日完成时间:2010 年月日课程设计成绩:学习态度及平时成绩(30)技术水平与实际能力(20)创新(5)说明书撰写质量(45)总分(100)指导教师签名:年月日目录摘要 (1)1 引言 (1)1.1 问题的提出 (1)1.2 如何解决高问题 (1)1.3国内外研究的现状 (1)1.4任务与分析 (2)2.设计方案 (3)3. 功能需求 (3)3.1.1 录入功能 (3)3.1.2 查找功能 (3)3.1.3 交换功能 (3)3.1.4计算功能 (3)3.1.5回代功能 (3)3.1.6输出功能 (3)3.2总体要求 (4)4.程序编码及模块分析 (4)4.1 程序代码 (5)4.2 程序模块分析 (9)4.3程序流程图 (11)5.比较有色的函数 (12)6. 系统测试 (12)6.1设计测试数据 (13)6.2 测试结及分析 (14)总结 (15)致谢 (16)参考资料 (16)摘要此程序是通过建立矩阵基类,然后由基类派生出方程组的系数类。
然后通过输入方程组左右两边的数据给基类的矩阵指针,方程右边给派生类自身的指针。
然后在实现时将指针地址给一个二维数组和一个一维数组,通过对两个数组的运算来实现对系数进行的选主元、交换行、消元和回带,然后将结果给方程组类的结果指针。
最后输出结果指针。
高斯列主元消元法解线性方程组的方法将通过下面对n元的方程组在下文中将得到讲诉,并在讲诉过程中理解到高斯列主元消元法在c++程序中的运用方法。
关键词:矩阵高斯列主元消元法线性方程组1 引言1.1 问题的提出随着计算机的普及,网络进入大众的家庭,在各个领域都起到了不可忽视的作用。
在现代化的教学方法中,对于数值计算方法中的一种很重要的解题方法——高斯主元消元法有着十分重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计说明书 题 目:高斯消去法的理论总结与应用 学生姓名 学 院:理学院 班 级:信计10-2 指导教师:
2013年 1月 11日
学校代码: 摘要 当今很多科学与工程计算问题都可以化为线性方程组的形式,所以有效地求解线性方程组在科学和工程计算中是非常重要的. 直接法是经过有限步算术运算,若没有舍入误差可求得方程组精确解的方法.由于实际计算过程中总存在着舍入误差,因此,用直接法得到的结果并不是准确的.直接法中最基本的方法是高斯消去法,矩阵三角分解法等. 本文主要研究高斯消去法.高斯消去法是反复运用消元与回代两个过程.将增广矩阵变成行阶梯型矩阵,使方程组变成同解的上三角方程组,然后再自下而上对上三角方程组求解.高斯消去法包括顺序高斯消去法、列主元高斯消去法、高斯约当消去法等,是求解线性方程组的重要方法. 文中分别编写顺序高斯消去法、列主元高斯消去法C语言程序,并结合实际的例子运行程序,最后对结果进行比较分析. 关键词 求解线性方程组;顺序高斯消去法;列主元高斯消去法;高斯-约当消
去法;C语言编程
Abstract Today a lot of science and engineering calculation problem can be turned into the form of linear equations, so effective in solving linear equations is very important in the calculation of science and engineering.
Direct method is limited step arithmetic operations, if there is no rounding error method of equations exact solutions can be obtained. As always there is a rounding error in the process of calculation, thus, the results by the direct method is not accurate. The direct method is the most basic methods in gaussian elimination method, matrix triangle decomposition method, etc.
This paper mainly studies the gaussian elimination method. Gauss elimination method is repeated use of elimination and go back two process. Will be augmented matrix into line when matrix, the equations into a triangle on the same solution of the equations, and then bottom-up on triangle equation. Gauss elimination method including sequence gauss elimination method, listed the main yuan gaussian elimination method, gaussian about when expunction method and so on, is an important method of solving linear equations.
The paper write order gaussian elimination method, principal component gaussian elimination method C language program, and combining with actual examples of the application, the comparative analysis of the results.
Key words Sequential gaussian elimination method; List the yuan gaussian
elimination method; Gauss - about when expunction method; C language programming 目录 引言 ................................................................... 1 第一章 高斯消去法 ...................................................... 2 §1.1 高斯消去法 .................................................... 2 §1.1.1 初等矩阵的变换 .......................................... 2 §1.1.2 基本思想 ................................................ 3 §1.1.3 高斯消去法的算法描述 .................................... 4 §1.1.4 高斯消去法的计算量 ...................................... 4 §1.2 高斯列主元消去法 .............................................. 5 §1.2.1简单介绍 ................................................. 5 §1.2.2 基本思想 ................................................ 5 §1.2.3 算法描述 ................................................ 6 §1.3 其他的高斯消去法 .............................................. 6 §1.3.1 高斯全主元消去法 ........................................ 6 §1.3.2 高斯-约当消去法 ......................................... 6 第二章 高斯消去法的应用 ................................................ 8 §2.1 高斯消去法的应用 .............................................. 8 §2.1.1 顺序高斯消去法的应用举例 ................................ 8 §2.1.2 高斯列主元消去法的应用举例 .............................. 9 §2.1.3 高斯-约当消去法的应用举例 .............................. 10 参考文献 .............................................................. 12 附录A ................................................................. 13 附录B ................................................................. 16 1
引言 直接法就是经过有限步算术运算,若计算过程中没有舍入误差可求得方程组精确解的方法.本文最主要的就是研究解线性方程组的一种直接法,即高斯消去法的理论知识及其应用. 对于n阶线性方程组
(1)
的问题,方程组的系数和右端项均为实数,且不全为零,方程组简记为Ax=b,其中
(2)
(3) 高斯消去法,又称高斯消元法,实际上就是我们俗称的加减消元法.数学上,高斯消去法或称高斯-约当消去法,由高斯和约当得名(很多人将高斯消去作为完整的高斯-约当消去的前半部分),它是线性代数中的一个算法,用于决定线性方程组的解.高斯消去法的基本思想是将增广矩阵利用线性方程组初等变换中的一种变换,变成行阶梯形矩阵,使方程组变成同解的上三角方程组,然后再自下而上对上三角方程组求解.
nnnnnnnnnnbxaxaxabxaxaxabxaxaa22112222212111212111x
nn2nn1n222211n1211aaaaaaaaaA
nbb21n21bb,xxxx 2
第一章 高斯消去法 §1.1高斯消去法 §1.1.1 初等矩阵的变换 定义1.1 初等矩阵对应着3种不同的行/列变换. ○1互换行/列: jiRR 这一变换 ijT,将一单位矩阵的第 i 行的所有元素与第 j 行互换.
101101Tij
○2把某行/列乘以一非零常数:,iiRkR其中k0 这一变换 Ti(m),将第 i 行的所有元素乘以一非零常数 m.
○3把第 i 行(列)加上第 j 行(列)的 k 倍:ijiRkRR 这一变换 Tij(m),将第 i 行加上第 j 行的 k 倍.
11m11mTi)(
