几种索力计算公式在短、长索中应用精度比较
绳子承重受力计算公式

绳子承重受力计算公式在工程学和物理学中,绳子承重受力计算是一个非常重要的问题。
绳子作为一种常见的材料,在吊装、牵引和支撑等方面都有着广泛的应用。
因此,了解绳子承重受力的计算公式对于工程设计和实际应用都具有重要意义。
绳子承重受力的计算公式主要涉及到绳子的材料特性、受力情况和外部环境等因素。
一般来说,绳子的承重受力可以通过以下公式进行计算:F = T / A。
其中,F代表绳子的承重受力,T代表绳子的张力,A代表绳子的横截面积。
这个公式表明,绳子的承重受力与绳子的张力成正比,与绳子的横截面积成反比。
也就是说,绳子的承重受力取决于绳子的张力大小和绳子的横截面积大小。
在实际应用中,绳子的承重受力计算还需要考虑到绳子的材料特性。
不同材料的绳子具有不同的拉伸强度和材料密度,因此需要根据具体的绳子材料来确定绳子的承重受力。
一般来说,绳子的承重受力可以通过以下公式进行计算:F = σ A。
其中,F代表绳子的承重受力,σ代表绳子的拉伸强度,A代表绳子的横截面积。
这个公式表明,绳子的承重受力与绳子的拉伸强度成正比,与绳子的横截面积成正比。
也就是说,绳子的承重受力取决于绳子的拉伸强度和绳子的横截面积大小。
除了绳子的材料特性,绳子的承重受力计算还需要考虑到绳子的受力情况。
在实际应用中,绳子通常会受到拉力、压力和弯曲等多种受力形式的作用,因此需要根据具体的受力情况来确定绳子的承重受力。
一般来说,绳子的承重受力可以通过以下公式进行计算:F = T / cosθ。
其中,F代表绳子的承重受力,T代表绳子的张力,θ代表绳子的受力角度。
这个公式表明,绳子的承重受力与绳子的张力和受力角度有关。
当绳子受到斜拉力时,其承重受力会随着受力角度的增大而减小,因此需要考虑到受力角度对绳子承重受力的影响。
此外,绳子的承重受力计算还需要考虑到外部环境的影响。
在实际应用中,绳子通常会受到温度、湿度和化学物质等外部环境的影响,因此需要根据具体的外部环境来确定绳子的承重受力。
斜拉索力计算公式
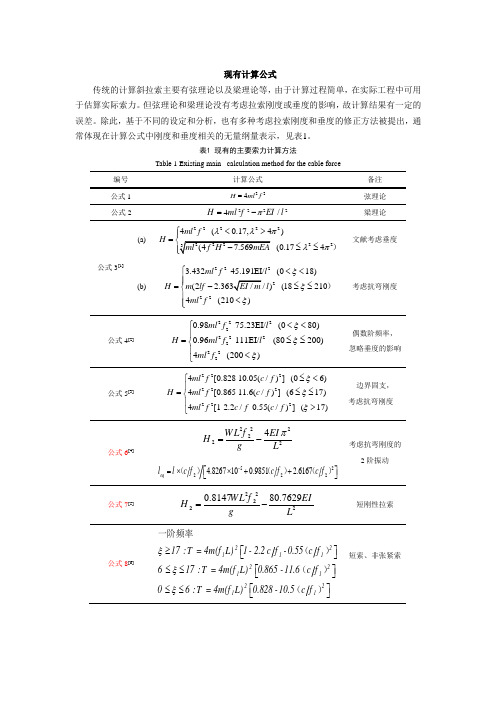
现有计算公式传统的计算斜拉索主要有弦理论以及梁理论等,由于计算过程简单,在实际工程中可用于估算实际索力。
但弦理论和梁理论没有考虑拉索刚度或垂度的影响,故计算结果有一定的误差。
除此,基于不同的设定和分析,也有多种考虑拉索刚度和垂度的修正方法被提出,通常体现在计算公式中刚度和垂度相关的无量纲量表示,见表1。
表1 现有的主要索力计算方法Table 1 Existing main calculation method for the cable force编号 计算公式 备注 公式1 224H ml f =弦理论 公式222224/H ml fEI l π=-梁理论公式3[1](a)22222224(0.17,4)(0.174ml f H λλπλπ⎧<>=≤≤)文献考虑垂度(b)2222223.432-45.191EI/(018)(2)(182104(210)ml f l H m lf l ml f ξξξ⎧<<⎪⎪=-≤≤⎨⎪<⎪⎩)考虑抗弯刚度公式4[2]222222222220.98-75.23EI/(080)0.96-111EI/(80200)4(200)ml f l H ml f l ml f ξξξ⎧<<⎪=≤≤⎨⎪<⎩偶数阶频率, 忽略垂度的影响公式5[3]2222222224[0.828-10.05(/)](06)4[0.865-11.6(/)](617)4[1-2.2/-0.55(/)](17)ml f c f H ml f c f ml f c f c f ξξξ⎧≤<⎪=≤≤⎨⎪>⎩边界固支, 考虑抗弯刚度公式6[4]2222224WL f EI H g L π=-522224.8267100.9851 2.6167eq l l c f c f c f -⎡⎤=⨯⨯++⎣⎦()()()考虑抗弯刚度的2阶振动公式7[5]2220.814780.7629WL f EIH g L =-22 短刚性拉索公式8[6]221112211221117:T =4m(f L)1-2.2c f -0.55c f 617:T =4m(f L)0.865-11.6c f 06:T =4m(f L)0.828-10.5c f ξξξ⎡⎤≥⎣⎦⎡⎤≤≤⎣⎦⎡⎤≤≤⎣⎦一阶频率()()()短索、非张紧索2222222222222260:T =m(f L)1-4.4c f -1.1c f 1760:T =m(f L) 1.03-6.33c f -1.58c 017:T =m(f L)0.882-85c ξξξ⎡⎤≥⎣⎦⎡⎤≤≤⎣⎦⎡⎤≤≤⎣⎦二阶频率()()()()()[]22n n 200:T =4m(f l)n 1-2.2nc ξ≥高阶频率注:(1)H 为斜拉索索力,为索的线密度,l 为拉索的长度;(2)f 为拉索的第一阶频率,即基频,2f 为拉索的第二阶频率;(3)EI 为拉索的抗弯刚度,EA 为拉索的轴向刚度,c为系数c =(4)ξ为反映抗弯刚度的无量纲量:ξ,λ为反映垂度的无量纲量: 22emgl EAl H HL λ⎡⎤=⎢⎥⎣⎦ 表1中公式1和公式2分别为传统的弦理论和梁理论;公式3由应用能量方法推导并辅以曲线拟合得到,分别了考虑垂度和考虑刚度的影响;公式4认为垂度只影响到奇数阶频率,在索力测量时选用偶数阶频率忽略垂度的影响推导的公式;公式5为考虑了边界条件为固支情况下的解。
吊杆索力的计算方法与应用研究

与 实测 的数 据进 行对 比 , 结果表 明 , 测试 吊杆 力 时 , 在 系杆拱 桥 特 别是 短 索 的测 试 中必 须 考虑 刚
度 以及 边界 条件 的影 响 。
本桥取其代表性 吊杆 , 施工时的实测频率如表 1 所示 。
1 8
石 家庄铁 道 大 学学报 (自然 科 学版 )
表 1 不 同 长 度 吊 杆 实 测 基 频
第. 2 4卷
3 模 型 计 算 结 果 分 析
将 上述各 个参 数放 . N种模 型计 算公 式 , 算可 得 四种情 况下 吊杆 的实 测索 力 、 、 和 , 其 AI 计 将 与理论 吊杆 力进 行 比较 , 析其 相对 误差 , 分 具体 数 值 见 表 2 同时 , 四种 模 型 吊杆 力 的误 差 进 行分 析 对 。 对
许 误差 范 围之 内 , 于钢管 混凝 土 吊杆 拱桥 而 言 已 经能 够 满 足工 程 实践 的需 要 , 刚 度 对 结构 的影 响 可 对 而
以忽略
4 结论
介 绍 了不 同情 况 下索 力 的求解方 法 , 在不 同索 力 以及 索长 时 , 如果 要 求 的精 度不 是 非 常高 , 么 可 以 那
第 3期
凌 知 民等 : 吊杆 索力 的计算 方 法 与应用研 究
根据 实 际的情 况选 择 较为 简单 的计 算方 法 。 ( ) 响 实测 吊杆 索力 精度 的 因素有 实 测频 率 的精度 以及 索 力计算 模 型 的精 度 , 中 吊杆 抗 弯 刚度 、 1影 其
吊杆 固定 端 长度 及所 用 模 型 的边 界条 件等 都 会 引起 吊杆 索力 的变 化 , 索力 计 算模 型 是否 能恰 当的 考虑 到 这些 影 响因素 将会 影 响到 吊杆 索力 的识 别精 度 。 () 2 系杆拱 桥 的 吊杆基 本属 短索 , 析表 明 , 分 其测试 索 力 的计算 模 型可 在计 算 模 型一 与 计 算模 型 三 之
重绳的各个点拉力计算公式

重绳的各个点拉力计算公式重绳是一种常见的工程结构,在吊桥、索道、吊车等领域都有广泛的应用。
在设计和使用重绳时,计算各个点的拉力是非常重要的,这可以帮助工程师确定结构的稳定性和安全性。
本文将介绍重绳的各个点拉力计算公式,以帮助读者更好地理解和应用重绳结构。
1. 单点拉力计算公式。
在重绳结构中,单点的拉力是指重绳上某一点的受力情况。
假设重绳的总长度为L,重绳的自重为W,重绳的线密度为λ,则重绳上某一点的拉力F可以通过以下公式计算得出:F = λgΔL + W。
其中,g为重力加速度,ΔL为该点到重绳下端的距离。
这个公式可以帮助工程师计算出重绳上任意一点的受力情况,从而确定结构的稳定性。
2. 多点拉力计算公式。
在实际工程中,重绳往往会有多个支点,每个支点都会受到不同的拉力。
为了计算多点的拉力,可以使用以下公式:F = λgΔL + W + T。
其中,T为该点的张力,可以通过张力平衡方程计算得出。
通过这个公式,工程师可以计算出重绳上每个支点的受力情况,从而确定结构的整体稳定性。
3. 重绳的弯曲和扭转计算公式。
除了拉力,重绳在使用过程中还会受到弯曲和扭转的影响。
为了计算重绳的弯曲和扭转情况,可以使用以下公式:弯曲应力σ = M / S。
扭转应力τ = T r / J。
其中,M为弯矩,S为截面的抗弯强度,T为扭矩,r为截面的半径,J为截面的极惯性矩。
这些公式可以帮助工程师计算重绳在弯曲和扭转情况下的受力情况,从而确定结构的稳定性和安全性。
4. 重绳的挠度计算公式。
在实际工程中,重绳往往会受到外部载荷的作用,从而产生挠度。
为了计算重绳的挠度,可以使用以下公式:y = F L^3 / (3 E I)。
其中,F为外部载荷,L为重绳的长度,E为弹性模量,I为截面的惯性矩。
这个公式可以帮助工程师计算出重绳在外部载荷作用下的挠度情况,从而确定结构的稳定性和安全性。
5. 重绳的动力学计算公式。
在一些特殊情况下,重绳还会受到动力学的影响,比如风载荷、地震等。
斜拉索桥需要计算的内容及对应的公式

斜拉索桥需要计算的内容及对应的公式以斜拉索桥需要计算的内容及对应的公式为标题,写一篇文章。
标题:斜拉索桥的设计与计算斜拉索桥是一种通过斜拉索来支撑主梁的桥梁结构,它具有美观、经济、适应性强等优点,因此在现代桥梁工程中得到了广泛应用。
在设计和建造斜拉索桥时,需要进行各种计算,以确保桥梁的安全性和可靠性。
本文将介绍斜拉索桥设计与计算中的几个关键内容及其对应的公式。
一、索力计算斜拉索桥的设计中,首先需要计算斜拉索的索力。
索力是指斜拉索中承受的拉力,它的大小决定了斜拉索的材料选择和结构设计。
斜拉索的索力计算可以通过以下公式得到:T = (P * L) / sinθ其中,T为索力,P为主梁上的荷载,L为主梁长度,θ为斜拉索与主梁的夹角。
二、斜拉索的布置斜拉索桥的设计中,斜拉索的布置是一个重要的问题。
合理的斜拉索布置可以使桥梁结构更加均衡和稳定。
斜拉索的布置需要考虑索力的分布、桥梁的几何形状和荷载情况等因素。
一般来说,斜拉索的布置可以通过以下公式计算:n = L / s其中,n为斜拉索的数量,L为主梁长度,s为斜拉索的间距。
三、主梁截面计算主梁的截面计算是斜拉索桥设计中的关键环节。
主梁的截面尺寸直接影响桥梁的承载能力和刚度。
主梁的截面计算需要考虑桥梁的几何形状、材料的力学性能和荷载情况等因素。
一般来说,主梁的截面计算可以通过以下公式得到:M = W * L / 8其中,M为主梁的弯矩,W为主梁上的荷载,L为主梁长度。
四、塔柱的尺寸计算斜拉索桥的设计中,塔柱的尺寸计算是非常重要的。
塔柱的尺寸直接影响桥梁的稳定性和承载能力。
塔柱的尺寸计算需要考虑塔柱的高度、横向刚度和纵向稳定性等因素。
一般来说,塔柱的尺寸计算可以通过以下公式得到:H = (T * L) / (2 * K * sinθ)其中,H为塔柱的高度,T为斜拉索的索力,L为主梁长度,K为塔柱的刚度,θ为斜拉索与主梁的夹角。
五、锚固设计斜拉索桥的设计中,锚固设计是一个关键的问题。
频率法测斜拉索索力的若干关键问题探讨

频率法测斜拉索索力的若干关键问题探讨摘要:斜拉索索力控制是斜拉桥施工控制的灵魂,斜拉索的索力关乎整个桥梁的内力和线形。
本文介绍了频率法测试索力的原理,并结合实际项目永川长江大桥,对频率法测索力的一些关键问题进行了探讨。
关键词:施工控制;索力测试;频率法0引言斜拉索作为斜拉桥最重要的结构构件之一,直接承担桥梁荷载,索力决定着整个桥的内力分布和线形。
因此,索力是斜拉桥状况评估的重要指标之一。
在桥梁施工和使用期限内,随时了解索力的状况十分重要。
而索力量测效果将直接对结构的施工质量和施工状态产生影响,要在施工过程中比较准确地了解索力的实际状态,选择适当的量测方法和仪器,并设法消除现场量测中各种因素的影响非常关键。
1工程概况永川长江大桥主桥为桥跨布置64+68×2+608+68×2+64=1008m的七跨连续半漂浮体系双塔混合梁斜拉桥。
斜拉索采用平行钢丝斜拉索,索面按扇形布置,每一扇面由19对斜拉索组成,全桥共设76对斜拉索。
根据索力的不同,采用PES7-109、PES7-121、PES7-139、PES7-151、PES7-163、PES7-187、PES7-199、PES7-211、PES7-223、PES7-241、PES7-253共11种规格。
斜拉索锚点之间的长度处于92.408m~332.086m之间。
2频率法测索力的原理频率法是根据拉索索力与振动频率之间的关系来求得索力。
频率法测索力的理论基础是弦振动理论,对于1根张紧的确定的拉索,只要测出其振动频率,其索力即可由拉索微元的动力平衡方程和边界条件求得。
对于两端铰支的索,若不考虑斜拉索抗弯刚度时,其动力平衡微分方程的解为:(1)对于两端铰支的索,考虑斜拉索抗弯刚度时,其动力平衡微分方程的解为:(2)式中:T为斜拉索索力;w为单位斜拉索长度的重量;为斜拉索的计算长度;g为重力加速度;为拉索的n阶固有振动频率;n为振动频率的阶数;为基频;m为斜拉索单位长度的质量;EI为斜拉索的弯曲刚度;K为索力系数。
建桥钢索拉力计算公式
建桥钢索拉力计算公式在桥梁建设中,钢索是一种常用的结构材料,用于支撑和加固桥梁结构。
而钢索的拉力计算是桥梁设计中的重要环节,它直接影响着桥梁的安全性和稳定性。
因此,建桥钢索拉力计算公式是桥梁设计中不可或缺的一部分。
钢索拉力计算的基本原理是根据钢索的受力情况,通过力学分析和公式推导,计算出钢索在不同受力情况下的拉力值。
这些受力情况包括静态荷载、动态荷载、温度变化等。
在实际的桥梁设计中,需要根据具体的桥梁结构和使用条件,选择合适的钢索拉力计算公式,并进行相应的计算和验证。
在桥梁设计中,常用的钢索拉力计算公式包括静态荷载下的拉力计算公式、动态荷载下的拉力计算公式和温度变化下的拉力计算公式。
这些公式基于力学原理和实际工程经验,可以较为准确地计算出钢索在不同受力情况下的拉力值。
静态荷载下的钢索拉力计算公式是桥梁设计中最基本的计算公式之一。
在静态荷载下,钢索受到的主要荷载是桥梁自重和行车荷载。
根据钢索的受力特点和受力分布,可以得到静态荷载下的钢索拉力计算公式。
这个公式一般包括了钢索的自重、桥梁荷载和其他附加荷载的影响,可以较为准确地计算出钢索的拉力值。
动态荷载下的钢索拉力计算公式是钢索设计中的另一个重要计算公式。
在桥梁使用过程中,钢索会受到来自行车和车辆的动态荷载,这些荷载会对钢索的受力情况产生较大影响。
因此,需要针对动态荷载情况,建立相应的钢索拉力计算公式。
这个公式一般包括了行车和车辆荷载的影响,可以较为准确地计算出钢索在动态荷载下的拉力值。
温度变化下的钢索拉力计算公式是桥梁设计中的另一个重要计算公式。
在桥梁使用过程中,由于气温的变化,钢索会受到温度变化的影响,从而产生拉力的变化。
因此,需要针对温度变化情况,建立相应的钢索拉力计算公式。
这个公式一般包括了温度变化对钢索长度的影响,可以较为准确地计算出钢索在温度变化下的拉力值。
在实际的桥梁设计中,需要根据具体的桥梁结构和使用条件,选择合适的钢索拉力计算公式,并进行相应的计算和验证。
索力测量
索力测量实验背景拉索是斜拉桥和悬索桥的重要承重构件,设计和施工时通过调整拉索的索力:使塔、梁处于最佳受力状态。
实验背景在运营过程中,亦应不断监测索力变化,及时调整索力,使之处于设计要求的状态。
因此,无论施工过程还是运营过程中均需准确地测知索力。
实验目的•1、学习索力测试的原理;2、学习索力测试方法。
实验仪器安装示意图实验原理•频率法目前是斜拉桥测索力的普遍应用方法,索的边界条件为两端固定,索的质量均匀分布,在本程序模块中,索力计算公式为:其中,T:索的拉力(N);M:索单位长度的质量(kg/m);L:缆索的长度(m):第n阶自振频率实验原理•在该试验中采用钢丝模拟索力的测试过程,钢丝的质量可以忽略不计,在钢丝上加一块质量块,形成集中的单自由度系统,激励质量块,产生自由衰减振动,测得其频率,就可通过以下公式来计算:实验原理•当采用三个集中质量块均匀分布,并且三个质量块质量相等为m 时,激励质量块,产生自由衰减振动,测得其三阶频率,就可通过以下公式来计算:•m:小质量块质量(kg)L:钢丝两端支承间距(m)•n:为频率阶数。
实验方法1、仪器安装按示意图安装配重块和钢丝质量块组成的三自由度悬索系统,电涡流位移传感器安装在质量块上面,距离约为4mm,电涡流传感器的输出接入数采仪的应变通道。
2、打开仪器电源进入控制分析软件,新建一个项目(文件名自定),设置采样频率、量程范围、工程单位和灵敏度等参数,在数据显示窗口内点击鼠标右键,选择信号,选择时间波形,另一窗口显示实时谱。
开始采集数据,数据同步采集显示在图形窗口内。
实验方法•3、用手在垂直方向使质量块离开平衡位置,放开手后,系统做自由衰减振动,在谱窗口读取共振频率,计算索力值。
•5、改变配重块质量,重复以上步骤。
实验结果和分析•实验结果和分析。
承载索的受力计算
承载索的受力计算承载索的受力计算是工程力学中非常重要的一个内容,它涉及到工程中吊装、挖掘、拖拉等多个方面。
下面我将从承载索的受力方式、力的分析方法和计算公式等几个方面来介绍承载索的受力计算。
1. 承载索的受力方式:承载索通常以绳索、钢丝绳等形式存在,其受力方式主要分为受张力和受轴向压力两种情况。
受张力是指承载索在机械系统中传递力的作用,常见于吊装、拖拉和绳索等应用中。
受轴向压力是指承载索在某些情况下由于受到压力作用而发生变形,常见于不需承受拉力而需要承受轴向力的预应力结构和框架结构中。
2. 力的分析方法:在进行承载索的受力计算时,通常采用力的分析方法进行求解。
力的分析方法包括力的平衡分析和力的曲线求解两种方法。
力的平衡分析是指在受力系统中,各个受力点处的合力为零,合力矩为零,从而求解受力点处的力。
力的曲线求解是通过对受力曲线进行积分,根据力、力矩、力的作用点的坐标等参数,求解出受力点处的力。
3. 承载索的受力计算公式:(1)受张力的承载索:当承载索在受张力的作用下时,其受力计算可以使用以下公式进行求解:张力 = 负载 / 张力系数其中,张力为承载索受到的张力,负载为需要承载的物体重量或拉力,张力系数为根据具体使用条件确定的参数,主要考虑到索的安全系数和使用环境等因素。
(2)受轴向压力的承载索:当承载索发生轴向压力时,可以使用以下公式进行计算:轴向压力 = 承载能力 / 断面积其中,轴向压力为承载索所受到的轴向压力,承载能力为承载索所能承受的最大力,断面积为承载索的横截面积。
此外,在实际工程中,还需要考虑到承载索的材料特性、使用环境、安全系数等因素,以及横向力、弯矩等其他外力的影响,对承载索的受力计算进行综合分析。
需要强调的是,承载索的受力计算应该由专业人员根据具体的工程要求和使用条件进行计算,确保安全可靠。
索夹强度计算
1)、吊杆索力取自全桥整体计算分析,每根吊杆的最大组合拉力为120t 。
2)、索夹内径计算公式如下: ctotw c V n d d -=12mm式中:c d ——索夹内径,或索夹处大缆直径;w d ——主缆的钢丝直径;tot n ——单根主缆中的钢丝总数;c V ——大缆空隙率,本设计索夹处的大缆空隙率取为18%。
取索夹内主缆直径为:c d =38618.01127371.52=-⨯⨯ mm同样地,索夹外空隙率取20%时,索夹外主缆直径为391 mm 。
3)、索夹长度的确定(1)索夹下滑力(吊杆力沿大缆切线方向的分力)c N ϕsin h c N N =,式中:h N ——吊索拉力,N ;ϕ——索夹在主缆上的安装倾角,取同类索夹中最大值计算;(2)索夹抗滑摩阻力fc Fc b cb tot P n P =tot fc P k F μ=式中:tot P ——索夹上螺杆总的设计夹紧力;cb n ——索夹上安装的螺杆总数;c b P ——索夹单根螺杆设计夹紧力,N ;本设计取355KN ;κ——紧固压力分布不均匀系数,取2.8;μ——摩擦系数,一般取0.15。
(3)索夹对大缆的抗滑安全系数fc K3≥=cfc fc N F K(4)索夹壁的应力计算σ=tot P /(2•L•t)+3•tot P •e/ L•2t 式中:L ——索夹长度;t ——索夹壁厚度;e ——螺栓夹紧力对索夹壁中心线的偏心距。
索夹由于吊索拉力及主缆倾角不同,所需夹紧力不同,索夹长度和螺杆数量均不相同。
为便于制造和施工,将相近长度的索夹并为:索夹A ~索夹G 共七类,其中索夹G 为主缆防护套处密闭索夹。
经计算,确定索夹参数如下面表格所示:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动对 称 模 态 会 在 运 动 过 程 中 产 生 一 种 额 外 分 力 ( Irvine, 1981) ,这一点已经得到证明 。 而 非对 称模 态下并不产生任何 额外分力 。 因此采用偶数 (2, 4, 6, 8 )阶来计算基频 ,此时可以 忽略垂度的影响 ,垂度 引起的误 差为 0 。通过仪器 读出这几 阶的频率 ,通过线性回归 方法换算 出基频 。精匹配阶 段各索 力基频及相关数据见表 2。各索力计算公式误差见表 3。
4 4 ) 式中 :α2 = (ξ +γ 4 令ξ = 1 2 2 2 4 4 β ξ ) -ξ ; = ( +γ 2 1 2 2 +ξ
器及简易的数据分析设备 ,方便 实用 ,可以方便地测试任意工 况下任意斜拉 索的索力 , 并且具有 令人满意的 测试精 度 。 因 此该方法成为目前应用最为广泛的斜拉索索力测试方法 。 由于频率法 有多 个索 力计算公式可供选择 ,有 必要分析 常用的索力计算公式的精 度 ,以及在满足 一定误差 要求情况 下 ,各公式的适用范围 ,以 便在 采用频 率法 测定 斜拉索 索力 时正确地选择计 算式 。 为 此 ,本文采用成 熟的非线 性有限元 程序 NLAB S计算出理 论索 力 , 在计 算理 论索 力时 模型 采用 实测温度数据 ,对常用的几种索力计算公 式的精度 在不同索 长情况下进行分 析和 讨论 。
工
程
结
构
几种索力计算公式在短 、 长索中应用精度比较
宋松科 ,陈定波 ,吴 铭
(西南交通大学 , 四川成都 610031 )
【 摘 要】 在斜拉桥中斜拉索索力的准确 与否 直接 关系到主梁的线 形 ,乃至 施工安全 。 因 此 ,在 施工中 必须 确保 索力 测试结果正确可靠 。对拉索索力影响较大的参 数有斜拉 索计算长度 ,拉索振 动基频 ,索的 重力 集度 。 通过对 现有 的索 力计算公式进行实测数据比较 , 拉索长度 范围从 100多 米到 500 多 米 ,对 不同的 公式 采用 短 、 长索计算索力 , 并且对其计算精度进行讨论和研究 。给 出不同索长 时采用哪种 公式计算 比较方 便而 且具 有较 高的 精度 。 【 关键词 】 斜拉桥 ; 索力 ; 频率法 ; 精度 【 中图分类号 】 U441 + 1 5 【 文献标识码 】 A 斜拉索是斜拉桥的重 要组 成部 分 ,它 承担了斜 拉桥在施 工阶段和成桥后正常运营 阶段 的大 部分荷载 ,桥跨 结构的重 量和桥上的和活 荷载 通过斜 拉索 传递到 桥塔 上面 。因 此它 是斜拉桥的主要 构件 之一 。斜 拉索的 索力 合理 与否直 接决 定了斜拉桥施工 阶段结构 的受 力安全 和成 桥后 结构内 力的 合理分布 ,因此对实测斜拉索索力和理论 索力偏差 的分析尤 为重要 。当前对 拉索的 研究 有 : 斜 拉索 非线 性振动 理论 、 环 境因素效应 、 测试系统 及测 试方 法 、 数据分 析理 论及方 法以 及基于振动的斜 拉索 索力计 算方 法等 。本 文研 究的是 提高 频率法计算索力精度的相 关理 论及 实用方法 ,以及 频率法计 算索力的各种不 同公 式 。
211 索为铰支
的关系 。在考虑抗弯刚度的情况下 ,斜拉 索的动力 平衡微分 方程为 :
m 92 y 94 y 92 y = 0 2 + EI 4 - T g 9t 9t 9 t2 (1 )
当索为铰支时解 微分 方程 ( 1 ) 的索力计算公式为 :
T= 4m l 2 f 2 n n2 g - EI n π l
2
c f 1
2
; ζ≥ 17
; 6 ≤ζ ≤ 17 ( 4 )
2
; 0 ≤ζ ≤ 6
2 频率法计算索力公式
利用弦振动 理论可得 到斜 拉索拉 力与 其自 振频率 之间
[ 收稿日期 ] 2007 - 09 - 03 [ 作者简介 ] 宋松科 ( 1982 ~) , 男 , 四川 邛崃人 , 硕 士研
T m ω 4 , γ = 2E I EI
由此式可以得出 斜拉 索索 力计算的实用公式 [ 2 ] : 用一阶振型的固 有频 率时 (垂度比较小的索 )
T = 4m ( f1 l) 2 1 - 2 12 c - 0 155 f1 T = 4m ( f1 l) 2 01865 - 11 16 T = 4m ( f1 l) 2 01828 - 10 15 c f1 c f1
究生 , 主要从事桥梁结构分析和桥梁施工控制的研究 。
001
四川建筑 第 2 8 卷 4 期 20 08 垂度比较大的索 )
T = m ( f2 l) T= m ( f2 l)
2
工
程
结
构
c 1 - 414 - 111 f2
c f2
2
; 60 ≤ζ c f 2
212不考虑抗弯刚度若不考虑抗弯刚度的影响则可得简化的斜拉索拉力213索为固结当索为固结时解微分方程coslcoshlsinlsinhlei由此式可以得出斜拉索索力计算的实用公式用一阶振型的固有频率时垂度比较小的索收稿日期200703作者简介四川邛崃人硕士研200808001四川建筑第用二阶振型的固有频率时垂度比较大的索110361630188285214实用公式在文献中采用能量法推导出了分别考虑索垂度和抗弯刚度影响时索基频与索力的关系进而用曲线拟合方法建立了索力的实用公式
研究 ,其测试精度已能 满足工程要 求 。 而且 仅需加速 度传感
若不考 虑 抗弯 刚度 的影 响 , 则 可得 简 化的 斜拉 索 拉力 为:
T = 213 索为固结 4m l 2 f 2 n n2 g (3 )
当索为固结时解 微分 方程 ( 1 ) 得 : 2 (αl) ( βl) [ 1 - cos(αl) cosh(βl) ] + βl) 2 - (αl) 2 ] sin (αl) sinh (βl) = 0 [ (
2
(2 )
式中 : L 为斜拉索 的 索长 ; fn 为斜 拉 索的 第 n 阶 自 振频 率 ; n为 振动阶数 。
212 不考虑抗弯刚度
1 测试方法
对斜拉桥索力 进行监控测 试的方法 主要有 :荷 重传感器 测量法 、 张拉千斤顶测量法 、 压力型 油压千斤顶 测量法 、 电阻 片测量法 、 缆索伸长测量法 、 主梁线 形测量法 、 缆索垂 度测量 法、 频率法等 ,这些方法在实桥测试中均有应用 。其中被证实 精度较高的有荷重传感器测量法以及频 率法 。 在实际工程中 测定索力时需要快 速准确地获 得拉索的 索力 ,振动 频率测试 法方便快捷 ,造价较低 ,并且随着考虑索结构参数影响的深入
