卧式储罐计算公式
卧式罐剩余容积计算公式

卧式罐剩余容积计算公式引言。
在工业生产和化工领域,储罐是一种常见的储存设备,用于储存液体或气体。
在储罐的设计和运行过程中,剩余容积的计算是非常重要的。
特别是对于卧式储罐来说,剩余容积的计算涉及到罐体的形状和尺寸等因素。
本文将介绍卧式罐剩余容积计算的公式和相关知识。
卧式罐剩余容积计算公式。
卧式罐剩余容积的计算公式可以通过以下步骤进行推导:1. 首先,我们需要了解卧式罐的基本形状。
卧式罐通常是一个长方形的容器,底部为平底,两侧为直立。
我们可以将卧式罐的形状简化为一个长方形底部和两个直立的侧面。
2. 接下来,我们需要确定卧式罐的尺寸。
具体来说,我们需要知道卧式罐的长度、宽度和高度。
3. 然后,我们可以使用以下公式来计算卧式罐的剩余容积:V = L W H (L 2x) (W 2x) H。
其中,V表示卧式罐的剩余容积,L表示卧式罐的长度,W表示卧式罐的宽度,H表示卧式罐的高度,x表示卧式罐的壁厚。
4. 最后,我们可以根据具体的尺寸和壁厚数据,代入公式进行计算,得到卧式罐的剩余容积。
卧式罐剩余容积计算公式的应用。
卧式罐剩余容积的计算公式可以应用于工业生产和化工领域的多个方面。
首先,它可以用于设计防溢流系统。
通过计算卧式罐的剩余容积,我们可以确定在罐体达到一定液位时需要启动防溢流系统,从而避免液体溢出造成安全事故。
其次,它可以用于优化储罐的储存效率。
通过计算卧式罐的剩余容积,我们可以确定最佳的填充液位,从而最大限度地利用储罐的容量,提高储存效率。
此外,它还可以用于计算液体的消耗量。
通过监测卧式罐的剩余容积变化,我们可以计算出液体的消耗量,从而进行生产计划和成本控制。
总之,卧式罐剩余容积计算公式在工业生产和化工领域具有重要的应用价值,可以帮助我们进行安全设计、提高效率和控制成本。
卧式罐剩余容积计算的注意事项。
在使用卧式罐剩余容积计算公式时,我们需要注意以下几个方面:首先,我们需要准确测量卧式罐的尺寸和壁厚。
尺寸和壁厚的不准确数据会导致计算结果的误差。
卧式储罐不同液位下的容积计算
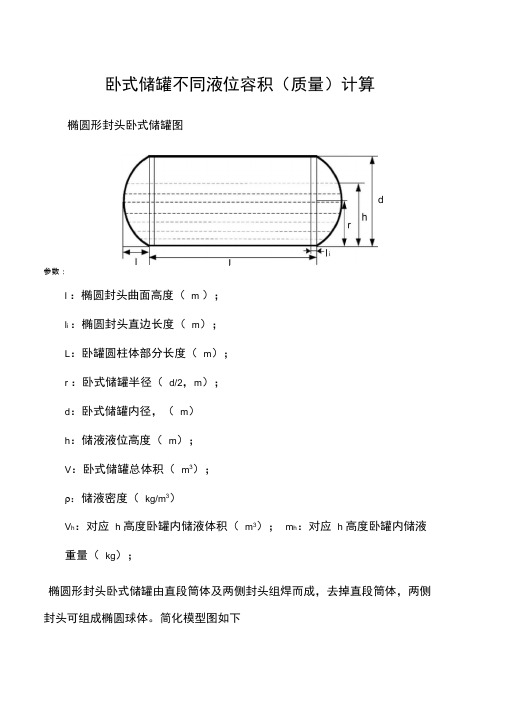
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆封头曲面高度(m );l i :椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h 高度卧罐内储液体积(m3);m h:对应h 高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为 ρ,则卧式储罐内储液总重量为:m h V h表 1 卧式储罐不同液位下容积(重量)ρrL h V hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度 (m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2 arcsin h-rrh-2rr 2rh-r 2以储罐底部为起点的液高该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
1) 椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2x 2 y 2 z 2 1 其中 a=b=r ,则有 x 2 y z2 1 a b c a c垂直于 y 轴分成无限小微元,任一微元面积为:S yic (a 2y 2)a当液面高度为 h 时,椭圆球体内液氨容积为2) 直段筒体部分:筒体的纵断面方程为 x 2 y 2 a 2 任一微元的面积为 S yj 2 a 2 y 2 dy 则筒体部分容积为:haS yjL a2 a 2 y 2dyLa 2(arcsinhahV1= a S yi dyhc2 2a a c(a 2 y 2)dyc(a 2ha33 h3 2a 3 33)3)卧式储罐储液总体积总容积为 V=V1+V2 ,此公式中液位高度 h 是以储罐内径中心为原点,其中 a=b=r 化简后 卧式储罐储液总体积为:实例:某热电厂液氨罐尺寸为:储罐体积 50m 3,直段筒体长度 L 1=8480mm , 封头直段长度 L 2=40mm (圆柱体部分长度为 (L 1+L 2/2)=8580mm ),筒体半径R=a=b=1300mm ,封头高度 c=650mmρV r l L h h 尺 V h m h误差 液体密度( kg/m 3)储罐总体积 (m 3) 储罐半 径 (m )封头高 度 (m )圆柱体部分 长度( m ) 储液液位高 度(中点为 坐标原点) (m )实际标尺 刻度储液体积 (m 3) 储液重量 (kg )不同液高下计算得到的 体积与实际 储液体积间 误差1 50 1.3 0.65 8.58 -1.3 0 0.000 0.0000.00%1501.30.658.58-0.9750.3253.6193.619arcsinhV=c(a 2h4h 2a2a 3)+ La 2(arcsinh3a 2rLr2arcsin h3Lh2r 2 -h 2r 2a1 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度 h 以卧罐底部为起点,如下图rroh则卧式储罐内储液总体积计算公式:若密度为 ρ,则卧式储罐内储液总重量为:m hV hρrL h V hm h液体密度 储罐半径 圆柱体部分长度 储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsin h-rrh r -2r r 2 rh-r 211.3 8.58 1.3 25.078 25.0781 1.3 8.58 2.275 46.537 46.537其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:(h r )2 h r2l (h r)[1 (h r3) ] L[(h r) 2hr h2 r2 arcsin( h r)]3r r若密度为ρ,则卧式储罐内储液总重量为:m h V hρV r l L h V h m h 误差V h V2此方式用到参数较多 ρ、V 、r 、l 、L 、h 。
卧式储罐体积计算公式

卧式储罐体积计算公式卧式储罐是一种广泛应用于石油、化工、医药等行业的容器,用于储存液体或气体物质。
其体积计算是设计、制造和使用储罐的基础。
卧式储罐的体积计算公式可以根据罐体形状和尺寸的不同而有所不同,下面将介绍几种常见的体积计算公式。
矩形卧式储罐一般由长方形和两个半圆柱体组成。
其体积可以通过以下公式计算:V=L*W*H+π*r²*L其中,V表示储罐的体积,L表示储罐的长,W表示储罐的宽,H表示储罐的高,r表示半圆柱体的半径。
圆柱型卧式储罐由一个长圆柱体和两个半圆锥体构成。
其体积可通过以下公式计算:V=π*r²*L+2/3*π*r³其中,L表示储罐的长度,r表示储罐的半径。
椭圆型卧式储罐由一个长椭球和两个半长椭球构成。
其体积可以通过以下公式计算:V=4/3*π*a*b*c其中,a、b、c分别表示椭圆长半轴、短半轴和半长轴。
需要注意的是,以上公式仅为简化计算公式,可能无法完全准确地计算出储罐的实际体积,因为储罐的形状、尺寸以及内部结构等因素都会对体积产生影响。
在实际工程设计中,还需要考虑到其他因素,如罐壁的厚度、罐底的形状等。
此外,卧式储罐的容积计算还需要考虑到液位的变化。
大多数卧式储罐会设置液位计来监测储罐内的液位,并通过液位计的信息计算出实际液位的体积。
通过根据液位的变化来计算储罐内的液体体积,可以更加准确地掌握储罐的储存能力。
综上所述,卧式储罐的体积计算需要结合储罐的形状和尺寸来确定合适的计算公式。
在实际应用中,设计和使用人员需要仔细考虑各种因素,并结合实际情况进行合理计算和判断。
卧室罐容积计算公式文

卧室罐容积计算公式文卧室罐容积计算公式。
在设计和装修卧室的过程中,计算卧室的罐容积是非常重要的一步。
罐容积指的是卧室内可容纳的物品和家具的总体积。
通过计算罐容积,我们可以更好地规划卧室的布局,选择合适大小的家具,以及合理利用空间。
在本文中,我们将介绍卧室罐容积的计算公式,并提供一些实用的技巧和建议。
卧室罐容积计算公式通常采用立方米或立方英尺作为单位。
计算公式如下:罐容积 = 长×宽×高。
其中,长、宽、高分别代表卧室内的三个方向的尺寸。
在实际应用中,我们需要先测量卧室的长、宽、高,然后将这些数值代入公式中进行计算。
在进行测量时,我们需要注意以下几点:1. 确保测量准确,使用尺子或测量工具进行测量时,要确保准确无误。
尽量避免估算或粗略测量,以免影响最终的计算结果。
2. 考虑特殊形状,如果卧室内有一些特殊形状的区域,比如斜顶或者凹凸不平的墙面,需要额外注意这些区域的测量方法,以确保计算结果的准确性。
3. 考虑家具和其他物品,在计算罐容积时,需要考虑卧室内已有的家具和其他物品。
通常情况下,我们会将这些物品的体积也计算在内,以便更好地规划空间。
除了计算公式外,我们在进行卧室罐容积计算时,还需要考虑一些实际情况和实用技巧:1. 灵活运用空间,有些卧室可能存在一些空间利用不当的情况,比如角落浪费、通道空间过大等。
在计算罐容积时,可以考虑如何更好地利用这些空间,比如增加储物柜、搁板或者定制家具等。
2. 考虑家具尺寸,在选择家具时,需要考虑家具的尺寸和卧室的罐容积。
如果卧室的罐容积较小,就需要选择尺寸较小的家具,以免造成空间拥挤和不便。
3. 考虑功能布局,在进行罐容积计算时,也需要考虑卧室的功能布局。
比如,如果卧室既要兼顾睡眠区域又要兼顾工作或学习区域,就需要合理规划空间,确保各个区域的功能得到充分发挥。
在实际应用中,卧室罐容积的计算可以帮助我们更好地规划卧室的布局,选择合适的家具和装饰,以及合理利用空间。
卧式储罐体积计算公式

卧式储罐体积计算公式卧式储罐是一种常见的储存液体或气体的设备,广泛应用于石油、化工、食品等行业。
储罐的体积计算是设计和运营过程中非常重要的一环,它直接关系到储罐的容量和使用效果。
下面将介绍几种常见的卧式储罐体积计算公式。
图形上看,卧式储罐的截面通常是一个椭圆形,因此椭圆罐容积计算公式是储罐设计中最常用的一种。
V=π*L*(b/2)^2*(1-(h/b*(2-h/b))^(1/2))其中,V表示储罐的容积,L表示储罐的长度,b表示椭圆的长轴长度,h表示液体的高度。
有些卧式储罐的底部是平坦的,这种情况下可以使用平底罐容积计算公式。
V=L*(b*c*d/3+d*h^2/2)其中,V表示储罐的容积,L表示储罐的长度,b表示椭圆的长轴长度,c表示椭圆的短轴长度,d表示椭圆的高度,h表示液体的高度。
另一种常见的卧式储罐底部是圆形的,这种情况下可以使用圆底罐容积计算公式。
V = L * (π * R^2 * (1 - cos(θ)) + R^2 * sin(θ) * h)其中,V表示储罐的容积,L表示储罐的长度,R表示圆底的半径,θ表示液体高度与L轴的夹角,h表示液体的高度。
需要注意的是,以上公式中的参数有些是设计过程中确定的,有些需要根据实际情况进行计算。
例如,椭圆罐容积计算中的L、b和h通常是设计参数,而平底罐容积计算中的c和d则需要根据椭圆的长轴和短轴长度计算得到。
此外,还有其他一些特殊形状的卧式储罐,例如锥底罐、双重底罐等,其容积计算公式略有不同,需要根据具体的形状和参数进行计算。
总之,卧式储罐的体积计算是设计和运营过程中非常重要的一步,它需要根据储罐的几何形状和液体高度来确定。
不同形状的储罐有不同的计算公式,设计和运营人员需要根据实际情况选择合适的公式进行计算,以保证储罐容量的准确性和安全性。
卧式储罐不同液位下的容积计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图d参数:l :椭圆圭寸头曲面高度(m );l i :椭圆圭寸头直边长度(m);L :卧罐圆柱体部分长度(m);r :卧式储罐半径(d/2, m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);P储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m h V h表1卧式储罐不同液位下容积(重量)PrLhV hm h液体密度 (kg/m 3)储罐半径 (m )圆柱体部分长度(m )储液液位高度(m )储液体积 (m 3)储液重量 (kg )2r 3LLr 2arcsi4r*r 2rh-r 2以储罐底部为起点的液咼该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2 2 2 2 2 2务告务 1 其中a=b=r,则有x 2 务 1 a b c a c垂直于y 轴分成无限小微元,任一微元面积为:S yi —(a 2 y 2)a当液面高度为h 时,椭圆球体内液氨容积为h「3 o 3V1=aS yj dya^(a 2 y 2)dy許2h自(2 )直段筒体部分:筒体的纵断面方程为x 2 y 2 a 2任一微元的面积为S yj 2、.、a 2 y 2dy则筒体部分容积为:L 2 a 2 y 2dy La 2(arcsin 」aahV2aSyj.2 _____________a 2八 2)( arcsin -)2a 2(3)卧式储罐储液总体积总容积为V 二V1+V2 ,232c 2- 4h 2a 2(. h h r .2、V= (a h)+ La (arcsin 2 ; a h ) a 3 3 a a2此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:21 三 Lr 2arcsin^ 3L rr 2-h 2r 21 50 1.3 0.65 8.58 0 1.3 25.078 25.0780.31%1 50 1.3 0.65 8.58 0.975 2.275 46.537 46.5371501.30.658.581.32.650.15550.1550.31%若液位高度h 以卧罐底部为起点,如下图/\ A / __________\rf (1)f\ y丿 1 二;o h \ ............. .... J V7\…一j... J■厶■N K A *则卧式储罐内储液总体积计算公式:若密度为p,则卧式储罐内储液总重量为:m hV hprLhV hm h液体密度 储罐半径 圆柱体部分长度储液液位高度储液体积 储液重量(kg )(kg/m 3)(m )(m )(m )(m 3)11.3 8.580.3253.619 3.6192r3LLr 2 arcsi®rh-r r 2h-r 2其它方法如下:第一种方法| PDF.卧式储罐不同液位 下的容积简化计算公卧式储罐内储液总体积计算公式:(hr ) 2--------------- K r2l (h r )[1」 宀]L[( h r)「2hr h 2 r 2 arcsi n( ---------------------------- )]3 rr若密度为p,则卧式储罐内储液总重量为:Vh V此方式用到参数较多P、V、r、l、L、h。
卧式圆柱罐体实际盛液的体积计算

卧式圆柱罐体实际盛液的体积计算
接下来,我们需要计算卧式圆柱罐体的高度。
卧式圆柱罐体通常有一个弓形的顶部,同时还有一个底部(通常为平面或球面)。
我们需要测量从底部到弓形顶部的垂直高度,即是罐体的高度。
最后,根据圆柱体的总体积公式:V=A*h,其中V为体积,A为底面积,h为高度,就可以得到卧式圆柱罐体的实际盛液体积。
举个例子来说明:
假设我们要计算一个卧式圆柱罐体的实际盛液体积,已知该罐体的底面直径为10米,高度为5米。
首先,根据半径计算底面积:
半径r=直径/2=10/2=5米
接下来,根据公式V=A*h,计算总体积:
V=78.54*5=392.7立方米
所以,该卧式圆柱罐体的实际盛液体积为392.7立方米。
需要注意的是,在实际运用中,我们可能会遇到一些额外的因素,比如罐体底部有凹陷或突出的结构,这样会影响到底面积的计算;另外,罐体内部可能有支撑物或导管等,也会对容积产生影响。
因此,在实际计算中需要根据具体情况进行调整。
除了通过计算卧式圆柱罐体的底面积和高度来求解体积,我们还可以通过其他方法来计算,比如浸没法、称重法等。
这些方法都是根据液体浸
没罐体的量或罐体的质量来计算容积。
不同的方法适用于不同的应用场景,具体选择哪种方法取决于具体情况和可行性。
总之,卧式圆柱罐体实际盛液的体积计算是一个基本的几何计算问题,在实际应用中需要考虑到具体情况和因素,选择合适的计算方法。
卧式储罐容积计算

卧式储罐容积计算一、卧式储罐容积计算的基础知识卧式储罐的形状就像一个躺着的大圆筒。
要计算它的容积,我们得先知道一些基本的东西。
比如说,储罐的长度、半径这些数据可重要啦。
你可以想象一下,要是储罐又长又粗,那它能装的东西肯定就多,容积就大呗。
就像大胖子能吃很多东西,大储罐就能装很多东西一样,嘿嘿。
二、不同形状卧式储罐的计算1. 标准圆柱形卧式储罐这种是最常见的啦。
它的容积计算就像算圆柱体的体积一样。
我们在高中学过,圆柱体体积公式是V = πr²h,在卧式储罐里,这个h就是储罐的长度,r就是半径。
但是要注意哦,这里的计算得精确,可不能马马虎虎的。
要是把半径量错了一点,那算出来的容积可就差得远了。
2. 带封头的卧式储罐这种储罐就稍微复杂一点了。
它的两端有封头,封头的形状会影响到整个储罐的容积。
一般来说,这种封头有椭圆形的、碟形的等等。
如果是椭圆形封头的卧式储罐,计算容积的时候,除了要算中间圆柱形部分的容积,还得加上两个封头部分的容积。
这就像做蛋糕,中间的圆柱体是蛋糕体,两边的封头就像是蛋糕上的装饰,都得算在整个蛋糕的大小里。
三、计算中的单位换算在计算卧式储罐容积的时候,单位可不能乱。
有时候给的数据可能是厘米,但是我们计算的时候可能要用米。
这就像换衣服一样,要把不合适的单位换成合适的。
比如说,1米等于100厘米,如果半径是50厘米,换算成米就是0.5米。
要是不换算好单位,计算结果就会错得很离谱,就像把冬天的衣服穿在夏天一样不合适。
四、实际测量中的要点1. 测量长度测量储罐长度的时候,要从一端到另一端,沿着储罐的中心轴线测量。
而且要测量多次,取平均值,这样才能减少误差。
就像量身高一样,一次量可能不准,多量几次就更准确了。
2. 测量半径测量半径可不容易呢。
因为储罐的壁可能有一定的厚度,我们要测量的是内径还是外径呢?如果是计算容积,一般是要测量内径的。
可以用专门的测量工具,比如卡尺之类的,小心地测量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卧式储罐计算公式
卧式储罐是一种常见的储存液体或气体的容器。
它采用水平放置的方式,通常用于储存石油、化工产品、液化气体等。
在设计和计算卧式储罐时,需要考虑到容器的结构、强度、稳定性和安全性等方面。
下面将介绍一些常用的卧式储罐计算公式。
1.储罐容积的计算:
储罐容积是指储罐能够容纳的液体或气体的总体积。
计算储罐容积一般需要考虑到容器的几何形状和尺寸等参数。
常用的计算公式包括:-矩形底储罐容积计算公式:
V=L*W*H
其中,V为容积,L为储罐长度,W为储罐宽度,H为储罐高度。
-圆形底储罐容积计算公式:
V=π*R^2*H
其中,V为容积,π取3.14,R为储罐半径,H为储罐高度。
2.储罐壁厚的计算:
储罐壁厚是指储罐壁体的厚度,主要用于承受内外压力差和容器自重等荷载。
计算储罐壁厚要考虑到材料的强度和应力等因素。
常用的计算公式包括:
-常规卧式储罐壁厚计算公式:
t=(P*D*S)/(2*F*E-0.2*P)
其中,t为壁厚,P为设计压力,D为储罐直径,S为材料允许应力,
F为安全系数,E为焊缝效率。
-强度计算公式:
σ=(P*D)/(2*t)
其中,σ为壁体应力,P为设计压力,D为储罐直径,t为壁厚。
3.储罐体积变化的计算:
储罐在受到温度变化、压力变化等外界因素的影响时,会发生体积的
变化。
计算储罐体积变化一般需要考虑到温度膨胀系数和压力系数等因素。
常用的计算公式包括:
-温度变化引起的体积变化计算公式:
ΔV=V*β*ΔT
其中,ΔV为体积变化,V为初始容积,β为温度膨胀系数,ΔT为
温度变化。
-压力变化引起的体积变化计算公式:
ΔV=V*α*ΔP
其中,ΔV为体积变化,V为初始容积,α为压力系数,ΔP为压力
变化。
以上是一些常用的卧式储罐计算公式,供设计和计算人员参考。
但需
要注意的是,不同的储罐结构和设计要求可能会有所不同,因此在实际应
用中,需要结合具体情况和相关标准进行计算和设计。
