几何画板中作二次函数图像与性质的步骤
几何画板二次函数案例

几何画板二次函数案例二次函数在几何画板中的应用非常广泛,下面我将为你提供一个案例,详细解释如何使用二次函数来构建一个几何图形。
案例:构建一个抛物线喷泉喷泉是一种常见的城市景观和装置,它通过一个喷水装置将水以特定的形式喷射出来,形成美丽的水柱。
在这个案例中,我们将使用二次函数来模拟喷泉的形状。
首先,让我们定义一个二次函数来描述喷泉的形状。
假设水柱的高度(h)是和喷射距离(x)相关的,我们可以使用以下二次函数来描述这种关系:h(x) = ax^2 + bx + c其中,a、b、c是需要确定的常数。
喷泉的形状通常是一个开口朝下的抛物线,所以a的值应该小于0。
接下来,我们将确定a、b和c的值。
为了简化问题,我们假设喷泉的最高高度是10米,并且喷射的最远距离是20米。
我们可以选择两个点来确定这个二次函数的值。
假设我们选择喷泉的两个关键点分别是(0,0)和(20,10)。
将这两个点带入二次函数的方程,我们可以得到以下两个方程:0=a*0^2+b*0+c=>c=010=a*20^2+b*20+0=>400a+20b=10通过解这个方程组,我们可以得到a和b的值。
解方程组可以得到a=-0.0125和b=0.25、所以二次函数的方程为:h(x)=-0.0125x^2+0.25x现在,我们可以使用这个二次函数来绘制喷泉的形状。
通过在几何画板上画出一系列点,然后使用平滑曲线连接这些点,我们可以得到整个喷泉的形状。
首先,我们选择几个x的值,例如x=0,2,4,...,20。
然后,我们使用二次函数计算对应的h(x)的值。
最后,在几何画板上画出这些点,并使用平滑曲线连接它们。
通过加入适当的颜色和细节,我们可以使这个几何图形更加真实和立体感。
我们还可以添加其他元素,如水柱顶部的喷雾效果。
通过调整二次函数的参数,我们可以自由地改变喷泉的形状和高度。
这使得几何画板成为优秀的工具,用于设计和模拟各种喷泉的形状,并选择出最佳的设计。
几何画板在二次函数y=ax2 ( a ≠0)中的应用

几何画板在二次函数y=ax2 ( a ≠0)中的应用二次函数y=ax^2 (a ≠0)是高中数学学习中的重要内容,它描述了一条抛物线的图像,具有许多重要的性质和应用。
而近年来,随着科技的发展,几何画板已经成为学习和教学的利器,它不仅可以帮助学生更好地理解和学习二次函数,还可以拓展二次函数的应用,使学习更加生动、深入和有趣。
一、几何画板的基本功能几何画板是一种数字化的绘图工具,它可以在屏幕上实现多种几何图形的绘制、变换和动态展示。
通过几何画板,学生可以绘制出二次函数y=ax^2的图像,观察抛物线的特征和性质,比如顶点坐标、对称轴、开口方向等。
几何画板还可以通过拖拽和调节参数,实现二次函数的变换和变形,如平移、伸缩、翻转等,从而加深学生对函数变化的理解和认识。
二、几何画板在二次函数图像的展示和分析中的应用1. 展示不同参数对图像的影响通过几何画板,学生可以通过调节参数a,观察二次函数图像的变化。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
a的绝对值越大,抛物线越“瘦长”,开口越“尖锐”;a的绝对值越小,抛物线越“扁平”,开口越“圆滑”。
通过这种方式,学生可以直观地感受到参数a对二次函数图像的影响,从而加深对二次函数的认识和理解。
2. 讨论特殊情况下的图像特征几何画板可以帮助学生讨论特殊情况下的图像特征,如a=0时,二次函数的图像将是一条水平直线;a=1时,抛物线与y=x^2的图像完全重合,学生可以通过画板进行观察和比较。
通过这种方式,学生可以更好地理解和掌握二次函数图像的性质和特征。
3. 探讨顶点、对称轴和轴线方程几何画板可以帮助学生观察和分析顶点、对称轴和轴线方程的关系。
通过观察,学生可以发现顶点的横坐标就是对称轴的方程,而对称轴的方程就是抛物线的轴线方程。
这种发现有助于学生对抛物线性质的理解和掌握。
除了上述基本功能和应用外,几何画板还可以在二次函数的应用中有更进一步的拓展。
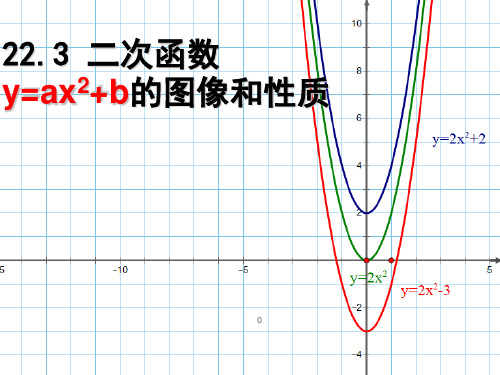
二次函数y=ax^2+b的图像及性质
0
复习巩固
二次函数 y=ax2(a>0) 1. 图像的特点 开口向上,向x轴左右方向 无限延伸 函数的性质 自变量x的取值范围 是全体实数
观察下面函数图像,完成下表:
2.
是轴对称图形,对称轴是y 轴
在y轴的左侧是下降的,在y 轴的右侧是上升的
对于x和-x可得到相 同y值
图象的形状相同吗?
观察图像回答问题:
1.y=2x2、y=2x2+1和y=2x2-1的图像,它们的开口方向如何?顶点坐标、对称轴 分别是什么?
它们开口向上,顶点坐标分别是(0,0)、(0,1)、(0,-1),对称轴都是y 轴。 2.对于同一个x值,二次函数y=2x2、y=2x2+1和y=2x2-1的值之间有什么 关系?这三个函数的图像在位置上有什么关系? 对于同一个x值,它们的函数值关于y轴对称,这三个 函数图像在位置上是沿y轴上下平移一个单位得到的 3.当x取何值时,二次函数y=2x2、y=2x2+1和y=2x2-1 取得最小值?最小值分别是多少? 当x取0时,函数y=2x2、y=2x2+1和y=2x2-1取 得最小值,最小值分别是0、1和-1
10
y
8
y=2x2+1
y=2x2 y=2x2-2
5
4
y
2
y=-2x2+3
5
6
4
-10
-5
O
-2
x
10
2
y=-2x2 y=-2x2-2
-4
-10 -5
O
-2
x
10
-6
-8
当a>0时,抛物线y=ax2+c的开口 向上 ,对称轴 是 y轴 ,顶点坐标是(0,c),在对称轴的左侧,y随x的 增大而 减小 ,在对称轴的右侧,y随x的增大而增大 , dfdfdfgfgfdfdfdfdf 当x= 0 时,取得最 小 值,这个值等于 c dfffdfdfdfdfdfdffdff ; fffdfdfdffffdfdfdfdf 当a<0时,抛物线y=ax2+c的开口 向下 ,对称轴 dfdfdfdfdffffdffdffd y 轴 是 ,顶点坐标是(0,c) ,在对称轴的左侧,y 随 x的 fdfffdfffdfdfdfffffffdf dff 增大而增大 ,在对称轴的右侧,y随x的增大而减小 , 当x= 0 时,取得最 大 值,这个值等于 c 。
讲解详细讲解二次函数的像绘制方法和常见的性质解答学生提出的疑问

讲解详细讲解二次函数的像绘制方法和常见的性质解答学生提出的疑问二次函数是高中数学中的重要内容之一,它在数学和物理等学科中都有广泛的应用。
本文将详细讲解二次函数的像绘制方法和常见的性质,以解答学生提出的疑问。
一、二次函数的像绘制方法要绘制二次函数的像,首先需要确定函数的一般式或标准式。
一般式表示为 y = ax^2 + bx + c,其中 a、b、c 为实数且a ≠ 0;标准式表示为 y = a(x - h)^2 + k,其中 a、h、k 为实数且a ≠ 0。
1. 一般式的像绘制方法根据给定的一般式 y = ax^2 + bx + c,可以通过以下步骤来绘制二次函数的像:(1)求出二次函数的顶点坐标。
二次函数的顶点坐标可以通过公式 x = -b/2a 和 y = f(-b/2a) 求得,其中 f(-b/2a) 表示将 x = -b/2a 代入函数中得到的 y 值。
(2)确定对称轴。
对称轴是通过二次函数的顶点且与 x 轴垂直的直线。
它的方程可以表示为 x = -b/2a。
(3)计算函数值 y。
在对称轴两侧任选几个 x 值,并带入函数中计算对应的 y 值,得到一些点坐标。
通过这些点坐标可以绘制出二次函数的像。
2. 标准式的像绘制方法对于标准式 y = a(x - h)^2 + k,绘制二次函数的像可以采用以下步骤:(1)求出二次函数的顶点坐标。
顶点坐标为 (h, k)。
(2)确定对称轴。
对称轴是通过二次函数的顶点且与 x 轴垂直的直线。
它的方程可以表示为 x = h。
(3)计算函数值 y。
在对称轴两侧任选几个 x 值,并带入函数中计算对应的 y 值,得到一些点坐标。
通过这些点坐标可以绘制出二次函数的像。
二、二次函数的常见性质除了像的绘制方法,我们还需要了解二次函数的常见性质。
以下是几个重要的性质:1. 对称性:二次函数的图像以对称轴为轴对称,即对称轴两侧的像完全相同。
2. 零点:二次函数的零点是函数值为零的 x 坐标。
二次函数图像画法与特性分析

二次函数图像画法与特性分析二次函数是高中数学中的重要内容之一,它在数学、物理、经济等领域都有广泛的应用。
本文将介绍二次函数图像的画法和特性分析。
一、二次函数图像的画法要画出二次函数的图像,首先需要确定函数的顶点和开口方向。
二次函数的一般形式为y = ax^2 + bx + c,其中a、b、c为常数。
根据a的正负可以判断二次函数的开口方向,当a>0时,开口向上;当a<0时,开口向下。
确定开口方向后,可以通过计算顶点的坐标来确定图像的位置。
二次函数的顶点坐标为(-b/2a, f(-b/2a)),其中f(x)为二次函数的值。
通过计算可以得到顶点坐标,然后将顶点标记在坐标轴上。
接下来,可以选择一些特殊点来确定图像的形状。
例如,可以选择x=0和x=1两个点来计算函数值,然后将这些点连接起来,就可以得到二次函数的大致形状。
二、二次函数图像的特性分析1. 对称轴:二次函数的图像关于对称轴对称。
对称轴的方程为x = -b/2a,通过计算可以得到对称轴的位置。
2. 最值点:二次函数的最值点即为顶点,通过计算顶点的坐标可以得到最值点的位置。
当a>0时,最值点为最小值;当a<0时,最值点为最大值。
3. 零点:二次函数的零点即为函数与x轴的交点。
通过求解二次方程ax^2 + bx + c = 0,可以得到零点的位置。
当判别式b^2-4ac>0时,函数有两个不同的零点;当判别式b^2-4ac=0时,函数有一个重根;当判别式b^2-4ac<0时,函数无实数根。
4. 函数的增减性:当a>0时,二次函数是上升的;当a<0时,二次函数是下降的。
通过计算函数的导数可以得到函数的增减性。
5. 函数的凹凸性:当a>0时,二次函数是凹的;当a<0时,二次函数是凸的。
通过计算函数的二阶导数可以得到函数的凹凸性。
通过对二次函数图像的特性进行分析,可以更好地理解函数的性质和变化规律。
如何用几何画板作函数图像

如何用几何画板作函数图像本人在教学工作中常用几何画板作函数图像,总结了一些基本方法现成文与广大数学教师共享。
一、坐标法坐标法适用于已知函数解析式求作函数图像的方法。
构造一个坐标满足函数解析式的点,用几何画板的轨迹工具画出图象。
下以二次函数为例。
步骤如下:1、新建一个绘图,选择菜单里的“图表”,鼠标单击“建立坐标轴”。
2、选择轴,右击鼠标显示快捷菜单,选择作图,对象上的点,确保该点处在被选中状态,选择工具栏里的“标出文本&标签”工具,鼠标单击刚画出的点,将显示出该点的“标签”(假设为“C”)。
确保C点处于被选中状态,右击鼠标显示快捷菜单选择“度量”,鼠标单击“坐标”,得到C点的坐标。
3、选择工具栏里的“选择&平移”工具,鼠标单击C点的坐标,使它处于被选中状态,再选择菜单栏里的“度量”,鼠标单击“计算”,出现“计算器”窗口,用鼠标单击“数值”按钮,把鼠标放在“点C”上,选择x,然后用鼠标单击“计算器”窗口里“确定”按钮,这样我们就得到了C点的横坐标的度量值。
如果用鼠标拖动点C的话,你会发现它的横坐标的度量值在随之变化。
4、下面我们把界面稍微整理一下,用鼠标单击C点的坐标,使它处于被选中状态,然后同时按下Ctrl和H键,把C点的坐标隐藏掉。
再选择工具栏里的“标出文本&标签”工具,用鼠标双击C点横坐标的度量值,在出现的“度量值格式”窗口里选择“文本格式”,出现两个文本框,将左面文本框内的“X[C]=”改成“x=”,按下“度量值格式”窗口里的“确定”按钮。
经过上面的工作,我们已经把二次函数的自变量构造出来了。
5、选择工具栏里的“选择&平移”按钮,按住Shift键,鼠标单击度量值x(确保别的对象不处于选中状态),选择菜单栏里的“度量”,鼠标单击“计算…”,在出现的“计算器”窗口里,鼠标单击“数值”按钮,选择“2”,鼠标单击“*”号按钮,鼠标单击“数值”按钮,选择“x”,鼠标单击“^”号按钮,鼠标单击“2”按钮,鼠标单击“-”号按钮,鼠标单击“数值”按钮,选择“3”,鼠标单击“*”号按钮,鼠标单击“数值”按钮,选择“x”,鼠标单击“+”号按钮,鼠标单击“数值”按钮,选择“1”,最后按下确定按钮,得到一个新的度量值。
二次函数y=ax^2+b的图像及性质

想一想:y=-2x 、y=-2x +3和y=-2x -
2 2 2
2的图像,它们的开口方向如何?位置关系如何?
教师几何画板演示a<0情况
jkjj ff ff ff ff ff ff ff ff f
函数y=-2x2+3的图象可由y=2x2的图象沿y轴向上平移3个 单位长度得到.
-10 -5
4
y
2
y=-2x2+3
当x=0时,函数取得最大 值, y最大值=0,且y没 有最小值,即y≤0
问题1:在同一平面直角坐标系中,画出函数y=2x2、
y=2x2+1和y=2x2-1的图像? 一、填表:
x
... ... ... ... -2 -3/2 -1 -1/2 0 1/2 1 3/2 2 ... ... ... ...
当x<0时,函数值y随 x值的增大而减小; 当x>0时,函数值y随 x值的增大而增大
3.
y=ax2(a>0)
4.
顶点就是原点(0,0),顶 点是图像的最低点,开口向 上,图像向上无限延伸
二次函数及其作图

二次函数及其作图二次函数是数学中的一种特殊函数类型,其表达式为f(x) = ax^2 +bx + c,其中a、b、c为常数,且a ≠ 0。
二次函数在数学及实际问题中都有广泛的应用,了解二次函数及其作图方法对于解决相关问题具有重要意义。
一、二次函数的基本形式及性质二次函数的基本形式为f(x) = ax^2 + bx + c,并且图像一定是抛物线。
根据a的正负及大小,可以得出以下性质:1. 当a > 0时,抛物线开口向上,图像在x轴上方有最小值。
2. 当a < 0时,抛物线开口向下,图像在x轴下方有最大值。
3. 当a的绝对值越大,抛物线的开口越宽。
4. 函数的零点即为二次方程ax^2 + bx + c = 0的解,可以通过求解该方程得到。
二、二次函数的作图方法为了更好地理解和应用二次函数,我们可以通过作图来展示其图像。
1. 确定基准点:找出抛物线的顶点,即最值点,可以通过求对称轴的坐标进行确定。
对称轴的坐标公式为x = -b / (2a),将这个值代入函数中即可得到顶点的坐标。
2. 确定关键点:找出抛物线与x轴的交点,即零点。
可以通过求解二次方程ax^2 + bx + c = 0来得到,求解出的根即为关键点的横坐标,将其代入函数中可以得到纵坐标。
3. 绘制抛物线:连接顶点和关键点,并逐渐绘制出整个抛物线的形状。
4. 补全图像:根据图像的开口方向和函数的定义域,补全抛物线的形状。
三、例题分析与实践例题:已知二次函数f(x) = 2x^2 - 4x + 3,求解以下问题:1. 函数f(x)的最值点坐标和最值;2. 函数f(x)的零点坐标;3. 根据所得信息画出函数f(x)的图像。
答案:1. 首先求解对称轴的坐标。
根据公式x = -b / (2a),代入a = 2,b = -4,得到对称轴的横坐标为 x = -(-4) / (2*2) = 1。
将x = 1代入函数中,得到最值点P的纵坐标:f(1) = 2 * 1^2 - 4 * 1 + 3 = 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数y=a(x^2)+bx+c图像与性质
1.确定系数a、b、c
几何画板中,“绘图”“定义坐标系”
选定X轴,“构造”“轴上的点”,重复3次,得X轴上三个点
选定X轴与此3点,“构造”,“垂线”,得X轴3条垂线
分别选定垂线,“构造”“垂线上的点”,
分别选定垂足和构造的点,“构造”“线段”,并隐藏垂线,并标记。
如下图
选定点A、B、C,“度量”“纵坐标”。
(说明:此方法与席老师所教有点不同,此方法得到的A、B、C只有纵坐标会发生变化,横坐标不会变化)
依次选定三个文本,“属性”“标签”修改为a、b、c。
如下图
2.新建并绘制函数
2.1 “数据”,“新建函数”,“方程”,“Y=”
2.2 输入函数表达式:a*(x^2)+b*x+c.(注意:a、b、c的输入须点击上图右之a、b、c)
2.3 选定y=a(x^2)+bx+c,“绘图”,“绘制函数”,如下图:。
