高考数学 考前最后一轮基础知识巩固之第六章 第2课 一元二次不等式 2
高考数学总复习 第6章 第2讲 一元二次不等式的解法课件 理 新人教A版

2.一元二次不等式中的恒成立问题 一元二次不等式中的恒成立问题,应结合相应的二次函 数图象和方程根的情况(用判别式),寻找其成立的条件. (1)一元二次不等式 ax2+bx+c>0 恒成立的等价条件为 a>0, Δ<0;
12
(2)一元二次不等式 ax2+bx+c<0 恒成立的等价条件为 a<0, Δ<0;
端点与相应的一元二次方程的根及相应的二 次函数图象与x轴交点的横坐标相同.
4
• 2种必会方法 • 1. 解一元二次不等式时,首先将不等式标准
化,再确定相应的方程的根,最后根据图象 写出解集. 对于Δ<0,Δ=0等特殊情况的解集 要从本质上理解. • 2. 解含参的一元二次不等式恒成立问题,一 是转化为一元二次不等式解集为R的情况来解, 二是分离参变量,转化为最值问题去处理.
25
• ③当a2-a=0,即a=0或a=1时, • 原不等式的解为x≠a. • 综上①②③得a>1或a<0时不等式解集为
{x|x>a2或x<a} • 当0<a<1时,不等式解集为{x|x<a2或x>a} • 当a=0或a=1时,不等式解集为{x|x≠a}. • (2)原不等式化为(ax-1)(x-1)<0. • ①当a=0时,其解为x>1;
14
• 不等式ax2+2ax+4≥0恒成立,对一切x的值, 求a的取值范围.
15
• 不等式ax2-x+2a<0的解集为∅,则a的取值 范围________.
16
1. {x|x<x1 或 x>x2} {x∈R|x≠-2ba} R {x|x1<x<x2}
∅∅
填一填:(1){x|x<-3
高考数学一轮复习 第六章 不等式、推理与证明 第二节 一元二次不等式及其解法学案 文

第二节一元二次不等式及其解法1.会从实际问题的情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.知识点一一元二次不等式的解法{x|x<x1或x>x2} {x|x≠-b2a }{x |x 1<x <x 2} ∅ ∅1.(2016·新课标全国卷Ⅲ)设集合S ={x |(x -2)(x -3)≥0},T ={x |x >0},则S ∩T =( )A .[2,3]B .(-∞,2]∪[3,+∞)C .[3,+∞)D .(0,2]∪[3,+∞)解析:集合S =(-∞,2]∪[3,+∞),结合数轴,可得S ∩T =(0,2]∪[3,+∞). 答案:D2.不等式x -12x +1≤0的解集为( )A.⎝ ⎛⎦⎥⎤-12,1B.⎣⎢⎡⎦⎥⎤-12,1 C.⎝⎛⎭⎪⎫-∞,-12∪[1,+∞) D.⎝⎛⎦⎥⎤-∞,-12∪[1,+∞) 解析:由数轴标根法可知原不等式的解集为⎝ ⎛⎦⎥⎤-12,1,选A.答案:A3.设一元二次不等式ax 2+bx +1>0的解集为{x |-1<x <2},则ab 的值为( ) A .1 B .-14C .4D .-12解析:因为一元二次不等式ax 2+bx +1>0的解集为 {x |-1<x <2}.所以方程ax 2+bx +1=0的解为-1,2.所以-1+2=-b a,(-1)×2=1a.所以a =-12,b =12,所以ab =-14.答案:B知识点二 一元二次不等式恒成立的条件 1.ax 2+bx +c >0(a ≠0)恒成立的充要条件是:______ (x ∈R ).2.ax 2+bx +c <0(a ≠0)恒成立的充要条件是:______ (x ∈R ).答案1.⎩⎪⎨⎪⎧a >0Δ<0 2.⎩⎪⎨⎪⎧a <0Δ<04.若不等式mx 2+2mx +1>0的解集为R ,则m 的取值范围是________. 解析:①当m =0时,1>0显然成立. ②当m ≠0时,由条件知⎩⎪⎨⎪⎧m >0,Δ=4m 2-4m <0.得0<m <1,由①②知0≤m <1. 答案:[0,1)5.不等式x 2+ax +4<0的解集不是空集,则实数a 的取值范围是________. 解析:∵不等式x 2+ax +4<0的解集不是空集,∴Δ=a 2-4×4>0,即a 2>16, ∴a >4或a <-4.答案:(-∞,-4)∪(4,+∞)热点一 一元二次不等式的解法 【例1】 解关于x 的不等式: (1)-2x 2+4x -3>0; (2)12x 2-ax >a 2(a ∈R );(3)a x -x -2>1(a >0).【解】 (1)原不等式可化为2x 2-4x +3<0.又判别式Δ=42-4×2×3<0, ∴原不等式的解集为∅.(2)由12x 2-ax -a 2>0⇒(4x +a )(3x -a )>0⇒(x +a 4)(x -a3)>0,①当a >0时,-a 4<a 3,解集为{x |x <-a 4或x >a3};②当a =0时,x 2>0,解集为{x |x ∈R 且x ≠0}; ③当a <0时,-a 4>a 3,解集为{x |x <a 3或x >-a4}. (3)a x -x -2-1>0⇒a -x +2-a x -2>0⇒[(a -1)x +2-a ](x -2)>0.①当a =1时,不等式的解为x >2. ②当a ≠1时,关键是(a -1)的符号和比较a -2a -1与2的大小. ∵a -2a -1-2=-aa -1,又a >0. ∴当0<a <1时,a -2a -1>2, 不等式的解为2<x <a -2a -1; 当a >1时,a -2a -1<2, 不等式的解为x <a -2a -1或x >2. 综上所述,当0<a <1时,原不等式的解集为{x |2<x <a -2a -1};当a =1,原不等式的解集为{x |x >2};当a >1时,原不等式的解集为{x |x <a -2a -1或x >2}.解下列不等式: (1)0<x 2-x -2≤4; (2)x 2-4ax -5a 2>0(a ≠0). 解:(1)原不等式等价于⎩⎪⎨⎪⎧x 2-x -2>0,x 2-x -2≤4⇔⎩⎪⎨⎪⎧x 2-x -2>0,x 2-x -6≤0⇔⎩⎪⎨⎪⎧x -x +,x -x +⇔⎩⎪⎨⎪⎧x >2或x <-1,-2≤x ≤3.借助于数轴,如图所示,原不等式的解集为{x |-2≤x <-1或2<x ≤3}. (2)由x 2-4ax -5a 2>0知(x -5a )(x +a )>0. 由于a ≠0故分a >0与a <0讨论. 当a <0时,x <5a 或x >-a ; 当a >0时,x <-a 或x >5a .综上,a <0时,解集为{x |x <5a 或x >-a };a >0时,解集为{x |x >5a 或x <-a }. 热点二 一元二次不等式恒成立问题 考向1 形如f (x )≥0(x ∈R )恒成立问题【例2】 已知不等式mx 2-2x -m +1<0,是否存在实数m 对所有的实数x ,不等式恒成立?若存在,求出m 的取值范围;若不存在,请说明理由.【解】 不等式mx 2-2x -m +1<0恒成立,即函数f (x )=mx 2-2x -m +1的图象全部在x 轴下方.当m =0时,1-2x <0,则x >12,不满足题意;当m ≠0时,函数f (x )=mx 2-2x -m +1为二次函数,需满足开口向下且方程mx 2-2x -m +1=0无解,即⎩⎪⎨⎪⎧m <0,Δ=4-4m-m ,不等式组的解集为空集,即m 无解. 综上可知不存在这样的m .考向2 形如f (x )≥0(x ∈[a ,b ])恒成立问题【例3】 设函数f (x )=mx 2-mx -1(m ≠0),若对于x ∈[1,3],f (x )<-m +5恒成立,求m 的取值范围.【解】 要使f (x )<-m +5在[1,3]上恒成立,则mx 2-mx +m -6<0,即m ⎝ ⎛⎭⎪⎫x -122+34m -6<0在x ∈[1,3]上恒成立.有以下两种方法:解法1:令g (x )=m ⎝ ⎛⎭⎪⎫x -122+34m -6,x ∈[1,3].当m >0时,g (x )在[1,3]上是增函数, 所以g (x )max =g (3)=7m -6<0. 所以m <67,则0<m <67.当m <0时,g (x )在[1,3]上是减函数, 所以g (x )max =g (1)=m -6<0. 所以m <6.所以m <0. 综上所述,m 的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪0<m <67或m <0. 解法2:因为x 2-x +1=⎝ ⎛⎭⎪⎫x -122+34>0,又因为m (x 2-x +1)-6<0,所以m <6x 2-x +1.因为函数y =6x 2-x +1=6⎝ ⎛⎭⎪⎫x -122+34 在[1,3]上的最小值为67,所以只需m <67即可.因为m ≠0,所以m 的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪m <0或0<m <67 . 考向3 形如f (x )≥0(参数m ∈[a ,b ])恒成立问题【例4】 对任意m ∈[-1,1],函数f (x )=x 2+(m -4)x +4-2m 的值恒大于零,求x 的取值范围.【解】 由f (x )=x 2+(m -4)x +4-2m =(x -2)m +x 2-4x +4, 令g (m )=(x -2)m +x 2-4x +4.由题意知在[-1,1]上,g (m )的值恒大于零.∴⎩⎪⎨⎪⎧g -=x --+x 2-4x +4>0,g =x -+x 2-4x +4>0,解得x <1或x >3.故当x 的取值为(-∞,1)∪(3,+∞)时,对任意的m ∈[-1,1],函数f (x )的值恒大于零.函数f (x )=x 2+ax +3.(1)当x ∈R 时,f (x )≥a 恒成立,求实数a 的范围; (2)当x ∈[-2,2]时,f (x )≥a 恒成立,求实数a 的范围; (3)当a ∈[4,6]时,f (x )≥0恒成立,求实数x 的范围.解析:(1)∵x ∈R 时,有x 2+ax +3-a ≥0恒成立,须Δ=a 2-4(3-a )≤0,即a 2+4a -12≤0,所以-6≤a ≤2.(2)当x ∈[-2,2]时,设g (x )=x 2+ax +3-a ≥0,分如下三种情况讨论(如图所示): ①如图①,当g (x )的图象恒在x 轴上方时,满足条件时,有Δ=a 2-4(3-a )≤0,即-6≤a ≤2.②如图②,g (x )的图象与x 轴有交点, 但在x ∈[-2,+∞)时,g (x )≥0,即⎩⎪⎨⎪⎧Δ≥0,x =-a2<-2,g -,即⎩⎪⎨⎪⎧a 2--a,-a2<-2,4-2a +3-a ≥0⇔⎩⎪⎨⎪⎧a ≥2或a ≤-6,a >4,a ≤73,解之得x ∈∅.③如图③,g (x )的图象与x 轴有交点, 但在x ∈(-∞,2]时,g (x )≥0.即⎩⎪⎨⎪⎧Δ≥0,x =-a 2>2,g ,即⎩⎪⎨⎪⎧a 2--a,-a 2>2,7+a ≥0⇔⎩⎪⎨⎪⎧a ≥2或a ≤-6,a <-4,a ≥-7.∴-7≤a ≤-6,综上,得-7≤a ≤2.(3)令h (a )=xa +x 2+3.当a ∈[4,6]时,h (a )≥0恒成立.只需⎩⎪⎨⎪⎧h ,h,即⎩⎪⎨⎪⎧x 2+4x +3≥0,x 2+6x +3≥0,解之得x ≤-3-6或x ≥-3+ 6. 答案:(1)[-6,2] (2)[-7,2](3)(-∞,-3-6)∪[-3+6,+∞)1.二次项系数中含有参数时,则应先考虑二次项是否为零,然后再讨论二次项系数不为零时的情形,以便确定解集的形式.2.当Δ<0时,易混ax 2+bx +c >0(a >0)的解集为R 还是∅.3.解含参数的一元二次不等式,可先考虑因式分解,再对根的大小进行分类讨论;若不能因式分解,则可对判别式进行分类讨论,分类要不重不漏.4.对于恒成立问题,常用到以下两个结论:(1)a≥f(x)恒成立⇔a≥f(x)max;(2)a≤f(x)恒成立⇔a≤f(x)min.。
高三总复习数学优质课件 第六章 不等式 第2节 一元二次不等式及其解法

Δ=b -4ac
Δ>0
Δ=0
Δ<0
2
y=ax +bx+c(a>0)的图象
2
ax +bx+c=0(a>0)的根
有两相异实根
x1,x2(x1<x2)
有两相等实根
x1=x2=-
没有实数根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
{x|x>x2或x<x1} .
{x|x1<x<x2}
< ,
≥ ,
所以 f(x)>3⇔
或
- + > 3
+ > 3
≥ ,
< ,
≥ ,
< ,
⇔
或
⇔
或
⇒x>1.
(-)( + ) > - + < 0
< -或 >
∈⌀
所以原不等式的解集为{x|x>1}.
答案:{x|x>1}
6<0},则A∩B等于( B
)
(A)(-2,3)
(B)(1,3)
(C)(3,4)
(D)(-2,4)
解析:由题意知A={x|1<x<4},B={x|-2<x<3},
所以A∩B=(1,3).故选B.
3.不等式2x2-x-3>0的解集为
.
2
解析:由 2x -x-3>0,得(x+1)(2x-3)>0,
高考数学一轮复习第6章不等式第2讲一元二次不等式及其解法学案
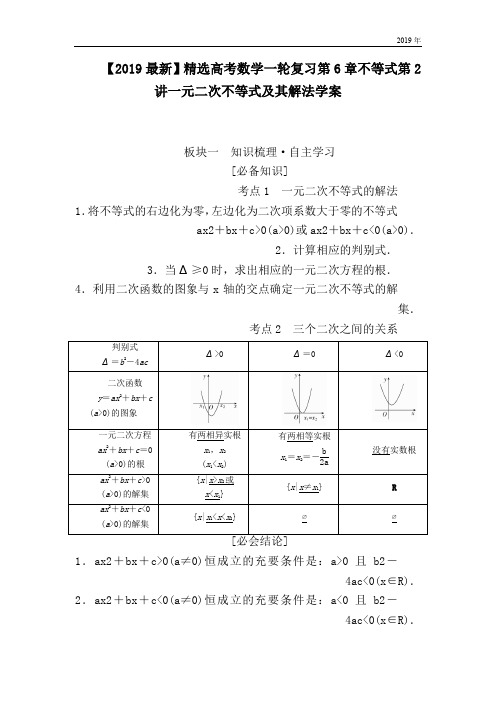
【2019最新】精选高考数学一轮复习第6章不等式第2讲一元二次不等式及其解法学案板块一知识梳理·自主学习[必备知识]考点1 一元二次不等式的解法1.将不等式的右边化为零,左边化为二次项系数大于零的不等式ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0).2.计算相应的判别式.3.当Δ≥0时,求出相应的一元二次方程的根.4.利用二次函数的图象与x轴的交点确定一元二次不等式的解集.考点2 三个二次之间的关系1.ax2+bx+c>0(a≠0)恒成立的充要条件是:a>0且b2-4ac<0(x∈R).2.ax2+bx+c<0(a≠0)恒成立的充要条件是:a<0且b2-4ac<0(x∈R).[考点自测]1.判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)若不等式ax2+bx +c<0的解集为(x1,x2),则必有a>0.( )(2)若不等式ax2+bx +c>0的解集是(-∞,x1)∪(x2,+∞),则方程ax2+bx +c =0的两个根是x1和x2.( )(3)若方程ax2+bx +c =0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R.( )(4)不等式ax2+bx +c≤0在R 上恒成立的条件是a<0且Δ=b2-4ac≤0.( )答案 (1)√ (2)√ (3)× (4)×2.[课本改编]不等式(x -1)(2-x)≥0的解集为( ) A .{x|1≤x≤2} B .{x|x≤1或x≥2} C .{x|1<x<2}D .{x|x<1或x>2}答案 A解析 因为(x -1)(2-x)≥0,所以(x -2)(x -1)≤0,所以结合二次函数的性质可得1≤x≤2.故选A.3.[2018·辽阳统考]不等式≤0的解集是( )A .(-∞,-1)∪(-1,2]B .[-1,2]C .(-∞,-1)∪[2,+∞)D .(-1,2] 答案 D解析 ≤0⇔(x +1)(x -2)≤0,且x≠-1,即x∈(-1,2].故选D.4.若不等式ax2+bx +c>0的解集为(-4,1),则不等式b(x2-1)+a(x +3)+c>0的解集为( )A.B .(-∞,1)∪⎝ ⎛⎭⎪⎫43,+∞ C .(-1,4)D .(-∞,-2)∪(1,+∞) 答案 A解析 由不等式ax2+bx +c>0的解集为(-4,1),知a<0且-4,1是方程ax2+bx +c =0的两根.∴-4+1=-,且-4×1=,即b =3a ,c =-4a.则所求不等式转化为3a(x2-1)+a(x +3)-4a>0, 即3x2+x -4<0,解得-<x<1.5.不等式(a -2)x2+2(a -2)x -4<0,对一切x∈R 恒成立,则实数a 的取值范围是( )A .(-∞,2]B .(-2,2]C .(-2,2)D .(-∞,2)答案 B解析 ∵∴-2<a<2,另a =2时,原式化为-4<0,不等式恒成立,∴-2<a≤2.故选B.板块二 典例探究·考向突破 考向 一元二次不等式的解法例 1 解下列关于x 的不等式:(1)0<x2-x -2≤4; (2)ax2-(a +1)x +1<0. 解 (1)原不等式等价于 ⎩⎪⎨⎪⎧ x2-x -2>0,x2-x -2≤4⇔⇔错误!⇔⎩⎪⎨⎪⎧x>2或x<-1,-2≤x≤3.借助于数轴,如图所示,原不等式的解集为{x|-2≤x<-1或2<x≤3}.(2)原不等式化为(ax -1)(x -1)<0.①当a =0时,其解为x>1; ②当0<a<1时,其解为1<x<; ③当a>1时,其解为<x<1;④当a =1时,无解;⑤当a<0时,不等式化为(x -1)>0,其解为x<或x>1.综上所述a =0时,不等式解集为{x|x>1};0<a<1时,不等式解集为;a>1时,不等式解集为;a<0时,不等式解集为;当a=1时,不等式解集为∅.触类旁通解含参数的一元二次不等式时分类讨论的依据(1)二次项中若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为一次不等式或二次项系数为正的形式.(2)当不等式对应方程的根的个数不确定时,讨论判别式Δ与0的关系.(3)确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集形式.【变式训练1】解不等式:(1)≥-1;(2)x2-(a2+a)x+a3>0.解(1)将原不等式移项通分得≥0,等价于错误!所以原不等式的解集为.(2)原不等式化为(x-a)(x-a2)>0,①当a2-a>0,即a>1或a<0时,原不等式的解为x>a2或x<a.②当a2-a<0,即0<a<1时,原不等式的解为x<a2或x>a;③当a2-a=0,即a=0或a=1时,原不等式的解为x≠a.综上①②③得a>1或a<0时不等式解集为{x|x>a2或x<a};当0<a<1时,不等式解集为{x|x<a2或x>a};当a=0或a=1时,不等式解集为{x|x≠a}.考向一元二次不等式恒成立问题例 2 [2018·正定模拟]已知函数f(x)=mx2-mx -1. (1)若对于x∈R,f(x)<0恒成立,求实数m 的取值范围; (2)若对于x∈[1,3],f(x)<5-m 恒成立,求实数m 的取值范围.解 (1)当m =0时,f(x)=-1<0恒成立.当m≠0时,则即-4<m<0.综上,-4<m≤0,故m 的取值范围是(-4,0].(2)不等式f(x)<5-m ,即(x2-x +1)m<6, ∵x2-x +1>0,∴m<对于x ∈[1,3]恒成立, 只需求的最小值,记g(x)=,x∈[1,3],记h(x)=x2-x +1=2+,h(x)在x∈[1,3]上为增函数,则g(x)在[1,3]上为减函数,∴[g(x)]min =g(3)=,∴m<.所以m 的取值范围是.本例中(1)变为:若f(x)<0对于m∈[1,2]恒成立,求实数x 的取值范围.解 设g(m)=mx2-mx -1=(x2-x)m -1,其图象是直线,当m∈[1,2]时,图象为一条线段,则即⎩⎪⎨⎪⎧x2-x -1<0,2x2-2x -1<0,解得<x<,故x 的取值范围为.本例中(2)条件“f(x)<5-m 恒成立”改为“f(x)<5-m 无解”,如何求m 的取值范围?解 若f(x)<5-m 无解,即f(x)≥5-m 恒成立,即m≥恒成立,又x∈[1,3],得m≥6,即m 的取值范围为[6,+∞).本例中(2)条件“f(x)<5-m 恒成立”改为“存在x ,使f(x)<5-m 成立”,如何求m 的取值范围.解 由题知f(x)<5-m 有解,即m<有解,则m<max ,又x∈[1,3],得m<6,即m 的取值范围为(-∞,6).触类旁通解决一元二次不等式恒成立问题的方法(1)对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x 轴上方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x 轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.(2)解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.【变式训练2】 (1)[2018·九江模拟]若关于x 的不等式x2-4x-2-a>0在区间(1,4)内有解,则实数a 的取值范围是( )A .(-∞,-2)B .(-2,+∞)C .(-6,+∞)D .(-∞,-6)答案 A解析 不等式x2-4x -2-a>0在区间(1,4)内有解等价于a<(x2-4x -2)max ,令g(x)=x2-4x -2,x∈(1,4),∴g(x)<g(4)=-2,∴a<-2.(2)若关于x 的不等式ax2-x +2a<0的解集为∅,则实数a 的取值范围是________.答案 ⎣⎢⎡⎭⎪⎫24,+∞ 解析 依题意可知,问题等价于ax2-x +2a≥0恒成立,当a =0时,-x≥0不恒成立;当a≠0时,要使ax2-x +2a≥0恒成立, 即f(x)=ax2-x +2a 的图象不在x 轴的下方,∴即⎩⎪⎨⎪⎧a>0,1-8a2≤0,解得a≥,即a的取值范围是.核心规律1.“三个二次”的关系是解一元二次不等式的理论基础,一般可把a<0时的情形转化为a>0时的情形.2.f(x)>0的解集即为函数y=f(x)的图象在x轴上方的点的横坐标的集合,充分利用数形结合思想.3.简单的分式不等式可以等价转化,利用一元二次不等式解法进行求解.满分策略1.对于不等式ax2+bx+c>0,求解时不要忘记讨论a=0时的情形.2.当Δ<0时,ax2+bx+c>0(a≠0)的解集为R还是∅由a确定,要注意区别.3.含参数的不等式要注意选好分类标准,避免盲目讨论.板块三 启智培优·破译高考数学思想系列7——转化与化归思想在不等式中的应用[2018·江苏模拟]已知函数f(x)=x2+ax +b(a ,b∈R)的值域为[0,+∞),若关于x 的不等式f(x)<c 的解集为(m ,m +6),则实数c 的值为________.解题视点 利用“三个二次”之间的关系,将不等式、函数、方程之间相互转化.解析 由题意知f(x)=x2+ax +b=2+b -.∵f(x)的值域为[0,+∞), ∴b -=0,即b =,∴f(x)=2.又∵f(x)<c,∴2<c,即--<x<-+.∴⎩⎪⎨⎪⎧-a2-c =m , ①-a2+c =m +6. ②②-①得2=6,∴c =9.答案 9答题启示 1本题的解法充分体现了转化与化归思想:函数的值域和不等式的解集转化为a ,b 满足的条件;不等式恒成立可以分离常数,转化为函数值域问题.()(2注意函数fx 的值域为[0,+∞与fx≥0的区别.)())() 跟踪训练若不等式a·4x-2x +1>0对一切x∈R 恒成立,则实数a 的取值范围是________.答案 a>14解析 不等式可变形为a>=x -x , 令x =t ,则t>0.∴y =x -x =t -t2=-2+,因此当t =时,y 取最大值,故实数a 的取值范围是a>.板块四 模拟演练·提能增分[A 级 基础达标]1.[2018·潍坊模拟]函数f(x)=的定义域是( )A .(-∞,1)∪(3,+∞)B .(1,3)C .(-∞,2)∪(2,+∞)D .(1,2)∪(2,3) 答案 D解析由题意知即⎩⎪⎨⎪⎧1<x<3,x≠2, 故函数f(x)的定义域为(1,2)∪(2,3).2.关于x 的不等式x2+px -2<0的解集是(q,1),则p +q 的值为( )A .-2B .-1C .1D .2答案 B解析 依题意得q,1是方程x2+px -2=0的两根,q +1=-p ,即p +q =-1.选B.3.[2018·郑州模拟]已知关于x 的不等式>0的解集是(-∞,-1)∪,则a 的值为( ) A .-1 B. C .1 D .2答案 D解析 由题意可得a≠0且不等式等价于a(x +1)x ->0,由解集的特点可得a>0且=,故a =2.故选D.4.[2018·福建模拟]若集合A ={x|ax2-ax +1<0}=∅,则实数a 的取值范围是( )A .(0,4)B .[0,4)C .(0,4]D .[0,4]答案 D解析 由题意知a =0时,满足条件.a≠0时,由得0<a≤4,所以实数a 的取值范围是[0,4].5.[2018·梧州模拟]不等式<1的解集是( )A .(-∞,-1)∪(1,+∞)B .(1,+∞)C .(-∞,-1)D .(-1,1) 答案 A解析 ∵<1,∴-1<0,即<0,该不等式可化为(x +1)(x -1)>0,∴x<-1或x>1.6.不等式(2x -1)(1-|x|)<0成立的充要条件是( )A .x>1或x<B .x>1或-1<x<12 C .-1<x< D .x<-1或x>12答案 B解析原不等式等价于或⎩⎪⎨⎪⎧2x -1<0,1-|x|>0. ∴或⎩⎪⎨⎪⎧x<12,-1<x<1.∴x>1或-1<x<.故选B.7.[2018·重庆模拟]关于x 的不等式x2-2ax -8a2<0(a>0)的解集为(x1,x2),且x2-x1=15,则a =( )A. B. C. D.152答案 A解析 由条件知x1,x2为方程x2-2ax -8a2=0的两根,则x1+x2=2a ,x1x2=-8a2.故(x2-x1)2=(x1+x2)2-4x1x2=(2a)2-4×(-8a2)=36a2=152,得a =.故选A.8.[2018·青岛模拟]不等式2x2-3|x|-35>0的解集为________.答案 {x|x<-5或x>5}解析 2x2-3|x|-35>0⇔2|x|2-3|x|-35>0⇔(|x|-5)(2|x|+7)>0⇔|x|>5或|x|<-(舍)⇔x>5或x<-5.9.已知关于x 的不等式ax2+2x +c>0的解集为,则不等式-cx2+2x -a>0的解集为________.答案 (-2,3)解析 依题意知,⎩⎪⎨⎪⎧-13+12=-2a ,-13×12=c a , ∴解得a =-12,c =2,∴不等式-cx2+2x -a>0,即为-2x2+2x +12>0,即x2-x -6<0,解得-2<x<3.所以不等式的解集为(-2,3).10.对于任意a∈[-1,1],f(x)=x2+(a -4)x +4-2a 的值恒大于0,那么x 取值范围是________.答案 (-∞,1)∪(3,+∞)解析 令g(a)=x2+(a -4)x +4-2a =(x -2)a +x2-4x +4,由题意得g(-1)>0且g(1)>0,即解得x<1或x>3.[B 级 知能提升]1.[2018·保定模拟]若不等式x2+ax -2>0在区间[1,5]上有解,则a 的取值范围是( )A. B.⎣⎢⎡⎦⎥⎤-235,1 C .(1,+∞)D.⎝ ⎛⎦⎥⎤-∞,-235 答案 A解析 由Δ=a2+8>0,知方程恒有两个不等实根,又知两根之积为负,所以方程必有一正根、一负根.于是不等式在区间[1,5]上有解,只需满足f(5)>0,即a>-.2.[2018·辽宁模拟]若不等式2kx2+kx -<0对一切实数x 都成立,则k 的取值范围为( )A .(-3,0)B .[-3,0)C .[-3,0]D .(-3,0] 答案 D解析 当k =0时,显然成立;当k≠0时,即一元二次不等式2kx2+kx-<0对一切实数x都成立,则解得-3<k<0.综上,满足不等式2kx2+kx-<0对一切实数x都成立的k的取值范围是(-3,0].3.[2018·西安质检]在R上定义运算:=ad-bc.若不等式≥1对任意实数x恒成立,则实数a的最大值为________.答案32解析原不等式等价于x(x-1)-(a-2)(a+1)≥1,即x2-x-1≥(a+1)(a-2)对任意x恒成立,x2-x-1=2-≥-,所以-≥a2-a-2,解得-≤a≤.4.[2018·池州模拟]已知函数f(x)=的定义域为R.(1)求a的取值范围;(2)若函数f(x)的最小值为,解关于x的不等式x2-x-a2-a<0.解(1)∵函数f(x)=的定义域为R,∴ax2+2ax+1≥0恒成立,当a=0时,1≥0恒成立.当a≠0时,则有解得0<a≤1,综上,a的取值范围是[0,1].(2)∵f(x)==,∵a>0,∴当x=-1时,f(x)min=,由题意,得=,∴a=.∴x2-x-2-<0,即(2x+1)(2x-3)<0,-<x<.故不等式的解集为. 5.已知函数f(x)=ax2+(b-8)x-a-ab,当x∈(-∞,-3)∪(2,+∞)时,f(x)<0.当x∈(-3,2)时,f(x)>0.(1)求f(x)在[0,1]内的值域;(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.解(1)因为当x∈(-∞,-3)∪(2,+∞)时,f(x)<0,当x∈(-3,2)时,f(x)>0,所以-3,2是方程ax2+(b -8)x -a -ab =0的两根,可得所以a=-3,b =5,f(x)=-3x2-3x +18=-32+18.75,函数图象关于x =-对称,且抛物线开口向下,所以在区间[0,1]上f(x)为减函数,所以函数的最大值为f(0)=18,最小值为f(1)=12,故f(x)在[0,1]内的值域为[12,18].(2)由(1)知,不等式ax2+bx +c≤0化为-3x2+5x +c≤0,因为二次函数y =-3x2+5x +c 的图象开口向下,要使-3x2+5x +c≤0的解集为R ,只需⎩⎪⎨⎪⎧a =-3<0,Δ=b2-4ac≤0, 即25+12c≤0⇒c≤-,所以实数c 的取值范围为.。
通用版2022届高考数学一轮总复习第六章不等式第2讲一元二次不等式及其解法课件

综上所述,k≥1 时,不等式的解集为∅; 0<k<1 时,
不等式的解集为x1-
题组二 走进教材 2.( 必修 5P78 例 2 改编)不等式-x2+2x-3>0 的解集为 ________. 解析:不等式-x2+2x-3>0 化简得 x2-2x+3<0,因为 Δ=-8<0,所以原不等式的解集为∅. 答案:∅
3.(必修 5P104 第 3 题改编)若关于 x 的不等式-12x2+2x>mx 的解集为{x|0<x<2},则 m=________.
解析:不等式-12x2+2x>mx 化简得 x2+2(m-2)x<0,其解 集为{x|0<x<2},则 x=0 或 x=2 是方程 x2+2(m-2)x=0 的根, 代入得 m=1.
答案:1
题组三 真题展现
4.(2018 年全国Ⅰ)已知集合 A={x|x2-x-2>0},则∁RA=
()
A.{x|-1<x<2}
1<0.
令 g(m)=(x2-x)m-1,m∈[-1,1].
则gg- 1<10<,0, 即- x2-x2+ x-x- 1<10<. 0,
解得1-2
5 1+ <x< 2
5 .
则实数 x 的取值范围为1-2 5,1+2 5.
【策略指导】一元二次不等式恒成立问题:
(1)在 R 上恒成立.
①一元二次不等式 ax2+bx+c>0(或≥0)对于一切 x∈R 恒
高考数学一轮复习 第六章 不等式、推理与证明 第二节 一元二次不等式及其解法学案 文

第二节一元二次不等式及其解法1.会从实际问题的情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.知识点一一元二次不等式的解法{x|x<x1或x>x2} {x|x≠-b2a }{x |x 1<x <x 2} ∅ ∅1.(2016·新课标全国卷Ⅲ)设集合S ={x |(x -2)(x -3)≥0},T ={x |x >0},则S ∩T =( )A .[2,3]B .(-∞,2]∪[3,+∞)C .[3,+∞)D .(0,2]∪[3,+∞)解析:集合S =(-∞,2]∪[3,+∞),结合数轴,可得S ∩T =(0,2]∪[3,+∞). 答案:D2.不等式x -12x +1≤0的解集为( )A.⎝ ⎛⎦⎥⎤-12,1B.⎣⎢⎡⎦⎥⎤-12,1 C.⎝⎛⎭⎪⎫-∞,-12∪[1,+∞) D.⎝⎛⎦⎥⎤-∞,-12∪[1,+∞) 解析:由数轴标根法可知原不等式的解集为⎝ ⎛⎦⎥⎤-12,1,选A.答案:A3.设一元二次不等式ax 2+bx +1>0的解集为{x |-1<x <2},则ab 的值为( ) A .1 B .-14C .4D .-12解析:因为一元二次不等式ax 2+bx +1>0的解集为 {x |-1<x <2}.所以方程ax 2+bx +1=0的解为-1,2.所以-1+2=-b a,(-1)×2=1a.所以a =-12,b =12,所以ab =-14.答案:B知识点二 一元二次不等式恒成立的条件 1.ax 2+bx +c >0(a ≠0)恒成立的充要条件是:______ (x ∈R ).2.ax 2+bx +c <0(a ≠0)恒成立的充要条件是:______ (x ∈R ).答案1.⎩⎪⎨⎪⎧a >0Δ<0 2.⎩⎪⎨⎪⎧a <0Δ<04.若不等式mx 2+2mx +1>0的解集为R ,则m 的取值范围是________. 解析:①当m =0时,1>0显然成立. ②当m ≠0时,由条件知⎩⎪⎨⎪⎧m >0,Δ=4m 2-4m <0.得0<m <1,由①②知0≤m <1. 答案:[0,1)5.不等式x 2+ax +4<0的解集不是空集,则实数a 的取值范围是________. 解析:∵不等式x 2+ax +4<0的解集不是空集,∴Δ=a 2-4×4>0,即a 2>16, ∴a >4或a <-4.答案:(-∞,-4)∪(4,+∞)热点一 一元二次不等式的解法 【例1】 解关于x 的不等式: (1)-2x 2+4x -3>0; (2)12x 2-ax >a 2(a ∈R );(3)a x -x -2>1(a >0).【解】 (1)原不等式可化为2x 2-4x +3<0.又判别式Δ=42-4×2×3<0, ∴原不等式的解集为∅.(2)由12x 2-ax -a 2>0⇒(4x +a )(3x -a )>0⇒(x +a 4)(x -a3)>0,①当a >0时,-a 4<a 3,解集为{x |x <-a 4或x >a3};②当a =0时,x 2>0,解集为{x |x ∈R 且x ≠0}; ③当a <0时,-a 4>a 3,解集为{x |x <a 3或x >-a4}. (3)a x -x -2-1>0⇒a -x +2-a x -2>0⇒[(a -1)x +2-a ](x -2)>0.①当a =1时,不等式的解为x >2. ②当a ≠1时,关键是(a -1)的符号和比较a -2a -1与2的大小. ∵a -2a -1-2=-aa -1,又a >0. ∴当0<a <1时,a -2a -1>2, 不等式的解为2<x <a -2a -1; 当a >1时,a -2a -1<2, 不等式的解为x <a -2a -1或x >2. 综上所述,当0<a <1时,原不等式的解集为{x |2<x <a -2a -1};当a =1,原不等式的解集为{x |x >2};当a >1时,原不等式的解集为{x |x <a -2a -1或x >2}.解下列不等式: (1)0<x 2-x -2≤4; (2)x 2-4ax -5a 2>0(a ≠0). 解:(1)原不等式等价于⎩⎪⎨⎪⎧x 2-x -2>0,x 2-x -2≤4⇔⎩⎪⎨⎪⎧x 2-x -2>0,x 2-x -6≤0⇔⎩⎪⎨⎪⎧x -x +,x -x +⇔⎩⎪⎨⎪⎧x >2或x <-1,-2≤x ≤3.借助于数轴,如图所示,原不等式的解集为{x |-2≤x <-1或2<x ≤3}. (2)由x 2-4ax -5a 2>0知(x -5a )(x +a )>0. 由于a ≠0故分a >0与a <0讨论. 当a <0时,x <5a 或x >-a ; 当a >0时,x <-a 或x >5a .综上,a <0时,解集为{x |x <5a 或x >-a };a >0时,解集为{x |x >5a 或x <-a }. 热点二 一元二次不等式恒成立问题 考向1 形如f (x )≥0(x ∈R )恒成立问题【例2】 已知不等式mx 2-2x -m +1<0,是否存在实数m 对所有的实数x ,不等式恒成立?若存在,求出m 的取值范围;若不存在,请说明理由.【解】 不等式mx 2-2x -m +1<0恒成立,即函数f (x )=mx 2-2x -m +1的图象全部在x 轴下方.当m =0时,1-2x <0,则x >12,不满足题意;当m ≠0时,函数f (x )=mx 2-2x -m +1为二次函数,需满足开口向下且方程mx 2-2x -m +1=0无解,即⎩⎪⎨⎪⎧m <0,Δ=4-4m-m ,不等式组的解集为空集,即m 无解. 综上可知不存在这样的m .考向2 形如f (x )≥0(x ∈[a ,b ])恒成立问题【例3】 设函数f (x )=mx 2-mx -1(m ≠0),若对于x ∈[1,3],f (x )<-m +5恒成立,求m 的取值范围.【解】 要使f (x )<-m +5在[1,3]上恒成立,则mx 2-mx +m -6<0,即m ⎝ ⎛⎭⎪⎫x -122+34m -6<0在x ∈[1,3]上恒成立.有以下两种方法:解法1:令g (x )=m ⎝ ⎛⎭⎪⎫x -122+34m -6,x ∈[1,3].当m >0时,g (x )在[1,3]上是增函数, 所以g (x )max =g (3)=7m -6<0. 所以m <67,则0<m <67.当m <0时,g (x )在[1,3]上是减函数, 所以g (x )max =g (1)=m -6<0. 所以m <6.所以m <0. 综上所述,m 的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪0<m <67或m <0. 解法2:因为x 2-x +1=⎝ ⎛⎭⎪⎫x -122+34>0,又因为m (x 2-x +1)-6<0,所以m <6x 2-x +1.因为函数y =6x 2-x +1=6⎝ ⎛⎭⎪⎫x -122+34 在[1,3]上的最小值为67,所以只需m <67即可.因为m ≠0,所以m 的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫m ⎪⎪⎪m <0或0<m <67 . 考向3 形如f (x )≥0(参数m ∈[a ,b ])恒成立问题【例4】 对任意m ∈[-1,1],函数f (x )=x 2+(m -4)x +4-2m 的值恒大于零,求x 的取值范围.【解】 由f (x )=x 2+(m -4)x +4-2m =(x -2)m +x 2-4x +4, 令g (m )=(x -2)m +x 2-4x +4.由题意知在[-1,1]上,g (m )的值恒大于零.∴⎩⎪⎨⎪⎧g -=x --+x 2-4x +4>0,g =x -+x 2-4x +4>0,解得x <1或x >3.故当x 的取值为(-∞,1)∪(3,+∞)时,对任意的m ∈[-1,1],函数f (x )的值恒大于零.函数f (x )=x 2+ax +3.(1)当x ∈R 时,f (x )≥a 恒成立,求实数a 的范围; (2)当x ∈[-2,2]时,f (x )≥a 恒成立,求实数a 的范围; (3)当a ∈[4,6]时,f (x )≥0恒成立,求实数x 的范围.解析:(1)∵x ∈R 时,有x 2+ax +3-a ≥0恒成立,须Δ=a 2-4(3-a )≤0,即a 2+4a -12≤0,所以-6≤a ≤2.(2)当x ∈[-2,2]时,设g (x )=x 2+ax +3-a ≥0,分如下三种情况讨论(如图所示): ①如图①,当g (x )的图象恒在x 轴上方时,满足条件时,有Δ=a 2-4(3-a )≤0,即-6≤a ≤2.②如图②,g (x )的图象与x 轴有交点, 但在x ∈[-2,+∞)时,g (x )≥0,即⎩⎪⎨⎪⎧Δ≥0,x =-a2<-2,g -,即⎩⎪⎨⎪⎧a 2--a,-a2<-2,4-2a +3-a ≥0⇔⎩⎪⎨⎪⎧a ≥2或a ≤-6,a >4,a ≤73,解之得x ∈∅.③如图③,g (x )的图象与x 轴有交点, 但在x ∈(-∞,2]时,g (x )≥0.即⎩⎪⎨⎪⎧Δ≥0,x =-a 2>2,g ,即⎩⎪⎨⎪⎧a 2--a,-a 2>2,7+a ≥0⇔⎩⎪⎨⎪⎧a ≥2或a ≤-6,a <-4,a ≥-7.∴-7≤a ≤-6,综上,得-7≤a ≤2.(3)令h (a )=xa +x 2+3.当a ∈[4,6]时,h (a )≥0恒成立.只需⎩⎪⎨⎪⎧h ,h,即⎩⎪⎨⎪⎧x 2+4x +3≥0,x 2+6x +3≥0,解之得x ≤-3-6或x ≥-3+ 6. 答案:(1)[-6,2] (2)[-7,2](3)(-∞,-3-6)∪[-3+6,+∞)1.二次项系数中含有参数时,则应先考虑二次项是否为零,然后再讨论二次项系数不为零时的情形,以便确定解集的形式.2.当Δ<0时,易混ax 2+bx +c >0(a >0)的解集为R 还是∅.3.解含参数的一元二次不等式,可先考虑因式分解,再对根的大小进行分类讨论;若不能因式分解,则可对判别式进行分类讨论,分类要不重不漏.4.对于恒成立问题,常用到以下两个结论:(1)a≥f(x)恒成立⇔a≥f(x)max;(2)a≤f(x)恒成立⇔a≤f(x)min.。
高考数学一轮复习 第六章 不等式 第2讲 一元二次不等式及其解法课时作业 理
第2讲 一元二次不等式及其解法1.(2016年湖北模拟)若关于x 的不等式ax -b >0的解集是(-∞,1),则关于x 的不等式(ax +b )(x -3)>0的解集是( )A .(-∞,-1)∪(3,+∞)B .(-1,3)C .(1,3)D .(-∞,1)∪(3,+∞)2.如果kx 2+2kx -(k +2)<0恒成立,那么实数k 的取值范围是( ) A .-1≤k ≤0 B .-1≤k <0 C .-1<k ≤0 D .-1<k <03.已知函数f (x )=⎩⎪⎨⎪⎧x +2,x ≤0,-x +2,x >0,则不等式f (x )≥x 2的解集是( )A .[-1,1]B .[-2,2]C .[-2,1]D .[-1,2]4.(2016年江西九江一模)若关于x 的不等式x 2-4x -2-a >0在区间(1,4)内有解,则实数a 的取值范围是( )A .(-∞,-2)B .(-2,+∞)C .(-6,+∞) D.(-∞,-6)5.已知不等式x 2-2x -3<0的解集为A ,不等式x 2+x -6<0的解集为B ,不等式x 2+ax +b <0的解集是A ∩B ,则a +b =( )A .-3B .1C .-1D .36.已知f (x )是定义域为R 的偶函数,当x ≤0时,f (x )=x 2+2x ,则不等式f (x +2)<3的解集是_________.7.已知a ∈Z ,关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则所有符合条件的a 的值之和是________.8.不等式ax 2+bx +c >0的解集为⎝ ⎛⎭⎪⎫-13,2,对于系数a ,b ,c ,有如下结论:①a <0;②b >0;③c >0;④a +b +c >0;⑤a -b +c >0.其中正确的结论的序号是________.9.(2016年北京朝阳统一考试)已知函数f (x )=x 2-2ax -1+a ,a ∈R .(1)若a =2,试求函数y =f xx(x >0)的最小值; (2)对于任意的x ∈[0,2],不等式f (x )≤a 成立,试求a 的取值范围.10.设f (x )=ax 2+bx +c ,若f (1)=72,问是否存在a ,b ,c ∈R ,使得不等式x 2+12≤f (x )≤2x 2+2x +32对一切实数x 都成立?证明你的结论.第2讲 一元二次不等式及其解法1.B 解析:由题意关于x 的不等式ax -b >0的解集是(-∞,1),可得ba=1,且a <0.则(ax +b )(x -3)>0可变形为(x -3)⎝⎛⎭⎪⎫x +b a <0,即得(x -3)(x +1)<0.所以-1<x <3.所以不等式的解集是(-1,3).故选B.2.C 解析:当k =0时,原不等式等价于-2<0,显然恒成立,∴k =0符合题意.当k ≠0时,由题意,得⎩⎪⎨⎪⎧k <0,k 2-4k ·[-k +<0.解得-1<k <0.∴-1<k ≤0. 3.A 解析:依题意,得⎩⎪⎨⎪⎧x ≤0,x +2≥x2或⎩⎪⎨⎪⎧x >0,-x +2≥x2⇒-1≤x ≤0或0<x ≤1⇒-1≤x ≤1.4.A 解析:不等式x 2-4x -2-a >0在区间(1,4)内有解等价于a <(x 2-4x -2)max .令g (x )=x 2-4x -2,x ∈(1,4),∴g (x )<g (4)=-2.∴a <-2.5.A 解析:由题意,得A ={x |-1<x <3},B ={x |-3<x <2}.A ∩B ={x |-1<x <2},由根与系数的关系可知,a =-1,b =-2.∴a +b =-3.6.{x |-5<x <1} 解析:设x ≥0,因为f (x )是定义域为R 的偶函数,所以f (x )=f (-x )=x 2-2x .又f (x +2)=f (|x +2|),所以f (x +2)<3⇔f (|x +2|)=(|x +2|)2-2|x +2|<3.所以(|x +2|-3)(|x +2|+1)<0.所以0≤|x +2|<3,解得-5<x <1.所以原不等式的解集为{x |-5<x <1}.7.21 解析:设f (x )=x 2-6x +a ,其图象是开口向上,对称轴是x =3的抛物线,图象如图D115.图D115关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则⎩⎪⎨⎪⎧f ,f>0即⎩⎪⎨⎪⎧f =4-12+a ≤0,f =1-6+a >0,解得5<a ≤8.又a ∈Z ,所以a =6,7,8,则所有符合条件的a 的值之和是6+7+8=21.8.①②③④ 解析:∵不等式ax 2+bx +c >0的解集为⎝ ⎛⎭⎪⎫-13,2,∴a <0;-13,2是方程ax 2+bx +c =0的两根,-13+2=-b a>0,∴b >0;f (0)=c >0,f (1)=a +b +c >0,f (-1)=a -b +c <0.故正确结论的序号为①②③④.9.解:(1)依题意,得y =f x x =x 2-4x +1x =x +1x-4.因为x >0,所以x +1x≥2,当且仅当x =1x,即x =1时,等号成立,所以y ≥-2.所以当x =1时,y =f xx 的最小值为-2. (2)因为f (x )-a =x 2-2ax -1,所以要使得“∀x ∈[0,2],不等式f (x )≤a 成立”只要“x 2-2ax -1≤0在[0,2]上恒成立”.不妨设g (x )=x 2-2ax -1,则只要g (x )≤0在[0,2]上恒成立即可.所以⎩⎪⎨⎪⎧ g ,g 即⎩⎪⎨⎪⎧0-0-1≤0,4-4a -1≤0.解得a ≥34.故a 的取值范围为⎣⎢⎡⎭⎪⎫34,+∞. 10.解:由f (1)=72,得a +b +c =72.令x 2+12=2x 2+2x +32⇒x =-1.由f (x )≤2x 2+2x +32推得f (-1)≤32.由f (x )≥x 2+12推得f (-1)≥32.∴f (-1)=32.∴a -b +c =32.故a +c =52,且b =1.∴f (x )=ax 2+x +52-a .依题意ax 2+x +52-a ≥x 2+12对一切x ∈R 都成立,∴a ≠1,且Δ=1-4(a -1)(2-a )≤0.由a -1>0,得a =32.∴f (x )=32x 2+x +1.证明如下: ∵32x 2+x +1-2x 2-2x -32 =-12x 2-x -12=-12(x +1)2≤0.∴32x 2+x +1≤2x 2+2x +32对x ∈R 都成立. ∴存在实数a =32,b =1,c =1,使得不等式x 2+12≤f (x )≤2x 2+2x +32对一切x ∈R 都成立.。
高考数学 第六章 第二节 一元二次不等式及其解法课件 文
(2)由 x2-4ax-5a2>0 知(x-5a)(x+a)>0.
由于 a≠0 故分 a>0 与 a<0 讨论.
当 a<0 时,x<5a 或 x>-a;
当 a>0 时,x<-a 或 x>5a.
综上,a<0
时,解集为x|x<
5a,或x>-a;a>0
时,解
集为x|x>5a,或x<-a.
当 a=1 时,解集为∅;
当 0<a<1 时,解为 1<x<1a.
综上,当 0<a<1 时,不等式的解集为x1<x<1a
;
当 a=1 时,不等式的解集为∅;
当 a>1 时,不等式的解集为x1a<x<1
.
第六页,共14页。
[例 2] 解:法一:f(x)=(x-a)2+2-a2,此二次函数图象的 对称轴为 x=a. ①当 a∈(-∞,-1) 时,f(x)在[-1,+∞)上单调递增,f(x)min =f(-1)=2a+3. 要使 f(x)≥a 恒成立,只需 f(x)min≥a,即 2a+3≥a,解得-3≤a <-1; ②当 a∈[-1,+∞)时,f(x)min=f(a)=2-a2,由 2-a2≥a, 解得-1 ≤a≤1. 综上所述,a 的取值范围为[-3,1].
第十二页,共14页。
高分障障碍要破除 [针对训练 1] 选 C ∵x2+ax+1≥0,在 x∈0,12时恒 成立, ∴a≥-x-1x. 又-x-1x=-x+1x≤-52, ∴a≥-52,即 amin=-52.
第十三页,共14页。
[针对训练 2] 选 C 函数图象恒在 x 轴上方,即不等式 (a2+4a-5)x2-4(a-1)x+3>0 对于一切 x∈R 恒成立. ①当 a2+4a-5=0 时,有 a=-5 或 a=1.若 a=-5,不等式 化为 24x+3>0,不满足题意;若 a=1,不等式化为 3>0,满 足题意. ②当 a2+4a-5≠0 时,应有 a2+4a-5>0, 16a-12-12a2+4a-5<0. 解得 1<a<19. 综上可知,a 的取值范围是 1≤a<19.
高考数学复习第六章不等式推理与证明第2节一元二次不等式及其解法市赛课公开课一等奖省名师优质课获奖PP
即-6 000x2+2 000x>0 0<x<1
解得 0<x<13,
所以投入成本增加的比例应在0,13范围内.
30/35
求解不等式应用题的四个步骤
31/35
[跟踪训练] (导学号 14576475)某农贸公司按每担 200 元收购某农产品,并每 100 元纳税 10 元(又称征税率为 10 个百分点),计划可收购 a 万担, 政府为了鼓励收购公司多收购这种农产品,决定将征税率降低 x(x≠0) 个百分点,预测收购量可增加 2x 个百分点. (1)写出降税后税收 y(万元)与 x 的函数关系式; (2)要使此项税收在税率调节后,不少于原计划税收的 83.2%,试 确定 x 的取值范围.
5/35
[思考辨析]
判断下列说法是否正确,正确的在它后面的括号里打“√”,
错误的打“×”.
(1)若不等式 ax2+bx+c<0 的解集为(x1,x2),则必有 a>0.(
)
(2)若不等式 ax2+bx+c>0 的解集是(-∞,x1)∪(x2,+∞),则
方程 ax2+bx+c=0 的两个根是 x1 和 x2.(
解析:由题意,知 Δ=4-4×1×(k2-1)<0, 即 k2>2,∴k> 2或 k<- 2. 答案:(-∞,- 2)∪( 2,+∞)
12/35
考点一 一元二次不等式的解法(自主练透) (导学号 14576469)解关于 x 的不等式: (1)x2+3x+4<0; (2)-3x2-2x+8≤0; (3)ax2-(a+1)x+1<0.
13/35
解:(1)由 Δ=9-16=-7<0,故不等式的解集为∅. (2)原不等式等价于 3x2+2x-8≥0⇔(x+2)(3x-4)≥0⇔x≤-2 或 x≥43, 故不等式的解集为x|x≤-2或x≥43.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
亿库教育网 http://www.eku.cc 亿库教育网 http://www.eku.cc 第2课 一元二次不等式 【考点导读】 1. 会解一元二次不等式,了解一元二次不等式与相应函数、方程之间的联系和转化。 2. 能运用一元二次不等式解决综合性较强的问题. 【基础练习】
1.解不等式:
(1)23440xx解 (2)213022xx (3)21322xxxx (4)2232142xx 解:(1)原不等式化为23440xx,解集为223x (2)原不等式化为2230xx,解集为R (3)原不等式化为210xx,解集为
(4)由22222134210132224,,1322250222xxxxxxxxxx得得 得2121,6161xxx或 (61,21)(21,61)x 点拨:解一元二次不等式要注意二次项系数的符号、对应方程的判断、以及对应方程两根大小的比较.
2. 函数)1(log221xy的定义域为 2,11,2
3..二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
则不等式ax2+bx+c>0的解集是),3()2,( 4.若不等式02cbxx的解集是}13{xxx或,则b=__-2____ c=__-3____.
x -3 -2 -1 0 1 2 3 4
y 6 0 -4 -6 -6 -4 0 6 亿库教育网 http://www.eku.cc 亿库教育网 http://www.eku.cc 5.关于x的不等式axax210的解集是空集,那么a的取值区间是[0,4] 【范例导析】
【例1】已知关于x的不等式(m-2)x 2-mx-1≥0的解集为[x 1,x 2]且1≤|x1-x 2|≤3,求实数m的取值范围.
分析: a应满足三个条件: ①m-2<0,保证抛物线y=(m-2)x 2-mx-1开口向下, ②其判别式Δ≥0,
③1≤|x1-x2|=||42aacb≤3 解: 令y=(m-2)x 2-mx-1
则由3||100221xxm3|2|)2(410)2(4222mmmmmm233222322mmmm或23≤m<2 点拨:通过二次函数的图像特点,寻找m的满足的充要条件,是数学中“等价转化”思想的体现.
例2.设f(x)=ax2+bx+c,若f(1)=27,问是否存在a、b、c∈R,使得不等式:
x2+21≤f(x)≤2x2+2x+23对一切实数x都成立,证明你的结论.
分析:抓住特殊状态寻找解题突破口. 解:由f(1)=27得a+b+c=27,令x2+21=2x2+2x+23xx=-1,由f(x)≤2x2+2x+23推得 f(-1)≤23.
由f(x)≥x2+21推得f(-1)≥23,∴f(-1)=23,∴a-b+c=23,故 2(a+c)=5,a+c=25且b=1,∴f(x)=ax2+x+(25-a). 依题意:ax2+x+(25-a)≥x2+21对一切x∈R成立, ∴a≠1且Δ=1-4(a-1)(2-a)≤0,得(2a-3)2≤0, ∴f(x)=23x2+x+1
易验证:23x2+x+1≤2x2+2x+23对x∈R都成立. ∴存在实数a=23,b=1,c=1,使得不等式:x2+21≤f(x)≤2x2+2x+23对一切x∈R都成立. 亿库教育网 http://www.eku.cc 亿库教育网 http://www.eku.cc 点拨:一元二次不等式恒成立的问题可以结合二次函数图像找出参数满足的条件. 【例3】解关于x的不等式)1(12)1(axxa 分析:本题可以转化为含参的一元二次不等式,要注意分类讨论. 解:原不等式等价于02)2()1(xaxa∵1a∴等价于:
02121x
a
axa
(*)
当a>1时,(*)式等价于212xaax>0∵11112aaa<1∴x<12aa或x>2 a<1时,(*)式等价于212xaax<0由2-12aa=1aa知:
当02,∴2当a<0时,12aa<2,∴12aa当a=0时,当12aa=2,∴x∈φ 综上所述可知:当a<0时,原不等式的解集为(12aa,2);当a=0时,原不等式的解集为φ;当01时,原不等式的解集为(-∞,12aa)∪(2,+∞)。 思维点拨:含参数不等式,应选择恰当的讨论标准对所含字母分类讨论,要做到不重不漏. 反馈练习:
1.已知不等式①2430xx②2680xx③2290xxm,若要使同时满足①
②的x也满足③,则m的范围是9m 2.若,mnpq,且0pmpn,0qmqn,则m、n、p、q的大小关系为mpqn 3.若关于x的不等式210,axaxa的解集为R,则a的取值范围是,0 4.不等式220axbx解集为1123x,则ab值分别为-12,-2 5.不等式22106xpx有唯一解,则实数p=4 亿库教育网 http://www.eku.cc 亿库教育网 http://www.eku.cc 6.若函数f(x) = 2221xaxa的定义域为R,则a的取值范围为10,
7.设111222,,,,,abcabc均为非零实数,不等式21110axbxc和22220axbxc的解集分别为集合M和N,那么111222abcabc是M=N的既非充要又非必要(填充分非必要、必要非充分、充要条件、既非充要又非必要) 8.不等式ax2+bx+c>0的解集为{x|α<x<β}其中β>α>0,则不等式cx2+bx+a<0的解集
是11|xxx或
9.若存在1,3,a使得不等式2220axax成立,则实数x的取值范围是213xx或
10.已知M是关于x的不等式2x2+(3a-7)x+3+a-2a2<0解集,且M中的一个元素是0,求实数a的取值范围,并用a表示出该不等式的解集. 解:原不等式即(2x-a-1)(x+2a-3)<0,
由0x适合不等式故得0)32)(1(aa,所以1a,或23a.
若1a,则5)1(252132aaa,∴2123aa, 此时不等式的解集是}2321|{axax; 若23a,由45)1(252132aaa,∴2123aa, 此时不等式的解集是}2123|{axax。 11.解不等式:0122xaax 分析:本题二次项系数含有参数,044222aaa,故只需对二次项 系数进行分类讨论。 解:∵044222aaa
解得方程 0122xaax两根,24221aaaxaaax24222 ∴当0a时,解集为aaaxaaaxx242242|22或 亿库教育网 http://www.eku.cc 亿库教育网 http://www.eku.cc 当0a时,不等式为012x,解集为21|xx 当0a时, 解集为aaaxaaax242242|22 12.已知方程4x2+(m-2)x+(m-5)=0,①是否存在实数m使方程有一正根和一负根,若存在求出m的值,若不存在请说明理由;②是否存在实数m使方程两根都大于1,若存在求出m的值,若不存在说明理由。
解 :设方程42x+(m-2)x+(m-5)=0的两根为1x、2x
①若方程42x+(m-2)x+(m-5)=0有一正根和一负根,则需满足:
0021xx0450)5(16)2(2mmmm<5.
∴此时m的取值范围是(-,5). ②错解:若方程42x+(m-2)x+(m-5)=0的两根都大于1,则需满足:
1202121xxxx1450432084202mmmm m∈(23,6)
∴此时m的取值范围是(23,6),即原方程不可能两根都大于1. 正解:若方程42x+(m-2)x+(m-5)=0的两根都大于1,则需满足:
0)1()1(0)1)(1(02121xxxx0460432084202mmmm m∈φ.
∴此时m的取值范围是φ,即原方程不可能两根都大于1. 说明:解这类题要充分利用判别式和韦达定理.
