Rossler系统的比例微分控制
Rossler系统的混沌控制

Rossler系统的混沌控制
李贤丽;李贤善;赵逢达
【期刊名称】《东北石油大学学报》
【年(卷),期】2004(028)003
【摘要】采用无反馈控制的3种方法,即参数周期扰动、周期激励和周期脉冲(拍)激励,对非线性Rossler系统的混沌态进行控制,均将混沌运动控制为规则的周期运动.
【总页数】3页(P106-108)
【作者】李贤丽;李贤善;赵逢达
【作者单位】大庆石油学院,电子工程系,黑龙江,大庆,163318;燕山大学,信息科学与工程学院,河北,秦皇岛,066004;燕山大学,信息科学与工程学院,河北,秦皇岛,066004【正文语种】中文
【中图分类】O415.5
【相关文献】
1.利用Rossler系统对心脏搏动实现混沌反控制 [J], 周燕瑜;杜妍辰
2.超混沌Lorenz系统与超混沌Rossler系统的异结构同步 [J], 蒋楠
3.超混沌Rossler系统混沌同步的反馈控制实现 [J], 吴琛义;高明成;李勇
4.超混沌Lorenz系统与超混沌Rossler系统的自适应控制同步 [J], 蒋楠
5.双时滞Rossler系统的分支分析与混沌控制 [J], 杨纪华;刘媚;李艳秋
因版权原因,仅展示原文概要,查看原文内容请购买。
伺服控制,伪微分调节

伺服控制,伪微分调节 伺服控制是一种通过对系统进行精确的调节和控制,使其能够按照预定要求完成特定任务的技术手段。而伪微分调节是一种基于微分控制的调节方法,它通过对系统输出信号进行微分运算,从而实现对系统动态性能的提高和稳定性的改善。本文将分别介绍伺服控制和伪微分调节的原理、应用及优缺点。
一、伺服控制的原理和应用 伺服控制是一种以反馈原理为基础的控制方法,它通过对系统输出信号进行监测和测量,然后与期望输出进行比较,从而计算出控制量,以达到使系统输出与期望输出一致的目的。
伺服控制广泛应用于自动控制系统中,例如机械工业中的机床、机器人等。它可以实现对机器运动轨迹、速度和力矩等参数的精确控制,从而提高生产效率和产品质量。
二、伪微分调节的原理和应用 伪微分调节是一种基于微分控制的调节方法,它通过对系统输出信号进行微分运算,从而实现对系统动态性能的提高和稳定性的改善。
伪微分调节通常可以分为两种类型:一种是基于硬件实现的伪微分调节,例如使用电路元件实现对输出信号的微分运算;另一种是基于软件实现的伪微分调节,例如使用数学模型进行离散化计算。
伪微分调节在控制系统中常用于对系统的阶跃响应进行优化,可以提高系统的响应速度和抑制超调量,从而使系统更加稳定和可靠。 三、伺服控制与伪微分调节的优缺点比较 1. 伺服控制的优点: - 可以实现对系统输出的精确控制,提高系统的稳定性和精度; - 适用于各种不同的控制对象和控制要求,具有广泛的应用范围; - 可以通过参数调节和参数整定等手段进行系统的优化和改进。
2. 伺服控制的缺点: - 对系统的参数变化和外界干扰较为敏感,需要进行复杂的系统建模和参数整定; - 控制系统的实现和调试比较复杂,需要专业的知识和技能。
3. 伪微分调节的优点: - 可以通过对输出信号进行微分运算,提高系统的动态响应和稳定性; - 可以通过调整微分增益等参数进行系统的优化和改进; - 硬件实现和软件实现两种方式灵活多样,适用于不同的应用场景。
无人机姿态控制pid内外环控制原理

无人机姿态控制pid内外环控制原理无人机姿态控制PID内外环控制原理无人机姿态控制是指控制无人机在飞行过程中保持期望的姿态,如平稳飞行、悬停、转弯等动作。
PID控制是一种常用的控制算法,它通过反馈误差来调整控制器的输出,使系统达到期望的状态。
本文将介绍无人机姿态控制中的PID内外环控制原理。
PID控制器由比例项(P项)、积分项(I项)和微分项(D项)组成,它们分别对应控制器的输出与误差的比例关系、积分关系和微分关系。
在无人机姿态控制中,通常将姿态误差作为PID控制器的输入,输出控制量用于调整无人机的姿态。
在PID内外环控制中,内环控制器用于控制无人机的角速度,外环控制器用于控制无人机的姿态。
内环控制器和外环控制器之间存在耦合关系,内环控制器的输出作为外环控制器的输入。
通过将无人机的姿态误差转化为角速度误差,PID内环控制器可以计算出相应的角加速度,进而通过姿态动力学模型将角加速度转化为电机控制量。
PID内环控制器的作用是将无人机的角速度与期望角速度进行比较,计算出角速度误差,并根据误差大小调整控制器的输出。
比例项使无人机快速响应期望角速度,积分项消除系统静态误差,微分项抑制系统的震荡和过冲。
通过调整PID内环控制器的参数,可以实现无人机角速度的精确控制。
PID外环控制器的作用是将无人机的姿态与期望姿态进行比较,计算出姿态误差,并根据误差大小调整控制器的输出。
外环控制器的输入是PID内环控制器的输出,通过将角速度误差转化为姿态误差,PID外环控制器可以计算出相应的角加速度。
同样地,比例项、积分项和微分项分别起到快速响应期望姿态、消除系统静态误差和抑制系统震荡的作用。
在实际应用中,PID内外环控制器的参数需要进行调整,以达到最佳的控制效果。
调整参数的方法有很多种,常用的方法包括试验法、经验法和自整定法。
通过调整参数,可以提高无人机姿态控制的稳定性和精确度。
总结起来,无人机姿态控制PID内外环控制原理是通过PID控制器对无人机的角速度和姿态进行控制,实现无人机在飞行过程中保持期望的姿态。
第三讲1 常规数字控制器设计方法—PID_上传-1答辩

数字量
模拟量
数字部分 A A/D B 连续部分
A’
B’
D/A
v 设计方法:离散化设计方法和连续化设计方法
2014年7月23日10时11分
总目录 章目录 返回 上一页 下一页
2
连续化设计
到最终消除偏差,但积分作用太强会使
系统超调加大,甚至使系统出现振荡;
积分
Kpe(t)
微分环节作用:有助于系统减小超调, 克服振荡,加快系统的响应速度,减小 调节时间,从而改善了系统的动态性能。 但Td 过大,会使系统出现不稳定
t
总目录 章目录 返回 上一页 下一页
16
PID控制规律主要具有以下优点:
v 离散化方法的选取非常重要 D(s)
r(t) e(t) e(k)
u(k)
T
D(z) T
u(t)
y(t)
H0(s)
G(s)
2014年7月23日10时11分
总目录 章目录 返回 上一页 下一页
3
按连续系统设计方法设计数字控制系统的条件:
v 若系统的采样频率相对于系统的工作频率是足够高的, 以至于采样保持器所引起的附加滞后影响可忽略时, 系统的数字控制器可用模拟控制器代替,使整个系统 成为模拟系统,从而可用模拟化方法进行设计。
v 缺点:不易直接观察或想象数字控制器的零极点设置 在何位置,才能改善系统特性,需要多次试算
v 常用分析方法:解析设计法、频率响应法、根轨迹法 等
2014年7月23日10时11分
总目录 章目录 返回 上一页 下一页
6
D(s)
2023年机器人控制系统练习题及答案

机器人控制系统练习题及答案一、填空题1. 伺服系统的三种控制方式:速度控制方式、转矩控制方式、位置控制方式。
2. 对于一个具有高度智能的机器人,它的控制系统实际上包含了“任务规划”、“任务规划”“轨迹规划”和基于模型的“伺服控制”等多个层次。
3. 机器人控制系统按其控制方式可分为程序输入型机器人、示教再现型机器人、智能型机器人三类。
4. ROS可以分成两层,低层是上面描述的操作系统层,高层则是广大用户群贡献的实现不同功能的各种软件包,如定位绘图、行动规划、感知、模拟等。
5. 伺服系统组成系统主要由触摸屏、 PLC 、伺服驱动器、永磁同步伺服电机组成,其中伺服电机是运动的执行机构,对其进行位置、速度和电流三环控制,从而达到用户的功能要求。
二、判断题1. 交流伺服电机主要由定子和转子构成。
(√)2. 如果用人来比喻机器人的组成的话,那么控制系统相当于人的“大脑”,感知系统相当于人的“视觉与感觉器官”,驱动系统相当于人的“肌肉”,执行机构相当于人的“身躯和四肢”。
(√)3. ROS基于一种图状架构,不同节点的进程都能接受、发布、聚合各种信息(如传感、控制、状态、规划等)。
目前ROS主要支持Ubuntu。
(√)4. ROS(低层)使用BSD许可证,是开源软件,并能大部分免费用于研究和商业用途。
而高层的用户提供的软件包则可以使用很多种不同的许可证。
(×)5. 机器人控制系统实际上包含了“任务规划”“动作规划”“轨迹规划”和基于模型的“伺服控制”等多个层次。
(√)三、选择题1. 实现机器人和其他设备的信息交换,一般有串行接口、并行接口等。
(A)A. 通信接口B. 网络接口C. 传感器接口D. 控制计算机2. 对于大多数控制系统来说,它一般由四个部分组成:输入、输出、控制元件和算法。
其中电机输出属于哪个部分?(B)A. 输入B. 输出C. 控制元件D. 算法3. 机器人控制系统按其控制方式可分为三类。
【国家自然科学基金】_混沌态_基金支持热词逐年推荐_【万方软件创新助手】_20140802
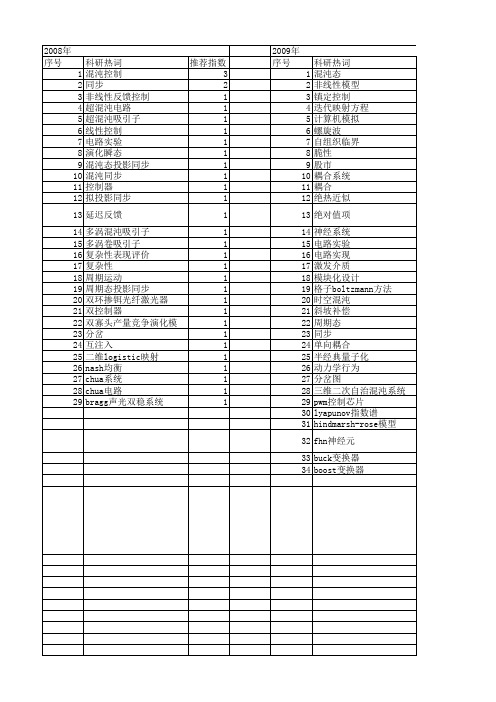
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
科研热词 推荐指数 混沌控制 4 混沌 3 混沌电路 2 平衡点 2 四维节能减排系统 2 非光滑系统 1 超混沌系统 1 螺旋波 1 自适应滞环调制 1 脉宽调制 1 线性反馈控制. 1 线性反馈控制 1 符号序列 1 突发混沌 1 离散映射 1 研发 1 电力市场 1 电光双稳态 1 滑模控制 1 有限理性 1 时空混沌 1 断续导通模式 1 技术溢出 1 延迟反馈 1 圆映射 1 可激发介质 1 变换器 1 动态模型 1 动力学分析 1 分支理论 1 分岔 1 倍周期分岔 1 介质阻挡放电 1 不同预期报价决策 1 nash均衡 1 four-dimensional energy-saving1 and emission-reduc buck变换器 1
科研热词 混沌 频谱分析 频率检测 非线性动力学 非线性共振 闭轨 超点阵 螺旋波 耦合 纳什均衡 相变 电力市场 激发介质 混沌现象 混沌振子 混沌态 比例微分控制 束流 束晕 晶格boltzmann方法 时空混沌 时滞反馈混沌控制 放电丝结构 强流离子束 平衡态 小世界 同步控制器 同宿轨道 古诺博弈 双重吸引子 分数阶 传输系统 介质阻挡放电 rossler混沌系统 newton-leipnik系统 melnikov函数
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
科研热词 混沌 duffing 非线性电路 镇定控制 过渡带 超混沌电路 被动介质 螺旋波 累积释放模型 符号动力学 相变 电压-电流转换器 激光光学 混沌控制 正交偏振调制 检测 时间延迟耦合 时滞电路 排列熵 弱正弦信号检测 复杂度 同步 半导体激光器 半导体光放大器 分岔 光纤环 光电子学 偏振混沌 偏振度 v2控制 buck变换器
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第22卷第4期V01.22No.4重庆工学院学报(自然科学)JournalofChongqingInstituteofTechnology(Natural
science)
2008年4月Apr.2008
Rossler系统的比例微分控制’王伟8,张秋富b(兰州交通大学a.数理与软件工程学院;b.非线性研究中心,兰州7313070)
摘要:采用比例微分控制器(PDC)实现Rossler系统的混沌控制.给出了混沌系统的控制结果.tong—guo理论分析和数值仿真表明:这种控制方法可以实现混沌控制的2个目标,即稳定系统中的不稳定周期轨道和产生新的稳定动力学行为.关键词:比例微分控制器;混沌控制;Rossler系统中图分类号:TP273文献标识码:A文章编号:1671—0924(2008)04—0136—03
ProponionalDifferentialControllingforRosslerSystem
WangWei8,ZhangQiu—fub(a.CollegeofMathematicsandSoftwareEngineering;b.TheCentreofNonlinearsIudy,
【舢z}louJiaotongUniversity,【anzhou730070,C&ina);Abstract:ProportionalDifferentialControlling(PDC)isusedtorealizechaoscontrollingforRosslersys—tem,andtheresultsofchaoscontrollingofthissystemprovided;Finally,analysisofthemeoretical
analysisandnumericalsimulationresultsdemonstratethatthiscontrollingmethodcall
realizetwogoalsof
chaoscontrolling,namely,instableperiodic
orbitinthestablesystemandproductionof
n州stable
dynam-
iCS.
Keywords:ProportionalDifferentialControlling;chaoscontrolling;Rosslersystem
近年来,混沌的控制与同步成为非线性科学中的一个研究热点,科学工作者已提出了大量的混沌控制与同步的方法u_6J,如系统状态变量延迟反馈法…3、系统变量正比例脉冲反馈法[2]2、系统变量的数值仿法[4J等.本研究采用经典的比例微分控制器实现Rossler系统的混沌控制.由于这种控制方法只需要单个状态变量对系统的部分状态方程进行反馈就可以实现混沌控制的目的,这就克服了目前大多数状态变量反馈法需要多个进行全局反馈的缺陷,所以这种控制方法在工程中十分容易实现,因而具有较高的应用价值.’
1控制方法
系统考虑如下的n阶自制或非自制非线性动力学
·收稿日期:2007—12—25作者简介:王伟(1980一),男,河北张家口人,硕士研究生,主要从事混沌控制理论研究.
万方数据王伟,等:Rossler系统的比例微分控制137
露=F(菇,弘,t)(1)其中:并∈R“,F=(^,f2,f3,…,厶)是/1,维光滑的向量场;/1为系统的参数.当肛取一定范围的值时,系统(1)处于混沌运动.现对式(1)所表示的系统的状态变量茹i取比例微分控制得:茹’i=kl戈i+k2xf(2)其中:k1,k2是本控制方法中的2个可调参数.调整k1,k2的值可以实现不同的控制目标.将露f按如下方法进行反馈f巧=is(Xl笫2…XPi名。产)1誓2is(茗lX,2…X,iXn∥’(3)L龙’f2kl茗f+k2x’iJ=i,J=1,2,…,r1.由式(3)所示的反馈方式可知:F()中的子系统五()不受反馈控制作用而自由演化.若系统Z()中无状态变量戤,也不受控制作用而自由演化,则本控制方法只需对系统的一部分子系统进行控制.这就大大减小了控制的代价和在实际工程系统中实现控制的难度,因为非线性系统的可观测性和可控性仍是一个未解决的难题.2Rossler系统的理论分析0.E.Rossler构造了几个简单但具有混沌行为蒯}线性方程组,其中最具有代表性的是他在1976年提出的如下方程组[7]:f露=一(Y一石)r{夕=算+ay(4)L2=z(戈一c)+b其中:口=0.2,b=0.2,c=5.7.和a=0.2,b=O.2,c=11.混沌吸引子分别如图1中的a),b)所示.本研究中主要研究当a=0.2,b=0.2,c=5时混沌的控制.令系统(4)的右端为零:这样得到系统的2个平衡点为:sl=(o,0,0),s2=(一曲+c,(ab—c)/a,一(ab—c)/a).当口=0.3,b=0.2,c=5时,得到系统的2个实平衡点为:sl=(0,0,0),s2=(4.94,一16.86,16.47)下面讨论这2个实平衡点的稳定性.对于平衡点sl=(0,0,0)其雅可比矩阵为:㈠-01]㈣
它的特征方程为P3+4.7p2—0.3p+4.94=0所以其特征值为:P1=0.1306+0.9893i,P2=0.1306—0.9893i,P3=一4.961
2,故5l=(0,0,O)是不
对于平衡点32=(4.94,一16.86,16.67),其雅可比矩阵为:f-o-1-1]l1o.3oI(6)
其特征值分别为:Pl=一0.0199+4.202
7i,P2=
一0.0199—4.2027i,P3=0.279
7,所以52为不稳
40¨20
10050O50
-50-50b)
图1混沌系统在不同参数下的吸引子
混沌系统的比例微分控制对于不动点s2=(4.94,一16.86,16.钾).在该条件下取状态变量Y为受控变量设置比例微分控制器Y’=klY+后2于.原系统变形为:r露=一k2·髫一Y一0.2·詹2‘Y+彳{少=石+0∥2Y(7)
【2:z.(菇一5)+0.2
万方数据】38熏庆.Y-擎院学报对于实施反馈后的系统(7),当kl=1时其与原系统有檑同的不动点.将系统(7)遴行线性佬,褥其Jacobian矩阵为:|一k2一(1+0.2k2)1|A=|10。20l(s)名。石一5把A,点投入其特征多项式为:A,一Al=A3+(5.4297+k2)A2+(5.6297k2—0.0908)A+5.6227由Routh.Hurwitz判据【83得:豢0.0163<k2<287653。4667酵,系统的不动点是稳定的.图2为k2=10时,混沌系统(4)的Maflab仿真结果。获蚕2中可看高这种控制方法是有效的,系统通过这种控制能很好地控制到平衡点.柚乐统撼制后的相田50t∞b)系蠡屯控制后变量★的时城田050l∞d)系跪旌稍后主重x神时城霹图2系统控制后的相图及时域图4结束语本研究分析了Rossler混沌系统的稳定性,设计了比例微分控制器,实现了它的混沌控制与同步,用Lyapunov定壤证明了这种控制方法的有效性.理论分析和数值仿真都表明了这种控制方法是有效的.该方法可以用来实现一般系统的混沌控制与同步.
参考文献:【1]LiZ,ZhangB,MaoZY.Strangeattl'ltCtol曝inpermanent-
magnetsynchronousnlotols[C]//ProeoftheIEEEt999
InterationalConferencePowerElectronicsandDriveSrs—
tellgq.HongKong:【s.n.],1999:150—155.
【2]ZhangBo,Li
Zhong,Mao
Zongyuan。‰numericalalg抄
rithmofPoincaremapanditsapphcafiontotheanalysisofthechaoticphenomenoninpermanent-magnet
synchronous
motors[J】.controlTheoryandApplications,2001,18(5):
796—800。,[3]GuckenheimerJ,HolmesP
J.NonlinearOscillations,Dr-
rmmicalSyst目ns,andBL妇rcagomofVerctor翻e出【聪j。
Berlin:Springervea,a{;,Heidelberg,1983。[4]WigginsS.IntroductiontoAppliedNonlinear
ny枷cai
%姗andChaos【M】.Be戒n:Springer-Verlag,Herdel-
be瑁,1984。[5]GuemezJM.Controlofchaosinunidimensionalmaps[J].
PlaysLettA,1993,181:29—32。【6】珞嘲涔K.Continunouscontrolofchaos酶self-controUing
feedback[J].Phy¥LeaA,1992,170:421—428.[7]陈荚荣,吕金虎.I础rlz系统族的动力学分析,控翎尚
同步[1ll】.北京:辩学出版社,2004:5—7.[8]刘秉正,彭建华.j}线性动力学[M].北京:高等教育出版社.2003:137—141.
(责任编辑刘舸)
万方数据
