张三慧大学物理上册习题答案详解(1章-9章)
张三慧《大学物理学:力学、电磁学》(第3版)(B版)(课后习题 静电场中的导体)【圣才出品】

第9章 静电场中的导体9.1 求导体外表面紧邻处场强的另一方法。
设导体面上某处面电荷密度为σ,在此处取一小面积ΔS,将ΔS 面两侧的电场看成是ΔS 面上的电荷的电场(用无限大平面算)和导体上其他地方以及导体外的电荷的电场(这电场在ΔS 附近可以认为是均匀的)的叠加,并利用导体内合电场应为零求出导体表面紧邻处的场强为σ/ε0(即教材式(8.2))。
解:如图8-1所示,导体表面小面积ΔS 上所带电荷在它的两侧分别产生场强为σ/2ε的电场E'1和E'2,ΔS以外的电荷在ΔS 附近产生的电场为E",可视为均匀的。
由电场叠加原理,在ΔS 的导体内一侧应有于是在ΔS的导体外一侧,则合电场应为这说明E ex 的大小为2σ/(2ε0)=σ/ε0,而其方向垂直于导体表面。
图8-19.2 一导体球半径为R1,其外同心地罩以内、外半径分别为R2和R3的厚导体壳,此系统带电后内球电势为φ1,外球所带总电量为Q 。
求此系统各处的电势和电场分布。
解:设内球带电为q 1,则球壳内表面带电将为-q1,而球壳外表面带电为q 1+Q ,这样就有由此式可解得于是,可进一步求得9.3 在一半径为R1=6.0 cm 的金属球A 外面套有一个同心的金属球壳B 。
已知球壳B 的内、外半径分别为R2=8.0 cm ,R3=10.0 cm 。
设A 球带有总电量QA =3×10-8 C ,球壳B 带有总电量QB =2×10-8C 。
(1)求球壳B 内、外表面上各带有的电量以及球A 和球壳B 的电势;(2)将球壳B 接地然后断开,再把金属球A 接地。
求金属球A 和球壳B内、外表面上各带有的电量以及球A 和球壳B 的电势。
解:(1)由高斯定律和电荷守恒可得球壳内表面带的电量为球壳外表面所带电量为于是(2)B 接地后断开,则它带的总电量变为然后球A 接地,则φ'a=0。
设此时球A 带电量为q'A ,则由此解得9.4 一个接地的导体球,半径为R ,原来不带电。
大学物理简程 张三慧主编第1章 质点运动学

at
a
R
an
o
a rc ta n
an at
14
1.7
y
相对运动
y
E
V
S:小球
V:马车
B
rS E A0 rV E
A
E:地面
rS V
o
o
x
rS E rS V rV E v S E v S V vV E
a lim
v t
t 0
lim
vn t
t 0
lim
vt t
t 0
an at
12
切向加速度:
vt v (t t ) v (t ) v
a t lim v t dv dt d ( R ) dt R d dt
v B A y v B y v A y v B sin 30 v A 600 km / h
v BA v B A x v B A y 9 1 7 km / h
2 2
v AB v A v B
23
0
16
dv dt
dv dt
du dt
若两个参考系相对做匀速直线运动,即 a r 则
a a
矢量合成的平行四边形法则:
A
A
B
C
B
C
矢量合成的三角形法则:
A A
C
B
C
B
17
矢量的分解:
A B B
y
A
第1章 质点运动学
大学物理(上册)参考答案

第一章作业题P211.1; 1.2; 1.4;1.9 质点沿x 轴运动,其加速度和位置的关系为 a =2+62x,a 的单位为2sm -⋅,x 的单位为 m. 质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值. 解: ∵x v v t x x v t v a d d d d d d d d ===分离变量:x x adx d )62(d 2+==υυ 两边积分得 cx x v ++=322221由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v1.10已知一质点作直线运动,其加速度为 a =4+3t 2sm -⋅,开始运动时,x =5 m ,v =0,求该质点在t =10s 时的速度和位置.解:∵ t t va 34d d +==分离变量,得 t t v d )34(d +=积分,得 12234c t t v ++=由题知,0=t ,00=v ,∴01=c故2234t t v += 又因为2234d d t t t x v +== 分离变量, tt t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c故 521232++=t t x所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1.11一质点沿半径为1 m 的圆周运动,运动方程为 θ=2+33t ,θ式中以弧度计,t 以秒计,求:(1) t = 2 s 时,质点的切向和法向加速度;(2)当加速度的方向和半径成45°角时,其角位移是多少?解:t t t t 18d d ,9d d 2====ωβθω(1)s 2=t 时, 2s m 362181-⋅=⨯⨯==βτR a2222s m 1296)29(1-⋅=⨯⨯==ωR a n(2)当加速度方向与半径成ο45角时,有145tan ==︒na a τ即βωR R =2亦即t t 18)9(22= 则解得 923=t 于是角位移为rad67.29232323=⨯+=+=t θ1.12 质点沿半径为R 的圆周按s =2021bt t v -的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,求:(1)t 时刻质点的加速度;(2) t 为何值时,加速度在数值上等于b .解:(1) bt v t sv -==0d d R bt v R v a btv a n 202)(d d -==-==τ则 240222)(R bt v b a a a n -+=+=τ加速度与半径的夹角为20)(arctanbt v Rb a a n --==τϕ(2)由题意应有2402)(R bt v b b a -+== 即 0)(,)(4024022=-⇒-+=bt v R bt v b b∴当b v t 0=时,b a = 第二章作业题P612.9 质量为16 kg 的质点在xOy 平面内运动,受一恒力作用,力的分量为x f =6 N ,y f =-7 N ,当t =0时,==y x 0,x v =-2 m ·s -1,y v =0.求当t = 2 s时质点的 (1)位矢;(2)速度.解:2s m 83166-⋅===m f a x x 2s m 167-⋅-==m f a y y(1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=20101200s m 872167s m 452832dt a v v dt a v v y y y x x x于是质点在s 2时的速度1s m 8745-⋅--=ji v(2)m874134)167(21)4832122(21)21(220j i ji jt a i t a t v r y x--=⨯-+⨯⨯+⨯-=++=2.10 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mk ev )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m ke )(-];(3)停止运动前经过的距离为)(0k m v ;(4)证明当k m t =时速度减至0v 的e 1,式中m 为质点的质量.答: (1)∵t v m kv a d d =-= 分离变量,得m t k v v d d -= 即 ⎰⎰-=v v t m tk vv 00d dmkt e v v -=ln ln 0∴tm kev v -=0(2)⎰⎰---===tttm k m k e k mv t ev t v x 000)1(d d(3)质点停止运动时速度为零,即t →∞,故有⎰∞-=='00d k mv t ev x tm k(4)当t=k m时,其速度为e v e v ev v kmm k 0100===-⋅-即速度减至0v 的e 1.2.11一质量为m 的质点以与地的仰角θ=30°的初速0v从地面抛出,若忽略空气阻力,求质点落地时相对抛射时的动量的增量. 解: 依题意作出示意图如题2-6图题2-6图在忽略空气阻力情况下,抛体落地瞬时的末速度大小与初速度大小相同,与轨道相切斜向下, 而抛物线具有对y 轴对称性,故末速度与x 轴夹角亦为o30,则动量的增量为0v m v m p -=∆由矢量图知,动量增量大小为v m,方向竖直向下.2.13作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s后,这物体的动量和速度的变化,以及力给予物体的冲量.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则it i t t F p t10401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,i p I im p v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t ttF v m t m F v m p v m p 000000d )d (,于是 ⎰∆==-=∆t p t F p p p 0102d, 同理, 12v v∆=∆,12I I =这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t解得s 10=t ,(s 20='t 舍去)3.14一质量为m 的质点在xOy 平面上运动,其位置矢量为j t b i t a rωωsin cos +=求质点的动量及t =0 到ωπ2=t 时间内质点所受的合力的冲量和质点动量的改变量.解: 质点的动量为)cos sin (j t b i t a m v m pωωω+-==将0=t 和ωπ2=t 分别代入上式,得j b m pω=1,i a m p ω-=2,则动量的增量亦即质点所受外力的冲量为)(12j b i a m p p p I+-=-=∆=ω2.15 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得b a t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将b at =代入,得b a I 22=(3)由动量定理可求得子弹的质量202bv a v I m ==第三章作业题P883.1; 3.2; 3.7;3.13计算题2-27图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为M ,半径为r ,在绳与轮缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,设1m =50kg ,2m =200 kg,M =15 kg, r =0.1 m解: 分别以1m ,2m 滑轮为研究对象,受力图如图(b)所示.对1m ,2m 运用牛顿定律,有a m T g m 222=- ① a m T 11= ②对滑轮运用转动定律,有β)21(212Mr r T r T =- ③又, βr a = ④联立以上4个方程,得2212s m 6.721520058.92002-⋅=++⨯=++=M m m g m a题2-27(a)图 题2-27(b)图题2-28图3.14 如题2-28图所示,一匀质细杆质量为m ,长为l ,可绕过一端O 的水平轴自由转动,杆于水平位置由静止开始摆下.求: (1)初始时刻的角加速度; (2)杆转过θ角时的角速度. 解: (1)由转动定律,有β)31(212ml mg=∴l g 23=β (2)由机械能守恒定律,有22)31(21sin 2ωθml l mg =∴ l g θωsin 3=题2-29图3.15 如题2-29图所示,质量为M ,长为l 的均匀直棒,可绕垂直于棒一端的水平轴O 无摩擦地转动,它原来静止在平衡位置上.现有一质量为m 的弹性小球飞来,正好在棒的下端与棒垂直地相撞.相撞后,使棒从平衡位置处摆动到最大角度=θ30°处. (1)设这碰撞为弹性碰撞,试计算小球初速0v 的值; (2)相撞时小球受到多大的冲量?解: (1)设小球的初速度为0v,棒经小球碰撞后得到的初角速度为ω,而小球的速度变为v ,按题意,小球和棒作弹性碰撞,所以碰撞时遵从角动量守恒定律和机械能守恒定律,可列式:mvl I l mv +=ω0 ①2220212121mv I mv +=ω ②上两式中231Ml I =,碰撞过程极为短暂,可认为棒没有显著的角位移;碰撞后,棒从竖直位置上摆到最大角度o30=θ,按机械能守恒定律可列式:)30cos 1(2212︒-=lMg I ω ③由③式得2121)231(3)30cos 1(⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒-=l g I Mgl ω由①式ml I v v ω-=0 ④由②式m I v v 2202ω-= ⑤所以22001)(2ωωm v ml I v -=-求得glmM m m M l ml I l v +-=+=+=31232(6)311(2)1(220ωω (2)相碰时小球受到的冲量为⎰-=∆=0d mvmv mv t F由①式求得ωωMl l I mv mv t F 31d 0-=-=-=⎰glM 6)32(6--=负号说明所受冲量的方向与初速度方向相反.第五章作业题P1455.1; 5.2;5.7 质量为kg 10103-⨯的小球与轻弹簧组成的系统,按)SI ()328cos(1.0ππ+=x 的规律作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差;解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==m m a FJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时,有p E E 2=,即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t5.8 一个沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表示.如果0=t 时质点的状态分别是:(1)A x -=0;(2)过平衡位置向正向运动;(3)过2Ax =处向负向运动; (4)过2Ax -=处向正向运动.试求出相应的初位相,并写出振动方程.解:因为 ⎩⎨⎧-==000sin cos φωφA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππφ+==t TA x)232cos(232πππφ+==t T A x)32cos(33πππφ+==t T A x)452cos(454πππφ+==t T A x5.9 一质量为kg 10103-⨯的物体作谐振动,振幅为cm 24,周期为s 0.4,当0=t 时位移为cm 24+.求:(1)s 5.0=t 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到cm 12=x 处所需的最短时间; (3)在cm 12=x 处物体的总能量.解:由题已知 s 0.4,m 10242=⨯=-T A∴ 1s rad 5.02-⋅==ππωT又,0=t 时,0,00=∴+=φA x故振动方程为m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=φ,t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt(3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J 101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E5.11 图为两个谐振动的t x -曲线,试分别写出其谐振动方程.题4-8图解:由题4-8图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4-8图(b)∵0=t 时,35,0,2000πφ=∴>=v A x01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65=故 m t x b )3565cos(1.0ππ+= 5.12 一轻弹簧的倔强系数为k ,其下端悬有一质量为M 的盘子.现有一质量为m 的物体从离盘底h 高度处自由下落到盘中并和盘子粘在一起,于是盘子开始振动. (1)此时的振动周期与空盘子作振动时的周期有何不同? (2)此时的振动振幅多大?(3)取平衡位置为原点,位移以向下为正,并以弹簧开始振动时作为计时起点,求初位相并写出物体与盘子的振动方程.解:(1)空盘的振动周期为k M π2,落下重物后振动周期为km M +π2,即增大. (2)按(3)所设坐标原点及计时起点,0=t 时,则kmgx -=0.碰撞时,以M m ,为一系统动量守恒,即0)(2v M m gh m +=则有 Mm ghm v +=20于是gM m khk mg M m gh m k mg v x A )(21))(2()()(22222++=++=+=ω(3)g m M khx v )(2tan 000+=-=ωφ (第三象限),所以振动方程为 ⎥⎦⎤⎢⎣⎡+++++=g m M kh t M m k gM m khk mg x )(2arctan cos )(215.15 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:(1) ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x (2)⎪⎩⎪⎨⎧+=+=cm)343cos(5cm )33cos(521ππt x t x解: (1)∵ ,233712πππφφφ=-=-=∆∴合振幅 cm 1021=+=A A A(2)∵ ,334πππφ=-=∆∴合振幅 0=A5.16 一质点同时参与两个在同一直线上的简谐振动,振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x 试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。
大学物理张三慧版第9章磁介质
0 dI
b
B
19
求磁矩m 半径为r的dr园环产生的磁矩dm为
2 2
2 dm r dI r dr r dr 2 2
O
m dm
a b
2
a 3
r dr
3
2
r
a
A
dr
6
a b a
b
B
20
例9 求半径为R的无限长半圆形柱面导体轴线上 p点的磁场。其上流有电流I,电流均匀分布。 dI I 0 解: dB dI dl dl R 2R R 0 dI dBx dB cos90 sin I 2R 0 dI B dB x sin 2R 0 sin I 0 I dl sin Rd y 2 2 2R R 2 R dl 0 I 0 I sin d 2 2 2 R 0 R x dB 沿x轴正方向 21
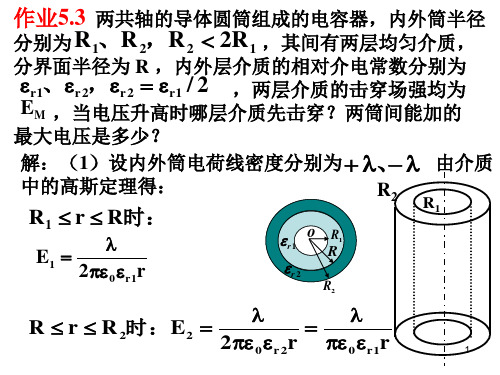
r1 o r2
E1
E2
R
R2
R1
2 0 r1r
0 r1r
2
第8章 磁场的源
本章研究电流激发磁场的规律, 磁场的高斯定律和环路定理,讨论非 均匀磁场中电流、线圈、运动电荷受 力问题,掌握电流磁场的计算。
3
8.1 毕奥 — 萨伐尔定律(稳恒电流磁场)
一、电流元产生的磁场 0 Idl r ˆ 实验发现: dB 2
2
0 0
2
I
Idl
l o
r
r0
1
dB
I r sin d I B sin d 4 r 4 r 0 I B (cos 1 cos 2 ) 方向: 4 r0
清华大学张三慧大学物理第一册第一章

§1.1 参考系 、坐标系
一.参考系(frame of reference, reference system)
由运动的相对性,描述运动必须选取参考系。
参考系:用来描述物体运动而选作参考的物体
或物体系。 运动学中参考系可任选,不同参考系中物体
的运动形式(如轨迹、速度等)可以不同。 常用的参考系:
一个任意的平面曲线运动,可以视为由一系
列小段圆周运动所组成。 加速度:
et1
·e
P1
n1
· 1 O1
曲率圆2 运动轨迹
O2
·· 2 P2 en2
et2
a
dv dt
et
v2
en
―曲率半径
在曲线上的各点固结一系列由
当地的切线和法线所组成的坐标
曲率圆1
系称自然坐标系。
21
§1.7 相对运动(relative motion)
v (t+Δt )
0
y
x
加速度:a lim
t 0
v t
d v dt
d2 r dt2
r
加速度的方向:v 变化的方向
加速度的大小:a
a
d v
dv
dt dt
12
§1.4 匀加速运动 (uniformly acceleration motion)
特点:a const.
由
a dv dt
t
v(t)
adt dv
t0
v(t0 )
由
v dr dt
t
r (t )
vdt dr
t0
r (t0 )
r(t
)
r (t0
)
v(t0
张三慧《大学物理学:力学、电磁学》(第3版)(B版)【章节题库】(1-3章)【圣才出品】

第1章质点运动学一、选择题1.一质点沿x轴运动,其运动方程为,式中时间t以s为单位.当t=2s时,该质点正在()A.加速B.减速C.匀速D.静止【答案】A2.一物体在位置1的矢径是,速度是,如图1-1所示,经Δt时间后到达位置2,其矢径是,速度是,则在Δt时间内的平均速度是()。
图1-1A.B.C.D.【答案】C【解析】平均速度。
3.一物体从某一确定高度以的速度水平抛出,已知它落地时的速度为,则它运动的时间是()。
A.B.C.D.【答案】C【解析】落地时的速度与水平速度和竖直方向速度有关系式,所以,下落的时间为。
4.瞬时速度υ的大小|υ|可以用下列哪个式子来表示()。
【答案】C【解析】由于速度,所以速度υ的大小。
5.质点以速度作直线运动,沿质点运动直线作Ox轴,并已知t=3s时,质点位于x=9m处,则该质点的运动学方程为()。
A.x=2tB.C.D.【答案】C6.(多选)质点沿半径为R的圆周按规律运动,其中b、c是常数,则在切向加速度和法向加速度大小相等以前所经历的时间为()。
【答案】AB【解析】由求出速率及切向加速度,进一步求出法向加速度,再由切向加速度大小等于法向加速度的条件,即可解出时间t。
依题可知,而。
当可得。
即7.(多选)以下说法中,正确的是()。
A.质点具有恒定的速度,但仍可能具有变化的速率B.质点具有恒定的速率,但仍可能具有变化的速度C.质点加速度方向恒定,但速度方向仍可能在不断变化着D.质点速度方向恒定,但加速度方向仍可能在不断变化着E.某时刻质点加速度的值很大,则该时刻质点速度的值也必定很大F.质点作曲线运动时,其法向加速度一般并不为零,但也有可能在某时刻法向加速度为零【答案】BCDF二、填空题1.一质点作匀加速直线运动,在ts时间内走过路程sm,而其速度增为初速的n倍。
此过程中的加速度a为______。
【答案】【解析】由,并利用,可解出。
2.有一水平飞行的飞机,速度为,在飞机上以水平速度υ向前发射一颗炮弹,略去空气阻力,并设发炮过程不影响飞机的速度,则(1)以地球为参考系,炮弹的轨迹方程为______。
张三慧《大学物理学:力学、电磁学》(第3版)(B版)【课后习题】(7-16章)【圣才出品】
第2篇电磁学第7章静电场7.1在边长为a的正方形的四角,依次放置点电荷q,2q,-4q和2q,它的正中放着一个单位正电荷,求这个电荷受力的大小和方向。
解:如图7-1所示,两个2q对q0的作用力相抵消,q0受的即q和-4q对它的合力,其大小为力的方向指向-4q。
图7-17.2三个电量为-q的点电荷各放在边长为r的等边三角形的三个顶点上,电荷放在三角形的重心上。
为使每个负电荷受力为零,Q之值应为多大?解:如图7-2所示,Q受其他三个电荷的合力等于0,与Q的大小无关。
一个-q受其他三个电荷的合力的大小为此合力为零给出图7-27.3如图7-3所示,用四根等长的线将四个带电小球相连,带电小球的电量分别是-q,Q,-q和Q。
试证明当此系统处于平衡时,。
图7-3解:如图7-3所示,电荷-q受合力为零要求化简后可得同理,电荷Q受合力为零要求将上两式相比,即得各电荷受力均为零时,7.4一个正π介子由一个u夸克和一个反d夸克组成。
u夸克带电量为,反d夸克带电量为。
将夸克作为经典粒子处理,试计算正π介子中夸克间的电力(设它们之间的距离为)。
解:7.5精密的实验已表明,一个电子与一个质子的电量在实验误差为的范围内是相等的,而中子的电量在的范围内为零。
考虑这些误差综合的最坏情况,问一个氧原子(具有8个电子、8个质子和8个中子)所带的最大可能净电荷是多少?若将原子看成质点,试比较两个氧原子间电力和万有引力的大小,其净力是相吸还是相斥?解:一个氧原子所带的最大可能净电荷为两个氧原子间的最大库仑力为两个氧原子间的引力为所以两氧原子间净力为引力。
7.6一个电偶极子的电矩为p=ql,证明此电偶极子轴线上距其中心为处的一点的场强为证:电偶极子的+q和-q两个电荷在轴线上距中心为r处的合场强为由于,并考虑到方向可得7.7电偶极子电场的一般表示式。
将电矩为p的电偶极子所在位置取作原点,电矩方向取作x轴正向。
由于电偶极子的电场具有对x轴的轴对称性,所以可以只求xy平面内的电场分布E(x,y)。
张三慧《大学物理学:力学、电磁学》(第3版)(B版)【课后习题】(1-6章)【圣才出品】
(1)求质点运动的轨道方程并画出轨道曲线;
(2)求
和
时,质点的位置、速度和加速度。
图 1-1
解:(1)在运动函数中消去 t,可得轨道方程为 1-1 所示。
(2)由
轨道曲线为一抛物线如图
可得在 t=1 s 时, 在 t=2 s 时,
1.8 男子排球的球网高度 2.43 m,球网两侧的场地大小都是 9.0 m×9.0 m。一运动 员采用跳发球姿势,其击球点高度为 3.5 m,离网的水平距离是 8.5 m。
由此可知θ无实数解,所以该目标不在可能的轨道上,所以不能被石头击中。 只有当
时,θ才有解,由此得 所以在 L=50 m 这个距离上,他能击中的目标的最高高度为 12.3 m。附带算出相应的
1.11 为迎接香港回归,柯受良 1997 年 6 月 1 日驾车飞越黄河壶口瀑布(见图 1-4)。 东岸跑道长 265 m,柯驾车从跑道东端起动,到达跑道终端时速度为 150 km/h,他随即 以仰角 5°冲出,飞越跨度为 57 m,安全落到西岸木桥上。
,他能击中一个与他的手水平距离 L
=50 m,高 h=13 m 处的一个目标吗?在这个距离内他能击中的目标的最高高度是多少?
解:如图 1-3 所示,石头的轨道方程为
图 1-3
以
代入可得
能击中该目标的θ角需满足上式,即条件为
将已知数据代入后,可得根号下的值
7 / 125
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书
第1篇 力 学
十万种考研考证电子书、题库视频学习平台
第 1 章 质点运动学
1.1 木星的一个卫星——木卫 1——上面的珞玑火山喷发出的岩块上升高度可达 200
a热学《大学物理》课本习题解答(张三慧)
1 .•• E:���*W.����T,-� •• ��.ftm�.�������� ���,��������±���m*Tf���m$Q����f���*T��rp �z;b�.ljL� 02.�§:����ft�X��T¥����*������o�����.ljL��Il��f�o3. �:h���J:EW: PD*�i;t A ;fI:l�i;t B *Jl�mJ:j�.C �[IiI-��9tT�f1Jj, Jl� � � A ;fD B mJIDkB-T, 'EfrJi.i1&\��T�3f�, it -�1$�1JII J:li!tilia.lllt, �_:tljffi\�'F, �ii: Jl/!ltii:ilia.ll ��1illI04. 11UB�tt;:;.gtF: �Jt:lf�m tID � ;fU�jJ �ia;t'F-f{, lZ:#m;t'F�tfL:l1:��D T :It ��f:tj * I-lJ � , JJll;m.9, i* �p V * {g..R � ii. J.t ff *. � JJt 5E)/...�;tIl 9, 1* iKi t'F T(K)iY!:Tee p V�5Ex-ii.J.t��--*�=m�;.g��T a = 273.16 KT=�T3P a VaAtfl ,Pa ,V3 �-JEJ9t:it9,i*::t£-*-� =�i;\iffi J.t T�ffiJifD{;$:m ;P.V ��9,{;$:::t£��iIia J.t T (f] ffiJii! ;fI:l1* m Q:ff:fJl!m 9,1*m;t'Fff��Wil'fil � ,'E ;fI:lfljJ Jjj(ilia.t'F7t�-f{ Q第2篇热学摄氏温标与热力学温标的关系tCC)=T-273.15(K)S.熟力学第三定幸事:费力学骂季度是不能达到的G6.理盟气体棋盎方程:描述在平衡态的理想气体的宏现量有下述关系:T 'E n-P TR m -M一T R UW, 一v ay式中R为普适气排常量,R =8圄31J/(mol • K)是为藏耳兹曼常量,是:录=1. 38 X 10-23 JI区式中,η为分子散密度,M为气体摩尔质量,.m 为气体的质量。
张三慧版大学物理第三版静电学练习1
1静电学练习11. 关于电场强度定义式0/q F E=,下列说法中哪个是正确的?(A) 场强E 的大小与试探电荷q 0的大小成反比.(B) 试探电荷受力F 的方向就是场强E 的方向.(C) 对场中某点,试探电荷受力F 与q 0的比值不因q 0而变.(D) 若场中某点不放试探电荷q 0,则F =0,从而E=0. [ ]2.设有一“无限大”均匀 带负电荷的平面.取x 轴垂直带电平面,坐标原 点位于带电平面上,则其 周围空间各点的电场强 度E 随距离平面的位置坐标x 变化的关系曲线为 (规定场强方向沿x 轴正向 为正、反之为负):[ ]3.正方形的两对角上,各置电荷Q ,在其余两对角上各置电荷q ,若Q 所受合力 为零,则Q 与q 的大小关系为(A) Q =-22q . (B) Q =-2q .(C) Q =-4q . (D) Q =-2q . [ ]4.一电矩为p 的电偶极子在场强为E 的均匀电场中,p与E 间的夹角为α,则它所受的电场 力F=___________,力矩的大小M =_________.5. 如图所示,真空中两个正点电荷Q ,相距2R .若以其中一点电荷所在处O 点为中心,以 R 为半径作高斯球面S ,则通过该球面的电场强度通量=______________;若以0r表示高斯面外法线方向的单位矢量,则高斯面上a 、b 两点的电场强度分别为_____ ______________________________.6.三个平行的“无限大”均匀带电平面,其电荷面密度都是+σ,如图所示,设向右为正方向,则A 、B 、C 、D 四个区域的电场强度分别为:E A =_________________,E B =_____________,E C =_______________,E D =_________________.+σ+σ+σABCD2d EO 7. 如图所示,真空中一长为L 的均匀带正电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度.8.真空中一立方体形的高斯面,边长a =0.1 m ,位于图中所示位置.已知空间的场强分布为:E x =bx , E y =0 , E z =0. 常量b =1000 N/(C ·m).试求通过该高斯面的电通量.9.图示闭合面包围了两个等量异号点电荷±q .下列说法是否正确?如有错误请改正.(1) 高斯定理∑⎰⋅=0/d εq S E S成立.(2) 因闭合面内包围净电荷∑q i =0,得到0d =⎰⋅S E S故闭合面上场强E 处处为零. (3) 通过闭合面上任一面元的电场强度通量等于零.10.用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心O 点的电场强度.静电学练习1答案1.(C ) 2.(B ) 3.(A ) 4. 0,pE sin α5. Q / ε0 )R /(r Q E ,E b a 2001850πε ==6. -3σ / (2ε0) ,-σ / (2ε0) ,σ / (2ε0) ,3σ / (2ε0)7.设杆的左端为坐标原点O ,x 轴沿直杆方向.带电直杆的电荷线密度为λ=q / L ,在x 处取一电荷元d q = λd x = q d x / L ,它在P 点的场强大小: LP3()204d d x d L q E -+π=ε()20x d L L ε4x d q -+=π总场强大小为 ⎰+π=Lx d L x L q E 020)(d 4-ε()d L d q+π=04ε 方向沿x 轴,即杆的延长线方向.8. 通过x =a 处平面1的电场强度通量Φ1 = -E 1 S 1= -b a 3通过x = 2a 处平面2的电场强度通量Φ2 = E 2 S 2 = 2b a 3其它平面的电场强度通量都为零.因而通过该高斯面的总电场强度通量为Φ = Φ1+ Φ2 = 2b a 3-b a 3 = b a 3 =1 N ·m 2/C9. (1) 正确.(2) 错误,虽然有0d =⎰⋅S E S,但本题中闭合面上各点场强均不为零.(3) 错误,通过整个闭合面的电场强度通量为零,而通过任一面元的电场强 度通量不一定为零(本题中任一面元上都不为零). 10.选取圆心O 为原点,坐标Oxy 如图所示,其中Ox 轴沿半圆环的对称轴。
