小学奥数训练专题 数阵图(二).学生版【推荐】.doc
66666小学奥数专题之数阵图练习题例

小学奥数专题之——————数阵图数阵是由幻方演化出来的另一种数字图。
幻方一般均为正方形。
图中纵、横、对角线数字和相等。
数阵则不仅有正方形、长方形,还有三角形、圆、多边形、星形、花瓣形、十字形,甚至多种图形的组合。
变幻多姿,奇趣迷人。
一般按数字的组合形式,将其分为三类,即辐射型数阵、封闭型数阵、复合型数阵。
数阵的特点是:每一条直线段或由若干线段组成的封闭线上的数字和相等。
它的表达形式多为给出一定数量的数字,要求填入指定的图中,使其具备数阵的特点。
解数阵问题的一般思路是:1.求出条件中若干已知数字的和。
2.根据“和相等”,列出关系式,找出关键数——重复使用的数。
3.确定重复用数后,对照“和相等”的条件,用尝试的方法,求出其他各数。
有时,因数字存在不同的组合方法,答案往往不是唯一的。
\1.10.5.2辐射型数阵例1 将1~5五个数字,分别填入下图的五个○中,使横、竖线上的三个数字和都是10。
解:已给出的五个数字和是:1+2+3+4+5=15题中要求横、竖每条线上数字和都是10,两条线合起来便是20了。
20-15=5,怎样才能增加5呢?因为中心的一个数是个重复使用数。
只有5连加两次才能使五个数字的和增加5,关键找到了,中心数必须填5。
确定中心数后,按余下的1、2、3、4,分别填在横、竖线的两端,使每条线上数的和是10便可。
例2将1~7七个数字,分别填入图中的各个○内,使每条线上的三个数和相等。
:解:图中共有3条线,若每条线数字和相等,三条线的数字总和必为3的倍数。
设中心数为a,则a被重复使用了2次。
即,1+2+3+4+5+6+7+2a=28+2a,28+2a应能被3整除。
(28+2a)÷3=28÷3+2a÷3其中28÷3=9…余1,所以2a÷3应余2。
由此,便可推得a只能是1、4、7三数。
当a=1时,28+2a=30 30÷3=10,其他两数的和是10-1=9,只要把余下的2、3、4、5、6、7,按和为9分成三组填入两端即可。
小学奥林匹克数学 数阵练习(2)(无答案)
小学奥林匹克数学数阵练习(2)(无答案)
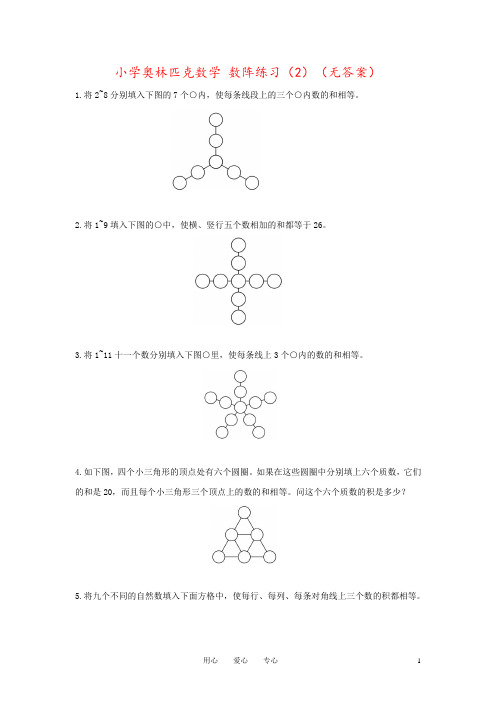
1.将2~8分别填入下图的7个○内,使每条线段上的三个○内数的和相等。
2.将1~9填入下图的○中,使横、竖行五个数相加的和都等于26。
3.将1~11十一个数分别填入下图○里,使每条线上3个○内的数的和相等。
4.如下图,四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数的和相等。
问这个六个质数的积是多少?
5.将九个不同的自然数填入下面方格中,使每行、每列、每条对角线上三个数的积都相等。
6.将1~9九个自然数分别填入下图的九个小三角形中,使靠近大三角形每条边上五个数的和
相等,并且尽可能大,这五个数之和最大是多少?
7.在空格中填入不同的数,使每一横行、竖行、斜行的三个数的和等于18。
8.将5、6、7、9、10、11六个数分别填在下面图的小圆圈里,使每个大圆的三个数及每条
直线上的三个数加起来分别等于24。
9.将1~7七个自然数分贝填入图中圆圈里,使每条线上三个数的和相等。
10.将1~8八个数分别填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四
格以及对角线四格内四个数的和都是18。
11.将1~8八个数分别填入下图的○内,使每边上的三个数的和相等。
12.将2~9八个数分别填入下图○内,使外圆四个数的和,内圆四个数的和以及横行、竖行
上四个数的和都等于22。
13.将1~9九个数分别填入下图○内,使外三角形边上○内数字和等于里面三角形边上○内数字的和。
二年级奥数数阵图
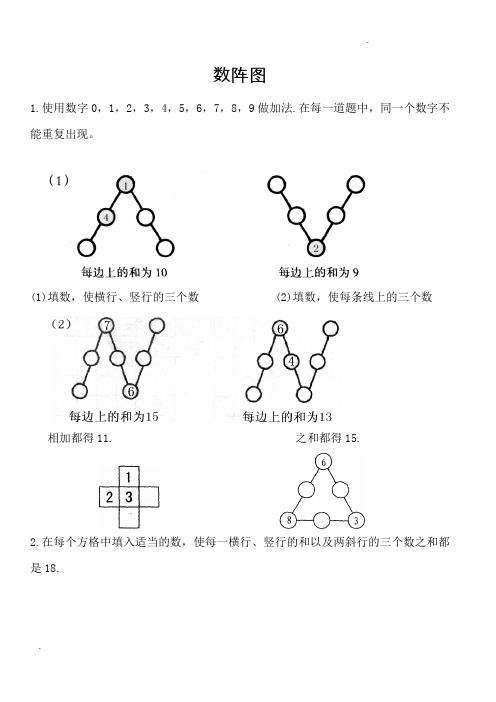
数阵图1.使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现。
(1)填数,使横行、竖行的三个数 (2)填数,使每条线上的三个数相加都得11. 之和都得15.2.在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.在空格中填入适当的数,使横行和竖行或每条对角线上的三个数相加都等于15。
3.把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数之和都等于14。
拓展练习(1)把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于12。
(2)把1,2,3,4,5,6分别填入○里,使每一个大椭圆上的四个数之和等于13.例4. 把1,3,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为17。
简单数阵图例1、把1—5 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
例2、把1—7这七个数分别填入图中的各○内,使每条线段上三个○内数的和等于10。
例3、在下图圆圈内分别填入数字1~9,使两条直线上五个数的和相等,和是多少?例4、把1~6这六个数分别填在下图中三角形三条边的六个○内,使每条边上三个○内数的和等于9。
例5、将2—9这八个数分别填入右图的○里,使每条边上的三个数之和都等于18。
例6、将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中,使三角形每边上四个数的和是17。
1、把2—6 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于13。
2、在图中填入2—9,使每边3个数的和等于15。
3、将数字1—9分别填在图中的○内使每条线上五个○内数的和等于27。
4、把1、4、7、10、13、16、19七个数填入图中7朵花里,使每条线上三个数的和等于30。
二年级奥数数阵图

专题五简单数阵图一、辐射型数阵图从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中心数,多算的次数,公共的和数和+中心数×重复次数=公共的和×线数数和:指所有要填的数字加起来的和中心数:指中间那数字,即重复计算那数字重复次数:中心数多算的次数,一般比线数少1公共的和:指每条直线上几个数的和线数:指算公共和的线条数例1、把1—5 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
例2、把1—7这七个数分别填入图中的各○内,使每条线段上三个○内数的和等于10。
例3、在下图圆圈内分别填入数字1~9,使两条直线上五个数的和相等,和是多少?二、封闭型数阵图多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
突破关键:确定顶点上的数字,公共的和数和+重叠数的和=公共的和×边数数和、公共的和跟辐射型数阵图一样的意思重叠数的和:指数阵图顶角重复算的数全加起来的和边数:指封闭图形的边数例4、把1~6这六个数分别填在下图中三角形三条边的六个○内,使每条边上三个○内数的和等于9。
例5、将2—9这八个数分别填入右图的○里,使每条边上的三个数之和都等于18。
例6、将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中,使三角形每边上四个数的和是17。
练习五1、把2—6 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于13。
2、在图中填入2—9,使每边3个数的和等于15。
3、将数字1—9分别填在图中的○内使每条线上五个○内数的和等于27。
4、把1、4、7、10、13、16、19七个数填入图中7朵花里,使每条线上三个数的和等于30。
二年级奥数数阵图

数阵图小朋友们,你喜欢填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!例1.使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现。
(1)填数,使横行、竖行的三个数 (2)填数,使每条线上的三个数相加都得11. 之和都得15.例2.在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.在空格中填入适当的数,使横行和竖行或每条对角线上的三个数相加都等于15。
例3.把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数之和都等于14。
拓展练习(1)把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于12。
(2)把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.例4.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12。
把1,3,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为17。
简单数阵图一、辐射型数阵图从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中心数,多算的次数,公共的和数和+中心数×重复次数=公共的和×线数数和:指所有要填的数字加起来的和中心数:指中间那数字,即重复计算那数字重复次数:中心数多算的次数,一般比线数少1公共的和:指每条直线上几个数的和线数:指算公共和的线条数例1、把1—5 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
例2、把1—7这七个数分别填入图中的各○内,使每条线段上三个○内数的和等于10。
例3、在下图圆圈内分别填入数字1~9,使两条直线上五个数的和相等,和是多少?二、封闭型数阵图多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
小学一年级奥数 简单的数阵图_PDF压缩
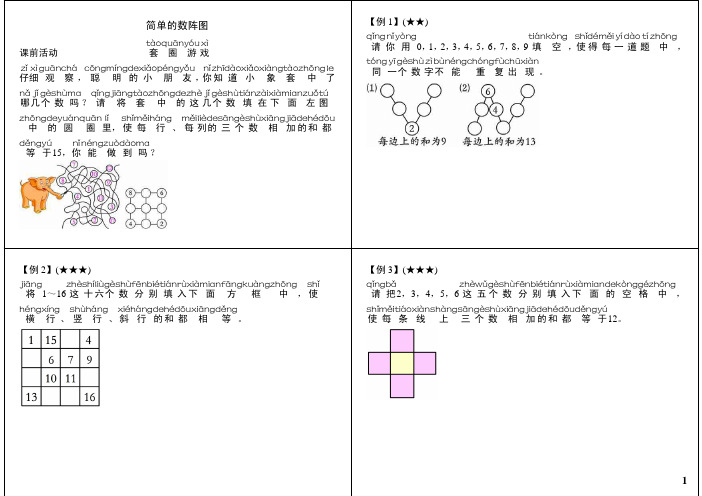
【例 3】(★★★)
qǐngbǎ
zhèwǔgèshùfēnbiétiánrùxiàmiandekònggézhōng
请 把2,3,4,5,6 这 五 个 数 分 别 填 入 下 面 的 空 格 中 ,
zhōngdeyuánquān lǐ shǐměiháng měilièdesāngèshùxiāngjiādehédōu 中 的 圆 圈 里, 使 每 行 、 每 列的 三 个 数 相 加 的 和 都
děngyú nǐnéngzuòdàoma 等 于15,你 能 做 到 吗 ?
【例 1】(★★)
qǐng nǐ yòng
fúshèxíngshùzhèntú zhǐyǒu yī gèchóngdiéshù 三、辐 射 型 数 阵 图( 只 有 一个 重 叠 数 )
liánxùshù shìtóu shìwěi shìzhōngjiān qíyúxiǎoshǒulā dàshǒu 连 续 数 :试 头 、试 尾 、试 中 间 ;其余 小 手 拉大 手 。
xiàn shùxiàn xiéxiànliánjiēqǐláidesāngèyuánquānnèideshùzhīhédōu 线 、 竖 线 、 斜 线 连 接起来的 三 个 圆 圈 内 的 数 之 和 都
děngyú 等 于15。
【拓展】(★★★★)
qǐng nǐ bǎ
zhèqīgèshùfēnbiétiánrùyuánquān lǐ shǐ
tiáozhíxiànshàngdesāngèshùxiāngjiādehédōuwéi
条 直 线 上 的 三 个 数 相 加 的 和 都 为 12。
小学奥数—数阵图
数阵图
[同步巩固演练]
1、把1—7这七个数填入图中的○中,使每条直线上三个数的和都等于14。
2、将1—9这九个数填入图中的○中,使每条边上四个数的和都等于17。
3、将数字1,2,3,4,5,6填入图中的小圆圈内,使每个大圆上4个数字的和都是16。
4,将1—8填在图中的○中,使每条线上的三个数的和都相等,并求出这个和的取值范围。
5、将1—8填在图中的○中,使大圆上、小圆上、横线上、竖线上四个数的和都相等,而且在大圆上的四个数中最大的数尽可能小。
[能力拓展平方]
1、将1,2,3,4,8,12这六个数分别填入图中的○内,使每条线上的三个数的积相等。
2、右图是一部古怪的电话,中间的十二个键分别为四个圆形、四个椭圆形和四个正方形,若想打电话,必须首先将1~12这十二个数填入其中,使四个椭圆、四个圆形、四个正方形以及四条直线上的四个数之和都为26,假如你要打电话,那么你将怎样填数?
3、请在下图的空格内填入1~46这四十六个自然数,使每一笔直线上各数之和都等于93,应怎样填?
4、将1~9九个数分别填入图中○内,使外三角形边上○内数字之和等于里面三角形边上○内数字之和。
第4题
5、在下左图中,将1~9这九个数,填入圆圈内,使每个三角形三个顶点的数字之和都相等。
6、把1~10这十个自然数填入图中的10个方格中,要求图中3个2×2的正方形中四数之和相等,那么,这个和的最小值是几?。
五年级奥数-数阵图与数字谜(含解析)
数阵图与数字谜教学目标1. 熟悉数阵图与数字谜的题目特点;2. 掌握数阵图与数字谜的解题思路。
精讲讲练数阵图数阵图是把一些数按照一定规则填在某一特定图形的规定位置上而来的图形,有时简称数阵。
【例1】 (2007年“希望杯”第二试)在右图所示○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点的三个数的和是__________。
【分析】 由于每条边上的三个数的和都是12,所以把这三条边上的三个数的和都加起来,总和应为12336⨯=,在其中,A 、B 、C 各算了一次,三个顶点的三个数各算了两次,所以三个顶点的三个数的和为(3618)29-÷=。
【例2】 (2007年天津“陈省身杯”国际青少年数学邀请赛)将112:这十二个自然数分别填入右图的12个圆圈内,使得每条直线上的四个数之和都相等,这个相等的和为__________。
【分析】 由于每条直线上的四个数之和都相等,设这个相等的和为S ,把所有6条直线上的四个数之和相加,得到总和为6S ;另一方面,在这样相加中,由于每个数都恰好在两条直线上,所以每个数都被计算了两遍。
所以,6(12312)2S =++++⨯L ,得到26S =,即所求的相等的和为26。
【例3】 (2007年“走进美妙的数学花园”决赛)如右图所示,A ,B ,C ,D ,E ,F ,G ,H ,I ,J 表示110:这10个各不相同的数字。
表中的数为所在行与列的对应字母的和,例如“14G C +=”。
请将表中其它的数全部填好。
C BA【分析】 由于5A F +=,14B F +=,所以1459B A -=-=,所以A 和B 只能是0和9。
因此可以推出:0A =,9B =,6C =,3D =,2E =,5F =,8G =,1H =,4I =,7J =。
可得右下图。
【例4】 (2007年“走进美妙的数学花园”初赛)从1、2、3…20这20个数中选出9个不同的数放入33⨯的方格表中,使得每行、每列、每条对角线上的三个数的和都相等。
1.12小学必学奥数 数阵图综合
1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?例题精讲知识点拨教学目标5-1-3-1.数阵图)【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
CBA【例 4】 将1至6这六个数字填入图中的六个圆圈中(每个数字只能使用一次),使每条边上的数字和相等.那么,每条边上的数字和是 .789fedcba 789【例 5】 将1到8这8个自然数分别填入如图数阵中的8个圆圈,使得数阵中各条直线上的三个数之和都相等,那么A 和B 两个圆圈中所填的数之差(大数减小数)是______.BA【例 6】 如图所示,圆圈中分别填人0到9这10个数,且每个正方形顶点上的四个数之和都是18,则中间两个数A 与B 的和是________。
BA【例 7】 把2~11这10个数填到右图的10个方格中,每格内填一个数,要求图中3个22 的正方形中的4个数之和相等.那么,这个和数的最小值是多少?111098765432【例 8】 下图中有五个正方形和12个圆圈,将1~12填入圆圈中,使得每个正方形四角上圆圈中的数字之和都相等.那么这个和是多少?861102912311457【例 9】 如图,大、中、小三个正方形组成了8个三角形,现在把2、4、6、8四个数分别填在大正方形的四个顶点;再把2、4、6、8分别填在中正方形的四个顶点上;最后把2、4、6、8分别填在小正方形的四个顶点上.⑴能不能使8个三角形顶点上数字之和都相等?⑵能不能使8个三角形顶点上数字之和各不相同?如果能,请画图填上满足要求的数;如果不能,请说明理由.246824688642【例 10】 将1~16分别填入下图(1)中圆圈内,要求每个扇形上四个数之和及中间正方形的四个数之和都为34,图中已填好八个数,请将其余的数填完.【例 11】一个3 3的方格表中,除中间一格无棋子外,其余梅格都有4枚一样的棋子,这样每边三个格子中都有12枚棋子,去掉4枚棋子,请你适当调整一下,使每边三格中任有12枚棋子,并且4个角上的棋子数仍然相等(画图表示)。
第四讲 有趣地数阵图学生版 奥数教程 讲义
经典精讲:数阵图:将一些数按照一定的要求排列成各种各样的图形。
数阵图是一种趣味性很强的填数游戏,它的形式多样,绚丽奇妙。
这里给同学们介绍三种形式的数阵图,即封闭型数阵图、辐射型数阵图和复合型数阵图。
(一)辐射型数阵图(像雪花)从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中间数,多算的次数,公共的和线数x 公共的和=数和+中心数x 重复次数【例1】把1—5 这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
【例2】把1—7这七个数分别填入图1中的各○内,使每条线段上三个○内数的和相等。
【课堂练习】将1~11这11个数分别填入图11中的方格内,每个数只许用一次,使相邻两个或三个方格内数的和都相等。
第四讲 有趣的数阵图(二)封闭型数阵图(像围墙)多边形的每条边放同样多的数,使它们的和都等于一个不变的数。
突破关键:确定顶点上的数字,公共的和边数x公和=数和+重叠数和【例3】把1~6这六个数分别填在下图中三角形三条边的六个○内,使每条边上三个○内数的和相等。
(本题有24种填法,你能想出几种?)【例4】将2—9这八个数分别填入右图的○里,使每条边上的三个数之和都等于18。
【课堂练习】 1、1—10这十个数,分别填在图9中五边形五条边上的十个○内,并使五条边上的三个○内数的和相等。
2、把1—8这8个数,填入图13中的八个○内,使每条线段上的四个数的和,与每个四边形四个顶点上的四个数的和都相等。
(三)复合型数阵图既有辐射型数阵图的特点,又有封闭型数阵图的特点。
突破点:找出关键位置重复次数。
【例5】将1~7这七个数分别填入下图的○里,使得每条直线上三个数之和与每个圆圈上的三个数之和都相等。
【课堂练习】1、将1、2、3、4、5、6六个数字填入图中的小圆圈内,使每个大圆上四个数字的和是16。
2、将1—8这八个数,分别填入图10中两个圆圈的八个○内,使每个圆圈上五个○内数的和分别为20、21、22。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
1. 了解数阵图的种类
2. 学会一些解决数阵图的解题方法
3. 能够解决和数论相关的数阵图问题
.
一、数阵图定义及分类:
1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.
2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数
阵图、辐射型数阵图和复合型数阵图.
3.
二、解题方法:
解决数阵类问题可以采取从局部到整体再到局部的方法入手:
第一步:区分数阵图中的普通点(或方格)和关键点(或方格);
第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得
到关键点上所填数的范围;
第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学
方法的综合运用.
复合型数阵图
【例 1】 由数字1、2、3组成的不同的两位数共有9个,老师将这9个数写在一个九宫格上,让同学选
数,每个同学可以从中选5个数来求和.小刚选的5个数的和是120,小明选的5个数的和是
111.如果两人选的数中只有一个是相同的,那么这个数是_____________.
313233
212223
131211
【例 2】 如图1,圆圈内分别填有1,2,……,7这7个数。如果6个三角形的顶点处圆圈内的数字的
和是64,那么,中间圆圈内填入的数是 。
例题精讲
知识点拨
教学目标
5-1-3-2.数阵图
|初一·数学·基础-提高-精英·学生版| 第1讲 第页
2
【例 3】 如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈
上三个数的和.
(1)
17
8
9
4
【例 4】 请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之
和与每条直线上的三个数之和相等.应怎样填?
【例 5】 在左下图的每个圆圈中填上一个数,各数互不相等,每个圆圈有3个相邻(即有线段相连的圆圈)
的圆圈。将左下图中每个圆圈中的数改为3个相邻圆圈所填数的平均值,便得到右下图。如果
左下图中已有一个数1,请填出左下图中的其它数,使得右下图中的数都是自然数。
【例 6】 将1至8这八个自然数分别填入图中的正方体的八个顶点处的内,并使每个面上的四个内
的数字之和都相等。求与填入数字1的有线段相连的三个内的数的和的最大值。
【例 7】 将自然数1到11分别填在右图的圆圈内,使得图中每条直线上的三个圆圈内的数的和相等.
3
18-c-d
18-b-c
c+d-6
b+c-6
12-d
12-c
12-b
d
c
b
6
1110987543
216
【例 8】 在下图中,在每个圆圈中填入一个数,使每条直线上所有圆圈中数的和都是234,那么标有★
的圆圈中所填的数是_____________.
★
f
e
d
cb
a
★
【例 9】 请将1,2,3,…,10这10个自然数填入图中的10个小圆圈内,使得图中的10条直线上圆圈
内数字之和都相等.那么乘积ABC ?
C
B
A
【例 10】 下图中有11条直线.请将1至11这11个数分别填在11个圆圈里,使每一条直线上所有数的
和相等.求这个相等的和以及标有*的圆圈中所填的数.
﹡
|初一·数学·基础-提高-精英·学生版| 第1讲 第页
4
【例 11】 “美妙的数学花园”这7个字各代表1~7中的一个数,并且每个圆中4个数的和都是15。如果
学比美大,美比园大,那么,园表示 。
【例 12】 图2中的五个问号分别表示五个连续的自然数,它们的和等于130,三角形内两个数的和等于
53,圆内三个数的和等于79,正方形内两个数的和等于50。那么,从左向右,这五个问号依次
是
?????
【例 13】 右图是大家都熟悉的奥林匹克五环标志.请将19分别填入五个圆相互分割的九个部分,并且
使每个圆环内的数字之和都相等.
【例 14】 2008年奥运会在北京举行。“奥”、“运”、 “会”、“北”、“京”这五个汉字代表五个连续的自然数,
将其分别填在五环图案的五个环内,满足“奥”+“运”+“会”=“北”+“京”。这五个自然数的和最大
是 。
京
北
会运奥
【例 15】 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填
数的和都等于2008。这九个数总和最小为 。
5
【例 16】 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,A,B,C,D,
E,F,G,H,I的总和是2008,并且每个圆中所填的数和都等于M。(1)M
最大为多少?
(2)
M
最小为多少?
【例 17】 将数字1~9分别填在下图空白的正六边形格子中,使得箭头所指直线方向上空格中所填的数字
和等于该箭头所在格中的给定数(每个方向上所填的数互不相同,且到写有另一个给定数字的
格为止)。例如:20,22,19ABCDEFGHCIJKMN。当填写完后,字母C处所写的数字是_____________。
D
CAHEGMFIBKN102720282269
19241020
20
26J23
A. 4 B. 5 C. 7 D. 9
【例 18】 用数字1至9填满空格,一个格子只能填入一个数字,每个数字在每一行,每一列(相连或不相
连)及每个粗线围成的区域中至多出现一次。
【例 19】 用l—9填满三角形空格,一个格子只能填入一个数字,使每个数字在每一行,每一列(包括不相
连的行,列)及每个粗黑线围成的区域中至多出现一次.
|初一·数学·基础-提高-精英·学生版| 第1讲 第页
6
