二叉树的创建及先序、中序、后序遍历
前序遍历和后续遍历

首先明确:一颗二叉树的前序遍历=根节点+左子树前序遍历+右子树前序遍历
一颗二叉树的中序遍历=左子树中序遍历+根节点+右子树中序遍历
那么从前序遍历中取第一个点,就是根节点,知道了根节点,就可以找到中序遍历中跟节点的位置,那么就可以在中序遍历中找到左子树和右子树。
首先,我们看看前序、中序、后序遍历的特性:
前序遍历:
1.访问根节点
2.前序遍历左子树
3.前序遍历右子树
中序遍历:
1.中序遍历左子树
2.访问根节点
3.中序遍历右子树
后序遍历:
1.后序遍历左子树
2.后序遍历右子树
3.访问根节点
好了,先说说用前序遍历和中序遍历求后序遍历
假设前序遍历为adbgcefh, 中序遍历为dgbaechf
前序遍历是先访问根节点,然后再访问子树的,而中序遍历则先访问左子树再访问根节点
那么把前序的a 取出来,然后查找a 在中序遍历中的位置就得到dgb a echf
那么我们就知道dgb 是左子树echf 是右子树,因为数量要吻合
所以前序中相应的dbg 是左子树cefh 是右子树
然后就变成了一个递归的过程,具体代码如下:
而已知后序遍历和中序遍历求前序遍历的过程差不多,但由于后序遍历是最后才访问根节点的所以要从后开始搜索,例如上面的例子,后序遍历为gbdehfca,中序遍历为dgbaechf
后序遍历中的最后一个元素是根节点,a,然后查找中序中a的位置
把中序遍历分成dgb a echf,而因为节点个数要对应
后序遍历分为gbd ehfc a,gbd为左子树,ehfc为右子树,这样又可以递归计算了
其他一些附带的代码上面已经有,这里就不重复贴了,具体代码如下:。
二叉树的基本操作课件浙教版(2019)高中信息技术选修1(24张PPT)

A
B
D
C
E
F
G
头指针
二叉树的list实现
二叉树节点可以看成是一个三元组,元素是左、右子树和本节点数据。
Python的list可以用于组合这样的三个元素。
下面介绍用list构造二叉树的方法。
(1)空树用None表示。
(2)非空二叉树用包含三个元素的列表[d,l,r]表示,其中:d表示根节点的元素,l和r是两棵子树,采用与整个二叉树同样结构的list表示。
二叉树的遍历
在完成二叉树的建立操作后,就可以对二叉树的各个节点进行访问,即遍历操作。二叉树的遍历,是指按照一定的规则和次序访问二叉树中的所有节点,使得每个节点都被访问一次且仅被访问一次。按照不同的遍历方式对节点进行访问,其处理效率不完全相同。二叉树的遍历方式有很多,主要有前序遍历、中序遍历和后序遍历等。
1.数组实现
用数组来表示二叉树时,分为以下两种情况。
(1)完全二叉树从二叉树的根节点开始,按从上而下、自左向右的顺序对n个节点进行编号,根节点的编号为0,最后一个节点的编号为n-1。然后依次将二叉树的节点用一组连续的数组元素来表示,节点编号与数组的下标一一对应。如下图中图甲所示的完全二叉树所对应的一维数组表示如图乙所示。
A
B
C
A
B
C
甲 原二叉树
乙 补全后的二叉树
0
1
2
3
4
5
6
7
丙 数组实现示意图
A
B
C
对于完全二叉树而言,一维数组的表示方式既简单又节省存储空间。但对于一般的二叉树来说,采用一维数组表示时,结构虽然简单,却容易造成存储空间的浪费。
二叉树的建立与先序中序后序遍历 求叶子节点个数 求分支节点个数 求二叉树的高度

/*一下总结一些二叉树的常见操作:包括建立二叉树先/中/后序遍历二叉树求二叉树的叶子节点个数求二叉树的单分支节点个数计算二叉树双分支节点个数计算二叉树的高度计算二叉树的所有叶子节点数*/#include<stdio.h> //c语言的头文件#include<stdlib.h>//c语言的头文件stdlib.h千万别写错了#define Maxsize 100/*创建二叉树的节点*/typedef struct BTNode //结构体struct 是关键字不能省略结构体名字可以省略(为无名结构体)//成员类型可以是基本型或者构造形,最后的为结构体变量。
{char data;struct BTNode *lchild,*rchild;}*Bitree;/*使用先序建立二叉树*/Bitree Createtree() //树的建立{char ch;Bitree T;ch=getchar(); //输入一个二叉树数据if(ch==' ') //' '中间有一个空格的。
T=NULL;else{ T=(Bitree)malloc(sizeof(Bitree)); //生成二叉树(分配类型*)malloc(分配元素个数*sizeof(分配类型))T->data=ch;T->lchild=Createtree(); //递归创建左子树T->rchild=Createtree(); //地柜创建右子树}return T;//返回根节点}/*下面先序遍历二叉树*//*void preorder(Bitree T) //先序遍历{if(T){printf("%c-",T->data);preorder(T->lchild);preorder(T->rchild);}} *//*下面先序遍历二叉树非递归算法设计*/void preorder(Bitree T) //先序遍历非递归算法设计{Bitree st[Maxsize];//定义循环队列存放节点的指针Bitree p;int top=-1; //栈置空if(T){top++;st[top]=T; //根节点进栈while(top>-1) //栈不空时循环{p=st[top]; //栈顶指针出栈top--;printf("%c-",p->data );if(p->rchild !=NULL) //右孩子存在进栈{top++;st[top]=p->rchild ;}if(p->lchild !=NULL) //左孩子存在进栈{top++;st[top]=p->lchild ;}}printf("\n");}}/*下面中序遍历二叉树*//*void inorder(Bitree T) //中序遍历{if(T){inorder(T->lchild);printf("%c-",T->data);inorder(T->rchild);}}*//*下面中序遍历二叉树非递归算法设计*/void inorder(Bitree T) //中序遍历{Bitree st[Maxsize]; //定义循环队列,存放节点的指针Bitree p;int top=-1;if(T){p=T;while (top>-1||p!=NULL) //栈不空或者*不空是循环{while(p!=NULL) //扫描*p的所有左孩子并进栈{top++;st[top]=p;p=p->lchild ;}if(top>-1){p=st[top]; //出栈*p节点,它没有右孩子或右孩子已被访问。
二叉树遍历算法——包含递归前、中、后序和层次,非递归前、中、后序和层次遍历共八种

⼆叉树遍历算法——包含递归前、中、后序和层次,⾮递归前、中、后序和层次遍历共⼋种⾸先,要感谢⽹上的参考资料。
1. /876134/1178079(作者:BlackAlpha)2. /fzh1900/article/details/14056735(作者:_云淡风轻)3. /stpeace/article/details/8138458(作者:stpeace)⼆叉树是使⽤的⽐较⼴泛的⼀种数据结构,这⾥我写了⼆叉树的相关操作,包括初始化、新建、以及遍历。
这⾥主要是为了学习⼆叉树的遍历算法,我总结后,写了⼋种⼆叉树的遍历算法,分别是:1.递归先序遍历2.递归中序遍历3.递归后序遍历4.⾮递归先序遍历(单栈辅助)5.⾮递归中序遍历(单栈辅助)6.⾮递归后序遍历(单栈辅助)7.递归层次遍历8.⾮递归层次遍历(队列辅助)当然,这⾥还要⽤到栈和队列,博客中以前有提到过(链式的栈和链式队列),其实还可以⽤顺序栈和顺序队列的(博客中后⾯将补上这块)。
下⾯直接上代码:LinkStack.h 链式栈头⽂件[cpp]1. #ifndef _LINK_STACK_H_H2. #define _LINK_STACK_H_H3.4. #include "BiTree.h"5.6. typedef pBiTree LStackEle;7.8. typedef struct LSNODE9. {10. LStackEle ele;11. struct LSNODE *pnext;12. }LSNode, *pLSNode;13.14. typedef struct LSTACK15. {16. pLSNode top;17. }LStack, *pLStack;18.19. //栈初始化20. void InitLinkStack(LStack &s);21.22. //⼊栈23. void PushLinkStack(LStack &s, LStackEle ele);24.26. void PopLinkStack(LStack &s, LStackEle &ele);27.28. //判断栈是否为空29. bool IsemptyLinkStack(LStack s);30.31. //获得栈顶值32. LStackEle GetTopLinkStack(LStack s);33.34. #endifLinkQueue.h 链式队列头⽂件[html]1. #ifndef _LINK_QUEUE_H_H2. #define _LINK_QUEUE_H_H3.4. #include "BiTree.h"5.6. typedef pBiTree LQueueEle;7.8. typedef struct LQNODE9. {10. LQueueEle ele;11. struct LQNODE *pnext;12. }LQNode, *pLQNode;13.14. typedef struct LQUEUE15. {16. pLQNode rear;17. pLQNode front;18. }LQueue, *pLQueue;19.20. //初始化队列21. void InitLinkQueue(LQueue &q);22.23. //⼊队24. void EnLinkQueue(LQueue &q, LQueueEle ele);25.26. //出队27. void DeLinkQueue(LQueue &q, LQueueEle &ele);28.29. //判断队列是否为空30. bool IsemptyLinkQueue(LQueue q);31.32. //获得队头元素值33. LQueueEle GetFrontLinkQueue(LQueue q);34.35. #endifBiTree.h ⼆叉树头⽂件[cpp]1. #ifndef _BITREE_H_H2. #define _BITREE_H_H3.4. typedef struct BINODE5. {7. struct BINODE *plchild;8. struct BINODE *prchild;9. }BiNode, *pBiTree;10.11. //初始化⼆叉树(含根节点)12. void InitBiTree(pBiTree &bt, int ele);13.14. //创建⼆叉树节点15. BiNode *CreateBiTreeNode(pBiTree lchild, pBiTree rchild, int ele);16.17. //插⼊左⼦⼆叉树18. void InsertLChild(pBiTree parent, pBiTree lchild);19.20. //插⼊右⼦⼆叉树21. void InsertRChild(pBiTree parent, pBiTree rchild);22.23. //计算⼆叉树的深度24. int DeepBiTree(pBiTree bt);25.26. //递归先序遍历27. void RePreOrderTraverse(pBiTree bt);28.29. //递归中序遍历30. void ReInOrderTraverse(pBiTree bt);31.32. //递归后序遍历33. void RePostOrderTraverse(pBiTree bt);34.35. //⾮递归先序遍历⼆36. void NonRePreOrderTraverse(pBiTree bt);37.38. //⾮递归中序遍历39. void NonReInOrderTraverse(pBiTree bt);40.41. //⾮递归后序遍历42. void NonRePostOrderTraverse(pBiTree bt);43.44. //⾮递归层次遍历45. void NonReLevelOrderTraverse(pBiTree bt);46.47. //递归层次遍历48. void ReLevelOrderTraverse(pBiTree bt);49.50. void PrintLevelNode(pBiTree bt, int level);51.52. #endifLinkStack.cpp 链式栈源⽂件[html]1. #include "LinkStack.h"2. #include <stdlib.h>3. #include <stdio.h>4.5. //栈初始化6. void InitLinkStack(LStack &s)7. {8. s.top= NULL;9. }10.11. //⼊栈12. void PushLinkStack(LStack &s, LStackEle ele)13. {14. pLSNode pnew = (pLSNode)malloc(sizeof(LSNode));15. if (pnew == NULL)16. {17. printf("内存分配失败!\n");18. exit(EXIT_FAILURE);19. }20.21. pnew->ele = ele;22. pnew->pnext = s.top;23. s.top = pnew;24. }25.26. //出栈27. void PopLinkStack(LStack &s, LStackEle &ele)28. {29. pLSNode pt = NULL;30. if (IsemptyLinkStack(s))31. {32. printf("栈为空,不能出栈操作!\n");33. exit(EXIT_FAILURE);34. }35. else36. {37. ele = s.top->ele;38. pt = s.top;39. s.top = pt->pnext;40. free(pt);41. pt = NULL;42. }43.44. }45.46. //判断栈是否为空47. bool IsemptyLinkStack(LStack s)48. {49. if (s.top == NULL)50. return true;51. else52. return false;53. }54.55. //获得栈顶元素56. LStackEle GetTop(LStack s)57. {58. if (IsemptyLinkStack(s))59. {60. printf("栈为空,不能获得栈顶元素值!\n");61. exit(EXIT_FAILURE);62. }63. else64. return s.top->ele;65. }LinkQueue.cpp 链式队列源⽂件[cpp]1. #include <stdlib.h>2. #include <stdio.h>3. #include "LinkQueue.h"4.5. //初始化队列6. void InitLinkQueue(LQueue &q)7. {8. q.front = (pLQNode)malloc(sizeof(LQNode));9. if (q.front == NULL)10. {11. printf("内存分配失败!\n");12. exit(EXIT_FAILURE);13. }14.15. q.rear = q.front;16. }17.18. //⼊队19. void EnLinkQueue(LQueue &q, LQueueEle ele)20. {21. pLQNode pnew = (pLQNode)malloc(sizeof(LQNODE));22. if (pnew == NULL)23. {24. printf("内存分配失败!\n");25. exit(EXIT_FAILURE);26. }27.28. pnew->ele = ele;29. pnew->pnext = NULL;30. q.rear->pnext = pnew;31. q.rear = pnew;32. }33.34. //出队35. void DeLinkQueue(LQueue &q, LQueueEle &ele)36. {37. pLQNode pt = NULL;38.39. if (IsemptyLinkQueue(q))40. {41. printf("队列为空,不能出队操作!\n");42. exit(EXIT_FAILURE);43. }44.45. ele = q.front->pnext->ele;46. pt = q.front->pnext;47. q.front->pnext = pt->pnext;48. free(pt);49. /*50. pt是最后⼀个节点时,释放完了以后,尾指针指向的51. 是随机内存,所以让它和头指针指向同⼀个地址。
二叉树的先序,中序,后序遍历c语言

二叉树的先序,中序,后序遍历c语言
二叉树是常见的数据结构,具有广泛的应用场景,例如搜索树、哈夫曼树等。
其中比较重要的一点就是对二叉树的遍历。
二叉树遍历有三种方式:先序遍历、中序遍历、后序遍历。
接下来,我将通过C语言来详细介绍这三种遍历方式。
一、先序遍历(Preorder Traversal)
先序遍历是指根节点->左子树->右子树的遍历方式。
C语言中的先序遍历算法如下:
```
void preorderTraversal(Node *node) {
if (node != NULL) {
printf("%d ", node->data); // 打印节点值
preorderTraversal(node->left); // 递归遍历左子树
preorderTraversal(node->right); // 递归遍历右子树
}
}
```
先序遍历的实现通过递归调用实现,当节点为空即遍历完成时返回。
总结:
以上三种遍历方式是二叉树遍历中最基本的方法,它们都是基于递归实现的。
通过学习这三种遍历方式,可以更好地理解二叉树的结构特点,提高数据结构算法的学习效果。
c语言二叉树的先序,中序,后序遍历
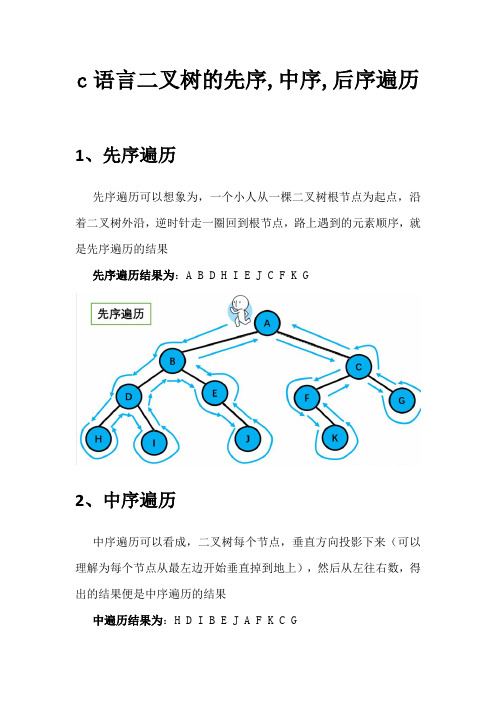
c语言二叉树的先序,中序,后序遍历1、先序遍历先序遍历可以想象为,一个小人从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果先序遍历结果为:A B D H I E J C F K G2、中序遍历中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果中遍历结果为:H D I B E J A F K C G3、后序遍历后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。
还记得我上面提到先序遍历绕圈的路线么?(不记得翻上面理解)就是围着树的外围绕一圈,如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄)(也就是葡萄要一个一个掉下来,不能一口气掉超过1个这样),就把它剪下来,组成的就是后序遍历了。
后序遍历中,根节点默认最后面后序遍历结果:H I D J E B K F G C A4、口诀先序遍历:先根再左再右中序遍历:先左再根再右后序遍历:先左再右再根这里的根,指的是每个分叉子树(左右子树的根节点)根节点,并不只是最开始头顶的根节点,需要灵活思考理解5、代码展示#include<stdio.h>#include<stdlib.h>typedef struct Tree{int data; // 存放数据域struct Tree *lchild; // 遍历左子树指针struct Tree *rchild; // 遍历右子树指针}Tree,*BitTree;BitTree CreateLink(){int data;int temp;BitTree T;scanf("%d",&data); // 输入数据temp=getchar(); // 吸收空格if(data == -1){ // 输入-1 代表此节点下子树不存数据,也就是不继续递归创建return NULL;}else{T = (BitTree)malloc(sizeof(Tree)); // 分配内存空间T->data = data; // 把当前输入的数据存入当前节点指针的数据域中printf("请输入%d的左子树: ",data);T->lchild = CreateLink(); // 开始递归创建左子树printf("请输入%d的右子树: ",data);T->rchild = CreateLink(); // 开始到上一级节点的右边递归创建左右子树return T; // 返回根节点}}// 先序遍历void ShowXianXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}printf("%d ",T->data);ShowXianXu(T->lchild); // 递归遍历左子树ShowXianXu(T->rchild); // 递归遍历右子树}// 中序遍历void ShowZhongXu(BitTree T) // 先序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowZhongXu(T->lchild); // 递归遍历左子树printf("%d ",T->data);ShowZhongXu(T->rchild); // 递归遍历右子树}// 后序遍历void ShowHouXu(BitTree T) // 后序遍历二叉树{if(T==NULL) //递归中遇到NULL,返回上一层节点{return;}ShowHouXu(T->lchild); // 递归遍历左子树ShowHouXu(T->rchild); // 递归遍历右子树printf("%d ",T->data);}int main(){BitTree S;printf("请输入第一个节点的数据:\n");S = CreateLink(); // 接受创建二叉树完成的根节点printf("先序遍历结果: \n");ShowXianXu(S); // 先序遍历二叉树printf("\n中序遍历结果: \n");ShowZhongXu(S); // 中序遍历二叉树printf("\n后序遍历结果: \n");ShowHouXu(S); // 后序遍历二叉树return 0;}。
二叉树教案
二叉树教案一、教学目标:1.了解二叉树的定义和性质。
2.学会二叉树的遍历算法(前序遍历、中序遍历、后序遍历)。
3.掌握二叉树的基本操作(创建二叉树、插入节点、删除节点)。
二、教学重点和难点:1.二叉树的定义和性质。
2.二叉树的遍历算法。
3.二叉树的基本操作。
三、教学准备:1.教师准备:PPT、计算机、投影仪。
2.学生准备:课前预习、纸笔。
四、教学过程:Step 1 导入新课教师通过提问的方式,引导学生回顾树的基本概念,并激发学生对二叉树的兴趣。
Step 2 二叉树的定义和性质教师给出二叉树的定义,并带领学生讨论二叉树的性质(每个节点最多有两个子节点,左子树和右子树)。
Step 3 二叉树的遍历算法1.前序遍历:先访问根节点,然后递归遍历左子树,再递归遍历右子树。
2.中序遍历:先递归遍历左子树,然后访问根节点,再递归遍历右子树。
3.后序遍历:先递归遍历左子树,然后递归遍历右子树,最后访问根节点。
Step 4 二叉树的基本操作1.创建二叉树:教师通过示例向学生展示二叉树的创建过程。
2.插入节点:教师通过示例向学生展示如何插入节点,并解释插入节点的规则。
3.删除节点:教师通过示例向学生展示如何删除节点,并解释删除节点的规则。
Step 5 练习与拓展1.教师设计练习题,让学生运用所学知识进行练习。
2.鼓励学生拓展二叉树的其他应用领域,并进行讨论。
五、教学反思本节课通过讲解二叉树的定义和性质,以及二叉树的遍历算法和基本操作,使学生对二叉树有了基本的了解和掌握。
通过练习和拓展,巩固了学生的学习成果,并培养了学生的分析和解决问题的能力。
但是,由于时间有限,学生的实际操作机会较少,可以在课后布置相关的作业,加深学生的理解和应用能力。
数据结构实验3:二叉树的操作
TextFile中。
(4) P:打印代码文件(Print)。
将文件CodeFile以紧凑格式显示在终端上,每行50个代码。
同时将此字符形式的编码文件写入文件CodePrin中。
(5) T:打印哈夫曼树(Tree printing)。
将已在内存中的哈夫曼树以直观的方式显示在终端上,同时将此字符形式的哈夫曼树写入文件TreePrint中。
3) 实现提示:(1) 文件CodeFile的基类型可以设为字节型。
(2) 用户界面可以设计为“菜单”方式:显示上述功能符号,再加上“Q”,表示退出运行Quit。
请用户键入一个选择功能符。
此功能执行完毕后再显示此菜单,直至某次用户选择了“E”为止。
(3) 在程序的一次执行过程中,第一次执行I、D或C命令之后,哈夫曼树已经在内存了,不必再读入。
每次执行中不一定执行I命令,因为文件hfmTree可能早已建好。
三、实验过程与实验结果实验3-01:以二叉链表为存储结构,实现二叉树的创建、遍历数据结构定义:typedef struct BiTNode{char data;BiTNode *lchild, *rchild;}BiTNode;typedef BiTNode *BiTree;算法设计思路简介:本实验需要实现以下操作:二叉树的初始化、前中后序遍历等基本操作1.利用递归实现前后序遍历,思路简洁,仅需要调整递归体的执行顺序即可实现。
2.利用非递归实现中序遍历,需要利用栈操作,按照中序遍历规则将节点依次入栈后出栈实现。
算法描述:图1 中序遍历(非递归)实现算法的实现和测试结果(参考OJ)实验3-02:编写算法交换二叉树中所有结点的左、右子树数据结构定义:typedef struct BiTNode{char data;BiTNode *lchild, *rchild;}BiTNode;typedef BiTNode *BiTree;算法设计思路简介:本实验需要实现以下操作:二叉树的初始化、前中后序遍历等基本操作1.利用递归实现前后序遍历,思路简洁,仅需要调整递归体的执行顺序即可实现。
由前序跟中序遍历序求后序遍历序的设计与实现
(中文)由前序跟中序遍历序求后序遍历序的设计与实现(英文)The design and implementation of getting postorder traversal according to preorderand inorder traversal of a binary tree蔡智聪摘要:树的遍历问题在应用开发过程中是一个很经典且常遇到的问题,在实际工程中,经常可能需要进行某种遍历充的求解。
本文介绍如何由一棵二叉树的前序遍历序和中序遍历序来后序遍历序的设计思路与具体C++实现。
首先根据前序遍历序和中序遍历序来建立(还原)出二叉树的原型,文中详细介绍了建立(还原)树的算法及原理。
然后再用后后序遍历算法求后序遍历序(一串字符串序列)。
关键字:二叉树前序遍历序中序遍历序后序遍历序Binary –Tree ,Preorder traversal, inorder traversal, postorder traversal正文:几个术语的介绍:二叉树:在计算机科学中,二叉树是每个结点最多有两个子树的有序树。
通常子树的根被称作“左子树”(left subtree)和“右子树”(right subtree)。
前序遍历序:在对一个树进行前序遍历而得到的一个访问结点的序列。
遍历的顺序是:先父结点,然后左子树,然后右子树。
中序遍历序:在对一个树进行中序遍历而得到的一个访问结点的序列。
遍历的顺序是:先左子树,然后父结点,然后右子树。
前序遍历序:在对一个树进行前序遍历而得到的一个访问结点的序列。
遍历的顺序是:先左子树,然后右子树,然后父结点。
引言:树的遍历问题在应用开发过程中是一个很经典且常遇到的问题,在实际工程中,经常可能需要进行某种遍历充的求解。
为了描述和实现的简化,本文中以二叉树来代替为例,并将二叉树的结点抽象成一个字符来代替,在实现运用中可以自己加以灵活变通。
问题的引出:那么对于一棵给定的二叉树,如何根据前序遍历序和中序遍历序来求出后序遍历序呢?如图A:这样的一棵树的前序遍历序为:ABDGHCEIFJ中序遍历序为:GDHBAEICFJ那么如何求出后序遍历序(GHDBIEJFCA)呢?算法原理及分析:1.先建立还原二叉树。
二叉树的遍历PPT-课件
4 、二叉树的创建算法
利用二叉树前序遍历的结果可以非常方便地生成给定的
二叉树,具体做法是:将第一个输入的结点作为二叉树的 根结点,后继输入的结点序列是二叉树左子树前序遍历的 结果,由它们生成二叉树的左子树;再接下来输入的结点 序列为二叉树右子树前序遍历的结果,应该由它们生成二 叉树的右子树;而由二叉树左子树前序遍历的结果生成二 叉树的左子树和由二叉树右子树前序遍历的结果生成二叉 树的右子树的过程均与由整棵二叉树的前序遍历结果生成 该二叉树的过程完全相同,只是所处理的对象范围不同, 于是完全可以使用递归方式加以实现。
void createbintree(bintree *t) { char ch; if ((ch=getchar())==' ') *t=NULL; else { *t=(bintnode *)malloc(sizeof(bintnode)); /*生成二叉树的根结点*/ (*t)->data=ch; createbintree(&(*t)->lchild); /*递归实现左子树的建立*/ createbintree(&(*t)->rchild); /*递归实现右子树的建立*/ }
if (s.top>-1) { t=s.data[s.top]; s.tag[s.top]=1; t=t->rchild; }
else t=NULL; }
}
7.5 二叉树其它运算的实现
由于二叉树本身的定义是递归的,因此关于二叉树的许多 问题或运算采用递归方式实现非常地简单和自然。 1、二叉树的查找locate(t,x)
(1)对一棵二叉树中序遍历时,若我们将二叉树严
格地按左子树的所有结点位于根结点的左侧,右子树的所
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
程序源代码(含注释)
#include <dos.h>
#include <conio.h>
#include <stdio.h>
#include <stdlib.h>
enum BOOL{False,True};
typedef struct BiTNode //定义二叉树节点结构
{char data; //数据域
struct BiTNode *lchild,*rchild; //左右孩子指针域
}BiTNode,*BiTree;
void CreateBiTree(BiTree &); //生成一个二叉树
void PreOrder(BiTree); //先序递归遍历二叉树
void InOrder(BiTree); //中序递归遍历二叉树
void PostOrder(BiTree); //后序递归遍历二叉树
void main()
{BiTree T;
int flag=1,j;
//---------------------程序解说-----------------------
printf("本程序实现二叉树的操作。
\n\n");
printf("可以进行建立二叉树,递归先序、中序、后序遍历等操作。
\n");
printf("请将先序遍历二叉树的结果输入以建立二叉树。
\n");
printf("对于叶子结点以空格表示。
\n");
printf("例如:\nabc de g f (回车),建立如下二叉树:\n"); printf(" a \n");
printf(" / \n");
printf(" b \n");
printf(" / \\ \n");
printf(" c d \n");
printf(" / \\ \n");
printf(" e f \n");
printf(" \\ \n");
printf(" g \n");
CreateBiTree(T); //初始化队列
getchar();
while(flag)
{
printf("请选择: \n");
printf("1.递归先序遍历\n");
printf("2.递归中序遍历\n");
printf("3.递归后序遍历\n");
printf("4.退出程序\n");
scanf("%d",&j);
switch(j)
{
case 1:if(T)
{printf("\n先序遍历二叉树:\n\t\t");
PreOrder(T);
printf(" ");
printf("\n");
}
else
printf("二叉树为空!\n");
break;
case 2:if(T)
{printf("\n中序遍历二叉树:\n\t\t");
InOrder(T);
printf(" ");
printf("\n");
}
else
printf("二叉树为空!\n");
break;
case 3:if(T)
{printf("\n后序遍历二叉树:\n\t\t");
PostOrder(T);
printf(" ");
printf("\n");
}
else
printf("二叉树为空!\n");
break;
default:flag=0;printf("程序运行结束,按任意键退出!\n");
}
getchar();
}
}
void CreateBiTree(BiTree &T)
{char ch;
scanf("%c",&ch); //读入一个字符
if(ch==' ') T=NULL;
else {T=(BiTNode *)malloc(sizeof(BiTNode)); //生成一个新结点T->data=ch;
CreateBiTree(T->lchild); //生成左子树
CreateBiTree(T->rchild); //生成右子树
}
}
void PreOrder(BiTree T)
{if(T)
{printf("%c",T->data); //访问结点
PreOrder(T->lchild); //遍历左子树PreOrder(T->rchild); //遍历右子树}}
void InOrder(BiTree T)
{if(T)
{
InOrder(T->lchild); //遍历左子树
printf("%c",T->data); //访问结点
InOrder(T->rchild); //遍历右子树}
}
void PostOrder(BiTree T)
{
if(T)
{
PostOrder(T->lchild); //遍历左子树
PostOrder(T->rchild); //访问结点
printf("%c",T->data); //遍历右子树}
}
四. 实验数据、结果分析。
