基于大功率led准直透镜的研究设计

合集下载

led光准直的方法

led光准直的方法（原创实用版5篇）《led光准直的方法》篇1以下是LED光准直的方法：1. 打开三脚架，将准直仪安装在前臂上，通过旋钮调整倾斜补偿和风偏补偿。

2. 将激光器的输出尾部与准直仪连接，并调整激光器位置，使激光器发出的激光沿着目标线方向。

3. 打开望远镜，调整望远镜系统，使其对准激光线。

4. 打开计算机屏幕上的软件，将激光器的输出尾部与计算机连接，并调整激光器位置，使激光器发出的激光沿着目标线方向。

5. 调整望远镜系统，使其对准激光线。

6. 打开计算机屏幕上的软件，将激光器的输出尾部与计算机连接，并调整激光器位置，使激光器发出的激光沿着目标线方向。

7. 调整望远镜系统，使其对准激光线。

8. 打开计算机屏幕上的软件，将激光器的输出尾部与计算机连接，并调整激光器位置，使激光器发出的激光沿着目标线方向。

《led光准直的方法》篇2LED准直的方法有三种：透镜准直、反射镜准直和棱镜准直。

1. 透镜准直：利用LED透镜可以使LED光线聚焦，达到准直的效果。

2. 反射镜准直：利用平面反射镜或球面反射镜，可以使LED光线发生全反射，从而达到准直的效果。

3. 棱镜准直：利用两个相对放置的直角棱镜，可以使LED光线偏转90度，从而达到准直的效果。

《led光准直的方法》篇3LED准直的方法有三种：透镜准直、反射镜准直和棱镜准直。

1. 透镜准直：使用透镜或透镜组将目标聚焦到视场中。

这种方法的优点是可以控制光束发散角，但缺点是价格相对较高。

2. 反射镜准直：使用反射镜或反射镜组将光束反射到视场中。

这种方法的价格相对较低，但控制光束发散角的能力有限。

3. 棱镜准直：使用棱镜或棱镜组将光束折射到视场中。

这种方法的价格相对较低，但控制光束发散角的能力也有限。

《led光准直的方法》篇4以下是LED光准直的方法：1. 打开三脚架，将准直仪安装在前臂上，将反射目标调整到准直仪镜头中间位置。

2. 打开反射板电源开关，使准直仪和反射板正常工作。

LED(准直)光源的SMS非成像光学设计方法的开题报告

LED（准直）光源的SMS非成像光学设计方法的开题报告标题：基于LED（准直）光源的SMS非成像光学设计方法的研究一、研究背景与意义随着现代光学技术的不断发展，光学成像技术在众多领域广泛应用。

但是，在某些特殊的应用场合，如高速运动目标跟踪、目标探测、测量等领域中，传统的成像技术已经无法满足需求。

因为这些场合所需的光学系统具有高速、高精度测量、精确定位等特殊要求，同时又不需要实现对目标的实时成像，传统的光学成像方法在这些方面存在很大局限性。

面对这种情况，在非成像光学方面的研究变得越来越重要。

近年来，LED（准直）光源作为一种新型的非成像光源，由于其高强度、高亮度、低能量消耗的特点，已经被广泛应用于非成像光学系统中。

但是，目前为止，关于基于LED（准直）光源的SMS（Spatial Modulation Spectroscopy）非成像光学设计方法的研究还比较有限。

因此，对于如何选择合适的LED（准直）光源进行SMS非成像光学系统的设计以及如何优化系统的光学特性等问题，仍然需要深入研究。

本研究旨在探索一种基于LED（准直）光源的SMS非成像光学设计方法，以解决现有SMS非成像光学系统中存在的问题，从而推动非成像光学技术的发展。

二、研究内容1. 分析LED（准直）光源的特点，构建LED（准直）光源的光学模型；2. 研究SMS非成像光学系统的原理以及其对LED（准直）光源的要求；3. 建立基于LED（准直）光源的SMS非成像光学设计模型，并进行优化；4. 利用Zemax等光学设计软件对所设计的SMS非成像光学系统进行建模和模拟分析；5. 实验验证SMS非成像光学系统的设计效果和性能指标。

三、研究方法1. 前期文献调研和实验研究，收集和总结相关的研究成果；2. 使用Matlab、Zemax、LabVIEW等软件进行SMS非成像光学设计模型的建立和模拟；3. 在实验室中搭建实验平台，验证SMS非成像光学系统的设计效果和性能指标。

基于LED光源的TIR透镜设计

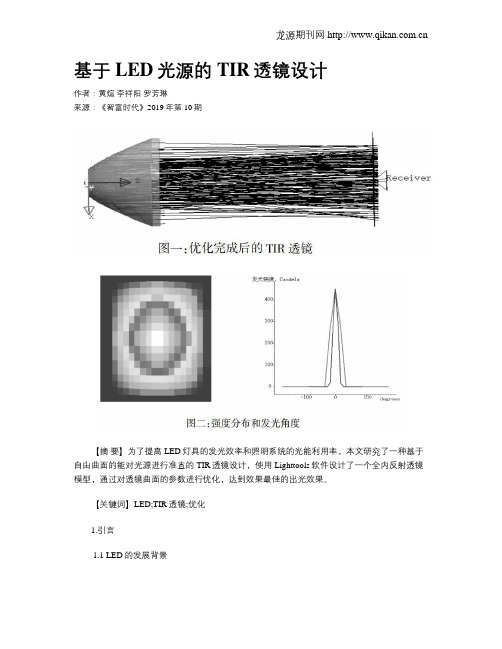
基于LED光源的TIR透镜设计作者：黄煊李祥阳罗芳琳来源：《智富时代》2019年第10期【摘要】为了提高LED灯具的发光效率和照明系统的光能利用率，本文研究了一种基于自由曲面的能对光源进行准直的TIR透镜设计，使用Lighttools软件设计了一个全内反射透镜模型，通过对透镜曲面的参数进行优化，达到效果最佳的出光效果。

【关键词】LED;TIR透镜;优化1.引言1.1 LED的发展背景近年来，各个国家和行业都花费了大量的人力、财力资源在发光二极管及其灯具的研究和发展应用上。

与传统的光源相比，LED作为第四代照明光源和绿色光源，它具有效率高、节能环保、寿命长、可靠性强等优点、广泛应用于各种指示器件、显示器件、装饰器件、户外照明器件、背光板等领域。

大功率LED是第四代光源的代表，普通大功率LED发光效率很高，是白炽灯的八倍，荧光灯的两倍多，这就意味着在满足相同的光照时可以节约大量的电能，降低了耗能成本。

1.2 研究背景实际生活中，LED发光亮度比较低，并且发散角比较大，一般不能直接用于光學系统中，而是经过二次光学系统设计，也就是经过一个TIR透镜汇聚并准直后，才能应用于照明器件中。

由于TIR透镜具有减小光束发散角度实现准直的作用，所以它在实际应用中的用处很大。

在微型投影系统中，TIR透镜结构的优化设计是关键，它的光束收集整形能力从很大程度上决定了系统的光能利用率和均匀度。

在LED微型投影仪照明系统中，以系统光能利用率和照明均匀性构建评价函数，采用光纤追迹和结构优化相结合的方法，对TIR透镜进行优化设计，将大角度扩展光束压缩到小角度范围以内，并且使得投影屏幕达到一定的照明均匀性。

2.结构原理TIR透镜的设计基于全内反射的原理，透镜由4部分组成，中间内凹的非球面柱面镜部分、侧面的全反射棱镜部分、两端的全反射棱镜部分、以及上表面“W”型的自由曲面组成。

透镜将郎伯型LED的光配成沿X方向120°（水平方向）以及Y方向60°（垂直方向）的光度分布。

基于自由曲面的LED全反射准直透镜的设计

摘要：为在特定角度范围内实现所需照明，满足各类ＬＥＤ照明系统的要求，提出一种适用于扩展光源的透射一全反射复合曲面的ＬＥＤ透镜设计方法。根据光源的大小由非成像光学原理确
定反射面面型并计算光源发散角度，再根据照射的角度要求进行自由曲面的透镜设计。文章给
ｓｉｇｎｅｄｆｒｅｅ — ｆｏｒｍｓｕｒｆａｃｅｌｅｎｓ．Ｗｅｐｒｏｖｉｄｅｄｔｈｅｄｅｓｉｇｎｉｄｅａａｎｄｍｅｔｈｏｄ，ｄｅｓｉｇｎｅｄａＬＥＤｌｅｎｓｗｉｔｈｅｍｅｒｇｅｎｃｅｈａｌｆａｎｇｌｅｏｆ２．５ｄｅｇｒｅｅ，ａｎｄａｎａｌｙｚｅｄｔｈｅｉｎｆｌｕｅｎｃｅｓｏｆｅｒｒｏｒｏｎｔｈｅａｃｔｕａｌｒｅ —
樊露青，李湘宁，王瑜，刘杰
（１．上海理工大学光电信息与计算机工程学院，上海２０００９３；２．上海市现代光学系统重点实验室，上海２０００９３；３．教育部光学仪器与系统工程研究中心，上海２０００９３）
（１．Ｓｃｈｏｏｌｏｆ０ｐｔｉｃａｌ＿ＥｌｅｃｔｒｉｃａｌａｎｄＣｏｍｐｕｔｅｒＥｎｇｉｎｅｅｒｉｎｇ，ＵｎｉｖｅｒｓｉｔｙｏｆＳｈａｎｇｈａｉｆｏｒＳｃｉｅｎｃｅａｎｄＴｅｃｈｎｏｌｏｇｙ，Ｓｈａｎｇｈａｉ２０００９３，Ｃｈｉｎａ；２．ＳｈａｎｇｈａｉＫｅｙＬａｂｏｆＭｏｄｅｒｎＯｐｔｉｃａｌＳｙｓｔｅｍ，Ｓｈａｎｇｈａｉ２０００９３，Ｃｈｉｎａ；３．ＲｅｓｅａｒｃｈＣｅｎｔｅｒｏｆＯｐｔｉｃａｌＩｎｓｔｒｕｍｅｎｔｓａｎｄＳｙｓｔｅｍＥｎｇｉｎｅｅｒｉｎｇ，ＭｉｎｉｓｔｒｙｏｆＥｄｕｃａｔｉｏｎ，Ｓｈａｎｇｈａｉ２０００９３，Ｃｈｉｎａ）

基于自由曲面的LED准直透镜设计

基于自由曲面的LED准直透镜设计张巧淞;徐春云;程灏波;TAM Hon Yuen【摘要】本文基于准直光束照明的自由曲面透镜设计方法,设计了一种以单颗LED 为光源的准直透镜,其可应用于投影仪的照明系统.根据几何光学原理构造自由曲面,该方法无需求解复杂的偏微分方程,计算简单.准直透镜由内自由曲面折射面、球面、抛物面全反射曲面以及平面组成,利用Matlab编程求出自由曲面轮廓曲线的离散数据点,导入Solidworks中进行曲线拟合,建立透镜的实体模型.为探讨LED光源尺寸对准直透镜光斑影像的影响,在Tracepro中对透镜进行非序列光线追迹,模拟结果表明:当光源半径不大于1 mm时,其光学效率达到86.26％以上,视场半角达到3.3度以内.【期刊名称】《影像科学与光化学》【年(卷),期】2016(034)001【总页数】7页(P36-42)【关键词】LED;准直;二次光学设计;自由曲面【作者】张巧淞;徐春云;程灏波;TAM Hon Yuen【作者单位】北京理工大学光电学院光机电工程联合研究中心,北京100081;北京理工大学深圳研究院,广东深圳518057;北京理工大学光电学院光机电工程联合研究中心,北京100081;北京理工大学深圳研究院,广东深圳518057;北京理工大学光电学院光机电工程联合研究中心,北京100081;北京理工大学深圳研究院,广东深圳518057;香港城市大学机械与生物医学工程系,香港999077;香港城市大学机械与生物医学工程系,香港999077【正文语种】中文影像信息学是一个从图像挖掘信息和提炼知识的过程，是一种边缘科学，是人类通过影像来认识和解释世界的重要手段。

随着影像信息学的发展，使人们能够更加充分的利用大量未被利用的影像信息。

能源是人类赖以生存的基础。

现今，地球上的许多能源都已告竭，因此发展“绿色能源”成为当今世界的主流[1]。

LED是一种可将电能转变为光能的半导体发光器件，属于固态光源，被全球公认为新一代的环保高科技光源。

一种用LED光源的准直系统设计[技巧]

一种用LED光源的准直系统设计1 引言半导体发光二级管(LED)光源具有体积小、效率高、响应快、易调光、色域范围宽、无汞污染、使用寿命长等特点，是一种节能环保的新型光源。

随着LED技术的不断完善，特别是光效的不断提高，在投影显示、背光光源、城市照明等领域有着广泛的应用前景。

然而，由于LED的空间光强近似Lambertian型分布，使其在被照面上所形成的照度随出射角的增大而迅速衰减，很难满足远距离照明如手电、港口或码头用信号投射灯的实际需要，为了使光束平行出射以提高光能利用率，光学设计人员尝试通过各种途径来设计反射器、折射器或折反射器来改善光线在目标面的布局，以符合实际情况的需要。

目前，LED二次光学设计主要有两种方法：直接经验法和求解方程法。

直接经验法主要通过CAE三维机械建模软件绘制出光学元件的结构，并将此结构导入到光学仿真软件中如Tracepro中，并对此结构赋予某种光学属性，最后通过蒙特卡罗非序列光线追迹来判断照明面上的照度分布及整个系统的光强分布。

由于这种设计的随意性很强，相关设计者往往需要多次修改光学元件的结构，多次模拟来完成设计，此类方法并不需要太多的理论计算，设计的关键往往取决于设计者的个人经验。

方程求解法基于光源的发光特性和所需实现的照明要求而构建方程组，其未知数即为所求自由曲面上个点的坐标，在给定初始条件后，通过求解方程组的解析解或数值解，即可得到自由曲面的面型数据并可实现所需照明要求。

此种方法免去了反复试验所需的时间，提高了设计效率，但对设计人员的光学构建能力和数学功底的要求比较高。

本文针对旋转对称折射器，根据LED光源特性和目标面的光强分布要求，依据snell 定律和非成像光学中的光学扩展量要求，设计了一种较为简便的自由曲面折射器，实现了系统的长距离均匀照明。

2 设计原理建立如图1所示的坐标系。

设LED光源位于坐标系的原点，透镜前表面为平面，后表面为为曲面，即为需要设计的自由曲面。

LED光源的透镜设计方法

LED光源的透镜设计方法光学元件是很精密的元件，制作成本较高，如果能减少元件的厚度，甚至做成片状透镜，则不但可以减少光学元件的尺寸，从而缩小灯具或其他设备的大小，还可以节省材料，降低成本。

由于厚度减少，光吸收也减少，灯具或仪器效率也会随之提高，因此做成高质量的薄片形的光学零件一直是光学设计追求的目标之一。

菲涅尔（Fresnel）透镜是一种片状的薄形透镜，它一直以其轻、薄、价格低廉优势而在一些方面得到应用。

但市场上的菲涅尔透镜多为等差半径的同心圆结构，其制作缺乏精确的光学设计过程，导致成像质量不是很高，有的甚至只是简单的波纹结构，其光学质量就更差了。

即使是较好的菲涅尔透镜，也是通常将普通透镜分为小段后，近似为折线，并经过不同距离的简单平移而形成，这些设计方法上的缺陷造成了菲涅尔透镜的低质量。

LED体积很小，但市场上销售的LED用杯状透镜大都厚度在10mm以上，这成为LED 在某些场合应用的致命问题，虽然可以用菲涅尔透镜来减薄透镜的厚度和减少光吸收，但如何进行精确的光学设计却很少见到文献报道。

本文介绍的是能获得精确的超薄锯齿形透镜的设计方法，其光学质量好，光线利用率较高。

因为一般的菲涅尔透镜在理论上就存在浪费，即透过透镜的光线理论上就有一部分不能到达设计的目的地，本方法得到的透镜对点光源来说理论上不存在浪费。

此外，各个小锯齿之间的距离也可根据需要而不同，而且在同一透镜中不同位置的锯齿间距也可变化，从而使这种方法设计的锯齿形透镜有更广泛的适应性，即它可以适应不同的使用条件和不同的加工条件的需求。

这种锯齿形透镜适用LED为光源的二次光学透镜。

对于LED这种尺寸很小的光源，具有小而薄的光学透镜是非常有意义的。

一、设计原理单个透镜一般是一个表面形状为曲面的透明材料，其作用是改变光线的方向，形成所需的光强空间分布。

其缺点是往往比较厚，因此体积大成本高，而且吸收也就大，特别是曲率大的透镜更是如此。

为简单计，举一个平凸透镜的例子，原始的平凹透镜见图1（a），相应地传统的菲涅尔透镜见图1（b），为了说明原理，图中齿距画得比较大。

一种基于自由曲面的LED准直透镜设计

一种基于自由曲面的LED准直透镜设计周镇;苏成悦;付倩;张春华【摘要】A design algorithm that can realize the collimating beam of light was proposed based on free-form surface lens,and an illumination optical system for a single LED source was designed based on the algorithm. The equations of the points on the profile curve about the back surface of the lens were established . By using the iterative method and Matlab programming, a number of discrete points of the free-form profile curve were calculated and fitted to optical entity with the SolidWorks software. Then the optical entity was imported into TracePro software for non-sequential ray tracing. The simulation results show that the optical system can a-chieve uniform illumination and collimate beam.%提出一种能实现准直光束照明的自由曲面透镜设计算法,并基于此算法设计一种以单颗LED为光源的准直透镜.通过建立透镜后表面轮廓曲线上的点所满足的方程,利用迭代方法并结合Matlab编程求出自由曲面轮廓曲线的离散数据点,将数据点导入SolidWorks中进行曲线拟合并建模,进而得到透镜的实体模型.在TracePro中对该透镜进行非序列光线追迹,模拟结果表明:该光学系统能够实现均匀照明,并对最终光线可实现准直出射.【期刊名称】《应用光学》【年(卷),期】2012(033)006【总页数】5页(P1058-1062)【关键词】LED;二次光学;自由曲面;准直透镜;非序列光线【作者】周镇;苏成悦;付倩;张春华【作者单位】广东工业大学物理与光电工程学院,广东广州510006;广东工业大学物理与光电工程学院,广东广州510006;广东工业大学物理与光电工程学院,广东广州510006;广东工业大学物理与光电工程学院,广东广州510006【正文语种】中文【中图分类】TN312.8引言LED为半导体固体光源，具有体积小、质量轻、耗能少、寿命长、响应时间短以及抗震性能好等优点，尤其是其抗震动能力，可以经受住各种剧烈的抖动和碰撞，这一特性使得LED手电特别适用于军队、警察、保安、户外探险等特种照明使用场合［1］。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

基于大功率LED准直透镜的研究设计常见的大功率LED二次透镜的剖面一般具有如下结构：其作用是通过曲面1的折射和曲面2的全反射改变LED发出的光线方向以实现配光的重新分布。

本文主要通过理论计算分析适用于准直透镜的曲面设计。

以下将曲面1和曲面2，分开讨论，讨论前需假设他们具有一个共同的分界角A，这样从LED发出的光线必然能被曲面1折射或曲面2全反射。

第一部分：首先讨论中间的准直透镜部分：如下图所示，取透镜中心为Y轴，径向为决定TIR 透镜的中心准直透镜的参数主要为：r n A max,所以可以把这三个参数当做已知参数，进而推导出y 与x 的关系，然后拟合成非球面曲线，那么就可以得到中心准直透镜的非球面系数。

具体推导如下：(a) 先求出Pn+1点所在光线方程：由坐标图，我们可以知道，Pn+1点所在光线所在的直线的斜率为1k ，其中1cot k A =，那么其光线方程为1cot y A x =⋅ (1)(b) 再求Pn 点所在切线方程：设Pn 点所在切线切线的斜率2k ，且为过点Pn (Xn ,Yn)，因此应该具有如下形式： Yn Xn x k y +-⋅=)(22由于角D 与角C 的和为90°，那么Pn 所在切线斜率2cot tan k D C ==，这样只需求出C 既可。

由折射定律sin sin B n C =，则角arcsin(sin )B n C =⋅ 于是问题转换为求角度B 。

这可以通过光线的斜率1k 和Pn 所在法线的斜率231k k -=求出。

由两直线夹角公式:111cot 132tan tan 1cot 113112tan k A k k k C B k A k k k C ++-===+⋅-- 于是有:1cot tan tan[arcsin(sin )]cot 1tan A C n C A C+⋅=- 经过进一步的计算，便可以解得：212121212)1(*1k k n k k n k -+-+=于是得Pn 点所在切线方程：Yn Xn x k y +-⋅=)(22 (2)可以近似认为Pn 的邻点Pn+1也在该切线上。

x k y ⋅=11 (3)22()cot y k x r r A =⋅-+ (4)解方程组（3）、（4）可得P1（X1，Y1）再次将P1（X1,Y1）坐标作为P0，然后我们依次递减A 的角度，这边每次递减为1°直到角A 为0°，所以这样第二次取A=39°代入（1）、（2）可得新的方程组x k y ⋅=11 (5)1)1()(12Y X x k F y +-⋅= (6)同理，解方程（5）、（6）可得P2（X2,Y2）以此类推，从Amax 递减到0°，可以求得一系列P 点坐标。

将离散的点，用MATLAB 多项式拟合成非球面的曲线方程，便可以得到非球面系数。

第二部分：全反射曲面的一个切面如下图所示，取透镜中心为Y 轴，径向为X 轴，为简化问题，将LED 简化为原点处的点光源，图中的光线发生全反射现象。

决定全反射部分的透镜参数为r 、R 、n 、Amin(即等同于中心准直透镜的Amax)，可以把这几个参数当做已知参数，进而推导出y 与x 的关系，然后拟合成非球面曲线，那么就可以得到透镜的全反射部分的非球面系数。

具体推导如下：(a)先求Pn 点所在切线方程，由坐标图可以知道它的斜率为()tan f x D '=由于(90C)2180D ︒-+=︒，所以90()tan 2C f x ︒+⎛⎫'= ⎪⎝⎭由折射定律：sin sin cos n C B A ==，得cos arcsin()A C n=，那么过该点的直线方程斜率： cos 90arcsin tan 2A n k ⎛⎫⎛⎫︒+ ⎪ ⎪⎝⎭ ⎪= ⎪ ⎪⎝⎭将Pn(Xn,Yn)坐标代入，则过Pn 的切线满足方程：cos 90arcsin tan ()2n n A n y x X Y ⎛⎫⎛⎫︒+ ⎪ ⎪⎝⎭ ⎪=-+ ⎪ ⎪⎝⎭……………………..（1）可以近似认为Pn 的邻点Pn+1也在该切线上。

(b)再求Pn+1点所在光线方程，由坐标图很容易得到其所在的直线方程为tan ()cot y C x r r A =⋅-+其中cos tan tan[arcsin()]A C n = 即Pn+1点所在光线方程: cos tan[arcsin()]()cot A y x r r A n=-+……. .(2)在坐标图中，我们是假设光发生全反射，但是还没有考虑是否遵循全反射定律，所以我们必须进一步来验证。

验证如下：由全反射定律可以知，要发生全反射，则入射角E 必须大于全反射临界角。

既是必须满足1tan tan[arcsin()]E n ≥,由于tanE=k ，所以只要1tan[arcsin()]k n≥ 于是有： cos 90arcsin 1arcsin()2A n n⎛⎫︒+ ⎪⎝⎭≥ 由上面式，可以知道1arcsin()n 只要小于等于cos 90arcsin 2A n ⎛⎫︒+ ⎪⎝⎭的最小值便可，而当A=90°时，cos 90arcsin 2A n ⎛⎫︒+ ⎪⎝⎭可以取得最小值为45°，既是1arcsin()45n≤︒，则414.12=≥n 可以全反射，这对于制造TIR 透镜常用的PMMA 和PC 材料可以实现。

因此该曲线对于任意的光线初始入射角a 都能发生全反射，设计时仅需考虑透镜结构高度上的要求。

（c ）求曲线方程离散解,拟合得到全反射部分透镜的非球面系数解方程组（1）（2），将P0坐标作为Pn ，取A=90°代入，可得关于X 与Y 的方程组。

0)(290cos arcsin 90tan +-⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛︒+︒=R x n y ………………..……….（3） ︒+-︒=90cot ))](90cos (tan[arcsin r r x ny …………………..………..（4) 解方程组（3）、（4）可得P1（X1，Y1）再次将P1（X1,Y1）坐标作为P0，然后我们依次递减A 的角度，这边每次递减为1°取A=89°代入（1）、（2）可得新的方程组1)1(289cos arcsin 90tan Y X x n y +-⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛︒+︒=……………………...（5） ︒+-︒=89cot ))](89cos (tan[arcsin r r x ny ……………………….......（6）同理，解方程（5）、（6）可得P2（X2,Y2）以此类推，一直递减到Amin 可以求得一系列P 点坐标。

将离散的点，用MATLAB 拟合成非球面方程，便可以得到非球面系数。

程序如下：% By Ruibin 08-9-25% Instruction ：This program help design LED collimating lens , feedback aspheric parameters and several chief dimensions.clear all;clc% The Frist Step: Define independent parametersr=3.25; %选择开孔半径R=4.25; %定义曲面底部半径d=1; %设置透镜前方平板高度n=1.4935; %定义材料折射率dividing_angle=24; %定义Core 与TIR 的分界角min_angle=1; %设置计算精度N=4; %设定拟合非球面系数阶数% The Second Step ：Caculate induced variableangles_Core=(dividing_angle:-min_angle:0);angles_TIR=(90:-min_angle:dividing_angle); num_Core=length(angles_Core);num_TIR=length(angles_TIR);for i=1:(num_Core)a_Core(i)=(angles_Core(i)*pi/180);k1(i)=cot(a_Core(i));k2(i)=(k1(i)+(n^2*k1(i)^2+n^2)^(1/2))/(n^2*k1(i)^2-1.*k1(i)^2+n^2); endk1(num_Core)=999;k2(num_Core)=0;for i=1:num_TIRa_TIR(i)=(angles_TIR(i)*pi/180);k3(i)=tan((pi/2+asin(cos(a_TIR(i))/n))/2);k4(i)=tan(asin(cos(a_TIR(i))/n));endX0_TIR=R;X0_Core=r;Y0_TIR=0;Y0_Core=r*cot(a_Core(1));% The Third Step:Solve functionsfor i=1:num_Core %Solve the curve of Core syms x;f1=k1(i)*x;f2=k2(i)*(x-X0_Core)+Y0_Core;f=f1-f2;x=double(solve(f));y=k1(i)*x;X0_Core=x;Y0_Core=y;Px_Core(i)=X0_Core;Py_Core(i)=Y0_Core;endfor i=1:num_TIR %Solve the curve of TIR syms x;f1=k3(i)*(x-X0_TIR)+Y0_TIR;f2=k4(i)*(x-r)+r*cot(a_TIR(i));f=f1-f2;x=double(solve(f));y=k3(i)*(x-X0_TIR)+Y0_TIR;X0_TIR=x;Y0_TIR=y;Px_TIR(i)=X0_TIR;Py_TIR(i)=Y0_TIR;end% The furth Step:Fitting the curveP_Core=polyfit(Px_Core,Py_Core,4);P_TIR=polyfit(Px_TIR,Py_TIR,4);% The fifth Step:Feedback chief dimensions of the lens and Create it %Feedback dimensions of the whole lensresult='透镜尺寸如下：'Diameter_of_lens=2*Px_TIR(num_TIR)Thickness_of_lens=Py_TIR(num_TIR)+dDiameter_of_Core=2*rThickness_of_front_pannel=dBottom_thickness=R-rLowest_Core=P_Core(5)%Feedback dimensions of Lens part TIRresult='TIR系数如下：'Thickness=Py_TIR(num_TIR)-P_TIR(5)+dAperture=Px_TIR(num_TIR)Obstruction=rPosition=P_TIR(5)format short e;Aspheric=[P_TIR(4) P_TIR(3) P_TIR(2) P_TIR(1)]format short;%DDE ConnectionTP_COMMAND = ddeinit('TracePro','Scheme');%Create TIRcmd =['(define TIR (insert:lens-element "PLASTIC" "pmma" (list 0 0 7.0306e-002 1.2580e-001 -2.5732e-003 -2.5281e-006) 18.6774 (list 0 0)(list "cir" 13.6051 0 0 0)(list "cir"3.25 0 0 0)))'];ddeexec(TP_COMMAND,cmd);cmd =['(entity:move TIR 0 0 -2.3712)'];ddeexec(TP_COMMAND,cmd);cmd =['(property:apply-name TIR "TIR")'];ddeexec(TP_COMMAND,cmd);%Feedback dimensions of Lens part TIRresult='Core系数如下：'Thickness=Py_TIR(num_TIR)-P_Core(5)+dAperture=rObstruction='None'Position=P_Core(5)format short e;Aspheric=[P_Core(4) P_Core(3) P_Core(2) P_Core(1)]format short;%Create Corecmd =['(define Core (insert:lens-element "PLASTIC" "pmma" (list 0 0 -2.6211e-002 1.9124e-001 -1.7949e-002 2.8016e-004) 10.3569 (list 0 0)(list "cir" 3.2500 0 0 0)))']; ddeexec(TP_COMMAND,cmd);cmd =['(entity:move Core 0 0 5.9493)'];ddeexec(TP_COMMAND,cmd);cmd =['(property:apply-name Core "Core")'];ddeexec(TP_COMMAND,cmd);%Create Lenscmd =['(define Unite (bool:unite TIR Core))'];ddeexec(TP_COMMAND,cmd);cmd =['(define block (insert:block 100 100 100))']; ddeexec(TP_COMMAND,cmd);cmd =['(entity:move block 0 0 -50)'];ddeexec(TP_COMMAND,cmd);cmd =['(define Lens (bool:subtract Unite block))']; ddeexec(TP_COMMAND,cmd);cmd =['(property:apply-name Lens "Lens")']; ddeexec(TP_COMMAND,cmd);%Close the DDE connectionddeterm(TP_COMMAND);。