4第四节 最大公因式
高等代数几个重要定理的证明-毕业论文

---文档均为word文档,下载后可直接编辑使用亦可打印--- 摘要代数是学学的心础课程,是其它课程的要提.本文共分三大部分,第一大部分主要介绍了高等代数课程的七个重要定理的内容、证明.因高等代数中提出了许多新概念、新定义、新定理,譬如多项式、数域、线性空间、映射等,且都是较为抽象的内容,故此将其中各章节中的重要定理列举出来,并寻找多个定理证明来加深对其的理解及认识.第二大部分主要介绍了在高等代数学习中遇到的问题及解决的方法.第三大部分则主要讲了高等代数在实际问题中的应用中的两种应用方法,即矩阵密码与保密通讯和情报信息检索模型.关键词:定理证明;矩阵;行列式;线性空间;高等代数应用AbstractHigher algebra is the core curriculum of university mathematics,and it is an important prerequisite for learning other courses. This paper is divided into three parts,and the first part mainly introduces the seven important theorems in advanced algebra course content. Because of Higher Algebra put forward many new concepts and new definition, theorems, such as polynomial, the number of domain, linear space mapping, etc., which are more abstract content.Therefore one of the important theorem of various sections of the list, and to find a proof of the theorem to deepen understanding and understanding of these.The second part mainly introduces the problems and solutions in the study of higher algebra. The third part focuses on the application of advanced algebra in the practical application of the two methods, namely, matrix cryptography and secure communications and information retrieval model.Key words:Theorem proving;matrix;determinant;application of Advanced algebra目录TOC \o "1-2" \u 前言11 定理阐述及证明21.1因式分解及唯一性定理21.2最大公因式存在定理41.3最小数原理51.4替换定理61.5哈密尔顿-凯莱定理81.6带余除法101.7行列式计算定理121.8定理:在数域上,任意一个对称矩阵都合同于一对角矩阵132 高等代数的重要定理在相关的对应理论中的作用、地位与应用132.1因式分解及唯一性定理142.2 最大公因式存在定理142.3 最小数定理142.4 替换定理142.5 哈密尔顿-凯莱定理152.6 带余除法152.7 行列式计算定理152.8 对称矩阵合同于对角矩阵153 高等代数的学习15结束语17参考文献18引言高代数是范学校学业的学生所学习的一门主要,是学的继与高.它的内容由多项式理论、解理论、线性空间理论三大部分组成.这三大部分的特殊性在于其中的定理和概念较多,具体的模型稀少,,可引导用的例题较少,计算性弱,逻辑性强.在对高等代数几个重要定理的证明方法的探索中,能够改变我们的思维,增强大家都思维能力,辑思维能力和代数计算.此外,高等代数已经是从事科学研究的科技人员必备的数学基础知识,因它是理论化学与理论物理的不可替代的代数基础知识,也已经渗透到了管理、经济、科学技术等多项领域,除此以外,矩阵又有了新的意,尤其是对矩阵的数值分析方面的贡献.由是对于本文探索高等代数的定理新证明又有了重大意义.1 定理阐述及证明1.1因式分解及唯一性定理:理容:数上有的多式都可一地解为域,一些可多项的积,所说的性是说,如有个分式,则,同在当排因的次后有,,且是些零数.证法一:首先要证明的式分解式是否存在,我们对的次数作数学归纳法.因为一次性多项式都是不可约的,所以当时结论成立.先,同设此论对于数的多项式已成立.如果,那么然论成,不是约的,,其的次数都.由归纳假和都可以分解成数上一些多式的积.把,的分式来就可以得到的一个式.由归纳法原理,可知结论普遍成立.下证它的一性.设可以解成约项式的积.如果还有另一个分解,其中都可约多项式,于是. (1)我们对作归纳法.当,是不可约多项式,由定义一定有且现在设可约式的时性已证.由(1)因此,能尽中的一个,.因为也可多式,,(2)在(1)式两边消去,就有.由归纳假设,有,即,(3)并且适当排列次序之后有,,(4)即(2),(3),(4)三式加起来就是我们所要证得,即证明了分解的唯一性.[1]证法二:可以对因式的用数学归纳法.对于可多式,也是对于的情来说,理成立.假定对于能分解成个不可约因式的乘积的多项式来说,定理成立.们明对于能可因的积的多项来说也立.等(1)表明,积可以被可多式整.性,若项与的积能被可多式,则有一能被的,且某一能被.适当调整的次序,可以假定即.但不是可约多项式,而的次数是零,所以必须是一个多项式:(2), 把的表示式代入式(1)的右端,得:,等端除为的多项式,得出式,令那么是一个能分解成不约多项式乘积的多项式.于是由归纳假定得,亦即,并且可以假定(3)其及都是次多式.令,由(2)及(3)得,这样得到明1.2最大公因式存在定理:如果中意个项在中存一个大因,且表示为的一个合,即中项式使.证法一:数学归纳法证明:将定理证明过程中会用到的引理列出:引理[1]:如有式成,和有同的因式.下面用归纳证明大因式在定理.(种形证)证明当或时,的最大公因式为或,显然有或当且时,不妨设,令,下面对n实行归纳法:.当时设,则(非零常数)或,当时,,于是的最大公因式为,有. 当(非零常数)时,由于,故的最大公因式为,由引理,的最大公因式也为,且有定理成立..假对于的自然,定都成.看n时情形设,则或,⑴时,,于是的最大公因式为,有.⑵时,设,则或⑶时,的最大公因式为,由引理,的最大公因式也为,且有.⑷当时,由归纳假设,存在最大公因式,且由引理,的最大公因式也为,进而的最大公因式也是.所以,对于一切都存在最大公因式.由于所以,取,,则有.[3]1.3最小数原理:负整数集合的任意一个非空子集一定含一个最小数,接下来通过构造的方法证明最大公因式存在定理.证明:分成两种情况当或时,的最大公因式为或,显然有或当且时,令,记,由于,所以,则是非负整数集的一个非空子集.由最小数原理,中存在最小数,故存在,且,即是中最小次数多项式.于是,有中多项式使由带余除法或或’若则,但,即,于是,与是中最小次数多项式矛盾.因此,从而.同理可证:.于是是与的公因式.设是与的任一公因式,则,,由得:,所以是与的最大公因式,且有.1.4替换定理:设无关的量组(1)可由组(2)线表,则,且(2)中个量使得向组,(3)与量(2).证法1.由可知性无的向组由量(2)表示,则有:可由向量组线性表示.从而,由可向量线性表示,得(3)性关.那么根据前面所提供的定理,可知至少有一个向量能用其前个向量线性表示.在向量组(3)中将除去,剩下个向量为(4)这时向量组(4)与(2)等价.同理可得(6)如果线性无关向量组的元素个数,则进行次可得向量组(7)则这个组(7)不含向,但量组(7)与向组(2)价.此又于可由,则可由性出.这与性关,故.由以上的证明过程可以的知向量组同向量组(2)等价. [4]证法2.运极无组的性质证,之后过扩极大关组来证明向量的价.设向组的极大无关组(8),然,因(1)可由线性表示,所也是的一个大无关,又因为性无关,因,又,故.因为的秩为,然,当选,可以把(1)为的一个极无关.因为,均是的极无关组,因此和等价,因此是极1.5哈密尔顿-凯莱定理:设是数上一个阵,是的,则:.证法一:是.因为矩阵都是的多项式,次数不超过,故此由矩阵的运算性质,可以写成.其中都是数字矩阵.设(6)而(7)比较(6)和(7)得(8)以依次从右边乘以(8)的第一式,第二式,…,第式,第式,得(9)把的个式子一块儿起来,就成了,右边,故.证法二:幂级数证法对于,由行列的拉普公式可得标准方程其中表示的伴随矩阵,的系数取自于的形式幂级数.因为所以可逆且为其逆矩阵,因此:将写成的次数取自于的形式幂级数,可得可以注意到中的元素都是的次数不超过的多项式,因此是零矩阵,等式两的系数,可得:,即. [5]1.6带余除法:对于中两个多项,其中,中的项存在,使(1)成立,其中,并且这样是唯一决定的.证法一:(1)中的存在性可以由高等代数北师大第四版课本上第八页所提及的除法直接得出,如果.下面设.令的次数分别为.对的次数作第二数学归纳法.当时,显然取,(1)式成立接下来讨论的情形,假设当次数时,的存在已证,现在看当次数等于时的情形.令的项,然有同的,因多项的数或为0.7对于者,取对于者,由归假,对在使其中,于是,也就是说,有,使成立.由归纳法原理,对的存在性就证明了.下面明性,设另有项使,其中,于是,即如果,又,那么,且有,但,所以不可能立,这就,因此证法二:用限维性来证明的带除法理.引理1:数上的任何线性关向量组构的一基;引理2:上一元多项式中,小于的组成的是上的;引理3:在中,一个互相同的项式组都是无关的.叙述:设是一元多项式环中的任意两个多项式,并且,那么存在唯一一对多项式满足:(1)(2)证明:设先证存在性,如果,那么就是满足定理条件(1)和(2)的唯一,如果,那么由引理2可知,中的个多项式组成的集合是线性空间的一组基.事实上,由引理3知,是一个线性无关集合,再由引理1和引理2的结论可知,它构成了的一组基.因为,所以在数域中存在唯一的一组数令,,于是满足定理的条件.再证唯一性:由于数域中的数是唯一的,所以也是唯一的1.7行列式计算定理:1.首先给出一个上三角行列式行列其实于主对线上素乘积即行列式计算定理.2.定义:数域上列式转化为三角行列式i ;ii ,;iii 换列式中的.比如把行列式的-2倍加到,得到再把第一行加到第三行,得到-2,我们将形如,,其分为三行列式和.1.8定理:在数域上,任意一个对称矩阵都合同于一对角矩阵对角矩阵:形式为的矩阵,其中是数,通常称为对角矩阵.对称矩阵:矩阵称为对称矩阵,如果:数域上矩阵之,如果有上的矩阵,使.合同是间的一个关系,具备下列三个特点:1)自反性:;2)对称性:由即得;3) 传递性:由和即得.2 高等代数的重要定理在相关的对应理论中的作用、地位与应用2.1因式分解及唯一性定理,我们前把它成几个能再,只是续分解这个是由于我们,并它不能,实际上这是相对于系数的数域而言的,并不是绝对的.因式分解及唯一性定理是对我们初中多项式分解知识有更深刻更宽广的认知,可是该并给出能够解多项式的以上便是多项式理论中的地位与局限.此外,初阶的因式分解定理常应用于初中考试题中.2.2 最大公因式存在定理我们在维纳的经典控制论等学科里常常会用到最大公因式,这说明最大公因式不仅是数学中的重要概念,而且在多个学科里都占据着不可替代的地位,因此在求解两个多项式之间的最大公因式时所用的辗转相除法是最大公因式定理的核心内容,它又被称为欧几里得算法,历史源远流长,是现代人们已得知的最古老的算法,这就是最大公因式存在定理的地位.辗转相除法是证明与计算最大公因式的核心,并且应用范围十分广泛.当需要寻找剩余定理的数时,它会被用来解丢翻图方程;在现代密码学里,RSA的主要构成部分就是它……这些都是辗转相除法应用里的沧海一粟.2.3 最小数定理,它等故此在解决许多存在性问题时常会用到最小数定理,证法与之结合解题常有2.4 替换定理替换定理是高等代数量空间理论的又.它应用广泛,可以被,也可被用于比较大无关量组向量的;亦;也可被用于证明基的扩充性,替换定理可以使这些问题可以得到更好的解决.2.5 哈密尔顿-凯莱定理哈密尔顿-凯莱定理是线性代数中的,是式所具备的一个,它揭示了和它式之间的关系,并且在解决.哈密尔顿-凯莱定理的应用可谓十分广泛,在计算方面可以辅助证明方阵的幂与方阵的逆阵,在证明方面即矩阵多项式等于零的有关问题中,可以使问难快速的得到解决.2.6 带余除法高等代数课程中占有重要地位的多项式的整除理论的基础就是带余除法,它是初等代数中最最基础,最最重要也是最直白的定理及工具.带余除法在初等代数中常被用到,常在小学初中的试卷中以应用题的形式出现,而在做这一类题的时候,就需要把题目外面包裹的各种各样的情境忽略掉而直接注意题目的本2.7 行列式计算定理,计算理,学习行列式的计算是学好高等代数的重要基石.,也很要,学会行列式的,我们可以应用它,还可以应用它求.2.8 对称矩阵合同于对角矩阵矩阵概念在高等代数课程的应用与内容中占据了非常广泛且重要的地位.首先,线性方程组的重要性质里就包含了矩阵的知识,例如它的系数矩阵和增广矩阵,除了线性方程组之外,许多问题的研究也常常会用到矩阵,甚至会研究有关于矩阵的方面.此外,对称矩阵、对角矩阵也是矩阵理论的重要研究对象.矩阵的应用方面包括,保密通讯技术时常会用到矩阵,信息的解码和编码也是需要用到矩阵密码这个技巧的.3 高等代数的学习《等代数》与相同,是学习的大学生要学习的核心课程之,是数学在,通过对高等代数的学习,我们可以加强自身的数学素养.在对高等代数的学习过程中,我们应该注意以下几点要求,可以让我们对这门课程的学习领悟更加深刻,更加透彻.高等代数里的抽象概念非常多,学生理解起来就有困难,譬如数域,映射,线性空间等概念,这些概念的特点就在于它们从很多具体的例子中被抽象出来的,总的来说学习高等代数时首要的是注意解相关.一方面,等代数这门课程的理与概念基本属于学专业的,由此,学生首先应注重对课程义的领会和运用,在充分理解定义定理后,我们对这门课的理解也就更深刻,在面对一些复杂的题目时更容易领会解答,从而使学生解高等代数象的内容,也会使学生对这门课程产生,唯有这样,才能对数学学习有正的度.另一方面,寻求正确的学习策略是在以培养学习的兴趣,端正学习的态度的条件下所进行的十足紧要的学习步骤.有些同学学习刻苦努力,但是成绩不算太好,就把原因归结为自己太笨,自暴自弃,其实这不是计算能力的问题,而是因为概念理解能力不行,即习对大家来说,要从、象的高等代数思维蛮困难的,故此我们在学习过程中,不应只是一味努力,也要注重学习方法,课前预习,课后复习,借力于具体的例子来理解抽象的定义定理,加深对定理的理解和掌握,寻找正确的途径学习高等代数.总而言之,学习高等代数,基本上就是在熟练掌握代数方法的同时尝试深入理解几何意义.结束语在完成这篇论文的近一百天的过程中,我再次复习了OFFICE的使用方法,对此更加熟练;阅读了许多关于高等代数重要定理的书本与论文,使我对高等代数的理解变得深刻,兴趣愈发浓厚,这也是我在大学真真正正用心去做,独立思考的稚嫩的成果,希望写论文的这段人生体验能让我在以后的学习生活中乘风破浪,积极进取.参考文献[1]王萼芳,石生明.高等代数[M].第四版.北京:高等教育出版社,2013:18.[2]张禾瑞,郝鈵新.高等代数上[M].第二版.北京人民教育出版社,1979:58.[3]苏白云,张瑞.最大公因式存在定理的两个新证法[D].河南郑州:河南财经政法大学数学与信息科学系,2013.[4]杜奕秋.替换定理的若干证明方法[D].吉林四平:吉林师范大学数学学院,2006.[5]邓勇.关于Cayley-Hamilton定理的新证明[D].新疆喀什:喀什师范学院数学系,2015.[6]王萼芳,石生明.高等代数[M].第四版高等教育出版社2013:8.[7]邓勇.多项式带余除法定理的一种新证明[D].新疆喀什:喀什大学数学与统计学院,[8]韦城东,尹长明,何世榕,庞伟才.大学数学学习成败的原因的成败分析[D].广西:广西师范学院学报,2006.[9]王喜建.高等代数课程教学中的几点体会[D].广东:广东五邑大学数学物理系[10]白永成,郑亚林.数学中的基本元素[D].陕西:安康师专学报,1998.[11]欧阳伦群,欧阳伦键.高等代数学习中的困惑与解决对策[D].湖南:当代教育理论与实践,2015.[12]熊斌,周瑶.最小数原理[D].数学通讯:教师阅读,2017.[13]李丽花.哈密尔顿-凯莱定理的应用[D].上海电力学院学报,2008.[14]侯波,郭艳红.高等代数教学的几点探索[D].学园,2015.[15]张爱萍.可逆矩阵的判定及求法[D].赤峰学院学报(自然科学版),2011.。
求最大公因数

求最大公因数最大公因数,也被称为最大公约数,是指两个或多个数共有的最大的约数。
在数论中,求最大公因数是一个常见的问题,它有着广泛的应用,比如在分数的化简、多项式的因式分解等领域。
本文将介绍几种常见的求最大公因数的方法。
一、质因数分解法质因数分解法是一种常用而简便的求最大公因数的方法。
它的基本思想是将两个数分别进行质因数分解,然后求其公共质因数的乘积。
例如,假设我们需要求出120和150的最大公因数。
首先,我们对这两个数进行质因数分解:120 = 2^3 × 3 × 5150 = 2 × 3 × 5^2然后,我们将它们的公共质因数的乘积取出:公共质因数为2、3、5,乘积为2 × 3 × 5 = 30所以,120和150的最大公因数为30。
二、辗转相除法辗转相除法,也叫欧几里德算法,是一种高效的求最大公因数的方法。
它的基本思想是通过连续除法的过程来逐步减小两个数的差距,直到找到它们的最大公因数。
例如,假设我们需要求出120和150的最大公因数。
首先,我们用150除以120得到商1和余数30,即:150 ÷ 120 = 1 (30)然后,我们用120除以30得到商4和余数0,即:120 ÷ 30 = 4 0由于余数为0,我们可以得出结论:120和150的最大公因数为30。
三、更相减损术更相减损术是一种求最大公因数的传统方法,它的基本思想是通过反复相减的过程,将两个数的差距逐渐减小,直到找到它们的最大公因数。
例如,假设我们需要求出120和150的最大公因数。
首先,我们用较大的数减去较小的数,即:150 - 120 = 30然后,我们继续用较大的数(30)减去较小的数(120)的差值,即:120 - 30 = 90接着,我们继续用较大的数(90)减去较小的数(30)的差值,即:90 - 30 = 60继续进行相减,直到两数相等或相差较小为止。
相减法求最大公因式的原理

相减法求最大公因式的原理
相减法求最大公因式的原理是一种简单而有效的求解公因式的方法。
该方法基于一个简单的原理:如果两个数a和b的最大公因式是d,那么a-b 和b的最大公因式也是d。
具体来说,我们可以用相减法来不断减小两个数中较大的数,直到两个数相等为止。
在这个过程中,不断计算两个数的差值,并用这个差值替换原先的较大数。
重复这个过程,直到两个数相等为止,这个相等的数就是它们的最大公因式。
举个例子来说,我们要求36和48的最大公因式。
首先计算两个数的差值48-36=12,然后用12替换较大的数48,得到36和12。
继续计算差值36-12=24,用24替换36,得到12和24。
继续计算差值24-12=12,用12替换24,最终得到12和12,这两个数相等,因此它们的最大公因式是12。
通过相减法求最大公因式的原理,我们可以在简单的步骤内求解两个数的最大公因式,是一种很实用的数学方法。
高等代数--第八章 多项式_OK

因此有
但是 (q(x) q(x)) (g(x)) (r(x) r(x))
矛盾。这就证明了
(g(x)) (r(x) r(x))
q(x)称为g(x)除f(x)的商,r(x)为余式
q(x) q(x),r(x) r(x)
25
例题
f 3x3 4x2 5x 6, g x2 3x 1
an :首项系数;
n为(1)的次数,记为 ( f (x)) 。 零多项式不定义次数。
11
运算:
n
m
f (x) ai xi , g (x) bj x j
i0
j0
加法:如n≥m,为方便,在g(x)中令
,
bn bn1 bm1 0
对于加减法: f (x) g(x)
n
(ai bi )xi
p(x)|f(x). 反过来,如果p(x)|f(x),p(x)|g(x),那 么p(x)一
定整除它们的线性组合 r(x)=f(x)-q(x)g(x)
由此可见,如果g(x),r(x)有一个最大 公因式 d(x),那么d(x)也是f(x),g(x)的一个 最大公因式。
36
定理2 对于P[x]中任意两个多项式 f(x),g(x),在P[x]中存在一个最大公因式d(x), 且d(x)可以表示成f(x),g(x)的一个线性组合,即有P[x]中多项式u(x),v(x)使
定义4 所有系数在数域P中的多项式的全体,
称为数域P上的一元多项式环,记为P[x],
P称为P[x]的系数域
BACK
19
§3 整除的概念
以后讨论都是在某一固定的数域P上的 多项式环中进行。 带余除法 整除 整除的性质
20
带余除法
对于P[x]中任意两个多项式f(x)与g(x),其
初中数学竞赛讲座——数论部分4(辗转相除法与最大公约数)
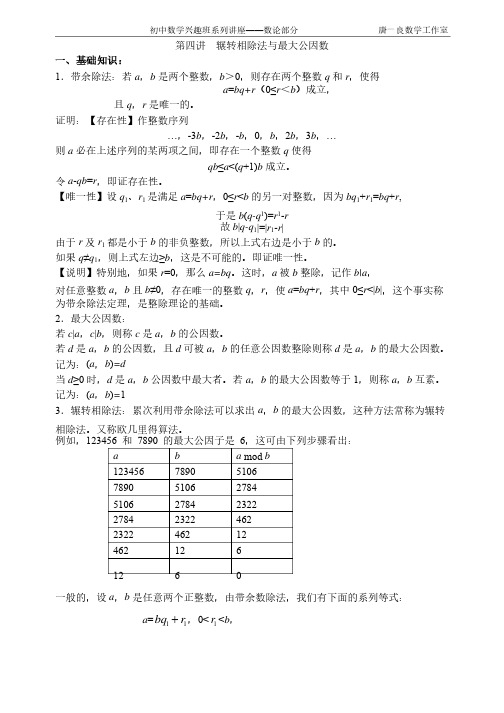
初中数学兴趣班系列讲座——数论部分初中数学兴趣班系列讲座——数论部分 唐一良数学工作室唐一良数学工作室第四讲第四讲 辗转相除法与最大公因数辗转相除法与最大公因数一、基础知识:1.带余除法:若a ,b 是两个整数,b >0,则存在两个整数q 和r ,使得,使得a =bq+r (0≤r <b )成立,)成立,且q ,r 是唯一的。
是唯一的。
证明:【存在性】作整数序列证明:【存在性】作整数序列…,-3b ,-2b ,-b ,0,b ,2b ,3b ,…则a 必在上述序列的某两项之间,即存在一个整数q 使得使得qb ≤a <(q +1)b 成立。
成立。
令a -qb =r ,即证存在性。
,即证存在性。
【唯一性】设q 1、r 1是满足a =bq+r ,0≤r <b 的另一对整数,因为bq 1+r 1=bq +r ,于是b (q-q 1)=r 1-r 故b |q-q 1|=|r 1-r |由于r 及r 1都是小于b 的非负整数,所以上式右边是小于b 的。
的。
如果q ≠q 1,则上式左边≥b ,这是不可能的。
即证唯一性。
,这是不可能的。
即证唯一性。
【说明】特别地,如果r =0,那么a=bq 。
这时,a 被b 整除,记作b|a ,对任意整数a ,b 且b ≠0,存在唯一的整数q ,r ,使a =bq +r ,其中0≤r <|b |,这个事实称为带余除法定理,是整除理论的基础。
为带余除法定理,是整除理论的基础。
2.最大公因数:.最大公因数:若c |a ,c |b ,则称c 是a ,b 的公因数。
的公因数。
若d 是a ,b 的公因数,且d 可被a ,b 的任意公因数整除则称d 是a ,b 的最大公因数。
记为:(a ,b )=d当d ≥0时,d 是a ,b 公因数中最大者。
若a ,b 的最大公因数等于1,则称a ,b 互素。
互素。
记为:(a ,b )=13.辗转相除法:累次利用带余除法可以求出a ,b 的最大公因数,这种方法常称为辗转相除法。
公因数公式(二)

公因数公式(二)公因数公式1. 概述在数学中,公因数公式用于求两个或多个数的公因数。
公因数是指能够同时整除给定数的数,而公因数公式则是通过一定的运算方式来求解公因数的公式。
2. 公因数公式列表以下是一些常见的公因数公式:最大公因数(Greatest Common Divisor,GCD)最大公因数是指能够同时整除给定数的最大正整数。
最大公因数的求解常用的有以下两种公式:•辗转相除法:将两个数的较大数除以较小数,然后用余数替代较大数,继续进行相同的除法运算,直到余数为0时,被除数即为最大公因数。
例如,求解94和65的最大公因数:94 / 65 = 1 (29)65 / 29 = 2 (7)29 / 7 = 4 (1)7 / 1 = 7 0因此,最大公因数为7。
•更相减损术:将两个数相减,然后用差值替代较大数,继续进行相同的相减运算,直到差值为0时,被减数即为最大公因数。
例如,求解94和65的最大公因数:94 - 65 = 2965 - 29 = 3636 - 29 = 729 - 7 = 2222 - 7 = 1515 - 7 = 88 - 7 = 17 - 1 = 66 - 1 = 55 - 1 = 44 - 1 = 33 - 1 = 22 - 1 = 1因此,最大公因数为1。
公因数计算公式除了求解最大公因数的公式,还存在一些用于计算公因数的公式,包括:•因式分解法:将给定的数进行因式分解,并找出它们的公因数。
将每个数的因式分解的结果中,相同的因式相乘即可得到公因数。
例如,对于30和45,先对这两个数进行因式分解得到:30 = 2 * 3 * 545 = 3 * 3 * 5公因数为3和5,相乘得到15。
•素数分解法:将给定的数分解为素数的乘积,并找出它们的公因数。
将每个数的素数分解结果中,相同的素数相乘即可得到公因数。
例如,对于35和70,先对这两个数进行素数分解得到:35 = 5 * 770 = 2 * 5 * 7公因数为5和7,相乘得到35。
求两个数的最大公因数的方法
求两个数的最大公因数的方法求两个数的最大公因数是数学中的基本问题之一,关于这个问题,可以用多种方法进行求解。
以下是几种经典的求最大公因数的方法:一、因式分解法这种方法适用于数比较小的时候。
1. 将两个数分别进行因式分解;2. 找出两个数中所有的公共因数;3. 取出所有公共因数中的最大值,即为所求的最大公因数。
例如:求48和60的最大公因数。
48=2^4×3,60=2^2×3×548和60的公共因数有2和3,所以它们的最大公因数为6。
二、辗转相除法辗转相除法,又称欧几里得算法,这种方法适用于数较大时的求解。
1. 用较大的数除以较小的数,将余数记作r1;2. 用较小的数除以r1,将余数记作r2;3. 再用r1除以r2,余数为r3;4. 依此类推,直到求得的余数为0为止;5. 最后,除数即为最大公因数。
例如:求48和60的最大公因数。
60÷48=1 (12)48÷12=4 0所以,48和60的最大公因数为12。
三、质因数分解法这种方法是一种将数进行质因数分解的方法,利用质因数分解后的结果求得最大公因数。
1. 将两个数进行质因数分解;2. 把同一质因数的次数较小的那个数的该质因数次方用于最大公因数的分解式中;3. 通过上述方法可以得到最大公因数的分解式,从而得到最大公因数的值。
例如:求48和60的最大公因数。
48=2^4×3,60=2^2×3×52:2^2×3所以,它们的最大公因数为2^2×3=12。
总的来说,根据具体情况可以采用不同的方法求最大公因数。
因此我们需要全方位了解这几种方法,为不同情况下的求解提供方法选择的依据。
第五章多项式
第一章多项式教学目的:1、理解一元多项式的的概念,掌握一元多项式的加法、减法和乘法的运算法则。
2、理解带余除法定理和整除的概念,掌握整除的性质,能熟练运用余除法计算商式和余式,学会整除性的判断和证明。
3、理解多项式的公因式,最大公因式和互素的概念与性质,掌握辗转相除法。
4、理解不可约多项式、因式分解定理和标准分解式,掌握不可约多项式的性质。
5、理解多项式的K重因式和导读(微商)的概念,掌握K重因式的性质和判断法。
6、理解多项式函数,多项式的根和K重要的概念,掌握余数定理和带余除法。
7、掌握复(实)系数多项式中的不可约多项式和因式分解定理,会把一些多项式在复数域或实数域进行因式分解。
8、理解本原多项式的概念和性质,掌握整系数多项式有理根的性质和求法,会运用艾森斯坦因判别法别有理数域上的不可约多项式。
教学重难点:整除的基本性质和整除性的判别和证明,最大公因式和互素的概念和性质,不可约多项式的性质,K重因式的性质,余数定理和综合除法,因式分解定理在复数域,实数域和有理数域上的具体形式。
教学方法:讲授、习题和讨论相互结合。
教学过程:§1 一元多项式在讨论多项式的有关内容中,我们总是预先给定一个数域P ,并且设x 是一个符号(或文字)。
1、定义:一元多项式:设10,,n n a a a ≥ 是数域P 上的元素,我们称1110nn n n a x a xa x a --+++为系数在数域P 上的一元多项式或称为数域P 上的一元多项式,常用(),(),,f x g x f g 或来表示,如:1()110n n x n n f a x a xa x a --=+++(1)ii a x称为多项式(1)的i 次项,i a 称为i 次项的系数,若0n a ≠,称n n a x 为(1)的首项,n a 为首项系数,n 称为多项式(1)的次数,记为(())f x ∂。
零多项式:如果多项式的系数全为0,则称多项式为零多项式。
多项式最大公因式的几种求法
多项式最大公因式的几种求法
发表时间:2015-09-21T16:46:59.207Z 来源:《教育学》2015年10月总第86期供稿作者:陈萍[导读] 华南师范大学数学科学学院多项式理论是高等代数的重要组成部分,求最大公因式在多项式理论研究中占有显著地位。
陈萍华南师范大学数学科学学院广东广州510631
摘要:多项式既是初高中课本的重要内容,也是大学数学高等代数的重要组成部分,而求多项式的最大公因式也成为了高等代数中最基本同时也是最重要的一个知识点。
而本文将从辗转相除、矩阵的初等变换以及矩阵的初等变换等不同角度给出了一元多项式的最大公因式的不同求法。
关键词:最大公因式辗转相除初等变换
多项式理论是高等代数的重要组成部分,求最大公因式在多项式理论研究中占有显著地位。
如何求多项式最大公因式,除了《高等代数》介绍的辗转相除法外,还有一些其他的较为便捷的方法,作者经过大量地查阅资料后,总结出较为经典的算法,并于此文一一介绍。
由上面的介绍,我们可以知道,多项式的最大公因式有多种解法,它们都是从多项式最大公因式的性质推广发展而来的,可见性质的重要性,并且三种方法都各有优劣,读者可以根据题目需要,选择一种最简便的方法进行计算,最好熟练掌握一种基本解法。
参考文献
[1]张禾瑞赫炳新高等代数(第三版)[M].北京:高等教育出版社,1983。
[2]蒋忠樟高等代数典型问题研究.高等教育出版社。
[3]骆公志一元多项式的最大公因式的几种求法.[J]连云港师范高等专科学校学报,2006。
一元多项式
所以 r2 x就是 f x与 gx的最大公因式:
f x, gx x 3
定理 1.4.2
若dx 是 P[x] 的多项式 f x与 gx的最大公因 式,那么在 P[x] 里可以求得多项式 ux与vx ,
二、教学目的
1.掌握一元多项式整除的概念及其性质。 2.熟练运用带余除法。
三、重点、难点
多项式的整除概念,带余除法定理
1.3.1 多项式的整除概念
设P是一个数域. P[x]是P上一元多项式.
定义1
设f x, gx P[x] ,如果存在 hx P[x] ,使得
f x gxhx,则称 gx整除 f x ,记为
3
虽然 a1,b1, a2,b2 Z,
不一定属于Z ,所以
不是数域.
a1aa不222 一33bb定122b2属, a于a2b221Z(3ab132b2)2
,因此 Z (
3)
定理1.1 任何数域都包含有理数域 Q. (有理数域是最小的数域).
定理1.2 若数域 P R,则P C. (实数域和复数域之间没有其它的数域).
则 (a1 a2) b1 b2 2 Q 2 ,
a1 b1 2 a2 b2 2
(a1a2 2b1b2 ) a1b2 a2b1 2 Q 2
显然,Q Q( 2) R.
再设 a2 b2 2 0, 即 a2,b2 不全为零,从
而 a2 b2 2 0 , a1 b1 2 a1 b1 2 a2 b2 2 a2 b2 2 a2 b2 2 a2 b2 2
a 叫做 i 次项, i叫做 i 次项的系数.
注 2:在一个多项式中,可以任意添上或去掉一些系
数为零的项;若是某一个i次项的系数是1 ,那 么这个系数可以省略不写。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因此在有限次之后,必然有余式为零。于是有一串
等式:
返回
上页
下页
f ( x ) q1 ( x ) g ( x ) r1 ( x ), g ( x ) q2 ( x )r1 ( x ) r2 ( x ), ri 2 ( x ) qi ( x )ri 1 ( x ) ri ( x ), rs 3 ( x ) q s 1 ( x )rs 2 ( x ) rs 1 ( x ), rs 2 ( x ) q s ( x )rs 1 ( x ) rs ( x ), rs 1 ( x ) q s 1 ( x )rs ( x ) 0.
推论 如果f1(x)|g(x),f2(x)|g(x),且(f1(x), f2(x))=1,
27 1 1 ( 27 x 9 ) f ( x ) 1 ( x 9 )( x 5 5 3 9 ) g ( x )
返回上页下页 Nhomakorabea是2 3 2 ( f ( x ), g( x )) ( 5 x 1) f ( x ) ( 1 x 5 5 x ) g( x ).
返回 上页 下页
例 证明:如果f(x), g(x)不全为0,且
u(x)f(x)+v(x)g(x)= (f(x),g(x)) 则 (u(x),v(x))=1 . 证 因为f(x), g(x)不全为0,故(f(x),g(x)) ≠0,由 u(x)f(x)+v(x)g(x)= (f(x),g(x)) 可得
返回 上页 下页
例
求下列各题中f(x)和g(x)的最大公因式.
n n1 f ( x ) x a x an1 x an, (n 1) 1. 1
g( x) x n1 a1 x n2 an2 x an1
解 1. 用g(x)除f(x)得
f ( x) xg( x ) an。
解 2. 作带余除法有
f ( x) x g( x) x 1, g( x) x
n n
n
mn
( x 1) 2,
n
1 n x 1 2 x 1 2
所以-2是f(x) 和g(x)的一个最大公因式,即 (f(x), g(x))=1 .
返回 上页 下页
r(x)=f(x)-q(x)g(x)
这就是说, ( x )是g(x), r(x)的公因式 . 由此可见,如 果g(x), r(x)有一个最大公因式d(x),那么d(x)也就是 f(x), g(x)的一个最大公因式 .
返回 上页 下页
定理2 对于P[x]中任意两个多项式f(x), g(x),在
P[x]中存在一个最大公因式d(x),且d(x)可以表成 f(x), g(x)的一个组合,即有P[x]中多项式u(x),v(x)使 d(x)=u(x)f(x)+v(x)g(x) 那么f(x)就是一个最大公因式,且 f(x)=1· f(x) +1· 0 下面来看一般的情形. 不妨设g(x)≠0. 按带余 除法,用 g(x) 除 f(x),得到商 q1(x),余式 r1(x);
入上式可消去rs-1(x),得到
rs ( x ) (1 qs ( x )qs 1 ( x ))rs 2 ( x ) qs ( x )rs 3 ( x ).
然后根据同样的方法用它上面的等式逐个地消去 rs-2(x) , … , r1(x),再并项就得到
rs ( x ) u( x ) f ( x ) v( x ) g( x )
返回 上页 下页
在有了以上的定义之后,我们首先要解决的
是最大公因式的存在问题,以下的证明也给出了 一个具体的求法. 最大公因式的存在性的证明主要根据带余除法, 关于带余除法我们指出以下事实:如果有等式 f(x)=q(x)g(x)+r(x) (1) 成立,那么f(x), g(x) 和g(x) , r(x) 有相同的公因式 .
如果an=0,那么(f(x), g(x))=g(x);如果an≠0,那 么用an除g(x) 得余式为0,所以an是f(x), g(x)的最 大公因式,亦即(f(x), g(x))=1 .
返回 上页 下页
2.
f ( x) x
m
m n
x x 1
m n
g( x) x x
mn
2, (m n)
证明 由(f(x), g(x))=1 可知,有u(x),v(x)使 u(x) f(x)+v(x) g(x)=1
等式两边乘h(x),得
u(x)f(x)h(x)+v(x)g(x)h(x)=h(x) 因为f(x)|g(x)h(x) ,所以f(x)整除等式左端,从而
f(x)|h(x) .
返回
证毕 .
上页 下页
1) d(x) 是f(x), g(x) 的公因式;
2) f(x), g(x) 的公因式全是d(x) 的因式.
那么就称d(x) 为f(x), g(x) 的一个最大公因式
例如,对于任意多项式 f(x), f(x) 就是f(x) 与0的一 个最大公因式 . 特别的,根据定义,两个零多项式 的最大公因式就是0。
定理3 P[x]中两个多项式f(x), g(x)互素的充分必要
条件是有P[x]中的多项式u(x),v(x)使 u(x)f(x)+v(x)g(x)=1
证明 必要性是定理2的直接推论 .
现在设有u(x),v(x)使 u(x)f(x)+v(x)g(x)=1
而d(x)是f(x)与g(x)的一个最大公因式 . 有d(x)| f(x), d(x)|g(x),从而d(x)|1,即f(x), g(x)互素 . 证毕.
返回 上页 下页
定理证明中用来求最大公因式的方法通常称
为辗转相除法。
例
设
f ( x ) x 4 3 x 3 x 2 4 x 3, g( x ) 3 x 3 10 x 2 2 x 3,
求(f(x), g(x)),并求 u(x),v(x) 使
( f ( x ), g( x )) u( x ) f ( x ) v ( x ) g( x ).
而 5 2 25 10 x 9 )( x x 9 x 27 g( x ) ( 27 5 9 9 3) 1 1 g( x ) ( 27 5 x 9) f ( x ) ( 3 x 9 ) g ( x )
9 2 18 ( 27 x 9 ) f ( x ) ( x 5 5 5 x ) g ( x ),
r2 ( x ) 9 x 27
r1 ( x ) 5 2 25 10 x x 9 9 3
5 2 5 x x 9 3
10 10 x 9 3 10 10 x 9 3
5 10 x 81 81 q3 ( x )
0
返回 上页 下页
用等式写出来,就是
10 f ( x ) ( x ) g ( x ) ( x 25 x 9 3 ), 1 3 1 9 5 9 2 2 5 25 10 g ( x ) ( 27 x 9 )( x x 5 9 9 3 ) ( 9 x 27), 2 25 10 5 10 5 x x ( x 9 9 3 81 81 )( 9 x 27). 因之 ( f ( x ), g( x )) x 3
返回
上页
下页
事实上,如果 ( x )|g(x), ( x )|r(x),那么由(1) 有, ( x ) |f(x).这就是说,g(x) , r(x)的公因式全是
( x) f(x), g(x)的公因式. 反过来,如果 | f(x), | ( x)
g(x),那么 ( x ) 一定能整除它们的组合
第四节
最大公因式
如果多项式 ( x ) 既是f(x)的因式,又是g(x)的 因式. 那么 ( x )就称为f(x)与g(x)的一个公因式. 在公因式中占有特殊重要地位的是所谓最大公因 式.
返回
上页
下页
定义 6
设f(x), g(x), d(x) 是P[x] 中的多项式,如
果d(x) 满足下面两个条件:
f ( x) g( x ) u( x ) v( x ) 1 ( f ( x ),g( x )) ( f ( x ),g( x ))
证毕 .
上页 下页
故由互素的充分条件知 (u(x) , v(x))=1 .
返回
定理4 如果(f(x), g(x))=1,且f(x)|g(x)h(x) ,那么
f(x)|h(x) .
这里
3 u( x ) x 1 5
v( x )
1 2 2 x x 5 5
定义7 如果 P[x] 中的两个多项式 f(x), g(x) 满足
(f(x), g(x))=1 ,那么就称 f(x), g(x)是互素的 .
显然,如果两个多项式互素,那么它们除去 零次多项外式(非零常数)没有其它的公因式, 反之亦然 .
这就是定理中的(2)式 .
返回
证毕.
上页 下页
由最大公因式的定义不难看出,如果 d1(x),
d2(x)是f(x)与g(x)的两个最大公因式,那么一定有 d1(x)|d2(x)与d2(x)|d1(x),也就是d1(x)=cd2(x), c≠0. 这就是说,两个多项式的最大公因式在可以 相差一个非零常数倍的意义下是唯一确定的. 我们知道,两个不全为零的多项式的最大公因式总 是一个非零多项式。在这个情形,我们约定,用 (f(x), g(x)) 来表示首项系数是1的那个最大公因式.
1 1 x 3 9 q1 ( x )
1 3 5 2 x x 3x 3 2 5 x 16 x 3 3 3 1 5 x 2 25 x 30 1 3 10 2 2 x x x 3 9 9 3
