八年级数学上册《121轴对称(1)》学案
第一章轴对称图形复习教学案(1)(苏科版八年级上)

2、轴对称图形的对称轴的条数( )
(A)只有一条 (B)2条 (C)3条 (D)至少一条
3、下列图形中,不是轴对称图形的是( )
A.两条相交直线B.线段
C.有公共端点的两条相等线段D.有公共端点的两条不相等线段
4、到三角形的三个顶点距离相等的点是( )
A.三条角平分线的交点B.三条中线的交点
1)当MN满足什么条件时,将长方形ABED以MN为折痕翻折,翻折后能使C点恰好和A点重合;
2)梯形ABMN的面积与梯形CDNM的面积相等吗?为什么?
24、已知直线 及其两侧两点A、B,如图.
(1)在直线 上求一点P,使PA=PB;
(2)在直线 上求一点Q,使 平分∠AQB.
第23题
25、在矩形ABCD中,将△ABC绕AC对折至△AEC位置,CE与AD交于点F,如图.试说明EF=DF.
18、如图,己知AB=AC,DE垂直平分AB交AC、AB于D、E两点,若AB=12cm,BC=10cm,∠A=49º,求△BCE的周长和∠EBC的度数.
19、“西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置。(保留画图痕迹,不写画法)
7、如图,A、B是安达公路边两个新建的居民小区,某镇需在公路边增加一个公共汽车站,这个公共汽车站建在什么位置,才能使两个小区到车站的路程一样,找出汽车站的位置并说明理由。
8、点Q在∠AOB的平分线上,QA⊥OA于A,QB⊥OB于B,则AQ=____ ,理由是_____________________________________。
江苏省张家港市南沙中学八年级数学上册 轴对称的性质(第1课时)学案

轴对称的性质预学目标1.阅读线段的垂直平分线的概念,初步了解垂直平分线是一条直线,它垂直于一条线段且平分这条线段.通常说成直线l垂直平分线段AB或直线l是线段AB的垂直平分线.2.学习讲义上的两个定理:成轴对称的两个图形全等;对称轴是对称点连线的垂直平分线.3.尝试找出画成轴对称的两个图形的对称轴的方式,能够熟练地找出它们的对称点.4.探讨两个结论:①成轴对称的两个图形中,对称点的连线相互平行;②若是对称线段或延长线相交,那么交点在对称轴上.预习讲义p43-44问题:成轴对称的两个图形具有哪些性质呢?它们的大小和位置有什么关系?操作:在纸上任意画一点A,把纸对折,用针在点A处穿孔,再把纸展开,并连接两针孔A、A'.l探讨:两针孔A、A'和线段A A'与折痕l之间有什么关系?‘问题1:若是把纸从头折叠,因为A、A'重合,那么线段OA、O A'呢?,现在O是线段A A'的。
问题2:∠1与∠2有什么关系?问题3:折痕l与A A'什么关系?新课概念探讨:,叫做这条线段的垂直平分线。
一、操作:取一张长方形的纸片,按下面步骤做一做。
将长方形纸片对折,折痕为l,(1)在纸上画△ABC;(2)用针尖沿△ABC各边扎几个小孔(3)将纸展开,连接AA’、BB’、CC’二、探讨:线段AA’、BB’、CC’与折痕l有什么关系?问题1:图中,线段AB 与''B A 有什么关系?BC 与''C B 呢?线段'BB 与l 有什么关系?'AA 与l 呢?说说你的理由。
问题2:图中,A ∠与'A ∠有什么关系?B ∠与'B ∠呢?ABC ∆与'''C B A ∆有什么关系?什么缘故?3、归纳:轴对称的性质:。
例题精讲例1 以下说法中,正确的选项是 ( )A .设点A 、B 关于直线EF 对称,那么线段AB 垂直平分EFB .假设△ABC ≌△DEF ,那么△ABC 和△DEF 成轴对称C .关于直线EF 成轴对称的两个图形全等D .假设两个图形关于直线EF 对称,那么这两个图形别离在直线EF 的双侧例2 如图,在Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上的A'处,折痕为CD ,那么∠A'DB 的度数为 ( )A .40°B .30°C .20°D .10°课堂练习1.两个全等的三角形_______关于某条直线对称;关于某条直线对称的两个三角形_______全等(填“必然”或“不必然”).对称轴上的点的对称点是_______.2.一只猫以40 cm /s 的速度走向一面镜子,猫距离镜子中的像8m ,那么猫通过_______s 碰着镜子.3.如图,点A 和点C 关于直线l 对称,点B 和点D 也关于直线l 对称,那么线段_______和线段_______关于直线l 对称,线段______和线段_______关于直线l 对称,因此_______=_______,_______=_______.4.如图,△ABC 与△A'B'C'关于直线l 对称,且∠A =78°,∠C'=48°,那么∠B 的度数为 ( )A .48°B .54°C .74°D .78°5.如图,先将△ABC沿DE折叠,使△CDE与△BDE完全重合,然后沿BD折叠,使△ABD与△EBD也完全重合,那么∠ABC的度数为( )A.30°B.40°C.50°D.60°6.如图,把一张长方形纸片沿EF折叠后,点D、C别离落在D'、C'的位置.假设∠EFB=65°,那么∠AED'的度数为( )A.70°B.65°C.50°D.25°巩固练习1.当你看到镜子中的你在用右手往左梳理你的头发时,事实上你是( )A.右手往左梳B.右手往右梳C.左手往左梳D.左手往右梳2.如图,将一块正方形纸片沿对角线折叠一次,然后在取得的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,取得的图案是( )3.以下说法不正确的选项是A.两个关于某直线对称的图形必然全等B.轴对称图形的对称点必然在对称轴的双侧C.两个轴对称的图形对称点的连线的垂直平分线是它们的对称轴D.平面上两个全等的图形不必然关于某直线对称4.桌面上有A、B两球,假设要将B球射向桌面任意一边,使一次反弹后击中A球,那么如下图8个点中,能够对准的点的个数是( )A.2 B.4 C.6 D.85.(2020.山东济南)如图,△ABC与△A'B'C'关于直线l对称,那么∠B的度数为( ) A.50°B.30°C.100°D.90°6.我国传统的木结构衡宇,窗子经常使用各类图案装饰,如图是一种常见的图案,那个图案有_______条对称轴.7.如图,已知四边形ABCD与四边形EFGH关于直线l成轴对称,图中与AB相等的线段有_______,与AE平行的线段有_______,直线l必然是线段_______的垂直平分线.8.如图,AB垂直平分CD,AC=6,BD=4,那么四边形ADBC的周长是_______.9.如图,若是直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°,那么∠D的值等于______.10.将一张长方形纸片按如下图的方式折叠,BC、BD为折痕,那么∠CBD为____度.12.以下图是由两个等边三角形组成的图形,它是轴对称图形吗?若是不是,请移动其中一个三角形,使它与另一个三角形一路组成轴对称图形,如何移动,才能使所组成的图形具有尽可能多的对称轴?试画出平移后的图形.13.如图,菱形ABCD(图①)与菱形EFGH(图②)的形状、大小完全相同.请从以下序号当选择正确选项的序号填写;①点E,F,G,H;②点G,F,E,H;③点E,H,G,F;④点G,H,E,F.(1)若是图①通过一次平移后取得图②,那么点A,B,C,D对应点别离是_______;(2)若是图①通过一次轴对称后取得图②,那么点A,B,C,D对应点别离是_______.。
八年级数学上册 12.1轴对称(第二课时)教案 人教新课标版

§12.1 轴对称的性质(第2课时)教学目标:(一)知识与技能. 1.掌握线段垂直平分线的概念. 2.掌握轴对称图形的性质.(二)过程与方法:经历探索轴对称图形性质的过程,进一步体验轴对称的特点,发展空间观察(三)情感态度与价值观通过对轴对称图形性质的探索,促使学生对轴对称有了更进一步的认识,活动与探究的过程可以更大程度地激发学生学习的主动性和积极性,•并使学生具有一些初步研究问题的能力.教学重点:轴对称的性质..教学难点:轴对称的特征.教学过程:一.创设问题情境上节课我们欣赏了许多生活中具有轴对称特征的图片,对轴对称图形已经有了初步的认识,今天我们要进一步深入学习轴对称的知识提问:这几组图片中,直线两旁的图案分别有什么关系?;学生观察比较后总结:只有第一组中直线两旁的图形是关于中间的直线对称;通过以上4组图形的比较,我们对图形的轴对称已经有了一个整体的认识:折叠后能够完全重合。
今天我们要更加深入、更加细致地研究轴对称图形的性质,那么应该从什么地方入手?引导:图形由点组成,从点开始入手研究。
二.探究一――――探索轴对称的性质(一)折一折提问:在纸上任意画出一条直线,那么如何作出两个点关于直线对称?学生活动:小组讨论、交流,小组代表发言教师活动:充分肯定学生的想法,并引导学生通过折纸得到两个点关于直线对称。
做法:先将纸张沿着直线对折,用笔尖在纸上穿一个孔,然后再把纸展开,就得到两个点对称。
学生活动:按照以上做法操作,并按照多媒体演示给相应的点标上字母。
(设计意图:这里采用让学生动手折一折,目的是让学生在折纸中体验对称性。
)(二)说一说(1)问:在上面的扎孔过程中,点A与点A'重合,设折痕为MN,连接点A与点A'的线段与MN有什么关系?设AA'交MN与点O,因为折叠时点A 与点A'重合,所以OA与OA'重合,即O是AA'的中点。
又因为∠1=∠2,∠1+∠2=1800,所以∠1=∠2=900,所以MN垂直AA'A AOMNB BCCA A‘OMN12(设计意图:先选取一个点进行实验,一是解决一个点,就解决了其他的点,二是从简单入手分析问题本身是我们推理和解决问题的一种手段。
八年级数学上12.1轴对称导学案(2)(人教新课标)

归纳:与一条线段两个端点距离相等的点,在这条线段的上.
形
式
个人备课
集体研讨与个案补充
导
学
活
动
过
三、巩固练习
(一)思考:教材P34思考
学生相互讨论,教师巡视班级,观察监督学生的活动情况。
看学生动手操作,肯定学生的积极表现,
总结归纳:作轴对称图形的对称轴的方法是:找到一对,作出连接它们的,就可以得到这两个图形的对称轴.
2、如图,角是轴对称图形吗?如果是,画出它的对称轴
3、如图,与图形A成轴对称的是哪个图形?画出它们的对称轴
4、如图所示在方格纸上画出的一棵树的一半,请你以树干为对称轴画出树的另一半
反
思
12.1轴对称导学案(2)
授课人:2009-9-23
科目
数学
集体研讨主持人
教案序号
集体研讨与个案补充
课题
轴对称(2)
课型
新
课时
1
形式
个人备课
导
学
活
动
过
程
教学目标:
1、理解线段垂直平分线的性质和判定,初步体会线段垂直平分线的集合定义。
2、会作轴对称图形的对称轴。
3、通过实践探究图形轴对称的性质和线段垂直平分线的性质,培养作图能力和解决实际问题的能力
4、通过小组合作交流,培养团队协作的精神和集体意识。
教学重点和难点:
重点:理解轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;理解线段垂直平分线的性质和判定;会作线段的垂直平分线和轴对称图形的对称轴。
难点:线段垂直平分线的集合定义
教学过程设计:
一、回顾旧知,引入新知
引导学生回顾上节课的内容,强调轴对称的数学本质以及垂直平分线的相关概念和性质。
内蒙古鄂尔多斯市八年级数学上册《作轴对称》学案(无
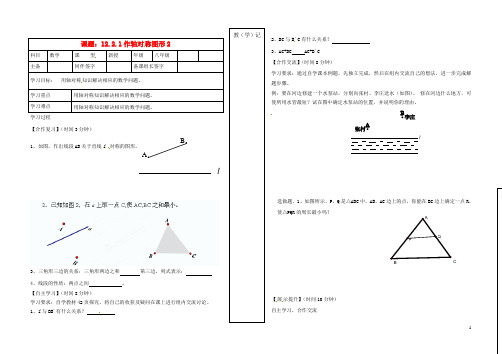
1教(学)记学习过程【合作复习】(时间3分钟)1、如图,作出线段AB 关于直线l 对称的图形。
3、三角形三边的关系:三角形两边之和 第三边。
列式表示:4、线段的性质:两点之间 。
【自主学习】(时间8分钟)学习要求:自学教材42页探究,将自己的收获及疑问在课上进行组内交流讨论。
1、l 与BB'有什么关系?2、BC 与B 'C 有什么关系?3、AC+BC AC+B'C 【合作交流】(时间8分钟)学习要求:通过自学课本例题,先独立完成,然后在组内交流自己的想法,进一步完成解题步骤。
例:要在河边修建一个水泵站,分别向张村、李庄送水(如图)。
修在河边什么地方,可使所用水管最短?试在图中确定水泵站的位置,并说明你的理由。
选做题、1、如图所示,P ,Q 是△ABC 中,AB ,AC 边上的点,你能在BC 边上确定一点R ,使△PQR 的周长最小吗?【展示提升】(时间10分钟) 自主学习,合作交流课题:12.2.1作轴对称图形2科目 数学 课 型 新授 年级八年级主备同伴签字备课组长签字学习目标: 用轴对称知识解决相应的数学问题。
学习重点 用轴对称知识解决相应的数学问题。
学习难点 用轴对称知识解决相应的数学问题。
A .B .l张村李庄lABACBPQ【课堂检测】学习要求:独立完成班级:姓名:1、如图所示,要在街道旁修建一个牛奶站,向居民区A、B提供牛奶,牛奶站应建在什么地方?才能使A、B到它的距离之和最短?选做2。
八上 1.2 轴对称的性质(1)
1.2 轴对称的性质(教案)
班级姓名学号
教学目标:
1、掌握轴对称性质;
2、会利用轴对称的性质,作对称点,对称图形等
教学重点:作已知图形的轴对称图形的一般步骤.
教学难点:怎样确定已知图形的关键点并根据这些点作出对称图形.
教学过程:
一、创设情境:
试一试
如下图,方格子内的两图形都是成轴对称的,请画出它们的对称轴.
做一做1
请试着画出下图所示图形的对称轴.
(1)(2)
你可以用折叠的方法来检验自己画的对称轴是否准确,如果准确的话,能总结你的方法吗?你是如何判断对称轴位置的呢?
做一做2
1、实践、操作:
在纸上画出线段AB 及它的中点O ,再过O 点画出与AB 垂直的直线CD ,
沿直线CD 将纸对折,看看线段OA 与OB 是否重合?
从上面的操作我们可以看出,线段是轴对称图形.
直线CD 是线段AB 的对称轴,它垂直于线段AB ,又平分线段AB ,
我们把这样垂直并且平分一条线段的直线,叫做这条线段的垂直平分线.
2、动手、操作
(1
直平分;
(2)说出图中相等的线段和角.
成轴对称的两个图形全等.
如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线
二、例题示范:
例题 用针扎重叠的纸得到下面关于l 成轴对称的两个图案:
(1) 找出它的两对对称点,两条对称线段;
(2) 用测量的方法验证你找到的对称点所连线段被对称轴垂直平分.
F
三、课堂小结:
1、能找到轴对称中的对称点;
2、会画出对称点、对称线段;
3、能找到对称轴
四、课后作业:P13-14 1,2,3
五、教学后记:。
(精编)八年级数学上册 12.1.2 轴对称的性质导学案(2)(无答案) 新人教版
ABC l轴对称的性质【学习目标】1.能够按要求作出简单平面图形经过一次对称后的图形 .2、能设计简单的轴对称图案 .3、通过画轴对称图形 ,增强学生学习几何的趣味感 ,培养审美情操 .【重点难点】:重点:利用对称轴作轴对称图形 .难点:利用对称轴进行图案设计 .【自主学习】一、预习新知P39 - - -P411、如图:你能做出它关于虚线的对称图形吗 ?(1 )找到点A的对称点A′(2) A A′与对称轴有什么关系 ?(3 )在图中另找一对对称点 ,连接对称点的线段与对称轴还有上述关系吗 ?2、连接任意一对对称点的线段被对称轴____________3、如图 ,点A和直线l ,试画出点A关于直线l的对称点A′ .请说说你的画法lA·4、作△ABC关于直线l的对称的图形△A′B′C′5、课本P41练习题1【合作探究】1、△ABC ,及点A的对称点A′ ,请作出对称轴直线l ,并画出△ABC关于直线l的对称图形 .A .A′思路分析:BC2、如图(1) ,请画出三角形关于直线l对称的图形 .3、身高的人站在平面镜前2米处 ,它在镜子中的像高______米 ,人与像之间距离为_______米;如果他向前走 ,人与像之间距离为_________米.【能力检测】1、请用四个半圆设计对称图形 .2、课本P46习题5【拓展延伸】为了美化环境 ,在一块按以下要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等.现已有两种不同的分法:⑴分别作两条对角线(如图中的图1 );⑵过一条边的四等分点作这边的垂线段 (图2 ) (图2中两个图形的分割看作同一方法 ).请你按照上述三个要求 ,分别在下面两个正方形中给出另外两种不同......的分割...方法.... (正确画图 ,不写画法 )图(1 ) 图(2 ) 图(3 ) 图(4 )小组评价:教师评价:【课后反思】。
八上 1.1 轴对称和轴对称图形
第一章轴对称图形教案1.1 轴对称和轴对称图形班级姓名学号教学目标:1、认识轴对称与轴对称图形;2、会画出对称轴,找出对称点;3、能设计简单轴对称图案、标志;教学重点:正确辨认轴对称图形,画出它们的对称轴;教学难点:设计简单轴对称图案;教学过程:一、情境创设:活动一:将一张矩形的纸对折,用针在纸上扎出简单的图形或数字,将纸打开铺平.仔细观察回答下列问题:1.纸上的图案有什么关系?2.找出图形中的两组对应点,并连接,看看你连接的的线段与对称轴之间有什么关系?3.在扎字中的对应线段,对应角又有什么样的关系?由此可得:把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形关于这条直线对称,也称这两个图形成轴对称,这条直线叫对称轴,两个图形中的对应点叫做对称点做一做1用一张半透明的纸描出图所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有多少条对称轴.做一做2请你标出图中A、B、C三点的对称点A1、B1、C1.我们再看图中的两组图形.试一试把一张纸对折,然后从折叠处剪出一个图形,想一想展开后会是一个什么样的图形?观察图10.1.1中的各个图形,它们都是对称图形.这些图形有什么特点呢?如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴.图10.1.1轴对称与轴对称图形的区别与联系.区别:轴对称是指两个图形沿某直线对折能够完全重合,而轴对称图形是指一个图形的两个部分能完全重合.联系:两部分都完全重合,都有对称轴,都有对称点.二、例题示范:例1 下列汉字,如果用一样粗细的笔写出来,哪些是轴对称图形?是轴对称图形的,有几条对称轴?大小口中朋木三、课堂小结:1、什么是轴对称和轴对称图形;2、如何画出对称轴、如何找对称点?3、生活中的轴对称和轴对称图形.四、课后作业:P9 1,2,3五、教学后记:。
八年级数学学案11:轴对称图形复习(1)教案
轴对称图形复习(1) 1.学习目标: (1)复习回顾轴对称图形概念和相关性质;(2)复习回顾线段与角的轴对称性质和判定.
2.自学指导: 复习回顾相关知识点并填空: (1)下列语句中正确的有 .(填序号) ①关于一条直线对称的两个图形一定能重合;②两个能重合的图形一定关于某条直线对称; ③一个轴对称图形不一定只有一条对称轴;④两个轴对称图形的对应点一定在对称轴的两侧; ⑤对称轴上的点到对应点的距离相等. 轴对称的性质:成轴对称的两个图形,对应点的连线被对称轴 .
(2) 线段的对称轴: . 线段中垂线的性质:线段垂直平分线上的点到 的距离相等. 符号语言:
线段中垂线的判定:到线段两端距离相等的点在线段的 上. 符号语言:
(3)角的对称轴: . 角平分线的性质:角平分线上的点到 的距离相等. 符号语言:
角平分线的判定:角的内部到角两边距离相等的点在角的 上. 符号语言:
3.自学检测: 1、在如图的网格中, (1)画△A1B1C1,使它与△ABC关于l1对称; (2)画△A2B2C2,使它与△A1B1C1关于l2对称; (3)画出△A2B2C2与△ACB的对称轴
2、如图,在ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB与点E、F、G..点F到ABC的边 、 距离相等,点F到ABC的顶点 、 的距离相等.
l A B
M
BACEDOP
GFED
C
BA例1 3. 已知:如图,点B、C分别在MAN的两边上,BD⊥AN,CE⊥AM,垂足分别为D、E,BD、CE相交于点F,且BE=CD.求证:点F在MAN的角平分线上.
4、如图,OE、OF分别是△ABC边AB、AC的垂直平分线,BP、CP分别是OBC、OCB的角平分线.求证:(1)OP是BOC的角平分线. (2)OP⊥BC
5.如图,在△ABC中,DE,FG分别是AB,AC的垂直平分线,连接AE,AF,已知∠BAC=80°,则 ∠EAF=________°
八年级数学上册 12.1.2 轴对称的性质及线段垂直平分线的性质教案 新人教版
轴对称的性质 及线段垂直平分线的性质 年级 八年级 学科 数学 审核
课题 轴对称的性质 及线段垂直平分线的性质
学习目标
1、了解轴对称图形的性质。 2、探究线段垂直平分线的性质。
重点 1、轴对称的性质。 2、线段垂直平分线的性质。
难点 探索并总结出线段垂直平分线的性质,能运用其性质解答实际问题。
预习导学
如图,△ABC和△A′B′C′关于直线MN对称。 1点A′、B′、C′的对称点分别是 、 、 ,线段AB与A′B′有什么关系?∠A与∠A’ 有什么关系?∠B与∠B′呢? △ABC与△A′B′C′有什么关系?为什么? 2设AA′交对称轴MN于点P,将△ABC和△A′B′C′沿MN折叠后,点A与A′重合吗?有PA= , ∠MPA= = 度 那么MN与线段AA′、BB′、CC′的连线有什么关系呢?AA′、BB′和 CC′与MN除了 以外,MN还经过线段AA′、BB′和CC′的 . 由此得到:对称轴所在直线经过对称点所连线段的 ,并且 这条线段.我们把经过线段中点并且垂直于这条线段的直线,叫做这条线段的 . 可以发现:如果两个图形关于某条直线对称,那么 是任何一对对应点所连线段 。(即两个图形成轴对称的性质) 随感 反思
感知训练
上诉性质是对两个成轴对称的图形来说的,如果是一个轴对称图形,那么它的对应点连线与对称轴之间是否也有同样的关系呢? 大家画一个轴对称图形,并找出两个对称点,看一下对称轴和两个对称点连线的关系. 同学们以小组讨论、探索、归纳,最后以组为单位出示结果作补充交流:
类似地,轴对称图形的对称轴,是 。 合作探究
见课本P32 探究 用平面图将上述问题进行转化,先作出线段AB, 过AB中点作AB的垂直平分线L,在L上取P1、 P2、P3…,连结AP1、AP2、AP3、BP1、BP2、BP3… 作好图后用直尺量出AP1、AP2、AP3、BP1、BP2、BP3… 讨论发现什么样的规律?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、学习目标:
1.理解轴对称图形及轴对称的定义,认识轴对称与全等的关系,了解轴对称图形与轴对
称的联系与区别 。
2.通过独立思考、小组合作、展示质疑,发展学生的观察、归纳、想象能力。
3.激情投入,快乐学习,感受对称美。
二、重点难点
重点:对轴对称图形与轴对称概念的理解
难点:轴对称图形与轴对称的联系与区别
三、合作探究(同学合作,教师引导)
1、在一张半透明的纸上画△ABC,使AB=AC,作BC上的高AD,沿直线AD折叠,直线两旁
的部分重合吗?
轴对称图形的定义:
叫做轴对称图形,这条直线..叫做它的
2、在一张半透明的纸上建立一个平面直角坐标系,并描出点A(-1,3)、B(-2,-4)、C
(-3,-1)、
A1(1,3)、B1(2,-4)、C1(3,-1),画出△ABC和△A1B1C1,沿y轴折叠,这两个三角形重
合吗?
轴对称的定义:
那么就说这两个图形关于这条直线对称,这条直线..叫做,折叠后重合的点是对应点,叫做。
3、第2中的△ABC和△A1B1C1全等吗?把其中的△A1B1C1向下平移一个单位,得到△A2B2C2,
△ABC和△A2B2C2全等吗?折一折,△ABC和△A2B2C2成轴对称吗?
轴对称与全等的关系:两个图形成轴对称,则它们一定;两个图形全等,
成轴对称。
4、你能说说轴对称图形与轴对称的区别和联系吗?
区别:
联系:
四、精讲精练
例1下列图案中,不是轴对称图形的是( )
(A)
(B
)))
(C)
(D)
例2、下面四组图形中,右边与左边成轴对称的是( )
A. B. C. D.
例3、仔细观察下列图案,并按规律在横线上画出合适的图形
_________
例4、在镜中看到的一串数字是“309087 ”,则这串数字是。
例5、下列图形中对称轴最多的是 ( )
A、圆 B、正方形 C、等腰三角形 D、线段
练习1、在实际生活中,轴对称无处不在,请你用给定的图形“○○,△△,————”
(两个圆,两个三角形,两条线段)为构件,尽可能多地构思独特且有实际生活意义的成
轴对称的一对图形,并写出一两句诙谐、贴切的解说词。如:
2、如图,把一个正方形三次对折后沿虚线剪下,
则所得图形大致是( )
3、写出10个“轴对称”的汉字,如“十、中”。
五、课堂小结:轴对称图形及轴对称的定义
六、作业:P36 1、2
教后反思:本节课分为体会轴对称图形特征、揭示概念、判断轴对称图形、拓展四个环节。
开课用动手操作让学生观察老师撕图形的过程,从而引入新课的学习,使学生初步感知轴
对称图形的特点。而后面让学生动手撕图形的验证过程,是使学生更好的感知什么是完全
重合,并加深了对对称轴的认识,培养了他们空间想象力。接着,通过判断轴对称图形的
活动,使学生通过观察、动手操作更深刻的掌握了对轴对称图形及对称轴的理解,发展学
生的空间观念。最后一个环节引导学生领略自然世界的美妙,对称美的认识,激发学生的
数学审美情趣。
新课标第一网系列资料www.xkb1.com新课标第一网不用注册,免费下载!
○○
△△
∣∣
两个棒棒糖
