启新教育三年级奥数第六讲找规律二
三年级奥数 第六讲 数字谜

三年级奥数 --- 算式谜 1观察特征找突破口逐一尝试两个数字相加,十位数字最大是1,两个数字相乘,十位数字最大是9,还要注意进位和借位例题1.+ 1 + 8 + 6例题2.- 8 5 - - 56 378 7 3 6例题3.学力成才数学学数学努力要成才爱数学爱数学要努力定要成才+喜爱数学 + 我爱数学 + 我要努力 +我定要成才 1 9 9 2 1 9 9 2 1 7 5 2 3 1 2 5 6巩固练习2. 不重复使用0,1,2,3,4,5,6,7,8,9这10个数字组成下面算式。
2 8三年级奥数 --- 算式谜 2两个数字相加,十位数字最大是1,两个数字相乘,十位数字最大是9,还要注意进位和借位例题1 在下面的空格内填上合适的数字,使算式成立。
﹙审题选择突破口;利用“倒推”实验求解。
﹚题2 在下面的算式中A 、B 、C 、D 表示不同的数字,相同的字母表示相同的数字,字母D 表示数字1时,B表示什么数字?A B A B A 腾 飞 中 国 A B C A - C B C 龙 腾 飞 爱 中 国 - C D C D C A C 3 + 巨 龙 腾 飞 + 爱 我 中 国 A B C D 2 0 0 1 1 9 8 9题3 下面算式中,每个文字表示一个数字,当它们代表什么数字时,算式成立?爱 听 想 看 兵 炮 马 卒 + 边 听 边 看 + 兵 炮 马 卒 边 看 想 爱 看 车 卒 马 兵 卒题4 下面的加法算式中,相同的字母代表相同的数字,不同的字母,代表不同的数字,求这个算式。
F O R T YT E N T E NS IX T Y+ F I V E T W O ONEEIGHT+S E VE NT H R E E T W OTWE L V E+A B C D E F C B AGDHE+三年级奥数 --- 算式谜 31.在 内填上合适的数字,使算式成立:4 3 0- 21 9 5 32、下面是三个数的加法算式,每个 内有一个数字,则三个加数中最大的是 。
(完整word)三年级奥数6-植树问题

课题寻规律填图
教学目标通过研究数列,发现数列中数排列的规律,并依据这个规律来填写空缺的数
重点通过观察、猜想、实验、推理等活动发现数列的排列规律
通过观察、猜想、实验、推理等活动发现数列的排列规律
难点
我们通常把研究植树的棵数、段数与线路长之间的关系称为植树问题。
另外,生活中还有一些问题,也可以用植树间题的方法来解答。
比如锯木头、爬楼梯问题等等。
植树间题通常有两种情况:
例1
同学们在马路一侧植树,先植1棵树,以后每隔5米植一棵,已经植了8棵,第1棵和第8棵相距多少米?
两棵小树之间最少有几米?
例5
在相连的四个正方形花圃边,已知每个小正方形每边上种5株菊花,且在交错点上都需种有一株,那么共种多少株?
练一练
学校有一个大三角形花坛,如图,由四个大小相同的小三角形组成,在这个花坛上种花。
已知每个小不角形每边上种8棵。
一共有花多少棵?
你学会了吗
1,把一捆电线剪成5米长的一段,剪了6次正好剪完,这捆电线长多少米?。
奥数状元必读专家点拨三年级上册第6课《找简单数列的规律》试题附答案

第三种:题目分类本。和错题本一样,专门记录自己做过的试题,并进行分类:一类是极其简单,自己一看就会的;一类是有一定难度,需要思考找到突破口的;一类是难度很大,需要综合运用很多知识并进行推理才能解答的。后两类都应该是我们的记录重点。
-------------------------谢谢喜欢------------------------
第四种:旧题新解。不时翻翻原来做过的试题,重点分析有没有新的解题思路和技巧。不断地增加思考有利于形成思考习惯,也有利于形成发散思维,开展多角度分析敏锐思路,随时利用新学知识去解决难题。
第五种:学习小组。定期地和小组成员分享好试题,好方法,好技巧,好经验,即可以增加同学之间的情感,又可以在交朋友的过程学习到新的东西,提高学习效率,培养合作精神,增强协调能力。
状元必读专家点拨
小学三年级上册数学奥数知识点讲解第6课《找简单数列的规律》试题附答案
答案
三年级奥数上册:第六讲找简单数列的规律习题解答
-------------------------赠予-------------------实很普遍也很简单,但恰恰是很多同学不容易做到的,记笔记有很多好处,记录老师讲课精华,练习书写能力,养成边听边写能力,这对于提高学习效率是非常有效的。
三年级奥数-2寻找规律

上课老师:陈婷婷
知识点及作业回顾: 1、数出下图有几个正方形? 2、有1~6六个数字,这些数 字能组成多少个个位上的 数字与十位上的数字不同 的两位数?
寻找宝藏的密码
小朋友你能帮他破解密码吗?
1,3,7,15,(
?),63,127
例1:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
练习1:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
2,4,8 ,10,( 2,5,8,11,(
),(
),···
),17,20,··· ),3,··· ),19,···
33,28,23,( ),13,( 55,49,43,( ),31,(
练习1:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
5 5 5
5 10
9 14
7 12
11 16
9 14
13
18
还有其他规律吗?
加强版(隐藏很深的规律) 4 8 7 2 8 9 4 4 3
16
14
加强版(隐藏很深的规律) 4 8 7 2 8 9 4 4 12 3
16
14
培优升级 例4:按规律填数
(1 ) (2 )
187,286,385 ,(
23 31 41 23
2,4,8 ,10,(12),(14),··· 2,5,8,11,(14),17,20,··· 33,28,23,(18),13,(8),3,··· 55,49,43,(37),31,(25),19,··· 变化缓慢,用加减法
练习2:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
3,5,12 ,( 2,6,18,(
1, 2, 3, 4, 5, 6,······
2022年小学三年级奥数找规律知识点与习题

第5讲找规律(一)这一讲我们先简介什么是“数列”,然后讲怎样发现和寻找“数列”旳规律。
按一定次序排列旳一列数就叫数列。
例如,(1) 1,2,3,4,5,6,…(2) 1,2,4,8,16,32;(3) 1,0,0,1,0,0,1,…(4) 1,1,2,3,5,8,13。
一种数列中从左至右旳第n个数,称为这个数列旳第n项。
如,数列(1)旳第3项是3,数列(2)旳第3项是4。
一般地,我们将数列旳第n项记作a n。
数列中旳数可以是有限多种,如数列(2)(4),也可以是无限多种,如数列(1)(3)。
许多数列中旳数是按一定规律排列旳,我们这一讲就是讲怎样发现这些规律。
数列(1)是按照自然数从小到大旳次序排列旳,也叫做自然数数列,其规律是:后项=前项+1,或第n项a n=n。
数列(2)旳规律是:后项=前项×2,或第n项数列(3)旳规律是:“1,0,0”周而复始地出现。
数列(4)旳规律是:从第三项起,每项等于它前面两项旳和,即a3=1+1=2,a4=1+2=3,a5=2+3=5,a6=3+5=8,a7=5+8=13。
常见旳较简朴旳数列规律有这样几类:第一类是数列各项只与它旳项数有关,或只与它旳前一项有关。
例如数列(1)(2)。
第二类是前后几项为一组,以组为单元找关系才可找到规律。
例如数列(3)(4)。
第三类是数列自身要与其他数列对比才能发现其规律。
此类情形稍为复杂些,我们用背面旳例3、例4来作某些阐明。
例1找出下列各数列旳规律,并按其规律在( )内填上合适旳数:(1)4,7,10,13,( ),…(2)84,72,60,( ),( );(3)2,6,18,( ),( ),…(4)625,125,25,( ),( );(5)1,4,9,16,( ),…(6)2,6,12,20,( ),( ),…解:通过对已知旳几种数旳前后两项旳观测、分析,可发现(1)旳规律是:前项+3=后项。
因此应填16。
(2)旳规律是:前项-12=后项。
三年级奥数教材第六讲之数图形
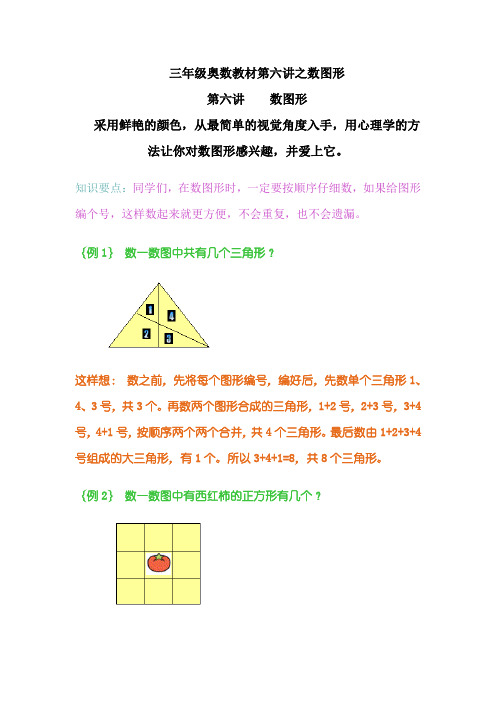
三年级奥数教材第六讲之数图形第六讲数图形采用鲜艳的颜色,从最简单的视觉角度入手,用心理学的方法让你对数图形感兴趣,并爱上它。
知识要点:同学们,在数图形时,一定要按顺序仔细数,如果给图形编个号,这样数起来就更方便,不会重复,也不会遗漏。
{例1}数一数图中共有几个三角形?这样想:数之前,先将每个图形编号,编好后,先数单个三角形1、4、3号,共3个。
再数两个图形合成的三角形,1+2号,2+3号,3+4号,4+1号,按顺序两个两个合并,共4个三角形。
最后数由1+2+3+4号组成的大三角形,有1个。
所以3+4+1=8,共8个三角形。
{例2}数一数图中有西红柿的正方形有几个?这样想:先数单个正方形,有西红柿的正方形有1个。
再数四个正方形合成的大正方形,有西红柿的大正方形有4个。
最后数由9个小正方形组成的大正方形,有1个。
所以1+4+1=6,有西红柿的正方形共6个。
{例3}数一数图中共有几个正方形?这样想:先数单个正方形1、2、3、4、5、6号,共6个。
再数四个正方形合成的大正方形,1+2+4+5号,2+3+5+6号,按顺序四个四个合并,共2个正方形。
所以6+2=8,共8个正方形。
{例4}数一数图中共有几个正方形?这样想:先数小正方形,共4个。
再数稍大的正方形,共5个。
最后数大正方形,有1个。
4+5+1=10,所以图中共有10个正方形。
{例5}数一数图中共有几个圆形?这样想:先数小圆,共5个。
再数大圆有1个。
图中共有6个圆。
数图形晚饭过后,妈妈给小小出了一道“试眼力”的题目:数数窗户上一共有多少个正方形。
小小一看,立即回答:“窗户上一共有6个正方形。
”妈妈笑了,爸爸在一旁也笑了,小小给弄了个“丈二和尚莫不着头脑”。
小朋友,你知道小小的爸爸妈妈为什么笑吗?小小数得难道不对吗?如果不对,那么窗户上究竟有几个正方形呢?下面我们就一起来研究数图形的问题。
典型例题例【6】下图中有多少条线段?A B C D E分析我们把图中的线段AB、BC、CD、DE看作是基本线段,那么:由1条基本线段构成的线段有AB、BC、CD、DE 4条;由2条基本线段构成的线段有AC、BD、CE 3条;由3条基本线段构成的线段有AD、BE 2条;由4条基本线段构成的线段有AE 1条。
小学奥数全国推荐三年级奥数通用学案附带练习题解析答案14找规律:数列规律、图形规律(二)

年级三年级学科奥数版本通用版课程标题找规律:数列规律、图形规律(二)在前面的学习中,我们已经了解了寻找数列规律的方法,这节课我们将来研究图形规律问题。
通过研究几何图形,学会正确观察思考图形规律,并且掌握观察思考复杂图形变化规律的方法,进一步培养我们全面地、由浅入深、由简到繁观察思考问题的良好习惯,并提高我们利用规律解决问题的能力。
一般地说,在观察图形变化规律时,应抓住以下几方面来考虑问题:(1)图形数量的变化;(2)图形形状的变化;(3)图形大小的变化;(4)图形颜色的变化;(5)图形位置的变化;(6)图形繁简的变化。
对于较复杂的图形,也可分成几部分来分别考虑,总而言之,只要全面观察、勤于思考,就一定能抓住规律,解决问题。
例1. 按顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形。
【分析与解】仔细观察,发现本题不只是箭方向上有变化,箭尾“羽毛”数量上也有变化,在同一行中,每旋转90°,箭尾上的“羽毛”将减少一对,依照这个规律,空格中的箭,其尾部应没有“羽毛”,成了光秃秃的一支箭,所以空格中应填:例2. 根据左边图形的关系,画出右边图形的另一半。
【分析与解】(1)由左边图形的变化,即阴影部分从内环变为外环,可得“?”处应填:(2)已知图形是两层圆形对应两层方形,则三层圆形应对应三层方形,阴影部分变为非阴影部分,所以“?”处应填:(3)图形都是△和□,阴影部分两个图形的位置正好相反,△的阴影部分在上面,即“?”处□的阴影应该在下方,应填:例3.观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【分析与解】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:四只脚、一条尾、背上五个点。
即:例4.根据下列图形的变化规律,接着画下去。
【分析与解】观察得知,每幅图只有四个小图形,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点,丁图中应填:例5. 将“猫”“狗”“兔”“鸡”“猴”“虎”六个动物名称分别写在乙个正方体的六个面上,从下面三种不同摆法中,判断这个正方体相对面上的动物名称。
三年级奥数如何解答找规律的奥数题(详细讲解解题方法)

三年级奥数:如何解答找规律的奥数题(详细讲解解题方法)展开全文三年级的学生在解答数学题的时候会经常遇到找规律的题目。
解答数学题和做事情一样,都有一定的方法。
我们先来看一个有趣的计算题:152415789971041×9×9=12345678987654321(这样排列的数字叫回文数)你有没有发现这个得数很有趣呢?这个得数里面的数字排列是有规律的。
同学们,其实学习数学是很有趣的哦。
下面,我来讲一讲找规律题的解题方法。
找规律题就是要求我们根据已知的数字、图形等摆放、变化的情况,推理出某一个(或几个)数字或者图形是什么。
例题1根据下面各题数字的排列规律,在()里填上适当的数。
(1)1,6,11,16,(),(),()。
(2)1,2,6,15,31,(),(),()。
(3)80,79,76,71,64,(),(),()。
【分析】(1)前面的数字排列规律是:前一个数字+5就得到下一个数字。
(2)前面的数字排列规律是:后一个数字=前一个数字分别+1、2、3……的平方得到的。
如:2=1+1×1;6=2+2×2;15=6+3×3;31=15+4×4。
(3)前面的数字排列规律是:从左到右连续减1、3、5、7(奇数)……【答案】(1)1,6,11,16,(21),(26),(31)。
(2)1,2,6,15,31,(56),(92),(141)。
(3)80,79,76,71,64,(55),(46),(37)。
例题2仔细地观察、分析表格中数字的排列规律,将正确的答案填在()里。
(1)(2)【分析】这类的题目,我们可以这样观察、分析:横的看,竖的看,斜的看,找出其中的规律,就可以完成需要解决的问题了。
(1)此题是横看:横排的三个数字之和是25,我们就得出()里是5。
【答案】【分析】(2)此题是竖看:竖排三个数字的排列规律是:前两个数字之差再除以2得到第三个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
启新教育三年级奥数第六讲找规律二
这一讲主要介绍如何发现和寻找图形、数表的变化规律。
例1 观察下列图形的变化规律,并按照这个规律将第四个图形补充完整。
解:观察前三个图,从左至右,黑点数依次为4,3,2个,并且每个图
形依次按逆时针方向旋转90°,所以第四个图如右图所示。
观察图形的变化,主要从各图形的形状、方向、数量、大小及各组成部分的相对位置入手,从中找出变化规律。
例2 在下列各组图形中寻找规律,并按此规律在“?”处填上合适的数:
解:(1)观察前两个图形中的数可知,大圆圈内的数等于三个小圆圈内的数的乘积的一半,故
第三个图形中的“?”=5×3×8÷2=60;
第四个图形中的“?”=(21×2)÷3÷2=7。
(2)观察前两个图形中的已知数,发现有
10=8+5-3, 8=7+4-3,
即三角形里面的数的和减去三角形外面的数就是中间小圆圈内的数。
故
第三个图形中的“?”=12+1-5=8;
第四个图形中的“?”=7+1-5=3。
例3寻找规律填数:
解:(1)考察上、下两数的差。
32-16=16,31-15=16,33-17=16,可知,上面那个“?”=35-16=19,下面那个“?”=18+16=34。
(2)从左至右,一上一下地看,由1,3,5,?,9,…知,12下面的“?”=7;一下一上看,由6,8,10,12,?,…知,9下面的“?”=14。
例4寻找规律在空格内填数:
解:(1)因为前两图中的三个数满足:
256=4×64,72=6×12,
所以,第三图中空格应填12×15=180;第四图中空格应填169÷
13=13。
第五图中空格应填224÷7=32。
(2)图中下面一行的数都是上一行对应数的3倍,故43下面应填43×3=129;87上面应填87÷3=29。
1 / 5
2 / 5
例5在下列表格中寻找规律,并求出“?”:
解:(1)观察每行中两边的数与中间的数的关系,发现3+8=11,4+2=6,所以,?=5+7=12。
(2)观察每列中三数的关系,发现1+3×2=7,7+2×2=11,所以,?=4+5×2=14。
例6 寻找规律填数:
解:观察其规律知:略。
观察比较图形、图表、数列的变化,并能从图形、数量间的关系中发现规律,这种能力对于同学们今后的学习将大有益处。
练习
寻找规律填数:
3 / 5
6.下图中第50个图形是△还是○?
○△○○○△○○○△○…
启新教育奥数天天练图形的排列规律 找规律是解决数学问题的一种重要手段。
而发现规律既需要敏锐的
观察力,又需要严密的逻辑推理能力。
同学们一定听说过福尔摩斯这个
人吧,他是世界著名的大侦。
我们从小说和电视剧中看到福尔摩斯的“破
案”简值神极了,什么疑难案件,他都能把业超级大国去肪分析清楚。
他靠的不仅是渊博的知识,还有细心敏锐的观察与严密的逻辑推理。
这一讲将为你提供很多图形,它们在某一个方面,比如颜色、形状、大小、
结构、位置或繁难等有些共同的特征或变化规律,我们要学会通过观察
找规律,并根据规律来推断结果。
例题与方法
例1 下面哪个图形和其他几个不一样,请你找出来,并打上“√”。
例2 形?
可供选项: 例3
(1)
(2)
(3) (4)
? ① ② ③ ④
例4 根据等号左边两个图形的变换关系,推断出“?”处应选择第几号图形?
例5 下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形。
例6
练习与思考
1.选择合适的图形,将图号填入虚线框内。
(1)
(2)
(3)
2.仔细观察下面图形,按其变化规律在“?”处填上合适的图形。
(1)
(2)
3.
(1)
)
?
?
?
4 / 5
5 / 5
(2)
(3)
4.从所给的6个图形中,选出一个适当的图形,将它的编号填入“?”处。
(1)
(2)
练习6
1.5。
提示:中间数=两腰数之和÷底边数。
2.45;1。
提示:中间数= 周围三数之和×3。
3.(1)13。
提示:中间数等于两边数之和。
(2)20。
提示:每行的三个数都成等差数列。
4.横行依次为60,65,70,75,325
; 竖行依次为40, 65, 90, 115, 325。
5.14。
提示:(23+ 5) ÷ 2=14。
6.△。
7. 714285;857142。
8. 8888886
; 9876543×9。
9.36。
提示:等于加式中心数的平方。
(注:可编辑下载,若有不当之处,请指正,谢谢!)
?
① ② ③ ④ ⑤ ①
②
③
④
⑤。
