学而思中考数学一轮复习第2讲.四边形.提高班.教师版
学而思中考数学第2讲.第二轮复习之图形变换与动手操作.提高班.教师版
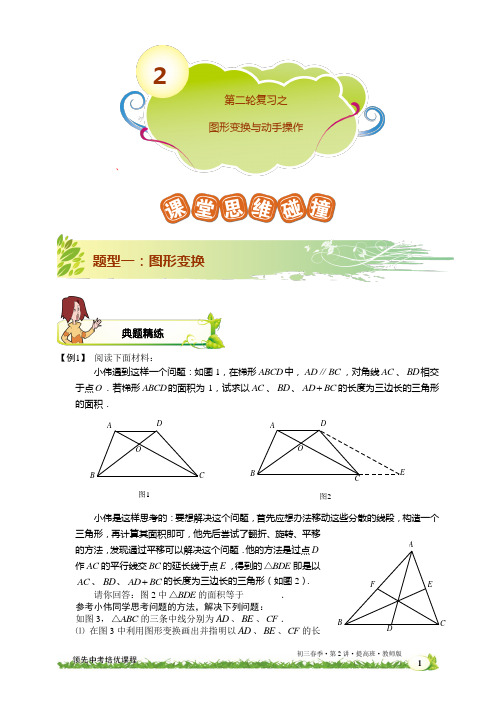
`【例1】 阅读下面材料:小伟遇到这样一个问题:如图1,在梯形ABCD 中,AD BC ∥,对角线AC 、BD 相交于点O .若梯形ABCD 的面积为1,试求以AC 、BD 、AD BC +的长度为三边长的三角形的面积.图1图2ADBCOADBCOE小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题.他的方法是过点D 作AC 的平行线交BC 的延长线于点E ,得到的BDE △即是以AC 、BD 、AD BC +的长度为三边长的三角形(如图2). 请你回答:图2中BDE △的面积等于________. 参考小伟同学思考问题的方法,解决下列问题:如图3,ABC △的三条中线分别为AD 、BE 、CF .⑴ 在图3中利用图形变换画出并指明以AD 、BE 、CF 的长典题精练2第二轮复习之 图形变换与动手操作题型一:图形变换图3AFE CD B度为三边长的一个三角形(保留画图痕迹);⑵ 若ABC △的面积为1,则以AD 、BE 、CF 的长度为三边长的三角形的面积等于________.(2011北京)【解析】BDE △的面积等于 1 .⑴ 如图.以AD 、BE 、CF 的长度为三边长的一个三角形是CFP △. ⑵ 以AD 、BE 、CF 的长度为三边长的三角形的面积等于34. 【例2】 阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC 面积相等的新的旋转对称图形.FDEF DBACOABCO图1 图2小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题: 如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点,P 1、P 2, M 1、M 2, N 1、N 2分别为 AB 、BC 、CA 的三等分点.(1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹); (2)若△ABC 的面积为a ,则图3中△FGH 的面积为 . (2012海淀二模) 【解析】(1)画图如下:(2)图3中△FGH 的面积为7a.图3H G F CBN 2N 1M 1M 2E 1E 2E 3P 2P 1AAPEFC DBH F GA BCE 1E 2E 3P 1P 2M 1M 2N 1N 2动手操作分为:1、立体图形及展开图;2、骰子问题;3、折纸问题;4、图形的分割;5、图形的剪拼.【例3】 ⑴如图,已知MN 是圆柱底面直径,NP 是圆柱的高.在圆柱的侧面上,过点M 、P 嵌有一圈路径最短的金属丝.现将圆柱侧面沿NP 剪开, 所得的侧面展开图是( )A. B. C. D. ⑵在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.开始时骰子如图 ①那样摆放,朝上的点数是2;最后翻动到如图②所示的位置,此时骰子朝上的点 数不可能...是下列数中( )A .5B .4C .3D .1⑶ 如图,矩形纸片ABCD 中,8AB =,将纸片折叠,使顶点B 落在边AD 上的点为E ,折痕的一端G 点在边BC 上()BG GC <,另一端F 落在矩形的边上,10BG =.①请你在备用图中画出满足条件的图形;典题精练题型二:动手操作PNM P /N /PNMP /N /PNMP /N /PNMM /P /N /PNM②求出折痕GF 的长为 .备用图(3)G 备用图(2)G DADG 备用图(1)【解析】 ⑴321n -2n ≥). ⑵ ①正确画出图⑴、图⑵ ②545情况一:如图⑴,当点F 在AB 上时,过点G 作GH AD ⊥,则四边形ABGH 为矩形,∴8GH AB ==,10AH BG ==,设BF x =, 由图形的折叠可知BFG EFG △≌△, ∴10EG BG ==,BF EF x ==,在Rt GEH △中,由勾股定理,得6EH =,∴4AE =. ∵90A ∠=︒,8AF x =-,EF x =,222EF AF AE =+ ∴()22284x x =-+解方程,得 5x .=∴5BF =,∵10BG =,∴2255FG BG BF .=+=情况二:如图⑵,当点F 在AD 边上时,因为四边形HFGE 由四边形ABGF 折叠得到, 由折叠可知,BG EG =,AB EH =,BGF EGF ∠=∠, ∵EF BG ∥,∴BGF EFG ∠=∠,∴EGF EFG ∠=∠, ∴EF EG =,∴BG EF =,∴四边形BGEF 为平行四边形 又∵EF EG =,∴平行四边形BGEF 为菱形 连结BE ,BE 与 FG 互相垂直平分,在Rt EFH △中,10EF BG ==,8EH AB ==, 由勾股定理可得6FH AF ==,∴16AE =, ∴2285BE AE AB =+∴45BO =∴222245FG OG BG BO ==-=.【例4】 ⑴在ABC △中,沿着中位线EF 一刀剪切后,用得到的AEF △和四边形EBCF 可以拼成平行四边形EBCP ,剪切线与拼图如图所示,仿上述的方法,按要求完成下列操作设计,并画出图示.①在ABC △中,增加条件 ,沿着 H E F 图(1)G DCBA O E(B)H(A)F图(2)GDCB AA一刀剪切后可以拼成矩形;②在ABC △中,增加条件 ,沿着 一刀剪切后可以拼成菱形;③在ABC △中,增加条件 ,沿着 一刀剪切后可以拼成正方形;④在ABC △()AB AC ≠中,一刀剪切后也可以拼成等腰梯形,首先要确定剪切线,其操作过程(剪切线的作法)是: .⑵在ABC △中,BC a =,BC 边上的高2h a =,沿图中线段DE 、CF 将ABC △剪开,分成的三块图形恰能拼成正方形CFHG ,如图⑴所示.请你解决如下问题: 在A B C '''△中,B C a ''=,B C ''边上的高12h a =.请你设计两种不同的分割方法,将A B C '''△ 沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图⑵、图⑶中,画出分割线及拼接后的图形.【解析】 ⑴ ①方法一:90B ∠=︒,中位线EF ,如图⑴.方法二:AB AC =,中线(或高)AD ,如图⑵.②2AB BC =(或者90C ∠=︒,30A ∠=︒),中位线EF ,如图⑶. ③方法一:90B ∠=︒且2AB BC =,中位线EF ,如图⑷.方法二:AB AC =且90BAC ∠=︒,中线(或高)AD ,如图⑸.④方法一:不妨设B C ∠>∠,在BC 边上取一点D ,作GDB B ∠=∠交AB 于G ,过AC 的中点E 作EF GD ∥交BC 于F ,则EF 为剪切线.如图⑹方法二:不妨设B C ∠>∠,分别取AB 、AC 的中点D 、E ,过D 、E 作BC 的垂线,G 、H 为垂足,在HC 上截取HF GB =,连结EF ,则EF 为剪切线.如图⑺图(1)①②③H F E D B图(4)图(3)图(2)图(1)P(E)C(A)FEBAP(E)FEC(A)BAP(D)D C(A)BAP(E)FEC(A)BA图(3)图(2)A'B 'C'C'B 'A'方法三:不妨设B C ∠>∠,作高AD ,在DC 上截取DG DB =,连结AG ,过AC 的中点E 作EF AG ∥交BC 于F ,则EF 为剪切线.如图⑻图(8)图(7)图(6)图(5)P(F)A(C)ECFG D BP(F)A(C)ECFH GBD EC FGD BP(F)A(C)P(D)D C(A)BA⑵ 答案如下图:【例5】 阅读下列材料:小明遇到一个问题:如图1,正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 和DA 边上靠近A 、B 、C 、D 的n 等分点,连结AF 、BG 、CH 、DE ,形成四边形MNPQ .求四边形MNPQ 与正方形ABCD 的面积比(用含n 的代数式表示).小明的做法是:先取2n =,如图2,将ABN △绕点B 顺时针旋转90︒至CBN '△,再将ADM △绕点D 逆时针旋转90︒至CDM '△,得到5个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是15;然后取3n =,如图3,将ABN △绕点B 顺时针旋转90︒至CBN '△,再将ADM △绕点D 逆时针旋转90︒至CDM '△,得到10个小正方形,所以四边形MNPQ 与正方形ABCD 的面积比是410,即25;……请你参考小明的做法,解决下列问题:⑴在图4中探究4n =时四边形MNPQ 与正方形ABCD 的面积比(在图4上画图并直接写出结果);⑵图5是矩形纸片剪去一个小矩形后的示意图,请你将它剪成三块后再拼成正方形(在图5中画出并指明拼接后的正方形).(3)(2)(1)M'N'GH GH G BCEFPQM N A BCD EF PQ M NN'M'N MQ PF ED CB A ①③②图(5)A'B 'C'C'B'A'①②②①【解析】 ⑴四边形MNPQ 与正方形ABCD 的面积比是917.⑵ 如图所示:【例6】 操作探究:一动点沿着数轴向右平移5个单位,再向左平移2个单位,相当于向右平移3个单位.用实数加法表示为 5+(2-)=3.若平面直角坐标系xOy 中的点作如下平移:沿x 轴方向平移的数量为a (向右为正,向左为负,平移a 个单位),沿y 轴方向平移的数量为b (向上为正,向下为负,平移b 个单位),则把有序数对{a ,b }叫做这一平移的“平移量”.规定“平移量”{a ,b }与“平移量”{c ,d }的加法运算法则为}{}{}{d b c a d c b a ++=+,,,. (1)计算:{3,1}+{1,2};(2)若一动点从点A (1,1)出发,先按照“平移量”{2,1}平移到点B ,再按照“平移量”{-1,2}平移到点C ;最后按照“平移量”{-2,-1}平移到点D ,在图中画出四边形ABCD ,并直接写出点D 的坐标;(3)将(2)中的四边形ABCD 以点A 为中心,顺时针旋转90°,点B 旋转到点E ,连结典题精练H G M'N'A BC DEF PQMN DCB(5)(4)H GAB C D EF P Q MN题型三:新定义AE、BE若动点P从点A出发,沿△AEB的三边AE、EB、BA平移一周.请用“平移量”加法算式表示动点P的平移过程.(2013丰台二模)【解析】(1){4,3}.(2)①画图②D(0,3).(3){1,-2}+{1,3}+{-2,-1}.yxO 11yxBACDO 11【例7】 如图1,四边形ABCD 中,AC 、BD 为它的对角线,E 为AB 边上一动点(点E 不与点A 、B 重合),EF ∥AC 交BC 于点F ,FG ∥BD 交DC 于点G ,GH ∥AC 交AD 于点H ,连接HE .记四边形EFGH 的周长为p ,如果在点E 的运动过程中,p 的值不变,则我们称四边形ABCD 为“Ω四边形”, 此时p 的值称为它的“Ω值”.经过探究,可得矩形是“Ω四边形”.如图2,矩形ABCD 中,若AB =4,BC =3,则它的“Ω值”为 .图1B FCGD HE A图2D CBA图3ODBA(1)等腰梯形 (填“是”或 “不是”)“Ω四边形”;(2)如图3,BD 是⊙O 的直径,A 是⊙O 上一点,=34AD AB =,,点C 为»AB 上的一动点,将△DAB 沿CD 的中垂线翻折,得到△CEF .当点C 运动到某一位置时,以A 、B 、C 、D 、E 、F 中的任意四个点为顶点的“Ω四边形”最多,最多有 个.(2013海淀二模)【解析】 “Ω值”为10.(1)是;(2)最多有5个.训练1. ⑴将如右图所示的圆心角为90︒的扇形纸片AOB 围成圆锥形纸帽,使扇形的两条半径OA 与OB 重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )⑵如图是一个等腰直角三角形纸片,按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成:(1)一个非矩形的平行四边形; (2)一个等腰梯形;(3)一个正方形.请画出拼接后的三个图形.【解析】 ⑴B. ⑵训练2. 图⑴、图⑵均为76⨯的正方形网格,点A 、B 、C 在格点上.⑴在图⑴中确定格点D ,并画出以A 、B 、C 、D 为顶点的四边形,使其为轴对称图形.(画一个即可)⑵在图⑵中确定格点E ,并画出以A 、B 、C 、E 为顶点的四边形,使其为中心对称图形.(画一个即可)(吉林长春)【解析】 ⑴ 有以下答案供参考:思维拓展训练(选讲)图(2)图(1)ABCCBADD A BCCBA⑵ 有以下答案供参考:EEABCCBA训练3. ⑴图⑴是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图⑵将纸板沿虚线进行切割,无缝隙无重叠的拼成图⑶所示的大正方形,其面积为842+则图⑶中线段AB 的长为 .(海淀二模)图(3)图(2)图(1)BA⑵如图⑶,在55⨯的网格中有一个正方形,把正方形的各边三等分,分别以居中那条线段为斜边向外作等腰直角三角形,去掉居中的那条线段,得到图⑷,请把图⑷中的图形剪拼成正方形,并在图⑷中画出剪裁线,在图⑸中画出剪拼后的正方形.(石景山一模)图(5)图(4)图(3)【解析】215.⑵如图所示:【练习1】 已知ABC △,63ABC ACB ∠=∠=°.如图1所示,取三边中点,可以把ABC △分割成四个等腰三角形.请你在图2中,用另外四种不同的方法把ABC △分割成四个等腰三角形,并标明分割后的四个等腰三角形的底角..的度数(如果经过变换后两个图形重合,则视为同一种方法).(海淀二模)【解析】 分割为等腰三角形常用方法:①角分线+平行线.如图⑴和图⑵ ②直角三角形+斜边中线.如图⑶(和图⑴)③顶角为特殊角度108︒的等腰三角形可以无限分割成36︒和72︒为底角的等腰三角形.如图⑷④知一等腰三角形,做此三角形的对称轴,然后再去分割.如图⑸复习巩固图1CBACB AAB C C B AAB C 图254°54°72°54°36°36°36°31.5°31.5°31.5°27°27°27°27°27°27°27°27°27°63°63°63°63°63°63°63°63°63°63°63°63°63°63°63°36°72°54°27°31.5°63°(5)(4)(3)(2)(1)【练习2】 现场学习题问题背景:在ABC △中,AB 、BC 、AC 21317三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点ABC △(即ABC △三个顶点都在小正方形的顶点处),如图⑴所示.这样不需求ABC △的高,而借用网格就能计算出它的面积. ⑴请你将ABC △的面积直接填写在横线上.________ 思维拓展:⑵我们把上述求ABC △面积的方法叫做构图法.若ABC △2a 、25a 26a (0)a >,请利用图⑵的正方形网格(每个小正方形的边长为a )画出相应的ABC △,并求出它的面积是: . 探索创新:⑶若ABC △三边的长分别为224m n +、2216m n +、222m n +(0,0,)m n m n >>≠ ,请运用构图法在图⑶指定区域内画出示意图,并求出ABC △的面积为: .【解析】 ⑴25. ⑵ 面积:23a .⑶ 面积:3mn .图(2)A B C 4m 2m 2m n n 2n C B A 图(3)图(3)图(2)图(1)A B C【练习3】 在如图1中,正方形ABCD 的边长为a ,等腰直角三角形FAE的斜边2AE b =,且边AD 和AE 在同一直线上. 操作示例:当2b a <时,如图1,在BA 上选取点G ,使BG b =,连结FG 和CG ,裁掉FAG △和CGB △并分别拼接到FEH △和CHD △的位置构成四边形FGCH .思考发现:小明在操作后发现:该剪拼方法就是先将FAG △绕点F 逆时针旋转90︒到FEH △的位置,易知EH 与AD 在同一直线上.连结CH ,由剪拼方法可得DH BG =,故CHD CBG △≌△,从而又可将CGB △绕点C 顺时针旋转90︒到CHD △的位置.这样,对于剪拼得到的四边形FGCH (如图1),过点F 作FM AE ⊥于点M (图略),利用SAS 公理可判断HFM CHD △≌△,易得FH HC GC FG ===,90FHC ∠=︒.进而根据正方形的判定方法,可以判断出四边形FGCH 是正方形.实践探究:⑴ 正方形FGCH 的面积是__________;(用含a ,b 的式子表示)⑵ 类比图1的剪拼方法,请你就如图2至如图4的三种情形分别画出剪拼成一个新正方形的示意图.联想拓展:小明通过探究后发现:当b a ≤时,此类图形都能剪拼成正方形,且所选取的点G 的位置在BA 方向上随着b 的增大不断上移.⑶ 当b a >时,如图5的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图;若不能,简要说明理由.【分析】 抓22a b +,结合四边形ABCD 为正方形及给出的图1中的作法,只需满足BG DH =,由全等三角形即可得出CG 和CH 互相垂直平分且相等.再按照提示方法可以证明四边形GCHF 为正方形.【解析】 ⑴ 22a b +; ⑵ 剪拼方法如图2至图4.⑶ 能;剪拼方法如图5(图中BG DH b ==).先沿FH 剪一刀,将FEH △拼接到图1(2b <a )H G FE DCB A 图2FA B C(E ) DH G F 图4ABC DF图3A BCEHD G C F图5ABDG H a<2b=a FEDC B A图3FD(E )C BA 图2a<2b<2a FEDCBA图3b>b=a 图4ABC DEF图5FEDCB A b>a 图5FE D C BA△即可.FAG△拼接到HDC△;再沿GC剪一刀,将GBC第十八种品格:坚持坚持即是成功有一个少年,拜在一位师傅门下,想学功夫。
学而思初二数学秋季班第2讲.倍长中线与截长补短.提高班.教师版

1初二秋季·第2讲·提高班·教师版三角形9级 全等三角形的经典模型(二)三角形8级全等三角形的经典模型(一) 三角形7级倍长中线与截长补短倍长中线与截长补短满分晋级漫画释义2倍长中线 与截长补短2初二秋季·第2讲·提高班·教师版定 义示例剖析倍长中线:即延长三角形的中线,使得延长后的线段是原中线的两倍.其目的是构造一对对顶的全等三角形; 其本质是转移边和角.EDABC其中BD CD =,延长AD 使得DE AD =,则BDE CDA △≌△.【例1】 已知ABC △中,AD 平分BAC ∠,且BD CD =,求证:AB AC =. 【解析】 延长AD 到E ,使DE AD =,连接CE .则CDE BDA △≌△,∴CE AB =,CED BAD ∠=∠, ∵AD 平分BAC ∠,∴BAD CAD ∠=∠, ∴CED CAD ∠=∠,∴CE AC =, ∴AB AC =.思路导航例题精讲知识互联网题型一:倍长中线EABCDABCD3初二秋季·第2讲·提高班·教师版【教师备选】教师可借用例1对等腰三角形三线合一性质的逆命题进行简单归纳:已知角平分线+中线证等腰三角形,如例1; 已知角平分线+高证等腰三角形,如拓展1; 已知中线+高证等腰三角形,如拓展2.【拓展1】已知△ABC 中,AD 平分∠BAC ,且AD ⊥BC ,求证:AB =AC . 【解析】∵AD 平分∠BAC ,∴∠BAD =∠CAD∵AD ⊥BC ,∴∠ADB =∠ADC =90° ∴△ABD ≌△ACD (SAS) ∴AB =AC .【拓展2】已知△ABC 中,AD ⊥BC ,且BD CD =,求证:AB =AC . 【解析】∵AD ⊥BC ,且BD CD =∴AD 所在直线是线段BC 的垂直平分线 根据垂直平分线上的点到线段两端点距离相等 故AB =AC .【例2】 ⑴如图,已知ABC △中,AB AC =,CE 是AB 边上的中线,延长AB 到D ,使BD AB =.给出下列结论:①AD =2AC ;②CD =2CE ;③∠ACE =∠BCD ;④CB 平分∠DCE ,则以上结论正确的是 . 【解析】 ①正确.∵AB AC =,BD AB =,∴AD =2AC .②、④正确.延长CE 到F ,使EF CE =,连接BF . ∵CE 是AB 的中线,∴AE EB =. 在EBF △和EAC △中 AE BEAEC BEF CE FE =⎧⎪∠=∠⎨⎪=⎩典题精练ABDEDCBA4初二秋季·第2讲·提高班·教师版∴EBF EAC ≌△△∴BF AC AB BD ===,EBF EAC ∠=∠ ∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠ 在FBC △和DBC △中 FB DB FBC DBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴FBC DBC ≌△△∴2CD CF CE ==,∠FCB =∠DCB 即CD =2CE ,CB 平分∠DCE .③错误.∵∠FCB =∠DCB ,而CE 是AB 边上中线而不是∠ACB 的角平分线故∠ACE 和∠BCD 不一定相等.⑵如图,在△ABC 中,点D 、E 为边BC 的三等分点,给出下列结论:①BD =DE =EC ;②AB +AE >2AD ;③AD +AC >2AE ;④AB +AC >AD +AE ,则以上结论正确的是 .NM ED CBAEDCBA【解析】 点D 、E 为边BC 的三等分点,∴BD =DE =CE 延长AD 至点M ,AE 至点N ,使得DM =AD ,EN =AE ,连接EM 、CN ,则可证明△ABD ≌△MED ,进而可得AB +AE >2AD ,再证明△ADE ≌△NCE ,进而可得AD +AC >2AE ,将两式相加可得到AB +AE +AD +AC >2AD +2AE ,即AB +AC >AD +AE . ∴①②③④均正确.【例3】 如图,已知在ABC △中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.FCAEBD5初二秋季·第2讲·提高班·教师版【解析】 延长AD 到G ,使DG AD =,连接BG∵BD CD =,BDG CDA ∠=∠,AD GD = ∴ADC GDB △≌△, ∴AC GB =,G EAF ∠=∠ 又∵AF EF =,∴EAF AEF BED ∠=∠=∠ ∴G BED ∠=∠,∴BE BG =,∴AC BE =.【例4】 在正方形ABCD 中,PQ ⊥BD 于P ,M 为QD 的中点,试探究MP 与MC 的关系.NABCDMPQ Q PMDCBA【解析】 延长PM 至点N ,使PM =MN ,连结CP 、CN 、DN .易证△PMQ ≌△NMD , ∴PB =PQ =DN ,∠PQD =∠NDM ∴PQ ∥DN ,又∵∠BPQ =∠BDN= 90° ∴∠PBQ =∠BDC=∠NDC =45° 再证△BPC ≌△DNC (SAS) 易证△PCN 为等腰直角三角形, 又∵PM =MN ,∴PM ⊥MC ,且PM =CM .GFEDCBA FE D CBA6初二秋季·第2讲·提高班·教师版定 义示例剖析截长:即在一条较长的线段上截取一段较短的线段DCBA在线段AB 上截取AD AC =补短:即在较短的线段上补一段线段使其和较长的线段相等AB C D延长AC ,使得AD AB =【例5】 在ABC △中,A ∠的平分线交BC 于D ,AB AC CD =+,40B ∠=︒,求C ∠的大小.(希望杯培训题)D C B AED CB A【解析】 在AB 上截取AE AC =,连接DE .∵AE AC =,BAD CAD ∠=∠,AD AD =,∴ACD AED △≌△, ∴C AED ∠=∠,CD DE =,∵AB AC CD =+,AE AC =,∴CD BE DE == ∴40EBD EDB ∠=∠=︒,80C AED ∠=∠=︒例题精讲思路导航题型二:截长补短7初二秋季·第2讲·提高班·教师版D CB AEDCB AD CEBAE DCB A【例6】 如图,在ABC △中,2B C ∠=∠,BAC ∠的平分线AD 交BC 于点D .求证:AB BD AC +=. 【解析】方法一:(截长)在AC 上截取AB AE =,连接DE .在ABD △和AED △中AB AE =,BAD EAD ∠=∠,AD AD =∴ABD AED △≌△∴BD ED =,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠ ∴EDC C ∠=∠,∴ED EC =∴AB BD AC +=. 方法二:(补短)延长AB 到点E 使得AC AE =,连接DE . 在AED △和ACD △中,AE AC =,EAD CAD ∠=∠,AD AD = ∴AED ACD △≌△,∴C E ∠=∠ 又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE BD =,∴AB BD AC +=.方法三:(补短)延长DB 到点E 使得AB BE =,连接AE 则有EAB E ∠=∠,2ABC E EAB E ∠=∠+∠=∠ 又∵2ABC C ∠=∠,∴C E ∠=∠ ∴AE AC = EAD EAB BAD E DAC ∠=∠+∠=∠+∠C DAC ADE =∠+∠=∠∴AE DE =,∴AB BD EB BD ED AE AC +=+=== ∴AB +BD=AC若题目条件或求证结论中含有“a b c =+”的条件,需要添加辅助线时多考虑“截长补短”.建议教师此题把3种解法都讲一下,方便学生更加深刻理解这种辅助线添加方法.【例7】 已知:在ABC △中,AB CD BD =-,AD BC ⊥,求证:2B C ∠=∠.【解析】 方法一:在DC 上取一点E ,使BD DE =,如图1,在ABD △和AED △中,AD BC ⊥,BD ED =,AD AD =.典题精练DC BA8初二秋季·第2讲·提高班·教师版∴ABD AED △≌△. ∴AB AE =,B AED ∠=∠.又∵AE AB CD BD CD DE EC ==-=-= ∴C EAC ∠=∠,∴2C EAC AED C ∠+∠=∠=∠ ∴2B C ∠=∠.图1E AB CD图2EAB CD方法二:延长DB 到点E ,使BE AB =,如图2, ∴E EAB ∠=∠.∵AB CD BD =-,∴ED CD =.在AED △和ACD △中,AD BC ⊥,ED CD =,AD AD =. ∴AED ACD △≌△. ∴E C ∠=∠. ∵2ABD E ∠=∠ ∴2B C ∠=∠.【探究对象】截长补短法是几何证明题中十分重要的方法,通常来证明几条线段的数量关系,常见做辅助线方法有: 截长法:⑴过某一点作长边的垂线;⑵在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
2025年广东中考数学一轮复习精讲提升-多边形与平行四边形

2.如图,在▱ABCD 中,BE 平分∠ABC 交 DC 于点 E.若∠A=60°,则 ∠DEB 的大小为( C ) A.130° B.125° C.120° D.115°
3.如图,在▱ABCD 中,点 E 在 AD 上,且 EC 平分∠BED.若∠EBC= 30°,BE=10,则▱ABCD 的面积为 50 .
4.如图,在▱ABCD 中,对角线 AC,BD 相交于点 O,点 E 是边 AB 的 中点.已知 BC=10,则 OE= 5 .
B 组 能力练 5.四边形 ABCD 是平行四边形,AB=6,∠BAD 的平分线交直线 BC 于 点 E,若 CE=2,则▱ABCD 的周长为 20或28 .
2025年广东中考数学一轮复习精讲提升第五章 四边形
多边形与平行四边形
1.了解多边形的有关概念,掌握多边形内角和与外角和公式. 2.理解平行四边形的概念,探索并证明平行四边形的性质和判定方法.会 综合运用它们进行有关的计算与推理证明. 3.灵活运用转化的数学思想将四边形或平行四边形问题转化成三角形的 问题进行解决.
知识点 1 多边形
1.多边形的性质 (1)内角和:n 边形的内角和等于 (n-2)×180° . (2)外角和:多边形的外角和等于 360°. (3)n 边形的对角线条数: n(n-3).
2
2.正多边形的性质
(1)定义:各边相等,各角也相等的多边形叫作正多边形.
(2)性质:正 n 边形的每个内角为 (n-2)·180° ,每一个外角都等于
证明:(1)∵四边形 ABCD 是平行四边形,∴AF∥EC. 又∵AE∥CF,∴四边形 AECF 是平行四边形. ∴∠1=∠2(平行四边形的对角相等). (2) ∵四边形 ABCD 是平行四边形, (3) ∴AB=CD,AD=BC. ∵四边形 AECF 是平行四边形, ∴AE=FC,AF=CE.∴BE=FD. 在△ABE 和△CDF 中,∵BE=DF,AE=CF,AB=CD, ∴△ABE≌△CDF(SSS).
2024河南中考数学一轮知识点复习专题 平行四边形与多边形 课件

考点1 平行四边形 重点
1.定义:两组对边分别平行的四边形叫做平行四边形.
2.性质与判定
性质
两组对边
分别平行
边
两组对边
分别④
相等
______
字母表示(如图)
// ,
①___
//
②___
= ,
=
A.若 // , = ,求证:四边形 是平行四边形.
B.若四边形 是平行四边形,且 = ,求证:四边形 是平行四
边形.
证明:A. ∵ // , ∴ ∠ = ∠ , ∠ = ∠ .
又 ∵ = , ∴△ ≌△ ,
得分速记
证明一个四边形是平行四边形的思路
证另一组对边相等,
(1)已知一组对边相等 ቊ
证这组对边平行;
证另一组对边平行,
(2)已知一组对边平行 ቊ
证这组对边相等;
(3)若图中有对角线——证对角线互相平分.
考点2 多边形
边形
( ≥ 3 ,且
为整数 )
内角和定理
边形的内角和为⑭______________.
22
(6)若 = 4 , = 3 ,则 ▱ 的周长为____.
考点1→
2.已知四边形 .
(1)如图(1),若 // ,添加下列条件中的一个:
①// ; ② = ; ③ = ; ④∠ = ∠ ;
⑤∠ + ∠ = 180∘ .能使四边形 成为平行四边形的
2
(3)若 = 4 , = 6 ,则 △ 比 △ 的周长小___.
5(答案不唯一,大于1小于7
人教版 初中数学中考一轮复习---特殊的平行四边形(含解析)

特殊的平行四边形例1. 如图,正方形ABCD的对角线BD长为2,若直线l满足:①点D到直线l的距离为;②A、C两点到直线l的距离相等.则符合题意的直线l的条数为()A.1 B.2 C.3 D.4例2. 正方形的对称轴的条数为()A.1 B.2 C.3 D.4例3. 边长为3cm的菱形的周长是()A.6cm B.9cm C.12cm D.15cm例4.下列命题是假命题的是()A.四个角相等的四边形是矩形 B.对角线相等的平行四边形是矩形C.对角线垂直的四边形是菱形 D.对角线垂直的平行四边形是菱形A组1、四个内角都相等的四边形是()A、矩形B、菱形C、正方形D、平行四边形2、符合下列条件的四边形不一定是菱形的是()A、四边都相等B、两组邻边分别相等C、对角线互相垂直平分D、两条对角线分别平分一组对角3、下列说法不正确...的是()A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形B组4、矩形的两边长分别是 3cm 和 4cm,则对角线长____cm。
5、如果矩形一条较短的边是 5,两条对角线的夹角是 60°,则对角线长是____。
6、菱形两条对角线的长分别是 12 和 16,则它的边长为____。
7、两条对角线_____的四边形是正方形。
8、如图,一张矩形的纸片,要折出一个正方形,只要把一个角沿折痕AE翻折上去,使AB和AD边上的AF重合,则四边形ABEF就是一个正方形,判断的根据是。
9、如图2,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为()A.20 B.18 C.16 D.1510、如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm 则∠1=度.11、如图,延长正方形ABCD的一边BC至E,使CE=AC,连结AE交CD于F,则∠AFC的度数是()A、112.5°B、120°C、122.5°D、135°12、如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是()A.125B.65C.245D.不确定13、如图,已知正方形ABCD 的边长为3,E 为CD 边上一点,1DE =.以点A 为中心,把△ADE 顺时针旋转90︒,得 △ABE ',连接EE ',则EE '的长等于 .14、已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1(如图2所示) 把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为___________.15、如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD .(1)试判断四边形OCED 的形状,并说明理由; (2)若AB =6,BC =8,求四边形OCED 的面积.16、如图,△ABC 中,点O 是边AC 上一个动点,过O 作直线MN ∥BC ,设MN 交∠BCA 的平分线于点E ,交∠BCA 的外角平分线于点F.(1)探究:线段OE 与OF 的数量关系并加以证明;(2)当点O 在边AC 上运动时,四边形BCFE 会是菱形吗?若是,请证明,若不是,则说明理由;(3)当点O 运动到何处,且△ABC 满足什么条件时,四边形AECF 是正方形?EDCBAFFDC BAOE图2C 组17、 (1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,∠AOF =90°.求证:BE =CF .(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH =90°, EF =4.求GH 的长.(3) 已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH =90°,EF =4. 直接写出下列两题的答案:①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长;②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n 的代数式表示).18、已知:菱形ABCD ,AC=8,BD=6,若将此菱形沿一条对角线剪开成为两个三角形,在平面上把这两个三角形拼成一个不重叠的凸四边形,画出所有拼成的四边形的示意图,并写出所拼四边形(不包括菱形)的对角线的长(不要求写计算过程).19、如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;(2)□APCD是否为矩形?请说明理由;(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN (点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.图1B 图2特殊的平行四边形例1. 如图,正方形ABCD的对角线BD长为2,若直线l满足:①点D到直线l的距离为;②A、C两点到直线l的距离相等.则符合题意的直线l的条数为()A. 1 B. 2 C. 3 D. 4考点:正方形的性质.分析:连接AC与BD相交于O,根据正方形的性质求出OD=,然后根据点到直线的距离和平行线间的距离相等解答.解答:解:如图,连接AC与BD相交于O,∵正方形ABCD的对角线BD长为2,∴OD=,∴直线l∥AC并且到D的距离为,同理,在点D的另一侧还有一条直线满足条件,故共有2条直线l.故选B.点评:本题考查了正方形的性质,主要利用了正方形的对角线互相垂直平分,点D到O 的距离小于是本题的关键.例2. 正方形的对称轴的条数为()A.1 B.2 C.3 D.4考点:轴对称的性质分析:根据正方形的对称性解答.解答:解:正方形有4条对称轴.故选D.点评:本题考查了轴对称的性质,熟记正方形的对称性是解题的关键.例3. 边长为3cm的菱形的周长是()A.6cm B.9cm C.12cm D.15cm考点:菱形的性质.分析:利用菱形的各边长相等,进而求出周长即可.解答:解:∵菱形的各边长相等,∴边长为3cm的菱形的周长是:3×4=12(cm).故选:C.点评:此题主要考查了菱形的性质,利用菱形各边长相等得出是解题关键.例4.下列命题是假命题的是()A.四个角相等的四边形是矩形B.对角线相等的平行四边形是矩形C.对角线垂直的四边形是菱形D.对角线垂直的平行四边形是菱形考点:命题与定理.分析:根据矩形的判定对A、B进行判断;根据菱形的判定方法对C、D进行判断.解答:解:A、四个角相等的四边形是矩形,所以A选项为真命题;B、对角线相等的平行四边形是矩形,所以B选项为真命题;C、对角线垂直的平行四边形是菱形,所以C选项为假命题;D、对角线垂直的平行四边形是菱形,所以D选项为真命题.故选C.点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.1、答、A【思路分析】正方形具有矩形、菱形的一切性质。
2020年中考数学一轮复习培优训练:《四边形》【有答案】

2020年中考数学一轮复习培优训练:《四边形》1.如图1,已知等腰Rt△ABC中,E为边AC上一点,过E点作EF⊥AB于F点,以为边作正方形,且AC=3,EF=.(1)如图1,连接CF,求线段CF的长;(2)将等腰Rt△ABC绕点旋转至如图2的位置,连接BE,M点为BE的中点,连接MC,MF,求MC与MF关系.2.如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.①求∠DAQ的度数;②若AB=6,求PQ的长度.3.在菱形ABCD中,∠ABC=60°,点P是对角线BD上一动点,将线段CP绕点C顺时针旋转120°到CQ,连接DQ.(1)如图1,求证:△BCP≌△DCQ;(2)如图2,连接QP并延长,分别交AB、CD于点M、N.①求证:PM=QN;②若MN的最小值为2,直接写出菱形ABCD的面积为.4.如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=2,BC=5,DC=3,点E在边BC 上,tan∠AEC=3,点M是射线DC上一个动点(不与点D、C重合),联结BM交射线AE于点N,设DM=x,AN=y.(1)求BE的长;(2)当动点M在线段DC上时,试求y与x之间的函数解析式,并写出函数的定义域;(3)当动点M运动时,直线BM与直线AE的夹角等于45°,请直接写出这时线段DM 的长.5.如图1,已知直角梯形ABCO中,∠AOC=90°,AB∥x轴,AB=6,若以O为原点,OA,OC所在直线为y轴和x轴建立如图所示直角坐标系,A(0,a),C(c,0)中a,c 满足|a+c﹣10|+=0(1)求出点A、B、C的坐标;(2)如图2,若点M从点C出发,以2单位/秒的速度沿CO方向移动,点N从原点出发,以1单位/秒的速度沿OA方向移动,设M、N两点同时出发,且运动时间为t秒,当点N从点O运动到点A时,点M同时也停止运动,在它们的移动过程中,当2S△ABN ≤S△BCM时,求t的取值范围:(3)如图3,若点N是线段OA延长上的一动点,∠NCH=k∠OCH,∠CNQ=k∠BNQ,其中k>1,NQ∥CJ,求的值(结果用含k的式子表示).6.在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:问题初探:(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为;问题再探:(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.成果运用(3)若边长AB=8,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L取最大值和最小值时E点的位置?7.实践与探究在平面直角坐标系中,四边形AOBC是矩形,点O0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.(1)如图①,当点D落在BC边上时,求点D的坐标;(2)如图②,当点D落在线段BE上时,AD与BC交于点H.①求证:△ADB≌△AOB;②求点H的坐标.8.实践与探究在综合实践课上,老师让同学们以两个全等的三角形纸片为操作对象,进行相关问题的探究.如图1,△ABC≌△DEF,其中∠ACB=90°,∠A=30°,AB=4.(1)请直接写出EF=;(2)新星小组将这两张纸片按如图2所示的方式放置后,经过观察发现四边形ACBF是矩形,请你证明这个结论.(3)新星小组在图2的基础上,将△DEF纸片沿AB方向平移至如图3的位置,其中点E与AB的中点重合,连接CE,BF.请你判断四边形BCEF的形状,并证明你的结论.9.(1)如图1,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD 上的点,且∠EAF=∠BAD,则BE,EF,DF之间的数量关系是.(2)如图2,若E,F分别是边BC,CD延长线上的点,其他条件不变,则BE,EF,DF之间的数量关系是什么?请说明理由.(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动命令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观察到舰艇甲、乙分别到达E,F处,且两舰艇与指挥中心O连线的夹角∠EOF=70°,试求此时两舰艇之间的距离.10.平面直角坐标系中,A(a,0),B(b,b),C(0,c),且满足:+(2b﹣a﹣c)2+|b﹣c|=0,E、D分别为x轴和y轴上动点,满足∠DBE=45°.(1)求A、B、C三点坐标;(2)如图1,若D为线段OC中点,求E点坐标;(3)当E,D在x轴和y轴上运动时,试探究CD、DE和AE之间的关系.11.【操作】如图①,在矩形ABCD中,E为对角线AC上一点(不与点A重合).将△ADE 沿射线AB方向平移到△BCF的位置,E的对应点为点F,易知△ADE≌△BCF(不需要证明)【探究】过图①的点E作BG∥BC交FB延长线于点G,连结AG,其它条件不变,如图②.求证:△EGA≌△BCF【拓展】将图②中的△BCF沿BC翻折得到△BCF′,连结GF′,其它条件不变,如图③当GF′最短时,若AB=4,BC=2,直接写出FF′的长和此时四边形BFCF′的周长.12.如1,在矩形ABCD中,AB=6,AD=10,E为AD上一点且AE=6,连接BE.(1)将△ABE绕点B逆时针旋转90°至△ABF(如图2),且A、B、C三点共线,再将△ABF沿射线BC方向平移,平移速度为每秒1个单位长度,平移时间为t(s)(t≥0),当点A与点C重合时运动停止.①在平移过程中,当点F与点E重合时,t=(s).②在平移过程中,△ABF与四边形BCDE重叠部分面积记为S,求s与t的关系式.(2)如图3,点M为直线BE上一点,直线BC上有一个动点P,连接DM、PM、DP,且EM=5,试问:是否存在点P,使得△DMP为等腰三角形?若存在,请直接写出此时线段BP的长;若不存在,请说明理由.13.在四边形ABCD中,AD=BC,AB=CD.(1)如图1,连接AC,求证:AB∥CD;(2)如图2,在CB的延长线上取一点M,连接DM,在DM上取一点L,连接BL,当∠CBL=2∠M时,求证:LB=MB;(3)如图3,在(2)条件下,CE平分∠ACB交DM于E点,连接AE,当AE⊥CE,BL=8时,求AC的长.14.阅读下面的例题及点拨,补全解题过程(完成点拨部分的填空),并解决问题:例题:如图1,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连结EM,易证△ABM≌△EBM(),可得AM=EM,∠1=∠2;又AM=MN,则EM =MN,可得∠=∠;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠.又因为∠2+∠6=120,所以∠5+∠6=120°,所以∠AMN=60°.问题:如图3,四边形ABCD的四条边都相等,四个角都等于90°,M是BC边上一点(不含端点B,C),N是四边形ABCD的外角∠DCH的平分线上一点,且AM=MN.求∠AMN的度数.15.在平面直角坐标系xOy中,四边形OADC为正方形,点D的坐标为(4,4),动点E 沿边AO从A向O以每秒1cm的速度运动,同时动点F沿边OC从O向C以同样的速度运动,连接AF、DE交于点G.(1)试探索线段AF、DE的关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图①中补全图形,并说明理由.(3)如图②当点E运动到AO中点时,点M是直线EC上任意一点,点N是平面内任意一点,是否存在点N使以O,C、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.参考答案1.解:(1)如图1,∵△ABC是等腰直角三角形,AC=3,∴AB=3,过点C作CM⊥AB于M,连接CF,∴CM=AM=AB=,∵四边形AGEF是正方形,∴AF=EF=,∴MF=AM﹣AF=﹣,在Rt△CMF中,CF===;(2)CM=FM,CM⊥FM,理由:如图2,过点B作BH∥EF交FM的延长线于H,连接CF,CH,∴∠BHM=∠EFM,∵四边形AGEF是正方形,∴EF=AF∵点M是BE的中点,∴BM=EM,在△BMH和△EMF中,,∴△BMH≌△EMF(AAS),∴MH=MF,BH=EF=AF ∵四边形AGEF是正方形,∴∠FAG=90°,EF∥AG,∵BH∥EF,∴BH∥AG,∴∠BAG+∠ABH=180°,∴∠CBH+∠ABC+∠BAC+∠CAG=180°.∵△ABC是等腰直角三角形,∴BC=AC,∠ABC=∠BAC=45°,∴∠CBH+∠CAG=90°,∵∠CAG+∠CAF=90°,∴∠CBH=∠CAF,在△BCH和△ACF中,,∴△BCH≌△ACF(SAS),∴CH=CF,∠BCH=∠ACF,∴∠HCF=∠BCH+∠BCF=∠ACF+∠BCF=90°,∴△FCH是等腰直角三角形,∵MH=MF,∴CM=FM,CM⊥FM;2.解:(1)如图1中,∵MN∥B′D′,∴∠C′MN=∠C′B′D′=45°,∠C′NM=∠C′D′B′=45°,∴∠C′MN=∠C′NM,∴C′M=C′N,∵C′B′=C′D′,'∴MB′=ND′,∵AB′=AD′,∠AB′M=∠AD′N=90°,∴△AB′M≌△AD′N(SAS),∴∠B′AM=∠D′AN,∵∠B′AD′=90°,∠MAN=45°,∴∠B′AM=∠D′AN=22.5°,∵∠BAC=45°,∴∠BAB′=22.5°,∴α=22.5°.(2)①如图2中,∵∠AB′Q=∠ADQ=90°,AQ=AQ,AB′=AD,∴Rt△AQB′≌Rt△AQD(HL),∴∠QAB′=∠QAD,∵∠BAB′=30°,∠BAD=90°,∴∠B′AD=30°,∴∠QAD=∠B′AD=30°.②如图2中,连接AP,在AB上取一点E,使得AE=EP,连接EP.设PB=a.∵∠ABP=∠AB′P=90°,AP=AP,AB=AB′,∴Rt△APB≌Rt△APB′(HL),∴∠BAP=∠PAB′=15°,∵EA=EP,∴∠EAP=∠EPA=15°,∴∠BEP=∠EAP+∠EPA=30°,∴PE=AE=2a,BE=a,∵AB=6,∴2a+a=6,∴a=6(2﹣).∴PB=6(2﹣),∴PC=BC﹣PB=6﹣6(2﹣)=6﹣6,∵∠CPQ+∠BPB′=180°,∠BAB′+∠BPB′=180°,∴∠CPQ=∠BAB′=30°,∴PQ===12﹣2.3.(1)证明:四边形ABCD是菱形,∴BC=DC,AB∥CD,∴∠PBM=∠PBC=∠ABC=30°,∠ABC+∠BCD=180°,∴∠BCD=180°﹣∠ABC=120°由旋转的性质得:PC=QC,∠PCQ=120°,∴∠BCD=∠DCQ,∴∠BCP=∠DCQ,在△BCP和△DCQ中,,∴△BCP≌△DCQ(SAS);(2)①证明:由(1)得:△BCP≌△DCQ,∴BP=DQ,∠QDC=∠PBC=∠PBM=30°.在CD上取点E,使QE=QN,如图2所示:则∠QEN=∠QNE,∴∠QED=∠QNC=∠PMB,在△PBM和△QDE中,,∴△PBM≌△QDE(AAS),∴PM=QE=QN.②解:由①知PM=QN,∴MN=PQ=PC,∴当PC⊥BD时,PC最小,此时MN最小,则PC=2,BC=2PC=4,∴菱形ABCD的面积=2S△ABC=2××42=8;故答案为:8.4.解:(1)如图1中,作AH⊥BC于H,∵AD∥BC,∠C=90°,∴∠AHC=∠C=∠D=90°,∴四边形AHCD是矩形,∴AD=CH=2,AH=CD=3,∵tan∠AEC=3,∴=3,∴EH=1,CE=1+2=3,∴BE=BC﹣CE=5﹣3=2.(2)延长AD交BM的延长线于G.∵AG∥BC,∴=,∴=,∴DG=,AG=2+=,∵=,∴=,∴y=(0<x<3).(3)①如图3﹣1中,当点M在线段DC上时,∠BNE=∠ABC=45°,∵△EBN∽△EAB,∴EB2=EN•AE,∴,解得x=.②如图3﹣2中,当点M在线段DC的延长线上时,∠ANB=∠ABE=45°,∵△B NA∽△EBA,∴AB2=AE•AN,∴(3)2=•[+解得x=13,综上所述DM的长为或13.5.解:(1)∵|a+c﹣10|+=0,∴a+c﹣10=0,且c﹣7=0,∴c=7,a+c=10,∴c=3,∴A(0,3),C(7,0),∵AB∥x轴,AB=6,∴B(6,3);(2)∴A(0,3),C(7,0),∴OA=3,OC=7,由题意得:ON=t,CM=2t,∴AN=3﹣t,∵2S△ABN≤S△BCM,∴2××(3﹣t)×6≤×2t×3,解得:t≥2,∵当点N从点O运动到点A时,点M同时也停止运动,∴0≤t≤3,∴t的取值范围为2≤t≤3;(3)设AB与CN交于点D,如图3所示:∵AB∥OC,∴∠BDC=∠OCD,∵∠BDC=∠BND+∠ABN,∠CNQ=k∠BNQ,∠NCH=k∠OCH,∴∠BDC=(k+1)∠BNQ+∠ABN,∠OCD=(k+1)∠OCH,∴(k+1)∠BNQ+∠ABN=∠OCD=(k+1)∠OCH,∴∠ABN═(k+1)∠OCH﹣(k+1)∠BNQ=(k+1)(∠OCH﹣∠BNQ),∵NQ∥CJ,∴∠NCJ=∠CNQ=k∠BNQ,∵∠HCJ+∠NCJ=∠NCH=k∠OCH,∴∠HCJ=k∠OCH﹣∠NCJ=k∠OCH﹣k∠BNQ=k(∠OCH﹣∠BNQ),∴==.6.解:(1)∵△ABC是等边三角形,∴∠B=∠C=60°,AB=BC,∵点D是BC的中点,∴BD=CD=BC=AB,∵∠DEB=90°,∴∠BDE=90°﹣∠B=30°,在Rt△BDE中,BE=BD,∵∠EDF=120°,∠BDE=30°,∴∠CDF=180°﹣∠BDE﹣∠EDF=30°,∵∠C=60°,∴∠DFC=90°,在Rt△CFD中,CF=CD,∴BE+CF=BD+CD=BC=AB,∵BE+CF=nAB,∴n=,故答案为:;(2)如图2,①,连接AD,过点D作DG⊥AB于G,DH⊥AC于H,∴∠DGB=∠AGD=90°,∵△ABC是等边三角形,∴∠BAC=60°,∴∠GDH=360°﹣∠AGD﹣∠AHD﹣∠A=120°,∵∠EDF=120°,∴∠EDG=∠FDH,∵△ABC是等边三角形,D是BC的中点,∴∠BAD=∠CAD,∵DG⊥AB,DH⊥AC,∴DG=DH,在△EDG和△FDH中,,∴△EDG≌△FDH(ASA),∴DE=DF,即DE始终等于DF;②同(1)的方法得,BG+CH=AB,由①知,△EDG≌△FDH,∴EG=FH,∴BE+CF=BG﹣EG+CH+FH=BG+CH=AB,∴BE与CF的和始终不变;(3)由(2)知,DE=DF,BE+CF=AB,∵AB=8,∴BE+CF=4,∴四边形DEAF的周长为L=DE+EA+AF+FD=DE+AB﹣BE+AC﹣CF+DF=DE+AB﹣BE+AB﹣CF+DE=2DE+2AB﹣(BE+CF)=2DE+2×8﹣4=2DE+12,∴DE最大时,L最大,DE最小时,L最小,当DE⊥AB时,DE最小,此时,BE=BD=2,当点F和点C重合时,DE最大,此时,∠BDE=180°﹣∠EDF=120°=60°,∵∠B=60°,∴△BDE是等边三角形,∴BE=BD=4,综上所述,周长L取最大值时,BE=4,周长L取最小值时,BE=2.7.解:(1)∵A(5,0),B(0,3),∴OA=5,OB=3,∵四边形AOBC是矩形,∴OB=AC=3,OA=BC=5,∠C=90°,∵矩形ADEF是由矩形AOBC旋转得到的,∴AD=OA=5,在Rt△ACD中,CD===4,∴BD=5﹣4=1,∴D(1,3);(2)①由旋转可知,OA=DA,∠AOB=∠ADE=90°,∴∠AOB=∠ADB=90°,在Rt△AOB与Rt△ADB中,,∴Rt△ADB≌Rt△AOB(HL);②∵△ADB≌△AOB,∴BD=BO=AC,在△BDH与△ACH中,,∴△BDH≌△ACH(AAS),∴DH=CH,∵DH+AH=AD=5,∴CH+AH=5,设CH=x,则AH=5﹣x,在Rt△ACH中,(5﹣x)2=x2+32,解得,x=,∴BH=5﹣=,∴点H的坐标为(,3).8.(1)解:∵△ABC≌△DEF,∴AB=DE=4,∠D=∠A=30°,∠ACB=∠DFE=90°,∴EF=DE=2;故答案为:2;(2)证明:∵△ABC≌△DEF,∴AC=DF=BF,BC=EF=AF,在四边形ACBF中,AC=BF,BC=AF,∴四边形ACBF是平行四边形,∵∠ACB=90°,∴四边形ACBF是矩形;(3)解:四边形BCEF是菱形;理由如下:由(2)可知:四边形ACBF是平行四边形,∴EF∥BC,EF=BC,∵△DEF是沿AB方向平移的,∴EF∥BC,EF=BC,∴四边形BCEF是平行四边形,∵点E是AB的中点,∠ACB=90°,∴CE=AB=2,∴CE=EF=2,∴四边形BCEF是菱形.9.解:(1)延长FD到点G,使DG=BE,连结AG,如图1所示:在△ABE和△ADG中,,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,在△AEF和△GAF中,,∴△AEF≌△AGF(SAS),∴EF=FG,∵FG=DG+DF=BE+DF,∴EF=BE+DF,故答案为:EF=BE+DF;(2)BE,EF,DF之间的数量关系是:EF=BE﹣DF;理由如下:在CB上截取BM=DF,连接AM,如图2所示:∵∠B+∠D=180°,∠ADC+∠ADF=180°,∴∠B=∠ADF,在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AF=AM,∠DAF=∠BAM,∴∠BAD=∠MAF,∵∠BAD=2∠EAF,∴∠MAF=2∠EAF,∴∠MAE=∠EAF,在△FAE和△MAE中,,∴△FAE≌△MAE(SAS),∴EF=EM=BE﹣BM=BE﹣DF,即EF=BE﹣DF;(3)连接EF,延长AE、BF相交于点C,如图3所示:∵∠AOB=30°+90°+(90°﹣70°)=140°,∠EOF=70°,∴∠EOF=∠AOB,∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(70°+50°)=180°,∴符合(1)中的条件,即结论EF=AE+BF成立,∴EF=1.5×(60+80)=210(海里).答:此时两舰艇之间的距离是210海里.10.解:(1)∵+(2b﹣a﹣c)2+|b﹣c|=0,∴a=4,b=c,2b﹣a﹣c=0,∴b=4,c=4,∴点A(4,0),点B(4,4),点C(0,4);(2)如图1,将△BCD绕点B逆时针旋转90°得到△BAH,∵点A(4,0),点B(4,4),点C(0,4),∴OA=OC=BC=AB=4,∵D为线段OC中点,∴CD=DO=2,∵将△BCD绕点B逆时针旋转90°得到△BAH,∴△BCD≌△BAH,∴BD=BH,∠CBD=∠HBA,CD=AH=2,∵∠DBE=45°,∴∠CBD+∠EBA=45°,∴∠EBA+∠ABH=45°=∠HBE=∠DBE,且BD=BH,BE=BE,∴△DBE≌△HBE(SAS)∴DE=EH,∵OH=OA+AH=4+2=6,∴DE=EH=6﹣OE,∵DE2=OD2+OE2,∴(6﹣OE)2=4+OE2,∴OE=,∴点E坐标为(,0);(3)如图1,若点E在x轴正半轴,点D在y轴正半轴上,由(2)可知:DE=EH,AH=CD,∴DE=AE+AH=AE+CD,如图2,点E在x轴负半轴,点D在y轴正半轴,将△BCD绕点B逆时针旋转90°得到△BAH,∴△BCD≌△BAH,∠DBH=90°,∴BD=BH,∠CBD=∠HBA,CD=AH,∵∠DBE=45°,∴∠DBE=45°=∠HBE,且BD=BH,BE=BE,∴△DBE≌△HBE(SAS)∴DE=EH,∴AE=AH+EH=CD+DE;如图3,点E在x轴正半轴,点D在y轴负半轴,将△BCD绕点B逆时针旋转90°得到△BAH,∴△BCD≌△BAH,∠DBH=90°,∴BD=BH,∠CBD=∠HBA,CD=AH,∵∠DBE=45°,∴∠DBE=45°=∠HBE,且BD=BH,BE=BE,∴△DBE≌△HBE(SAS)∴DE=EH,∴CD=AH=AE+EH=AE+DE.11.解:【探究】由平移可知:AE=BF,AE∥BF,∴∠CBF=∠ACB,∵四边形ABCD是矩形,∴AD=BC,∵EG∥BC,∴∠AEG=∠ACB,∴∠AEG=∠CBF,∵GE∥BC,AC∥BG,∴四边形EGBC是平行四边形,∴EG=BC,∴△EGA≌△BCF(SAS).【拓展】如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.∵四边形ABCD是矩形,∴∠ABC=90°,AB=4,BC=2,∴AC===2,∵•AB•CB=•AC•BK,∴BK=,∴OK===,由题意四边形AGFC是平行四边形,∴GF=AC=2,∵BF=BF′,可以假设BF=x,则BG=2﹣x,∵AC∥GF,∴∠BOK=∠HBF′,∵∠BKO=∠F′HB=90°,∴△F′HB∽△BKO,∴==,∴==,∴F′H=x,BH=x,GH=BG﹣BH=2﹣x﹣x=2﹣x,∴GF′===,∵>0,∴当x=﹣=时,GF′的值最小,此时点F′与O重合,可得FF′=4,四边形BFCF′的周长为4.12.解:(1)①如图1中,连接EF.由题意EF=AB=BF=6,∴t=6时,点F与点E重合,故答案为6.②如图2﹣1中,当0<t≤6时,重叠部分是△BMB′,S=t2.如图2﹣2中,当6<t≤10时,重叠部分是△AFB′,S=×6×6=18.如图2﹣3中,当10<t≤16时,重叠部分是△AMC,S=(16﹣t)2,综上所述,S=.(2)如图3中,总MH⊥AD于H,交BC于G.∵AB=AE=6,∠A=90°,∴BE=6,∵EM=5,∴BM=,∴BG=MG=AH=1,HM=HE=5,DH=AD﹣AH=9,∴DM===,当DM=DP时,可得CP1=CP2===,∴BP1=10﹣,BP2=10+.当MD=MP时,可得GP3=GP4===,∴BP3=﹣1,BP4=+1,当PM=PD时,设GP5=x,则=,解得x=,∴BP5=1+=.13.解:(1)证明:在△ADC与△CBA中,,∴△ADC≌△CBA(SSS),∴∠A CD=∠BAC,∴AB∥CD;(2)∵∠CBL=∠M+∠BLM,∠CBL=2∠M,∴∠M+∠BLM=2∠M,∴∠M=∠BLM,∴BM=BL;(3)延长AE交CM于H,∵CE平分∠ACB交DM于E点,∴∠ACE=∠HCE,∵AE⊥CE,∴∠AEC=∠HEC=90°,在△ACE与△HCE中,,∴△ACE≌△CHE(ASA),∴AE=EH,AC=CH,∵AD∥CM,∴∠ADE=∠M,在△ADE与△HME中,,∴△ADE≌△HME(AAS),∴AD=HM,∵AD=BC,∴HM=BC,∴CH=BM,∵BL=8,∴CH=BM=8,∴AC=CH=8.14.解:点拨:如图2,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连结EM,易证△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM=MN,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5.又因为∠2+∠6=120,所以∠5+∠6=120°,所以∠AMN=60°.问题:延长AB至E,使EB=AB,连接EMC、EC,如图所示:则EB=BC,∠EBM中=90°=∠ABM,∴△EBC是等腰直角三角形,∴∠BEC=∠BCE=45°,∵N是正方形ABCD的外角∠DCH的平分线上一点,∴∠MCN=90°+45°=135°,∴∠BCE+∠MCN=180°,∴E、C、N,三点共线,在△ABM和△EBM中,,∴△ABM≌△EBM(SAS),∴AM=EM,∠1=∠2,∵AM=MN,∴EM=MN,∴∠3=∠4,∵∠2+∠3=45°,∠4+∠5=45°,∴∠1=∠2=∠5,∵∠1+∠6=90°,∴∠5+∠6=90°,∴∠AMN=180°﹣90°=90°.故答案为:SAS,3,4,5.15.解:(1)AF=DE.理由如下:∵四边形OADC是正方形,∴OA=AD,∠DAE=∠AOF=90°,由题意得:AE=OF,在△AOF和△DAE中,,∴△AOF≌△DAE(SAS),∴AF=DE.(2)四边形HIJK是正方形.理由如下:如图①所示:∵H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,HI∥AF,HK∥ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△AOF≌△DAE,∴∠ADE=∠OAF,∵∠ADE+∠AED=90°,∴∠OAF+∠AED=90°,∴∠AGE=90°,∴AF⊥ED,∵HI∥AF,HK∥ED,∴HI⊥HK,∴∠KHI=90°,∴四边形HIJK是正方形.(3)存在,理由如下:∵四边形OADC为正方形,点D的坐标为(4,4),∴OA=AD=OC=4,∴C(4,0),∵点E为AO的中点,∴OE=2,E(0,2);分情况讨论:如图②所示,①当OC是以O,C、M、N为顶点的菱形的对角线时,OC与MN互相垂直平分,则M 为CE的中点,∴点M的坐标为(2,1),∵点M和N关于OC对称,∴N(2,﹣1);②当OC是以O,C、M、N为顶点的菱形的边时,若M在y轴的左侧时,∵四边形OCM'N'是菱形,∴OM'=OC=4,M'N'∥OC,∴△M'FE∽△COE,∴==2,设EF=x,则M'F=2x,OF=x+2,在Rt△OM'F中,由勾股定理得:(2x)2+(x+2)2=42,解得:x=,或x=﹣2(舍去),∴M'F=,FN=4﹣M'F=,OF=2+=,∴N'(,);若M在y轴的右侧时,作N''P⊥OC于P,∵ON''∥CM'',∴∠PON''=∠OCE,∴tan∠PON''==tan∠OCE==,设PN''=y,则OP=2y,在Rt△OPN''中,由勾股定理得:y2+(2y)2=42,解得:y=,∴PN''=,OP=,∴N''(,﹣);综上所述,存在点N使以O,C、M、N为顶点的四边形是菱形,点N的坐标为(2,﹣1)或(,)或(,﹣).。
学而思初一数学春季班第2讲-目标中考满分班-教师版

函数1级平面直角坐标系认识初步 函数2级平面直角坐标系中的变换函数3级 函数初步暑期班 第二讲春季班 第一讲减肥记漫画释义满分晋级阶梯2平面直角坐标系中的变换编写思路:本讲求面积时主要让学生掌握将点坐标转化为线段长度的过程.一:让学生亲自动手在坐标系中画出某个点关于横轴、纵轴以及原点的对应点,并且让他们自己总结两个对称点的横、纵坐标关系。
二:(1)对于点的平移:让学生亲自动手将某个点进行上、下、左、右平移,并且自己总结点的坐标变化规律。
对于任意的平移,可以将其理解先上下平移、后左右平移的组合。
(2)对于图形的平移:让学生充分认识本质就是图形上的每个点都进行同一过程的平移,即对应点之间的平移过程完全一样。
从而将图形的平移转化成为点的平移。
并让学生体会平移前后的两个图形完全一样。
三、简单的数形结合:求三角形面积问题。
让学生充分掌握割补法求三角形面积,并理解为何要用割补法。
让学生熟练掌握并体会坐标与线段长的计算关系。
四、找规律问题:老师可带着学生探索常见找规律问题的思路和方法.点()P a b ,关于x 轴的对称点是()P a b '-,,即横坐标不变,纵坐标互为相反数. 点()P a b ,关于y 轴的对称点是()P a b '-,,即纵坐标不变,横坐标互为相反数. 点()P a b ,关于坐标原点的对称点是()P a b '--,,即横坐标互为相反数,纵坐标也互为相反数. 点()P a b ,和点()Q c d ,的中点是22a c b d M ++⎛⎫⎪⎝⎭,.(选讲)思路导航知识互联网题型一:坐标系中的对称【引例】 在平面直角坐标系中,()45P -,关于x 轴的对称点的坐标是 ,关于y 轴的对称点的坐标是 ,关于原点的对称点是 .【解析】 关于x 轴的对称点横坐标不变,纵坐标互为相反数,坐标是()45--,; 关于y 轴的对称点纵坐标不变,横坐标互为相反数,坐标是()45,; 关于原点的对称点横、纵坐标都互为相反数,坐标是()45-,.【例1】 ⑴ 点()35P -,关于x 轴对称的点的坐标为( ) A .()35--, B .()53,C .()35-,D .()35,⑵ 点()21P -,关于y 轴对称的点的坐标为( ) A .()21--,B . ()21,C .()21-,D .()21-,⑶ 在平面直角坐标系中,点()23P -,关于原点对称点P '的坐标是 .⑷ 点()23,P 关于直线3x =的对称点为 ,关于直线5y =的对称点为 . ⑸ 已知点()121P a a +-,关于x 轴的对称点在第一象限,求a 的取值范围.【解析】 ⑴ D ;⑵ B ;⑶ ()2,3-;⑷ ()43,,()27,;⑸ 112a -<<.【例2】 如图,在平面直角坐标系中,直线l 是第一、三象限的角平分线.实验与探究:⑴ 由图观察易知()20A ,关于直线l 的对称点A '的坐标为()02,,请在图中分别标明()53B ,,()25C -,关于直线l 的对称点B '、C '的位置,并写出它们的坐标:B ' ,C ' ;归纳与发现:⑵ 结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点()P a b ,关于第一、三象限的角平分线l 的对称点P '的坐标为 (不必证明);⑶ 点()A a b ,在直线l 的下方,则a ,b 的大小关系为 ;若在直线l 的上方,则 .典题精练例题精讲【解析】 ⑴ ()35B ',,()52C '-,; ⑵ ()b a ,; ⑶ a b >,b a >.⑴ 点平移:①将点()x y ,向右(或向左)平移a 个单位可得对应点()x a y +,或()x a y -,. ②将点()x y ,向上(或向下)平移b 个单位可得对应点()x y b +,或()x y b -,.⑵ 图形平移:①把一个图形各个点的横坐标都加上(或减去)一个正数a ,相应的新图形就是把原图形向右(或向左)平移a 个单位.②如果把图形各个点的纵坐标都加上(或减去)一个正数a ,相应的新图形就是把原图形向上(或向下)平移a 个单位.注意:平移只改变图形的位置,图形的大小和形状不发生变化.【引例】 点()35M --,向上平移7个单位得到点1M 的坐标为 ;再向左平移3个单位得到点2M 的坐标为 .【解析】 点向上平移7个单位,则横坐标不变,纵坐标增加7,即1M 坐标为()32-,,再向左平移3个单位,则纵坐标不变,横坐标减少3,即2M 坐标为()62-,.【例3】 ⑴ 平面直角坐标系中,将(2,1)P -向右平移4个单位,向下平移3个单位,得到'P ,CB A'A-1-2-3-3-2-1O yx123456654321l 典题精练例题精讲思路导航题型二:坐标系中的平移⑵ 平面直角坐标系中,线段11A B ′′是由线段AB 经过平移得到的,点()14A --,的对应点为 ()111A -,′,那么此过程是先向 平移 个单位再向 平移 个单位得到的,则点B ()11,的对应点1B 坐标为 . ⑶将点()21,P m n -+沿x 轴负方向平移3个单位,得到()112,P m -,则点P 坐标是 . (一五六中学期中)⑷ 平面直角坐标系中,线段A B ′′是由线段AB 经过平移得到的,点()21,A -的对应点为 ()34,A ′,点B 的对应点为()40,B ′,则点B 的坐标为( )A .()93,B .()13,--C .()33,-D .()31,--(一五六中学期中)【解析】 ⑴ ()22-,; ⑵ 右2,上3,()3,4;⑶ ()12,.由题意知23112m m n --=-⎧⎨+=⎩,解得31m n =⎧⎨=⎩.故点()12P ,.⑷ B ;可知线段AB 向右平移5个单位,向上平移3个单位得到A B '',故点B 坐标是()13,--.【例4】 ⑴ 如下左图,在平面直角坐标系中,右边的图案是由左边的图案经过平移得到的,左边图案中左、右眼睛的坐标分别是(42)-,,(22)-,,右边图案中左眼的坐标是(34),,则右边图案中右眼的坐标是_______.(北京十二中期中) ⑵ 如下右图是由若干个边长为1的小正方形组成的网格,请在图中作出将“蘑菇”ABCDE 绕A 点逆时针旋转90︒再向右平移2个单位的图形(其中C 、D 为所在小正方形边的中点).⑶ 如图,把图1中的A e 经过平移得到O e (如图2),如果图1中A e 上一点P 的坐标为()m n ,,那么平移后在图2中的对应点P '的坐标为 .(三帆中学期中)【解析】 ⑴ 左眼坐标由(42)-,变为(34),,由此可知由左图得到右图是向上平移2个单位,向右平移7个单位,从而得到右眼平移后的坐标为(54),. ⑵ 图略;A B CDE -3图1-图2⑶ ()21m n +-,;A e 向右平移2个单位长度,再向下平移1个单位长度得到O e .在平面直角坐标系或网格中求面积,一般将难以求解的图形分割成易求解的图形的面积,可以用大图形的总面积减去周围小三角形的面积.一般方法有割补法和等积变换法.找规律的题目一定要先找123n =、、几个图形规律,再推广到n 的情况.从简单情形入手,从中发现规律,猜想、推测、归纳出结论,这是创造性思维的特点.【引例】 如图,直角坐标系中,ABC △的顶点都在网格点上,其中点A 坐标为()21-,,则ABC △的面积为 平方单位. 【解析】 长方形FDEB 的面积是12平方单位,ADC △的面积是1.5平方单位,AEB △的面积是4个平方单位,BFC △的面积是1.5平方单位,所以ABC △的面积为124 1.5 1.55---=平方单位.【例5】 ⑴ 直角坐标系中,已知()10A -,、()30B ,两点,点C 在y 轴上,ABC △的面积是4,则点C 的坐标是 .⑵ 如右图,已知直角坐标系中()14A -,、()02B ,,平移线段AB , 使点B 移到点()30C ,,此时点A 记作点D ,则四边形ABCD 的 面积是 .(161中学期中)【解析】 ⑴ ()02,或()02,-;⑵ 4;点A 平移后的坐标为()22D ,,所以BD x ∥轴,2BD =,故122242ABCD S =⨯⨯⨯=.【例6】 ⑴ 如下左图,在平面直角坐标系中,四边形ABCD 各顶点的坐标分别为(00)A ,,(90)B ,,(75)C ,,(27)D ,.求四边形ABCD 的面积.典题精练例题精讲思路导航题型三:坐标系中的面积与规律问题OF EDCBA y x1O yxDC BA54321Ay D (2,7)C (7,5)y⑵如上右图,ABC △,将ABC △向右平移3个单位长度,然后再向上平移2个单位长度,可以得到111A B C △.①画出平移后的111A B C △;②写出111A B C △三个顶点的坐标;(在图中标出)③已知点P 在x 轴上,以1A 、1B 、P 为顶点的三角形面积为4,求P 点的坐标.【解析】 ⑴ 本题的关键是根据平面直角坐标系的长度单位、原点和坐标轴方向的意义解决简单的面积问题.可以把图形分割成3个直角三角形和1个正方形,问题就迎刃而解了.如右图,分别过点D 、C 作x 轴的垂线,过C 作y 轴的垂线,则可把图形分割成特殊的4部分,因此(275225)25542ABCD S =⨯+⨯+⨯÷+⨯=四边形.⑵ ①略;②()()()111042041A B C ,,,,,;③ ()00,或()40,.【探究对象】平面直角坐标系中求面积的方法【探究目的】熟练利用几种方法快速准确求面积,为以后学习函数综合题打好基础 建议教师:先让学生自由发散,最后教师再总结方法 方法一、割补法(割:分割后再加;补:补全再减.)【探究1】如图所示,()()()1,4,4,3,5,0A B C ,求图形OABC 的面积.解析: 割:如上左图,分别过点A 、B 做x 轴的垂线段AD 、BE OAD BCE OABC ABED S S S S =++△△四边形梯形 ()111=14+4+33+13=14222⨯⨯⨯⨯⨯⨯补:如上右图,先补全为长方形再减去其余图形OAD BCE ABE OABC ODEC S S S S S =---△△△四边形四边形 111=54141414=14222⨯-⨯⨯-⨯⨯-⨯⨯【探究2】如下图所示,()()354,3A B -,,,求图形OAB 的面积.解析:补:如上右图所示,补全图形为ABD △OAB ABD AOD BOD S S S S =--△△△△111117838372222=⨯⨯-⨯⨯-⨯⨯=割:利用一次函数可求出直线AB 解析式为:811=77y x -,故117OC =()1111134272OAB OAC OBC S S S =+=⨯⨯+=△△△ 【此法教师备选】方法二、容斥法:面积差【探究3】如图所示,求12S S -的值.解析:1211=6424822ABD ACD S S S S --=⨯⨯-⨯⨯=△△【教师备选】B B方法三、转化法:平行线,一边转到轴上【探究4】如图所示,求三角形AOB 的面积.解析:过点A 做OB 的平行线,交y 轴于点C ,连接BC由一次函数知识可求出直线1=2OB y x :,设直线1=+2AC y x b :求得1=+22y x ,得()0,2C由等积变换可知1=24=42AOB BOC S S =⨯⨯△△【探究5】如图所示,求三角形ABC 的面积.解析:过点A 作BC 的平行线交y 轴于点D ,连接DC 利用一次函数求得:=2+2BC y x ,设直线:=2+AD y x b 求得=2+7y x ,()0,7D由等积变换可知15=15=22ABC DBC S S =⨯⨯△△【点评】方法一和二为坐标系中求面积的常用方法,方法三转化法用到了一次函数的知识,作为教师备选,建议教师可给学生传递这种求面积的思想,即把其中的一条边转化为坐标轴,从而快速的求出面积.【变式】已知,在平面直角坐标系中,A 、B 两点分别在x 轴、y 轴的正半轴上,且3OB OA ==.⑴直接写出点A 、B 的坐标; ⑵若点()22C -,,求BOC △的面积;⑶点P 是与y 轴平行的直线上一点,且点P 的横坐标为1,若ABP △的面积是6,求点P 的坐标.【解析】 ⑴()()3,00,3A B ,;⑵13232BOC S =⨯⨯=△;⑶ 分两种情况:①当点P 在第一象限时,设()1,,>0P a a ,如图1所示AOB ABP BDP AODP S S S S =++△△△四边形即()()1911+3=+6+3222a a ⨯-,解得=6a ()1,6P②当点P 在第四象限时,设()1,,<0P a a ,如图2所示 ABP AOB BDP AODP S S S S =+-△△△四边形 即()()911+1+313+=6222a a ⨯-⨯⨯解得=2,a 故=2a -. 即()1,2P -图1 图2【例7】 ⑴ 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,图中的正方形的四个顶点都在格点上,观察图中每一个正方形四 条边上的整点的个数,请你猜测由里向外第10个正方形四条边 上的整点个数共有 个.(清华附中期中)⑵ 如图,在平面直角坐标系中,第1次将OAB △变换成11OA B △,第二次将OAB △变换成22OA B △,第3次将OAB △变换成33OA B △.已知()13A ,,()123A ,,()243A ,,()383A ,,()20B ,,()140B ,,()280B ,,()3160B , 观察每次变化前后的三角形,找出规律,按此变化规律再将33OA B △变换成44OA B △,则点4A 的坐标是 ,点4B 的坐标是 ,点n A 的坐标是 ,点n B 的坐标是 .【解析】 ⑴ 40;⑵ ()163,,()320,,()23,n ,()120,n +【例8】 一个粒子在第一象限内及x 轴、y 轴上运动,在第1min 内它从原点运动到(10),,而后接着按如图所示方式在与x 轴、y 轴平行的方向上来回运动,且每分钟移动1个单位长度,那么,在2013min 后,求这个粒子所处的位置坐标.【解析】 弄清粒子的运动规律,并求出靠近1989min 后粒子所在的特殊点的坐标,最后确定所求点的坐标.对于这种运算数较大的题目,我们首先来寻找规律,先观察横坐标与纵坐标相同的点: (00),,粒子运动了0min .(11),,粒子运动了122(min)⨯=,向左运动. (22),,粒子运动了236(min)⨯=,向下运动. (33),,粒子运动了3412(min)⨯=,向左运动. (44),,粒子运动了4520(min)⨯=,向下运动.……于是点(4444),处粒子运动了44451980(min)⨯=.这时粒子向下运动,从而在运动了2013min 后,粒子所在的位置是(444433)-,,即(4411),.【变式】将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标()x y ,,且x ,y 均为整数.如数5对应的坐标为()11-,,则数 对应的坐标是()23-,,数2012对应的坐标是 . (2012年101中期中)【拓展】 数1950对应的坐标是 .【解析】 36,()922-,. ()22,9- 真题赏析12345678910111213141516171819202122232425262728293031323334353637 xy如右图所示,可观察到奇数平方数的规律如下数字 坐标21=1 ()0,023=9 ()11-, 25=25 ()22-,……那么由245=2025可得数2025对应的坐标为()2222-,, 故数2012对应的坐标为()221322--,,即()922-,. 拓展:由于2012比较接近45的平方,而1950接近44的平方,故观察偶数平方数的规律数字 坐标22=4 ()0,124=16 ()12-, 26=36 ()23-,……由244=1936可得数1936对应的坐标为()21,22-,此时再往左一个数字1937对应坐标为()22,22-,此后向下数字变大,故1950对应的坐标为()22,2213--,即()22,9-.【教师备选】【备选1】类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位,用实数加法表示为()321+-=.若坐标平面上的点作如下平移:沿x 轴方向平移的数量为a (向右为正,向左为负,平移a个单位),沿y 轴方向平移的数量为b (向上为正,向下为负,平移b 个单位),则把有序数对{}a b ,叫做这一平移的“平移量”;“平移量”{}a b ,与“平移量”{}c d ,的加法运算法则为{}{}{}a b c d a c b d +=++,,,. 解决问题:⑴ 计算:{}{}3112+,,; ⑵ 动点P 从坐标原点O 出发,先按照“平移量”{}31,平移到A ,再按照“平移量”{}12, 平移到B ;若先把动点P 按照“平移量”{}12,平移到C ,再按照“平移量”{}31,平移,最后的位置还是点B 吗?在图1中画出四边形OABC .⑶ 如图2,一艘船从码头O 出发,先航行到湖心岛码头()23P ,,再从码头P 航行到码头()55Q ,,最后回到出发点O ,请用“平移量”加法算式表示它的航行过程.(2012北京101中期中)【解析】 ⑴}{4,3;⑵是,如图所示;⑶}{}{}{}{2,3+3,2+5,5=0,0--.【备选2】观察下列有规律的点的坐标:()111A ,,()224A -,,()334A ,,()442A -,,()557A ,,6463A ⎛⎫- ⎪⎝⎭,,()7710A ,,()881A -,依此规律,11A 的坐标为 ,12A 的坐标为 .(2012年101中期中)【解析】 ()1111,16A ,12212,3A ⎛⎫- ⎪⎝⎭.横坐标的规律很明显,而纵坐标414,427,,10, 1 (3)----,,,中的奇数数列1,4,7,10是公差为3的等差数列,11A 的纵坐标为16,偶数数列可转化为4444,,,1234----,故12A 的纵坐标为42=63--. 【备选3】一个动点P 在平面直角坐标系中作折线运动,第一次从原点运动到(1,1),然后按图中箭头所示方向运动,每次移动三角形的一边长.即(1,1)→(2,0)→(3,2)→(4,0)→(5,1)→……,按这样的运动规律,经过第17次运动后,动点P 的坐标是 ,经过第2011次运动后,动点P 的坐标是 .【解析】 ()()17,12011,2,.【备选4】如图,在长方形网格中,每个小长方形的长为2,宽为1,A 、B两点在网格格点上,若点C 也在网格格点上,以A 、B 、C 为顶 点的三角形面积为2,则满足条件的点C 个数是( ) A .5 B .4 C .3 D .2(2012清华附中期中) 【解析】 B .【备选5】在平面直角坐标系中,已知()22A -,,在y 轴上确定点P ,使AOP △为等腰三角形,则符合条件的点P 共有( )A .2个B .3个C .4个D .5个(2012陈分期中考试)【解析】 C题型一 坐标系中的对称 巩固练习【练习1】 ⑴ 在平面直角坐标系中,点()25A ,与点B 关于y 轴对称,则点B 的坐标是( ) A .(52)--, B .()25--,C .()25,-D .()25,-⑵ 已知点()P x y ,,()Q m n ,,如果00x m y n +=+=,,那么点P Q ,( ) A .关于原点对称 B .关于x 轴对称C .关于y 轴对称D .关于过点()()0011,,,的直线对称 ⑶ 已知:()2|1|20x y -++=,则()x y ,关于原点对称的点为 .(12,0)(10,0)(8,0)(6,0)(4,0)(2,0)(11,2)(9,1)(7,2)(5,1)(3,2)(1,1)O 复习巩固(北京十二中)⑷ 已知点()33P a b +,与点()52Q a b -+,关于x 轴对称,则a = ,b = .【解析】 ⑴ C;⑵ A ;⑶ ()12-,;⑷ 12a b ==-,;由3523a b a b +=-⎧⎨+=-⎩解得12a b =⎧⎨=-⎩. 题型二 坐标系中的平移 巩固练习【练习2】 ⑴线段CD 是由线段AB 平移得到的,点()15A -,的对应点是()42C ,,则点()41B -,的对应点D 的坐标为 .⑵在平面直角坐标系中有一个已知点A ,现在x 轴向下平移3个单位,y 轴向左平移2个单 位,单位长度不变,得到新的坐标系,在新的坐标系下点A 的坐标为()12-,,在旧的坐标系下,点A 的坐标为 .【解析】 ⑴()9,4-;⑵()31--,.【练习3】 如图,在平面直角坐标系中,若每一个方格的边长代表一个单位.⑴ 线段DC 是线段AB 经过怎样的平移得到的? ⑵ 若C 点的坐标是()41,,A 点的坐标是()12--,,你能写出B 、D 两点的坐标吗?⑶ 求平行四边形ABCD 的面积.(首师大二附中期中)【解析】 ⑴ 先向右平移1个单位再向上平移3个单位.⑵ ()32B -,,()01D ,. ⑶ 4312ABCD S =⨯=Y .题型三 坐标系中的面积和规律问题 巩固练习【练习4】 ⑴ 已知()02,A -,()50,B ,()43,C ,求△ABC 的面积. (四中期中) ⑵ 已知:()40A ,,()10B x -,,()13C ,,ABC △的面积6=, 求代数式22225432x x x x x -++--的值.(人大附中期中)【解析】 ⑴ 172.⑵ 由题可得4AB =,得1441x x --=±⇒=或7x =-,原式化简222254322x x x x x x -++--=--,代入得3-或5【练习5】 如图,长为1,宽为2的长方形ABCD 以右下角的顶点为中心顺时针旋转90︒,此时A 点的坐标为 ;依次旋转2009次,则顶DCBA点A 的坐标为 .【解析】 ()32,,()30152,.第十四种品格:信念你的意念能跳多高布勃卡是举世闻名的奥运会撑杆跳冠军,享有“撑杆跳沙皇”的美誉。
《四边形中考复习》课件

。
图案设计
四边形作为基础图案元素,用于 纺织品、平面设计等领域。
科技中的应用
机械零件
四边形形状的机械零件用于各种机械设备中,确 保稳定性和功能性。
电路板设计
电子设备中的印刷电路板常采用四边形形状,以 提高空间利用率和信号传输效率。
交通标志
交通标志中的四边形元素用于指示方向、警告或 禁令,提高道路安全性。
02
四边形的判定
平行四边形的判定
定义法
定理法
定理法
对角线性质
两组对边分别平行的四 边形是平行四边形。
一组对边平行且相等的 四边形是平行四边形。
两组对边分别相等的四 边形是平行四边形。
对角线互相平分的四边 形是平行四边形。
矩形的判定
01
02
03
04
定义法
所有角都是直角的四边形是矩 形。
定理法
一组邻边相等的平行四边形是 矩形。
面积与形状关系
四边形的面积与其形状有 关,形状相同但大小不同 的四边形可能有不同的面 积。
四边形的周长计算
周长公式
四边形的周长是其所有边 的长度之和。
周长计算方法
对于不规则四边形,可以 通过测量每一边的长度然 后相加得到周长。
周长与形状关系
四边形的周长与其形状有 关,形状相同但大小不同 的四边形可能有不同的周 长。
定理法
对角线垂直且相等的平行四边形是正方形。
定理法
一组邻边相等的矩形是正方形。
定理法
有一个角是直角的菱形是正方形。
03
四边形的面积与周长
四边形的面积计算
01
02
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考试内容考试要求层次A B C多边形了解多边形及正多边形的概念;了解多边形的内角和与外角和公式;知道用任意一个三角形、四边形或正六边形可以进行镶嵌;了解四边形的不稳定性;了解特殊四边形之间的关系会用多边形的内角和与外角和公式解决计算问题;能依据图形条件分解与拼接简单图形平行四边形会识别平行四边形掌握平行四边形的概念、判定和性质,会用平行四边形的性质和判定解决简单问题会运用平行四边形的知识解决有关问题特殊的平行四边形会识别矩形、菱形、正方形掌握矩形、菱形、正方形的概念、判定和性质,会用矩形、菱形、正方形的性质和判定解决简单问题会运用矩形、菱形、正方形的知识解决有关问题梯形会识别梯形、等腰梯形;了解等腰梯形的性质和判定会用等腰梯形的性质和判定解决简单问题本讲结构新课标剖析2中考第一轮复习四边形G FEDCB A一、 四边形知识结构图直角梯形等腰梯形一个角是直角两腰相等四边形两组对边分别平行平行四边形一个角是直角一组邻边相等矩形菱形一组邻边相等一个角是直角正方形梯形一组对边平行另一组不平行二、平行四边形及特殊平行四边形的性质及其判定名称 定义 性质判定面积平 行 四 边 形 两组对边分别平行的四边形叫做平行四边形.①对边平行;②对边相等;③对角相等;④邻角互补;⑤对角线互相平分;⑥是中心对称图形. ①定义;②两组对边分别相等的四边形;③一组对边平行且相等的四边形;④两组对角分别相等的四边形;⑤对角线互相平分的四边形.S ah =(a 为一边长,h为这条边上的高).矩 形 有一个角是直角的平行四边形叫做矩形. 除具有平行四边形的性质外,还有:①四个角都是直角;②对角线相等;③既是中心对称图形又是轴对称图形. ①定义;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形. S ab =(a 、b 为一组邻边).菱 形有一组邻边相等的平行四边形叫做菱形. 除具有平行四边形的性质外,还有:①四条边相等;②对角线互相垂直,且每一条对角线平分一组对角;③既是中心对称图形又是轴对称图形.①定义;②四条边相等的四边形是菱形;③对角线垂直的平行四边形是菱形. ① S ah =(a 为一边长,h 为这条边上的高); ②12S bc =(b 、c 为两条对角线的长). 正方形 有一组邻边相等且有一个角是直角的平行四边形叫做正方形.具有平行四边形、矩形、菱形的性质:①四个角是直角,四条边相等;②对角线相等,互相垂直平分,每一条对角线平分一组对角;③既是中心对称图形又是轴对称图形.①定义;②有一组邻边相等的矩形是正方形;③有一个角是直角的菱形是正方形. ①2S a =(a 为边长); ②212S b =(b 为对角线长).三、梯形常见辅助线作法:DC B AEFFEEE FEEABCD ABC DABCDABC DDC BA四、特殊四边形性质特点:(以下性质需先证明后运用)知识导航OHABDEFN M E ODCBA60°ODCBA1. 对角线互相垂直的四边形:性质1 中点四边形EFGH 为矩形;如图1性质2 四边形面积等于对角线乘积的一半;即12ABCD S AC BD =⋅性质3 四边形对边的平方和相等. 即 2222AB CD AD BC +=+2. 筝形:两组邻边分别相等的四边形,称之为筝形,也称之为半菱形.如图,在筝形ABCD 中,AB=AD ,BC=DC ,AC 与BD 相交于点O . 性质1 ABC ADC △≌△性质2 一组对角相等,即ABC ADC ∠=∠性质3(1)对角线平分一组对角,即AC 平分,BAD BCD ∠∠.(2)对角线互相垂直,即AC BD ⊥.(3)一条对角线平分另一条对角线,即AC 平分BD (OB OD =). 性质4 12ABCD S AC BD =⋅筝形 性质5 筝形是轴对称图形,即AC 所在直线为其对称轴.【编写思路】本讲内容主要包括:平行四边形、矩形、菱形、正方形、梯形的性质与判定的应用,以及与其他知识点的综合运用,例如相似全等、几何变换等,由于近三年中考淡化了对梯形的考察,因此我们放入了平四、矩形、菱形、正方形的两问的中档题,而削弱了梯形的题量和难度. 本讲针对核心考点——中点的构造,进行探究,再次回顾、总结中点的重要辅助线构造.【例1】 ⑴如图,在平行四边形ABCD 中(AB ≠BC ),直线EF 经过其对角线的交点O ,且分别交AD 、BC 于点M 、N ,交BA 、DC 的延长线于点E 、 F ,下列结论:①AO=BO ;②OE=OF ;③△EAM ∽△EBN ; ④△EAO ≌△CNO ,其中正确的是( )A. ①②B. ②③C. ②④D. ③④(2)如图,在矩形ABCD 中,对角线AC 、BD 交于点O .已知∠AOB =60°,AC =16,则图中长度为8的线段有( )A. 2条B. 4 条C. 5条D. 6条(3)人教版八年级数学下册92页第14题是这样叙述的:如图1,Y ABCD 中,过对角线BD 上一点P 作EF ∥BC ,HG ∥AB ,图中哪两个平行四边形面 积相等?为什么?① 根据习题背景,写出面积相等的一对平行四边形的名称为 和 ; ② 如图2,点P 为Y ABCD 内一点,过点P 分别作AD 、AB 的平行线分别交Y ABCD 的四边于点E 、F 、G 、H . 已知S □BHPE = 3,S □PFDG = 5,则PAC S ∆= ;夯实基础模块一 平行四边形及特殊平行四边形的性质和判定③ 如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD 的面积为11,则菱形EFGH 的周长为 . (2013昌平一模)图2图3图1⑤④③②①H PA BGEH DF C ABGEP DF C HGFE DCBA(4)如图,点P 是正方形ABCD 的对角线BD 上一点,PE ⊥BC 于点E ,PF ⊥CD 于点F ,连接EF .给出下列五个结论:①AP =EF ;②AP ⊥EF ; ③△APD 一定是等腰三角形;④∠PFE =∠BAP ;⑤PD 2.其中 正确结论的序号是 .【解析】(1)B (2)D (3)①Y AEPH 和Y PGCF 或Y ABGH 和Y EBCF 或Y AEFD 和Y HGCD ;②1. ③24.(4)①②④⑤【例2】 1. 如图,在ABCD Y 中,F 是AD 的中点,延长BC 到点E ,使12CE BC =,连接DE ,CF .(1)求证:四边形CEDF 是平行四边形;(2)若4AB =,6AD =,60B ∠=︒,求DE 的长.(2013北京中考) 【解析】(1)在ABCD Y 中,AD BC ∥∵F 是AD 中点.∴12DF AD =,又∵12CE BC =.∴DF CE =且DF CE ∥ ∴四边形CEDF 为平行四边形 (2)过D 作DH BE ⊥于H在ABCD Y 中 ∵60B ∠=︒ ∴60DCE ∠=︒∵4AB =, ∴4CD = ∴2CH =,23DH = 在CEDF Y 中,132CE DF AD ===, ∴1EH =在Rt DHE △中,22(23)113DE +=g2. 如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连接DE 交AB 于点F ,∠AED =2∠CED ,点G 是DF 的中点. (1)求证:∠CED =∠DAG ;P F EDCBAAB CDEF(2)若BE =1,AG =4,求sin AEB ∠的值. (2013东城一模) 【解析】(1)证明:∵ 矩形ABCD ,∴ AD ∥BC .∴ ∠CED =∠ADE .又∵点G 是DF 的中点, ∴ AG =DG .∴ ∠DAG =∠ADE . ∴ ∠CED =∠DAG . (2)∵ ∠AED =2∠CED ,∠AGE =2∠DAG , ∴ ∠AED =∠AGE . ∴ AE =AG . ∵ AG =4,∴ AE =4.在Rt △AEB 中,由勾股定理可求AB 15 ∴ 15sin AB AEB AE ∠== 【例3】 1. 已知:如图,在菱形ABCD 中,F 为边BC 的中点,DF与对角线AC 交于点M ,过M 作ME ⊥CD 于点E ,∠1=∠2. (1)若CE =1,求BC 的长;(2)求证AM=DF+ME. (2012重庆)【解析】(1)解:∵四边形ABCD 是菱形,∴BC CD =,1DAC DCA ACB ∠=∠=∠=∠. ∵12∠=∠,∴2DCA ∠=∠, ∴DM CM =. 又∵ME CD ⊥,1CE =,∴22CD CE ==,∴2BC CD ==.(2)证明:延长AB 和DF 相交于点G . ∵F 为BC 的中点,∴22BC CF BF ==. ∵2CD CE =,BC CD =,∴CE CF = 又∵ECM FCM ∠=,CM CM =, ∴CEM △≌CFM △, ∴ME MF =. ∵四边形ABCD 是菱形, ∵AB CD ∥,∴2G ∠=∠.又∵DFC GFB ∠=∠,CF BF =, ∴DCF △≌GBF △, ∴DF GF =. ∵2G ∠=∠,12∠=∠, ∴1G ∠=∠, ∴AM GM =. ∵MG GF MF =+,DF GF =,ME MF =, ∴AM DF ME =+.2. 已知:如图,过正方形ABCD 的顶点B 作直线BE 平行于对角线AC ,AE=AC (E ,C 均在AB 的同侧).求证:∠CAE =2∠BAE . (2013大兴一模)【解析】过A 作AG ⊥BE 于G ,连结BD 交AC 于点O ,∴ AGBO 是正方形. ∴ AG=AO=21AC =21AE ∴ ∠AEG=30°.∵ BE ∥AC , ∴ ∠CAE =∠AEG = 30 º.E DBCAGOACBDE12MABGCD FE21MFEDCB A∴ ∠BAE = 45º – 30º = 15º . ∴ ∠CAE = 2∠BAE .【例4】 在ABCD Y中,BAD ∠的平分线交直线BC 于点E ,交直线DC 于点F . ⑴ 在图1中证明CE CF =;⑵ 若90ABC ∠=︒,G 是EF 的中点(如图2),直接写出BDG ∠的度数;⑶ 若120ABC ∠=︒,FG CE ∥,FG CE =,分别连结DB 、DG (如图3),求BDG ∠的度数.图1图2图3ABCF ED ADB E CGFADECG FB(2011北京中考) 【解析】⑴ 证明:∵AF 平分BAD ∠, ∴BAF DAF ∠=∠.∵四边形ABCD 是平行四边形, ∴AD BC AB CD ,∥∥.∴DAF CEF BAF F ∠=∠∠=∠,. ∴CEF F ∠=∠. ∴CE CF =. ⑵ BDC ∠=45︒.⑶ 解:分别连结GB 、GE 、GC . ∵120AB DC ABC ∠=︒,,∥ ∴120ECF ABC ∠=∠=︒∵FG CE ∥且FG CE =, ∴四边形CEGF 是平行四边形. 由⑴得CE CF =, ∴CEGF Y 是菱形.∴1602EG EC GCF GCE ECF =∠=∠=∠=︒,.∴ECG △是等边三角形.∴EG CG =, ①60GEC EGC ∠=∠=︒.∴GEC GCF ∠=∠. ∴BEG DCG ∠=∠. ②由AD BC ∥及AF 平分BAD ∠可得BAE AEB ∠=∠. ∴AB BE =. 在ABCD Y 中,AB DC =. ∴BE DC =. ③ 由①②③得BEG DCG ≅△△. ∴BG DE =,12∠=∠.∴132360BGD EGC ∠=∠+∠=∠+∠=∠=︒.能力提升321G图2ABCFED图3图2图1A E B F C D A E BF C GD A EB FC GD ∴180602BGDBDG ︒-∠∠==︒.【点评】 此题与第一讲的例3的第2问类似,第(2)问已知CEG △为等腰直角三角形,欲证BDG △为等腰 直角三角形,只需证DCG BEG △≌△; 第(3)问已知CEG △为等边三角形,欲证BDG △为等边三角形,只需证DCG BEG △≌△.【例5】 已知:如图1,正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连结DF ,G 为DF 中点,连接EG ,CG . ⑴ 求证:EG =CG ;⑵ 将图1中△BEF 绕B 点逆时针旋转45º,如图2所示,取DF 中点G ,连接EG ,CG .问⑴ 中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.⑶ 将图1中△BEF 绕B 点旋转任意角度,如图3所示,再连接相应的线段,问⑵中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)(2011平谷二模)【解析】(1)∵90DEF DCF ∠=∠=︒ ,G 为DF 中点, ∴EG =CG=12DF ;(2)方法一:如下图1,延长EG 交AD 延长线于点M ,连结CM 、CE ,易证DMG FEG △≌△、BDE DCM △≌△,然后可证ECM △为等腰直角三角形,于是EG =CG ,同时还可得EG ⊥CG ;方法二:如下图2,延长CG 到M ,使得MG=CG ,连结MF 、ME 、EC ,类似方法一通过证两次 全等和一个等腰直角三角形即可证得结论;方法三,如下图3,过点G 作GM ⊥AD 于点M ,延长MG 、EF 交于点N ,连结AG ,通过证明 AG=GE 、AG=GC 证得结论;图3图2图1MNG BCDEFFECBAGGABCEF图2图1DGEEGC(3)结论为EG =CG 且EG ⊥CG ,证明思路如下:方法一:如下图1,延长CG 到M ,使得MG=CG ,连结MF 、ME 、EC ,并延长MF 交BC 于点H , 先证MGF CGD △≌△,再通过证明四边形EBHF 对角互补证明EFM EBC ∠=∠,从而可证EFM EBC △≌△以及MEC △为等腰直角三角形,于是EG =CG 且EG ⊥CG ;方法二:如下图2,分别取FB 、DB 的中点M 、N ,连结EM 、CN 、MG 、GN ,通过证明EMG GNC △≌△ 证出结论;方法三:如下图3,延长FE 到M ,使FE=EM ,延长DC 到N ,使CN=DC ,连结BM 、BN 、MD 、FN ,通过证明MBD FBN △≌△证出结论.图1图2图3MNNABDEFGH ABD F GMMGFD BA【点评】回顾总结“中点”的辅助线构造:以下探究主题为:中点的构造【探究1】 在正方形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上(点 E 、C 不重合).且BN =NE ,请判断BN 与EN 的位置关系、以及CE 与BM 的数量关系并证明. 【解析】如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H . ∵ 四边形ABCD 是正方形,∴ AB ∥CG . ∴ ∠MBN =∠DGN ,∠BMN =∠GDN . ∵ N 为MD 的中点,∴ MN =DN . ∴ △BMN ≌△GDN .∴ MB =DG ,BN =GN .∵ BN =NE , ∴ BN =NE =GN .∴ ∠BEG =90°.∵ EH ⊥CE , ∴ ∠CEH =90°. ∴ ∠BEG =∠CEH . ∴ ∠BEC =∠GEH . 由(1)得∠DCF =45°.HGABCDEM NFFENM DCBA∴ ∠CHE =∠HCE =45°. ∴ EC=EH , ∠EHG =135°. ∵∠ECB =∠DCB +∠HCE =135°,∴ ∠ECB =∠EHG .∴ △ECB ≌△EHG .∴ EB =EG ,CB =HG . ∵ BN =NG ,∴ BN ⊥NE.∵ BM =DG= HG -HD= BC -HD =CD -HD =CH=2CE , ∴CEBM=22.【探究2】△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P 作PE ⊥AB 于点E ,PF ⊥AC 于点F .请判断ED 和FD 的数量关系并说明理由.【解析】 DE =DF理由如下:分别取BP 、CP 的中点M 、N ,联结EM 、DM 、FN 、DN .∵D 为BC 的中点,∴BP DN BP DN //,21=. ∵,AB PE ⊥∴BP BM EM 21==.∴21,∠=∠=EM DN .∴12213∠=∠+∠=∠.同理,524,//DM FN MD PC =∠=∠. ∴四边形MDNP 为平行四边形. ∴67∠=∠.∵,41∠=∠∴35∠=∠.∴EMD DNF ∠=∠. ∴△EMD ≌△DNF . ∴DE =DF .【例6】 如图,等腰梯形ABCD 中,AD ∥BC ,∠B =45°,P 是BC 边上一点,△P AD 的面积为21,设AB =x ,AD =y .(1)求y 与x 的函数关系式;(2)若∠APD =45°,当1=y 时,求PB•PC 的值;(3)若∠APD =90°,求y 的最小值. (2013福建福州)B CADDAC P B模块二 梯形2x m =()()200ax b m a m +=≠≥,()211x +=11x +=±11x +=11x +=-1202x x ==-,AEFPBD C7654321NMCD BPFEA【解析】(1)如图,过点A 作AE BC ⊥于点E在Rt ABE △中,45B ∠=︒,AB x =∴2sin AE AB B x ==g ∵1122APD S AD AE ==g △,∴12122y =g g , ∴2y =(2)∵APC APD CPD B BAP ∠=∠+∠=∠+∠ 又45APD B ∠=∠=︒ ∴BAP CPD ∠=∠∵四边形ABCD 是等腰梯形, ∴B C ∠=∠,AB DC =∴ABP △∽PCD △, ∴AB PBPC DC=, ∴PB PC AB DC =g g , ∴2PB PC AB =g 当1y =时,2x =即2AB =∴2(2)2PB PC ==g(3)如图,取AD 的中点F ,连接PF ,过点P 作PH AD ⊥于点H ∴PF PH ≥当PF PH =时,PF 有最小值又∵90APD ∠=︒,∴1122PF AD y ==,∴12PH y =∴1122APD S AD PH ==g g △, ∴111222y y =g g , 22y =∵0y >,∴2y =,即y 2【思维拓展训练】提高班训练1. 将两块全等的含30︒角的三角尺如图1摆放在一起,设较短直角边为1.30︒AB CD30︒图 1ABCDB 1C 1D 1图 2AB CD图 3图 4DCB A⑴ 四边形ABCD 是平行四边形吗?说出你的结论和理由:________________________. ⑵ 如图2,将Rt BCD △沿射线BD 方向平移到111Rt B C D △的位置,四边形11ABC D 是平行四边形吗?说出你的结论和理由:_________________________________________.⑶ 在Rt BCD △沿射线BD 方向平移的过程中,当点B 的移动距离为______时,四边形11ABC D 为矩形,其理由是_____________________________________;当点B 的移动距离为______时,四边形11ABC D 为菱形,其理由是___________________________.(图3、图4用于探究)【解析】(1)是,AD ∥BC ,AD=BC ;(2)是,因为始终有AB ∥11C D ;(33,此时190ABC ∠=︒311AC BD ⊥.DACE P B H B P ECADF训练2.如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=2,且AC︰BD=2︰3.(1)求AC的长;(2)求△AOD的面积.(2013西城一模)【解析】(1)∵平行四边形ABCD的对角线AC、BD交于点O,∴OA=12AC,OB=12BD .∵AC︰BD=2︰3,∴OA︰OB=2︰3 .设OA=2x (x >0),则OB=3x.∵AC⊥AB,∴∠BAC =90°.在Rt△OAB中,OA2+AB2=OB2.∵AB=2,∴(2x)2+22=(3x)2 .解得x=±255(舍负). ∴AC=2OA=855.(2)∵平行四边形ABCD的对角线AC、BD交于点O,∴OB=OD.∴S△AOD= S△AOB=12AO·AB =12×455×2=455.训练3.如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=42,∠C=45°,点P是BC边上一动点,设PB的长为x.⑴当x的值为____________时,以点P、A、D、E为顶点的四边形为直角梯形;⑵当x的值为____________时,以点P、A、D、E为顶点的四边形为平行四边形;⑶点P在BC边上运动的过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.【解析】(1)3或8;(2)1或11;(3)由(2)知,当BP=11时,以点P、A、D、E为顶点的四边形为平行四边形,∴EP=AD=5,过D作DF⊥BC于F,则DF=FC=4,∴FP=3,∴2222345DP FP DF=+=+=∴EP=DP,G故此时平四为菱形.模块一特殊平行四边形的性质和判定课后演练【演练1】⑴如图,矩形ABCD中,AB AD>,AB a=,AN平分DAB∠,DM AN⊥于点M,CN AN⊥于点N.则DM CN+的值为(用含a的代数式表示)()实战演练aNMD CBAP EAB CDS 2S 1A .aB .a 54 C .a 22 D . a 23⑵ 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积 分别为S 1,S 2,则S 1+S 2的值为( )A.16B.17C.18D.19【解析】(1)C (2)B【演练2】 在平行四边形ABCD 中,AC 、BD 交于点O ,过点O 作直线EF 、GH ,分别交平行四边形的四条边于E 、G 、F 、H 四点,连接EG 、GF 、FH 、HE . ⑴ 如图①,试判断四边形EGFH 的形状,并说明理由;⑵ 如图②,当EF ⊥GH 时,四边形EGFH 的形状是 ;⑶ 如图③,在⑵的条件下,若AC =BD ,四边形EGFH 的形状是 ;⑷ 如图④,在⑶的条件下,若AC ⊥BD ,试判断四边形EGFH 的形状,并说明理由.【解析】(1)由全等证得OE=OF ,OG=OH 即可;(2)菱形;(3)菱形;(4)四边形EGFH 为正方形,先证平行四边形ABCD 为正方形.【演练3】 已知:如图,在□ABCD 中,∠BAD ,∠ADC 的平分线AE ,DF 分别与线段BC 相交于点E ,F ,AE 与DF 相交于点G .(1)求证:AE ⊥DF ;(2)若AD =10,AB =6,AE =4,求DF 的长.(2013昌平一模) 【解析】(1)证明:∵四边形ABCD 是平行四边形, ∴AB ∥DC . ∴∠BAD +∠ADC=180°. ∵AE 、DF 分别平分∠BAD 、∠ADC , ∴111,222BAD ADC ∠=∠∠=∠ .∴112()902BAD ADC ∠+∠=∠+∠=︒ .∴∠AGD=90°. ∴AE ⊥DF .(2)由(1)知:AD ∥BC ,且BC= AD = 10,DC =AB =6,∠1=∠3,∠2=∠4 .∴∠1=∠AEB ,∠2=∠DFC . ∴∠3=∠AEB ,∠4=∠DFC .∴BE=AB =6,CF=DC =6. ∴BF =4. ∴EF =2. ∵AD ∥BC , ∴△EFG ∽△ADG . ∴15EG EF AGAD==.H G F E O D C B A 图① H G F E O D C B A 图② A B C D O E F G H 图③ A B C D O E F G H 图④GA EBCDF4321GAE B CDFPF EDCBA ∴145EGEG =-.∴EG=23.∴AG=103.由(1)知∠FGE=∠AGD=90°,由勾股定理,得2023,423∴DF=82.【演练4】 已知:如图,在正方形ABCD 中, E 、F 分别是BC 、DC 边上的点,且AE ⊥EF 于点E .⑴ 延长EF 交正方形ABCD 的外角平分线CP 于点P ,试判断AE 与EP 的大小关系,并说明理由;⑵ 在AB 边上是否存在一点M ,使得四边形DMEP 是平行四边形,若存在,请给予证明;若不存在,请说明理由.【解析】(1)AE =EP ,在AB 上截取BN=BE ,证明ANE ECP △≌△ 即可; (2)存在一点M ,使得四边形DMEP 是平行四边形,如图,过点D 作DM ∥PE ,交AE 于点K ,交AB 于点M ,连结ME 、DP.证明AMD BEA △≌△即可.模块二 梯形 课后演练【演练5】 如图,已知梯形ABCD 中,AD BC ∥,3cm AB CD ==,60C ∠=︒,BD CD ⊥.⑴ 求BC 、AD 的长度;⑵ 若点P 从点B 开始沿BC 边向点C 以2cm/秒的速度运动,点Q 从点 C 开始沿CD 边向点D 以lcm/秒的速度运动,当P 、Q 分别从B 、C 同时出发时,写出五边形ABPQD 的面积S 与运动时间t 之间的关系 式,并写出t 的取值范围(不包含点P 在B 、C 两点的情况);⑶ 在⑵的前提下,是否存在某一时刻t ,使线段PQ 把梯形ABCD 分成 两部分的面积比为15∶?若存在,求出t 的值;若不存在,请说明理由.【解析】(1)BC=6cm ,AD=3cm ;(2))()232627034S t t t =-+<< (3)当12t = 时,线段PQ 把梯形ABCD 分成两部分的面积比为15∶.DAP QBKMPFEDCBA第十八种品格:坚持万斯同闭门思过清朝初期的著名学者、史学家万斯同参与编撰了我国重要史书《二十四史》。
