【精品】2016-2017年广东省韶关市乐昌市七年级上学期数学期中试卷及解析答案word版
2017-2018学年韶关市乐昌市七年级上期末数学试卷含答案解析

2017-2018学年广东省韶关市乐昌市七年级(上)期末数学试卷一、选择题(每小题3分,共30分)1.(3分)﹣5的倒数是()A.5 B.﹣5 C.D.﹣2.(3分)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱3.(3分)如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为()A.2cm B.4cm C.8cm D.13cm4.(3分)如果代数式与ab是同类项,那么m的值是()A.0 B.1 C.D.35.(3分)如图,在数轴上点A表示的数最可能是()A.﹣2 B.﹣2.5 C.﹣3.5 D.﹣2.96.(3分)当x=3,y=2时,代数式的值是()A.B.2 C.0 D.37.(3分)下列式子中,是一元一次方程的有()A.x+5=2x B.x2﹣8=x2+7 C.5x﹣3 D.x﹣y=48.(3分)用代数式表示“a的3倍与b的差的平方”,正确的是()A.3(a﹣b)2B.(3a﹣b)2C.3a﹣b2D.(a﹣3b)29.(3分)数a,b在数轴上的位置如图所示,则a+b是()A.正数B.零C.负数D.都有可能10.(3分)观察下列算式并总结规律:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律,写出22016的末位数字是()A.2 B.4 C.6 D.8二、填空题(每小题3分,共24分)11.(3分)计算:①﹣2+1=②4﹣(﹣4)=③×()=2.12.(3分)计算:①﹣2=②=③﹣x+2x=.13.(3分)直接写出下列方程的解:①x=﹣x+2②﹣x=6③x=2x.14.(3分)把一根木条固定在墙上,至少要钉2根钉子,这是根据.15.(3分)若3 070 000=3.07×10x,则x=.16.(3分)如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=度.17.(3分)一个角是70°,则这个角的余角为度.18.(3分)某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T恤的成本为.三、解答题(一)(本大题共21分)19.(8分)计算:(1)26﹣17+(﹣6)﹣33(2)﹣14×[3﹣(﹣3)2].20.(8分)解方程:(1)4x=5x﹣5(2)﹣1=.21.(5分)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.四、解答题(二)(本大题共18分)22.(6分)一只船从甲码头到乙码头是顺流行驶,用了2小时;从乙码头返回到甲码头是逆流行驶,用了2.5小时.如果水流的速度是3千米/小时,求船在静水中的速度?23.(6分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°(1)求∠AOB的度数;(2)∠COD的度数.24.(6分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物x元(x>300).(1)请用含x代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?五、解答题(三)(本大题共7分)25.(7分)如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?2017-2018学年广东省韶关市乐昌市七年级(上)期末数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)﹣5的倒数是()A.5 B.﹣5 C.D.﹣【解答】解:﹣5的倒数是﹣.故选:D.2.(3分)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱【解答】解:如图所示:这个几何体是四棱锥.故选:A.3.(3分)如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为()A.2cm B.4cm C.8cm D.13cm【解答】解:∵BC=3cm,BD=5cm,∴CD=BD﹣BC=2cm,∵D是AC的中点,∴AC=2CD=4cm,故选:B.4.(3分)如果代数式与ab是同类项,那么m的值是()A.0 B.1 C.D.3【解答】解:根据题意得:2m=1,解得:m=.故选C.5.(3分)如图,在数轴上点A表示的数最可能是()A.﹣2 B.﹣2.5 C.﹣3.5 D.﹣2.9【解答】解:∵点A表示的数在﹣3与﹣2中间,∴A、C、D三选项错误,B选项正确.故选:B.6.(3分)当x=3,y=2时,代数式的值是()A.B.2 C.0 D.3【解答】解:==7.(3分)下列式子中,是一元一次方程的有()A.x+5=2x B.x2﹣8=x2+7 C.5x﹣3 D.x﹣y=4【解答】解:A、是一元一次方程,故A正确;B、不是方程,故B错误;C、是多项式,故C错误;D、二元一次方程,故D错误;故选:A.8.(3分)用代数式表示“a的3倍与b的差的平方”,正确的是()A.3(a﹣b)2B.(3a﹣b)2C.3a﹣b2D.(a﹣3b)2【解答】解:∵a的3倍与b的差为3a﹣b,∴差的平方为(3a﹣b)2.故选B.9.(3分)数a,b在数轴上的位置如图所示,则a+b是()A.正数B.零C.负数D.都有可能【解答】解:由图,可知:a<0,b>0,|a|>|b|.则a+b<0.故选:C.10.(3分)观察下列算式并总结规律:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律,写出22016的末位数字是()A.2 B.4 C.6 D.8【解答】解:由21=2,22=4,23=8,24=16,…;可以发现他们的末尾数字是4个数一个循环,2,4,8,6,…∵2016÷4=504,∴22016的与24的末尾数字相同是6.故选:C.二、填空题(每小题3分,共24分)11.(3分)计算:①﹣2+1=﹣1②4﹣(﹣4)=8③×(﹣4)=2.【解答】解:①﹣2+1=﹣1②4﹣(﹣4)=8③×(﹣4)=2故答案为:﹣1、8、﹣4.12.(3分)计算:①﹣2=﹣4②=﹣4.5③﹣x+2x=x.【解答】解:①﹣2=﹣4;②=﹣4.5;③﹣x+2x=x.故答案为:﹣4,﹣4.5,x.13.(3分)直接写出下列方程的解:①x=﹣x+2x=1②﹣x=6x=﹣18③x=2x x=0.【解答】解:①移项得,x+x=2,合并同类项得,2x=2,系数化为1得,x=1;②方程两边都乘以﹣3,系数化为1得,x=﹣18;③移项得,x﹣2x=0,合并同类项得,﹣x=0,系数化为1得,x=0.故答案为:①x=1;②x=﹣18;③x=0.14.(3分)把一根木条固定在墙上,至少要钉2根钉子,这是根据过两点有且只有一条直线.【解答】解:在墙上固定一根木条至少需要两根钉子,依据的数学道理是过两点有且只有一条直线或两点确定一条直线.15.(3分)若3 070 000=3.07×10x,则x=6.【解答】解:∵3 070 000=3.07×106=3.07×10x,∴x=6.16.(3分)如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=155度.【解答】解:∵点A、O、B在一条直线上,∴∠COB=180°﹣∠AOC=180°﹣50°=130°,∵OD平分∠AOC,∴∠COD=×50°=25°,∴∠BOD=∠COB+∠COD=130°+25°=155°.故答案为:155.17.(3分)一个角是70°,则这个角的余角为20度.【解答】解:∵一个角是70°,∴这个角的余角=90°﹣70°=20°.故答案为:20.18.(3分)某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T恤的成本为160元.【解答】解:设成本为x元,则获利为20%x元,售价为0.8×240元,由题意得:x+20%x=0.8×240,解得:x=160.答:这件T恤的成本为160元.故答案为160元.三、解答题(一)(本大题共21分)19.(8分)计算:(1)26﹣17+(﹣6)﹣33(2)﹣14×[3﹣(﹣3)2].【解答】解:(1)原式=26﹣17﹣6﹣33=26﹣56=﹣30;(2)原式=﹣1﹣×(﹣6)=﹣1+1=0.20.(8分)解方程:(1)4x=5x﹣5(2)﹣1=.【解答】解:(1)4x=5x﹣54x﹣5x=﹣5,则﹣x=﹣5,解得:x=5;(2)﹣1=去分母得:3(x+2)﹣12=2(2x﹣3),则3x+6﹣12=4x﹣6,3x﹣4x=﹣6﹣6+12,解得:x=0.21.(5分)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.【解答】解:原式=2ab2﹣3a2b﹣2a2b﹣2ab2=﹣5a2b;当a=1,b=﹣2时,原式=﹣5×12×(﹣2)=10.四、解答题(二)(本大题共18分)22.(6分)一只船从甲码头到乙码头是顺流行驶,用了2小时;从乙码头返回到甲码头是逆流行驶,用了2.5小时.如果水流的速度是3千米/小时,求船在静水中的速度?【解答】解:设船在静水中的速度为xkm/h.2(x+3)=2.5(x﹣3)﹣0.5x=﹣13.5x=27.答:船在静水中的平均速度是27千米/小时.23.(6分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°(1)求∠AOB的度数;(2)∠COD的度数.【解答】解:(1)∵∠BOC=2∠AOC,∠AOC=40°,∴∠BOC=80°,∴∠AOB=∠BOC+∠AOC=120°;(2)∵OD平分∠AOB,∴∠AOD=∠AOB=60°,∴∠COD=∠AOD﹣∠AOC=20°.24.(6分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物x元(x>300).(1)请用含x代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?,顾客在乙超市购物所【解答】解:(1)设顾客在甲超市购物所付的费用为y甲付的费用为y,乙0.8(x﹣300)=0.8x+60;y乙=200+0.85(x﹣200)=0.85x+30.根据题意得:y甲=300+(2)他应该去乙超市,理由如下:60=460,y乙=0.85x+30=455,当x=500时,y甲=0.8x+∵460>455,∴他去乙超市划算.0.8x+60=0.85x+30,(3)令y甲=y乙,即解得:x=600.答:李明购买600元的商品时,到两家超市购物所付的费用一样.五、解答题(三)(本大题共7分)25.(7分)如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是30.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?【解答】解:(1)OB=3OA=30.故B对应的数是30;(2)设经过x秒,点M、点N分别到原点O的距离相等①点M、点N在点O两侧,则10﹣3x=2x,解得x=2;②点M、点N重合,则3x﹣10=2x,解得x=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等;(3)设经过y秒,恰好使AM=2BN.①点N在点B左侧,则3y=2(30﹣2y),解得y=,3×﹣10=;②点N在点B右侧,则3y=2(2y﹣30),解得y=60,3×60﹣10=170;即点M运动到或170位置时,恰好使AM=2BN.故答案为:30.。
2016-2017年广东省韶关市乐昌市八年级上学期数学期中试卷与答案
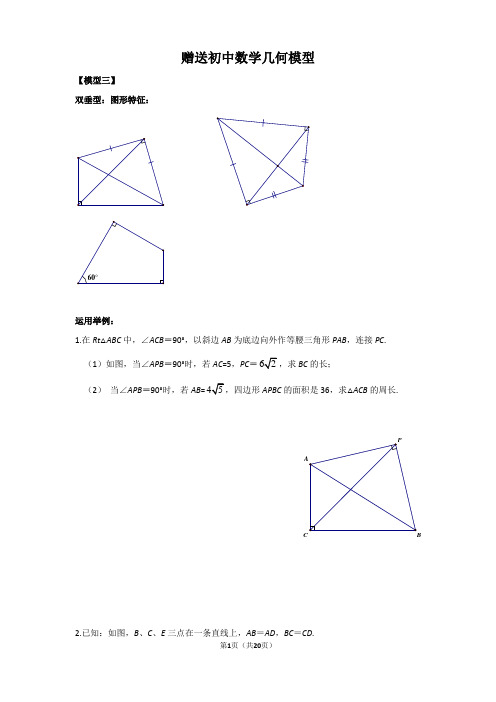
赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC. (1)如图,当∠APB=90°时,若AC=5,PC=62,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.P 2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
DBC2016-2017学年广东省韶关市乐昌市八年级(上)期中数学试卷一、选择题(共10小题,每小题2分,满分20分)1.(2分)在△ABC中,∠A=30°,∠B=60°,则∠C=()A.30°B.45°C.60°D.90°2.(2分)已知三角形的两边长分别是5、7,则第三边长a的取值范围是()A.2<a<12 B.2≤a≤12 C.a>2 D.a<123.(2分)下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.2,4,5 D.1,7,94.(2分)如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=()A.10°B.15°C.20°D.30°5.(2分)观察下列图形,是轴对称图形的是()A.B.C.D.6.(2分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定7.(2分)如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN8.(2分)如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为()A.1 B.2 C.3 D.49.(2分)如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为()A.55°B.65°C.75°D.85°10.(2分)如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是()A.AD=AE B.DB=EC C.∠ADE=∠AED D.DE=BC二、填空题(共6小题,每小题3分,满分18分)11.(3分)线段是轴对称图形,它的对称轴有条.12.(3分)一个多边形的内角和是720°,这个多边形的边数是.13.(3分)已知点A(3,1),则点A关于x轴的对称点A1的坐标是.14.(3分)正△ABC的两条角平分线BD和CE交于点I,则∠BIC等于.15.(3分)如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是.16.(3分)如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在图5中,互不重叠的三角形共有个.三、解答题(共9小题,满分62分)17.(6分)如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.18.(6分)如图,在△ABC中,AB=AC.(1)利用尺规作图法作边BC的高AD,垂足为D,(要求:保留作图痕迹,不写作法).(2)求证:BD=CD.19.(6分)如图.(1)求图形中的x的值;(2)求:∠A、∠B、∠C、∠D的度数.20.(7分)如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1B1C1.21.(7分)如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.22.(7分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.(1)求证:△ADC≌△CEB.(2)AD=6cm,DE=4cm,求BE的长度.23.(7分)如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.24.(8分)如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.25.(8分)如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.2016-2017学年广东省韶关市乐昌市八年级(上)期中数学试卷参考答案与试题解析一、选择题(共10小题,每小题2分,满分20分)1.(2分)在△ABC中,∠A=30°,∠B=60°,则∠C=()A.30°B.45°C.60°D.90°【解答】解:∵在△ABC中,∠A=30°,∠B=60°,∴∠C=180°﹣30°﹣60°=90°,故选:D.2.(2分)已知三角形的两边长分别是5、7,则第三边长a的取值范围是()A.2<a<12 B.2≤a≤12 C.a>2 D.a<12【解答】解:∵三角形的第三边大于两边之差小于两边之和,∴三角形的两边长分别是5、7,则第三边长a的取值范围是2<a<12.故选:A.3.(2分)下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.2,4,5 D.1,7,9【解答】解:A、错误.因为3+4<8.B、错误.因为5+6=11.C、正确.因为2+4>5.D、错误.因为1+7<9.故选:C.4.(2分)如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=()A.10°B.15°C.20°D.30°【解答】解:∵∠ADC是△ABD的外角,∴∠ADC=∠B+∠BAD=∠B+20°,∵∠AED是△CDE的外角,∴∠AED=∠C+∠EDC,∵∠B=∠C,∠ADE=∠AED,∴∠C+∠EDC=∠ADC﹣∠EDC=∠B+20°﹣∠EDC,解得∠EDC=10°.故选:A.5.(2分)观察下列图形,是轴对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选:A.6.(2分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定【解答】解:A、锐角三角形,三条高线交点在三角形内,故错误;B、钝角三角形,三条高线不会交于一个顶点,故错误;C、直角三角形的直角所在的顶点正好是三条高线的交点,可以得出这个三角形是直角三角形,故正确;D、能确定C正确,故错误.故选:C.7.(2分)如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN【解答】解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故B 选项符合题意;C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.故选:B.8.(2分)如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为()A.1 B.2 C.3 D.4【解答】解:过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,∴PQ=PW,PW=PR,∴PR=PQ,∵点P到AC的距离为3,∴PQ=PR=3,则点P到AB的距离为3,故选:C.9.(2分)如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为()A.55°B.65°C.75°D.85°【解答】解:∵∠BCA=35°,∠B=80°,∴∠BAC=180°﹣∠BCA﹣∠B=180°﹣35°﹣80°=65°,∵△ABC与△ADC关于AC所在的直线对称,∴∠DAC=∠BAC=65°.故选:B.10.(2分)如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是()A.AD=AE B.DB=EC C.∠ADE=∠AED D.DE=BC【解答】解:∵DE∥BC,∴=,∠ADE=∠B,∵AB=AC,∴AD=AE,DB=EC,∠B=∠C,∴∠ADE=∠AED,而DE不一定等于BC,故选:D.二、填空题(共6小题,每小题3分,满分18分)11.(3分)线段是轴对称图形,它的对称轴有2条.【解答】解:线段是轴对称图形,它的对称轴有2条.故答案为:2.12.(3分)一个多边形的内角和是720°,这个多边形的边数是6.【解答】解:∵多边形的内角和公式为(n﹣2)•180°,∴(n﹣2)×180°=720°,解得n=6,∴这个多边形的边数是6.故答案为:6.13.(3分)已知点A(3,1),则点A关于x轴的对称点A1的坐标是(3,﹣1).【解答】解:点A(3,1)关于x轴的对称点A1的坐标是(3,﹣1).故答案为:(3,﹣1).14.(3分)正△ABC的两条角平分线BD和CE交于点I,则∠BIC等于120°.【解答】解:∵△ABC是等边三角形,∴∠A=∠ABC=∠ACB=60°,∵BI平分∠ABC,CI平分∠ACB,∴∠IBC=∠ABC=30°,∠ICB=∠ACB=30°,∴∠BIC=180°﹣30°﹣30°=120°,故答案为:120°.15.(3分)如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是利用三角形的稳定性.【解答】解:这样做的道理是利用三角形的稳定性.16.(3分)如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在图5中,互不重叠的三角形共有16个.【解答】解:图1中互不重叠的三角形有4个图2中互不重叠的三角形有7=4+3个图3中互不重叠的三角形有10=4+3×2个按此规律图n中互不重叠的三角形有4+3(n﹣1)=3n+1个,∴当n=5时,3n+1=16,故答案为:16.三、解答题(共9小题,满分62分)17.(6分)如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.【解答】证明:在△ACB和△ADB中,,∴△ACB≌△ADB(AAS),∴BC=BD.18.(6分)如图,在△ABC中,AB=AC.(1)利用尺规作图法作边BC的高AD,垂足为D,(要求:保留作图痕迹,不写作法).(2)求证:BD=CD.【解答】(1)解:如图,点D即为所求;(2)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.在△ABD与△ACD中,∵,∴△ABD≌△ACD(HL),∴BD=CD.19.(6分)如图.(1)求图形中的x的值;(2)求:∠A、∠B、∠C、∠D的度数.【解答】解:(1)依题意有:3x+3x+4x+2x=360°,解得x=30°;(2)∠A=∠B=3×30°=90°,∠C=2×30°=60°,∠D=4×30°=120°.20.(7分)如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1(﹣1,2)B1(﹣3,1)C1(2,﹣1).【解答】解:(1)所作图形如下所示:(2)A1,B1,C1的坐标分别为:(﹣1,2),(﹣3,1),(2,﹣1).故答案为:(﹣1,2),(﹣3,1),(2,﹣1).21.(7分)如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.【解答】(1)解:∵AB=AC,∴∠B=∠C=30°,∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,∵∠DAB=45°,∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.22.(7分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.(1)求证:△ADC≌△CEB.(2)AD=6cm,DE=4cm,求BE的长度.【解答】(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,∴∠E=∠ADC=∠ACB=90°,∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,∴∠CAD=∠BCE,在△ADC和△CEB中∴△ADC≌△CEB(AAS);(2)解:∵△ADC≌△CEB,AD=6cm,∴CE=AD=6cm,BE=CD,∵DE=4cm,∴BE=CD=CE﹣DE=6cm﹣4cm=2cm.23.(7分)如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.【解答】解:如:AD=BC,BE∥AF,则DE=CF;理由是:∵BE∥AF,∴∠AFD=∠BEC,在△ADF和△BEC中,∵,∴△ADF≌△BCE,∴DF=CE,∴DF﹣EF=CE﹣EF,∴DE=CF.24.(8分)如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.【解答】证明:(1)∵△ABC、△ADE是等边三角形,∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,∴∠BAC+∠CAD=∠DAE+∠CAD,即:∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=EC,∵BD=BC+CD=AC+CD,∴CE=BD=AC+CD;(2)由(1)知:△BAD≌△CAE,∴∠ACE=∠ABD=60°,∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ECD=60°.25.(8分)如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.【解答】(1)证明:∵BE⊥AC,CF⊥AB,∴∠HFB=∠HEC=90°,又∵∠BHF=∠CHE,∴∠ABD=∠ACG,在△ABD和△GCA中,∴△ABD≌△GCA(SAS),∴AD=GA(全等三角形的对应边相等);(2)位置关系是AD⊥GA,理由为:∵△ABD≌△GCA,∴∠ADB=∠GAC,又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,∴∠AED=∠GAD=90°,∴AD⊥GA.。
韶关市乐昌市2016-2017学年八年级上期中数学试卷含答案解析(初中 数学试卷)

2016-2017学年广东省韶关市乐昌市八年级(上)期中数学试卷一、选择题(共10小题,每小题2分,满分20分)1.在△ABC中,∠A=30°,∠B=60°,则∠C=()A.30°B.45°C.60°D.90°2.已知三角形的两边长分别是5、7,则第三边长a的取值范围是()A.2<a<12 B.2≤a≤12 C.a>2 D.a<123.下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.2,4,5 D.1,7,94.如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=()A.10°B.15°C.20°D.30°5.观察下列图形,是轴对称图形的是()A. B. C. D.6.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定7.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN 的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN8.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为()A.1 B.2 C.3 D.49.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为()A.55°B.65°C.75°D.85°10.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是()A.AD=AE B.DB=EC C.∠ADE=∠AED D.DE=BC二、填空题(共6小题,每小题3分,满分18分)11.线段是轴对称图形,它的对称轴有条.12.一个多边形的内角和是720°,这个多边形的边数是.13.已知点A(3,1),则点A关于x轴的对称点A1的坐标是.14.正△ABC的两条角平分线BD和CE交于点I,则∠BIC等于.15.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是.16.如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在图5中,互不重叠的三角形共有个.三、解答题(共9小题,满分62分)17.如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.18.如图,在△ABC中,AB=AC.(1)利用尺规作图法作边BC的高AD,垂足为D,(要求:保留作图痕迹,不写作法).(2)求证:BD=CD.19.如图.(1)求图形中的x的值;(2)求:∠A、∠B、∠C、∠D的度数.20.如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1B1C1.21.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.22.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.(1)求证:△ADC≌△CEB.(2)AD=6cm,DE=4cm,求BE的长度.23.如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.24.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.25.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.2016-2017学年广东省韶关市乐昌市八年级(上)期中数学试卷参考答案与试题解析一、选择题(共10小题,每小题2分,满分20分)1.在△ABC中,∠A=30°,∠B=60°,则∠C=()A.30°B.45°C.60°D.90°【考点】三角形内角和定理.【分析】三角形内角和是180°,据此进行计算即可.【解答】解:∵在△ABC中,∠A=30°,∠B=60°,∴∠C=180°﹣30°﹣60°=90°,故选(D)2.已知三角形的两边长分别是5、7,则第三边长a的取值范围是()A.2<a<12 B.2≤a≤12 C.a>2 D.a<12【考点】三角形三边关系.【分析】根据三角形的第三边大于两边之差小于两边之和,即可解决问题.【解答】解:∵三角形的第三边大于两边之差小于两边之和,∴三角形的两边长分别是5、7,则第三边长a的取值范围是2<a<12.故选A.3.下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.2,4,5 D.1,7,9【考点】三角形三边关系.【分析】根据两边之和大于第三边即可判断.【解答】解:A、错误.因为3+4<8.B、错误.因为5+6=11.C、正确.因为2+4>5.D、错误.因为1+7<9.故选C.4.如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=()A.10°B.15°C.20°D.30°【考点】等腰三角形的性质.【分析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+22°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论.【解答】解:∵∠ADC是△ABD的外角,∴∠ADC=∠B+∠BAD=∠B+20°,∵∠AED是△CDE的外角,∴∠AED=∠C+∠EDC,∵∠B=∠C,∠ADE=∠AED,∴∠C+∠EDC=∠ADC﹣∠EDC=∠B+20°﹣∠EDC,解得∠EDC=10°.故选A.5.观察下列图形,是轴对称图形的是()A. B. C. D.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选A.6.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定【考点】三角形的角平分线、中线和高.【分析】根据三角形的高的特点对选项进行一一分析,即可得出答案.【解答】解:A、锐角三角形,三条高线交点在三角形内,故错误;B、钝角三角形,三条高线不会交于一个顶点,故错误;C、直角三角形的直角所在的顶点正好是三条高线的交点,可以得出这个三角形是直角三角形,故正确;D、能确定C正确,故错误.故选:C.7.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN 的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN【考点】全等三角形的判定.【分析】根据普通三角形全等的判定定理,有AAS、SSS、ASA、SAS四种.逐条验证.【解答】解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故B 选项符合题意;C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.故选:B.8.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为()A.1 B.2 C.3 D.4【考点】角平分线的性质;三角形的外角性质.【分析】过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,根据角平分线性质得出PQ=PR,即可得出答案.【解答】解:过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,∴PQ=PW,PW=PR,∴PR=PQ,∵点P到AC的距离为3,∴PQ=PR=3,则点P到AB的距离为3,故选C.9.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为()A.55°B.65°C.75°D.85°【考点】轴对称的性质.【分析】根据三角形的内角和等于180°求出∠BAC的度数,再根据轴对称的性质可得∠DAC=∠BAC.【解答】解:∵∠BCA=35°,∠B=80°,∴∠BAC=180°﹣∠BCA﹣∠B=180°﹣35°﹣80°=65°,∵△ABC与△ADC关于AC所在的直线对称,∴∠DAC=∠BAC=65°.故选B.10.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是()A.AD=AE B.DB=EC C.∠ADE=∠AED D.DE=BC【考点】等腰三角形的性质;平行线的性质.【分析】由DE与BC平行,得到三角形ADE与三角形ABC相似,由相似得比例,根据AB=AC,得到AD=AE,进而确定出DB=EC,再由两直线平行同位角相等,以及等腰三角形的底角相等,等量代换得到∠ADE=∠AED,而DE不一定为中位线,即DE不一定为BC的一半,即可得到正确选项.【解答】解:∵DE∥BC,∴=,∠ADE=∠B,∵AB=AC,∴AD=AE,DB=EC,∠B=∠C,∴∠ADE=∠AED,而DE不一定等于BC,故选D.二、填空题(共6小题,每小题3分,满分18分)11.线段是轴对称图形,它的对称轴有2条.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:线段是轴对称图形,它的对称轴有2条.故答案为:2.12.一个多边形的内角和是720°,这个多边形的边数是6.【考点】多边形内角与外角.【分析】根据内角和定理180°•(n﹣2)即可求得.【解答】解:∵多边形的内角和公式为(n﹣2)•180°,∴(n﹣2)×180°=720°,解得n=6,∴这个多边形的边数是6.故答案为:6.13.已知点A(3,1),则点A关于x轴的对称点A1的坐标是(3,﹣1).【考点】关于x轴、y轴对称的点的坐标.【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”求解即可.【解答】解:点A(3,1)关于x轴的对称点A1的坐标是(3,﹣1).故答案为:(3,﹣1).14.正△ABC的两条角平分线BD和CE交于点I,则∠BIC等于120°.【考点】等边三角形的性质.【分析】根据等边三角形性质得出∠ABC=∠ACB=60°,根据角平分线性质求出∠IBC和∠ICB,根据三角形的内角和定理求出即可.【解答】解:∵△ABC是等边三角形,∴∠A=∠ABC=∠ACB=60°,∵BI平分∠ABC,CI平分∠ACB,∴∠IBC=∠ABC=30°,∠ICB=∠ACB=30°,∴∠BIC=180°﹣30°﹣30°=120°,故答案为:120°.15.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是利用三角形的稳定性.【考点】三角形的稳定性.【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.【解答】解:这样做的道理是利用三角形的稳定性.16.如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在图5中,互不重叠的三角形共有16个.【考点】规律型:图形的变化类.【分析】根据图形结合题目所给数据寻找规律,发现图2比图1多3个互不重叠的三角形,即4+3个;图3比图2多3个互不重叠的三角形,即4+3×2个;依此类推,图n中互不重叠的三角形的个数是4+3(n﹣1),即3n+1个.【解答】解:图1中互不重叠的三角形有4个图2中互不重叠的三角形有7=4+3个图3中互不重叠的三角形有10=4+3×2个按此规律图n中互不重叠的三角形有4+3(n﹣1)=3n+1个,∴当n=5时,3n+1=16,故答案为:16.三、解答题(共9小题,满分62分)17.如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.【考点】全等三角形的判定与性质.【分析】根据全等三角形的判定和性质即可得到结论.【解答】证明:在△ACB和△ADB中,,∴△ACB≌△ADB(AAS),∴BC=BD.18.如图,在△ABC中,AB=AC.(1)利用尺规作图法作边BC的高AD,垂足为D,(要求:保留作图痕迹,不写作法).(2)求证:BD=CD.【考点】作图—基本作图;等腰三角形的性质.【分析】(1)分别以点BC为圆心,以大于BC为半径画圆,两圆相交于点E,连接AE,交线段于点D,则点D即为垂足;(2)根据HL定理得出△ABD≌△ACD,进而可得出结论.【解答】(1)解:如图,点D即为所求;(2)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.在△ABD与△ACD中,∵,∴△ABD≌△ACD(HL),∴BD=CD.19.如图.(1)求图形中的x的值;(2)求:∠A、∠B、∠C、∠D的度数.【考点】多边形内角与外角.【分析】(1)根据四边形内角和等于360°列出方程求解即可;(2)把x的值代入计算即可求解.【解答】解:(1)依题意有:3x+3x+4x+2x=360°,解得x=30°;(2)∠A=∠B=3×30°=90°,∠C=2×30°=60°,∠D=4×30°=120°.20.如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1(﹣1,2)B1(﹣3,1)C1(2,﹣1).【考点】作图-轴对称变换;点的坐标.【分析】(1)利用轴对称性质,作出A、B、C关于y轴的对称点A1、B1、C1,顺次连接A1B1、B1C1、C1A1,即得到关于y轴对称的△A1B1C1;(2)根据点关于y轴对称的性质,纵坐标相同,横坐标互为相反数,即可求出A1、B1、C1各点的坐标.【解答】解:(1)所作图形如下所示:(2)A1,B1,C1的坐标分别为:(﹣1,2),(﹣3,1),(2,﹣1).故答案为:(﹣1,2),(﹣3,1),(2,﹣1).21.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.【考点】等腰三角形的性质.【分析】(1)由AB=AC,根据等腰三角形的两底角相等得到∠B=∠C=30°,再根据三角形的内角和定理可计算出∠BAC=120°,而∠DAB=45°,则∠DAC=∠BAC﹣∠DAB=120°﹣45°;(2)根据三角形外角性质得到∠ADC=∠B+∠DAB=75°,而由(1)得到∠DAC=75°,再根据等腰三角形的判定可得DC=AC,这样即可得到结论.【解答】(1)解:∵AB=AC,∴∠B=∠C=30°,∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,∵∠DAB=45°,∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.22.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.(1)求证:△ADC≌△CEB.(2)AD=6cm,DE=4cm,求BE的长度.【考点】全等三角形的判定与性质;等腰直角三角形.【分析】(1)求出∠E=∠ADC=∠ACB=90°,∠CAD=∠BCE,根据AAS推出即可;(2)根据全等三角形的性质求出CE=AD=6cm,BE=CD,即可得出答案.【解答】(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,∴∠E=∠ADC=∠ACB=90°,∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,∴∠CAD=∠BCE,在△ADC和△CEB中∴△ADC≌△CEB(AAS);(2)解:∵△ADC≌△CEB,AD=6cm,∴CE=AD=6cm,BE=CD,∵DE=4cm,∴BE=CD=CE﹣DE=6cm﹣4cm=2cm.23.如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.【考点】全等三角形的判定与性质.【分析】只要以其中三个作为条件,能够得出另一个结论正确即可,下边以①③为条件,②为结论为例.【解答】解:如:AD=BC,BE∥AF,则DE=CF;理由是:∵BE∥AF,∴∠AFD=∠BEC,在△ADF和△BEC中,∵,∴△ADF≌△BCE,∴DF=CE,∴DF﹣EF=CE﹣EF,∴DE=CF.24.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.【考点】等边三角形的性质;对顶角、邻补角;全等三角形的判定与性质.【分析】(1)根据△ABC、△ADE都是等边三角形,得到AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,推出∠BAD=∠CAE,得到△BAD≌△CAE,根据全等三角形的性质得到BD=EC,即可推出答案;(2)由(1)知:△BAD≌△CAE,根据平角的意义即可求出∠ECD的度数.【解答】证明:(1)∵△ABC、△ADE是等边三角形,∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,∴∠BAC+∠CAD=∠DAE+∠CAD,即:∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=EC,∵BD=BC+CD=AC+CD,∴CE=BD=AC+CD;(2)由(1)知:△BAD≌△CAE,∴∠ACE=∠ABD=60°,∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ECD=60°.25.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.【考点】全等三角形的判定与性质.【分析】(1)由BE垂直于AC,CF垂直于AB,利用垂直的定义得∠HFB=∠HEC,由得对顶角相等得∠BHF=∠CHE,所以∠ABD=∠ACG.再由AB=CG,BD=AC,利用SAS可得出三角形ABD与三角形ACG全等,由全等三角形的对应边相等可得出AD=AG,(2)利用全等得出∠ADB=∠GAC,再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE,又∠GAC=∠GAD+∠DAE,利用等量代换可得出∠AED=∠GAD=90°,即AG与AD垂直.【解答】(1)证明:∵BE⊥AC,CF⊥AB,∴∠HFB=∠HEC=90°,又∵∠BHF=∠CHE,∴∠ABD=∠ACG,在△ABD和△GCA中,∴△ABD≌△GCA(SAS),∴AD=GA(全等三角形的对应边相等);(2)位置关系是AD⊥GA,理由为:∵△ABD≌△GCA,∴∠ADB=∠GAC,又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,∴∠AED=∠GAD=90°,∴AD⊥GA.2017年2月15日。
2016——2017 学年第一学期教学质量检测七年级数学试题及答案

2016——2017学年第一学期教学质量检测七年级数学试卷说明:本试卷考试时间90分钟,满分100分,答题必须在答题卷上作答,在试题卷上作答无效。
第一部分选择题一、选择题:(本题共12小题,每小题3分,共36分,每小题给出4个选项,其中只有一个是正确的)1.2-的相反数是()A .2B .12-C .2-D .122.2015年10月29日,中共十八届五中全会公报决定,实施普遍二孩政策,中国从1980年开始,推行了35年的城镇人口独生子女政策真正宣告终结。
“未来中国人口会不会突破15亿?”是政策调整决策中的重要考量,“经过高、中、低方案反复测算,未来中国人口不会突破。
”15亿用科学计数法表示为()A .81510⨯B .8510⨯C .91.510⨯D .91.53.下列调查方式合适的是()A .为了了解冰箱的使用寿命,采用普查的方式B .为了了解全国中学生的视力状况,采用普查的方式C .为了了解人们保护水资源的意识,采用抽样调查的方式D .对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式4.下列各组代数式中,不是同类项的是()A .22x y 和2yx -B .33-和3C .2ax 和2a xD .3xy 和2xy -5.若从n 边形的一个顶点出发,最多可以引()条对角线A .n B .1n -C .2n -D .3n -6.有理数a 、b 在数轴上的位置如图,则下列各式不成立的是()A .0a b +>B .0a b ->C .b a>D .0ab <7.下面说法,错误的是()A .一个平面截一个球,得到的截面一定是圆B .一个平面截一个正方体,得到的截面可以是五边形C .棱柱的截面不可能是圆D .下边甲、乙两图中,只有乙才能折成正方体8.某件产品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该件产品的进货价为()A .80元B .85元C .90元D .95元9.方程()1230a a x --+=是关于x 的一元一次方程,则a =()A .2B .2-C .1±D .2±10.下列说法正确的是()A .长方形的长是a 米,宽比长短25米,则它的周长可表示为()225a -米B .6h 表示底为6,高为h 的三角形面积C .10a b +表示一个两位数,它的个位数字是a ,十位数字是bD .甲、乙两人分别从相距40千米的两地同时相向出发,其行走的速度分别为3千米/小时和5千米/小时,经过x 小时相遇,则可列方程式为3540x x +=11.关于x 、y 的代数式()()33981kxy y xy x -++-+中不含有二次项,则k =()A .3B .13C .4D .1412.已知3a =,216b =;且a b a b +≠+,则代数式a b -的值为()A .1或7B .1或7-C .1-或7-D .±1或±7第二部分非选择题二、填空题:(本题共4小题,每小题3分,共12分)13.比较大小:8-________9-(填“<”、“=”、“>”).14.若1a b -=,则代数式()2a b --的值是________.15.在时钟的钟面上,九点半的时针与分针的夹角是________.16.a 是不为1的有理数,我们把11a-称为a 的差倒数,如:2的差倒数是1112--=,1-的差倒数是()11112--=,已知113a =,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,……,以此类推,则2015a =________.三、解答题:(本题共7小题,其中第17题11分,第18题8分,第19题6分,第20题6分,第21题6分,第22题7分,第23题8分,共52分)17.计算:(1)(本题3分)()137********⎛⎫--+⨯- ⎪⎝⎭(2)(本题3分)()()()324224⎡⎤-⨯-÷---⎣⎦(3)(本题5分)先化简,再求值:22221223333x x xy y x ⎛⎫--+-- ⎪⎝⎭,其中2x =,1y -=.18.(每小题4分,共8分)解方程:(1)()52323x x ---=(2)34153x x ---=19.(本题6分)校学生会体育部为更好的的开展同学们课外体育活动,现对学生最喜欢的一项球类运动进行了随机抽样调查,根据调查的结果绘制成如图2-①和图2-②所示的两幅不完整统计图,其中A .喜欢篮球B .喜欢足球C .喜欢乒乓球D .喜欢排球。
2016-2017年广东省韶关市乐昌市八年级(上)期末数学试卷和解析答案

2016-2017学年广东省韶关市乐昌市八年级(上)期末数学试卷一、选择题(每小题3分,满分30分)1.(3分)下列图形是轴对称图形地是()A.B.C.D.2.(3分)分式有意义,则x地取值范围是()A.x≠1 B.x=1 C.x≠﹣1 D.x=﹣13.(3分)已知等腰三角形地一个角为75°,则其顶角为()A.30°B.75°C.105° D.30°或75°4.(3分)下列计算正确地是()A.a3+a3=2a6B.a3•a2=a6 C.a6÷a2=a3D.(a3)2=a65.(3分)下列分解因式正确地是()A.x3﹣x=x(x2﹣1)B.x2﹣1=(x+1)(x﹣1)C.x2﹣x+2=x(x﹣1)+2 D.x2+2x﹣1=(x﹣1)26.(3分)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形地对数为()A.1 B.2 C.3 D.47.(3分)一个正多边形地每个外角都是36°,这个正多边形地边数是()A.9 B.10 C.11 D.128.(3分)点M(﹣2,3)关于x轴对称点地坐标为()A.(﹣2,﹣3)B.(2,﹣3)C.(﹣3,﹣2)D.(2,3)9.(3分)如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误地是()A.∠A=∠B B.AO=BO C.AB=CD D.AC=BD10.(3分)如图,△ABC中,AB=AC,AB地垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC地周长等于()A.4cm B.6cm C.8cm D.10cm二、填空题(每小题3分,满分18分)11.(3分)计算:a2•a3=.12.(3分)当m=时,分式地值为零.13.(3分)如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是.(只需填一个即可)14.(3分)将一副直角三角板,按如图所示叠放在一起,则图中∠α地度数是.15.(3分)若等腰三角形地两条边长分别为7cm和4cm,则它地周长为cm.16.(3分)观察:l×3+1=222×4+1=323×5+1=424×6+1=52…,请把你发现地规律用含正整数n(n≥2)地等式表示为(n=2时对应第1个式子,…)三、解答题(一)(共16分)17.(5分)解方程:=.18.(5分)把两个多项式:x2+2x﹣1,x2+4x+1进行加法运算,并把结果分解因式.19.(6分)已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.求证:BC=DE.四、解答题(二)(共18分)20.(6分)先化简,再求值:+,其中a=.21.(6分)如图,△ABC三个顶点地坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移5个单位长度后得到地△A1B1C1;(2)请画出△ABC关于原点对称地△A2B2C2;(3)在x轴上求作一点P,使△PAB地周长最小,请画出△PAB,并直接写出P 地坐标.22.(6分)如图,在△ABC中,∠BAC=75°,AD、BE分别是BC、AC边上地高,AD=BD,求∠C和∠AFB地度数.五、解答题(每小题6分,满分18分)23.(6分)如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH地长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.(1)求证:AB=AE;(2)若∠A=100°,求∠EBC地度数.24.(6分)某县为了落实中央地“强基惠民工程”,计划将某村地居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数地1.5倍.如果由甲、乙队先合做15天,那么余下地工程由甲队单独完成还需5天.这项工程地规定时间是多少天?25.(6分)已知:如图,△ABC和△DBE均为等腰直角三角形.(1)求证:AD=CE;(2)求证:AD和CE垂直.2016-2017学年广东省韶关市乐昌市八年级(上)期末数学试卷参考答案与试题解析一、选择题(每小题3分,满分30分)1.(3分)下列图形是轴对称图形地是()A.B.C.D.【解答】解:A、是轴对称图形,符合题意;B、不是轴对称图形,不符合题意;C、不是轴对称图形,不符合题意;D、不是轴对称图形,不符合题意.故选A.2.(3分)分式有意义,则x地取值范围是()A.x≠1 B.x=1 C.x≠﹣1 D.x=﹣1【解答】解:根据题意可得x﹣1≠0;解得x≠1;故选A.3.(3分)已知等腰三角形地一个角为75°,则其顶角为()A.30°B.75°C.105° D.30°或75°【解答】解:当75°角为底角时,顶角为180°﹣75°×2=30°;75°角为顶角时,其底角==52.5°,所以其顶角为30°或75°.故选D.4.(3分)下列计算正确地是()A.a3+a3=2a6B.a3•a2=a6 C.a6÷a2=a3D.(a3)2=a6【解答】解:A、系数相加字母部分不变,故A错误;B、底数不变指数相加,故B错误;C、底数不变指数相减,故C错误;D、底数不变指数相乘,故D正确;故选:D.5.(3分)下列分解因式正确地是()A.x3﹣x=x(x2﹣1)B.x2﹣1=(x+1)(x﹣1)C.x2﹣x+2=x(x﹣1)+2 D.x2+2x﹣1=(x﹣1)2【解答】解:A、x3﹣x=x(x2﹣1)=x(x+1)(x﹣1),故本选项错误;B、x2﹣1=(x+1)(x﹣1),故本选项正确;C、x2﹣x+2=x(x﹣1)+2右边不是整式积地形式,故本选项错误;D、应为x2﹣2x+1=(x﹣1)2,故本选项错误.故选B.6.(3分)如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形地对数为()A.1 B.2 C.3 D.4【解答】解:∵OP平分∠MON,PE⊥OM于E,PF⊥ON于F,∴PE=PF,∠1=∠2,在△AOP与△BOP中,,∴△AOP≌△BOP(SAS),∴AP=BP,在△EOP与△FOP中,,∴△EOP≌△FOP(AAS),在Rt△AOP与Rt△BOP中,,∴Rt△AOP≌Rt△BOP(HL_,∴图中有3对全等三角形.故选:C.7.(3分)一个正多边形地每个外角都是36°,这个正多边形地边数是()A.9 B.10 C.11 D.12【解答】解:360°÷36°=10,则这个正多边形地边数是10.故选B.8.(3分)点M(﹣2,3)关于x轴对称点地坐标为()A.(﹣2,﹣3)B.(2,﹣3)C.(﹣3,﹣2)D.(2,3)【解答】解:M(﹣2,3)关于x轴对称点地坐标为(﹣2,﹣3),故选:A.9.(3分)如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误地是()A.∠A=∠B B.AO=BO C.AB=CD D.AC=BD【解答】解:∵△AOC≌△BOD,∴∠A=∠B,AO=BO,AC=BD,∴A、B、D均正确,而AB、CD不是不是对应边,且CO≠AO,∴AB≠CD,故选C.10.(3分)如图,△ABC中,AB=AC,AB地垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC地周长等于()A.4cm B.6cm C.8cm D.10cm【解答】解:∵△ABC中,AB=AC,AB=5cm,∴AC=5cm,∵AB地垂直平分线交AC于P点,∴BP+PC=AC,∴△PBC地周长=(BP+PC)+BC=AC+BC=5+3=8cm.故选C.二、填空题(每小题3分,满分18分)11.(3分)计算:a2•a3=a5.【解答】解:a2•a3=a2+3=a5.故答案为:a5.12.(3分)当m=﹣2时,分式地值为零.【解答】解:依题意,得|m|﹣2=0,且m﹣2≠0,解得,m=﹣2.故答案是:﹣2.13.(3分)如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是∠A=∠F或AC∥EF或BC=DE(答案不唯一).(只需填一个即可)【解答】解:增加一个条件:∠A=∠F,显然能看出,在△ABC和△FDE中,利用SAS可证三角形全等(答案不唯一).故答案为:∠A=∠F或AC∥EF或BC=DE(答案不唯一).14.(3分)将一副直角三角板,按如图所示叠放在一起,则图中∠α地度数是75°.【解答】解:如图,∠1=90°﹣60°=30°,∴∠α=30°+45°=75°.故答案为:75°.15.(3分)若等腰三角形地两条边长分别为7cm和4cm,则它地周长为15或18cm.【解答】解:∵等腰三角形地两边分别是4cm和7cm,∴应分为两种情况:①4为底,7为腰,则4+7+7=18cm;②7为底,4为腰,则7+4+4=15cm;∴它地周长是15cm或18cm.故答案为:15或18.16.(3分)观察:l×3+1=222×4+1=323×5+1=424×6+1=52…,请把你发现地规律用含正整数n(n≥2)地等式表示为(n﹣1)(n+1)+1=n2(n≥2,且n为正整数)(n=2时对应第1个式子,…)【解答】解:n=2时,l×3+1=22,即(2﹣1)(2+1)+1=22,n=3时,2×4+1=32,即(3﹣1)(3+1)+1=32,n=4时,3×5+1=42,即(4﹣1)(4+1)+1=42,n=5时,4×6+1=52,即(5﹣1)(5+1)+1=52,…n=n时,(n﹣1)(n+1)+1=n2,故答案为(n﹣1)(n+1)+1=n2(n≥2,且n为正整数).三、解答题(一)(共16分)17.(5分)解方程:=.【解答】解:去分母得:90(x﹣6)=60x,去括号得:90x﹣540=60x,移项合并得:30x=540,解得:x=18,经检验x=18是分式方程地解.18.(5分)把两个多项式:x2+2x﹣1,x2+4x+1进行加法运算,并把结果分解因式.【解答】解:x2+2x﹣1+x2+4x+1=x2+6x=x(x+6).19.(6分)已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.求证:BC=DE.【解答】证明:∵AB∥EC,∴∠A=∠DCE,在△ABC和△CDE中,,∴△ABC≌△CDE,∴BC=DE.四、解答题(二)(共18分)20.(6分)先化简,再求值:+,其中a=.【解答】解:原式=+==,当a=时,原式==.21.(6分)如图,△ABC三个顶点地坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移5个单位长度后得到地△A1B1C1;(2)请画出△ABC关于原点对称地△A2B2C2;(3)在x轴上求作一点P,使△PAB地周长最小,请画出△PAB,并直接写出P 地坐标.【解答】解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示;(3)△PAB如图所示,P(2,0).22.(6分)如图,在△ABC中,∠BAC=75°,AD、BE分别是BC、AC边上地高,AD=BD,求∠C和∠AFB地度数.【解答】解:(1)在△ABC中,AD、BE分别是BC、AC边上地高,∴∠ADB=∠ADC=∠BEC=90°.∵AD=BD,∴∠ABD=∠BAD=45°.在△ABC中,∠BAC=75°,∴∠C=180°﹣(∠ABD+∠BAC)=180°﹣(45°+75°)=60°.(2)在四边形DCEF中,∵∠DFE=360°﹣(∠ADC+∠BEC+∠C)=360°﹣(90°+90°+60°)=120°.∴∠AFB=∠DFE=120°.五、解答题(每小题6分,满分18分)23.(6分)如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH地长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.(1)求证:AB=AE;(2)若∠A=100°,求∠EBC地度数.【解答】(1)证明:∵AD∥BC,∴∠AEB=∠EBC.由BE是∠ABC地角平分线,∴∠EBC=∠ABE,∴∠AEB=∠ABE,∴AB=AE;(2)由∠A=100°,∠ABE=∠AEB,得∠ABE=∠AEB=40°.由AD∥BC,得∠EBC=∠AEB=40°.24.(6分)某县为了落实中央地“强基惠民工程”,计划将某村地居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数地1.5倍.如果由甲、乙队先合做15天,那么余下地工程由甲队单独完成还需5天.这项工程地规定时间是多少天?【解答】解:设这项工程地规定时间是x天,根据题意得=1.解得:x=30.经检验x=30是方程地解.答:这项工程地规定时间是30天.25.(6分)已知:如图,△ABC和△DBE均为等腰直角三角形.(1)求证:AD=CE;(2)求证:AD和CE垂直.【解答】(1)证明:∵△ABC和△DBE是等腰直角三角形,∴AB=BC,BD=BE,∠ABC=∠DBE=90°,∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,即∠ABD=CBE,在△ABD和△CBE中,,∴△ABD≌△CBE(SAS),∴AD=CE;(2)延长AD分别交BC和CE于G和F,如图所示:∵△ABD≌△CBE,∴∠BAD=∠BCE,∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,又∵∠BGA=∠CGF,∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,∴∠AFC=∠ABC=90°,∴AD⊥CE.赠送:初中数学几何模型举例【模型四】 几何最值模型: 图形特征:l运用举例:1. △ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为AP的中点,则MF的最小值为EM FB2.如图,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F为AC上一动点,则EF+BF的最小值为_________。
2023-2024学年广东省韶关市七年级上学期期中数学学情检测模拟试卷(含答案)

2023-2024学年广东省韶关市七年级上学期期中数学质量检测模拟试题一、单选题9.当4x =-时,多项式3242x x ---与32534x x x ++-的和是()A .0B .4C .4-D .2-10.观察并找规律:122=,224=,328=,4216=,5232=,6264=,72128=,82256=,那么20182的个位数是()A .2B .4C .6D .8二、填空题三、计算题四、应用题五、解答题22.随着手机的普及,微信的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售.刚大学毕业的夏明把自家的冬枣产品放到网上销售,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入.下表是某周的销售情况(超出的量记为正数,不足的量记为负数.单位:斤,1斤500=克)六、计算题23.某城市居民生活用电基本价为每度a元,若每月用电超过70度,超出部分按基本价的150%收费.(1)若用户三月份用电30度,则应收费________元;(2)若用户三月份用电为100度,则应收费________元;(3)由(1)(2)可得:若平均价格________a元(选填“<”“>”或“=”),则用电量一定超过70度;(4)若每月用电量超过y度,超过部分按基本电价的150%收费,某户五月份用电84度,则应收费多少元.答案:【分析】(1)根据前三天销售量相加计算即可;(2)将销售量最多的一天与销售量最少的一天相减计算即可;(3)先将各数相加求得正负即可求解;(4)将总数量乘以价格差解答即可.【详解】(1)解:435300296--+=(斤).故296.(2)()21829--=(斤).故29.(3)达到了.理由:435148216170+--+-+-=>∴本周实际销售总量达到了计划销售量.(4)()()17100783+⨯⨯-7175=⨯3585=(元).答:夏明这一周一共收入3585元.本题考查正数和负数的问题,有理数的四则运算.解题的关键是读懂题意,列式计算.23.(1)30a(2)115a(3)>(4)84y >,则应收费84a 元,或84y <,则应收费()1260.5a ay -元【分析】(1)三月份没有超过70度,则用电基本价格为每度a 元,根据电费=用电量×单价列式即可.(2)三月份用电超过70度,超出部分按基本电价的150%收费,前70度按基本价格为每度a 元收费,超出的按每度1.5a 元收费.(3)根据(1)(2)的结论可得结论.(4)根据“基本电费+超出部分电费”列出代数式,再整理即可.【详解】(1)∵3070<,∴三月份用电量没有超过70度,∴三月份的电费为:30a (元);故30a ;(2)∵10070>,∴三月份电费为:7010070150%115a a a +-⨯⨯=(),故115a ;(3)由于超出部分的每度电的收费多150%10.5a a ⨯-=()元,故当平均价格大于a 元时,则用电量一定超过70度,故>;(4)根据题意得:当84y ≥时,应缴纳电费为84a 元;当84y <时,应缴纳电费为:()()84150%1260.5ay y a a ay ⎡⎤+-⨯=-⎣⎦元.本题考查了列代数式,整式加减的应用,明确计费方式是解答本题的关键.。
【名师精编】韶关市乐昌市七年级上期末数学试卷(有答案)
广东省韶关市乐昌市七年级(上)期末数学试卷一、选择题(每小题3分,共30分)1.(3分)﹣5的倒数是()A.5 B.﹣5 C.D.﹣2.(3分)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥 B.四棱柱C.三棱锥D.三棱柱3.(3分)如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC 的长为()A.2cm B.4cm C.8cm D.13cm4.(3分)如果代数式与ab是同类项,那么m的值是()A.0 B.1 C.D.35.(3分)如图,在数轴上点A表示的数最可能是()A.﹣2 B.﹣2.5 C.﹣3.5 D.﹣2.96.(3分)当=3,y=2时,代数式的值是()A.B.2 C.0 D.37.(3分)下列式子中,是一元一次方程的有()A.+5=2 B.2﹣8=2+7 C.5﹣3 D.﹣y=48.(3分)用代数式表示“a的3倍与b的差的平方”,正确的是()A.3(a﹣b)2 B.(3a﹣b)2C.3a﹣b2D.(a﹣3b)29.(3分)数a,b在数轴上的位置如图所示,则a+b是()A.正数B.零C.负数D.都有可能10.(3分)观察下列算式并总结规律:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律,写出22016的末位数字是()A.2 B.4 C.6 D.8二、填空题(每小题3分,共24分)11.(3分)计算:①﹣2+1=②4﹣(﹣4)=③×()=2.12.(3分)计算:①﹣2=②=③﹣+2=.13.(3分)直接写出下列方程的解:①=﹣+2②﹣=6③=2.14.(3分)把一根木条固定在墙上,至少要钉2根钉子,这是根据.15.(3分)若3 070 000=3.07×10,则=.16.(3分)如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=度.17.(3分)一个角是70°,则这个角的余角为度.18.(3分)某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T 恤的成本为.三、解答题(一)(本大题共21分)19.(8分)计算:(1)26﹣17+(﹣6)﹣33(2)﹣14×[3﹣(﹣3)2].20.(8分)解方程:(1)4=5﹣5(2)﹣1=.21.(5分)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.四、解答题(二)(本大题共18分)22.(6分)一只船从甲码头到乙码头是顺流行驶,用了2小时;从乙码头返回到甲码头是逆流行驶,用了2.5小时.如果水流的速度是3千米/小时,求船在静水中的速度?23.(6分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°(1)求∠AOB的度数;(2)∠COD的度数.24.(6分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物元(>300).(1)请用含代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?五、解答题(三)(本大题共7分)25.(7分)如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?2017-2018学年广东省韶关市乐昌市七年级(上)期末数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)﹣5的倒数是()A.5 B.﹣5 C.D.﹣【解答】解:﹣5的倒数是﹣.故选:D.2.(3分)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥 B.四棱柱C.三棱锥D.三棱柱【解答】解:如图所示:这个几何体是四棱锥.故选:A.3.(3分)如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC 的长为()A.2cm B.4cm C.8cm D.13cm【解答】解:∵BC=3cm,BD=5cm,∴CD=BD﹣BC=2cm,∵D是AC的中点,∴AC=2CD=4cm,故选:B.4.(3分)如果代数式与ab是同类项,那么m的值是()A.0 B.1 C.D.3【解答】解:根据题意得:2m=1,解得:m=.故选C.5.(3分)如图,在数轴上点A表示的数最可能是()A.﹣2 B.﹣2.5 C.﹣3.5 D.﹣2.9【解答】解:∵点A表示的数在﹣3与﹣2中间,∴A、C、D三选项错误,B选项正确.故选:B.6.(3分)当=3,y=2时,代数式的值是()A.B.2 C.0 D.3【解答】解:==7.(3分)下列式子中,是一元一次方程的有()A.+5=2 B.2﹣8=2+7 C.5﹣3 D.﹣y=4【解答】解:A、是一元一次方程,故A正确;B、不是方程,故B错误;C、是多项式,故C错误;D、二元一次方程,故D错误;故选:A.8.(3分)用代数式表示“a的3倍与b的差的平方”,正确的是()A.3(a﹣b)2 B.(3a﹣b)2C.3a﹣b2D.(a﹣3b)2【解答】解:∵a的3倍与b的差为3a﹣b,∴差的平方为(3a﹣b)2.故选B.9.(3分)数a,b在数轴上的位置如图所示,则a+b是()A.正数B.零C.负数D.都有可能【解答】解:由图,可知:a<0,b>0,|a|>|b|.则a+b<0.故选:C.10.(3分)观察下列算式并总结规律:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律,写出22016的末位数字是()A.2 B.4 C.6 D.8【解答】解:由21=2,22=4,23=8,24=16,…;可以发现他们的末尾数字是4个数一个循环,2,4,8,6,…∵2016÷4=504,∴22016的与24的末尾数字相同是6.故选:C.二、填空题(每小题3分,共24分)11.(3分)计算:①﹣2+1=﹣1②4﹣(﹣4)=8③×(﹣4)=2.【解答】解:①﹣2+1=﹣1②4﹣(﹣4)=8③×(﹣4)=2故答案为:﹣1、8、﹣4.12.(3分)计算:①﹣2=﹣4②=﹣4.5③﹣+2=.【解答】解:①﹣2=﹣4;②=﹣4.5;③﹣+2=.故答案为:﹣4,﹣4.5,.13.(3分)直接写出下列方程的解:①=﹣+2=1②﹣=6=﹣18③=2=0.【解答】解:①移项得,+=2,合并同类项得,2=2,系数化为1得,=1;②方程两边都乘以﹣3,系数化为1得,=﹣18;③移项得,﹣2=0,合并同类项得,﹣=0,系数化为1得,=0.故答案为:①=1;②=﹣18;③=0.14.(3分)把一根木条固定在墙上,至少要钉2根钉子,这是根据过两点有且只有一条直线.【解答】解:在墙上固定一根木条至少需要两根钉子,依据的数学道理是过两点有且只有一条直线或两点确定一条直线.15.(3分)若3 070 000=3.07×10,则=6.【解答】解:∵3 070 000=3.07×106=3.07×10,∴=6.16.(3分)如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=155度.【解答】解:∵点A、O、B在一条直线上,∴∠COB=180°﹣∠AOC=180°﹣50°=130°,∵OD平分∠AOC,∴∠COD=×50°=25°,∴∠BOD=∠COB+∠COD=130°+25°=155°.故答案为:155.17.(3分)一个角是70°,则这个角的余角为20度.【解答】解:∵一个角是70°,∴这个角的余角=90°﹣70°=20°.故答案为:20.18.(3分)某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T 恤的成本为160元.【解答】解:设成本为元,则获利为20%元,售价为0.8×240元,由题意得:+20%=0.8×240,解得:=160.答:这件T恤的成本为160元.故答案为160元.三、解答题(一)(本大题共21分)19.(8分)计算:(1)26﹣17+(﹣6)﹣33(2)﹣14×[3﹣(﹣3)2].【解答】解:(1)原式=26﹣17﹣6﹣33=26﹣56=﹣30;(2)原式=﹣1﹣×(﹣6)=﹣1+1=0.20.(8分)解方程:(1)4=5﹣5(2)﹣1=.【解答】解:(1)4=5﹣54﹣5=﹣5,则﹣=﹣5,解得:=5;(2)﹣1=去分母得:3(+2)﹣12=2(2﹣3),则3+6﹣12=4﹣6,3﹣4=﹣6﹣6+12,解得:=0.21.(5分)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.【解答】解:原式=2ab2﹣3a2b﹣2a2b﹣2ab2=﹣5a2b;当a=1,b=﹣2时,原式=﹣5×12×(﹣2)=10.四、解答题(二)(本大题共18分)22.(6分)一只船从甲码头到乙码头是顺流行驶,用了2小时;从乙码头返回到甲码头是逆流行驶,用了2.5小时.如果水流的速度是3千米/小时,求船在静水中的速度?【解答】解:设船在静水中的速度为m/h.2(+3)=2.5(﹣3)﹣0.5=﹣13.5=27.答:船在静水中的平均速度是27千米/小时.23.(6分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°(1)求∠AOB的度数;(2)∠COD的度数.【解答】解:(1)∵∠BOC=2∠AOC,∠AOC=40°,∴∠BOC=80°,∴∠AOB=∠BOC+∠AOC=120°;(2)∵OD平分∠AOB,∴∠AOD=∠AOB=60°,∴∠COD=∠AOD﹣∠AOC=20°.24.(6分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物元(>300).(1)请用含代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?,顾客在乙超市购物所付的费用为【解答】解:(1)设顾客在甲超市购物所付的费用为y甲y乙,0.8(﹣300)=0.8+60;y乙=200+0.85(﹣200)=0.85+30.根据题意得:y甲=300+(2)他应该去乙超市,理由如下:60=460,y乙=0.85+30=455,当=500时,y甲=0.8+∵460>455,∴他去乙超市划算.0.8+60=0.85+30,(3)令y甲=y乙,即解得:=600.答:李明购买600元的商品时,到两家超市购物所付的费用一样.五、解答题(三)(本大题共7分)25.(7分)如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是30.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?【解答】解:(1)OB=3OA=30.故B对应的数是30;(2)设经过秒,点M、点N分别到原点O的距离相等①点M、点N在点O两侧,则10﹣3=2,解得=2;②点M、点N重合,则3﹣10=2,解得=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等;(3)设经过y秒,恰好使AM=2BN.①点N在点B左侧,则3y=2(30﹣2y),解得y=,3×﹣10=;②点N在点B右侧,则3y=2(2y﹣30),解得y=60,3×60﹣10=170;即点M运动到或170位置时,恰好使AM=2BN.故答案为:30.。
2016-2017年广东省韶关市高二上学期数学期中试卷带答案(理科)
2016-2017学年广东省韶关市高二(上)期中数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)51.(5分)在△ABC中,A=60°,AB=2,且△ABC的面积S△ABC=,则边BC的长为()A.B.3 C.D.72.(5分)设命题p:对∀x∈R+,e x>lnx,则¬p为()A.∃x 0∈R+,e<lnx0B.∀x∈R+,e^x<lnxC.∃x0∈R+,e≤lnx0D.∀x∈R+,e^x≤lnx3.(5分)已知a、b、c满足c<b<a,且ac<0,那么下列选项中一定不成立的()A.ab>ac B.c(b﹣a)<0 C.cb2≤ab2D.ac(a﹣c)<04.(5分)当x>3时,不等式x+≥a恒成立,则实数a的取值范围是()A.(﹣∞,3]B.[3,+∞)C.[,+∞)D.(﹣∞,]5.(5分)已知等差数列{a n}的前n项和为S n,满足S5=S9,且a1>0.则S n中最大的是()A.S6B.S7C.S8D.S156.(5分)2x2﹣5x﹣3<0的一个必要不充分条件是()A.﹣<x<3 B.﹣<x<0 C.﹣3<x<D.﹣1<x<67.(5分)下列命题中,假命题是()A.“π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期”B.“m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充分不必要条件C.“若a≤b,则2a≤2b﹣1”的否命题D.“任意a∈(0,+∞),函数y=a x在定义域内单调递增”的否定8.(5分)已知x,y满足约束条件,若z=ax+y的最大值为4,则a=()A.3 B.2 C.﹣2 D.﹣39.(5分)数列{a n}足a1=2,a2=1,并且,则数列{a n}的第100项为()A.B. C. D.10.(5分)已知命题p:“∀x∈[1,2],x2﹣a≥0”,命题q:“∃x∈R,x2+2ax+2﹣a=0”,若命题“p∧q”是真命题,则实数a的取值范围是()A.(﹣∞,﹣2]∪{1}B.(﹣∞,﹣2]∪[1,2]C.[1,+∞)D.[﹣2,1]11.(5分)在△ABC中,角A,B,C所对边长分别为a,b,c,若a2+b2=2c2,则cosC的最小值为()A.B.C.D.12.(5分)定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{a n},{f(a n)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)=;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为()A.①②B.③④C.①③D.②④二、填空题(每小题5分,共20分).13.(5分)若直线+=1(a>0,b>0)过点(1,1),则a+b的最小值为.14.(5分)若在△ABC中,∠A=60°,b=1,S△ABC=,则=.15.(5分)已知等比数列{a n}的首项a1=1公比q=2,则log2a1+log2a2+…+log2a11=.16.(5分)已知点A(a,b)与点B(1,0)在直线3x﹣4y+10=0的两侧,给出下列说法:①3a﹣4b+10>0;②当a>0时,a+b有最小值,无最大值;③>2;④当a>0且a≠1,b>0时,的取值范围为(﹣∞,﹣)∪(,+∞).其中,所有正确说法的序号是.三.解答题(共70分)17.(10分)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.18.(12分)设命题p:实数x满足x2﹣4ax+3a2<0,命题q:实数x满足|x﹣3|<1.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;(Ⅱ)若a>0,且¬p是¬q的充分不必要条件,求实数a的取值范围.19.(12分)设数列{a n}的前n项和为S n,a1=1,且对任意正整数n,点(a n+1,S n)在直线2x+y﹣2=0上.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)是否存在实数λ,使得数列{S n+λ•n+}为等差数列?若存在,求出λ的值;若不存在,则说明理由.20.(12分)设函数f(x)=mx2﹣mx﹣1.(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;(2)对于x∈[1,3],f(x)<﹣m+5恒成立,求m的取值范围.21.(12分)已知数列{a n}的首项,.(1)证明:数列是等比数列;(2)求数列的前n项和为S n.22.(12分)设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)f(1)>0,求证:(Ⅰ)方程f(x)=0有实根.(Ⅱ)﹣2<<﹣1;(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则≤|x1﹣x2|<.2016-2017学年广东省韶关市高二(上)期中数学试卷(理科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)51.(5分)在△ABC中,A=60°,AB=2,且△ABC的面积S△ABC=,则边BC的长为()A.B.3 C.D.7【解答】解:∵=sin60°=,∴AC=1,△ABC中,由余弦定理可得BC==,故选:A.2.(5分)设命题p:对∀x∈R+,e x>lnx,则¬p为()A.∃x0∈R+,e<lnx0B.∀x∈R+,e^x<lnxC.∃x0∈R+,e≤lnx0D.∀x∈R+,e^x≤lnx【解答】解:因为全称命题的否定是特称命题,所以命题p:对∀x∈R+,e x>lnx,则¬p为:∃x0∈R+,e≤lnx0.故选:C.3.(5分)已知a、b、c满足c<b<a,且ac<0,那么下列选项中一定不成立的()A.ab>ac B.c(b﹣a)<0 C.cb2≤ab2D.ac(a﹣c)<0【解答】解:∵c<b<a,且ac<0,∴c<0,a>0,b﹣a<0;∴ab>ac,cb2≤ab2,c(b﹣a)>0;ac(a﹣c)<0;故选:B.4.(5分)当x>3时,不等式x+≥a恒成立,则实数a的取值范围是()A.(﹣∞,3]B.[3,+∞)C.[,+∞)D.(﹣∞,]【解答】解:解:∵x>3∴x﹣1>2,∴y=(x﹣1)++1,设t=x﹣1,t>2y=t++1,在t∈(2,+∞)上单调递增,∴y>2=,∵不等式x+≥a恒成立,∴,a的取值范围是(﹣∞,],故选:D.5.(5分)已知等差数列{a n}的前n项和为S n,满足S5=S9,且a1>0.则S n中最大的是()A.S6B.S7C.S8D.S15【解答】解:∵等差数列{a n}的前n项和为S n,且满足S5=S9,∴S9﹣S5=a6+a7+a8+a9=2(a7+a8)=0,结合a1>0可得a7>0,a8<0,∴S n中最大的S7,故选:B.6.(5分)2x2﹣5x﹣3<0的一个必要不充分条件是()A.﹣<x<3 B.﹣<x<0 C.﹣3<x<D.﹣1<x<6【解答】解:2x2﹣5x﹣3<0的充要条件为对于A是2x2﹣5x﹣3<0的充要条件对于B,是2x2﹣5x﹣3<0的充分不必要条件对于C,2x2﹣5x﹣3<0的不充分不必要条件对于D,是2x2﹣5x﹣3<0的一个必要不充分条件故选:D.7.(5分)下列命题中,假命题是()A.“π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期”B.“m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充分不必要条件C.“若a≤b,则2a≤2b﹣1”的否命题D.“任意a∈(0,+∞),函数y=a x在定义域内单调递增”的否定【解答】解:A.π是函数y=sinx的一个周期是假命题,2π是函数y=cosx的一个周期是真命题,则“π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期”是真命题.B.当x≥1时,log2x≥0,则f(x)≥m,若函数f(x)=m+log2x(x≥1)不存在零点,则m>0,则“m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充要条件,故B是假命题,C.“若a≤b,则2a≤2b﹣1”的否命题是,“若a>b,则2a>2b﹣1”为真命题.∵a>b,∴2a>2b>2b﹣1,故C是真命题.D.“任意a∈(0,+∞),函数y=a x在定义域内单调递增”是假命题,则“任意a ∈(0,+∞),函数y=a x在定义域内单调递增”的否定是真命题,故选:B.8.(5分)已知x,y满足约束条件,若z=ax+y的最大值为4,则a=()A.3 B.2 C.﹣2 D.﹣3【解答】解:作出不等式组对应的平面区域如图:(阴影部分).则A(2,0),B(1,1),若z=ax+y过A时取得最大值为4,则2a=4,解得a=2,此时,目标函数为z=2x+y,即y=﹣2x+z,平移直线y=﹣2x+z,当直线经过A(2,0)时,截距最大,此时z最大为4,满足条件,若z=ax+y过B时取得最大值为4,则a+1=4,解得a=3,此时,目标函数为z=3x+y,即y=﹣3x+z,平移直线y=﹣3x+z,当直线经过A(2,0)时,截距最大,此时z最大为6,不满足条件,故a=2,故选:B.9.(5分)数列{a n}足a1=2,a2=1,并且,则数列{a n}的第100项为()A.B. C. D.【解答】解:由得,故为等差数列,且首项为,公差为1﹣=.故,∴,,故选:D.10.(5分)已知命题p:“∀x∈[1,2],x2﹣a≥0”,命题q:“∃x∈R,x2+2ax+2﹣a=0”,若命题“p∧q”是真命题,则实数a的取值范围是()A.(﹣∞,﹣2]∪{1}B.(﹣∞,﹣2]∪[1,2]C.[1,+∞)D.[﹣2,1]【解答】解:∵“p∧q”为真命题,∴得p、q为真,若p为真则有a≤(x2)min=1;若q为真则有△=4a2﹣4(2﹣a)≥0.故得a≤﹣2或a=1.故选:A.11.(5分)在△ABC中,角A,B,C所对边长分别为a,b,c,若a2+b2=2c2,则cosC的最小值为()A.B.C.D.【解答】解:因为a2+b2=2c2,所以由余弦定理可知,c2=2abcosC,cosC==.故选:C.12.(5分)定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{a n},{f(a n)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)=;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为()A.①②B.③④C.①③D.②④【解答】解:由等比数列性质知,),故正确;①=f2(a n+1②≠=f2(a n),故不正确;+1③==f2(a n+1),故正确;④f(a n)f(a n+2)=ln|a n|ln|a n+2|≠=f2(a n+1),故不正确;故选:C.二、填空题(每小题5分,共20分).13.(5分)若直线+=1(a>0,b>0)过点(1,1),则a+b的最小值为4.【解答】解:∵直线过点(1,1),∴+=1.则a+b=(a+b)=2++≥2+=4,当且仅当a=b=2时取等号.故答案为:4.14.(5分)若在△ABC中,∠A=60°,b=1,S△ABC=,则=.【解答】解:由∠A=60°,得到sinA=,cosA=,又b=1,S△ABC=,∴bcsinA=×1×c×=,解得c=4,根据余弦定理得:a2=b2+c2﹣2bccosA=1+16﹣4=13,解得a=,根据正弦定理====,则=.故答案为:15.(5分)已知等比数列{a n}的首项a1=1公比q=2,则log2a1+log2a2+…+log2a11= 55.【解答】解:∵等比数列{a n}的首项a1=1公比q=2,∴a6=a1q5=25,又a1•a11=a2•a10=…=a5•a7=,∴a1•a2•…•a11=,∴log2a1+log2a2+…+log2a11=log2(a1•a2•…•a11)=log2=11log 2a6=11log225=55.故答案为:55.16.(5分)已知点A(a,b)与点B(1,0)在直线3x﹣4y+10=0的两侧,给出下列说法:①3a﹣4b+10>0;②当a>0时,a+b有最小值,无最大值;③>2;④当a>0且a≠1,b>0时,的取值范围为(﹣∞,﹣)∪(,+∞).其中,所有正确说法的序号是③④.【解答】解:∵点A(a,b)与点B(1,0)在直线3x﹣4y+10=0的两侧,故点A(a,b)在如图所示的平面区域内故3a﹣4b+10<0,即①错误;当a>0时,a+b>,a+b即无最小值,也无最大值,故②错误;设原点到直线3x﹣4y+10=0的距离为d,则d==2,则>d=2,故③正确;当a>0且a≠1,b>0时,表示点A(a,b)与B(1,0)连线的斜率∵当a=0,b=时,=﹣,又∵直线3x﹣4y+10=0的斜率为故的取值范围为(﹣∞,﹣)∪(,+∞),故④正确;故答案为:③④三.解答题(共70分)17.(10分)△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.【解答】解:(Ⅰ)∵在△ABC中,0<C<π,∴sinC≠0已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,整理得:2cosCsin(A+B)=sinC,即2cosCsin(π﹣(A+B))=sinC2cosCsinC=sinC∴cosC=,∴C=;(Ⅱ)由余弦定理得7=a2+b2﹣2ab•,∴(a+b)2﹣3ab=7,∵S=absinC=ab=,∴ab=6,∴(a+b)2﹣18=7,∴a+b=5,∴△ABC的周长为5+.18.(12分)设命题p:实数x满足x2﹣4ax+3a2<0,命题q:实数x满足|x﹣3|<1.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;(Ⅱ)若a>0,且¬p是¬q的充分不必要条件,求实数a的取值范围.【解答】解:(Ⅰ)由x2﹣4ax+3a2<0得(x﹣3a)(x﹣a)<0当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.由|x﹣3|≤1,得﹣1≤x﹣3≤1,得2≤x≤4,即q为真时实数x的取值范围是2≤x≤4,若p∧q为真,则p真且q真,所以实数x的取值范围是2≤x<3.(Ⅱ)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q⇏¬p,设A={x|¬p},B={x|¬q},则A⊊B,又A={x|¬p}={x|x≤a或x≥3a},B={x|¬q}={x≤2或x>3},则0<a≤2,且3a>3,所以实数a的取值范围是1<a≤2.19.(12分)设数列{a n}的前n项和为S n,a1=1,且对任意正整数n,点(a n+1,S n)在直线2x+y﹣2=0上.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)是否存在实数λ,使得数列{S n+λ•n+}为等差数列?若存在,求出λ的值;若不存在,则说明理由.【解答】解:(Ⅰ)∵点(a n+1,S n)在直线2x+y﹣2=0上,∴2a n+1+S n ﹣2=0.①n≥2时,2a n+s n﹣1﹣2=0.②①─②得2a n+1﹣2a n+a n=0,∴=(n≥2).再由a1=1,可得a2=.∴{a n}是首项为1,公比为的等比数列,∴a n =.(Ⅱ)由(Ⅰ)可得s n==2﹣.若数列{S n+λ•n+}为等差数列,则s1+λ+,s2+2λ+,s3+3λ+成等差数列,∴2(s 2+2λ+)=(s1+λ+)+(s3+3λ+),解得λ=2.又λ=2时,S n+λ•n+=2n+2,显然{2n+2}成等差数列,故存在实数λ=2,使得数列{S n+λ•n+}成等差数列.20.(12分)设函数f(x)=mx2﹣mx﹣1.(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;(2)对于x∈[1,3],f(x)<﹣m+5恒成立,求m的取值范围.【解答】解:(1)由题意,mx2﹣mx﹣1<0对任意实数x恒成立,若m=0,显然﹣1<0成立;若m≠0,则,解得﹣4<m<0.所以﹣4<m≤0.(2)由题意,f(x)<﹣m+5,即m(x2﹣x+1)<6因为x2﹣x+1>0对一切实数恒成立,所以m<在x∈[1,3]上恒成立.因为函数y=x2﹣x+1在x∈[1,3]上的最大值为7,所以只需m<即可.所以m的取值范围是{m|m<}.21.(12分)已知数列{a n}的首项,.(1)证明:数列是等比数列;(2)求数列的前n项和为S n.【解答】(1)证明:∵,∴,∴,又,∴,∴数列是以为首项,为公比的等比数列;(2)解:由(1)得,,即,∴设,①则,②由①﹣②得:,∴.又.∴数列的前n项和.22.(12分)设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)f(1)>0,求证:(Ⅰ)方程f(x)=0有实根.(Ⅱ)﹣2<<﹣1;(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则≤|x1﹣x2|<.【解答】证明:(Ⅰ)若a=0,则b=﹣c,f(0)f(1)=c(3a+2b+c)=﹣c2≤0,与已知矛盾,所以a≠0.方程3ax2+2bx+c=0的判别式△=4(b2﹣3ac),由条件a +b +c=0,消去b ,得△=4(a 2+c 2﹣ac )=故方程f (x )=0有实根. (Ⅱ)由条件,知,, 所以(x 1﹣x 2)2=(x 1+x 2)2﹣4x 1x 2=.因为,所以故赠送初中数学几何模型【模型二】半角型:图形特征:45°4321A1FDAB正方形ABCD 中,∠EAF =45° ∠1=12∠BAD 推导说明:1.1在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且∠FAE =45°,求证:EF =BE +DFE-a1.2在正方形ABCD中,点E、F分别在BC、CD上,且EF=BE+DF,求证:∠FAE=45°E-aa B E挖掘图形特征:a+bx-aa 45°DBa+b-a45°A运用举例:1.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM(2)当AE=1时,求EF的长.E2.如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,求△AMN的周长.ND CABM3.如图,梯形ABCD中,AD∥BC,∠C=90°,BC=CD=2AD=4,E为线段CD上一点,∠ABE=45°.(1)求线段AB的长;(2)动点P从B出发,沿射线..BE运动,速度为1单位/秒,设运动时间为t,则t为何值时,△ABP为等腰三角形;(3)求AE-CE的值.变式及结论:4.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图1),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图2),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图3),请你直接写出线段EF,BE,DF之间的数量关系.ABFEDCF。
广东省韶关市乐昌市2016-2017学年八年级(上)期中数学试卷(解析版)
2016-2017学年广东省韶关市乐昌市八年级(上)期中数学试卷一、选择题(共10小题,每小题2分,满分20分)1.在△ABC中,∠A=30°,∠B=60°,则∠C=()A.30°B.45°C.60°D.90°2.已知三角形的两边长分别是5、7,则第三边长a的取值范围是()A.2<a<12 B.2≤a≤12 C.a>2 D.a<123.下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.2,4,5 D.1,7,94.如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=()A.10°B.15°C.20°D.30°5.观察下列图形,是轴对称图形的是()A.B.C.D.6.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定7.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN 的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN8.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为()A.1 B.2 C.3 D.49.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为()A.55°B.65°C.75°D.85°10.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是()A.AD=AE B.DB=EC C.∠ADE=∠AED D.DE=BC二、填空题(共6小题,每小题3分,满分18分)11.线段是轴对称图形,它的对称轴有条.12.一个多边形的内角和是720°,这个多边形的边数是.13.已知点A(3,1),则点A关于x轴的对称点A1的坐标是.14.正△ABC的两条角平分线BD和CE交于点I,则∠BIC等于.15.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是.16.如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在图5中,互不重叠的三角形共有个.三、解答题(共9小题,满分62分)17.如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.18.如图,在△ABC中,AB=AC.(1)利用尺规作图法作边BC的高AD,垂足为D,(要求:保留作图痕迹,不写作法).(2)求证:BD=CD.19.如图.(1)求图形中的x的值;(2)求:∠A、∠B、∠C、∠D的度数.20.如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1B1C1.21.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.22.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.(1)求证:△ADC≌△CEB.(2)AD=6cm,DE=4cm,求BE的长度.23.如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.24.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.25.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.2016-2017学年广东省韶关市乐昌市八年级(上)期中数学试卷参考答案与试题解析一、选择题(共10小题,每小题2分,满分20分)1.在△ABC中,∠A=30°,∠B=60°,则∠C=()A.30°B.45°C.60°D.90°【考点】三角形内角和定理.【分析】三角形内角和是180°,据此进行计算即可.【解答】解:∵在△ABC中,∠A=30°,∠B=60°,∴∠C=180°﹣30°﹣60°=90°,故选(D)2.已知三角形的两边长分别是5、7,则第三边长a的取值范围是()A.2<a<12 B.2≤a≤12 C.a>2 D.a<12【考点】三角形三边关系.【分析】根据三角形的第三边大于两边之差小于两边之和,即可解决问题.【解答】解:∵三角形的第三边大于两边之差小于两边之和,∴三角形的两边长分别是5、7,则第三边长a的取值范围是2<a<12.故选A.3.下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.2,4,5 D.1,7,9【考点】三角形三边关系.【分析】根据两边之和大于第三边即可判断.【解答】解:A、错误.因为3+4<8.B、错误.因为5+6=11.C、正确.因为2+4>5.D、错误.因为1+7<9.故选C.4.如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=()A.10°B.15°C.20°D.30°【考点】等腰三角形的性质.【分析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+22°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论.【解答】解:∵∠ADC是△ABD的外角,∴∠ADC=∠B+∠BAD=∠B+20°,∵∠AED是△CDE的外角,∴∠AED=∠C+∠EDC,∵∠B=∠C,∠ADE=∠AED,∴∠C+∠EDC=∠ADC﹣∠EDC=∠B+20°﹣∠EDC,解得∠EDC=10°.故选A.5.观察下列图形,是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.故选A.6.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定【考点】三角形的角平分线、中线和高.【分析】根据三角形的高的特点对选项进行一一分析,即可得出答案.【解答】解:A、锐角三角形,三条高线交点在三角形内,故错误;B、钝角三角形,三条高线不会交于一个顶点,故错误;C、直角三角形的直角所在的顶点正好是三条高线的交点,可以得出这个三角形是直角三角形,故正确;D、能确定C正确,故错误.故选:C.7.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN 的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN【考点】全等三角形的判定.【分析】根据普通三角形全等的判定定理,有AAS、SSS、ASA、SAS四种.逐条验证.【解答】解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故B 选项符合题意;C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.故选:B.8.如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,若点P到AC的距离为3,则点P到AB的距离为()A.1 B.2 C.3 D.4【考点】角平分线的性质;三角形的外角性质.【分析】过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,根据角平分线性质得出PQ=PR,即可得出答案.【解答】解:过P作PQ⊥AC于Q,PW⊥BC于W,PR⊥AB于R,∵△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P,∴PQ=PW,PW=PR,∴PR=PQ,∵点P到AC的距离为3,∴PQ=PR=3,则点P到AB的距离为3,故选C.9.如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为()A.55°B.65°C.75°D.85°【考点】轴对称的性质.【分析】根据三角形的内角和等于180°求出∠BAC的度数,再根据轴对称的性质可得∠DAC=∠BAC.【解答】解:∵∠BCA=35°,∠B=80°,∴∠BAC=180°﹣∠BCA﹣∠B=180°﹣35°﹣80°=65°,∵△ABC与△ADC关于AC所在的直线对称,∴∠DAC=∠BAC=65°.故选B.10.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是()A.AD=AE B.DB=EC C.∠ADE=∠AED D.DE=BC【考点】等腰三角形的性质;平行线的性质.【分析】由DE与BC平行,得到三角形ADE与三角形ABC相似,由相似得比例,根据AB=AC,得到AD=AE,进而确定出DB=EC,再由两直线平行同位角相等,以及等腰三角形的底角相等,等量代换得到∠ADE=∠AED,而DE不一定为中位线,即DE不一定为BC的一半,即可得到正确选项.【解答】解:∵DE∥BC,∴=,∠ADE=∠B,∵AB=AC,∴AD=AE,DB=EC,∠B=∠C,∴∠ADE=∠AED,而DE不一定等于BC,故选D.二、填空题(共6小题,每小题3分,满分18分)11.线段是轴对称图形,它的对称轴有2条.【考点】轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:线段是轴对称图形,它的对称轴有2条.故答案为:2.12.一个多边形的内角和是720°,这个多边形的边数是6.【考点】多边形内角与外角.【分析】根据内角和定理180°•(n﹣2)即可求得.【解答】解:∵多边形的内角和公式为(n﹣2)•180°,∴(n﹣2)×180°=720°,解得n=6,∴这个多边形的边数是6.故答案为:6.13.已知点A(3,1),则点A关于x轴的对称点A1的坐标是(3,﹣1).【考点】关于x轴、y轴对称的点的坐标.【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”求解即可.【解答】解:点A(3,1)关于x轴的对称点A1的坐标是(3,﹣1).故答案为:(3,﹣1).14.正△ABC的两条角平分线BD和CE交于点I,则∠BIC等于120°.【考点】等边三角形的性质.【分析】根据等边三角形性质得出∠ABC=∠ACB=60°,根据角平分线性质求出∠IBC和∠ICB,根据三角形的内角和定理求出即可.【解答】解:∵△ABC是等边三角形,∴∠A=∠ABC=∠ACB=60°,∵BI平分∠ABC,CI平分∠ACB,∴∠IBC=∠ABC=30°,∠ICB=∠ACB=30°,∴∠BIC=180°﹣30°﹣30°=120°,故答案为:120°.15.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是利用三角形的稳定性.【考点】三角形的稳定性.【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.【解答】解:这样做的道理是利用三角形的稳定性.16.如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在图5中,互不重叠的三角形共有16个.【考点】规律型:图形的变化类.【分析】根据图形结合题目所给数据寻找规律,发现图2比图1多3个互不重叠的三角形,即4+3个;图3比图2多3个互不重叠的三角形,即4+3×2个;依此类推,图n中互不重叠的三角形的个数是4+3(n﹣1),即3n+1个.【解答】解:图1中互不重叠的三角形有4个图2中互不重叠的三角形有7=4+3个图3中互不重叠的三角形有10=4+3×2个按此规律图n中互不重叠的三角形有4+3(n﹣1)=3n+1个,∴当n=5时,3n+1=16,故答案为:16.三、解答题(共9小题,满分62分)17.如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.【考点】全等三角形的判定与性质.【分析】根据全等三角形的判定和性质即可得到结论.【解答】证明:在△ACB和△ADB中,,∴△ACB≌△ADB(AAS),∴BC=BD.18.如图,在△ABC中,AB=AC.(1)利用尺规作图法作边BC的高AD,垂足为D,(要求:保留作图痕迹,不写作法).(2)求证:BD=CD.【考点】作图—基本作图;等腰三角形的性质.【分析】(1)分别以点BC为圆心,以大于BC为半径画圆,两圆相交于点E,连接AE,交线段于点D,则点D即为垂足;(2)根据HL定理得出△ABD≌△ACD,进而可得出结论.【解答】(1)解:如图,点D即为所求;(2)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.在△ABD与△ACD中,∵,∴△ABD≌△ACD(HL),∴BD=CD.19.如图.(1)求图形中的x的值;(2)求:∠A、∠B、∠C、∠D的度数.【考点】多边形内角与外角.【分析】(1)根据四边形内角和等于360°列出方程求解即可;(2)把x的值代入计算即可求解.【解答】解:(1)依题意有:3x+3x+4x+2x=360°,解得x=30°;(2)∠A=∠B=3×30°=90°,∠C=2×30°=60°,∠D=4×30°=120°.20.如图,在平面直角坐标系xoy中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴的对称图形△A1B1C1.(2)写出点A1,B1,C1的坐标(直接写答案).A1(﹣1,2)B1(﹣3,1)C1(2,﹣1).【考点】作图-轴对称变换;点的坐标.【分析】(1)利用轴对称性质,作出A、B、C关于y轴的对称点A1、B1、C1,顺次连接A1B1、B1C1、C1A1,即得到关于y轴对称的△A1B1C1;(2)根据点关于y轴对称的性质,纵坐标相同,横坐标互为相反数,即可求出A1、B1、C1各点的坐标.【解答】解:(1)所作图形如下所示:(2)A1,B1,C1的坐标分别为:(﹣1,2),(﹣3,1),(2,﹣1).故答案为:(﹣1,2),(﹣3,1),(2,﹣1).21.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.(1)求∠DAC的度数;(2)求证:DC=AB.【考点】等腰三角形的性质.【分析】(1)由AB=AC,根据等腰三角形的两底角相等得到∠B=∠C=30°,再根据三角形的内角和定理可计算出∠BAC=120°,而∠DAB=45°,则∠DAC=∠BAC﹣∠DAB=120°﹣45°;(2)根据三角形外角性质得到∠ADC=∠B+∠DAB=75°,而由(1)得到∠DAC=75°,再根据等腰三角形的判定可得DC=AC,这样即可得到结论.【解答】(1)解:∵AB=AC,∴∠B=∠C=30°,∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,∵∠DAB=45°,∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.22.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.(1)求证:△ADC≌△CEB.(2)AD=6cm,DE=4cm,求BE的长度.【考点】全等三角形的判定与性质;等腰直角三角形.【分析】(1)求出∠E=∠ADC=∠ACB=90°,∠CAD=∠BCE,根据AAS推出即可;(2)根据全等三角形的性质求出CE=AD=6cm,BE=CD,即可得出答案.【解答】(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,∴∠E=∠ADC=∠ACB=90°,∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,∴∠CAD=∠BCE,在△ADC和△CEB中∴△ADC≌△CEB(AAS);(2)解:∵△ADC≌△CEB,AD=6cm,∴CE=AD=6cm,BE=CD,∵DE=4cm,∴BE=CD=CE﹣DE=6cm﹣4cm=2cm.23.如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.【考点】全等三角形的判定与性质.【分析】只要以其中三个作为条件,能够得出另一个结论正确即可,下边以①③为条件,②为结论为例.【解答】解:如:AD=BC,BE∥AF,则DE=CF;理由是:∵BE∥AF,∴∠AFD=∠BEC,在△ADF和△BEC中,∵,∴△ADF≌△BCE,∴DF=CE,∴DF﹣EF=CE﹣EF,∴DE=CF.24.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.求证:(1)CE=AC+DC;(2)∠ECD=60°.【考点】等边三角形的性质;对顶角、邻补角;全等三角形的判定与性质.【分析】(1)根据△ABC、△ADE都是等边三角形,得到AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,推出∠BAD=∠CAE,得到△BAD≌△CAE,根据全等三角形的性质得到BD=EC,即可推出答案;(2)由(1)知:△BAD≌△CAE,根据平角的意义即可求出∠ECD的度数.【解答】证明:(1)∵△ABC、△ADE是等边三角形,∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,∴∠BAC+∠CAD=∠DAE+∠CAD,即:∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=EC,∵BD=BC+CD=AC+CD,∴CE=BD=AC+CD;(2)由(1)知:△BAD≌△CAE,∴∠ACE=∠ABD=60°,∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,∴∠ECD=60°.25.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.【考点】全等三角形的判定与性质.【分析】(1)由BE垂直于AC,CF垂直于AB,利用垂直的定义得∠HFB=∠HEC,由得对顶角相等得∠BHF=∠CHE,所以∠ABD=∠ACG.再由AB=CG,BD=AC,利用SAS可得出三角形ABD与三角形ACG全等,由全等三角形的对应边相等可得出AD=AG,(2)利用全等得出∠ADB=∠GAC,再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE,又∠GAC=∠GAD+∠DAE,利用等量代换可得出∠AED=∠GAD=90°,即AG与AD垂直.【解答】(1)证明:∵BE⊥AC,CF⊥AB,∴∠HFB=∠HEC=90°,又∵∠BHF=∠CHE,∴∠ABD=∠ACG,在△ABD和△GCA中,∴△ABD≌△GCA(SAS),∴AD=GA(全等三角形的对应边相等);(2)位置关系是AD⊥GA,理由为:∵△ABD≌△GCA,∴∠ADB=∠GAC,又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,∴∠AED=∠GAD=90°,∴AD⊥GA.2017年2月15日。
韶关市乐昌市七年级上册期末数学试卷(有答案)【精编】.doc
广东省韶关市乐昌市七年级(上)期末数学试卷一、选择题(每小题3分,共30分)1.(3分)﹣5的倒数是()A.5 B.﹣5 C.D.﹣2.(3分)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱3.(3分)如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为()A.2cm B.4cm C.8cm D.13cm4.(3分)如果代数式与ab是同类项,那么m的值是()A.0 B.1 C.D.35.(3分)如图,在数轴上点A表示的数最可能是()A.﹣2 B.﹣2.5 C.﹣3.5 D.﹣2.96.(3分)当=3,y=2时,代数式的值是()A.B.2 C.0 D.37.(3分)下列式子中,是一元一次方程的有()A.+5=2 B.2﹣8=2+7 C.5﹣3 D.﹣y=48.(3分)用代数式表示“a的3倍与b的差的平方”,正确的是()A.3(a﹣b)2B.(3a﹣b)2C.3a﹣b2D.(a﹣3b)29.(3分)数a,b在数轴上的位置如图所示,则a+b是()A.正数B.零C.负数D.都有可能10.(3分)观察下列算式并总结规律:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律,写出22016的末位数字是()A.2 B.4 C.6 D.8二、填空题(每小题3分,共24分)11.(3分)计算:①﹣2+1=②4﹣(﹣4)=③×()=2.12.(3分)计算:①﹣2=②=③﹣+2=.13.(3分)直接写出下列方程的解:①=﹣+2②﹣=6③=2.14.(3分)把一根木条固定在墙上,至少要钉2根钉子,这是根据.15.(3分)若3 070 000=3.07×10,则=.16.(3分)如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=度.17.(3分)一个角是70°,则这个角的余角为度.18.(3分)某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T恤的成本为.三、解答题(一)(本大题共21分)19.(8分)计算:(1)26﹣17+(﹣6)﹣33(2)﹣14×[3﹣(﹣3)2].20.(8分)解方程:(1)4=5﹣5(2)﹣1=.21.(5分)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.四、解答题(二)(本大题共18分)22.(6分)一只船从甲码头到乙码头是顺流行驶,用了2小时;从乙码头返回到甲码头是逆流行驶,用了2.5小时.如果水流的速度是3千米/小时,求船在静水中的速度?23.(6分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°(1)求∠AOB的度数;(2)∠COD的度数.24.(6分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物元(>300).(1)请用含代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?五、解答题(三)(本大题共7分)25.(7分)如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?广东省韶关市乐昌市七年级(上)期末数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)﹣5的倒数是()A.5 B.﹣5 C.D.﹣【解答】解:﹣5的倒数是﹣.故选:D.2.(3分)一个几何体的表面展开图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱【解答】解:如图所示:这个几何体是四棱锥.故选:A.3.(3分)如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为()A.2cm B.4cm C.8cm D.13cm【解答】解:∵BC=3cm,BD=5cm,∴CD=BD﹣BC=2cm,∵D是AC的中点,∴AC=2CD=4cm,故选:B.4.(3分)如果代数式与ab是同类项,那么m的值是()A.0 B.1 C.D.3【解答】解:根据题意得:2m=1,解得:m=.故选C.5.(3分)如图,在数轴上点A表示的数最可能是()A.﹣2 B.﹣2.5 C.﹣3.5 D.﹣2.9【解答】解:∵点A表示的数在﹣3与﹣2中间,∴A、C、D三选项错误,B选项正确.故选:B.6.(3分)当=3,y=2时,代数式的值是()A.B.2 C.0 D.3【解答】解:==7.(3分)下列式子中,是一元一次方程的有()A.+5=2 B.2﹣8=2+7 C.5﹣3 D.﹣y=4【解答】解:A、是一元一次方程,故A正确;B、不是方程,故B错误;C、是多项式,故C错误;D、二元一次方程,故D错误;故选:A.8.(3分)用代数式表示“a的3倍与b的差的平方”,正确的是()A.3(a﹣b)2B.(3a﹣b)2C.3a﹣b2D.(a﹣3b)2【解答】解:∵a的3倍与b的差为3a﹣b,∴差的平方为(3a﹣b)2.故选B.9.(3分)数a,b在数轴上的位置如图所示,则a+b是()A.正数B.零C.负数D.都有可能【解答】解:由图,可知:a<0,b>0,|a|>|b|.则a+b<0.故选:C.10.(3分)观察下列算式并总结规律:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律,写出22016的末位数字是()A.2 B.4 C.6 D.8【解答】解:由21=2,22=4,23=8,24=16,…;可以发现他们的末尾数字是4个数一个循环,2,4,8,6,…∵2016÷4=504,∴22016的与24的末尾数字相同是6.故选:C.二、填空题(每小题3分,共24分)11.(3分)计算:①﹣2+1=﹣1②4﹣(﹣4)=8③×(﹣4)=2.【解答】解:①﹣2+1=﹣1②4﹣(﹣4)=8③×(﹣4)=2故答案为:﹣1、8、﹣4.12.(3分)计算:①﹣2=﹣4②=﹣4.5③﹣+2=.【解答】解:①﹣2=﹣4;②=﹣4.5;③﹣+2=.故答案为:﹣4,﹣4.5,.13.(3分)直接写出下列方程的解:①=﹣+2=1②﹣=6=﹣18③=2=0.【解答】解:①移项得,+=2,合并同类项得,2=2,系数化为1得,=1;②方程两边都乘以﹣3,系数化为1得,=﹣18;③移项得,﹣2=0,合并同类项得,﹣=0,系数化为1得,=0.故答案为:①=1;②=﹣18;③=0.14.(3分)把一根木条固定在墙上,至少要钉2根钉子,这是根据过两点有且只有一条直线.【解答】解:在墙上固定一根木条至少需要两根钉子,依据的数学道理是过两点有且只有一条直线或两点确定一条直线.15.(3分)若3 070 000=3.07×10,则=6.【解答】解:∵3 070 000=3.07×106=3.07×10,∴=6.16.(3分)如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD= 155度.【解答】解:∵点A、O、B在一条直线上,∴∠COB=180°﹣∠AOC=180°﹣50°=130°,∵OD平分∠AOC,∴∠COD=×50°=25°,∴∠BOD=∠COB+∠COD=130°+25°=155°.故答案为:155.17.(3分)一个角是70°,则这个角的余角为20度.【解答】解:∵一个角是70°,∴这个角的余角=90°﹣70°=20°.故答案为:20.18.(3分)某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,则这件T恤的成本为160元.【解答】解:设成本为元,则获利为20%元,售价为0.8×240元,由题意得:+20%=0.8×240,解得:=160.答:这件T恤的成本为160元.故答案为160元.三、解答题(一)(本大题共21分)19.(8分)计算:(1)26﹣17+(﹣6)﹣33(2)﹣14×[3﹣(﹣3)2].【解答】解:(1)原式=26﹣17﹣6﹣33=26﹣56=﹣30;(2)原式=﹣1﹣×(﹣6)=﹣1+1=0.20.(8分)解方程:(1)4=5﹣5(2)﹣1=.【解答】解:(1)4=5﹣54﹣5=﹣5,则﹣=﹣5,解得:=5;(2)﹣1=去分母得:3(+2)﹣12=2(2﹣3),则3+6﹣12=4﹣6,3﹣4=﹣6﹣6+12,解得:=0.21.(5分)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.【解答】解:原式=2ab2﹣3a2b﹣2a2b﹣2ab2=﹣5a2b;当a=1,b=﹣2时,原式=﹣5×12×(﹣2)=10.四、解答题(二)(本大题共18分)22.(6分)一只船从甲码头到乙码头是顺流行驶,用了2小时;从乙码头返回到甲码头是逆流行驶,用了2.5小时.如果水流的速度是3千米/小时,求船在静水中的速度?【解答】解:设船在静水中的速度为m/h.2(+3)=2.5(﹣3)﹣0.5=﹣13.5=27.答:船在静水中的平均速度是27千米/小时.23.(6分)如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠AOC=40°(1)求∠AOB的度数;(2)∠COD的度数.【解答】解:(1)∵∠BOC=2∠AOC,∠AOC=40°,∴∠BOC=80°,∴∠AOB=∠BOC+∠AOC=120°;(2)∵OD平分∠AOB,∴∠AOD=∠AOB=60°,∴∠COD=∠AOD﹣∠AOC=20°.24.(6分)甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物元(>300).(1)请用含代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?,顾客在乙超市购物所付的费用【解答】解:(1)设顾客在甲超市购物所付的费用为y甲为y,乙0.8(﹣300)=0.8+60;y乙=200+0.85(﹣200)=0.85+30.根据题意得:y甲=300+(2)他应该去乙超市,理由如下:60=460,y乙=0.85+30=455,当=500时,y甲=0.8+∵460>455,∴他去乙超市划算.0.8+60=0.85+30,(3)令y甲=y乙,即解得:=600.答:李明购买600元的商品时,到两家超市购物所付的费用一样.五、解答题(三)(本大题共7分)25.(7分)如图,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是30.(2)经过几秒,点M、点N分别到原点O的距离相等?(3)当点M运动到什么位置时,恰好使AM=2BN?【解答】解:(1)OB=3OA=30.故B对应的数是30;(2)设经过秒,点M、点N分别到原点O的距离相等①点M、点N在点O两侧,则10﹣3=2,解得=2;②点M、点N重合,则3﹣10=2,解得=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等;(3)设经过y秒,恰好使AM=2BN.①点N在点B左侧,则3y=2(30﹣2y),解得y=,3×﹣10=;②点N在点B右侧,则3y=2(2y﹣30),解得y=60,3×60﹣10=170;即点M运动到或170位置时,恰好使AM=2BN.故答案为:30.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页(共13页) 2016-2017学年广东省韶关市乐昌市七年级(上)期中数学试卷 一、选择题:(每小题2分,共20分) 1.(2分)下列各数:3,0,﹣10,0.58,﹣(﹣6),﹣|﹣9|,(﹣4)2 中,负数有( ) A.1个 B.2个 C.3个 D.4个 2.(2分)中国月球探测工程的“嫦娥一号”发射升空飞向月球,已知地球距离月球表面约为384 000千米,那么这个距离用科学记数法表示为( ) A.3.84×l04 千米 B.3.84×l05千米 C.3.84×l06千米 D.38.4×l04 千米 3.(2分)若a2=4,那么a=( ) A.2 B.﹣2 C.±2 D.±4 4.(2分)下列各对数中互为相反数的是( ) A.32 与﹣23 B.﹣23 与(﹣2)3
C.﹣32 与(﹣3)2 D.(﹣3×2)2与 23×(﹣3) 5.(2分)下列各式:①②a ③﹣5ab2 ④x+y ⑤0 ⑥,是单项式的有( ) A.2个 B.3个 C.4个 D.5个 6.(2分)某礼堂第一排有m个座位,后面每排比前一排多一个座位,则第20排有( )个座位. A.m+21 B.m+20 C.m+19 D.m+18 7.(2分)若3am﹣2b3与abn+1是同类项,则m+n=( ) A._3 B.3 C.5 D.﹣5 8.(2分)的系数与次数分别为( ) A.,7 B.,6 C.4π,6 D.,4 9.(2分)已知一个多项式与3x2+9x的和等于3x2+4x﹣l,则这个多项式是( ) 第2页(共13页)
A.﹣5x﹣1 B.5x+1 C.13x﹣l D.6x2+13x﹣1 10.(2分)规定“!”是一种运算符号, 其中1!=1, 2!=1×2, 3!=1×2×3, 4!=1×2×3×4,… 则的值为( ) A.2014 B.2015 C.2016 D.2017
二、填空题:(每小题3分,共30分) 11.(3分)小华的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作 万元. 12.(3分)﹣2的相反数是 . 13.(3分)已知:点A在数轴上的位置如图所示,点B也在数轴上,且A、B两点之间的距离是2,则点B表示的数是 .
14.(3分)比较大小:﹣ ﹣. 15.(3分)计算:|3.14﹣π|= . 16.(3分)用四舍五入法把4.036精确到百分位的近似数是 . 17.(3分)若|a﹣1|+(b+2)2=0,则a+b= . 18.(3分)请写出一个含有两个字母、系数为﹣2的二次单项式 . 19.(3分)绝对值不大于6的整数的和是 . 20.(3分)观察下列单项式:x,﹣2x2,3x3,﹣4x4,5x5,…按此规律,可以得到第n个单项式表示为 .
三、计算与化简:(每小题24分,共24分) 21.(24分)计算与化简: (1)8+(﹣)﹣5﹣(﹣0.25)
(2)(﹣81)÷×÷16 第3页(共13页)
(3)(﹣﹣)×(﹣60) (4)﹣32﹣×[5﹣(﹣3)2] (5)4a2+18b﹣15a2﹣12b (6)3(2a﹣4b)﹣2(3a+b)
四、解答题:(共26分) 22.(6分)先化简再求值2a2﹣[(ab﹣4a2)+8ab]﹣ab,其中a=1,b=. 23.(6分)若a、b互为相反数,c是最大的负整数,d是最小的正整数. 求(a+b)d+d﹣c的值. 24.(8分)某检修小组乘一辆检修车沿铁路检修,规定向东走为正,向西走为负,小组的出发地记为0,某天检修完毕时,行走记录(单位:千米)如下:+10,﹣2,+3,﹣1,+9,﹣3,﹣2,+11,+3,﹣4,+6. (1)问收工时,检修小组距出发地有多远?在东侧还是西侧? (2)若检修车每千米耗油2.8升,求从出发到收工共耗油多少升? 25.(6分)观察下列等式: 13=12
13+23=32 13+23+33=62 13+23+33+43=102… (1)根据观察得到规律写出:13+23+33+43+53═ . (2)根据观察得到规律写出13+23+33+43+…+1003= . (3)13+23+33+43+53+…+n3= . 第4页(共13页)
2016-2017学年广东省韶关市乐昌市七年级(上)期中数学试卷 参考答案与试题解析
一、选择题:(每小题2分,共20分) 1.(2分)下列各数:3,0,﹣10,0.58,﹣(﹣6),﹣|﹣9|,(﹣4)2 中,负数有( ) A.1个 B.2个 C.3个 D.4个 【解答】解:∵﹣(﹣6)=6,﹣|﹣9|=﹣9,(﹣4)2=16, ∴3,0,﹣10,0.58,﹣(﹣6),﹣|﹣9|,(﹣4)2 中,负数有2个: ﹣10,﹣|﹣9|. 故选:B.
2.(2分)中国月球探测工程的“嫦娥一号”发射升空飞向月球,已知地球距离月球表面约为384 000千米,那么这个距离用科学记数法表示为( ) A.3.84×l04 千米 B.3.84×l05千米 C.3.84×l06千米 D.38.4×l04 千米 【解答】解:384 000=3.84×105. 故选:B.
3.(2分)若a2=4,那么a=( ) A.2 B.﹣2 C.±2 D.±4 【解答】解:a2=4, a=±2, 故选:C.
4.(2分)下列各对数中互为相反数的是( ) A.32 与﹣23 B.﹣23 与(﹣2)3 C.﹣32 与(﹣3)2 D.(﹣3×2)2与 23×(﹣3) 第5页(共13页)
【解答】解:A、32=9,﹣23=﹣8,9与﹣8 不是相反数,故本选项错误; B、﹣23=﹣8,(﹣2)3=﹣8,﹣8=﹣8,故本选项错误; C、﹣32=﹣9,(﹣3)2=9,﹣9与9互为相反数,故本选项正确; D、(﹣3×2)2=36,23×(﹣3)=﹣24,36与﹣24不是相反数,故本选项错误; 故选:C.
5.(2分)下列各式:①②a ③﹣5ab2 ④x+y ⑤0 ⑥,是单项式的有( ) A.2个 B.3个 C.4个 D.5个 【解答】解:① 是分式; ②a是单项式; ③﹣5ab2 是单项式; x+y是多项式; ⑤0是单项式; ⑥是多项式, 故选:B.
6.(2分)某礼堂第一排有m个座位,后面每排比前一排多一个座位,则第20排有( )个座位. A.m+21 B.m+20 C.m+19 D.m+18 【解答】解:由题意可得, 第20排有:m+(20﹣1)=(m+19)(个), 故选:C.
7.(2分)若3am﹣2b3与abn+1是同类项,则m+n=( ) A._3 B.3 C.5 D.﹣5 【解答】解:∵3am﹣2b3与abn+1是同类项, ∴m﹣2=1,n+1=3, ∴m=3,n=2, 第6页(共13页)
∴m+n=3+2=5, 故选:C.
8.(2分)的系数与次数分别为( ) A.,7 B.,6 C.4π,6 D.,4 【解答】解:的系数为,次数为6. 故选:B.
9.(2分)已知一个多项式与3x2+9x的和等于3x2+4x﹣l,则这个多项式是( ) A.﹣5x﹣1 B.5x+1 C.13x﹣l D.6x2+13x﹣1 【解答】解:根据题意列得:(3x2+4x﹣1)﹣(3x2+9x)=3x2+4x+1﹣3x2﹣9x=﹣5x﹣1. 故选:A.
10.(2分)规定“!”是一种运算符号, 其中1!=1, 2!=1×2, 3!=1×2×3, 4!=1×2×3×4,… 则的值为( ) A.2014 B.2015 C.2016 D.2017 【解答】解:根据题中的新定义得:原式==2017, 故选:D.
二、填空题:(每小题3分,共30分) 11.(3分)小华的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作 ﹣2 万元. 第7页(共13页)
【解答】解:“正”和“负”相对, ∵存入3万元记作+3万元, ∴支取2万元应记作﹣2万元. 故答案为:﹣2.
12.(3分)﹣2的相反数是 2 . 【解答】解:﹣2的相反数是:﹣(﹣2)=2, 故答案为:2.
13.(3分)已知:点A在数轴上的位置如图所示,点B也在数轴上,且A、B两点之间的距离是2,则点B表示的数是 ﹣5或﹣1 .
【解答】解:由图知:A=﹣3, |A﹣B|=2, 得出B=﹣5或﹣1. 故答案为:﹣5或﹣1.
14.(3分)比较大小:﹣ < ﹣. 【解答】解:根据两个负数,绝对值大的反而小的规律得出:﹣<﹣.
15.(3分)计算:|3.14﹣π|= π﹣3.14 . 【解答】解:|3.14﹣π|=π﹣3.14, 故答案为:π﹣3.14.
16.(3分)用四舍五入法把4.036精确到百分位的近似数是 4.04 . 【解答】解:4.036≈4.04(精确到百分位). 故答案为4.04.
17.(3分)若|a﹣1|+(b+2)2=0,则a+b= ﹣1 .
