概率论与数理统计习题集及答案
浙大版概率论与数理统计习题集和试卷

浙大版概率论与数理统计习题集和试卷第一讲1.2,?,N1. 由盛有号码为的球的箱子中有放回的摸了n 次, 依次记其号码,求这些号码按严格上升次序排列的概率.(2)对任意凑在一起的40 人, 求他们中没有两人生日相同的概率.2r(2r,n)3. 从n 双不同的鞋子中任取只, 求下列事件的概率:r(1) (1) 没有成双的鞋子; (2) 只有一双鞋子; (3) 恰有二双鞋子; (4) 有双鞋子. 4. 从52 张的一副扑克牌中, 任取 5 张, 求下列事件的概率:(1)(1) 取得以A为打头的顺次同花色5张;(3)(2) 有 4 张同花色;(4)(3) 5 张同花色;(5)(4) 3 张同点数且另 2 张也同点数.思考题:1.( 分房、占位问题) 把n 个球随机地放入N 个不同的格子中,每个球落入各格子内的概率相同(设格子足够大,可以容纳任意多个球)。
1.I. 若这n 个球是可以区分的,求(1) 指定的n 个格子各有一球的概率;(2)有n 个格子各有一球的概率;若这n 个球是不可以区分的,求(1) 某一指定的盒子中恰有k 个球的概率;(2)恰好有m个空盒的概率。
2.取数问题) 从1-9 这九个数中有放回地依次取出五个数,求下列各事件的概率: (1) (1) 五个数全不同;(2)1 恰好出现二次;(3) 总和为10.第二讲1.在一张打方格的纸上投一枚直径为 1 的硬币, 问方格要多小时才能使硬币与线不相交的概率小于0.01?2.在某城市中共发行三种报纸: 甲、乙、丙。
在这个城市的居民中,订甲报(记为A)的有45%订乙报(记为B)的有35%订内报(记为C)的有30%同时订甲、乙两报(记为D)的有10%同时订甲、丙两报(记为E)的有8%同时订乙、丙两报(记为F)的有5%同时订三中报纸(记为G)的有3%.试表示下列事件,并求下述百分比:(1) 只订甲报的;(2) 只订甲、乙两报的;(3) 只订一种报纸的;(4) 正好订两种报纸的;(5) 至少订一种报纸的;(6) 不订任何报纸的.3.在线段[0,1] 上任意投三个点, 求0 到这三点的三条线段能构成三角形的概率.4. 设A, B, C, D 是四个事件, 似用它们表示下列事件:(1)(1) 四个事件至少发生一个;(2)(2) 四个事件恰好发生两个;(3)(3) A,B 都发生而C, D 不发生;(4)(4) 这四个事件都不发生;(5)(5)这四个事件至多发生一个;(6)(6)这四个事件至少发生两个;(7)(7)这四个事件至多发生两个.m(m,n)n5. 考试时共有张考签, 有个同学参加考试. 若被抽过的考签立即放回求在考试结束后, 至少有一张考签没有被抽到的概率.k(k,n)6. 在?3例5中, 求恰好有个人拿到自己的枪的概率.p,P(A),q,P(B),r,P(A,B)P(AB)P(AB)7.给定, 求及. 思考题l(l,a)1.( 蒲丰投针问题续)向画满间隔为a的平行线的桌面上任投一直径为的半圆形纸片, 求事件“纸片与某直线相交”的概率;第三讲nm1. 件产品中有件废品, 任取两件, 求:(1)(1) 在所取两件中至少有一件是废品的条件下, 另一件也是废品的概率;(2)(2) 在所取两件中至少有一件不是废品的条件下, 另一件是废品的概率.a(a,3)2. 袋中有只白球, b 只黑球, 甲乙丙三人依次从袋中取出一球(取后不放回). 试用全概率公式分别求甲乙丙各取得白球的概率.3.敌机被击中部位分成三部分: 在第一部分被击中一弹, 或第二部分被击中两弹, 或第三部分被击中三弹时, 敌机才能被击落. 其命中率与各部分面积成正比假如这三部分面积之比为0.1, 0.2, 0.7. 若已中两弹, 求敌机被击落的概率.4.甲乙两人从装有九个球, 其中三个是红球的盒子中, 依次摸一个球, 并且规定摸到红球的将受罚.(1)(1) 如果甲先摸, 他不受罚的概率有多大?(2)(2) 如果甲先摸并且没有受罚, 求乙也不受罚的的概率.(3)(3) 如果甲先摸并且受罚, 求乙不受罚的的概率.(4)(4) 乙先摸是否对甲有利?(5)(5) 如果甲先摸, 并且已知乙没有受罚, 求甲也不受罚的概率.A,B,AB,A,B5. 设事件A, B, C 相互独立, 求证: 也相互独立.思考题1.甲、乙两人轮流掷一均匀的骰子。
概率论与数理统计习题集答案

概率论与数理统计习题集答案【篇一:《概率论与数理统计》第三版__课后习题答案._】出下列随机试验的样本空间:(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;解:连续5 次都命中,至少要投5次以上,故?1??5,6,7,??;(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;解:?2??2,3,4,?11,12?;(3) 观察某医院一天内前来就诊的人数;解:医院一天内前来就诊的人数理论上可以从0到无穷,所以?3??0,1,2,?(4) 从编号为1,2,3,4,5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解:属于不放回抽样,故两件产品不会相同,编号必是一大一小,故: ?4??i,j??i?j?5?;(5) 检查两件产品是否合格;解:用0 表示合格, 1 表示不合格,则?5???0,0?,?0,1?,?1,0?,?1,1??;(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于t1, 最高气温不高于t2); 解:用x表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间,故: ?6??x,y?1?x?y?t2?; ???;(7) 在单位圆内任取两点, 观察这两点的距离;解:?7?x0?x?2?;(8) 在长为l的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.解:?8??x,y?x?0,y?0,x?y?l?;1.2(1) a 与b 都发生, 但c 不发生; ab;(2) a 发生, 且b 与c 至少有一个发生;a(b?c);(3) a,b,c 中至少有一个发生; a?b?c;??(4) a,b,c 中恰有一个发生;a?b?;(5) a,b,c 中至少有两个发生; ab?ac?bc;(6) a,b,c 中至多有一个发生;??;(7) a;b;c 中至多有两个发生;abc(8) a,b,c 中恰有两个发生.bc?ac?ab ;注意:此类题目答案一般不唯一,有不同的表示方式。
概率论和数理统计课后习题答案解析
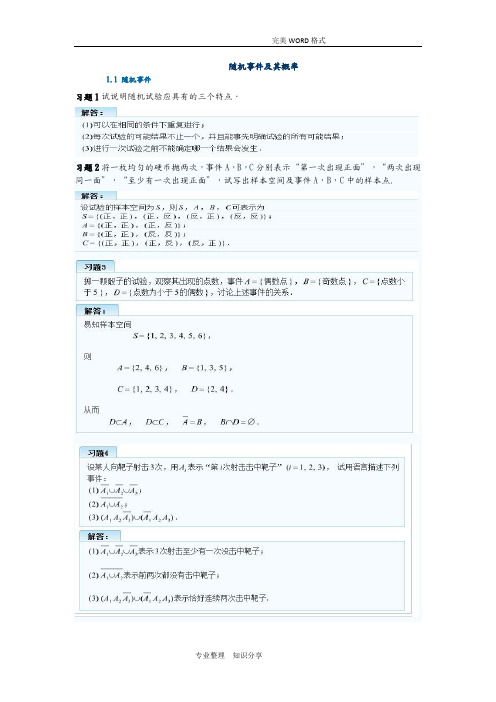
随机事件及其概率1.1 随机事件习题1试说明随机试验应具有的三个特点.习题2将一枚均匀的硬币抛两次,事件A,B,C分别表示“第一次出现正面”,“两次出现同一面”,“至少有一次出现正面”,试写出样本空间及事件A,B,C中的样本点.1.2 随机事件的概率1.3 古典概型与几何概型1.4 条件概率1.5 事件的独立性复习总结与总习题解答习题3. 证明下列等式:习题6.习题7习题9习题10习题12习题13习题14习题15习题16习题18习题20习题21习题23习题24习题26第二章随机变量及其分布2.1 随机变量习题1随机变量的特征是什么?解答:①随机变量是定义在样本空间上的一个实值函数.②随机变量的取值是随机的,事先或试验前不知道取哪个值.③随机变量取特定值的概率大小是确定的.习题2试述随机变量的分类.解答:①若随机变量X的所有可能取值能够一一列举出来,则称X为离散型随机变量;否则称为非离散型随机变量.②若X的可能值不能一一列出,但可在一段连续区间上取值,则称X为连续型随机变量.习题3盒中装有大小相同的球10个,编号为0,1,2,⋯,9, 从中任取1个,观察号码是“小于5”,“等于5”,“大于5”的情况,试定义一个随机变量来表达上述随机试验结果,并写出该随机变量取每一个特定值的概率.解答:分别用ω1,ω2,ω3表示试验的三个结果“小于5”,“等于5”,“大于5”,则样本空间S={ω1,ω2,ω3},定义随机变量X如下:X=X(ω)={0,ω=ω11,ω=ω2,2,ω=ω3则X取每个值的概率为P{X=0}=P{取出球的号码小于5}=5/10,P{X=1}=P{取出球的号码等于5}=1/10,P{X=2}=P{取出球的号码大于5}=4/10.2.2 离散型随机变量及其概率分布习题1设随机变量X服从参数为λ的泊松分布,且P{X=1}=P{X=2}, 求λ.解答:由P{X=1}=P{X=2}, 得λe-λ=λ^2/2e^-λ,解得λ=2.习题2设随机变量X的分布律为 P{X=k}=k15,k=1,2,3,4,5,试求(1)P{12<X<52; (2)P{1≤X≤3}; (3)P{X>3}.解答:(1)P{12<X<52=P{X=1}+P{X=2}=115+215=15;(2)P{≤X≤3}=P{X=1}+P{X=2}+P{X=3}=115+215+315=25;(3)P{X>3}=P{X=4}+P{X=5}=415+515=35.习题3已知随机变量X只能取-1,0,1,2四个值,相应概率依次为12c,34c,58c,716c, 试确定常数c, 并计算P{X<1∣X≠0}.解答:依题意知,12c+34c+58c+716c=1, 即3716c=1,解得c=3716=2.3125.由条件概率知 P{X<1∣X≠0}=P{X<1,X≠0}P{X≠0}=P{X=-1}P{X≠0}=12c1-34c=24c-3=26.25=0.32.习题4一袋中装有5只球,编号为1,2,3,4,5. 在袋中同时取3只,以X表示取出的3只球中的最大号码,写出随机变量X的分布律.解答:随机变量X的可能取值为3,4,5.P{X=3}=C22⋅1C53=110, P{X=4}=C32⋅1C53=310, P{X=5}=C42⋅1C53=35,所以X的分布律为设X表示取出3件产品的次品数,则X的所有可能取值为0,1,2,3. 对应概率分布为P{X=0}=C73C103=35120, P{X=1}=C73C31C103=36120,P{X=2}=C71C32C103=21120, P{X=3}=C33C103=1120.X的分布律为X 0123P 3512036120211201120习题9一批产品共10件,其中有7件正品,3件次品,每次从这批产品中任取一件,取出的产品仍放回去,求直至取到正品为止所需次数X的概率分布.解答:由于每次取出的产品仍放回去,各次抽取相互独立,下次抽取时情况与前一次抽取时完全相同,所以X的可能取值是所有正整数1,2,⋯,k,⋯.设第k次才取到正品(前k-1次都取到次品), 则随机变量X的分布律为P{X=k}=310×310×⋯×310×710=(310)k-1×710,k=1,2,⋯.习题10设随机变量X∼b(2,p),Y∼b(3,p), 若P{X≥1}=59, 求P{Y≥1}.解答:因为X∼b(2,p),P{X=0}=(1-p)2=1-P{X≥1}=1-5/9=4/9,所以p=1/3.因为Y∼b(3,p), 所以 P{Y≥1}=1-P{Y=0}=1-(2/3)3=19/27.习题11纺织厂女工照顾800个纺绽,每一纺锭在某一段时间τ内断头的概率为0.005, 在τ这段时间内断头次数不大于2的概率.解答:以X记纺锭断头数, n=800,p=0.005,np=4,应用泊松定理,所求概率为:P{0≤X≤2}=P{⋃0≤xi≤2{X=xi}=∑k=02b(k;800,0.005)≈∑k=02P(k;4)=e-4(1+41!+422!)≈0.2381.习题12设书籍上每页的印刷错误的个数X服从泊松分布,经统计发现在某本书上,有一个印刷错误与有两个印刷错误的页数相同,求任意检验4页,每页上都没有印刷错误的概率.解答:\becauseP{X=1}=P{X=2}, 即λ11!e-λ=λ22!e-λ⇒λ=2,∴P{X=0}=e-2,∴p=(e-2)4=e-8.2.3 随机变量的分布函数习题1F(X)={0,x<-20.4,-2≤x<01,x≥0, 是随机变量X的分布函数,则X是___________型的随机变量.解答:离散.由于F(x)是一个阶梯函数,故知X是一个离散型随机变量.习题2设F(x)={0x<0x20≤1,1x≥1 问F(x)是否为某随机变量的分布函数.解答:首先,因为0≤F(x)≤1,∀x∈(-∞,+∞).其次,F(x)单调不减且右连续,即F(0+0)=F(0)=0, F(1+0)=F(1)=1,且 F(-∞)=0,F(+∞)=1,所以F(x)是随机变量的分布函数.习题3已知离散型随机变量X的概率分布为P{X=1}=0.3,P{X=3}=0.5,P{X=5}=0.2,试写出X的分布函数F(x),并画出图形.解答:由题意知X的分布律为:X 135Pk 0.30.50.2所以其分布函数F(x)=P{X≤x}={0,x<10.3,1≤x<30.8,3≤x<51,x≥5.F(x)的图形见图.习题4设离散型随机变量X的分布函数为 F(x)={0,x<-10.4,-1≤x<10.8,1≤x<31,x≥3,试求:(1)X的概率分布; (2)P{X<2∣X≠1}.解答:(1)X -113pk 0.40.40.2(2)P{X<2∣X≠1}=P{X=-1}P{X≠1}=23.习题5设X的分布函数为F(x)={0,x<0x2,0≤x<1x-12,1≤x<1.51,x≥1.5,求P{0.4<X≤1.3},P{X>0.5},P{1.7<X≤2}.解答:P{0.4<X≥1.3}=P{1.3}-F(0.4)=(1.3-0.5)-0.4/2=0.6,P{X>0.5}=1-P{X≤0.5}=1-F(0.5)=1-0.5/2=0.75,P{1.7<X≤2}=F(2)-F(1.7)=1-1=0.习题6设随机变量X的分布函数为F(x)=A+Barctanx(-∞<x<+∞),试求:(1)系数A与B; (2)X落在(-1,1]内的概率.解答:(1)由于F(-∞)=0,F(+∞)=1,可知{A+B(-π2)A+B(π2)=1=0⇒A=12,B=1π,于是F(x)=12+1πarctanx, -∞<x<+∞;(2)P{-1<X≤1}=F(1)-F(-1)=(12+1πarctan1)-[12+1πarctanx(-1)]=12+1π⋅π4-12-1π(-π4)=12.习题7在区间[0,a]上任意投掷一个质点,以X表示这个质点的坐标.设这个质点落在[0,a]中任意小区间内的概率与这个小区间的长度成正比例,试求X的分布函数.解答: F(x)=P{X≤x}={0,x<0xa,0≤x<a.1,x≥a2.4 连续型随机变量及其概率密度习题1设随机变量X的概率密度为f(x)=12πe-(x+3)24(-∞<x<+∞),则Y=¯∼N(0,1).解答:应填3+X2.由正态分布的概率密度知μ=-3,σ=2由Y=X-μσ∼N(0,1), 所以Y=3+X2∼N(0,1).习题2已知X∼f(x)={2x,0<x<10,其它, 求P{X≤0.5};P{X=0.5};F(x).解答:P{X≤0.5}=∫-∞0.5f(x)dx=∫-∞00dx+∫00.52xdx=x2∣00.5=0.25,P{X=0.5}=P{X≤0.5}-P{X<0.5}=∫-∞0.5f(x)dx-∫-∞0.5f(x)dx=0.当X≤0时,F(x)=0;当0<x<1时,F(x)=∫-∞xf(t)dt=∫-∞00dt+∫0x2tdt=t2∣0x=x2;当X≥1时,F(x)=∫-∞xf(t)dt=∫-∞00dt+∫0x2tdt+∫1x0dt=t2∣01=1,故F(x)={0,x≤0x2,0<x<1.1,x≥1习题3设连续型随机变量X的分布函数为F(x)={A+Be-2x,x>00,x≤0,试求:(1)A,B的值;(2)P{-1<X<1}; (3)概率密度函数F(x).解答:(1)\becauseF(+∞)=limx→+∞(A+Be-2x)=1, ∴A=1;又 \becauselimx→0+(A+Be-2x)=F(0)=0, ∴B=-1.(2) P{-1<X<1}=F(1)-F(-1)=1-e-2.(3)f(x)=F′(x)={2e-x,x>00,x≤0.习题4服从拉普拉斯分布的随机变量X的概率密度f(x)=Ae-∣x∣, 求系数A及分布函数F(x).解答:由概率密度函数的性质知,∫-∞+∞f(x)dx=1,即∫-∞+∞Ae-∣x∣dx=1,而∫-∞+∞Ae-∣x∣dx=∫-∞0Aexdx+∫0+∞Ae-xdx=Aex∣-∞0+(-Ae-x∣0+∞)=A+A=2A或∫-∞+∞Ae-xdx=2∫0+∞Ae-xdx=-2Ae-x∣0+∞=2A,所以2A=1, 即A=1/2.从而f(x)=12e-∣x∣,-∞<x<+∞,又因为F(x)=∫-∞xf(t)dt,所以当x<0时,F(x)=∫-∞x12e-∣t∣dt=12∫-∞xetdt=12et∣-∞x=12ex;当x≥0时,F(x)=∫-∞x12e-∣x∣dt=∫-∞012etdt+∫0x12e-tdt=12et∣-∞0-12e-t∣0x=12-12e-x+12=1-12e-x,从而F(x)={12ex,x<01-12e-x,x≥0.习题5某型号电子管,其寿命(以小时计)为一随机变量,概率密度f(x)={100x2,x≥1000,其它,某一电子管的使用寿命为X, 则三个电子管使用150小时都不需要更换的概率.解答:设电子管的使用寿命为X, 则电子管使用150小时以上的概率为P{X>150}=∫150+∞f(x)dx=∫150+∞100x2dx=-100x∣150+∞=100150=23,从而三个电子管在使用150小时以上不需要更换的概率为 p=(2/3)3=8/27.习题6设一个汽车站上,某路公共汽车每5分钟有一辆车到达,设乘客在5分钟内任一时间到达是等可能的,试计算在车站候车的10位乘客中只有1位等待时间超过4分钟的概率.解答:设X为每位乘客的候车时间,则X服从[0,5]上的均匀分布. 设Y表示车站上10位乘客中等待时间超过4分钟的人数. 由于每人到达时间是相互独立的.这是10重伯努力概型. Y服从二项分布,其参数n=10,p=P{X≥4}=15=0.2,所以P{Y=1}=C101×0.2×0.89≈0.268.习题7设X∼N(3,22).(1)确定C, 使得P{X>c}=P{X≤c};(2)设d满足P{X>d}≥0.9, 问d至多为多少?解答:因为X∼N(3,22), 所以X-32=Z∼N(0,1).(1)欲使P{X>c}=P{X≤c}, 必有1-P{X≤c}=P{X≤c}, 即 P{X≤c}=1/2,亦即Φ(c-32)=12, 所以 c-32=0, 故c=3.(2)由P{X>d}≥0.9可得1-P{X≤d}≥0.9, 即 P{X≤d}≤0.1.于是Φ(d-32)≤0.1,Φ(3-d2)≥0.9.查表得3-d2≥1.282, 所以d≤0.436.习题8设测量误差X∼N(0,102), 先进行100次独立测量,求误差的绝对值超过19.6的次数不小于3的概率.解答:先求任意误差的绝对值超过19.6的概率p,p=P{∣X∣>19.6}=1-P{∣X∣≤19.6}=1-P{∣X10∣≤1.96=1-[Φ(1.96)-Φ(-1.96)]=1-[2Φ(1.96)-1]=1-[2×0.975-1]=1-0.95=0.05.设Y为100次测量中误差绝对值超过19.6的次数,则Y∼b(100,0.05).因为n很大,p很小,可用泊松分布近似,np=5=λ,所以P{Y≥3}≈1-50e-50!-51e-51!-52e-52!=1-3722-5≈0.87.习题9某玩具厂装配车间准备实行计件超产奖,为此需对生产定额作出规定. 根据以往记录,各工人每月装配产品数服从正态分布N(4000,3600).假定车间主任希望10%的工人获得超产奖,求:工人每月需完成多少件产品才能获奖?解答:用X表示工人每月需装配的产品数,则X∼N(4000,3600).设工人每月需完成x件产品才能获奖,依题意得P{X≥x}=0.1, 即1-P{X<x}=0.1,所以1-F(x)=0.1, 即 1-Φ(x-400060)=0.1, 所以Φ(x-400060)=0.9.查标准正态人分布表得Φ(1.28)=0.8997,因此 x-400060≈1.28, 即x=4077件,就是说,想获超产奖的工人,每月必须装配4077件以上.习题10某地区18岁女青年的血压(收缩压,以mm-HG计)服从N(110,122). 在该地区任选一18岁女青年,测量她的血压X.(1)求P{X≤105},P{100<X≤120};(2)确定最小的x, 使P{X>x}≤0.005.解答:已知血压X∼N(110,122).(1)P{X≤105}=P{X-11012≤-512≈1-Φ(0.42)=0.3372,P{100<X≤120}=Φ(120-11012)-Φ(100-11012)=Φ(0.833)-Φ(-0.833)=2Φ(0.833)-1≈0.595.(2)使P{X>x}≤0.05, 求x, 即1-P{X≤x}≤0.05, 亦即Φ(x-11012)≥0.95,查表得x-10012≥1.645, 从而x≥129.74.习题11设某城市男子身高X∼N(170,36), 问应如何选择公共汽车车门的高度使男子与车门碰头的机会小于0.01.解答:X∼N(170,36), 则X-1706∼N(0,1).设公共汽车门的高度为xcm,由题意P{X>x}<0.01, 而P{X>x}=1-P{X≤x}=1-Φ(x-1706)<0.01,即Φ(x-1706)>0.99, 查标准正态表得x-1706>2.33, 故x>183.98cm.因此,车门的高度超过183.98cm时,男子与车门碰头的机会小于0.01.习题12某人去火车站乘车,有两条路可以走. 第一条路程较短,但交通拥挤,所需时间(单位:分钟)服从正态分布N(40,102); 第二条路程较长,但意外阻塞较少,所需时间服从正态分布N(50,42), 求:(1)若动身时离开车时间只有60分钟,应走哪一条路线?(2)若动身时离开车时间只有45分钟,应走哪一条路线?解答:设X,Y分别为该人走第一、二条路到达火车站所用时间,则 X∼N(40,102),Y∼N(50,42).哪一条路线在开车之前到达火车站的可能性大就走哪一条路线.(1)因为P{X<60}=Φ(60-4010)=Φ(2)=0.97725,P{Y<60}=Φ(60-504)=Φ(2.5)=0.99379,所以有60分钟时应走第二条路.(2)因为P{X<45}=Φ(45-4010)=Φ(0.5)=0.6915,P{X<45}=Φ(45-504)=Φ(-1.25)=1-Φ(1.25)=1-0.8925=0.1075所以只有45分钟应走第一条路.当c>0时,fY(y)={1c(b-a),ca+d≤y≤cb+d0,其它,当c<0时,fY(y)={-1c(b-a),cb+d≤y≤ca+d0,其它.习题4设随机变量X服从[0,1]上的均匀分布,求随机变量函数Y=eX的概率密度fY(y).解答:f(x)={1,0≤x≤10,其它,f=ex,x∈(0,1)是单调可导函数,y∈(1,e), 其反函数为x=lny, 可得f(x)={fX(lny)∣ln′y,1<y<e0,其它={1y,1<y<e0,其它.习题5设X∼N(0,1),求Y=2X2+1的概率密度.解答:因y=2x2+1是非单调函数,故用分布函数法先求FY(y).FY(y)=P{Y≤y}=P{2X2+1≤y}(当y>1时)=P{-y-12≤X≤y-12=∫-y-12y-1212πe-x2dx,所以fY(y)=F′Y(y)=22πe-12⋅y-12⋅122y-1,y>1, 于是fY(y)={12π(y-1)e-y-14,y>10,y≤1.习题6设连续型随机变量X的概率密度为f(x), 分布函数为F(x), 求下列随机变量Y的概率密度:(1)Y=1X; (2)Y=∣X∣.解答:(1)FY(y)=P{Y≤y}=P{1/X≤y}.①当y>0时,FY(y)=P{1/X≤0}+P{0<1/X≤y}=P{X≤0}+P{X≥1/y}=F(0)+1-F(1/y),故这时fY(y)=[-F(1y)]′=1y2f(1y);;②当y<0时,FY(y)=P{1/y≤X<0}=F(0)-F(1/y),故这时fY(y)=1y2f(1y);③当y=0时,FY(y)=P{1/X≤0}=P{X<0}=F(0),故这时取fY(0)=0, 综上所述fY(y)={1y2⋅f(1y),y≠00,y=0.(2)FY(y)=P{Y≤y}=P{∣X∣≤y}.①当y>0时,FY(y)=P{-y≤X≤y}=F(y)-F(-y)这时fY(y)=f(y)+f(-y);②当y<0时,FY(y)=P{∅}=0, 这时fY(y)=0;③当y=0时,FY(y)=P{Y≤0}=P{∣X∣≤0}=P{X=0}=0,故这时取FY(y)=0, 综上所述 fY(y)={f(y)+f(-y),y>00,y≤0.习题7某物体的温度T(∘F)是一个随机变量, 且有T∼N(98.6,2), 已知θ=5(T-32)/9, 试求θ(∘F)的概率密度.解答:已知T∼N(98.6,2). θ=59(T-32), 反函数为T=59θ+32,是单调函数,所以fθ(y)=fT(95y+32)⋅95=12π⋅2e-(95y+32-98.6)24⋅95=910πe-81100(y-37)2.习题8设随机变量X在任一区间[a,b]上的概率均大于0, 其分布函数为FY(x), 又Y在[0,1]上服从均匀分布,证明:Z=FX-1(Y)的分布函数与X的分布函数相同.解答:因X在任一有限区间[a,b]上的概率均大于0, 故FX(x)是单调增加函数,其反函数FX-1(y)存在,又Y在[0,1]上服从均匀分布,故Y的分布函数为FY(y)=P{Y≤y}={0,y<0y,0≤y≤11,y>0,于是,Z的分布函数为FZ(z)=P{Z≤z}=P{FX-1(Y)≤z}=P{Y≤FX(z)}={0,FX(z)<0FX(z),0≤FX(z)≤1,1,FX(z)>1由于FX(z)为X的分布函数,故0≤FX(z)≤1.FX(z)<0和FX(z)>1均匀不可能,故上式仅有FZ(z)=FX(z), 因此,Z与X的分布函数相同.总习题解答习题1从1∼20的整数中取一个数,若取到整数k的概率与k成正比,求取到偶数的概率.解答:设Ak为取到整数k, P(Ak)=ck, k=1,2,⋯,20.因为P(⋃K=120Ak)=∑k=120P(Ak)=c∑k=120k=1,所以c=1210,P{取到偶数}=P{A2∪A4∪⋯∪A20} =1210(2+4+⋯+20)=1121.习题2若每次射击中靶的概率为0.7, 求射击10炮,(1)命中3炮的概率;(2)至少命中3炮的概率;(3)最可能命中几炮.解答:若随机变量X表示射击10炮中中靶的次数. 由于各炮是否中靶相互独立,所以是一个10重伯努利概型,X服从二项分布,其参数为n=10,p=0.7, 故(1)P{X=3}=C103(0.7)3(0.3)7≈0.009;(2)P{X≥3}=1-P{X<3}=1-[C100(0.7)0(0.3)10+C101(0.7)1(0.3)9+C102(0.7)2(0.3)8]≈0.998;(3)因X∼b(10,0.7), 而k0=[(n+1)p]=[(10+1)]×0.7=[7.7]=7,故最可能命中7炮.习题3在保险公司里有2500名同一年龄和同社会阶层的人参加了人寿保险,在1年中每个人死亡的概率为0.002,每个参加保险的人在1月1日须交120元保险费,而在死亡时家属可从保险公司里领20000元赔偿金,求:(1)保险公司亏本的概率;(2)保险公司获利分别不少于100000元, 200000元的概率.解答:1)以“年”为单位来考虑,在1年的1月1日,保险公司总收入为2500×120元=30000元.设1年中死亡人数为X, 则X∼b(2500,0.002), 则保险公司在这一年中应付出200000X(元),要使保险公司亏本,则必须 200000X>300000即X>15(人).因此,P{保险公司亏本}=P{X>15}=∑k=162500C2500k(0.002)k×(0.998)2500-k≈1-∑k=015e-55kk!≈0.000069,由此可见,在1年里保险公司亏本的概率是很小的.(2)P{保险公司获利不少于100000元}=P{300000-200000X≥100000}=P{X≤10}=∑k=010C2500k(0.002)×(0.998)2500-k≈∑k=010e-55kk!≈0.986305,即保险公司获利不少于100000元的概率在98%以上.P{保险公司获利不少于200000元}=P{300000-200000X≥200000}=P{X≤5}=∑k=05C2500k(0.002)k×(0.998)2500-k≈∑k=05e-55kk!≈0.615961,即保险公司获利不少于200000元的概率接近于62%.习题4一台总机共有300台分机,总机拥有13条外线,假设每台分机向总机要外线的概率为3%, 试求每台分机向总机要外线时,能及时得到满足的概率和同时向总机要外线的分机的最可能台数.解答:设分机向总机要到外线的台数为X, 300台分机可看成300次伯努利试验,一次试验是否要到外线. 设要到外线的事件为A, 则P(A)=0.03, 显然X∼b(300,0.03), 即P{X=k}=C300k(0.03)k(0.97)300-k(k=0,1,2,⋯,300),因n=300很大,p=0.03又很小,λ=np=300×0.03=9,可用泊松近似公式计算上面的概率. 因总共只有13条外线,要到外线的台数不超过13,故P{X≤13}≈∑k=0139kk!e-9≈0.9265, (查泊松分布表)且同时向总机要外线的分机的最可能台数k0=[(n+1)p]=[301×0.03]=9.习题5在长度为t的时间间隔内,某急救中心收到紧急呼救的次数X服从参数t2的泊松分布,而与时间间隔的起点无关(时间以小时计), 求:(1)某一天从中午12至下午3时没有收到紧急呼救的概率;(2)某一天从中午12时至下午5时至少收到1次紧急呼救的概率.解答:(1)t=3,λ=3/2, P{X=0}=e-3/2≈0.223;(2)t=5,λ=5/2, P{X≥1}=1-P{X=0}=1-e-5/2≈0.918.习题6设X为一离散型随机变量,其分布律为X -101pi 1/21-2qq2试求:(1)q的值; (2)X的分布函数.解答:(1)\because离散型随机变量的概率函数P{X=xi}=pi, 满足∑ipi=1, 且0≤pi≤1,∴ {1/2+1-2q+q2=10≤1-2q≤1q2≤1,解得q=1-1/2. 从而X的分布律为下表所示:因F(x)在x=π6处连续,故P{X=π6=12,于是有P{∣X∣<π6=P{-π6<X<π6=P{-π6<X≤π6=F(π6)-F(-π6)=12..习题8使用了x小时的电子管,在以后的Δx小时内损坏的概率等于λΔx+o(Δx),其中λ>0是常数,求电子管在损坏前已使用时数X的分布函数F(x),并求电子管在T小时内损坏的概率.解答:因X的可能取值充满区间(0,+∞),故应分段求F(x)=P{X≤x}.当x≤0时,F(x)=P{X≤x}=P(∅)=0;当x>0时,由题设知P{x<X≤x+Δx/X}=λΔx+o(Δx),而P{x<X≤x+Δx/X}=P{x<X≤x+Δx,X>x}P{X>x}=P{x<X≤x+Δx}1-P{X≤x}=F(x+Δx)-F(x)1-F(x),故F(X+Δx)-F(x)1-F(x)=λΔx+o(Δx),即F(x+Δx)-F(x)Δx=[1-F(x)][λ+o(Δx)Δx],令o(Δx)→0,得F′(x)=λ[1-F(x)].这是关于F(x)的变量可分离微分方程,分离变量dF(x)1-F(x)=λdx,积分之得通解为C[1-F(x)]=e-λx(C为任意常数).注意到初始条件F(0)=0, 故C=1.于是F(x)=1-e-λx,x>0,λ>0,故X的分布函数为F(x)={0,x≤01-e-λx,x>0(λ>0),从而电子管在T小时内损坏的概率为P{X≤T}=F(T)=1-e-λT.习题9设连续型随机变量X的分布密度为f(x)={x,0<x≤12-x,1<x≤20,其它,求其分布函数F(x).解答:当x≤0时,F(x)=∫-∞x0dt=0;当0<x≤1时,F(x)=∫-∞xf(t)dt=∫-∞00tdt+∫0xtdt=12x2;当1<x≤2时,F(x)=∫-∞xf(t)dt=∫-∞00dt+∫01tdt+∫1x(2-t)dt=0+12+(2t-12t2)∣1x=-1+2x-x22;当x>2时,F(x)=∫-∞00dt+∫01tdt+∫12(2-t)dt+∫2x0dt=1,故F(x)={0,x≤212x2,0<x≤1-1+2x-x22,1<x≤21,x>2.习题10某城市饮用水的日消费量X(单位:百万升)是随机变量,其密度函数为:f(x)={19xe-x3,x>00,其它,试求:(1)该城市的水日消费量不低于600万升的概率;(2)水日消费量介于600万升到900万升的概率.解答:先求X的分布函数F(x). 显然,当x<0时,F(x)=0, 当x≥0时有F(x)=∫0x19te-t3dt=1-(1+x3)e-x3故F(x)={1-(1+x3)e-x3,x≥00,x<0, 所以P{X≥6}=1-P{X<6}=1-P(X≤6}=1-F(6)=1-[1-(1+x3)e-x3]x=6=3e-2,P{6<X≤9}=F(9)-F(6)=(1-4e-3)-(1-3e-2)=3e-2-4e-3.习题11已知X∼f(x)={cλe-λx,x>a0,其它(λ>0),求常数c及P{a-1<X≤a+1}.解答:由概率密度函数的性质知∫-∞+∞f(x)dx=1,而∫-∞+∞f(x)dx=∫-∞a0dx+∫a+∞cλe-λxdx=c∫a+∞e-λxd(λx)=-ce-λx\vlinea+∞=ce-λa,所以ce-λa=1,从而c=eλa.于是P{a-1<X≤a+1}=∫a-1a+1f(x)dx=∫a-1a0dx+∫aa+1λeλae-λxdx=-eλae-λx\vlineaa+1=-eλa(e-λ(a+1)-e-λa)=1-e-λ.注意,a-1<a, 而当x<a时,f(x)=0.习题12已知X∼f(x)={12x2-12x+3,0<x<10,其它, 计算P{X≤0.2∣0.1<X≤0.5}.解答:根据条件概率;有P{X≤0.2∣0.1<X≤0.5}=P{X≤0.2,0.1<X≤0.5}P{0.1<X≤0.5}=P{0.1<X≤0.2}P{0.1<X≤0.5}=∫0.10.2(12x2-12x+2)dx∫0.10.5(12x2-12x+3) dx=(4x3-6x2+3x)∣0.10.2(4x3-6x2+3x)∣0.10.5=0.1480.256=0.578125.习题13若F1(x),F2(x)为分布函数,(1)判断F1(x)+F2(x)是不是分布函数,为什么?(2)若a1,a2是正常数,且a1+a2=1. 证明:a1F1(x)+a2F2(x)是分布函数.解答:(1)F(+∞)=limx→+∞F(x)=limx→+∞F1(x)+limx→+∞F2(x)=1+1=2≠1故F(x)不是分布函数.(2)由F1(x),F2(x)单调非减,右连续,且 F1(-∞)=F2(-∞)=0,F1(+∞)=F2(+∞)=1,可知a1F1(x)+a2F2(x)单调非减,右连续,且 a1F1(-∞)+a2F2(-∞)=0,a1F1(+∞)+a2F2(+∞)=1.从而a1F1(x)+a2F2(x)是分布函数.习题14设随机变量X的概率密度ϕ(x)为偶函数,试证对任意的a>0, 分布函数F(x)满足:(1)F(-a)=1-F(a); (2)P{∣X∣>a}=2[1-F(a)].解答:(1)F(-a)=∫-∞-aϕ(x)dx=∫a+∞ϕ(-t)dt=∫a+∞ϕ(x)dx=1-∫-∞aϕ(x)dx=1-F(a).(2)P{∣X∣>a}=P{X<-a}+P{X>a}=F(-a)+P{X≥a}F(-a)+1-F(a)=2[1-F(a)].习题15设K在(0,5)上服从均匀分布,求x的方程4x2+4Kx+K+2=0有实根的概率.解答:因为K∼U(0,5), 所以 fK(k)={1/5,0<k<50,其它,方程4x2+4Kx+K+2=0有实根的充要条件为(4K)2-4⋅4(K+2)≥0, 即 K2-K-2≥0,亦即(k-2)(K+1)≥0, 解得K≥2(K≤-1舍去), 所以P{方程有实根}=P{K≥2}=∫2515dx=35.习题16某单位招聘155人,按考试成绩录用,共有526人报名,假设报名者考试成绩X∼N(μ,σ2), 已知90分以上12人,60分以下83人,若从高分到低分依次录取,某人成绩为78分,问此人是否能被录取?解答:要解决此问题首先确定μ,σ2, 因为考试人数很多,可用频率近似概率.根据已知条件P{X>90}=12/526≈0.0228,P{X≤90}=1-P{X>90}≈1-0.0228}=0.9772;又因为P{X≤90}=P{X-μσ≤90-μσ, 所以有Φ(90-μσ)=0.9772, 反查标准正态表得90-μσ=2 ①同理:P{X≤60}=83/526≈0.1578; 又因为P{X≤60}=P{X-μσ≤60-μσ,故Φ(60-μσ)≈0.1578.因为0.1578<0.5,所以60-μσ<0, 故Φ(μ-60σ)≈1-0.1578=0.8422, 反查标准正态表得μ-60σ≈1.0 ②联立①,②解得σ=10,μ=70, 所以,X∼N(70,100).某人是否能被录取,关键看录取率. 已知录取率为155526≈0.2947, 看某人是否能被录取,解法有两种:方法1:P{X>78}=1-P{X≤78}=1-P{x-7010≤78-7010=1-Φ(0.8)≈1-0.7881=0.2119,因为0.2119<0.2947(录取率), 所以此人能被录取.方法2:看录取分数线. 设录取者最低分为x0, 则P{X≥x0}=0.2947(录取率),P{X≤x0}=1-P{X≥x0}=1-0.2947=0.7053,P{X≤x0}=P{x-7010≤x0-7010=Φ{x0-7010=0.7053,反查标准正态表得x0-7010≈0.54, 解得x0≈75. 此人成绩78分高于最低分,所以可以录取.习题17假设某地在任何长为t(年)的时间间隔内发生地震的次数N(t)服从参数为λ=0.1t的泊松分布,X表示连续两次地震之间间隔的时间(单位:年).(1)证明X服从指数分布并求出X的分布函数;(2)求今后3年内再次发生地震的概率;(3)求今后3年到5年内再次发生地震的概率.解答:(1)当t≥0时,P{X>t}=P{N(t)=0}=e-0.1t,∴F(t)=P{X≤t}=1-P{X>t}=1-e-0.1t;当t<0时,F(t)=0,∴ F(x)={1-e-0.1t,x≥00,x<0,X服从指数分布(λ=0.1);(2)F(3)=1-e-0.1×3≈0.26;(3)F(5)-F(3)≈0.13.习题18100件产品中,90个一等品,10个二等品,随机取2个安装在一台设备上,若一台设备中有i个(i=0,1,2)二等品,则此设备的使用寿命服从参数为λ=i+1的指数分布.(1)试求设备寿命超过1的概率;(2)已知设备寿命超过1,求安装在设备上的两个零件都是一等品的概率 .解答:(1)设X表示设备寿命. A表示“设备寿命超过1”,Bi表示“取出i个二等品”(i=0,1,2),则X的密度函数为fX(x)={λe-λx,x>00,x≤0 (λ=i+1,i=0,1,2),P(B0)=C902C1002, P(B1)=C901C102C1002, P(B2)=C102C1002,P(A∣B0)=∫1+∞e-xdx=e-1, P(A∣B1)=∫1+∞2e-2xdx=e-2,P(A∣B2)=∫1+∞3e-3xdx=e-3,由全概率公式:P(A)=∑i=02P(Bi)P(A∣Bi)≈0.32.(2)由贝叶斯公式:P(B0∣A)=P(B0)P(A∣B0)P(A)≈0.93.fX(x)={e-x,x>00,其它,求Y=eX的概率密度.解答:因为α=min{y(0),y(+∞)}=min{1,+∞}=1,β=max{y(0),y(+∞)}=max{1,+∞}=+∞.类似上题可得fY(y)={fX[h(y)]∣h′(y)∣,1<y<+∞0,其它={1/y2,1<y<+∞0,其它.习题22设随便机变量X的密度函数为 fX(x)={1-∣x∣,-1<x<10,其它,求随机变量Y=X2+1的分布函数与密度函数.解答:X的取值范围为(-1,1), 则Y的取值范围为[1,2). 当1≤y<2时, FY(y)=P{Y≤y}=P{X2+1≤y}=P{-Y-1≤x≤y-1}=∫-y-1y-1(1-∣x∣)dx=2∫0y-1(1-x)dx=1-(1-y-1)2,从而Y的分布函数为 FY(y)={0,y<11-(1-y-1)2,1≤y<2,1,其它Y的概率密度为fY(y)={1y-1-1,1<y<20,其它.第三章多维随机变量及其分布3.1 二维随机变量及其分布习题1设(X,Y)的分布律为X\Y 1231 1/61/91/182 1/3a1/9求a.解答:由分布律性质∑i⋅jPij=1, 可知 1/6+1/9+1/18+1/3+a+1/9=1,解得 a=2/9.习题2(1)2.设(X,Y)的分布函数为F(x,y),试用F(x,y)表示:(1)P{a<X≤b,Y≤c};解答:P{a<X≤b,Y≤c}=F(b,c)-F(a,c).习题2(2)2.设(X,Y)的分布函数为F(x,y),试用F(x,y)表示: (2)P{0<Y≤b};解答:P{0<Y≤b}=F(+∞,b)-F(+∞,0).习题2(3)2.设(X,Y)的分布函数为F(x,y),试用F(x,y)表示: (3)P{X>a,Y≤b}.解答:P{X>a,Y≤b}=F(+∞,b)-F(a,b).习题3(1)3.设二维离散型随机变量的联合分布如下表:试求: (1)P{12<X<32,0<Y<4;解答:P{12<X<23,0<Y<4P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=14+0+0=14.习题3(2)3.设二维离散型随机变量的联合分布如下表:试求: (2)P{1≤X≤2,3≤Y≤4};解答:P{1≤X≤2,3≤Y≤4}=P{X=1,Y=3}+P{X=1,Y=4}+P{X=2,Y=3}+P{X=2,Y=4}=0+116+0+14=516.习题3(3)3.设二维离散型随机变量的联合分布如下表:试求: (3)F(2,3).解答:F(2,3)=P(1,1)+P(1,2)+P(1,3)+P(2,1)+P(2,2)+P(2,3)=14+0+0+116+14+0=916.习题4设X,Y为随机变量,且 P{X≥0,Y≥0}=37, P{X≥0}=P{Y≥0}=47,求P{max{X,Y}≥0}.解答:P{max{X,Y}≥0}=P{X,Y至少一个大于等于0} =P{X≥0}+P{Y≥0}-P{X≥0,Y≥0}=47+47-37=57.习题5(X,Y)只取下列数值中的值: (0,0),(-1,1),(-1,13),(2,0)且相应概率依次为16,13,112,512, 请列出(X,Y)的概率分布表,并写出关于Y的边缘分布.解答:(1)因为所给的一组概率实数显然均大于零,且有16+13+112+512=1, 故所给的一组实数必是某二维随机变量(X,Y)的联合概率分布. 因(X,Y)只取上述四组可能值,故事件:{X=-1,Y=0}, {X=0,Y=13, {X=0,Y=1},{X=2,Y=13,{X=2,Y=1}均为不可能事件,其概率必为零. 因而得到下表:(2)P{Y=0}=P{X=-1,Y=0}+P{X=0,Y=0}+P{X=2,Y=0} =0+16+512=712,同样可求得 P{Y=13=112,P{Y=1}=13,关于的Y边缘分布见下表:Y 01/31pk 7/121/121/3习题6设随机向量(X,Y)服从二维正态分布N(0,0,102,102,0), 其概率密度为f(x,y)=1200πex2+y2200,求P{X≤Y}.解答:由于P{X≤Y}+P{X>Y}=1,且由正态分布图形的对称性,知P{X≤Y}=P{X>Y}, 故 P{X≤Y}=12.习题7设随机变量(X,Y)的概率密度为f(x,y)={k(6-x-y),0<x<2,2<y<40,其它,(1)确定常数k; (2)求P{X<1,Y<3}; (3)求P{X<1.5}; (4)求P{X+Y≤4}.解答:如图所示(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数k.∫02∫24k(6-x-y)dydx=k∫02(6-2x)dx=8k=1,所以k=18.(2)P{X<1,Y<3}=∫01dx∫2318(6-x-y)dy=38.(3)P{X<1.5}=∫01.5dx∫2418(6-x-y)dy=2732.(4)P{X+Y≤4}=∫02dx∫24-x18(6-x-y)dy=23.习题8已知X和Y的联合密度为 f(x,y)={cxy,0≤x≤1,0≤y≤10,其它,试求:(1)常数c; (2)X和Y的联合分布函数F(x,y).解答:(1)由于1=∫-∞+∞∫-∞+∞f(x,y)dxdy=c∫01∫01xydxdy=c4,c=4.(2)当x≤0或y≤0时,显然F(x,y)=0;当x≥1,y≥1时,显然F(x,y)=1;设0≤x≤1,0≤y≤1, 有F(x,y)=∫-∞x∫-∞yf(u,v)dudv=4∫0xudu∫0yvdv=x2y2.设0≤x≤1,y>1, 有 F(x,y)=P{X≤1,Y≤y}=4∫0xudu∫01ydy=x2.最后,设x>1,0≤y≤1, 有 F(x,y)=P{X≤1,Y≤y}=4∫01xdx∫0yvdv=y2.函数F(x,y)在平面各区域的表达式 F(x,y)={0,x≤0或y≤0x2,0≤x≤1,y>1x2y2,0≤x≤1,0≤y≤1.y2,x>习题9设二维随机变量(X,Y)的概率密度为 f(x,y)={4.8y(2-x),0≤x≤1,x≤y≤10,其它,求边缘概率密度fY(y).解答:fX(x)=∫-∞+∞f(x,y)dy={∫0x4.8y(2-x)dy,0≤x≤10,其它={2.4x2(2-x),0≤x≤10,其它.fY(y)=∫-∞+∞f(x,y)dx={∫0y4.8y(2-x)dx,0≤y≤10,其它={2.4y(4y-y2),0≤y≤10,其它.习题10设(X,Y)在曲线y=x2,y=x所围成的区域G里服从均匀分布,求联合分布密度和边缘分布密度.解答:区域G的面积A=∫01(x-x2)dx=16, 由题设知(X,Y)的联合分布密度为f(x,y)={6,0≤x≤1,x2≤y≤x0,其它,从而fX(x)=∫-∞+∞f(x,y)dy=6∫x2xdy=6(x-x2),0≤x≤1, 即 fX(x)={6(x-x2),0≤x≤10,其它fY(y)=∫-∞+∞f(x,y)dx=6∫yydx=6(y-y),0≤y≤1,即fY(y)={6(y-y),0≤y≤10,其它.3.2 条件分布与随机变量的独立性习题1二维随机变量(X,Y)的分布律为解答:由题意知X的密度函数为fX(x)={15,0≤x≤50,其它, 因为X与Y相互独立,所以X与Y的联合密度为:fXY(x,y)={2(5-y)125,0≤y≤5,0≤x≤50,其它,故此人能及时上火车的概率为P{Y>X}=∫05∫x52(5-y)125dydx=13.习题7设随机变量X与Y都服从N(0,1)分布,且X与Y相互独立,求(X,Y)的联合概率密度函数.解答:由题意知,随机变量X,Y的概率密度函数分别是fX(x)=12πe-x22,fY(y)=12πe-y22因为X与Y相互独立,所以(X,Y)的联合概率密度函数是f(x,y)=12πe-12(x+y)2.习题8设随机变量X的概率密度f(x)=12e-∣x∣(-∞<x<+∞),问:X与∣X∣是否相互独立?解答:若X与∣X∣相互独立,则∀a>0, 各有 P{X≤a,∣X∣≤a}=P{X≤a}⋅P{∣X∣≤a},而事件{∣X∣≤a}⊂{X≤a}, 故由上式有 P{∣X∣≤a}==P{X≤a}⋅P{∣X∣≤a},⇒P{∣X∣≤a}(1-P{X≤a})=0⇒P{∣X≤a∣}=0或1=P{X≤a}⋅(∀a>0)但当a>0时,两者均不成立,出现矛盾,故X与∣X∣不独立.习题9设X和Y是两个相互独立的随机变量,X在(0,1)上服从均匀分布,Y的概率密度为fY(y)={12e-y2,y>00,y≤0,(1)求X与Y的联合概率密度;(2)设有a的二次方程a2+2Xa+Y=0, 求它有实根的概率.解答:(1)由题设易知fX(x)={1,0<x<10,其它,又X,Y相互独立,故X与Y的联合概率密度为f(x,y)=fX(x)⋅fY(y)={12e-y2,0<x<1,y>00,其它;(2)因{a有实根}={判别式Δ2=4X2-4Y≥0}={X2≥Y},故如图所示得到: P{a有实根}=P{X2≥Y}=∫∫x2>yf(x,y)dxdy=∫01dx∫0x212e-y2dy=-∫01e-x22dx=1-[∫-∞1e-x22dx-∫-∞0e-x22dx] =1-2π[12π∫-∞1e-x22dx-12π∫-∞0e-x 22dx]=1-2π[Φ(1)-Φ(0),又Φ(1)=0.8413,Φ(0)=0.5,于是Φ(1)-Φ(0)=0.3413,所以 P{a有实根}=1-2π[Φ(1)-Φ(0)]≈1-2.51×0.3413=0.1433.3.3 二维随机变量函数的分布习题1设随机变量X和Y相互独立,且都等可能地取1,2,3为值,求随机变量U=max{X,Y}和V=min{X,Y}的联合分布.解答:由于U≥V, 可见P{U=i,V=j}=0(i<j).此外,有 P{U=V=i}=P{X=Y=i}=1/9(i=1,2,3),P{U=i,V=j}=P{X=i,Y=j}+P{X=j,Y=i}=2/9(i>j),于是,随机变量U和V的联合概率分布为\under2line令x+y=t{∫x+∞12te-tdt=12(x+1)e-x,x>00,x≤0,由对称性知fY(y)={12(y+1)e-y,y>00,y≤0, 显然f(x,y)≠fX(x)fY(y),x>0,y>0,所以X与Y不独立.(2)用卷积公式求fZ(z)=∫-∞+∞f(x,z-x)dx.当{x>0z-x>0 即 {x>0x<z时,f(x,z-x)≠0,所以当z≤0时,fZ(z)=0;当z>0时,fZ(z)=∫0z12xe-xdx=12z2e-z.于是,Z=X+Y的概率密度为 fZ(z)={12z2e-z,z>00,z≤0.习题6设随机变量X,Y相互独立,若X服从(0,1)上的均匀分布,Y服从参数1的指数分布,求随机变量Z=X+Y 的概率密度.解答:据题意,X,Y的概率密度分布为 fX(x)={1,0<x<10,其它, fY(y)={e-y,y≥00,y<0,由卷积公式得Z=X+Y的概率密度为fZ(z)=∫-∞+∞fX(x)fY(z-x)dx=∫-∞+∞fX(z-y)fY(y)dy =∫0+∞fX(z-y)e-ydy.由0<z-y<1得z-1<y<z,可见:当z≤0时,有fX(z-y)=0, 故fZ(z)=∫0+∞0⋅e-ydy=0;当z>0时,fZ(z)=∫0+∞fX(z-y)e-ydy=∫max(0,z-1)ze-ydy=e-max(0,z-1)-e-z,即 fZ(z)={0,z≤01-e-z,0<z≤1e1-z-e-z,z>1.习题7设随机变量(X,Y)的概率密度为f(x,y)={be-(x+y),0<x<1,0<y<+∞,0,其它.(1)试确定常数b;(2)求边缘概率密度fX(x),fY(y);(3)求函数U=max{X,Y}的分布函数.解答:(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数b. ∫01dx∫0+∞be-xe-ydy=b(1-e-1)=1,所以b=11-e-1,从而 f(x,y)={11-e-1e-(x+y),0<x<1,0<y<+∞,0,其它.(2)由边缘概率密度的定义得fX(x)={∫0+∞11-e-1e-(x+y)dy=e-x1-e-x,0<x<1,0,其它,fY(x)={∫0111-e-1e-(x+y)dx=e-y,0<y<+∞,0,其它(3)因为f(x,y)=fX(x)fY(y),所以X与Y独立,故 FU(u)=P{max{X,Y}≤u}=P{X≤u,Y≤u}=FX(u)FY(u),其中FX(x)=∫0xe-t1-e-1dt=1-e-x1-e-1,0<x<1,所以 FX(x)={0,x≤0,1-e-x1-e-1,0<x<1,1,x≥1.同理FY(y)={∫0ye-tdt=1-e-y,0<y<+∞,0,y≤0,因此 FU(u)={0,u<0,(1-e-u)21-e-1,0≤u<1,1-e-u,u≥1.习题8设系统L是由两个相互独立的子系统L1和L2以串联方式联接而成,L1和L2的寿命分别为X与Y, 其概率密度分别为ϕ1(x)={αe-αx,x>00,x≤0, ϕ2(y)={βe-βy,y>00,y≤0,其中α>0,β>0,α≠β,试求系统L的寿命Z的概率密度.解答:设Z=min{X,Y}, 则 F(z)=P{Z≥z}=P{min(X,Y)≤z}=1-P{min(X,Y)>z}=1-P{X≥z,Y≥z} =1-[1P{X<z}][1-P{Y<z}]=1-[1-F1{z}][1-F2{z}]由于F1(z)={∫0zαe-αxdx=1-e-αz,z≥00,z<0, F2(z)={1-e-βz,z≥00,z<0,故 F(z)={1-e-(α+β)z,z≥00,z<0,从而ϕ(z)={(α+β)e-(α+β)z,z>00,z≤0.习题9设随机变量X,Y相互独立,且服从同一分布,试明: P{a<min{X,Y}≤b}=[P{X>a}]2-[P{X>b}]2.解答:设min{X,Y}=Z,则 P{a<min{X,Y}≤b}=FZ(b)-FZ(a),。
概率论与数理统计课后习题答案(非常全很详细)

概率论与数理统计复旦大学此答案非常详细非常全,可供大家在平时作业或考试前使用,预祝大家考试成功习题一1.略.见教材习题参考答案.2.设A,B,C为三个事件,试用A,B,C的运算关系式表示下列事件:(1)A发生,B,C都不发生;(2)A与B发生,C不发生;(3)A,B,C都发生;(4)A,B,C至少有一个发生;(5)A,B,C都不发生;(6)A,B,C不都发生;(7)A,B,C至多有2个发生;(8)A,B,C至少有2个发生.【解】(1)A BC(2)AB C(3)ABC(4)A∪B∪C=AB C∪A B C∪A BC∪A BC∪A B C∪AB C∪ABC=ABC(5) ABC=A B C(6) ABC(7) A BC∪A B C∪AB C∪AB C∪A BC∪A B C∪ABC=ABC=A∪B∪C(8) AB∪BC∪CA=AB C∪A B C∪A BC∪ABC3.略.见教材习题参考答案4.设A,B为随机事件,且P(A)=0.7,P(A-B)=0.3,求P(AB).【解】P(AB)=1-P(AB)=1-[P(A)-P(A-B)]=1-[0.7-0.3]=0.65.设A,B是两事件,且P(A)=0.6,P(B)=0.7,求:(1)在什么条件下P(AB)取到最大值?(2)在什么条件下P(AB)取到最小值?【解】(1) 当AB =A 时,P (AB )取到最大值为0.6.(2) 当A ∪B =Ω时,P (AB )取到最小值为0.3.6.设A ,B ,C 为三事件,且P (A )=P (B )=1/4,P (C )=1/3且P (AB )=P (BC )=0,P (AC )=1/12,求A ,B ,C 至少有一事件发生的概率.【解】 P (A ∪B ∪C )=P (A )+P (B )+P (C )-P (AB )-P (BC )-P (AC )+P (ABC ) =14+14+13-112=347.从52张扑克牌中任意取出13张,问有5张黑桃,3张红心,3张方块,2张梅花的概率是多少?【解】 p =5332131313131352C C C C /C8.对一个五人学习小组考虑生日问题:(1) 求五个人的生日都在星期日的概率; (2) 求五个人的生日都不在星期日的概率;(3) 求五个人的生日不都在星期日的概率.【解】(1) 设A 1={五个人的生日都在星期日},基本事件总数为75,有利事件仅1个,故 P (A 1)=517=(17)5 (亦可用独立性求解,下同) (2) 设A 2={五个人生日都不在星期日},有利事件数为65,故P (A 2)=5567=(67)5 (3) 设A 3={五个人的生日不都在星期日}P (A 3)=1-P (A 1)=1-(17)5 9.略.见教材习题参考答案.10.一批产品共N 件,其中M 件正品.从中随机地取出n 件(n <N ).试求其中恰有m 件(m ≤M )正品(记为A )的概率.如果:(1) n 件是同时取出的;(2) n 件是无放回逐件取出的;(3) n 件是有放回逐件取出的.【解】(1) P (A )=C C /C mn m n M N M N --(2) 由于是无放回逐件取出,可用排列法计算.样本点总数有P n N 种,n 次抽取中有m次为正品的组合数为C mn 种.对于固定的一种正品与次品的抽取次序,从M 件正品中取m 件的排列数有P m M 种,从N -M 件次品中取n -m 件的排列数为P n m N M --种,故P (A )=C P P P mm n m n M N M n N-- 由于无放回逐渐抽取也可以看成一次取出,故上述概率也可写成P (A )=C C C m n m M N M n N-- 可以看出,用第二种方法简便得多.(3) 由于是有放回的抽取,每次都有N 种取法,故所有可能的取法总数为N n 种,n次抽取中有m 次为正品的组合数为C m n 种,对于固定的一种正、次品的抽取次序,m 次取得正品,都有M 种取法,共有M m 种取法,n -m 次取得次品,每次都有N -M 种取法,共有(N -M )n -m 种取法,故()C ()/m m n m n nP A M N M N -=- 此题也可用贝努里概型,共做了n 重贝努里试验,每次取得正品的概率为M N,则取得m 件正品的概率为 ()C 1m n m mn M M P A N N -⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭11.略.见教材习题参考答案.12. 50只铆钉随机地取来用在10个部件上,其中有3个铆钉强度太弱.每个部件用3只铆钉.若将3只强度太弱的铆钉都装在一个部件上,则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少?【解】设A ={发生一个部件强度太弱}133103501()C C /C 1960P A == 【解】 设A i ={甲进i 球},i =0,1,2,3,B i ={乙进i 球},i =0,1,2,3,则33312123330()(0.3)(0.4)C 0.7(0.3)C 0.6(0.4)i i i P A B ==+⨯⨯+22223333C (0.7)0.3C (0.6)0.4+(0.7)(0.6)⨯=0.3207617.从5双不同的鞋子中任取4只,求这4只鞋子中至少有两只鞋子配成一双的概率.【解】 4111152222410C C C C C 131C 21p =-= 18.某地某天下雪的概率为0.3,下雨的概率为0.5,既下雪又下雨的概率为0.1,求:(1) 在下雨条件下下雪的概率;(2) 这天下雨或下雪的概率.【解】 设A ={下雨},B ={下雪}.(1) ()0.1()0.2()0.5P AB p B A P A === (2) ()()()()0.30.50.10.7p A B P A P B P AB =+-=+-=19.已知一个家庭有3个小孩,且其中一个为女孩,求至少有一个男孩的概率(小孩为男为女是等可能的).【解】 设A ={其中一个为女孩},B ={至少有一个男孩},样本点总数为23=8,故 ()6/86()()7/87P AB P B A P A === 或在缩减样本空间中求,此时样本点总数为7. 6()7P B A =20.已知5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是男人的概率(假设男人和女人各占人数的一半).【解】 设A ={此人是男人},B ={此人是色盲},则由贝叶斯公式()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.50.05200.50.050.50.002521⨯==⨯+⨯ 21.两人约定上午9∶00~10∶00在公园会面,求一人要等另一人半小时以上的概率.题21图 题22图【解】设两人到达时刻为x,y ,则0≤x ,y ≤60.事件“一人要等另一人半小时以上”等价于|x -y |>30.如图阴影部分所示.22301604P == 22.从(0,1)中随机地取两个数,求:(1) 两个数之和小于65的概率; (2) 两个数之积小于14的概率. 【解】 设两数为x ,y ,则0<x ,y <1.(1) x +y <65. 11441725510.68125p =-== (2) xy =<14. 1111244111d d ln 242x p x y ⎛⎫=-=+ ⎪⎝⎭⎰⎰ 23.设P (A )=0.3,P (B )=0.4,P (A B )=0.5,求P (B |A ∪B )【解】 ()()()()()()()()P AB P A P AB P B A B P A B P A P B P AB -==+- 0.70.510.70.60.54-==+- 24.在一个盒中装有15个乒乓球,其中有9个新球,在第一次比赛中任意取出3个球,比赛后放回原盒中;第二次比赛同样任意取出3个球,求第二次取出的3个球均为新球的概率.【解】 设A i ={第一次取出的3个球中有i 个新球},i =0,1,2,3.B ={第二次取出的3球均为新球}由全概率公式,有30()()()i i i P B P B A P A ==∑33123213336996896796333333331515151515151515C C C C C C C C C C C C C C C C C C =•+•+•+•0.089=25. 按以往概率论考试结果分析,努力学习的学生有90%的可能考试及格,不努力学习的学生有90%的可能考试不及格.据调查,学生中有80%的人是努力学习的,试问:(1)考试及格的学生有多大可能是不努力学习的人?(2)考试不及格的学生有多大可能是努力学习的人?【解】设A ={被调查学生是努力学习的},则A ={被调查学生是不努力学习的}.由题意知P(A )=0.8,P (A )=0.2,又设B ={被调查学生考试及格}.由题意知P (B |A )=0.9,P (B |A )=0.9,故由贝叶斯公式知(1)()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+0.20.110.027020.80.90.20.137⨯===⨯+⨯ 即考试及格的学生中不努力学习的学生仅占2.702% (2) ()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.80.140.30770.80.10.20.913⨯===⨯+⨯ 即考试不及格的学生中努力学习的学生占30.77%.26. 将两信息分别编码为A 和B 传递出来,接收站收到时,A 被误收作B 的概率为0.02,而B 被误收作A 的概率为0.01.信息A 与B 传递的频繁程度为2∶1.若接收站收到的信息是A ,试问原发信息是A 的概率是多少?【解】 设A ={原发信息是A },则={原发信息是B }C ={收到信息是A },则={收到信息是B }由贝叶斯公式,得()()()()()()()P A P C A P A C P A P C A P A P C A =+ 2/30.980.994922/30.981/30.01⨯==⨯+⨯ 27.在已有两个球的箱子中再放一白球,然后任意取出一球,若发现这球为白球,试求箱子中原有一白球的概率(箱中原有什么球是等可能的颜色只有黑、白两种)【解】设A i ={箱中原有i 个白球}(i =0,1,2),由题设条件知P (A i )=13,i =0,1,2.又设B ={抽出一球为白球}.由贝叶斯公式知 111120()()()()()()()i i i P B A P A P A B P A B P B P B A P A ===∑ 2/31/311/31/32/31/311/33⨯==⨯+⨯+⨯ 28.某工厂生产的产品中96%是合格品,检查产品时,一个合格品被误认为是次品的概率为0.02,一个次品被误认为是合格品的概率为0.05,求在被检查后认为是合格品产品确是合格品的概率.【解】 设A ={产品确为合格品},B ={产品被认为是合格品}由贝叶斯公式得()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.960.980.9980.960.980.040.05⨯==⨯+⨯ 29.某保险公司把被保险人分为三类:“谨慎的”,“一般的”,“冒失的”.统计资料表明,上述三种人在一年内发生事故的概率依次为0.05,0.15和0.30;如果“谨慎的”被保险人占20%,“一般的”占50%,“冒失的”占30%,现知某被保险人在一年内出了事故,则他是“谨慎的”的概率是多少?【解】 设A ={该客户是“谨慎的”},B ={该客户是“一般的”},C ={该客户是“冒失的”},D ={该客户在一年内出了事故}则由贝叶斯公式得 ()()(|)(|)()()(|)()(|)()(|)P AD P A P D A P A D P D P A P D A P B P D B P C P D C ==++ 0.20.050.0570.20.050.50.150.30.3⨯==⨯+⨯+⨯ 30.加工某一零件需要经过四道工序,设第一、二、三、四道工序的次品率分别为0.02,0.03,0.05,0.03,假定各道工序是相互独立的,求加工出来的零件的次品率.【解】设A i ={第i 道工序出次品}(i =1,2,3,4).412341()1()i i P A P A A A A ==- 12341()()()()P A P A P A P A =-10.980.970.950.970.124=-⨯⨯⨯=31.设每次射击的命中率为0.2,问至少必须进行多少次独立射击才能使至少击中一次的概率不小于0.9?【解】设必须进行n 次独立射击.1(0.8)0.9n -≥即为 (0.8)0.1n ≤故 n ≥11至少必须进行11次独立射击.32.证明:若P (A |B )=P (A |B ),则A ,B 相互独立.【证】 (|)(|)P A B P A B =即()()()()P AB P AB P B P B = 亦即 ()()()()P AB P B P AB P B =()[1()][()()]()P AB P B P A P AB P B -=-因此 ()()()P AB P A P B =故A 与B 相互独立.33.三人独立地破译一个密码,他们能破译的概率分别为15,13,14,求将此密码破译出的概率.【解】 设A i ={第i 人能破译}(i =1,2,3),则 31231231()1()1()()()i i P A P A A A P A P A P A ==-=-42310.6534=-⨯⨯= 34.甲、乙、丙三人独立地向同一飞机射击,设击中的概率分别是0.4,0.5,0.7,若只有一人击中,则飞机被击落的概率为0.2;若有两人击中,则飞机被击落的概率为0.6;若三人都击中,则飞机一定被击落,求:飞机被击落的概率.【解】设A ={飞机被击落},B i ={恰有i 人击中飞机},i =0,1,2,3由全概率公式,得30()(|)()i i i P A P A B P B ==∑=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)0.2+(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)0.6+0.4×0.5×0.7=0.45835.已知某种疾病患者的痊愈率为25%,为试验一种新药是否有效,把它给10个病人服用,且规定若10个病人中至少有四人治好则认为这种药有效,反之则认为无效,求:(1) 虽然新药有效,且把治愈率提高到35%,但通过试验被否定的概率.(2) 新药完全无效,但通过试验被认为有效的概率.【解】(1) 3101100C(0.35)(0.65)0.5138k k k k p -===∑ (2) 10102104C(0.25)(0.75)0.2241kk k k p -===∑36.一架升降机开始时有6位乘客,并等可能地停于十层楼的每一层.试求下列事件的概率:(1) A =“某指定的一层有两位乘客离开”;(2) B =“没有两位及两位以上的乘客在同一层离开”;(3) C =“恰有两位乘客在同一层离开”;(4) D =“至少有两位乘客在同一层离开”.【解】 由于每位乘客均可在10层楼中的任一层离开,故所有可能结果为106种.(1) 2466C 9()10P A =,也可由6重贝努里模型: 224619()C ()()1010P A = (2) 6个人在十层中任意六层离开,故6106P ()10P B = (3) 由于没有规定在哪一层离开,故可在十层中的任一层离开,有110C 种可能结果,再从六人中选二人在该层离开,有26C 种离开方式.其余4人中不能再有两人同时离开的情况,因此可包含以下三种离开方式:①4人中有3个人在同一层离开,另一人在其余8层中任一层离开,共有131948C C C 种可能结果;②4人同时离开,有19C 种可能结果;③4个人都不在同一层离开,有49P 种可能结果,故1213114610694899()C C (C C C C P )/10P C =++ (4) D=B .故 6106P ()1()110P D P B =-=- 37. n 个朋友随机地围绕圆桌而坐,求下列事件的概率:(1) 甲、乙两人坐在一起,且乙坐在甲的左边的概率;(2) 甲、乙、丙三人坐在一起的概率;(3) 如果n 个人并排坐在长桌的一边,求上述事件的概率.【解】 (1) 111p n =- (2) 23!(3)!,3(1)!n p n n -=>- (3) 12(1)!13!(2)!;,3!!n n p p n n n n --''===≥ 38.将线段[0,a ]任意折成三折,试求这三折线段能构成三角形的概率【解】 设这三段长分别为x ,y ,a -x -y .则基本事件集为由0<x <a ,0<y <a ,0<a -x -y <a 所构成的图形,有利事件集为由()()x y a x y x a x y y y a x y x+>--⎡⎢+-->⎢⎢+-->⎣ 构成的图形,即02022a x a y a x y a ⎡<<⎢⎢⎢<<⎢⎢⎢<+<⎢⎣ 如图阴影部分所示,故所求概率为14p =. 39. 某人有n 把钥匙,其中只有一把能开他的门.他逐个将它们去试开(抽样是无放回的).证明试开k 次(k =1,2,…,n )才能把门打开的概率与k 无关.【证】 11P 1,1,2,,P k n k n p k n n --===40.把一个表面涂有颜色的立方体等分为一千个小立方体,在这些小立方体中,随机地取出一个,试求它有i 面涂有颜色的概率P (A i )(i =0,1,2,3).【解】 设A i ={小立方体有i 面涂有颜色},i =0,1,2,3.在1千个小立方体中,只有位于原立方体的角上的小立方体是三面有色的,这样的小立方体共有8个.只有位于原立方体的棱上(除去八个角外)的小立方体是两面涂色的,这样的小立方体共有12×8=96个.同理,原立方体的六个面上(除去棱)的小立方体是一面涂色的,共有8×8×6=384个.其余1000-(8+96+384)=512个内部的小立方体是无色的,故所求概率为01512384()0.512,()0.38410001000P A P A ====, 24968()0.096,()0.00810001000P A P A ====. 41.对任意的随机事件A ,B ,C ,试证P (AB )+P (AC )-P (BC )≤P (A ).【证】 ()[()]()P A P A B C P AB AC ≥=()()()P AB P AC P ABC =+-()()()P AB P AC P BC ≥+-42.将3个球随机地放入4个杯子中去,求杯中球的最大个数分别为1,2,3的概率.【解】 设i A ={杯中球的最大个数为i },i =1,2,3.将3个球随机放入4个杯子中,全部可能放法有43种,杯中球的最大个数为1时,每个杯中最多放一球,故3413C 3!3()48P A == 而杯中球的最大个数为3,即三个球全放入一个杯中,故1433C 1()416P A == 因此 213319()1()()181616P A P A P A =--=--= 或 12143323C C C 9()416P A == 43.将一枚均匀硬币掷2n 次,求出现正面次数多于反面次数的概率.【解】掷2n 次硬币,可能出现:A ={正面次数多于反面次数},B ={正面次数少于反面次数},C ={正面次数等于反面次数},A ,B ,C 两两互斥.可用对称性来解决.由于硬币是均匀的,故P (A )=P (B ).所以1()()2P C P A -= 由2n 重贝努里试验中正面出现n 次的概率为211()()()22n n n n P C C =故 2211()[1C ]22n n n P A =- 44.掷n 次均匀硬币,求出现正面次数多于反面次数的概率.【解】设A ={出现正面次数多于反面次数},B ={出现反面次数多于正面次数},由对称性知P (A )=P (B )(1) 当n 为奇数时,正、反面次数不会相等.由P (A )+P (B )=1得P (A )=P (B )=0.5(2) 当n 为偶数时,由上题知211()[1C ()]22nn n P A =-45.设甲掷均匀硬币n +1次,乙掷n 次,求甲掷出正面次数多于乙掷出正面次数的概率.【解】 令甲正=甲掷出的正面次数,甲反=甲掷出的反面次数.乙正=乙掷出的正面次数,乙反=乙掷出的反面次数. 显然有>正正(甲乙)=(甲正≤乙正)=(n +1-甲反≤n -乙反) =(甲反≥1+乙反)=(甲反>乙反)由对称性知P (甲正>乙正)=P (甲反>乙反) 因此P (甲正>乙正)=1246.证明“确定的原则”(Sure -thing ):若P (A |C )≥P (B |C ),P (A |C )≥P (B |C ),则P (A )≥P (B ).【证】由P (A |C )≥P (B |C ),得()(),()()P AC P BC P C P C ≥即有 ()()P AC P BC ≥ 同理由 (|)(|),P A C P B C ≥ 得 ()(),P AC P BC ≥故 ()()()()()()P A P AC P AC P BC P BC P B =+≥+= 47.一列火车共有n 节车厢,有k (k ≥n )个旅客上火车并随意地选择车厢.求每一节车厢内至少有一个旅客的概率.【解】 设A i ={第i 节车厢是空的},(i =1,…,n ),则121(1)1()(1)2()(1)1()(1)n k ki kki j ki i i n P A n nP A A n n P A A A n--==-=--=-其中i 1,i 2,…,i n -1是1,2,…,n 中的任n -1个. 显然n 节车厢全空的概率是零,于是2112111122111111123111()(1)C (1)2()C (1)1()C (1)0()(1)n n nk ki ni ki j n i j nn kn i i i n i i i nn nn i ni S P A n n n S P A A n n S P A A A nS P A S S S S --=≤<≤--≤<<≤+===-=-==--==-==-+-+-∑∑∑121121C (1)C (1)(1)C (1)kkn n kn n n n nnn--=---++--故所求概率为121121()1C (1)C (1)nk i i n ni P A n n=-=--+--+111(1)C (1)n n kn n n+----48.设随机试验中,某一事件A 出现的概率为ε>0.试证明:不论ε>0如何小,只要不断地独立地重复做此试验,则A 迟早会出现的概率为1. 【证】在前n 次试验中,A 至少出现一次的概率为1(1)1()n n ε--→→∞49.袋中装有m 只正品硬币,n 只次品硬币(次品硬币的两面均印有国徽).在袋中任取一只,将它投掷r 次,已知每次都得到国徽.试问这只硬币是正品的概率是多少? 【解】设A ={投掷硬币r 次都得到国徽}B ={这只硬币为正品} 由题知 (),()m nP B P B m n m n==++ 1(|),(|)12r P A B P A B ==则由贝叶斯公式知()()(|)(|)()()(|)()(|)P AB P B P A B P B A P A P B P A B P B P A B ==+121212rrrm m m n m nm n m n m n+==++++ 50.巴拿赫(Banach )火柴盒问题:某数学家有甲、乙两盒火柴,每盒有N 根火柴,每次用火柴时他在两盒中任取一盒并从中任取一根.试求他首次发现一盒空时另一盒恰有r 根的概率是多少?第一次用完一盒火柴时(不是发现空)而另一盒恰有r 根的概率又有多少? 【解】以B 1、B 2记火柴取自不同两盒的事件,则有121()()2P B P B ==.(1)发现一盒已空,另一盒恰剩r 根,说明已取了2n -r 次,设n 次取自B 1盒(已空),n -r 次取自B 2盒,第2n -r +1次拿起B 1,发现已空。
概率论和数理统计课后习题集答案解析徐雅静版

习题答案第1章 三、解答题1.设P (AB ) = 0,则下列说法哪些是正确的? (1) A 和B 不相容; (2) A 和B 相容; (3) AB 是不可能事件; (4) AB 不一定是不可能事件; (5) P (A ) = 0或P (B ) = 0 (6) P (A – B ) = P (A ) 解:(4) (6)正确.2.设A ,B 是两事件,且P (A ) = 0.6,P (B ) = 0.7,问: (1) 在什么条件下P (AB )取到最大值,最大值是多少? (2) 在什么条件下P (AB )取到最小值,最小值是多少? 解:因为)()()()(B A P B P A P AB P -+≤,又因为)()(B A P B P ≤即.0)()(≤-B A P B P 所以(1) 当)()(B A P B P =时P (AB )取到最大值,最大值是)()(A P AB P ==0.6.(2) 1)(=B A P 时P (AB )取到最小值,最小值是P (AB )=0.6+0.7-1=0.3. 3.已知事件A ,B 满足)()(B A P AB P =,记P (A ) = p ,试求P (B ).解:因为)()(B A P AB P =,即)()()(1)(1)()(AB P B P A P B A P B A P AB P +--=-== ,所以 .1)(1)(p A P B P -=-=4.已知P (A ) = 0.7,P (A – B ) = 0.3,试求)(AB P .解:因为P (A – B ) = 0.3,所以P (A )– P(AB ) = 0.3, P(AB ) = P (A )– 0.3, 又因为P (A ) = 0.7,所以P(AB ) =0.7– 0.3=0.4,6.0)(1)(=-=AB P AB P .5. 从5双不同的鞋子种任取4只,问这4只鞋子中至少有两只配成一双的概率是多少? 解:显然总取法有410C n=种,以下求至少有两只配成一双的取法k :法一:分两种情况考虑:15C k=24C 212)(C +25C 其中:2122415)(C C C 为恰有1双配对的方法数法二:分两种情况考虑:!2161815C C C k ⋅⋅=+25C其中:!2161815C C C ⋅⋅为恰有1双配对的方法数法三:分两种情况考虑:)(142815C C C k -=+25C其中:)(142815C C C -为恰有1双配对的方法数法四:先满足有1双配对再除去重复部分:2815C C k =-25C法五:考虑对立事件:410C k =-45C 412)(C其中:45C 412)(C 为没有一双配对的方法数法六:考虑对立事件:!4141618110410C C C C C k ⋅⋅⋅-=其中:!4141618110C C C C ⋅⋅⋅为没有一双配对的方法数所求概率为.2113410==C k p 6.在房间里有10个人,分别佩戴从1号到10号的纪念章,任取3人记录其纪念章的号码.求: (1) 求最小号码为5的概率; (2) 求最大号码为5的概率.解:(1) 法一:12131025==C C p ,法二:1213102513==A A C p (2) 法二:20131024==C C p ,法二:2013102413==A A C p 7.将3个球随机地放入4个杯子中去,求杯子中球的最大个数分别为1,2,3的概率. 解:设M 1, M 2, M 3表示杯子中球的最大个数分别为1,2,3的事件,则834)(3341==A M P , 1694)(324232=⨯=A C M P , 1614)(3143==C M P8.设5个产品中有3个合格品,2个不合格品,从中不返回地任取2个,求取出的2个中全是合格品,仅有一个合格品和没有合格品的概率各为多少?解:设M 2, M 1, M 0分别事件表示取出的2个球全是合格品,仅有一个合格品和没有合格品,则3.0)(25232==C C M P ,6.0)(2512131==C C C M P ,1.0)(25221==C C M P9.口袋中有5个白球,3个黑球,从中任取两个,求取到的两个球颜色相同的概率.解:设M 1=“取到两个球颜色相同”,M 1=“取到两个球均为白球”,M 2=“取到两个球均为黑球”,则φ==2121M M M M M 且.所以.2813C C C C )()()()(282328252121=+=+==M P M P M M P M P10. 若在区间(0,1)内任取两个数,求事件“两数之和小于6/5”的概率.解:这是一个几何概型问题.以x 和y 表示任取两个数,在平面上建立xOy 直角坐标系,如图. 任取两个数的所有结果构成样本空间Ω = {(x ,y ):0 ≤ x ,y ≤ 1} 事件A =“两数之和小于6/5”= {(x ,y ) ∈ Ω : x + y ≤ 6/5} 因此2517154211)(2=⎪⎭⎫ ⎝⎛⨯-=Ω=的面积的面积A A P . 图?11.随机地向半圆220x ax y -<<(a 为常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,求原点和该点的连线与x 轴的夹角小于4π的概率. 解:这是一个几何概型问题.以x 和y 表示随机地向半圆内掷一点的坐标,θ表示原点和该点的连线与x 轴的夹角,在平面上建立xOy 直角坐标系,如图.随机地向半圆内掷一点的所有结果构成样本空间Ω={(x ,y ):220,20x ax y a x -<<<<}事件A =“原点和该点的连线与x 轴的夹角小于4π” ={(x ,y ):40,20,202πθ<<-<<<<x ax y a x }因此211214121)(222+=+=Ω=πππa aa A A P 的面积的面积.12.已知21)(,31)(,41)(===B A P A B P A P ,求)(B A P . 解:,1213141)()()(=⨯==A B P A P AB P ,6121121)|()()(=÷==B A P AB P B P .311216141)()()()(=-+=-+=AB P B P A P B A P 13.设10件产品中有4件不合格品,从中任取两件,已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率是多少?解:题中要求的“已知所取两件产品中有一件是不合格品,则另一件也是不合格品的概率”应理解为求“已知所取两件产品中至少有一件是不合格品,则两件均为不合格品的概率”。
概率论和数理统计习题集与答案解析第七章

习题7-11. 选择题(1) 设总体X 的均值μ与方差σ2都存在但未知, 而12,,,n X X X 为来自X的样本, 则均值μ与方差σ2的矩估计量分别是( ) .(A) X 和S 2.(B) X 和211()nii X nμ=-∑. (C) μ和σ2.(D) X 和211()nii X X n=-∑.解 选(D). (2) 设[0,]XU θ, 其中θ>0为未知参数, 又12,,,n X X X 为来自总体X的样本, 则θ的矩估计量是( ) .(A) X . (B) 2X . (C) 1max{}i i nX ≤≤. (D) 1min{}i i nX ≤≤.解 选(B).2. 设总体X 的分布律为其中0<θ<12n , 试求θ的矩估计量.解 因为E (X )=(-2)×3θ+1×(1-4θ)+5×θ=1-5θ, 令15X θ-=得到θ的矩估计量为ˆ15X θ-=. 3. 设总体X 的概率密度为(1),01,(;)0, x x f x θθθ+<<=⎧⎨⎩其它. 其中θ>-1是未知参数, X 1,X 2,…,X n 是来自X 的容量为n 的简单随机样本, 求: (1) θ的矩估计量;(2) θ的极大似然估计量. 解 总体 X 的数学期望为1101()()d (1)d 2E X xf x x x x θθθθ+∞+-∞+==+=+⎰⎰. 令()E X X =, 即12X θθ+=+, 得参数θ的矩估计量为21ˆ1X X θ-=-. 设x 1, x 2,…, x n 是相应于样本X 1, X 2,… , X n 的一组观测值, 则似然函数为1(1),01,0,n n i i i x x L θθ=⎧⎛⎫+<<⎪ ⎪=⎨⎝⎭⎪⎩∏其它. 当0<x i <1(i =1,2,3,…,n )时, L >0且 ∑=++=ni ixn L 1ln )1ln(ln θθ,令1d ln ln d 1ni i L nx θθ==++∑=0, 得θ的极大似然估计值为 1ˆ1ln nii nxθ==--∑,而θ的极大似然估计量为 1ˆ1ln nii nXθ==--∑.4. 设总体X 服从参数为λ的指数分布, 即X 的概率密度为e ,0,(,)0,0,x x f x x λλλ->=⎧⎨⎩≤ 其中0λ>为未知参数, X 1, X 2, …, X n 为来自总体X 的样本, 试求未知参数λ的矩估计量与极大似然估计量.解 因为E (X )=1λ =X , 所以λ的矩估计量为1ˆXλ=. 设x 1, x 2,…, x n 是相应于样本X 1, X 2,… ,X n 的一组观测值, 则似然函数11nii inxx nni L eeλλλλ=--=∑==∏,取对数 1ln ln ()ni i L n x λλ==-∑.令1d ln 0,d ni i L n x λλ==-=∑ 得λ的极大似然估计值为1ˆxλ=,λ的极大似然估计量为1ˆXλ=. 5. 设总体X 的概率密度为,01(,)1,120,x f x x θθθ<<=-⎧⎪⎨⎪⎩,≤≤,其它,其中θ(0<θ<1)是未知参数. X 1, X 2, …, X n 为来自总体的简单随机样本, 记N 为样本值12,,,n x x x 中小于1的个数. 求: (1) θ的矩估计量; (2) θ的极大似然估计量.解 (1) 1213()d (1)d 2X E X x x x x θθθ==+-=-⎰⎰, 所以32X θ=-矩.(2) 设样本12,,n x x x 按照从小到大为序(即顺序统计量的观测值)有如下关系:x (1) ≤ x (2) ≤…≤ x (N ) <1≤ x (N +1)≤ x (N +2)≤…≤x (n ) .似然函数为(1)(2)()(1)(2)(1),1()0,,N n N N N N n x x x x x x L θθθ-++-<=⎧⎨⎩≤≤≤≤≤≤≤其它.考虑似然函数非零部分, 得到ln L (θ ) = N ln θ + (n − N ) ln(1−θ ),令d ln ()0d 1L Nn Nθθθθ-=-=-, 解得θ的极大似然估计值为ˆN nθ=. 习题7-21. 选择题: 设总体X 的均值μ与方差2σ都存在但未知, 而12,,,nX X X 为X 的样本, 则无论总体X 服从什么分布, ( )是μ和2σ的无偏估计量.(A)11nii Xn=∑和211()nii X X n=-∑. (B)111nii X n =-∑和211()1nii X X n =--∑.(C)111nii X n =-∑和211()1nii X n μ=--∑. (D)11nii X n=∑和211()nii X nμ=-∑.解 选(D).2. 若1X ,2X ,3X 为来自总体2(,)XN μσ的样本, 且Y 1231134X X kX =++为μ的无偏估计量, 问k 等于多少?解 要求1231111()3434E X X kX k μμμμ++=++=, 解之, k =512.3. 设总体X 的均值为0, 方差2σ存在但未知, 又12,X X 为来自总体X 的样本, 试证:2121()2X X -为2σ的无偏估计.证 因为22212112211[()][(2)]22E X X E X X X X -=-+2222112212[()2()()]22E X E X X E X σσ=-+==,所以2121()2X X -为2σ的无偏估计.习题7-31. 选择题(1) 总体未知参数θ的置信水平为0.95的置信区间的意义是指( ). (A) 区间平均含总体95%的值. (B) 区间平均含样本95%的值.(C) 未知参数θ有95%的可靠程度落入此区间. (D) 区间有95%的可靠程度含参数θ的真值. 解 选(D).(2) 对于置信水平1-α(0<α<1), 关于置信区间的可靠程度与精确程度, 下列说法不正确的是( ).(A) 若可靠程度越高, 则置信区间包含未知参数真值的可能性越大. (B) 如果α越小, 则可靠程度越高, 精确程度越低. (C) 如果1-α越小, 则可靠程度越高, 精确程度越低. (D) 若精确程度越高, 则可靠程度越低, 而1-α越小.解 选(C )习题7-41. 某灯泡厂从当天生产的灯泡中随机抽取9只进行寿命测试, 取得数据如下(单位:小时):1050, 1100, 1080, 1120, 1250, 1040, 1130, 1300, 1200. 设灯泡寿命服从正态分布N (μ, 902), 取置信度为0.95, 试求当天生产的全部灯泡的平均寿命的置信区间.解 计算得到1141.11,x = σ2 =902. 对于α = 0.05, 查表可得/20.025 1.96z z ==α.所求置信区间为/2/2(,)(1141.11 1.96,1141.11 1.96)(1082.31,1199.91).x x z +=-=αα2. 为调查某地旅游者的平均消费水平, 随机访问了40名旅游者, 算得平均消费额为105=x 元, 样本标准差28=s 元. 设消费额服从正态分布. 取置信水平为0.95, 求该地旅游者的平均消费额的置信区间.解 计算可得105,x = s 2 =282.对于α = 0.05, 查表可得0.0252(1)(39) 2.0227t n t α-==.所求μ的置信区间为22((1),(1))(105 2.0227,105 2.0227)x n x n αα--+-=+=(96.045, 113.955).3. 假设某种香烟的尼古丁含量服从正态分布. 现随机抽取此种香烟8支为一组样本, 测得其尼古丁平均含量为18.6毫克, 样本标准差s =2.4毫克. 试求此种香烟尼古丁含量的总体方差的置信水平为0.99的置信区间.解 已知n =8, s 2 =2.42, α = 0.01, 查表可得220.0052(1)(7)20.278n αχχ-==, 220.99512(1)(7)0.989n αχχ--==, 所以方差σ 2的置信区间为2222122(1)(1)(,)(1)(1)n S n S n n ααχχ---=--22(81) 2.4(81) 2.4(,)20.2780.989-⨯-⨯=(1.988, 40.768). 4. 某厂利用两条自动化流水线灌装番茄酱, 分别从两条流水线上抽取样本:X 1,X 2,…,X 12及Y 1,Y 2,…,Y 17, 算出221210.6g,9.5g, 2.4, 4.7x y s s ====. 假设这两条流水线上装的番茄酱的重量都服从正态分布, 且相互独立, 其均值分别为12,μμ. 又设两总体方差2212σσ=. 求12μμ-置信水平为0.95的置信区间,并说明该置信区间的实际意义.解 由题设22121210.6,9.5, 2.4, 4.7,12,17,x y s s n n ======2222112212(1)(1)(121) 2.4(171) 4.71.94212172wn s n s s n n -+--⨯+-⨯===+-+-120.0252(2)(27) 2.05181,t n n t α+-==所求置信区间为122(()(2)((10.69.5) 2.05181 1.94x y t n n s α-±+-=-±⨯ =(-0.40,2.60).结论“21μμ-的置信水平为0.95 的置信区间是(-0.40,2.60)”的实际意义是:在两总体方差相等时, 第一个正态总体的均值1μ比第二个正态总体均值2μ大-0.40~2.60,此结论的可靠性达到95%.5. 某商场为了了解居民对某种商品的需求, 调查了100户, 得出每户月平均需求量为10公斤, 方差为9 . 如果这种商品供应10000户, 取置信水平为0.99.(1) 取置信度为0.99,试对居民对此种商品的平均月需求量进行区间估计; (2) 问最少要准备多少这种商品才能以99%的概率满足需要? 解 (1) 每户居民的需求量的置信区间为2222((1),(1))()(10 2.575,10 2.575)(9.2275,10.7725).,x n x n x z x αααα-+-≈+=-=10000户居民对此种商品月需求量的置信度为0.99的置信区间为(92275,107725);(2)最少要准备92275公斤商品才能以99%的概率满足需要.。
概率与数理统计_习题集(含答案)
《概率与数理统计》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《概率与数理统计》(编号为01008)共有计算题1,计算题2等多种试题类型,其中,本习题集中有[]等试题类型未进入。
一、计算题11.设A,B,C表示三个随机事件,试将下列事件用A,B,C表示出来。
(1) A出现,B、C不出现;(2) A、B都出现,而C不出现;(3) 所有三个事件都出现;(4) 三个事件中至少一个出现;(5) 三个事件中至少两个出现。
2.在分别标有1,2,3,4,5,6,7,8的八张卡片中任抽一张。
设事件A为“抽得一张标号不大于4的卡片”,事件B为“抽得一张标号为偶数的卡片”,事件C为“抽得一张标号为奇数的卡片”。
试用样本点表示下列事件:(1)AB;(2)A+B;(3)B;(4)A-B;(5)BC3.写出下列随机试验的样本空间:(1)一枚硬币掷二次,观察能出现的各种可能结果;(2)对一目标射击,直到击中4次就停止射击的次数;(3)二只可辨认的球,随机地投入二个盒中,观察各盒装球情况。
4.设A,B,C为三事件,用A,B,C的运算关系表示下列事件。
(1)A发生,B与C不发生;(2)A,B,C都发生;(3)A,B,C中不多于一个发生。
5.甲、乙、丙三人各向目标射击一发子弹,以A、B、C分别表示甲、乙、丙命中目标。
试用A、B、C的运算关系表示下列事件:(1)至少有一人命中目标(2)恰有一人命中目标(3)恰有二人命中目标 (4)最多有一人命中目标 (5)三人均命中目标6. 袋内有5个白球与3个黑球。
从其中任取两个球,求取出的两个球都是白球的概率。
7. 两台车床加工同样的零件,第一台出现废品的概率是0.03,第二台出现废品的概率是0.02。
加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍,求任意取出的零件是合格品的概率。
8. 某地区的电话号码由7个数字组成(首位不能为0),每个数字可从0,1,2,…,9中任取,假定该地区的电话用户已经饱和,求从电话码薄中任选一个号码的前两位数字为24的概率。
概率论与数理统计习题1及答案
概率论与数理统计习题及答案习题 一1.写出下列随机试验的样本空间及下列事件包含的样本点. (1) 掷一颗骰子,出现奇数点. (2) 掷二颗骰子,A =“出现点数之和为奇数,且恰好其中有一个1点.”B =“出现点数之和为偶数,但没有一颗骰子出现1点.” (3)将一枚硬币抛两次, A =“第一次出现正面.” B =“至少有一次出现正面.”C =“两次出现同一面.” 【解】{}{}1123456135A Ω==(),,,,,,,,;{}{}{}{}{}(2)(,)|,1,2,,6,(12),(14),(16),(2,1),(4,1),(6,1),(22),(24),(26),(3,3),(3,5),(4,2),(4,4),(4,6),(5,3),(5,5),(6,2),(6,4),(6,6);(3)(,),(,),(,),(,),(,),(,),(,),(,),(i j i j A B A B ΩΩ=======,,,,,,正反正正反正反反正正正反正正正反反{}{},),(,),(,),C =正正正反反2.设A ,B ,C 为三个事件,试用A ,B ,C 的运算关系式表示下列事件: (1) A 发生,B ,C 都不发生; (2) A 与B 发生,C 不发生; (3) A ,B ,C 都发生;(4) A ,B ,C 至少有一个发生; (5) A ,B ,C 都不发生; (6) A ,B ,C 不都发生;(7) A ,B ,C 至多有2个发生; (8) A ,B ,C 至少有2个发生. 【解】(1) A BC (2) AB C (3) ABC(4) A ∪B ∪C =AB C ∪A B C ∪A BC ∪A BC ∪A B C ∪AB C ∪ABC =ABC(5) ABC =A B C (6) ABC(7) A BC ∪A B C ∪AB C ∪AB C ∪A BC ∪A B C ∪ABC =ABC =A ∪B ∪C (8) AB ∪BC ∪CA =AB C ∪A B C ∪A BC ∪ABC5.设A ,B 为随机事件,且P (A )=0.7,P (A -B )=0.3,求P (AB ). 【解】 P (AB )=1-P (AB )=1-[P (A )-P (A -B )]=1-[0.7-0.3]=0.67.设A ,B 是两事件,且P (A )=0.6,P (B )=0.7,求: (1) 在什么条件下P (AB )取到最大值? (2) 在什么条件下P (AB )取到最小值? 【解】(1) 当AB =A 时,P (AB )取到最大值为0.6.(2) 当A ∪B =Ω时,P (AB )取到最小值为0.3.9.对一个五人学习小组考虑生日问题: (1) 求五个人的生日都在星期日的概率; (2) 求五个人的生日都不在星期日的概率; (3) 求五个人的生日不都在星期日的概率. 【解】(1) 设A 1={五个人的生日都在星期日},基本事件总数为75,有利事件仅1个,故 P (A 1)=517=(17)5(亦可用独立性求解,下同) (2) 设A 2={五个人生日都不在星期日},有利事件数为65,故P (A 2)=5567=(67)5(3) 设A 3={五个人的生日不都在星期日}P (A 3)=1-P (A 1)=1-(17)510. 从一批由45件正品,5件次品组成的产品中任取3件,求其中恰有一件次品的概率. 【解】与次序无关,是组合问题.从50个产品中取3个,有350C 种取法.因只有一件次品,所以从45个正品中取2个,共245C 种取法;从5个次品中取1个,共15C 种取法,由乘法原理,恰有一件次品的取法为245C 15C种,所以所求概率为21455350C C P C =.11.一批产品共N 件,其中M 件正品.从中随机地取出n 件(n <N ).试求其中恰有m 件(m ≤M )正品(记为A )的概率.如果:(1) n 件是同时取出的;(2) n 件是无放回逐件取出的; (3) n 件是有放回逐件取出的.【解】(1) P (A )=C C /C m n m nM N M N --(2) 由于是无放回逐件取出,可用排列法计算.样本点总数有P nN 种,n 次抽取中有m次为正品的组合数为C mn 种.对于固定的一种正品与次品的抽取次序,从M 件正品中取m 件的排列数有P mM 种,从N -M 件次品中取n -m 件的排列数为P n mN M --种,故P (A )=C P P P m m n mn M N MnN -- 由于无放回逐渐抽取也可以看成一次取出,故上述概率也可写成P (A )=C C C m n mM N MnN-- 可以看出,用第二种方法简便得多.(3) 由于是有放回的抽取,每次都有N 种取法,故所有可能的取法总数为N n 种,n次抽取中有m 次为正品的组合数为C mn 种,对于固定的一种正、次品的抽取次序,m 次取得正品,都有M 种取法,共有M m 种取法,n -m 次取得次品,每次都有N -M 种取法,共有(N -M )n -m 种取法,故()C ()/m m n mn n P A M N M N -=- 此题也可用贝努里概型,共做了n 重贝努里试验,每次取得正品的概率为MN,则取得m 件正品的概率为()C 1m n mm n M M P A N N -⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭12. 50只铆钉随机地取来用在10个部件上,每个部件用3只铆钉.其中有3个铆钉强度太弱.若将3只强度太弱的铆钉都装在一个部件上,则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少? 【解】设A ={发生一个部件强度太弱}133103501()C C /C 1960P A ==13.一个袋内装有大小相同的7个球,其中4个是白球,3个是黑球,从中一次抽取3个,计算至少有两个是白球的概率. 【解】 设A i ={恰有i 个白球}(i =2,3),显然A 2与A 3互斥.213434233377C C C 184(),()C 35C 35P A P A ====故 232322()()()35P A A P A P A =+=14.有甲、乙两批种子,发芽率分别为0.8和0.7,在两批种子中各随机取一粒,求:(1) 两粒都发芽的概率; (2) 至少有一粒发芽的概率; (3) 恰有一粒发芽的概率.【解】设A i ={第i 批种子中的一粒发芽},(i =1,2)(1) 1212()()()0.70.80.56P A A P A P A ==⨯= (2) 12()0.70.80.70.80.94P A A =+-⨯=(3) 2112()0.80.30.20.70.38P A A A A =⨯+⨯=15.掷一枚均匀硬币直到出现3次正面才停止.(1) 问正好在第6次停止的概率;(2) 问正好在第6次停止的情况下,第5次也是出现正面的概率.【解】(1) 223151115()()22232p C ==(2) 1342111C ()()22245/325p ==18.某地某天下雪的概率为0.3,下雨的概率为0.5,既下雪又下雨的概率为0.1,求:(1) 在下雨条件下下雪的概率;(2) 这天下雨或下雪的概率. 【解】 设A ={下雨},B ={下雪}.(1) ()0.1()0.2()0.5P AB p B A P A === (2) ()()()()0.30.50.10.7p A B P A P B P AB =+-=+-=19.已知一个家庭有3个小孩,且其中一个为女孩,求至少有一个男孩的概率(小孩为男为女是等可能的).【解】 设A ={其中一个为女孩},B ={至少有一个男孩},样本点总数为23=8,故()6/86()()7/87P AB P B A P A ===或在缩减样本空间中求,此时样本点总数为7.6()7P B A =20.已知5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是男人的概率(假设男人和女人各占人数的一半).【解】 设A ={此人是男人},B ={此人是色盲},则由贝叶斯公式()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.50.05200.50.050.50.002521⨯==⨯+⨯ 21.两人约定上午9∶00~10∶00在公园会面,求一人要等另一人半小时以上的概率.题21图 题22图【解】设两人到达时刻为x,y ,则0≤x ,y ≤60.事件“一人要等另一人半小时以上”等价于|x -y |>30.如图阴影部分所示.22301604P ==22.从(0,1)中随机地取两个数,求:(1) 两个数之和小于65的概率; (2) 两个数之积小于14的概率.【解】 设两数为x ,y ,则0<x ,y <1. (1) x +y <65. 11441725510.68125p =-==(2) xy =<14.1111244111d d ln 242x p x y ⎛⎫=-=+⎪⎝⎭⎰⎰23.设P (A )=0.3,P (B )=0.4,P (A B )=0.5,求P (B |A ∪B ) 【解】 ()()()()()()()()P AB P A P AB P B AB P A B P A P B P AB -==+- 0.70.510.70.60.54-==+-24.在一个盒中装有15个乒乓球,其中有9个新球,在第一次比赛中任意取出3个球,比赛后放回原盒中;第二次比赛同样任意取出3个球,求第二次取出的3个球均为新球的概率.【解】 设A i ={第一次取出的3个球中有i 个新球},i =0,1,2,3.B ={第二次取出的3球均为新球}由全概率公式,有3()()()i i i P B P B A P A ==∑33123213336996896796333333331515151515151515C C C C C C C C C C C C C C C C C C =•+•+•+•0.089=25. 按以往概率论考试结果分析,努力学习的学生有90%的可能考试及格,不努力学习的学生有90%的可能考试不及格.据调查,学生中有80%的人是努力学习的,试问: (1)考试及格的学生有多大可能是不努力学习的人? (2)考试不及格的学生有多大可能是努力学习的人? 【解】设A ={被调查学生是努力学习的},则A ={被调查学生是不努力学习的}.由题意知P(A )=0.8,P (A )=0.2,又设B ={被调查学生考试及格}.由题意知P (B |A )=0.9,P (B |A )=0.9,故由贝叶斯公式知(1)()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.20.110.027020.80.90.20.137⨯===⨯+⨯即考试及格的学生中不努力学习的学生仅占2.702% (2) ()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.80.140.30770.80.10.20.913⨯===⨯+⨯即考试不及格的学生中努力学习的学生占30.77%.26. 将两信息分别编码为A 和B 传递出来,接收站收到时,A 被误收作B 的概率为0.02,而B 被误收作A 的概率为0.01.信息A 与B 传递的频繁程度为2∶1.若接收站收到的信息是A ,试问原发信息是A 的概率是多少?【解】 设A ={原发信息是A },则={原发信息是B }C ={收到信息是A },则={收到信息是B } 由贝叶斯公式,得()()()()()()()P A P C A P A C P A P C A P A P C A =+2/30.980.994922/30.981/30.01⨯==⨯+⨯27.在已有两个球的箱子中再放一白球,然后任意取出一球,若发现这球为白球,试求箱子中原有一白球的概率(箱中原有什么球是等可能的颜色只有黑、白两种) 【解】设A i ={箱中原有i 个白球}(i =0,1,2),由题设条件知P (A i )=13,i =0,1,2.又设B ={抽出一球为白球}.由贝叶斯公式知11112()()()()()()()i i i P B A P A P A B P A B P B P B A P A ===∑ 2/31/311/31/32/31/311/33⨯==⨯+⨯+⨯28.某工厂生产的产品中96%是合格品,检查产品时,一个合格品被误认为是次品的概率为0.02,一个次品被误认为是合格品的概率为0.05,求在被检查后认为是合格品产品确是合格品的概率.【解】 设A ={产品确为合格品},B ={产品被认为是合格品}由贝叶斯公式得()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.960.980.9980.960.980.040.05⨯==⨯+⨯29.某保险公司把被保险人分为三类:“谨慎的”,“一般的”,“冒失的”.统计资料表明,上述三种人在一年内发生事故的概率依次为0.05,0.15和0.30;如果“谨慎的”被保险人占20%,“一般的”占50%,“冒失的”占30%,现知某被保险人在一年内出了事故,则他是“谨慎的”的概率是多少?【解】 设A ={该客户是“谨慎的”},B ={该客户是“一般的”},C ={该客户是“冒失的”},D ={该客户在一年内出了事故} 则由贝叶斯公式得()()(|)(|)()()(|)()(|)()(|)P AD P A P D A P A D P D P A P D A P B P D B P C P D C ==++0.20.050.0570.20.050.50.150.30.3⨯==⨯+⨯+⨯30.加工某一零件需要经过四道工序,设第一、二、三、四道工序的次品率分别为0.02,0.03,0.05,0.03,假定各道工序是相互独立的,求加工出来的零件的次品率. 【解】设A i ={第i 道工序出次品}(i =1,2,3,4).412341()1()i i P A P A A A A ==-12341()()()()P A P A P A P A =-10.980.970.950.970.124=-⨯⨯⨯= 31.设每次射击的命中率为0.2,问至少必须进行多少次独立射击才能使至少击中一次的概率不小于0.9?【解】设必须进行n 次独立射击.1(0.8)0.9n -≥即为 (0.8)0.1n≤ 故 n ≥11 至少必须进行11次独立射击.32.证明:若P (A |B )=P (A |B ),则A ,B 相互独立.【证】 (|)(|)P A B P A B =即()()()()P AB P AB P B P B =亦即 ()()()()P AB P B P AB P B =()[1()][()()]()P AB P B P A P AB P B -=-因此 ()()()P AB P A P B = 故A 与B 相互独立. 33.三人独立地破译一个密码,他们能破译的概率分别为15,13,14,求将此密码破译出的概率.【解】 设A i ={第i 人能破译}(i =1,2,3),则31231231()1()1()()()i i P A P A A A P A P A P A ==-=-42310.6534=-⨯⨯= 34.甲、乙、丙三人独立地向同一飞机射击,设击中的概率分别是0.4,0.5,0.7,若只有一人击中,则飞机被击落的概率为0.2;若有两人击中,则飞机被击落的概率为0.6;若三人都击中,则飞机一定被击落,求:飞机被击落的概率. 【解】设A ={飞机被击落},B i ={恰有i 人击中飞机},i =0,1,2,3由全概率公式,得3()(|)()i i i P A P A B P B ==∑=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)0.2+(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)0.6+0.4×0.5×0.7 =0.45835.已知某种疾病患者的痊愈率为25%,为试验一种新药是否有效,把它给10个病人服用,且规定若10个病人中至少有四人治好则认为这种药有效,反之则认为无效,求: (1) 虽然新药有效,且把治愈率提高到35%,但通过试验被否定的概率. (2) 新药完全无效,但通过试验被认为有效的概率. 【解】(1) 310110C(0.35)(0.65)0.5138k k k k p -===∑(2) 10102104C(0.25)(0.75)0.2241kk k k p -===∑36.一架升降机开始时有6位乘客,并等可能地停于十层楼的每一层.试求下列事件的概率:(1) A =“某指定的一层有两位乘客离开”;(2) B =“没有两位及两位以上的乘客在同一层离开”; (3) C =“恰有两位乘客在同一层离开”; (4) D =“至少有两位乘客在同一层离开”.【解】 由于每位乘客均可在10层楼中的任一层离开,故所有可能结果为106种.(1) 2466C 9()10P A =,也可由6重贝努里模型: 224619()C ()()1010P A =(2) 6个人在十层中任意六层离开,故6106P ()10P B =(3) 由于没有规定在哪一层离开,故可在十层中的任一层离开,有110C 种可能结果,再从六人中选二人在该层离开,有26C 种离开方式.其余4人中不能再有两人同时离开的情况,因此可包含以下三种离开方式:①4人中有3个人在同一层离开,另一人在其余8层中任一层离开,共有131948C C C 种可能结果;②4人同时离开,有19C 种可能结果;③4个人都不在同一层离开,有49P 种可能结果,故1213114610694899()C C (C C C C P )/10P C =++(4) D=B .故6106P ()1()110P D P B =-=-37. n 个朋友随机地围绕圆桌而坐,求下列事件的概率: (1) 甲、乙两人坐在一起,且乙坐在甲的左边的概率; (2) 甲、乙、丙三人坐在一起的概率;(3) 如果n 个人并排坐在长桌的一边,求上述事件的概率. 【解】 (1) 111p n =- (2) 23!(3)!,3(1)!n p n n -=>-(3) 12(1)!13!(2)!;,3!!n n p p n n n n --''===≥ 38.将线段[0,a ]任意折成三折,试求这三折线段能构成三角形的概率【解】 设这三段长分别为x ,y ,a -x -y .则基本事件集为由0<x <a ,0<y <a ,0<a -x -y <a 所构成的图形,有利事件集为由()()x y a x y x a x y y y a x y x+>--⎡⎢+-->⎢⎢+-->⎣ 构成的图形,即02022a x a y ax y a ⎡<<⎢⎢⎢<<⎢⎢⎢<+<⎢⎣如图阴影部分所示,故所求概率为14p =. 39. 某人有n 把钥匙,其中只有一把能开他的门.他逐个将它们去试开(抽样是无放回的).证明试开k 次(k =1,2,…,n )才能把门打开的概率与k 无关.【证】 11P 1,1,2,,P k n k n p k n n--===40.把一个表面涂有颜色的立方体等分为一千个小立方体,在这些小立方体中,随机地取出一个,试求它有i 面涂有颜色的概率P (A i )(i =0,1,2,3). 【解】 设A i ={小立方体有i 面涂有颜色},i =0,1,2,3.在1千个小立方体中,只有位于原立方体的角上的小立方体是三面有色的,这样的小立方体共有8个.只有位于原立方体的棱上(除去八个角外)的小立方体是两面涂色的,这样的小立方体共有12×8=96个.同理,原立方体的六个面上(除去棱)的小立方体是一面涂色的,共有8×8×6=384个.其余1000-(8+96+384)=512个内部的小立方体是无色的,故所求概率为01512384()0.512,()0.38410001000P A P A ====,24968()0.096,()0.00810001000P A P A ====. 41.对任意的随机事件A ,B ,C ,试证P (AB )+P (AC )-P (BC )≤P (A ).【证】 ()[()]()P A P A B C P AB AC ≥=()()()P AB P AC P ABC =+-()()()P AB P AC P BC ≥+-42.将3个球随机地放入4个杯子中去,求杯中球的最大个数分别为1,2,3的概率.【解】 设i A ={杯中球的最大个数为i },i =1,2,3.将3个球随机放入4个杯子中,全部可能放法有43种,杯中球的最大个数为1时,每个杯中最多放一球,故3413C 3!3()48P A == 而杯中球的最大个数为3,即三个球全放入一个杯中,故1433C 1()416P A == 因此 213319()1()()181616P A P A P A =--=--= 或 12143323C C C 9()416P A == 43.将一枚均匀硬币掷2n 次,求出现正面次数多于反面次数的概率.【解】掷2n 次硬币,可能出现:A ={正面次数多于反面次数},B ={正面次数少于反面次数},C ={正面次数等于反面次数},A ,B ,C 两两互斥.可用对称性来解决.由于硬币是均匀的,故P (A )=P (B ).所以1()()2P C P A -= 由2n 重贝努里试验中正面出现n 次的概率为211()()()22n n n n P C C = 故 2211()[1C ]22n n n P A =- 44.掷n 次均匀硬币,求出现正面次数多于反面次数的概率.【解】设A ={出现正面次数多于反面次数},B ={出现反面次数多于正面次数},由对称性知P (A )=P (B )(1) 当n 为奇数时,正、反面次数不会相等.由P (A )+P (B )=1得P (A )=P (B )=0.5(2) 当n 为偶数时,由上题知211()[1C ()]22n n n P A =- 45.设甲掷均匀硬币n +1次,乙掷n 次,求甲掷出正面次数多于乙掷出正面次数的概率.【解】 令甲正=甲掷出的正面次数,甲反=甲掷出的反面次数.乙正=乙掷出的正面次数,乙反=乙掷出的反面次数.显然有>正正(甲乙)=(甲正≤乙正)=(n +1-甲反≤n -乙反) =(甲反≥1+乙反)=(甲反>乙反)由对称性知P(甲正>乙正)=P (甲反>乙反)因此P (甲正>乙正)=1246.证明“确定的原则”(Sure -thing ):若P (A |C )≥P (B |C ),P (A |C )≥P (B |C ),则P (A )≥P (B ).【证】由P (A |C )≥P (B |C ),得()(),()()P AC P BC P C P C ≥ 即有 ()()P AC P BC ≥同理由 (|)(|),P A C P B C ≥得 ()(),P AC P BC ≥故 ()()()()()()P A P AC P AC P BC P BC P B =+≥+=47.一列火车共有n 节车厢,有k (k ≥n )个旅客上火车并随意地选择车厢.求每一节车厢内至少有一个旅客的概率.【解】 设A i ={第i 节车厢是空的},(i =1,…,n ),则121(1)1()(1)2()(1)1()(1)n k k i k k i j k i i i n P A n nP A A nn P A A A n --==-=--=-其中i 1,i 2,…,i n -1是1,2,…,n 中的任n -1个.显然n 节车厢全空的概率是零,于是2112111122111111123111()(1)C (1)2()C (1)1()C (1)0()(1)n n nk k i n i ki j n i j n n k n i i i n i i i n n n n i ni S P A n n n S P A A n n S P A A A n S P A S S S S --=≤<≤--≤<<≤+===-=-==--==-==-+-+-∑∑∑121121C (1)C (1)(1)C (1)k k n n k n n n n n n n--=---++-- 故所求概率为 121121()1C (1)C (1)n k i i n n i P A n n =-=--+--+111(1)C (1)n nk n n n+---- 48.设随机试验中,某一事件A 出现的概率为ε>0.试证明:不论ε>0如何小,只要不断地独立地重复做此试验,则A 迟早会出现的概率为1.【证】在前n 次试验中,A 至少出现一次的概率为1(1)1()n n ε--→→∞49.袋中装有m 只正品硬币,n 只次品硬币(次品硬币的两面均印有国徽).在袋中任取一只,将它投掷r 次,已知每次都得到国徽.试问这只硬币是正品的概率是多少?【解】设A ={投掷硬币r 次都得到国徽}B ={这只硬币为正品}由题知 (),()m n P B P B m n m n==++ 1(|),(|)12r P A B P A B == 则由贝叶斯公式知()()(|)(|)()()(|)()(|)P AB P B P A B P B A P A P B P A B P B P A B ==+ 121212r r r m m m n m n m nm n m n+==++++ 50.巴拿赫(Banach )火柴盒问题:某数学家有甲、乙两盒火柴,每盒有N 根火柴,每次用火柴时他在两盒中任取一盒并从中任取一根.试求他首次发现一盒空时另一盒恰有r 根的概率是多少?第一次用完一盒火柴时(不是发现空)而另一盒恰有r 根的概率又有多少?【解】以B 1、B 2记火柴取自不同两盒的事件,则有121()()2P B P B ==.(1)发现一盒已空,另一盒恰剩r 根,说明已取了2n -r 次,设n 次取自B 1盒(已空),n -r 次取自B 2盒,第2n -r +1次拿起B 1,发现已空。
概率论与数理统计练习题附答案详解
概率论与数理统计练习题附答案详解第⼀章《随机事件及概率》练习题⼀、单项选择题1、设事件A 与B 互不相容,且P (A )>0,P (B )>0,则⼀定有()(A )()1()P A P B =-;(B )(|)()P A B P A =;(C )(|)1P A B =;(D )(|)1P A B =。
2、设事件A 与B 相互独⽴,且P (A )>0,P (B )>0,则()⼀定成⽴(A )(|)1()P A B P A =-;(B )(|)0P A B =;(C )()1()P A P B =-;(D )(|)()P A B P B =。
3、设事件A 与B 满⾜P (A )>0,P (B )>0,下⾯条件()成⽴时,事件A 与B ⼀定独⽴(A )()()()P AB P A P B =;(B )()()()P A B P A P B =;(C )(|)()P A B P B =;(D )(|)()P A B P A =。
4、设事件A 和B 有关系B A ?,则下列等式中正确的是()(A )()()P AB P A =;(B )()()P AB P A =;(C )(|)()P B A P B =;(D )()()()P B A P B P A -=-。
5、设A 与B 是两个概率不为0的互不相容的事件,则下列结论中肯定正确的是()(A )A 与B 互不相容;(B )A 与B 相容;(C )()()()P AB P A P B =;(D )()()P A B P A -=。
6、设A 、B 为两个对⽴事件,且P (A )≠0,P (B ) ≠0,则下⾯关系成⽴的是()(A )()()()P AB P A P B =+;(B )()()()P A B P A P B ≠+;(C )()()()P AB P A P B =;(D )()()()P AB P A P B =。
7、对于任意两个事件A 与B ,()P A B -等于()(A )()()P A P B - (B )()()()P A P B P AB -+;(C )()()P A P AB -;(D )()()()P A P B P AB +-。
概率论与数理统计题库及答案
概率论与数理统计题库及答案一、单选题1. 在下列数组中,( )中的数组可以作为离散型随机变量的概率分布.(A) 51,41,31,21 (B) 81,81,41,21 (C) 21,21,21,21- (D) 161,81,41,212. 下列数组中,( )中的数组可以作为离散型随机变量的概率分布.(A) 41414121(B)161814121(C)1631614121 (D)81834121-3. 设连续型随机变量X 的密度函数⎩⎨⎧<<=,,0,10,2)(其他x x x f 则下列等式成立的是( ).(A) X P (≥1)1=- (B) 21)21(==X P (C) 21)21(=<X P (D) 21)21(=>X P4. 若)(x f 与)(x F 分别为连续型随机变量X 的密度函数与分布函数,则等式( )成立.(A) X a P <(≤⎰∞+∞-=x x F b d )() (B) X a P <(≤⎰=bax x F b d )()(C) X a P <(≤⎰=bax x f b d )() (D) X a P <(≤⎰∞+∞-=x x f b d )()5. 设)(x f 和)(x F 分别是随机变量X 的分布密度函数和分布函数,则对任意b a <,有X a P <(≤=)b ( ). (A)⎰bax x F d )( (B)⎰bax x f d )((C) )()(a f b f - (D) )()(b F a F -6. 下列函数中能够作为连续型随机变量的密度函数的是( ).7. 设⎥⎦⎤⎢⎣⎡2.04.03.01.03210~X ,则=<)2(X P ( ). (A) 0.1 (B) 0.4 (C) 0.3 (D) 0.28. 设)1,0(~N X ,Φ)(x 是X 的分布函数,则下列式子不成立的是( ).(A) Φ5.0)0(= (B) Φ+-)(x Φ1)(=x (C) Φ=-)(a Φ)(a (D) 2)(=<a x P Φ1)(-a9. 下列数组中,不能作为随机变量分布列的是( ).(A )61,61,31,31 (B) 104,103,102,101 (C) 12141818,,, (D) 131619112,,,10. 若随机变量)1,0(~N X ,则~23-=X Y ( ).(A) )3,2(-N (B) )3,4(-N (C) )3,4(2-N (D) )3,2(2-N11. 随机变量X 服从二项分布),(p n B ,则有=)()(X E X D ( ). (A) n (B) p (C) 1- p (D)p-1112. 如果随机变量X B ~(,.)1003,则E X D X (),()分别为( ).(A) E X D X (),().==321(B) 9.0)(,3)(==X D X E(C) E X D X ().,()==033 (D) E X D X ().,().==032113. 设),(~p n B X ,2.1)(,2)(==X D X E ,则p n ,分别是( ).(A) 4.0,5 (B) 2.0,10 (C) 5.0,4 (D) 25.0,814. 设),(~p n B X ,且6.3)(,6)(==X D X E ,则=n ( ).(A) 30 (B) 20(C) 15 (D) 1015. 设)10,50(~2N X ,则随机变量( )~)1,0(N .(A)10050-X (B) 1050-X (C) 50100-X (D) 5010-X16. 对于随机事件A B ,,下列运算公式( )成立.(A) )()()(B P A P B A P +=+ (B) )()()(B P A P AB P =(C) )()()(A B P B P AB P = (D) )()()()(AB P B P A P B A P -+=+17. 下列事件运算关系正确的是( ).(A) A B BA B += (B) A B BA B += (C) A B BA B += (D) B B -=118. 设A ,B 为两个任意事件,那么与事件B A B A B A ++相等的事件是().(A) AB (B) B A + (C) A (D) B19. 设A B ,为随机事件,A 与B 不同时发生用事件的运算表示为( ).(A) A B + (B) A B + (C) AB AB + (D) A B20. 若随机事件A ,B 满足AB =∅,则结论( )成立. (A) A 与B 是对立事件 (B) A 与B 相互独立(C) A 与B 互不相容 (D) A 与B 互不相容21. 甲、乙二人射击,A B ,分别表示甲、乙射中目标,则AB 表示( )的事件.(A) 二人都没射中 (B) 至少有一人没射中 (C) 两人都射中 (D) 至少有一人射中22. 若事件A B ,的概率为6.0)(=A P ,5.0)(=B P ,则A 与B 一定( ).(A) 相互对立 (B) 相互独立 (C) 互不相容 (D) 相容23. 设A ,B 为两个任意事件,则P (A +B ) =( ).(A) P (A ) + P (B ) (B) P (A ) + P (B ) - P (A )P (B ) (C) P (A ) + P (B ) - P (AB ) (D) P (AB ) – [P (A ) + P (B ) ]24. 对任意两个任意事件A B ,,等式( )成立.(A) P AB P A P B ()()()= (B) P A B P A P B ()()()+=+ (C) P A B P A P B ()()(())=≠0 (D) P AB P A P B A P A ()()()(())=≠025. 设A ,B 是两个任意事件,则下列等式中( )是不正确的.(A) )()()(B P A P AB P =,其中A ,B 相互独立 (B) )()()(B A P B P AB P =,其中0)(≠B P (C) )()()(B P A P AB P =,其中A ,B 互不相容 (D) )()()(A B P A P AB P =,其中0)(≠A P26. 若事件A 与B 互斥,则下列等式中正确的是( ). (A) P AB P A P B ()()()= (B) P B P A ()()=-1(C) P A P A B ()()= (D) P A B P A P B ()()()+=+27. 设A ,B 为两个任意事件,则下列等式成立的是( ).(A) B A B A +=+ (B) B A AB ⋅= (C) B A B B A +=+ (D) B A B B A +=+28. 设A B ,为随机事件,下列等式成立的是( ).(A) )()()(B P A P B A P -=- (B) )()()(B P A P B A P +=+ (C) )()()(B P A P B A P +=+ (D) )()()(AB P A P B A P -=-29. 甲、乙两人各自考上大学的概率分别为0.7,0.8,则甲、乙两人同时考上大学的概率为( ).(A) 0.56 (B) 0.50 (C) 0.75 (D) 0.9430. 若A B ,满足( ),则A 与B 是对立事件.(A) 1)(=+B A P (B) A B U AB +==∅, (C) P A B P A P B ()()()+=+ (D) P AB P A P B ()()()=31. 若A 与B 相互独立,则等式( )成立.(A) P A B P A P B ()()()+=+ (B) P AB P A ()()=(C) P A B P A ()()= (D) P AB P A P B ()()()=32. 设n x x x ,,,21 是正态总体),(2σμN (2σ已知)的一个样本,按给定的显著性水平α检验0H :0μμ=(已知);1H :0μμ≠时,判断是否接受0H 与( )有关. (A) 样本值,显著水平α (B) 样本值,样本容量(C) 样本容量n ,显著水平α (D) 样本值,样本容量n ,显著水平α33. 假设检验时,若增大样本容量,则犯两类错误的概率( ). (A) 有可能都增大 (B) 有可能都减小(C) 有可能都不变 (D) 一定一个增大,一个减小34. 从正态总体),(2σμN 中随机抽取容量为n 的样本,检验假设0H :,0μμ=1H :0μμ≠.若用t 检验法,选用统计量t ,则在显著性水平α下的拒绝域为( ). (A) )1(-<n t t α (B) t ≥)1(1--n t α (C) )1(->n t t α (D) )1(1--<-n t t α35. 在对单正态总体N (,)μσ2的假设检验问题中,T 检验法解决的问题是( ).(A) 已知方差,检验均值 (B) 未知方差,检验均值 (C) 已知均值,检验方差 (D) 未知均值,检验方差36. 对正态总体),(2σμN 的假设检验问题中,U 检验解决的问题是( ).(A) 已知方差,检验均值 (B) 未知方差,检验均值 (C) 已知均值,检验方差 (D) 未知均值,检验方差37. 设n x x x ,,,21 是正态总体),(2σμN 的一个样本,2σ是已知参数,μ是未知参数,记∑==ni i x n x 11,函数)(x Φ表示标准正态分布)1,0(N 的分布函数,975.0)96.1(=Φ,900.0)28.1(=Φ,则μ的置信水平为0.95的置信区间为( ).(A) (x -0.975n σ,x +0.975nσ) (B) (x -1.96n σ,x +1.96n σ)(C) (x -1.28nσ,x +1.28nσ) (D) (x -0.90nσ,x +0.90nσ)38. 设321,,x x x 是来自正态总体N (,)μσ2的样本,则μ的无偏估计是( ).(A)3321x x x -+ (B) 321x x x -+(C) 321x x x ++ (D) 321x x x --39. 设x x x n 12,,, 是来自正态总体N (,)μσ2的样本,则( )是μ无偏估计.(A) 321x x x ++ (B)321525252x x x ++ (C) 321515151x x x ++ (D) 321535151x x x ++40. 设21,x x 是取自正态总体)1,(μN 的容量为2的样本,其中μ为未知参数,以下关于μ的估计中,只有( )才是μ的无偏估计.(A) 213432x x + (B) 214241x x + (C) 214143x x - (D)215352x x +41. 设总体X 的均值μ与方差2σ都存在,且均为未知参数,而n x x x ,,,21 是该总体的一个样本,记∑==ni i x n x 11,则总体方差2σ的矩估计为( ).(A) x (B) ∑=-ni i x n 12)(1μ(C) ∑=-n i i x x n 12)(1 (D) ∑=n i i x n 12142. 设n x x x ,,,21 是来自正态总体22,)(,(σμσμN 均未知)的样本,则( )是统计量.(A) 1x (B) μ+x (C)221σx (D)1x μ43. 对来自正态总体X N ~(,)μσ2(μ未知)的一个样本X X X 123,,,∑==3131i i X X ,则下列各式中( )不是统计量. (A ) X (B)∑=31i iX(C) ∑=-312)(31i i X μ (D) ∑=-312)(31i i X X44. 设X 是连续型随机变量,其密度函数为⎩⎨⎧∉∈=],,1(,0],,1(,ln )(b x b x x x f 则常数b =( ).(A) e (B) e + 1 (C) e – 1 (D) e 245. 随机变量)21,3(~B X ,则X P (≤=)2( ).(A) 0 (B) 81(C)21 (D) 8746. 设),2(~2σN X ,已知2(P ≤X ≤4.0)4=,则X P (≤=)0( ).(A) 0.4 (B) 0.3 (C) 0.2 (D) 0.147. 已知)2,2(~2N X ,若)1,0(~N b aX +,那么( ).(A) 2,2-==b a (B) 1,2-=-=b a (C) 1,21-==b a (D) 2,21==b a48. 设随机变量X 的密度函数为f x (),则E X ()2=( ).(A) xf x x ()-∞+∞⎰d (B)x x f x d )(2⎰∞+∞-(C)x x xf d )(2⎰∞+∞- (D)(())()x E X f x x --∞+∞⎰2d49. 若随机变量X 的期望和方差分别为)(X E 和)(X D ,则等式( )成立.(A) )]([)(X E X E X D -= (B) 22)]([)()(X E X E X D += (C) )()(2X E X D = (D) 22)]([)()(X E X E X D -=50. 设随机变量X 服从二项分布B (n , p ),已知E (X )=2.4, D (X )=1.44,则( ). (A) n = 8, p =0.3 (B) n = 6, p =0.6 (C) n = 6, p =0.4 (D) n = 24, p =0.1二、证明题1. 试证:已知事件A ,B 的概率分别为P (A ) = 0.3,P (B ) = 0.6,P (B A +) = 0.1,则P (AB ) =0.2. 试证:已知事件A ,B 相互独立,则)()(1)(B P A P B A P -=+.3. 已知事件A ,B ,C 相互独立,试证)(B A +与C 相互独立.4. 设事件A ,B 的概率分别为21)(=A P ,32)(=B P ,试证:A 与B 是相容的.5. 设随机事件A ,B 相互独立,试证:B A ,也相互独立.6. 设A ,B 为随机事件,试证:)()()(AB P A P B A P -=-.7. 设随机事件A ,B 满足AB =∅,试证:P A B P B ()()+=-1.8. 设A ,B 为随机事件,试证:P A P A B P AB ()()()=-+.9. 设B A ,是随机事件,试证:)()()()(AB P B A P B A P B A P ++=+.10. 已知随机事件A ,B 满足A B ⊃,试证:)()()(B P A P B A P -=-.三、计算题1. 设B A ,是两个随机事件,已知5.0)(=A P , 4.0)(=A B P ,求)(B A P .2. 某种产品有80%是正品,用某种仪器检查时,正品被误定为次品的概率是3%,次品被误定为正品的概率是2%,设A 表示一产品经检查被定为正品,B 表示一产品确为正品,求P (A ).3. 某单位同时装有两种报警系统A 与B ,每种系统独立使用时,其有效概率9.0)(=A P ,95.0)(=B P ,在A 有效的条件下B 有效的概率为97.0)(=A B P ,求)(B A P +.4. 设A , B 是两个独立的随机事件,已知P (A ) = 0.4,P (B ) = 0.7,求A 与B 只有一个发生的概率.5. 设事件A ,B 相互独立,已知6.0)(=A P ,8.0)(=B P ,求A 与B 只有一个发生的概率.6. 假设B A ,为两事件,已知4.0)(,6.0)(,5.0)(===A B P B P A P ,求)(B A P +.7. 设随机变量)2,3(~2N X ,求概率X P <-3(≤)5 (已知Φ3841.0)1(=,Φ7998.0)3(=φ).8. 设A , B 是两个随机事件,已知P (A ) = 0.6,P (B ) = 0.8,P (A B )=0.2,求)(B A P .9. 从大批发芽率为8.0的种子中,任取4粒,问(1)4粒中恰有一粒发芽的概率是多少?(2)至少有1粒种子发芽的概率是多少?10. 已知21)(,31)(,41)(===B A P A B P A P ,求)(B A P +.11. 已知4.0)(=A P ,8.0)(=B P ,5.0)(=B A P ,求P B A ().12. 已知7.0)(=A P ,3.0)(=B P ,5.0)(=B A P ,求)(B A P .13. 已知P (B ) = 0.6,)(B A P =0.2,求)(AB P .14. 设随机变量X ~ N (3,4).求 P (1< X < 7)(Φ3841.0)1(=,Φ2977.0)2(=).15. 设)5.0,3(~2N X ,求2(P ≤X ≤)6.3.已知Φ9884.0)2.1(=,2977.0)2(=Φ.16. 设B A ,是两个随机事件,已知4.0)(=A P ,5.0)(=B P ,45.0)(=A B P ,求)(B A P +.17.已知某批零件的加工由两道工序完成,第一道工序的次品率为0.03,第二道工序的次品率为0.01,两道工序的次品率彼此无关,求这批零件的合格率.18.已知袋中有3个白球7个黑球,从中有放回地抽取3次,每次取1个,试求⑴恰有2个白球的概率;⑵有白球的概率.19. 268-16.某篮球运动员一次投篮投中篮框的概率为0.8,该运动员投篮3次,⑴求投中篮框不少于2次的概率;⑵求至少投中篮框1次的概率.20.某篮球运动员一次投篮投中篮框的概率为0.9,该运动员投篮3次,⑴求投中篮框不少于2次的概率;⑵求至少投中篮框1次的概率.21.某气象站天气预报的准确率为70%,在4次预报中,求⑴恰有3次准确的概率;⑵至少1次准确的概率.22.已知某批产品的次品率为0.1,在这批产品中有放回地抽取4次,每次抽取一件,试求⑴有次品的概率;⑵恰有两件次品的概率.23.某射手射击一次命中靶心的概率是08.,该射手连续射击5次,求:⑴命中靶心的概率;⑵至少4次命中靶心的概率.24.设箱中有3个白球2个黑球,从中依次不放回地取出3球,求第3次才取到黑球的概率.25.一袋中有10个球,其中3个黑球7个白球.今从中有放回地抽取,每次取1个,共取5次.求⑴恰有2次取到黑球的概率;⑵至少有1次取到白球的概率.26.有甲、乙两批种子,发芽率分别是0.85和0.75,在这两批种子中各随机取一粒,求至少有一粒发芽的概率.27.机械零件的加工由甲、乙两道工序完成,甲工序的次品率是0.01,乙工序的次品率是0.02,两道工序的生产彼此无关,求生产的产品是合格品的概率.28.一袋中有10个球,其中3个黑球7个白球.今从中依次无放回地抽取两个,求第2次抽取出的是黑球的概率.29. 两台车床加工同样的零件,第一台废品率是1%,第二台废品率是2%,加工出来的零件放在一起。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《概率论与数理统计》作业集及答案第1章 概率论的基本概念§1 .1 随机试验及随机事件1. (1) 一枚硬币连丢3次,观察正面H ﹑反面T 出现的情形. 样本空间是:S= ;(2) 一枚硬币连丢3次,观察出现正面的次数. 样本空间是:S= ;2.(1) 丢一颗骰子. A :出现奇数点,则A= ;B:数点大于2,则B= .(2) 一枚硬币连丢2次, A :第一次出现正面,则A = ;B:两次出现同一面,则= ; C :至少有一次出现正面,则C= .§1 .2 随机事件的运算1. 设A 、B、C 为三事件,用A 、B 、C 的运算关系表示下列各事件: (1)A 、B 、C 都不发生表示为: .(2)A 与B 都发生,而C 不发生表示为: . (3)A 与B都不发生,而C 发生表示为: .(4)A、B 、C 中最多二个发生表示为: .(5)A 、B 、C 中至少二个发生表示为: .(6)A 、B 、C 中不多于一个发生表示为: .2. 设}42:{},31:{},50:{≤<=≤<=≤≤=x B x x A x x S :则(1)=⋃B A ,(2)=AB ,(3)=B A ,(4)B A ⋃= ,(5)B A = 。
§1 .3 概率的定义和性质1. 已知6.0)(,5.0)(,8.0)(===⋃B P A P B A P ,则(1) =)(AB P , (2)()(B A P )= , (3))(B A P ⋃= .2. 已知,3.0)(,7.0)(==AB P A P 则)(B A P = .§1 .4 古典概型1. 某班有30个同学,其中8个女同学, 随机地选10个,求:(1)正好有2个女同学的概率,(2)最多有2个女同学的概率,(3) 至少有2个女同学的概率.2. 将3个不同的球随机地投入到4个盒子中,求有三个盒子各一球的概率.§1 .5 条件概率与乘法公式1.丢甲、乙两颗均匀的骰子,已知点数之和为7, 则其中一颗为1的概率是 。
2. 已知,2/1)|(,3/1)|(,4/1)(===B A P A B P A P 则=⋃)(B A P 。
§1 .6 全概率公式1. 有10个签,其中2个“中”,第一人随机地抽一个签,不放回,第二人再随机地抽一个签,说明两人抽“中‘的概率相同。
2. 第一盒中有4个红球6个白球,第二盒中有5个红球5个白球,随机地取一盒,从中随机地取一个球,求取到红球的概率。
§1 .7 贝叶斯公式1. 某厂产品有70%不需要调试即可出厂,另30%需经过调试,调试后有80%能出厂,求(1)该厂产品能出厂的概率,(2)任取一出厂产品, 求未经调试的概率。
2. 将两信息分别编码为A和B 传递出去,接收站收到时,A 被误收作B 的概率为0.02,B 被误收作A的概率为0.01,信息A 与信息B 传递的频繁程度为3 : 2,若接收站收到的信息是A,问原发信息是A 的概率是多少?§1 .8 随机事件的独立性1. 电路如图,其中A,B,C ,D 为开关。
设各开关闭合与否相互独立,且每一开关闭合的概率均为p,求L 与R为通路(用T表示)的概率。
A BL R C D3. 甲,乙,丙三人向同一目标各射击一次,命中率分别为0.4,0.5和0.6,是否命中,相互独立, 求下列概率: (1) 恰好命中一次,(2) 至少命中一次。
第1章作业答案§1 .1 1:(1)},,,,,,,{TTT TTH THT HTT THH HTH HHT HHH S =; (2)}3,2,1,0{=S2:(1)}6,5,4,3{}5,3,1{==B A ;(2){=A 正正,正反{},=B 正正,反反{},=C 正正,正反,反正}。
§1 .2 1: (1) ABC ;(2) C AB ;(3) C B A ;(4)C B A ⋃⋃;(5)BC AC AB ⋃⋃;(6) C B C A B A ⋃⋃ 或 C B A C B A C B A C B A +++; 2:(1)}41:{<<=⋃x x B A ;(2)}32:{≤≤=x x AB ;(3)}43:{<<=x x B A ;(4)10:{≤≤=⋃x x B A 或}52≤≤x ;(5)}41:{<<=x x B A 。
§1 .3 1: (1) )(AB P =0.3, (2))(B A P = 0.2, (3) )(B A P ⋃ = 0.7. 2:)(B A P )=0.4.§1 .4 1:(1)103082228/C C C ,(2)(103082228922181022/C C C C C C )(++,(3)1-(1030922181022/C C C C )+.2: 3344/P .§1 .5 1:. 2/6; 2: 1/4。
§1 .6 1: 设A 表示第一人“中”,则 P (A ) = 2/10设B 表示第二人“中”,则 P(B) = P(A )P(B|A) + P(A )P(B|A ) =1029210891102=⋅+⋅ 两人抽“中‘的概率相同, 与先后次序无关。
2: 随机地取一盒,则每一盒取到的概率都是0.5,所求概率为:p = 0.5 × 0.4 + 0.5 × 0.5 = 0.45§1 .7 1:(1)94% (2)70/94; 2: 0.993;§1 .8. 1: 用A,B,C,D表示开关闭合,于是 T = AB ∪CD, 从而,由概率的性质及A,B,C,D 的相互独立性P (T) = P(A B) + P(CD) - P(AB CD )= P (A)P(B) + P(C)P(D ) – P(A)P(B)P(C )P (D)424222p p p p p -=-+=2: (1) 0.4(1-0.5)(1-0.6)+(1-0.4)0.5(1-0.6)+(1-0.4)(1-0.5)0.6=0.38;(2) 1-(1-0.4)(1-0.5)(1-0.6)=0.88.第2章 随机变量及其分布§2.1 随机变量的概念,离散型随机变量1 一盒中有编号为1,2,3,4,5的五个球,从中随机地取3个,用X 表示取出的3个球 中的最大号码., 试写出X 的分布律.2 某射手有5发子弹,每次命中率是0.4,一次接一次地射击,直到命中为止或子弹用尽为止,用X 表示射击的次数, 试写出X 的分布律。
§2.2 10-分布和泊松分布1 某程控交换机在一分钟内接到用户的呼叫次数X 是服从λ=4的泊松分布,求(1)每分钟恰有1次呼叫的概率;(2)每分钟只少有1次呼叫的概率; (3)每分钟最多有1次呼叫的概率;2 设随机变量X 有分布律: X 2 3 , Y ~π(X ), 试求: p 0.4 0.6(1)P(X =2,Y ≤2); (2)P(Y≤2); (3) 已知 Y ≤2, 求X=2 的概率。
§2.3 贝努里分布1 一办公室内有5台计算机,调查表明在任一时刻每台计算机被使用的概率为0.6,计算机是否被使用相互独立,问在同一时刻(1) 恰有2台计算机被使用的概率是多少?(2) 至少有3台计算机被使用的概率是多少? (3) 至多有3台计算机被使用的概率是多少? (4) 至少有1台计算机被使用的概率是多少?2 设每次射击命中率为0.2,问至少必须进行多少次独立射击,才能使至少击中一次的概率不小于0.9 ?§2.4 随机变量的分布函数1设随机变量X 的分布函数是: F (x) = ⎪⎩⎪⎨⎧≥<≤--<11115.010x x x(1)求 P(X ≤0 ); P ()10≤<X ;P(X ≥1),(2) 写出X 的分布律。
2 设随机变量X 的分布函数是:F(x ) = ⎪⎩⎪⎨⎧≤>+001x x xAx , 求(1)常数A, (2) P ()21≤<X .§2.5 连续型随机变量1 设连续型随机变量X 的密度函数为:⎩⎨⎧<<=他其010)(x kx x f(1)求常数k 的值;(2)求X 的分布函数F(x),画出F (x) 的图形,(3)用二种方法计算 P(- 0.5<X<0.5).2 设连续型随机变量0≥x 的分布函数为:F(x) = ⎪⎩⎪⎨⎧≥<≤<e x e x x x 11ln 10(1)求X 的密度函数)(x f ,画出)(x f 的图形,(2)并用二种方法计算 P(X >0.5).§2.6 均匀分布和指数分布1设随机变量K 在区间 (0, 5) 上服从均匀分布, 求方程 42x + 4Kx + K + 2 = 0 有实根的概率。
2 假设打一次电话所用时间(单位:分)X 服从2.0=α的指数分布,如某人正好在你前面走进电话亭,试求你等待:(1)超过10分钟的概率;(2)10分钟 到20分钟的概率。
§2.7 正态分布1 随机变量X ~N (3, 4), (1) 求 P(2<X ≤5) , P (- 4<X≤10), P(|X|>2), P(X>3);(2)确定c ,使得 P(X>c ) = P (X <c)。
2 某产品的质量指标X 服从正态分布,μ=160,若要求P(120<X<200)≥0.80,试问σ最多取多大?§2.81设随机变量X 的分布律为; 0.3Y = 2X – 1, 求随机变量的分布律。
2设随机变量X 的密度函数为:⎩⎨⎧<<-=他其010)1(2)(x x x f ,2X Y =;求随机变量Y 的密度函数。
3. 设随机变量X 服从(0, 1)上的均匀分布,X Y ln 2-= ,求随机变量Y的密度函数。
第2章作业答案§2.1 1:p 2: X 1 2 3 4 5 p 0.4 0.6×0.4 0.6×0.6×0.4 0.6×0.6×0.6×0.4 0.6×0.6×0.6×0.6×1§2.2 1: (1) P(X = 1) = P(X ≥1) – P (X ≥2) = 0.981684 – 0.908422 = 0.073262,(2) P(X≥1) = 0.981684,(3) P(X ≤1) = 1 - P(X ≥2) = 1 – 0.908422 = 0.091578。
