平面直角坐标系及轴对称变换专题

合集下载

备考2021年中考数学二轮复习：图形的变换_轴对称变换_作图﹣轴对称,综合题专训及答案

备考2021年中考数学二轮复习：图形的变换_轴对称变换_作图﹣轴对称，综合题专训及答案备考2021中考数学二轮复习：图形的变换_轴对称变换_作图﹣轴对称，综合题专训1、(2017鹤岗.中考真卷) 如图，在平面直角坐标系中，Rt △ABC 三个顶点都在格点上，点A 、B 、C 的坐标分别为A （﹣1，3），B （﹣3，1），C （﹣1，1）．请解答下列问题：（1）画出△ABC 关于y 轴对称的△A B C ，并写出B 的坐标．（2）画出△A B C 绕点C 顺时针旋转90°后得到的△A B C ，并求出点A 走过的路径长．2、(2016哈尔滨.中考真卷) 图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC 的两个端点均在小正方形的顶点上．（1）如图1，点P 在小正方形的顶点上，在图1中作出点P 关于直线AC 的对称点Q ，连接AQ 、QC 、CP 、PA ，并直接写出四边形AQCP 的周长；（2）在图2中画出一个以线段AC 为对角线、面积为6的矩形ABCD，且点B 和点D 均在小正方形的顶点上．3、(2019丹东.中考模拟) 如图，平面直角坐标系中，的顶点都在正方形（每个小正方形边长为单位1）网格的格点上.（1）的形状是（直接写答案）（2）画出沿轴翻折后的；111111112211（3）画出绕点顺时针旋转的并求出旋转过程中扫过的面积.（结果保留）4、(2017大庆.中考模拟) 如图，△ABC 三个顶点的坐标分别为A （2，4），B （1，1），C （4，3）．①请画出△ABC 关于x 轴对称的△A B C ，并写出点A 的坐标；②请画出△ABC 绕点B逆时针旋转90°后的△A BC ，并写出点A 、C 的坐标．5、(2017淳安.中考模拟) 在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系，已知格点三角形A BC （三角形的三个顶点都在小正方形上）（1）画出△ABC 关于直线l ：x=﹣1的对称三角形△A B C ；并写出A 、B 、C 的坐标．（2）在直线x=﹣l 上找一点D ，使BD+CD 最小，满足条件的D 点为．6、(2017太和.中考模拟) 如图，方格中，每个小正方形的边长都是单位1，△ABC 在平面直角坐标系中的位置如图．（1）①画出△ABC 关于y 轴对称的△A B C ；②画出△ABC 绕点O 按顺时针方向旋转90°后的△A B C ；（2）判断△A B C 和△A B C 是不是成轴对称？如果是，请在图中作出它们的对称轴．111122221111111112221112227、(2017和.中考模拟) 如图，在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）．（1）请画出△ABC 关于直线l 对称的△A B C ；（2）将线段AC 向左平移3个单位，再向下平移5个单位，画出平移得到的线段A C ，并以它为一边作一个格点△A B C ，使A B =C B ．8、(2017安徽.中考真卷) 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC 和△DEF （顶点为网格线的交点），以及过格点的直线l．（1）将△ABC 向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形．（2）画出△DEF 关于直线l 对称的三角形．（3）填空：∠C+∠E=．9、(2017鹰潭.中考模拟) 如图，在平面直角坐标系中，△ABC 的三个顶点坐标分别为A （﹣2，1），B （﹣1，4），C （﹣3，2）．111222222222（1）①画出△ABC 关于y 轴对称的图形△A B C ，并直接写出C 点坐标；②以原点O 为位似中心，位似比为1：2，在y 轴的左侧，画出△ABC 放大后的图形△A B C ，并直接写出C 点坐标；（2）如果点D （a ，b ）在线段AB 上，请直接写出经过（1）②的变化后点D 的对应点D 的坐标．10、(2016钦州.中考真卷) 如图，在平面直角坐标系中，△ABC 的三个顶点分别为A （﹣1，﹣1），B （﹣3，3），C （﹣4，1）（1）画出△ABC 关于y 轴对称的△A B C ，并写出点B 的对应点B 的坐标；（2）画出△ABC 绕点A 按逆时针旋转90°后的△AB C ，并写出点C 的对应点C 的坐标．11、(2016玉林.中考真卷) 如图，在平面直角坐标系网格中，将△ABC 进行位似变换得到△A B C．（1）△A B C 与△ABC 的位似比是；（2）画出△A B C 关于y 轴对称的△A B C ；（3）设点P （a ，b ）为△ABC 内一点，则依上述两次变换后，点P 在△A B C 内的对应点P 的坐标是．1111222221111222111111111222222212、(2017南岸.中考模拟) 如图1，在平面直角坐标系中，抛物线y=与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，抛物线的顶点为点D ，过点B 作BC 的垂线，交对称轴于点E ．（1）求证：点E 与点D 关于x 轴对称；（2）点P 为第四象限内的抛物线上的一动点，当△PAE 的面积最大时，在对称轴上找一点M ，在y 轴上找一点N ，使得OM+MN+NP 最小，求此时点M 的坐标及OM+MN+NP 的最小值；（3）如图2，平移抛物线，使抛物线的顶点D 在射线AD 上移动，点D 平移后的对应点为D′，点A 的对应点A′，设抛物线的对称轴与x 轴交于点F ，将△FBC 沿BC 翻折，使点F 落在点F′处，在平面内找一点G ，若以F′、G 、D′、A′为顶点的四边形为菱形，求平移的距离．13、(2017眉山.中考真卷) 在如图的正方形网格中，每一个小正方形的边长为1．格点三角形ABC （顶点是网格线交点的三角形）的顶点A 、C 的坐标分别是（﹣4，6），（﹣1，4）．（1）请在图中的网格平面内建立平面直角坐标系；（2）请画出△ABC 关于x 轴对称的△A B C ；（3）请在y 轴上求作一点P ，使△PB C 的周长最小，并写出点P 的坐标．14、(2017靖远.中考模拟) 如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为A （﹣1，1），B （﹣3，1），C （﹣1，4）．①画出△ABC 关于y 轴对称的△A B C ；②将△ABC 绕着点B 顺时针旋转90°后得到△A BC ，请在图中画出△A BC ，并求出线段BC 旋转过程中所扫过的面积（结果保留π）．1111111222215、(2020梧州.中考模拟) 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）和直线l 及点O.（1）画出△ABC 关于直线l 对称的△A B C ；（2）连接OA ，将OA 绕点O 顺时针旋转180°，画出旋转后的线段；（3）在顺时针旋转的过程中，当OA 与△A B C 有交点时，旋转角ɑ的取值范围是________备考2021中考数学二轮复习：图形的变换_轴对称变换_作图﹣轴对称，综合题答案1.答案：2.答案：1111113.答案：4.答案：5.答案：6.答案：7.答案：8.答案：9.答案：10.答案：11.答案：12.答案：13.答案：14.答案：15.答案：。

图形变换之轴对称变换

轴对称变换姓名_________一、轴对称定义及性质:1.定义:(1)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也叫轴对称.两个图形中的对应点叫做关于这条直线的_____,这条直线叫做_____.说明:定义中包含两层意思:①两个图形是全等形(即形状、大小相同)；②沿着某一条直线对折能够完全重合。

(2)轴对称图形:如果一个图形图形沿着一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形.(3)轴对称与轴对称图形的区别与联系:区别:轴对称涉及两个图形,而轴对称图形是对一个图形而言.联系:①定义中都有沿某条直线折叠重合;②如果把轴对称图形沿对称轴分成两个部分,那么这两个图形就是关于这条直线成轴对称(即一分为二);反过来,如果把两个成轴对称的图形看成一个整体,那么它就是一个轴对称图形(即合二而一).例.选择：(1)．在下列图形中，既是中心对称图形，又是轴对称图形，且对称轴只有两条的是（）A．等腰梯形B．平行四边形C．菱形D．正方形(06北京市) （2）．下列图形中，既是中心对称图形又是轴对称图形的是( )（A）矩形（B）等腰梯形（C）平行四边形（D）等边三角形(06崇文一模)（3）观察下列用纸折叠成的图案，其中轴对称图形和中心对称图形的个数分别是( )（05东城一）A.4、1 B. 3、1 C. 2、2 D. 1、3（4）剪纸艺术是我国文化宝库中的优秀遗产，在民间广泛流传．我们扬州的民间剪纸作品享誉中外．下面的一组剪纸作品，属于中心对称图形的是 ( ) （5）如图，下列图案是我国几家银行的标志，其中是轴对称图形的有（）A 、1个B 、2个C 、3个D 、4个（6）下列四个图形中，从几何图形的对称性考虑，哪一个与其他三个不同？( ) 2.性质:①关于某条直线对称的两个图形是全等形;②如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点必在对称轴上.逆定理:如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称. 例.1．如图，△ABC 和△A’B’C’关于直线MN 对称，△A’B’C’和△A’’B’’C’’关于直线EF 对称。

平面直角坐标系坐标变化

平面直角坐标系中的变换彳----------- 必标系屮的对称平而l'i角坐标系屮的变换坐标系中的平移\------------ 怡标系屮的面枳和规律问题编写思路:本讲求而积时主要让学生掌握将点坐标转化为线段长度的过程•让学生亲自动手在坐标系中画出某个点关于横轴、纵轴以及原点的对应点，并且让他们自己总结两个对称点的横.纵坐标关系。

二：(1)对于点的平移：让学生亲自动手将某个点进行上、下、左、右平移，并且自己总结点的坐标变化规律。

对于任意的平移，可以将貝理解先上下平移、后左右平移的组合。

(2)对于图形的平移：让学生充分认识本质就是图形上的每个点都进行同一过程的平移，即对应点之间的平移过程完全一样。

从而将图形的平移转化成为点的平移。

并让学生体会平移前后的两个图形完全一样。

三、简单的数形结合：求三角形而积问题。

让学生充分掌握割补法求三角形而积，并理解为何要用割补法。

让学生熟练掌握并体会坐标与线段长的讣算关系。

四.找规律问题：老师可带着学生探索常见找规律问题的思路和方法.点P(-b)关于X轴的对称点是叫，-巧,即横坐标不变，纵坐标互为相反数.点P(a,b)关于y轴的对称点是P©,b),即纵坐标不变，横坐标互为相反数.点P(a.b)关于坐标原点的对称点是P'(—d),即横坐标互为相反数，纵坐标也互为相反数.【引例】在平而直角坐标系中，卩(-4 5)关于X 轴的对称点的坐标是 __________ 坐标是 ________ ,关于原点的对称点是 ___________【例1】(1)点P(3, -5)关于x 轴对称的点的坐标为()⑵点"-2, 1)关于y 轴对称的点的坐标为()⑶ 在平而直角坐标系中，点P(2, -3)关于原点对称点P 的坐标是 _____________ ⑷ 点P(2, 3)关于直线x = 3的对称点为 ________ ,关于直线y = 5的对称点为 ________ ⑸已知点P(“ + l,加-1)关于x 轴的对称点在第一彖限，求d 的取值范围.【例2】如图，在平而直角坐标系中，直线/是第一、三象限的角平分线.实验与探究：(1) 由图观察易知A(2, 0)关于直线/的对称点/V 的坐标为(0,2),请在图中分别标明3(5,3), C(-2,5)关于直线/的对称点X 、C'的位置，并写岀它们的坐标： B' __________ ，C ____________ ；归纳与发现：(2) 结合图形观察以上三组点的坐标，你会发现：坐标平而内任一点关于第一、三象限的角平分线/的对称点P 的坐标为 ______________ (不必证明)： ⑶点A(a , b)在直线/的下方，则d, 〃的大小关系为 ________________ :若在直线/的上方，则 __________ ・h + d\丁 >・(选讲),关于y 轴的对称点的A. (—3, —5)B. (5, 3)C. (一3, 5) D ・(3, 5)B. (2,1)C. (2, -1)D. (-2, 1)点P(a ,b)和点Q(c , d)的中点是M(1)点平移：①将点(x, y)向右(或向左)平移4个单位可得对应点(x + a t y)或(x-“, y).②将点(x, y)向上(或向下)平移〃个单位可得对应点(x，＞'+/?)或(x, y-h).⑵图形平移：①把一个图形％个点的横坐标都加上(或减去)一个正数d ,相应的新图形就是把原图形向右(或向左)平移Q个单位.②如果把图形各个点的纵坐标都加上(或减去)一个正数d ,相应的新图形就是把原图形向上(或向下)平移a个单位.注意：平移只改变图形的位置，图形的大小和形状不发生变化.【弓I例】点M(-3, -5)向上平移7个单位得到点M,的坐标为：再向左平移3个单位得到【例3】(1)平而直角坐标系中，将P(-2,l)向右平移4个单位，向下平移3个单位，得到P __________ ,□平而直角坐标系中，线段虫妨'是由线段佔经过平移得到的，点A(-1,-4)的对应点为人(1, -1),那么此过程是先向________ 平移____ 个单位再向______ 平移 _____ 个单位得到的，则点B (1, 1)的对应点$坐标为______________ .⑶将点P(m-2,” + 1)沿求轴负方向平移3个单位，得到P^i-rn, 2),则点P坐标是_____________⑷ 平而直角坐标系中，线段A'B'是由线段初经过平移得到的，点A(-2, 1)的对应点为A f (3. 4),点B 的对应点为B'(4,0),则点B 的坐标为()A ・(9,3) B. (一 1，一3) C ・(3, — 3) D. (一3, —1)【例4】二如下左图，在平面直角坐标系中，右边的图案是由左边的图案经过平移得到的，左边图案中左.右眼睛的坐标分别是(-4, 2), (-2, 2),右边图案中左眼的坐标是(3, 4),则右边图案中右眼的坐标是 _____________________ .-如下右图是由若干个边长为1的小正方形组成的网格，请在图中作岀将“蘑菇”ABCDE 绕A点逆时针旋转奸再向右平移2个单位的图形(其中C 、D 为所在小正方形边的中点).二如图，把图1中的04经过平移得到00(如图2),如果图1中04上一点P 的坐标为伽皿),那么平移后在图2中的对应点P 的坐标为 __________ ・大图形的总而积减去周用小三角形的面积.一般方法有割补法和等积变换法.找规律的题目一左要先找/7 = 1、2、3几个图形规律，再推广到“的情况.从简单情形入手，从中发现规律，猜想、推测.归纳出结论，这是创造性思维的特点.i/\ V1例题精讲A ・v图1 图2在平面直角坐标系或网格中求而积，一般将难以求解的图形分割成易求解的图形的面积，可以用F二兀一 - —【引例】如图，直角坐标系中，△ABC的顶点都在网格点上，英中点A坐k标为(2,-1),则△4BC 的而积为 _____________ 平方单位.二如上右图，AABC,将△ABC 向右平移3个单位长度，然后再向上平移2个单位长度，可以得到△ ・ ① 画出平移后的△人妨6 :② 写出△ AB.C,三个顶点的坐标：(在图中标岀)③ 已知点P 在x 轴上，以B“ P 为顶点的三角形面积为4,求P 点的坐标.【探究1】如图所示,4(1,4),B(4,3),(7(5,0),求图形如C 的面积.【例5】□直角坐标系中，已知人(-1,0)、5(3, 0)两点，点C 在y 轴上，△ABC 的而积是4,则点C 的坐标是 ___________ ■0如右图，已知直角坐标系中A(-1,4)、B(0,2),平移线段初,使点B 移到点C(3,0),此时点A 记作点D ，贝IJ 四边形ABCD 的而积是 ___________ .【例6】□如下左图，在平而直角坐标系中，四边形ABCD 各顶点的坐标分别为A(0,0), 8(9,0), C(7,5),D(2, 7)・求四边形ABCD 的而积.「41「J 1_1 T 丿r k —厂」I 厂 11- T 4—n T klrLIr典题精练L LIL」I- T -I- +• -1 ~J_L J•V A【探究2】如下图所示，A(-3,5), B(4,3),求图形OAB的而积.【教师备选】方法三、转化法：平行线，一边转到轴上【探究4】如图所示，求三角形AOB的而积.解析：过点A做0B的平行线，交y轴于点C,连接BC由一次函数知识可求出直线OB：y=-x t设直线AC：y=-x+b -2 - 2 求得y=l x+2 ,得C(0,2)由等积变换可知S厶AOB = S^Bg. ―― x 2x 4=4解析：过点A作BC的平行线交y轴于点D,连接DC利用一次函数求得BC：y=2x+2 ,设直线AD：y=2x+b 求得尸2x+7, D(0,7) 由等积变换可知S沁=S沁弓x 1 x 5=|【变式】已知，在平而直角坐标系中，A「B两点分别在才轴、y轴的正半轴上，且OB = OA = 3. ⑴直接写出点A、B的坐标：⑵若点C(-2, 2),求△BOC的面积；⑶点P是与〉，轴平行的直线上一点，且点P的横坐标为1.若的面积是6,求点P的坐标.【例7】□任平而直角坐标系中，横坐标、纵坐标都为整数的点称为整点,图中的正方形的四个顶点都在格点上，观察图中每一个正方形四条边上的整点的个数，请你猜测由里向外第10个正方形四条边上的整点个数共有_______ 个.□如图，在平而直角坐标系中，第1次将MAB变换成△ OA.B.,第二次将变换成第3次将MAB 变换成△0比尽・已知A(l, 3), 4(2, 3), 4(4, 3), A(8, 3), B(2, 0), $(4, 0) , BJ8, 0),耳(16, 0)观察每次变化前后的三角形，找岀规律，按此变化规律再将△OA&3变换成△ O儿则点比的坐标是 _____ ，点厲的坐标是 _____ ,点人的坐标是_______ ，点乞的坐标是 ___________ ・【例8】一个粒子在第一象限内及x轴、y轴上运动，在第lmin内它从原点运动到(1, 0),而后接着按如图所示方式在与X轴、轴平行的方向上来回运动，且每分钟移动1个单位长度，那么，在2013min后，求这个粒子所处的位置坐标・【变式】将正整数按如图所示的规律在平而直角坐标系中进行排列，每个正整数对应一个整点坐标(X, y)9且x, y均为整数.如数5对应的坐标为(-1,1)，则数_________________ 对应的坐标是(-2,3),数2012对应的坐标是__________________【拓展】数1950对应的坐标是______________ ・【教师备选】【备选1】类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1 个单位，用实数加法表示为3 + （-2） = 1.若坐标平而上的点作如下平移：沿*轴方向平移的数屋为d （向右为正，向左为负，平移冋个单位），沿y 轴方向平移的数量为方（向上为正，向下为负，平移问个单位），则把有序数对{“，b}叫做这一平移的“平移量”;“平移量” {a, b}与“平移量” {c, d}的加法运算法则为{“，b} + {c, d} = {a+c, b + d}. 解决问题：（1）计算：{3, 1} + {1, 2}；（2）动点P 从坐标原点O 出发，先按照"平移量”{3, 1}平移到A,再按照"平移量”{1, 2} 平移到若先把动点P 按照“平移量” {1, 2}平移到C,再按照“平移量” {3, 1}平移，最后的位置还是点B 吗？在图1中画出四边形OABC.（3）如图2, 一艘船从码头O 出发，先航行到湖心岛码头P （2,3）,再从码头P 航行到码头0（5, 5）,最后回到出发点O,请用“平移量”加法算式表示它的航行过程.37 36 35 34 3332 31 30 297 16 15 1413 12 11 18 19 61 2 2() 78 ,10 27 2122 23 2425 26图1【备选2】观察下列有规律的点的坐标：儿(1, 1), 4(2, -4), 4(3, 4),人(4, 一2),人(5, 7),肩6, -寸，4(7, 10), 4(8, —1)依此规律，人|的坐标为______________ ，州2的坐标为 ______________________________【备选3】一个动点P在平而直角坐标系中作折线运动，第一次从原点运动到(b 1)＞然后按图中箭头所示方向运动，每次移动三角形的一边长•即(1, 1)-* (2, 0) - (3, 2) - (4, 0)-(5, 1)—........... ,按这样的运动规律，经过第17次运动后，动点P的坐标是___________ ,经过第2011次运动后，动点P的坐标是 __________ .【备选4】如图，在长方形网格中，每个小长方形的长为2,宽为1, B 两点在网格格点上，若点C也在网格格点上，以A、3、C为顶点的三角形面积为2,则满足条件的点C个数是( )A. 5B. 4B AD・2【备选5】在平而直角坐标系中，已知八(2・-2),任y轴上确左点P.使8"为等腰三角形，则符合条件的点P共有( )A. 2个B. 3个C. 4个D. 5个题型一坐标系中的对称巩固练习【练习1】□在平面直角坐标系中，点A(2,5)与点B关于y轴对称，则点B的坐标是( )A. (—5,—2)B. (一2, —5)C. (一2,5)D. (2, —5)□已知点P(x, y), n),如果x +加=0, y + 〃= 0 ,那么点P, Q ( )A・关于原点对称 B.关于x轴对称C・关于y轴对称D・关于过点(0,0), (1,1)的直线对称□已知：lx-ll+(.y + 2『=0,则(x, y)关于原点对称的点为_________________ .□已知点P(" + 3b,3)与点0(-5,“ + 2b)关于x轴对称，贝比= ______________ , b = _________ .题型二坐标系中的平移巩固练习【练习2】⑴线段CD是由线段初平移得到的，点A(-l, 5)的对应点是C(4, 2),则点B(4, -1)的对应点D的坐标为__________ ・⑵在平面直角坐标系中有一个已知点A ,现在x轴向下平移3个单位，y轴向左平移2个单位，单位长度不变，得到新的坐标系，在新的坐标系下点A的坐标为(-1，2),在旧的坐标系下，点A的坐标为_______ ・【练习3】如图，在平而直角坐标系中，若每一个方格的边长代表一个单位.□线段DC是线段经过怎样的平移得到的？□若C点的坐标是(4, 1), A点的坐标是(-1，-2),你能写岀B、D两点的坐标吗？□求平行四边形ABCD的而积.题型三坐标系中的面积和规律问题巩固练习【练习4】□已知A(0,—2), B(5,0), C(4,3),求△ABC的而积.□已知：A(4,0), 3(1-斗0), 0(1, 3), ZVWC 的而积=6,1)A B求代数式2A-2-5X + X2+4X-3X2 -2 的值.【练习5】如图，长为1,宽为2的长方形ABCQ以右下角的顶点为中心顺时针旋转90°,此时A点的坐标为________ :依次旋转2009次，则顶点A的坐标为___________ ・。

轴对称及轴对称变换

第3讲轴对称及轴对称变换考点·方法·破译1．轴对称及其性质把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线成轴对称，这条直线叫对称轴.轴对称的两个图形有如下性质：①关于某直线对称的两个图形是全等形；②对称轴是任何一对对应点所连线段的垂直平分线；③两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上.2．线段垂直平分线线段垂直平分线也叫线段中垂线，它反映了与线段的两种关系：①位置关系——垂直；②数量关系——平分.性质定理：线段垂直平分线上的点与这条线段两个端点的距离相等. 判定定理：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.3．当已知条件中出现了等腰三角形、角平分线、高（或垂线）、或求几条折线段的最小值等情况时，通常考虑作轴对称变换，以“补齐”图形，集中条件.经典·考题·赏析【例１】（兰州）如图所示，将一张正方形纸片对折两次，然后在上面打 3 个洞，则纸片展开后是（）【解法指导】对折问题即是轴对称问题，折痕就是对称轴.故选 D.【变式题组】01．将正方形纸片两次对折，并剪出一个菱形小洞后铺平，得到的图形是（）02．（荆州）如图，将矩形纸片ABCD 沿虚线EF 折叠，使点A 落在点G 上，点D 落在点H 上；然后再沿虚线GH 折叠，使 B 落在点 E 上，点 C 落在点F 上，叠完后，剪一个直径在BC 上的半圆，再展开，则展开后的图形为（）【例2】（襄樊）如图，在边长为 1 的正方形网格中，将△ABC 向右平移两个单位长度得到△A’B’C’，则与点B’关于x 轴对称的点的坐标是（）A．（0，－1）B．（1，1）C．（2，－1）D．（1，－1）【解法指导】在△ABC 中，点 B 的坐标为（－1，1），将△ ABC向右平移两个单位长度得到△A’B’C’，由点的坐标平移规律可得B’（－1＋2，1），即B’（1，1）.由关于x 轴对称的点的坐标的规律可得点B’关于x 轴对称的点的坐标是（1，－1），故应选D.【变式题组】01．若点P（－2，3）与点Q（a，b）关于x 轴对称，则a、b 的值分别是（）A．－2，3 B．2，3 C．－2，－3 D．2，－302．在直角坐标系中，已知点P（－3，2），点Q 是点P 关于x 轴的对称点，将点Q 向右平移4 个单位得到点R，则点R 的坐标是___________.03．（荆州）已知点P（a＋1，2a－1）关于x 轴的对称点在第一象限，则a 的取值范围为___________.【例3】如图，将一个直角三角形纸片ABC（∠ACB＝90°），沿线段CD 折叠，使点B 落在B1 处，若∠ACB1＝70°，则∠ACD ＝（）A．30° B．20° C．15° D．10°【解法指导】由折叠知∠BCD＝∠B1CD.设∠ACD＝x，则∠BCD＝∠B1CD＝∠ACB1＋∠ACD＝70°＋x.又∠ACD＋∠BCD＝∠ACB，即x＋（70°＋x）＝90°，故x＝10°.故选D.【变式题组】01．（东营）如图，把一个长方形纸片沿EF 折叠后，点D、C 分别落在点D’、C’的位置. 若∠EFB＝65°，则∠AED’等于（）A．70° B．65° C．50° D．25°02．如图，△ABC 中，∠A＝30°，以BE 为边，将此三角形对折，其次，又以BA 为边，再一次对折，C 点落在BE 上，此时∠CDB＝82°，则原三角形中∠B＝___________.03．（江苏）⑴观察与发现：小明将三角形纸片ABC（AB＞AC）沿过点A 的直线折叠，使得AC 落在AB 边上，折痕为AD，展平纸片（如图①）；再次折叠该三角形纸片，使点 A 和点 D 重合，折痕为EF，展平纸片后得到△AEF （如图②）.小明认为△AEF 是等腰三角形，你同意吗？请说明理由. ⑵实践与运用：将矩形纸片ABCD 沿过点 B 的直线折叠，使点 A 落在BC 边上的点 F 处，折痕为BE （如图③）；再沿过点 E 的直线折叠，使点 D 落在BE 上的点D’处，折痕为EG（如图④）；再展平纸片（如图⑤）.求图⑤中∠α 的大小.【例4】如图，在△ABC 中，AD 为∠BAC 的平分线，EF 是AD 的垂直平分线，E 为垂足，EF 交BC 的延长线于点F，求证：∠B＝∠CAF．【解法指导】∵EF 是AD 的中垂线，则可得△AEF ≌△DEF，∴∠EAF＝∠EDF．从而利用角平分线的定义与三角形的外角转化即可．证明：∵EF 是AD 的中垂线，∴AE＝DE，∠AEF ＝∠DEF，EF＝EF，∴△AEF≌△DEF，∴∠2＋∠4 ＝∠3，∴∠3＝∠B＋∠1，∴∠2＋∠4＝∠B＋∠1，∵∠1＝∠2，∴∠B＝∠4【变式题组】01．如图，点D 在△ABC 的BC 边上，且BC＝BD＋AD，则点D 在__________的垂直平分线上．02．如图，△ABC 中，∠ABC＝90°，∠C＝15°，DE⊥AC 于E，且AE＝EC，若AB＝3cm，则DC＝___________cm．03．如图，△ABC 中，∠BAC＝126°，DE、FG 分别为AB、AC 的垂直平分线，则∠EAG ＝___________．04.△ABC 中，AB＝AC，AB 边的垂直平分线交AC 于F，若AB＝12cm，△BCF 的周长为20cm，则△ABC 的周长是___________cm．【例5】（眉山）如图，在3³3 的正方形格点图中，有格点△ABC 和△DEF，且△ABC 和△DEF 关于某直线成轴对称，请在下面的备用图中画出所有这样的△DEF．【解法指导】在正方形格点图中，如果已知条件中没有给对称轴，在找对称轴时，通常找图案居中的水平直线、居中的竖直直线或者斜线作为对称轴．若以图案居中的水平直线为对称轴，所作的△DEF 如图①②③所示；若以图案居中的竖直直线为对称轴，所作的△DEF 如图④所示；若以图案居中的斜线为对称轴，所作的△DEF 如图⑤⑥所示．【变式题组】01．（泰州）如图，在2³2 的正方形格点图中，有一个以格点为顶点的△ABC，请你找出格点图中所有与△ABC 成轴对称且也以格点为顶点的三角形，这样的三角形共有___________个．02．（绍兴）如图甲，正方形被划分成16 个全等的三角形，将其中若干个三角形涂黑，且满足下列条件：⑴涂黑部分的面积是原正方形面积的一半；⑵涂黑部分成轴对称图形．如图乙是一种涂法，请在图1－3 中分别设计另外三种涂法．（在所设计的图案中，若涂黑部分全等，则认为是同一种不同涂法，如图乙与图丙）【例6】如图，牧童在 A 处放牛，其家在 B 处，若牧童从 A 处出发牵牛到河岸CD 处饮水后回家，试问在何处饮水，所求路程最短？【解法指导】⑴所求问题可转化为CD 上取一点M，使其AM ＋BM 为最小；⑵本题利用轴对称知识进行解答．解:先作点A 关于直线CD 的对称点A’，连接A’B 交CD 于点M，则点M 为所求，下面证明此时的AM＋BM 最小．证明：在CD 上任取与M 不重合的点M’，∵AA’关于CD 对称，∴CD 为线段AA’的中垂线，∴AM＝A’M，M’＝A’M’,在△A’M’B 中，有A’B＜A’M’＋BM’，∴A’M＋BM＜A’M’＋BM’，∴AM＋BM＜AM’＋BM’，即AM＋BM 最小．【变式题组】01．（山西）设直线l 是一条河，P、Q 两地相距8 千米，P、Q 两地到l 地距离分别为2 千米、5 千米，欲在l 上的某点M 处修建一个水泵站向P、Q 两地供水．现在如下四种铺设管道方案，图中的实线表示辅设的管道，则铺设的管道最短的是（）02．若点A、B 是锐角∠MON 内两点，请在OM、ON 上确定点C、点D，使四边形ABCD 周长最小，写出你作图的主要步骤并标明你确定的点．演练巩固·反馈提高01．（黄冈）如图，△ABC 与△A’B’C’关于直线l 对称，且∠A＝78°，∠C’＝48°，则∠B 的度数是（）．A．48° B．54° C．74° D．7802．（泰州）如图，把一张长方形纸片对折，折痕为AB，再以AB 的中点O 为顶点把平角∠ AOB 三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O 为顶点的等腰三角形，那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是（）A．正三角形B．正方形C．正五边形D．正六边形03．1 是四边形纸片ABCD，图其中∠B＝120°，∠D＝50°，若将其右下角向内折出△PCR，恰使CP∥AB，RC∥AD，如图2 所示，则∠C＝（）A．80° B．85° C．95° D．110°04．如图，阴影部分组成的图案既是关于x 轴成轴对称的图形又是关于y 轴成轴对称的图形，若点 A 的坐标是（1，3），则点M 和点N 的坐标分别是（）A．M（1，－3），N（－1，－3）B．M（－1，－3），N（－1，3）C．M（－1，－3），N（1，－3）D．M（－1，3），N（1，－3）05．点P 关于x 轴对称的对称点P’的坐标是（－3，5），则点P 关于y 轴对称的对称点的坐标是（）A．（3，－5）B．（－5，3）C．（3，5）D．（5，3）06．已知M（1－a，2a＋2）关于y 轴对称的点在第二象限，则a 的取值范围是（）A．－1＜a＜1 B．－1≤a≤1 C．a＞1 D．a＞－107．（杭州）如图，镜子中号码的实际号码是___________．08．（贵阳）如图，正方形ABCD 的边长为4cm，则图中阴影部分的面积为___________cm .09．已知点A（2a＋3b，－2）和B（8，3a＋2b）关于x 轴对称，则a＋b＝___________.10．如图，在△ABC 中，OE、OF 分别是AB、AC 中垂线，且∠ABO ＝20°，∠ABC＝45°，求∠BAC 和∠ACB 的度数．11．如图，C、D、E、F 是一个长方形台球桌的4 个顶点，A、B 是桌面上的两个球，怎样击打 A 球，才能使 A 球撞击桌面边缘CF 后反弹能够撞击 B 球？请画出A 球经过的路线，并写出作法．12．如图，P 为∠ABC 的平分线与AC 的垂直平分线的交点，PM⊥BC 于M，PN⊥BA 的延长线于N．求证：AN＝MC．13．（荆州）有如图“”的8 张纸条，用每4 张拼成一个正方形图案，拼成的正方形的每一行和每一列中，同色的小正方形仅为 2 个，且使每个正方形图案都是轴对称图形，在网格中画出你拼成的图．（画出的两个图案不能全等）培优升级·奥赛检测01．（浙江竞赛试题）如图，直线l1 与直线l2 相交，∠α ＝60°，点P 在∠α 内（不在l1l2 上）．小明用下面的方法作P 的对称点：先以l1 为对称轴作点P 关于l1 的对称点P1,再以l2 为对称轴作P1 关于l2 的对称点P2，然后再以l1 为对称轴作P2 关于l1 的对称点P3，以l2 为对称轴作P3 关于l2 的对称点P4，……如此继续，得到一系列P1、P2、P3……Pn 与P 重合，则n 的最小值是（）A．5 B．6 C．7 D．802．在平面直角坐标系中，直线l 过点M（3，0），且平行于y 轴．⑴如果△ABC 三个顶点的坐标分别是A（－2，0），B（－1，0），C（－1，2），△ABC 关于y 轴的对称图形△A1B1C1，△A1B1C1 关于直线l 的对称图形是△A2B2C2，写出△ A2B2C2 的三个顶点的坐标；⑵如果点P 的坐标是（－a，0），其中a＞0，点P 关于y 轴的对称点是点P1，点P1 关于直线l 的对称点是P2，求PP2 的长．03．（荆州）某住宅小区拟栽种12 棵风景树，若想栽成6 行，每行4 棵，且6 行树所处位置连成线后能组成精美的对称图案，请你仿照举例在下面方框中再设计两种不同的栽树方案．04．（宜昌）已知：如图，AF 平分∠BAC，BC⊥AF，垂足为E，点D 与点A 关于点E 对称，PB 分别与线段CF、AF 相交于P、M．⑴求证：AB＝CD；⑵若∠BAC＝2∠MPC，请你判断∠F 与∠MCD 的数量关系，并说明理由．05．在△ABC 中，∠BAC＝90°，点A 关于BC 边的对称点为A’，点B 关于AC 边的对称点为B’，点C 关于AB 边的对称点为C’，若S△ABC＝1，求S△A’B’C’．06．（湖州市竞赛试题）小王同学在小组数学活动中，给本小组出了这样一道“对称跳棋” 题：如图，在作业本上画一条直线l，在直线l 两边各放一粒围棋子A、B，使线段AB 长a 厘米，并关于直线l 对称，在图中P1 处有一粒跳棋子，P1 距A 点b 厘米、与直线l 的距离C 厘米，按以下程序起跳：第1 次，从P1 点以A 为对称中心跳至P2 点；第 2 次，从P2 点以l 为对称轴跳至P3 点；第 3 次，从P3 点以 B 为对称中心跳至P4 点；第4 次，从P4 以l 为对称轴跳至P1 点；⑴画出跳棋子这 4 次跳过的路径并标注出各点字母；（画图工具不限）⑵棋子按上述程序跳跃2011 次后停下，假设a＝8，b ＝6，c＝3，计算这时它与 A 的距离是多少？07．（湖州）如图，已知平面直角坐标系，A、B 两点的坐标分别为A（2，－3），B（4，－1）．⑴若P（p，0）是x 轴上的一个动点，则当p＝___________时，△PAB 的周长最短；⑵若C（a，0），D（a＋3，0）是x 轴上的两个动点，则当a＝___________时，四边形ABCD 的周长最短；⑶设M、N 分别为x 轴和y 轴上的动点，请问：是否存在这样的点M（m，0）、N（0，n）使四边形ABMN 的周长最短？若存在，，请求出m＝___________，n＝___________ （不必写解答过程）；若不存在，请说明理由．。

图形的变化——轴对称备战2023年中考数学考点微专题

考向5.2 图形的变化——轴对称[知识要点] 1、定义把一个图形沿着某条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线成轴对称，该直线叫做对称轴。

2、性质（1）关于某条直线对称的两个图形是全等形。

（2）如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。

（3）两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。

3、判定如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

4、轴对称图形把一个图形沿着某条直线折叠，如果直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴。

例题1．在ABC 中，90ACB ∠=︒，ACm BC=，D 是边BC 上一点，将ABD △沿AD 折叠得到AED ，连接BE ．（1）特例发现：如图1，当1m =，AE 落在直线AC 上时， ①求证：DAC EBC ∠=∠； ②填空：CDCE的值为______；（2）类比探究：如图2，当1m ≠，AE 与边BC 相交时，在AD 上取一点G ，使ACG BCE ∠=∠，CG 交AE 于点H ．探究CGCE的值（用含m 的式子表示），并写出探究过程；（3）拓展运用：在（2）的条件下，当22m =，D 是BC 的中点时，若6EB EH ⋅=，求CG 的长．解：（1）①证明：延长AD 交BE 于点F ．由折叠得90AFB ACB ∠=︒=∠．∴90DAC ADC BDF EBC ∠+∠=∠+∠=︒． ∵ADC BDF ∠=∠， ∴DAC EBC ∠=∠． ②当1m =，即1ACBC=时，可知AC =BC ，在ACD △和BCE 中， 90DAC EBC ACD BCE AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴ACD ≌BCE (AAS )， ∴CD CE =， ∴1CDCE=．故答案为：1；（2）解：CGm CE=．理由：延长AD 交BE 于点F ，由折叠得90AFB ACB ∠=︒=∠．∴90ADC DAC BDF CBE ∠+∠=∠+∠=︒， ∵ADC BDF ∠=∠，∴DAC CBE ∠=∠， ∵ACG BCE ∠=∠， ∴ACG BCE △∽△， ∴CG ACm CE BC==．（3）解：由折叠得90AFB ∠=︒，BF FE =， ∵D 是BC 的中点， ∴//DF CE ，∴90BEC BFD ∠=∠=︒，AGC ECG ∠=∠，GAH CEA ∠=∠，由（2）知ACG BCE △∽△， ∴90AGC BEC ∠=∠=︒， 22AG CG AC m BE CE BC ====， D 是BC 的中点，2,BC CD ∴=∴2ACCD=， ∴1tan 2CG DC GAC AG AC =∠==，设CG x =，则2AG x =，2CE x =，2BE x =， ∴AG CE =，,,GAH HEC AHG CHE ∠=∠∠=∠∴AGH ECH ≌△△， ∴AH EH =，GH CH =， ∴12GH x =，在Rt AGH 中，由勾股定理得2232AH AG GH x EH =+==， ∵6EB EH ⋅=， ∴3262x x ⋅=，解得2x =±（负值舍去）， ∴2CG =．【点拨】本题．1、轴对称图形和折叠的关系：折叠形成的图形就是轴对称图形，其中折痕所在的直线就是对称轴；2、“对称点的连线被对称轴垂直平分”这个知识点常常是解题的突破口；3、本题为三角形综合题，考查折叠的性质，全等三角形判定与性质，相似三角形的判定及性质，勾股定理等知识点，根据折叠性质找到角度之间的关系是解题的关键一、单选题1．（2022·重庆·模拟预测）下列图形中既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．2．（2021·甘肃兰州·中考真题）在平面直角坐标系xOy 中，点()3,4A -关于y 轴对称的点B 的坐标是（） A ．()3,4-B ．()3,4--C ．()3,4-D ．()3,43．（2021·山东青岛·中考真题）如图，在四边形纸片ABCD 中，//AD BC ，10AB =，60B ∠=︒．将纸片折叠，使点B 落在AD 边上的点G 处，折痕为EF ．若45BFE ∠=︒，则BF 的长为（）A ．5B ．35C ．53D 34．（2021·山东滨州·中考真题）在四张反面无差别的卡片上，其正面分别印有线段、等边三角形、平行四边形和正六边形．现将四张卡片的正面朝下放置，混合均匀后从中随机抽取两张，则抽到的卡片正面图形都是轴对称图形的概率为（） A ．12B ．13C ．14D ．345．（2018·四川内江·中考真题）如图，将矩形ABCD 沿对角线BD 折叠，使点C 落在F 处，BF 交AD 于点E ．若∠BDC ＝62°，则∠DEF 的度数为（）A ．31°B ．28°C ．62°D ．56°6．（2021·山东潍坊·中考真题）如图，某机器零件的三视图中，既是轴对称图形，又是中心对称图形的是（）A ．主视图B ．左视图C ．俯视图D ．不存在7．（2021·四川凉山·中考真题）如图，ABC 中，90,8,6ACB AC BC ∠=︒==，将ADE 沿DE 翻折，使点A 与点B 重合，则CE 的长为（）A ．198B ．2C ．254 D ．748．（2011·甘肃天水·中考真题）把一张长方形的纸片按如图所示的方式折叠，EM 、FM 为折痕，折叠后的C 点落在B′M 或B′M 的延长线上，那么∠EMF 的度数是( )A ．85°B ．90°C ．95°D ．100°9．（2020·山东济南·中考真题）如图，在ABC 中，AB ＝AC ，分别以点A 、B 为圆心，以适当的长为半径作弧，两弧分别交于E ，F ，作直线EF ，D 为BC 的中点，M 为直线EF 上任意一点．若BC ＝4，ABC 面积为10，则BM +MD 长度的最小值为（）A ．52B ．3C ．4D ．5二、填空题10．（2021·四川内江·中考真题）有背面完全相同，正面分别画有等腰三角形、平行四边形、矩形、菱形、等腰梯形的卡片5张，现正面朝下放置在桌面上，将其混合后，并从中随机抽取一张，则抽中正面的图形一定是轴对称图形的卡片的概率为 __．11．（2021·河南·中考真题）小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt ABC △中，90ACB ∠=︒，30B ∠=︒，1AC =．第一步，在AB 边上找一点D ，将纸片沿CD 折叠，点A落在A '处，如图2，第二步，将纸片沿CA '折叠，点D 落在D 处，如图3．当点D 恰好在原直角三角形纸片的边上时，线段A D ''的长为__________．12．（2014·贵州黔西·中考真题）如图．将长方形纸片ABCD 折叠，使边AB 、CB 均落在对角线BD 上，得折痕BE 、BF ，则∠EBF 的大小为_____ .13．（2021·湖南湘西·中考真题）如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB 、CD ，若//CD BE ，1=20∠︒，则2∠的度数是____．14．（2021·湖南株洲·中考真题）《蝶几图》是明朝人戈汕所作的一部组合家具的设计图（蜨，同“蝶”），它的基本组件为斜角形，包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只，共十三只（图①中的“様”和“隻”为“样”和“只”）．图②为某蝶几设计图，其中ABD △和CBD 为“大三斜”组件（“一様二隻”的大三斜组件为两个全等的等腰直角三角形），已知某人位于点P 处，点P 与点A 关于直线DQ 对称，连接CP 、DP ．若24ADQ ∠=︒，则DCP ∠= ___________度．15．（2014·四川德阳·中考真题）如图，△ABC 中，∠A=60°，将△ABC 沿DE 翻折后，点A 落在BC 边上的点A′处．如果∠A′EC=70°，那么∠A′DE 的度数为___．16．（2017·山东泰安·中考真题）如图，30BAC ∠=︒，M 为AC 上一点，2AM =，点P 是AB 上的一动点，PQ AC ⊥，垂足为点Q ，则PM PQ +的最小值为_________．17．（2015·四川内江·中考真题）如图，在四边形ABCD 中，AD ∥BC ，∠C=90°，E 为CD 上一点，分别以EA ，EB 为折痕将两个角（∠D ，∠C ）向内折叠，点C ，D 恰好落在AB 边的点F 处．若AD=2，BC=3，则EF 的长为____．18．（2012·山东潍坊·中考真题）点P 在反比例函数ky x= (k ≠0)的图象上，点Q (2，4)与点P 关于y 轴对称，则反比例函数的解析式为____ 三、解答题19．（2021·湖北武汉·二模）如图，在下列88⨯的网格中，横、纵坐标均为整点的数叫做格点，ABC 的顶点的坐标分别为()3,0A ，()0,4B ，()4,2C ．（1）直接写出ABC 的形状；（2）要求在下图中仅用无刻度的直尺作图：将ABC 绕点B 逆时针旋转角度2α得到11A BC ，其中ABC α=∠，A ，C 的对应点分别为1A ，1C ，请你完成作图；（3）在网格中找一个格点G ，使得1C G AB ⊥，并直接写出G 点的坐标；（4）作点1C 关于BC 的对称点D ．20．（2021·北京东城·二模）如图，在等腰△ABC中，AB=AC，直线l过点A．点B与点D 关于直线l对称，连接AD，CD．求证：∠ACD=∠ADC．21．（2017·山东威海·中考真题）如图，四边形为一个矩形纸片，，，动点自点出发沿方向运动至点后停止.以直线为轴翻折，点落到点的位置.设，与原纸片重叠部分的面积为.（1）当为何值时，直线过点？（2）当为何值时，直线过的中点？（3）求出与的函数关系式.一、单选题1．（2021·湖北荆门·中考真题）下列图形既是中心对称又是轴对称的是（）A ．B ．C ．D ．2．（2021·内蒙古鄂尔多斯·中考真题）如图，在Rt ABC 中，90,8,6ACB AC BC ∠=︒==，将边BC 沿CN 折叠，使点B 落在AB 上的点B ′处，再将边AC 沿CM 折叠，使点A 落在CB '的延长线上的点A '处，两条折痕与斜边AB 分别交于点N 、M ，则线段A M '的长为（）A ．95B ．85C ．75D ．653．（2021·黑龙江绥化·中考真题）已知在Rt ACB 中，90,75C ABC ∠=︒∠=︒，5AB =．点E 为边AC 上的动点，点F 为边AB 上的动点，则线段FE EB +的最小值是（）A 53B ．52C 5D 34．（2021·江苏苏州·中考真题）如图，在平行四边形ABCD 中，将ABC 沿着AC 所在的直线翻折得到AB C '，B C '交AD 于点E ，连接B D '，若60B ∠=︒，45ACB ∠=︒，6AC =则B D '的长是（）A ．1B ．2C ．3D ．625．（2021·湖北湖北·中考真题）若抛物线2y x bx c =++与x 轴两个交点间的距离为4．对称轴为2x =，P 为这条抛物线的顶点，则点P 关于x 轴的对称点的坐标是（） A ．()2,4B ．()2,4-C ．()2,4--D ．()2,4-6．（2021·内蒙古·中考真题）如图，在ABC 中，AB AC =，DBC △和ABC 关于直线BC 对称，连接AD ，与BC 相交于点O ，过点C 作CE CD ⊥，垂足为C ，与AD 相交于点E ．若8AD =，6BC =，则2+OE AEBD的值为（）A ．43B ．34C ．53D ．547．（2021·河北·中考真题）如图，直线l ，m 相交于点O ．P 为这两直线外一点，且 2.8OP =．若点P 关于直线l ，m 的对称点分别是点1P ，2P ，则1P ，2P 之间的距离可能．．是（）A ．0B ．5C ．6D ．78．（2021·湖北武汉·中考真题）如图，AB 是O 的直径，BC 是O 的弦，先将BC 沿BC 翻折交AB 于点D ．再将BD 沿AB 翻折交BC 于点E ．若BE DE =，设ABC α∠=，则α所在的范围是（）A ．21.922.3α︒<<︒B ．22.322.7α︒<<︒C ．22.723.1α︒<<︒D ．23.123.5α︒<<︒9．（2021·四川宜宾·中考真题）如图，在矩形纸片ABCD 中，点E 、F 分别在矩形的边AB 、AD 上，将矩形纸片沿CE 、CF 折叠，点B 落在H 处，点D 落在G 处，点C 、H 、G 恰好在同一直线上，若AB ＝6，AD ＝4，BE ＝2，则DF 的长是（）A ．2B ．74C ．322D ．3二、填空题10．（2021·山东青岛·中考真题）已知正方形ABCD 的边长为3，E 为CD 上一点，连接AE 并延长，交BC 的延长线于点F ，过点D 作DG AF ⊥，交AF 于点H ，交BF 于点G ，N 为EF 的中点，M 为BD 上一动点，分别连接MC ，MN ．若14DCG FCE S S =△△，则MN MC +的最小值为__________．11．（2021·青海西宁·中考真题）如图，ABC 是等边三角形，6AB =，N 是AB 的中点，AD 是BC 边上的中线，M 是AD 上的一个动点，连接,BM MN ，则BM MN +的最小值是________．12．（2021·辽宁鞍山·中考真题）如图，90POQ ∠=︒，定长为a 的线段端点A ，B 分别在射线OP ，OQ 上运动（点A ，B 不与点O 重合），C 为AB 的中点，作OAC 关于直线OC 对称的OA C '，A O '交AB 于点D ，当OBD 是等腰三角形时，OBD ∠的度数为_____________．13．（2021·广东广州·中考真题）如图，在ABC 中，AC BC =，38B ∠=︒，点D 是边AB 上一点，点B 关于直线CD 的对称点为B '，当//B D AC '时，则BCD ∠的度数为________．14．（2021·贵州毕节·中考真题）如图，在菱形ABCD 中，2BC =，120C ∠=︒，Q 为AB 的中点，P 为对角线BD 上的任意一点，则AP PQ +的最小值为_____________．15．（2021·辽宁大连·中考真题）如图，在菱形ABCD 中，60BAD ∠=︒，点E 在边BC 上，将ABE △沿直线AE 翻折180°，得到'AB E △，点B 的对应点是点B '若AB BD '⊥，2BE =，则BB '的长是__________．16．（2021·辽宁营口·中考真题）如图，40MON ∠=︒，以O 为圆心，4为半径作弧交OM 于点A ，交ON 于点B ，分别以点A ，B 为圆心，大于12AB 的长为半径画弧，两弧在MON ∠的内部相交于点C ，画射线OC 交AB 于点D ，E 为OA 上一动点，连接BE ，DE ，则阴影部分周长的最小值为_________．17．（2021·山东聊城·中考真题）有四张大小和背面完全相同的不透明卡片，正面分别印有等边三角形、平行四边形、菱形和圆，将这四张卡片背面朝上洗匀，从中随机抽取两张卡片，所抽取的卡片正面上的图形都既是轴对称图形，又是中心对称图形的概率是__________． 18．（2021·四川广安·中考真题）如图，将三角形纸片ABC 折叠，使点B 、C 都与点A 重合，折痕分别为DE 、FG .已知15ACB ∠=︒，AE EF =，3DE =，则BC 的长为_______．19．（2021·内蒙古鄂尔多斯·中考真题）如图，已知正方形ABCD 的边长为6，点F 是正方形内一点，连接,CF DF ，且ADF =DCF ∠∠，点E 是AD 边上一动点，连接,EB EF ，则EB EF +长度的最小值为___________．三、解答题20．（2021·辽宁阜新·中考真题）下面是小明关于“对称与旋转的关系”的探究过程，请你补充完整．（1）三角形在平面直角坐标系中的位置如图1所示，简称G ，G 关于y 轴的对称图形为1G ，关于x 轴的对称图形为2G ．则将图形1G 绕____点顺时针旋转____度，可以得到图形2G ．（2）在图2中分别画出．．．．G 关于 y 轴和直线1y x =+的对称图形1G ，2G ．将图形1G 绕____点（用坐标表示）顺时针旋转______度，可以得到图形2G ．（3）综上，如图3，直线1:22l y x =-+和2:l y x =所夹锐角为α，如果图形G 关于直线1l 的对称图形为1G ，关于直线2l 的对称图形为2G ，那么将图形1G 绕____点（用坐标表示）顺时针旋转_____度（用α表示），可以得到图形2G ．21．（2021·山东济宁·中考真题）研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．（1）阅读材料立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．例如，正方体ABCD A B C D ''''-（图1）．因为在平面AA C C ''中，//CC AA ''，AA '与AB 相交于点A ，所以直线AB 与AA '所成的BAA '∠就是既不相交也不平行的两条直线AB 与CC '所成的角．解决问题如图1，已知正方体ABCD A B C D ''''-，求既不相交也不平行的两条直线BA '与AC 所成角的大小．（2）如图2，M ，N 是正方体相邻两个面上的点．①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是； ②在所选正确展开图中，若点M 到AB ，BC 的距离分别是2和5，点N 到BD ，BC 的距离分别是4和3，P 是AB 上一动点，求PM PN +的最小值．22．（2021·湖北荆门·中考真题）如图，抛物线2y ax bx c =++交x 轴于(1,0)A -，(3,0)B 两点，交y 轴于点(0,3)C -，点Q 为线段BC 上的动点．（1）求抛物线的解析式；（2）求||||QO QA +的最小值；（3）过点Q 作//PQ AC 交抛物线的第四象限部分于点P ，连接P A ，PB ，记PAQ △与PBQ △的面积分别为1S ，2S ，设12S S S =+，求点P 坐标，使得S 最大，并求此最大值．1．C【解析】【分析】根据中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形就叫做中心对称图形；轴对称图形的定义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形．【详解】解：A．是轴对称图形，不是中心对称图形，故本选项不符合题意；B．既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；C．既是轴对称图形，又是中心对称图形，故本选项符合题意；D．既不是轴对称图形，也不是中心对称图形，故本选项不符合题意．故选：C【点拨】本题考查了中心对称图形与轴对称图形的概念，正确掌握相关定义是解题关键．2．D【解析】【分析】根据关于y轴对称的点的横坐标互为相反数，纵坐标相等，可得答案．【详解】解：点A（-3，4）关于y轴对称的点的坐标是（3，4），【点拨】本题考查了关于y 轴对称的点的坐标，明确关于y 轴对称的点的横坐标互为相反数，纵坐标相等是解题的关键 3．C 【解析】【分析】过点A 作AH BC ⊥ 于H ，由折叠知识得：90BFG ∠=︒ ，再由锐角三角函数可得53AH =，然后根据//AD BC ，可证得四边形AHFG 是矩形，即可求解．【详解】解：过点A 作AH BC ⊥ 于H ，由折叠知：BF =GF ，∠BFE =∠GFE ，45BFE ∠=︒， 90BFG ∴∠=︒ ，在Rt ABH 中，10AB =，60B ∠=︒， 3sin sin 60101053AH B AB =⨯=︒⨯==， //AD BC ，90GAH AHB ∴∠=∠=︒ ， 90GAH AHB BFG ∴∠=∠=∠=︒ ，∴ 四边形AHFG 是矩形， 3FG AH ∴==， 3BF GF ∴==．故选：C ．【点拨】本题主要考查了折叠变换，解直角三角形，矩形的判定和性质，熟练掌握相关知识点是解题的关键． 4．A 【解析】【分析】首先判断各图形是否是轴对称图形，再根据题意画出树状图，然后由树状图求得所有等可能的结果与抽到卡片上印有的图案都是轴对称图形的情况，再利用概率公式求解即可求得答案．解：∵线段是轴对称图形，等边三角形是轴对称图形，平行四边形不是轴对称图形，正六边形是轴对称图形，分别用A 、B 、C 、D 表示线段、等边三角形、平行四边形和正六边形，∴随机抽取两张，则抽到的卡片正面图形都是轴对称图形的概率为612=12，故选：A ．【点拨】本题考查概率公式、轴对称图形，解答本题的关键是写出题目中的图形是否为轴对称图形，明确两张都是轴对称图形是同时发生的． 5．D 【解析】【分析】先利用互余计算出∠BDE ＝28°，再根据平行线的性质得∠CBD ＝∠BDE ＝28°，接着根据折叠的性质得∠FBD ＝∠CBD ＝28°，然后利用三角形外角性质计算∠DEF 的度数，于是得到结论．【详解】解：∵四边形ABCD 为矩形， ∴AD ∥BC ，∠ADC ＝90°，∵90906228BDE BDC ∠︒-∠︒-︒︒＝＝＝， ∵AD ∥BC ，∴∠CBD ＝∠BDE ＝28°， ∵矩形ABCD 沿对角线BD 折叠， ∴∠FBD ＝∠CBD ＝28°，∴∠DEF ＝∠FBD +∠BDE ＝28°+28°＝56°．故选：D ．【点拨】本题考查了矩形的性质，平行线和折叠的性质，综合运用以上性质是解题的关键． 6．C 【解析】【分析】根据该几何体的三视图，结合轴对称图形的定义：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形及中心对称的定义：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形称为中心对称图形进行判断即可．【详解】解：该几何体的三视图如下：三视图中既是轴对称图形，又是中心对称图形的是俯视图，故选：C．【点拨】本题考查简单几何体的三视图，中心对称、轴对称，理解视图的意义，掌握简单几何体三视图的画法以及轴对称、中心对称的意义是正确判断的前提．7．D【解析】【分析】先在RtABC中利用勾股定理计算出AB=10，再利用折叠的性质得到AE=BE，AD=BD=5，设AE=x，则CE=AC-AE=8-x，BE=x，在Rt△BCE中根据勾股定理可得到x2=62+（8-x）2，解得x，可得CE．【详解】解：∵∠ACB=90°，AC=8，BC=6，∴AB22AC BC+，∵△ADE沿DE翻折，使点A与点B重合，∴AE=BE，AD=BD=12AB=5，设AE=x，则CE=AC-AE=8-x，BE=x，在Rt△BCE中∵BE2=BC2+CE2，∴x2=62+（8-x）2，解得x=254，∴CE=2584-=74，故选：D．【点拨】本题考查了折叠的性质：折叠前后两图象全等，即对应角相等，对应边相等．也考查了勾股定理．8．B 【解析】【分析】根据折叠性质可得∠EMB′=∠EMB＝12∠BMC′，∠FMB′＝∠FMC＝12∠CMC′，再根据平角定义即可解答．【详解】解：∠EMF＝∠EMB′＋∠FMB′＝12∠BMC′＋12∠CMC′＝12×180°＝90°，故选：B．【点拨】本题考查折叠的性质、平角定义，熟练掌握折叠的性质求角度是解答的关键．9．D【解析】【分析】由基本作图得到得EF垂直平分AB，则MB＝MA，所以BM+MD＝MA+MD，连接MA、DA，如图，利用两点之间线段最短可判断MA+MD的最小值为AD，再利用等腰三角形的性质得到AD⊥BC，然后利用三角形面积公式计算出AD即可．【详解】解：由作法得EF垂直平分AB，∴MB＝MA，∴BM+MD＝MA+MD，连接MA、DA，如图，∵MA+MD≥AD（当且仅当M点在AD上时取等号），∴MA+MD的最小值为AD，∵AB＝AC，D点为BC的中点，∴AD⊥BC，∵110,2ABCS BC AD==∴1025,4AD⨯==∴BM+MD长度的最小值为5．故选：D．【点拨】本题考查的是线段的垂直平分线的性质，利用轴对称求线段和的最小值，三角形的面积，两点之间，线段最短，掌握以上知识是解题的关键．10．45【解析】【分析】卡片中，轴对称图形有等腰三角形、矩形、菱形、等腰梯形，再根据概率公式P =满足条件的样本个数÷总体的样本个数，可求出最终结果．【详解】解：卡片中，轴对称图形有等腰三角形、矩形、菱形、等腰梯形，根据概率公式，P （轴对称图形）45=．故答案为：45．【点拨】本题主要考查概率问题，属于基础题，掌握轴对称图形的性质以及概率公式是解题关键．11．12或2【解析】【分析】因为点D 恰好在原直角三角形纸片的边上，所以分为当D 落在AB 边上和BC 边上两种情况分析，勾股定理求解即可．【详解】解：当D 落在AB ：设DD '交AB 于点E ，由折叠知：60EA D A '∠=∠=︒, AD A D A D '''==,DD A E ''⊥,A C AC '=90ACB ∠=︒，30B ∠=︒，1AC =2,AB BC ∴==设AD x =，则在Rt A ED '中，12A E x '=在Rt ECB 中，12EC BC ==A C AC '=112x ∴=即2x =当D 落在BC 边上时，如图（2）因为折叠，30,ACD A CD A CD '''∠=∠=∠=︒∴ 11,122A D A C A B A C A B AC ''''''===== 12AD A D ''∴==．故答案为：12或23【点拨】本题考查了轴对称变换，勾股定理，直角三角形中30的性质，正确的作出图形是解题的关键．12．45°【解析】【分析】根据折叠的性质可以得出∠EBD=12∠ABD, ∠FBD=12∠CBD,即可求出∠EBF.【详解】解：将长方形纸片ABCD 折叠，使边AB 、CB 均落在对角线BD 上，得折痕BE 、BF 得到∠EBD=∠ABE=12∠ABD, ∠FBD=∠CBF=12∠CBD∵ ∠ABC=90°∴∠EBF=∠EBD+∠FBD=12∠ABD+12∠CBD=12∠ABC=45°故答案为：45°【点拨】本题主要考查了折叠的性质及角度的计算，掌握概念是解题的关键.13．40°【解析】【分析】如图，由折叠的性质可得1=20BAF ∠=∠︒，进而可得40CHB HAB HBA ∠=∠+∠=︒，然后易得四边形CHBD 是平行四边形，最后根据平行四边形的性质可求解．【详解】解：如图所示：∵1=20∠︒，由折叠的性质可得1=20BAF ∠=∠︒，∵//CD BE ，∴20HBA BAF ∠=∠=︒，∴40CHB HAB HBA ∠=∠+∠=︒，∵//CH BD ，∴四边形CHBD 是平行四边形，∴240CHB ∠=∠=︒；故答案为40°．【点拨】本题主要考查平行四边形的性质与判定、平行线的性质及折叠的性质，熟练掌握平行四边形的性质与判定、平行线的性质及折叠的性质是解题的关键．14．21【解析】【分析】由题意易得四边形ABCD 是正方形，进而根据轴对称的性质可得AD =DP ，24PDQ ADQ ∠=∠=︒，则有CD =DP ，然后可得138CDP ∠=︒，最后根据等腰三角形的性质可求解．【详解】解：∵CBD ABD ≌，且都为等腰直角三角形，∴四边形ABCD 是正方形，∴90,CDA CD AD ∠=︒=，∵点P 与点A 关于直线DQ 对称，24ADQ ∠=︒，∴24PDQ ADQ ∠=∠=︒，AD =DP ，∴CD =DP ，48ADP ∠=︒，∴138CDP ∠=︒， ∴180212CDP DCP DPC ︒-∠∠=∠==︒，故答案为21．【点拨】本题主要考查正方形的判定与性质、轴对称的性质及等腰三角形的性质，熟练掌握正方形的判定与性质、轴对称的性质及等腰三角形的性质是解题的关键．15．65°．【解析】【详解】试题分析：：∵∠AEA′=180°﹣∠A′EC=180°﹣70°=110°，又∵∠A′ED=∠AED=12∠AEA′=55°，∠DA′E=∠A=60°，∴∠A′DE=180°﹣∠A′ED ﹣∠DA′E=180°﹣55°﹣60°=65°．故答案是65°．考点：翻折变换（折叠问题）．16．【解析】【详解】试题分析：作点M 关于AB 的对称点N ，过N 作NQ ⊥AC 于Q 交AB 于P ，则NQ 的长即为PM+PQ 的最小值，连接MN 交AB 于D ，则MD ⊥AB ，DM=DN ，∵∠NPB=∠APQ ，∴∠N=∠BAC=30°，∵∠BAC=30°，AM=2，∴MD=AM=1，∴MN=2，∴NQ=MN•cos∠N=2×=，故答案为．考点：轴对称﹣最短路线问题17．6．【解析】【详解】试题分析：先根据折叠的性质得DE=EF，CE=EF，AF=AD=2，BF=CB=3，则DC=2EF，AB=5，再作AH⊥BC于H，由于AD∥BC，∠B=90°，则可判断四边形ADCH为矩形，所以AH=DC=2EF，HB=BC﹣CH=BC﹣AD=1，然后在Rt△ABH中，利用勾股定理计算出AH=2，所以EF=．考点：翻折变换（折叠问题）．.18．8yx=-．【解析】【分析】根据轴对称的定义，利用点Q（2，4），求出P点坐标，将P点坐标代入解析式，即可求出反比例函数解析式．【详解】解：∵点Q（2，4）和点P关于y轴对称，关于y轴对称的点的坐标特征是纵坐标不变，横坐标互为相反数∴P点坐标为（－2，4）．将（－2，4）解析式kyx=得，k=xy=－2×4=－8．∴函数解析式为8yx=-．故答案为：8yx=-．【点拨】本题考查了待定系数法求反比例函数解析式、关于x轴、y轴对称的点的坐标，熟悉待定系数法是解题的关键．19．（1）ABC 是直角三角形；（2）见解析；（3）图见解析，()0,3G ；（4）见解析【解析】【分析】（1）利用勾股定理以及勾股定理的逆定理解决问题即可．（2）利用数形结合的思想解决问题即可．（3）利用数形结合的思想解决问题即可．（4）取格点T ，作直线1TC ，取格点P ，连接OP 交1TC 于点D ，点D 即为所求作．【详解】解：（1）∵()3,0A ，()0,4B ，()4,2C ， ∴22345AB =+=，22521AC =+=，224225BC =+=，∴222AB AC BC =+，∴90ACB ∠=︒，∴ABC 是以AB 为斜边的直角三角形．（2）11A BC 如图所示．先将AB 绕点B 逆时针旋转2α到达1BA ，点1(5,4)A ；再将CB 绕点B 逆时针旋转2α到达1BC ，点1(4,6)C ，连接11A C ，即可得到11A BC ；（3）如图，过点1C 作直线1C G AB ⊥ 交y 轴于点G ，由图可知：点()0,3G ．（4）如图，取格点T （1，0），作直线1TC ，取格点P （4，-2），连接OP 交1TC 于点D ，点D 即为所求作．【点拨】本题考查作图-旋转变换，轴对称，勾股定理以及逆定理等知识，解题的关键是学会利用数形结合的思想解决问题．20．证明见解析【解析】【分析】要证明∠ACD=∠ADC，只需证明AD=AC，又AB=AD，AB=AC，等量代换即可．【详解】证明：∵点B与点D关于直线l对称，∴AB=AD，又∵AB=AC，∴AD=AC．∴∠ACD=∠ADC．【点拨】本题考查的是等腰三角形的相关定理，能根据要求进行条件的等量转换是解题关键．21．（1）当x=时，直线AD1过点C（2）当x=时，直线AD1过BC的中点E（3）当0＜x≤2时，y=x；当2＜x≤3时，y=【解析】【详解】试题分析：（1）根据折叠得出AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，在Rt△ABC中，根据勾股定理求出AC，在Rt△PCD1中，根据勾股定理得出方程，求出即可；（2）连接PE，求出BE=CE=1，在Rt△ABE中，根据勾股定理求出AE，求出AD1=AD=2，PD=PD1=x，D1E=﹣2，PC=3﹣x，在Rt△PD1E和Rt△PCE中，根据勾股定理得出方程，求出即可；（3）分为两种情况：当0＜x≤2时，y=x；当2＜x≤3时，点D1在矩形ABCD的外部，PD1交AB于F，求出AF=PF，作PG⊥AB于G，设PF=AF=a，在Rt△PFG中，由勾股定理得出方程（x﹣a）2+22=a2，求出a即可．试题解析：（1）如图1，∵由题意得：△ADP≌△AD1P，∴AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，∵直线AD1过C，∴PD1⊥AC，在Rt△ABC中，AC=，CD1=﹣2，在Rt△PCD1中，PC2=PD12+CD12，即（3﹣x）2=x2+（﹣2）2，解得：x=，∴当x=时，直线AD1过点C；（2）如图2，连接PE，∵E为BC的中点，∴BE=CE=1，在Rt△ABE中，AE==，∵AD1=AD=2，PD=PD1=x，∴D1E=﹣2，PC=3﹣x，在Rt△PD1E和Rt△PCE中，x2+（﹣2）2=（3﹣x）2+12，解得：x=，∴当x=时，直线AD1过BC的中点E；（3）如图3，当0＜x≤2时，y=x，如图4，当2＜x≤3时，点D1在矩形ABCD的外部，PD1交AB于F，∵AB∥CD，∴∠1=∠2，∵∠1=∠3（根据折叠），∴∠2=∠3，∴AF=PF，作PG⊥AB于G，设PF=AF=a，由题意得：AG=DP=x，FG=x﹣a，在Rt△PFG中，由勾股定理得：（x﹣a）2+22=a2，解得：a=，所以y==，综合上述，当0＜x≤2时，y=x；当2＜x≤3时，y=．考点：1、勾股定理，2、折叠的性质，3、矩形的性质，4、分类推理思想1．C【解析】【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．【详解】解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项不符合题意．B 、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故此选项不符合题意；C 、此图形旋转180°后能与原图形重合，此图形是中心对称图形，是轴对称图形，故此选项符合题意；D 、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故此选项不符合题意．故选：C ．【点拨】此题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．2．B【解析】【分析】利用勾股定理求出AB =10，利用等积法求出CN ＝245，从而得AN ＝325，再证明∠NMC ＝∠NCM ＝45°，进而即可得到答案．【详解】解：∵90,8,6ACB AC BC ∠=︒==∴AB 10，∵S △ABC ＝12×AB ×CN ＝12×AC ×BC∴CN ＝245，∵AN 325=， ∵折叠∴AM ＝A'M ，∠BCN ＝∠B'CN ，∠ACM ＝∠A'CM ，∵∠BCN +∠B'CN +∠ACM +∠A'CM =90°，∴∠B'CN +∠A'CM ＝45°，∴∠MCN ＝45°，且CN ⊥AB ，∴∠NMC ＝∠NCM ＝45°，∴MN ＝CN ＝245， ∴A'M ＝AM ＝AN −MN ＝325-245=85．故选B ．【点拨】本题考查了翻折变换，勾股定理，等腰直角三角形的性质，熟练运用折叠的性质是本题的关键．3．B【解析】【分析】作点F关于直线AB的对称点F’，如下图所示，此时EF+EB=EF’+EB，再由点到直线的距离垂线段长度最短求解即可．【详解】解：作点F关于直线AB的对称点F’，连接AF’，如下图所示：由对称性可知，EF=EF’，此时EF+EB= EF’+EB，由“点到直线的距离垂线段长度最小”可知，当BF’⊥AF’时，EF+EB有最小值BF0，此时E位于上图中的E0位置，由对称性知，∠CAF0=∠BAC=90°-75°=15°，∴∠BAF0=30°，由直角三角形中，30°所对直角边等于斜边的一半可知，BF0=12AB=15522⨯=，故选：B．【点拨】本题考查了30°角所对直角边等于斜边的一半，垂线段最短求线段最值等，本题的核心思路是作点F关于AC的对称点，将EF线段转移，再由点到直线的距离最短求解．4．B【解析】【分析】利用平行四边形的性质、翻折不变性可得△AEC为等腰直角三角形，根据已知条件可得CE得长，进而得出ED的长，再根据勾股定理可得出B D'；【详解】解：∵四边形ABCD是平行四边形∴AB=CD∠B=∠ADC=60°，∠ACB＝∠CAD由翻折可知：BA＝AB′＝DC，∠ACB＝∠AC B′=45°，∴△AEC为等腰直角三角形。

2020年上海中考数学·一轮复习第14讲平面直角坐标系

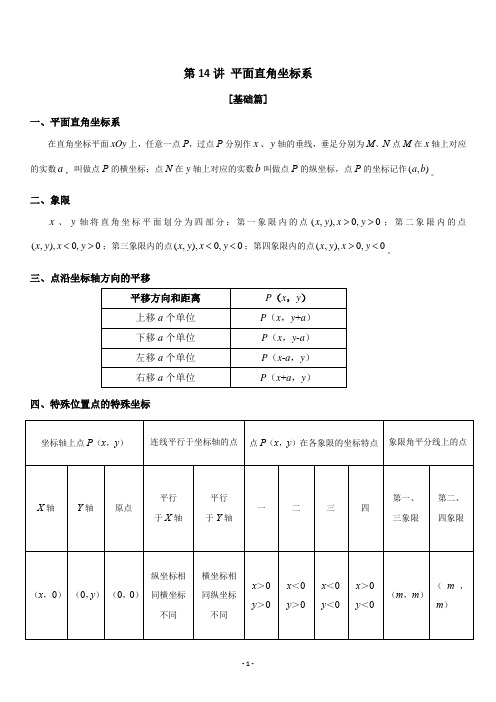
第14讲平面直角坐标系[基础篇]一、平面直角坐标系在直角坐标平面xOy 上，任意一点P ，过点P 分别作x 、y 轴的垂线，垂足分别为M 、N 点M 在x 轴上对应的实数a ，叫做点P 的横坐标；点N 在y 轴上对应的实数b 叫做点P 的纵坐标，点P 的坐标记作(,)a b 。

二、象限x、y 轴将直角坐标平面划分为四部分：第一象限内的点(,),0,x y x y >>0；第二象限内的点(,),0,x y x y <>0；第三象限内的点(,),0,x y x y <<0；第四象限内的点(,),0,x y x y ><0。

三、点沿坐标轴方向的平移四、特殊位置点的特殊坐标五、点关于坐标轴、原点的对称变换在直角坐标平面内，与点(,)M x y 关于x 轴对称点的坐标为(,)x y -；与点(,)M x y 关于y 轴对称点的坐标为(,)x y -；与点(,)M x y 关于原定对称点的坐标为(,)x y --．六、点的简单旋转变换点(,)P x y 绕原点O 按逆时针方向旋转90︒到达点Q ，则Q '(,)y x -．七、坐标轴上两点间的距离设A 、B 的直线坐标分别为1122(,)(,)A x y B x y 、，分别过A 、B 引x 轴的垂线，垂足分别满足12(,0)(,0)A B M x M x 、；引y 轴的垂线，垂足分别为12(0,)(0,)A B N y N y 、，则：2121,A B A B M M x x N N y y ||=|-|||=|-|．八、中点坐标设A 、B 的直角坐标分别为1122(,),(,)A x y B x y ，(,)M x y 是A 、B 的中点，则122x x x +=，122y y y +=．九、平面直角坐标系中的等腰三角形问题利用两腰相等进行求解。

十、平面直角坐标系中三角形面积的求法1、当三角形的一边在坐标轴上或与坐标轴平行时，可借助坐标轴或平行于坐标轴的直线上的某一条线段作为三角形的边，第三点到这条边的距离作为三角形的高，直接利用三角形的面积公式求解。

平面直角坐标系篇(解析版)--中考数学必考考点总结+题型专训

知识回顾微专题专题12平面直角坐标系考点一：平面直角坐标系之坐标特点1.有序数对：有顺序的两个数a 与b 组成的数对叫做有序数对。

表示为()b a ，，可以用来表示位置。

2.平面直角坐标系各部分的坐标特点：①x 轴上的所有点的坐标可表示为()0 ，x 。

②y 轴上的所有点的坐标可表示为()y ，0。

③第一象限内的所有点的坐标横纵坐标都是正数。

即（﹢，﹢）。

④第二象限内的所有点的坐标横坐标是负数，纵坐标是正数。

即（﹣，﹢）。

⑤第三象限内的所有点的坐标横纵坐标都是负数。

即（﹣，﹣）。

⑥第四象限内的所有点的坐标横坐标是正数，纵坐标是负数。

即（﹢，﹣）。

3.点到坐标轴的距离：点()b a ，到横坐标的距离等于纵坐标的绝对值。

即b 。

点()b a ，到纵坐标的距离等于横坐标的绝对值。

即a 。

1．（2022•六盘水）两个小伙伴拿着如图的密码表玩听声音猜动物的游戏，若听到“咚咚﹣咚咚，咚﹣咚，咚咚咚﹣咚”表示的动物是“狗”，则听到“咚咚﹣咚，咚咚咚﹣咚咚，咚﹣咚咚咚”时，表示的动物是（）A ．狐狸B ．猫C ．蜜蜂D ．牛【分析】根据点的坐标解决此题．【解答】解：由题意知，咚咚﹣咚咚对应（2，2），咚﹣咚对应（1，1），咚咚咚﹣咚对应（3，1）．∴咚咚﹣咚对应（2，1），表示C；咚咚咚﹣咚咚对应（3，2），表示A；咚﹣咚咚咚对应（1，3），表示T．∴此时，表示的动物是猫．故选：B．2．（2022•柳州）如图，这是一个利用平面直角坐标系画出的某学校的示意图，如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向，并且综合楼和食堂的坐标分别是（4，1）和（5，4），则教学楼的坐标是（）A．（1，1）B．（1，2）C．（2，1）D．（2，2）【分析】根据综合楼和食堂的坐标分别是（4，1）和（5，4），建立适当的平面直角坐标系，即可解答．【解答】解：建立如图所示的平面直角坐标系：∴教学楼的坐标是（2，2），故选：D．3．（2022•铜仁市）如图，在矩形ABCD中，A（﹣3，2），B（3，2），C（3，﹣1），则D的坐标为（）A．（﹣2，﹣1）B．（4，﹣1）C．（﹣3，﹣2）D．（﹣3，﹣1）【分析】先根据A、B的坐标求出AB的长，则CD＝AB＝6，并证明AB∥CD∥x轴，同理可得AD∥BC ∥y轴，由此即可得到答案．【解答】解：∵A（﹣3，2），B（3，2），∴AB＝6，AB∥x轴，∵四边形ABCD是矩形，∴CD＝AB＝6，AB∥CD∥x轴，同理可得AD∥BC∥y轴，∵点C（3，﹣1），∴点D的坐标为（﹣3，﹣1），故选：D．4．（2022•宜昌）如图是一个教室平面示意图，我们把小刚的座位“第1列第3排”记为（1，3）．若小丽的座位为（3，2），以下四个座位中，与小丽相邻且能比较方便地讨论交流的同学的座位是（）A．（1，3）B．（3，4）C．（4，2）D．（2，4）【分析】直接利用点的坐标特点得出与小丽相邻且能比较方便地讨论交流的同学的座位位置．【解答】解：如图所示：与小丽相邻且能比较方便地讨论交流的同学的座位是（4，2）．故选：C．5．（2022•扬州）在平面直角坐标系中，点P（﹣3，a2+1）所在象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据平方数非负数判断出点P的纵坐标是正数，再根据各象限内点的坐标特征解答．【解答】解：∵a2≥0，∴a2+1≥1，∴点P（﹣3，a2+1）所在的象限是第二象限．故选：B．6．（2022•乐山）点P（﹣1，2）在（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据各象限内点的坐标符号直接判断的判断即可．【解答】解：∵P（﹣1，2），横坐标为﹣1，纵坐标为：2，∴P点在第二象限．故选：B．7．（2022•攀枝花）若点A（﹣a，b）在第一象限，则点B（a，b）在（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】直接利用第一象限内点的坐标特点得出a、b的符号，进而得出答案．【解答】解：∵点A（﹣a，b）在第一象限内，∴﹣a＞0，b＞0，∴a＜0，∴点B（a，b）所在的象限是：第二象限．故选：B．8．（2022•衢州）在平面直角坐标系中，点A（﹣1，﹣2）落在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【分析】根据第三象限中点的坐标特征：横坐标为负数，纵坐标为负数，由此可确定A 点位置．【解答】解：∵﹣1＜0，﹣2＜0，∴点A （﹣1，﹣2）在第三象限，故选：C ．9．（2022•河池）如果点P （m ，1+2m ）在第三象限内，那么m 的取值范围是（）A ．﹣21＜m ＜0B ．m ＞﹣21C ．m ＜0D ．m ＜﹣21【分析】根据点P 在第三象限，即横纵坐标都是负数，据此即可列不等式组求得m 的范围．【解答】解：根据题意得，解①得m ＜0，解②得m ＜．则不等式组的解集是m ＜﹣．故选：D ．10．（2022•兰州）如图，小刚在兰州市平面地图的部分区域建立了平面直角坐标系，如果白塔山公园的坐标是（2，2），中山桥的坐标是（3，0），那么黄河母亲像的坐标是．【分析】根据白塔山公园的坐标是（2，2），中山桥的坐标是（3，0）画出直角坐标系，然后根据点的坐标的表示方法写出黄河母亲像的坐标；【解答】解：如图，根据白塔山公园的坐标是（2，2），中山桥的坐标是（3，0）画出直角坐标系，∴黄河母亲像的坐标是（﹣4，1）．故答案为：（﹣4，1）．11．（2022•广安）若点P（m+1，m）在第四象限，则点Q（﹣3，m+2）在第象限．【分析】根据点P（m+1，m）在第四象限，求出m的取值范围，得到1＜m+2＜2，进而得到点Q所在的象限．【解答】解：∵点P（m+1，m）在第四象限，∴，∴﹣1＜m＜0，∴1＜m+2＜2，∴点Q（﹣3，m+2）在第二象限，故答案为：二．12．（2022•鄂州）中国象棋文化历史久远．某校开展了以“纵横之间有智慧攻防转换有乐趣”为主题的中国象棋文化节．如图所示是某次对弈的残局图，如果建立平面直角坐标系，使“帥”位于点（﹣1，﹣2），“馬”位于点（2，﹣2），那么“兵”在同一坐标系下的坐标是．【分析】应用平面内点的平移规律进行计算即可得出答案．【解答】解：根据平面内点的平移规律可得，把“帅”向左平移两个单位，向上平移3个单位得到“兵”的位置，∴（﹣1﹣2，﹣2+3），即（﹣3，1）．故答案为：（﹣3，1）．13．（2022•烟台）观察如图所示的象棋棋盘，若“兵”所在的位置用（1，3）表示，“炮”所在的位置用（6，4）表示，那么“帅”所在的位置可表示为．【分析】直接利用已知点坐标得出原点位置进而得出答案．【解答】解：如图所示：“帅”所在的位置：（4，1），故答案为：（4，1）．考点二：平面直角坐标系之坐标变换知识回顾微专题1.平行于x 轴（垂直于y 轴）的直线上的点的坐标：纵坐标相等。

平移旋转轴对称练习题

平移旋转轴对称练习题一、选择题1. 下列图形中，哪一个图形可以通过平移得到另一个图形？A. 正方形B. 长方形C. 梯形D. 平行四边形2. 在平面直角坐标系中，点A(2, 3)经过平移后得到点B，若点B 的坐标为(5, 7)，则平移向量为？A. (3, 4)B. (4, 3)C. (3, 5)D. (5, 3)3. 下列哪个图形是轴对称图形？A. 正三角形B. 正方形C. 等腰梯形D. 所有选项都是4. 下列哪个图形可以通过旋转90度得到自身？A. 正方形B. 长方形C. 等边三角形D. 圆二、填空题1. 图形平移时，对应点的连线__________。

2. 图形的旋转中心称为__________。

3. 轴对称图形的对称轴可以是__________、__________或__________。

4. 一个图形绕着某一点旋转180度后与原图形重合，这个点称为__________。

三、判断题1. 平移不改变图形的大小和形状。

（）2. 旋转会改变图形的大小和形状。

（）3. 轴对称图形的对称轴必须经过图形的中心。

（）4. 平移和旋转都是刚体变换。

（）四、作图题1. 请画出下列图形经过平移后的图形：（1）正方形，平移向量：(3, 2)（2）等腰三角形，平移向量：(4, 1)2. 请画出下列图形绕点O旋转90度后的图形：（1）正方形（2）等边三角形3. 请画出下列图形的对称轴：（1）正方形（2）等腰梯形五、解答题1. 请描述一个正方形绕其中心旋转180度后的位置变化。

2. 画出两个全等三角形，其中一个三角形通过平移、旋转或轴对称变换得到另一个三角形，并说明变换过程。

3. 请举例说明生活中平移、旋转和轴对称现象的应用。

六、应用题1. 在平面直角坐标系中，点P(1, 2)经过平移后到达点Q，点Q 的坐标是(4, 1)。

求平移向量，并画出平移后的图形。

2. 一个长方形的长是8厘米，宽是4厘米。

如果将这个长方形绕其一个顶点旋转90度，求旋转后长方形的面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三讲平面直角坐标系与轴对称变换专题第一节：直角坐标系与轴对称变换知识点回忆知识点一：轴对称、轴对称图形1、轴对称图形：如果一个图形沿*条直线对折，对折的两局部是重合的，则就称这样的图形为轴对称图形。

这条直线称为对称轴，对称轴一定为直线。

2、轴对称：把一个图形沿着*一条直线翻折过去，如果它能与另一个图形重合，则这两个图形成轴对称，两个图形中的对应点叫对称点。

知识点二：轴对称图形的性质1、轴对称图形的对应线段相等，对应角相等，对应点的连线被对称轴垂直平分。

轴对称的两个图形，对应线段或延长线相交，交点在对称轴上。

2、轴对称图形变换的特征是不改变图形的大小和形状，只改变图形的位置，新旧图形具有对称性。

例2：〔2009****〕如图，Rt △ABC 中，∠ACB =90°，∠A =50°，将其折叠，使点A 落在边CB 上A ′处，折痕为CD ，则∠A ′DB =〔〕A ．40° B．30° C．20° D．10°解析：有关折叠问题是中考常考的题型，必须要区分清楚折叠前后图形和数量关系。

此题中，将∠A 折叠，出现了轴对称，∠CA ′D =∠A ，因为∠A =50°，所以∠CA ′D =50°。

在Rt △ABC 中，∠ACB =90°，∠B =90°-∠A =40°。

∠CA ′D 是△ A ′B D 的一个外角，等于∠A ′DB 与∠B 之和，所以∠A ′DB =∠A ′DB -∠B =50°- 40°=10°。

应选择D 。

2.〔2009****〕点(35)p ，关于x 轴对称的点的坐标为〔〕A ．(3,5)B ．(5,3)C ．(3,5)D ．(3,5)【答案】D知识点三：中心对称、中心对称图形1、中心对称图形：一个图形绕着*点旋转一定角度后能与自身重合，这种图形叫中心对称图形，该点叫作旋转中心。

2、中心对称：把一个图形绕着*一点旋转一定角度后，如果它能与另一个图形重合，则，A 'B D A C这两个图形成中心对称，该点叫作对称中心。

知识点四：中心对称图形的性质在中心对称的两个图形中，连接对称点的线段都经过对称中心且被对称中心平分。

1、如图,在平面直角坐标系中有一矩形ABCD,其中(0,0),B(8,0),C(0,4,)假设将△ABC 沿AC 所在直线翻折,点B 落在点E 处,则E 点的坐标是__________.2、如图，将正六边形放在直角坐标系中中心与坐标原点重合，假设A 点的坐标为〔-1,0)，则点C 的坐标为______.3、：如图，O 为坐标原点，四边形OABC 为矩形，A(10，0)，C(0，4)，点D 是OA 的中点，点P 在BC 上运动，当△ODP 是腰长为5的等腰三角形时，则P 点的坐标为．4.对任意实数x ，点2(2)P x x x ，一定不在．．〔〕 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限〔1〕当0＜*＜2时，*＞0，*2-2*=**〔*-2〕＜0，故点P 在第四象限；〔2〕当*＞2时，*＞0，*2-2*=**〔*-2〕＞0，故点P 在第一象限；〔3〕当*＜0时，*2-2*＞0，点P 在第二象限．故对任意实数*，点P 可能在第一、二、四象限，一定不在第三象限，应选C ．5如图的坐标平面上有一正五边形ABCDE ，其中C 、D 两点坐标分别为(1,0)、(2,0) ．假设在没有滑动的情况下，将此正五边形沿着*轴向右滚动，则滚动过程中，以下会经过(75 , 0)的点是〔〕A ． AB ． BC ． CD ． D∵C、D 两点坐标分别为〔1，0〕、〔2，0〕．∴按题中滚动方法点E 经过点〔3，0〕，点A 经过点〔4，0〕，点B 经过点〔5，0〕，∵点〔75，0〕的横坐标是5的倍数，而该正五边形滚动5次正好一周，∴可知经过〔5，0〕的点经过〔75，0〕，∴点B 经过点〔75，0〕．应选B ．6、当b=______时,点B(3,|b-1|)在第一.三象限角平分线上.点在角平分线上的特点：一、三象限的角平分线上的点：横纵坐标相等；二、四象限的角平分线上的点：横纵坐标互为相反数7.〔2013****〕如图，在△ABC 中,∠ CAB ＝70。

. 在同一平面内, 将△ABC 绕点A 旋转到△AB’C’的位置, 使得AB //CC’, 则∠BAB 〔〕A. 30.B. 35.C. 40.D. 50.8、如图，已经四边形ABCD 是矩形，把矩形沿直线AC 折叠，点B 落在点E 处，连接DE ，假设DE:AC=3:5,求AD /AB 的值第二节：最短路径问题A BC D E y(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求．如下图，点A，B分别是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短，这时点C是直线l与AB的交点．(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，则与该直线的交点即为所求．如下图，点A，B分别是直线l同侧的两个点，在l上找一个点C，使CA＋CB最短，这时先作点B关于直线l的对称点B′，则点C是直线l与AB′的交点．为了证明点C的位置即为所求，我们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′，证明AC＋CB＜AC′＋C′B.如下：证明：由作图可知，点B和B′关于直线l对称，所以直线l是线段BB′的垂直平分线．因为点C与C′在直线l上，所以BC＝B′C，BC′＝B′C′.在△AB′C′中，AB′＜AC′＋B′C′，所以AC＋B′C＜AC′＋B′C′，所以AC＋BC＜AC′＋C′B.【例1】在图中直线l上找到一点M，使它到A，B两点的距离和最小．分析：先确定其中一个点关于直线l的对称点，然后连接对称点和另一个点，与直线l的交点M即为所求的点．解：如下图：(1)作点B关于直线l的对称点B′；(2)连接AB′交直线l于点M.(3)则点M即为所求的点．点拨：运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上，然后用"两点之间线段最短〞解决问题.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题的根本思路，不管题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上*点的距离和最小这个核心，所有作法都一样．警误区利用轴对称解决最值问题应注意题目要求根据轴对称的性质、利用三角形的三边关系，通过比拟来说明最值问题是常用的一种方法．解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问．3．利用平移确定最短路径选址选址问题的关键是把各条线段转化到一条线段上．如果两点在一条直线的同侧时，过两点的直线与原直线的交点处构成线段的差最大，如果两点在一条直线的异侧时，过两点的直线与原直线的交点处构成的线段的和最小，都可以用三角形三边关系来推理说明，通常根据最大值或最小值的情况取其中一个点的对称点来解决．解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．在解决最短路径问题时，我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上，从而作出最短路径的方法来解决问题．【例2】如图，小河边有两个村庄A，B，要在河边建一自来水厂向A村与B村供水．(1)假设要使厂部到A，B村的距离相等，则应选择在哪建厂？(2)假设要使厂部到A，B两村的水管最短，应建在什么地方？分析：(1)到A，B两点距离相等，可联想到"线段垂直平分线上的点到线段两端点的距离相等〞，又要在河边，所以作AB的垂直平分线，与EF的交点即为符合条件的点．(2)要使厂部到A村、B村的距离之和最短，可联想到"两点之间线段最短〞，作A(或B)点关于EF的对称点，连接对称点与B点，与EF的交点即为所求．解：(1)如图1，取线段AB的中点G，过中点G画AB的垂线，交EF于P，则P到A，B的距离相等．也可分别以A、B为圆心，以大于12AB为半径画弧，两弧交于两点，过这两点作直线，与EF的交点P即为所求．(2)如图2，画出点A关于河岸EF的对称点A′，连接A′B交EF于P，则P到A，B的距离和最短．【例3】如图，从A地到B地经过一条小河(河岸平行)，今欲在河上建一座与两岸垂直的桥，应如何选择桥的位置才能使从A地到B地的路程最短？思路导引：从A到B要走的路线是A→M→N→B，如下图，而MN是定值，于是要使路程最短，只要AM＋BN最短即可．此时两线段应在同一平行方向上，平移MN到AC，从C到B 应是余下的路程，连接BC的线段即为最短的，此时不难说明点N即为建桥位置，MN即为所建的桥．解：(1)如图2，过点A作AC垂直于河岸，且使AC等于河宽．(2)连接BC与河岸的一边交于点N.(3)过点N作河岸的垂线交另一条河岸于点M.则MN为所建的桥的位置．4．生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知，求距离之和最小问题，就是运用等量代换的方式，把几条线段的和想方法转化在一条线段上，从而解决这个问题，运用轴对称性质，能将两条线段通过类似于镜面反射的方式转化成一条线段，如图，AO＋BO＝AC的长．所以作点关于*直线的对称点是解决这类问题的根本方法．【例4】(实际应用题)茅坪民族中学八(2)班举行文艺晚会，桌子摆成如图a所示两直排(图中的AO，BO)，AO桌面上摆满了橘子，OB桌面上摆满了糖果，站在C处的学生小明先拿橘子再拿糖果，然后到D处座位上，请你帮助他设计一条行走路线，使其所走的总路程最短？图a 图b解：如图b.(1)作C点关于OA的对称点C1，作D点关于OB的对称点D1，(2)连接C1D1，分别交OA，OB于P，Q，则小明沿C→P→Q→D的路线行走，所走的总路程最短．5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键．先做出其中一点关于对称轴的对称点，然后连接对称点和另一个点，所得直线与对称轴的交点，即为所求．根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值．破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法．【例5】如下图，A，B两点在直线l的两侧，在l上找一点C，使点C到点A、B的距离之差最大．分析：此题的突破点是作点A(或B)关于直线l的对称点A′(或B′)，作直线A′B(AB′)与直线l交于点C，把问题转化为三角形任意两边之差小于第三边来解决．解：如下图，以直线l为对称轴，作点A关于直线l的对称点A′，A′B的连线交l于点C，则点C即为所求．理由：在直线l上任找一点C′(异于点C)，连接CA，C′A，C′A′，C′B.因为点A，A′关于直线l对称，所以l为线段AA′的垂直平分线，则有CA＝CA′，所以CA －CB＝CA′－CB＝A′B.又因为点C′在l上，所以C′A＝C′A′.在△A′BC′中，C′A－C′B＝C′A′－C′B＜A′B，所以C′A′－C′B＜CA－C B.点拨：根据轴对称的性质、利用三角形的三边关系，通过比拟来说明最值问题是常用的一种方法．不等式补充：1. 对于整数a ，b ，c ，d ，定义bd ac c d b a -=，3411<<d b ，则b ＋d 的值为_________． 2. 假设m 、n 为有理数，解关于*的不等式(－m 2－1)*＞n ． 3. A ＝2*2＋3*＋2，B ＝2*2－4*－5，试比拟A 与B 的大小． 4.|21||3|x x -+<-。