图的表示与图同构-南京大学
图的同构分类
图同构
,定义
性质：自反、对称、传递 必要条件：
I度数列相等
-10.3图与子图及其分类
定义10.5
设G为n阶无向简单图，若G中每一对结点间都有边相连，则称G为n阶无向完全图，
简称n阶完全图，记作K（（n>=1）o设D为n阶有向简单图，若D中每个顶点都邻接到 其余
的n-1个顶点，则称D是n阶有向完全图。设D为n阶有向简单图，若D的基图为n阶 无向完 全图，则称D是n阶竞赛图。
、定义10.7 /
设图G=<V, E>,如果有图（；=（广£），且（； =（，".£'），则称G'为图G的 子图。G为G，的母图，记作。又若Lu厂或E'uE，则称G'为G的 真子图。若厂'=厂， 则称G'为G的生成子图。
例 10.4
求
图10.16生成子图。
解：图10.16的生成子图如下
图10.16求生成子图
-图的分类及运算
-10.2图的同构
定义10.4
设图G=〈V, E〉及G,=<V,, E'〉。若存在一一映射
寸"/匚服七)* 且e=(vi, vj)(或〈vi, vj〉)是。的一条边，
当且仅当迎=(M, )•,«： )) 的点集和边集的重数相等，则
)•、".)〉：是G，的一条边，当且仅当所对应
称G与G，同构，记作G三3
O O-------O
图10.14 0-正则、1-正则、2-正则、3-正则
-10.3图与子图及其分类
补图：给定一个图G,由G中所有的结点，以及能使G成为完全图的所有添 加边所组成的图, 称为G相对于完全图的补图，简称为G的补图，记为&。
图论----同构图（详解）
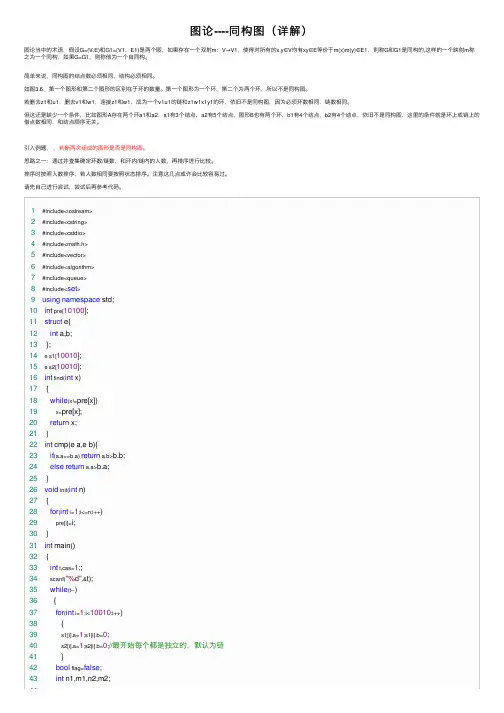
图论----同构图（详解）图论当中的术语，假设G=(V,E)和G1=(V1，E1)是两个图，如果存在⼀个双射m：V→V1，使得对所有的x,y∈V均有xy∈E等价于m(x)m(y)∈E1，则称G和G1是同构的,这样的⼀个映射m称之为⼀个同构，如果G=G1，则称他为⼀个⾃同构。
简单来说，同构图的结点数必须相同，结构必须相同。
如图3.6，第⼀个图形和第⼆个图形的区别在于环的数量。
第⼀个图形为⼀个环，第⼆个为两个环，所以不是同构图。
若删去z1和u1，删去v1和w1，连接z1和w1，成为⼀个v1u1的链和z1w1x1y1的环，依旧不是同构图，因为必须环数相同，链数相同。
但这还是缺少⼀个条件，⽐如图形A存在两个环a1和a2，a1有3个结点，a2有5个结点，图形B也有两个环，b1有4个结点，b2有4个结点，依旧不是同构图，这⾥的条件就是环上或链上的借点数相同，和结点顺序⽆关。
引⼊例题，，判断两次组成的图形是否是同构图。
思路之⼀：通过并查集确定环数/链数，和环内/链内的⼈数，再排序进⾏⽐较。
排序时按照⼈数排序，若⼈数相同要按照状态排序。
注意这⼏点或许会⽐较容易过。
请先⾃⼰进⾏尝试，尝试后再参考代码。
1 #include<iostream>2 #include<cstring>3 #include<cstdio>4 #include<math.h>5 #include<vector>6 #include<algorithm>7 #include<queue>8 #include<set>9using namespace std;10int pre[10100];11struct e{12int a,b;13 };14 e s1[10010];15 e s2[10010];16int find(int x)17 {18while(x!=pre[x])19 x=pre[x];20return x;21 }22int cmp(e a,e b){23if(a.a==b.a) return a.b>b.b;24else return a.a>b.a;25 }26void init(int n)27 {28for(int i=1;i<=n;i++)29 pre[i]=i;30 }31int main()32 {33int t,cas=1;;34 scanf("%d",&t);35while(t--)36 {37for(int i=1;i<10010;i++)38 {39 s1[i].a=1;s1[i].b=0;40 s2[i].a=1;s2[i].b=0;//最开始每个都是独⽴的，默认为链41 }42bool flag=false;43int n1,m1,n2,m2;444445 scanf("%d%d",&n1,&m1);46 init(n1);47for(int i=0;i<m1;i++)48 {49int a,b;50 scanf("%d%d",&a,&b);51int dx=find(a);52int dy=find(b);53if(dx!=dy)54 {55 pre[dx]=dy;56 s1[dy].a+=s1[dx].a;57 s1[dx].a=0;//把拉⼿的孩⼦数量加起来，下同58 }59else s1[dy].b=1;//成环60 }6162 scanf("%d%d",&n2,&m2);63 init(n2);64for(int i=0;i<m2;i++)65 {66int a,b;67 scanf("%d%d",&a,&b);68int dx=find(a);69int dy=find(b);70if(dx!=dy)71 {72 pre[dx]=dy;73 s2[dy].a+=s2[dx].a;74 s2[dx].a=0;75 }76else s2[dy].b=1;77 }78if(n1==n2){7980 sort(s1+1,s1+n1+1,cmp);81 sort(s2+1,s2+n2+1,cmp);//排序，若孩⼦的数量相同则对是否是环进⾏排序，这⾥要注意8283for(int i=0;i<n1;i++)84if(s1[i].a!=s2[i].a||s1[i].b!=s2[i].b) {//判断数量，状态85 flag=true;86break;87 }88 }89if(n1!=n2) flag=true;9091if(flag) printf("Case #%d: NO\n",cas++);92else printf("Case #%d: YES\n",cas++);93 }94return0;95 }。
图论中的图的同构与同构问题
图论中的图的同构与同构问题在图论中，同构是一个重要的概念。
图的同构指的是两个图结构完全相同，只是节点的标签或者边的标签不同。
而图的同构问题则是判断两个给定的图是否同构的问题。
本文将详细探讨图的同构与同构问题。
一、图的同构图的同构是指两个图结构完全相同，只是节点的标签或者边的标签不同。
为了更好地理解图的同构，我们先来了解一些基本概念。
1.1 图的定义在图论中，图由节点（也称为顶点）和边组成。
通常用G=(V, E)来表示一个图，其中V是节点（顶点）的集合，E是边的集合。
边可以用有序或无序对(u, v)来表示，表示节点u和v之间存在一条边。
1.2 同构图的定义给定两个图G1=(V1, E1)和G2=(V2, E2)，如果存在一一对应关系f: V1→V2，使得对于每条边(u, v)∈E1，有(f(u), f(v))∈E2，则称图G1与G2同构。
其中，f被成为同构映射。
二、图的同构问题图的同构问题是判断两个给定的图是否同构的问题，它是图论中的一个经典问题。
在实际应用中，图的同构问题非常重要，对于计算机视觉、网络安全等领域都有广泛应用。
2.1 图的同构问题的定义给定两个图G1=(V1, E1)和G2=(V2, E2)，判断它们是否同构。
2.2 图的同构问题的解决方法图的同构问题是一个NP问题，目前还没有确定的多项式时间解决算法。
在实际应用中，为了解决图的同构问题，通常采用以下方法：（1）特征向量法：通过计算图的特征向量，并比较两个图的特征向量来判断是否同构。
（2）图分类器法：通过训练一个图分类器，将同构和非同构的图进行分类。
（3）哈希算法法：通过为图节点和边生成一个唯一的哈希值，并比较两个图的哈希值来判断是否同构。
以上方法都有各自的优缺点，在不同的应用场景下选择合适的方法。
三、图的同构性质图的同构性质是指图的某些特征在同构映射下保持不变。
在判断图的同构性质时，可以利用这些性质来简化问题。
3.1 路径在判断图的同构性质时，路径是一个重要的性质。
图论中的图的同构与同胚
图论中的图的同构与同胚图论是数学中的一个分支，研究了如何描述图以及图的性质和特征。
在图论中，同构和同胚是两个重要的概念，它们用来描述不同图之间的关系。
本文将介绍图的同构和同胚的概念、定义以及应用。
一、图的同构在图论中，如果两个图具有相同的结构，即结点和边的对应关系相同，但结点和边的标签可以不同，那么这两个图被称为同构的。
图的同构关系可以理解为，它们具有相同的拓扑结构，只是标签的不同。
二、图的同构的定义设G=(V,E)和G'=(V',E')是两个图，如果存在一个双射函数f:V→V'，使得(u,v)∈E当且仅当(f(u), f(v))∈E'，则称G和G'是同构的。
其中，V和V'分别表示两个图的结点集合，E和E'分别表示两个图的边集合。
三、图的同构的判断方法判断两个图是否同构是图论中一个典型的问题，有很多方法可以判断两个图是否同构，以下是几种常用的方法：1. 度序列法：图的度序列是指将图中结点按照度的大小排列得到的序列。
如果两个图的度序列相同，则它们可能是同构的。
2. 邻接矩阵法：将图用邻接矩阵表示，即一个n×n的矩阵，矩阵中的元素a[i][j]表示结点i和结点j之间是否有边。
如果两个图的邻接矩阵相同，则它们可能是同构的。
3. 搜索法：通过对图进行深度优先搜索或广度优先搜索，得到图的某种特征序列。
如果两个图的特征序列相同，则它们可能是同构的。
四、图的同胚在图论中，如果两个图具有相同的结构，即结点和边的对应关系相同，并且结点和边的标签也相同，那么这两个图被称为同胚的。
同胚可以理解为同构的一个特殊情况。
五、图的同胚的判断方法判断两个图是否同胚是图论中的一个难题，其复杂性在于需要同时考虑结点和边的对应关系。
目前还没有有效的算法可以快速地判断两个图是否同胚，只能通过试探的方法进行判断。
六、图的同构与同胚的应用图的同构和同胚在实际应用中有许多重要的应用，以下是几个典型的应用场景：1. 化学分子结构的比较：化学分子可以用图来表示，通过对比不同分子的图的同构关系，可以判断它们的相似性以及化学性质的差异。
离散数学中的图的同构与同构不变性
离散数学中的图的同构与同构不变性离散数学是数学的一个分支，研究离散的结构和对象。
图论是离散数学的一个重要分支，研究图的性质和结构。
在图论中，同构和同构不变性是两个重要的概念。
一、同构的定义和性质在图论中，如果两个图具有相同的结构，即它们的顶点集和边集相同，那么这两个图就是同构的。
具体来说，对于两个图G=(V, E)和G'=(V', E')，如果存在一个双射函数f: V→V'，使得对于任意的u, v∈V，(u, v)∈E当且仅当(f(u), f(v))∈E'，那么图G和图G'就是同构的，记作G≅G'。
同构是图论中的一个重要概念，它可以帮助我们研究图的性质和结构。
同构关系具有以下性质：1. 同构关系是等价关系。
即对于任意的图G，它与自身是同构的；对于任意的图G和图G'，如果G与G'是同构的，则G'与G也是同构的；对于任意的图G、G'和图G''，如果G与G'是同构的，G'与G''是同构的，则G与G''也是同构的。
2. 同构关系保持图的基本性质。
如果两个图是同构的，则它们具有相同的顶点数和边数。
3. 同构关系与图的表示方式有关。
同一个图可以有不同的表示方式，而不同的表示方式可能导致不同的同构判断结果。
二、同构不变性同构不变性是指图在同构变换下保持某些性质不变。
具体来说，如果两个图是同构的，那么它们在某些性质上是相同的。
同构不变性在图论中有重要的应用，可以帮助我们简化问题的分析和求解。
在图的同构不变性中，有一些重要的性质是不变的，包括：1. 度序列：图的度序列是指图中每个顶点的度按非递减顺序排列的序列。
对于同构的图，它们的度序列是相同的。
2. 连通性：图的连通性指的是图中任意两个顶点之间存在路径。
对于同构的图，它们的连通性是相同的。
3. 路径和回路：图中的路径是指顶点之间的连续边构成的序列，回路是指起点和终点相同的路径。
图论中的图的同构与同构问题
图论中的图的同构与同构问题同构是图论中一个非常重要的概念，它用于描述两个图结构之间的相似性和等价性。
在图论中，通过同构的概念，我们可以比较和研究不同的图，并找出它们之间的相似性和差异性。
本文将对图的同构和同构问题进行探讨。
一、图的同构首先，我们来了解一下什么是图的同构。
在图论中，同构指的是两个图结构之间存在一一对应的关系，使得它们具有相同的顶点数和边数，并且顶点之间的关联关系也相同。
简而言之，两个同构的图在结构上是完全相同的，只是顶点和边的命名可能不同。
图的同构是一种等价关系，具有自反性、对称性和传递性。
即对于任意的图G，它和自身一定是同构的；如果图G和图H是同构的，那么图H和图G也一定是同构的；如果图G和图H是同构的，图H和图I是同构的，那么图G和图I也一定是同构的。
二、图的同构问题图的同构问题是指确定两个给定图是否同构的问题。
在实际应用中，图的同构问题是一个具有挑战性的难题，因为当图的规模增大时，判断两个图是否同构变得非常困难。
为了解决图的同构问题，人们提出了许多算法和方法。
其中最著名的是Weisfeiler-Lehman算法，它是一种基于图的局部结构的判定同构的算法。
该算法通过不断迭代地更新图中每个顶点的标签，来判断两个图是否同构。
另外，还有许多其他的图同构算法，如VF2算法、Nauty算法等都被广泛应用于图的同构问题的解决。
三、图的同构应用图的同构问题在许多领域中都有重要的应用。
在化学领域，图的同构可以帮助确定分子结构的相似性和差异性，从而在药物设计等方面发挥关键作用。
在计算机科学领域，图的同构可以用于数据挖掘、图数据库的查询和图网络的分析等方面。
此外，在社交网络、电路设计、通信网络等领域，图的同构也具有广泛的应用。
图的同构和同构问题是图论中的一个重要研究领域，它涉及到图结构的相似性和等价性的判定。
通过研究图的同构，我们可以深入理解不同图之间的关系，挖掘图结构中的规律和特性。
在实际应用中，图的同构问题有着广泛的应用价值，对于解决复杂的实际问题具有重要的意义。
同构图形的四种原理
同构图形的四种原理同构图形是指在平面上进行变换后形状、大小、相对位置都完全相同的图形。
同构图形的判断和研究在几何学中具有重要的意义。
同构图形有四种原理：射影原理、长度比较原理、角度比较原理和相区对照原理。
1. 射影原理：同构图形的射影是指将两个同构图形上的对应点用直线射影到同一直线上的操作。
射影原理指出：如果两个图形在同一直线上的任意两个对应点，经过射影之后也在同一直线上，则这两个图形是同构的。
射影原理是同构图形判断的基本原理，也是其他原理的重要依据。
例如，若有两个平面上的正方形ABCDEF和A'B'C'D'E'F'，要判断它们是否同构，可以将这两个正方形的对应顶点A和A'进行射影，得到直线l1；再将对应顶点C和C'进行射影，得到直线l2。
如果直线l1和l2重合，则可以判断这两个正方形是同构的。
2. 长度比较原理：同构图形的长度比较是指将两个同构图形上的对应线段的长度进行比较的操作。
长度比较原理指出：如果两个同构图形上的所有对应线段的长度相等，则这两个图形是同构的。
长度比较原理是判断同构图形时常用的方法。
例如，若有两个平面上的三角形ABC和A'B'C'，要判断它们是否同构，可以将这两个三角形上的对应边AB和A'B'的长度进行比较，如果它们相等，再将对应边BC和B'C'的长度进行比较，如果也相等，最后再将对应边AC和A'C'的长度进行比较，如果仍然相等，那么就可以判断这两个三角形是同构的。
3. 角度比较原理：同构图形的角度比较是指将两个同构图形上的对应角度进行比较的操作。
角度比较原理指出：如果两个同构图形上的所有对应角度相等，则这两个图形是同构的。
角度比较原理是判断同构图形时常用的方法。
例如，若有两个平面上的平行四边形ABCD和A'B'C'D'，要判断它们是否同构，可以将这两个平行四边形上的对应角度进行比较，如果对应角A和A'、角B和B'、角C和C'、角D和D'都相等，那么就可以判断这两个平行四边形是同构的。
图形创意之图形同构ppt课件
Design
.
14
由于大气中二氧化碳排放量 过多造成全球变暖，大气和海洋 温度上升，全球大气层和地表这
图形创意
一系统就如同一个巨大的“玻璃
温室”，企鹅面临生存危机。图
把企鹅身上的“煎熬”和人们生 活中身心上的“酷热”“痛苦” 联系起来，以“身心难以承受”
为核心创决，用比喻的手法将企
鹅拟人化．把全球变暖，既危害
图形创意
这种将两个以上不同的 形象巧妙地结合在一起，构 成一种具有创造意义的超现 实的新异图形，称为“异形 同构”。
Design
《为什么和平迟未实现》（海报）金特·凯瑟（德国）
.
11
这是一幅宣传招贴，用真实 的树皮制作成小号模型，形成小 号的形与树皮的质的两种元素的 同构。两种元素的同构象征了爵 士乐母体，而从树侧生长出的一 支嫩叶则象征着爵士乐的新生。 这是一种诗化的隐喻，传达出了 新生代音乐的主题。
Graphic Creative
图形创意
——之图形同构
Graphic creative curriculum
LOGO
引入情境
图形创意
❖ 水果超市视觉形象！——图形设计
Design
.
2
图形创意
Design
.
3
图形创意
Design
.
4
图形创意
Design
.
5
图形创意
Design
.
6
图形创意
Design
图形创意
使用一种物体的材质来替 换另一物体的材质，构成一种 新异的图形，给人以强烈的视 觉刺激，使人们对图形内涵有 更深层次的认识，称为“异质 同构”。
它是用其他物体的材质来 取代原来物体组织结构中的材 质，结构关系不变，面貌却焕 然一新。
图论中的图的同构与同胚
图论中的图的同构与同胚在学习图论的过程中，我们常常会遇到同构和同胚这两个概念。
这两个概念在图论中有着重要的意义，它们帮助我们研究图的结构和性质。
接下来，我们将深入探讨图的同构与同胚的含义及其在图论中的应用。
首先，让我们了解一下什么是图的同构。
在图论中，如果两个图的结构相同，也就是说它们的顶点集合和边集合相同，并且边的连接关系也相同，那么这两个图就是同构的。
简而言之，同构的两个图可以通过一种双射关系相互映射，保持图的结构不变。
同构的图虽然在外表上可能看起来不一样，但在本质上却是相同的。
接下来，让我们来了解一下图的同胚。
同胚是指通过一种特定的映射，将一个图变换为另一个图，使得它们在拓扑结构上保持一致。
也就是说，同胚将保持图中顶点和边的连接方式，并且保持顶点的度数和邻接关系不变。
同胚的两个图在拓扑结构上并无差异，只是它们的顶点和边的实际标记可能不同。
在图论中，同胚和同构是两个常见且重要的概念。
同构关系更加严格，要求图之间的双射关系，而同胚更侧重于拓扑结构的相似性。
通过研究图的同构与同胚关系，我们可以更好地理解图的性质和特征。
在实际应用中，同构和同胚关系对于解决图论中的问题起着重要作用。
例如，在网络路由、社交网络分析、电路设计等领域，通过判断图之间的同构或同胚关系，可以帮助我们更好地设计和优化系统。
此外，在化学中，同构和同胚的概念也被广泛运用于分子结构的研究中。
总的来说，图的同构与同胚是图论中非常重要的概念，它们帮助我们理解图的结构和性质，为解决实际问题提供了有力的工具和方法。
通过深入学习和应用图的同构与同胚，我们可以更好地掌握图论知识，拓展思维，提升问题解决能力。
希望本文能给读者带来一些启发和帮助，引起更多对图论研究的兴趣与关注。
图论中的图的同构与同胚
图论中的图的同构与同胚在图论中，图的同构和同胚是两个基本的概念。
它们用来描述两个图之间的关系，帮助我们理解图的结构和性质。
本文将介绍图的同构和同胚的定义、性质以及它们在实际问题中的应用。
一、同构与同胚的定义在图论中，如果两个图的顶点集合和边集合都一样，那么我们称这两个图是同构的。
具体地说，给定两个图G1=(V1, E1)和G2=(V2, E2)，如果存在一个一一对应的函数f:V1→V2，使得对于任意的顶点u和v，(u, v)是边集E1中的边当且仅当(f(u), f(v))是边集E2中的边，那么我们称G1和G2是同构的。
同胚是图同构的一种特殊情况。
如果两个图的顶点集合和边集合一样，并且它们之间的连接方式也完全相同，那么我们称这两个图是同胚的。
换句话说，同胚是同构的一种更强的关系。
二、同构与同胚的性质1. 同构和同胚是等价关系。
即对于任意的图G，它与自身是同构的，并且如果图G与图H是同构的，那么图H与图G也是同构的。
2. 同构和同胚是保持图的结构的。
即如果两个图是同构的（或同胚的），那么它们具有相同的图的性质，例如连通性、欧拉回路等。
3. 同构和同胚是可传递的。
即如果图G1与图G2是同构的，图G2与图G3是同构的，那么图G1与图G3也是同构的。
三、同构与同胚的应用同构和同胚在实际问题中有着广泛的应用，特别是在网络安全、化学结构分析等领域。
1. 网络安全：在网络安全中，通过判断两个网络是否同构或同胚，可以判断它们之间的相似性和联系。
这对于检测网络攻击、识别恶意行为等非常重要。
2. 化学结构分析：在化学中，分子的结构可以用图来表示。
通过判断两个分子的图是否同构或同胚，可以比较它们的结构和性质。
这对于药物设计、化学反应等有着重要的意义。
3. 图像处理：在计算机视觉领域，图像可以看作是一个由像素组成的图。
通过判断两个图像的图是否同构或同胚，可以进行图像的匹配、相似性比较等操作。
四、总结在图论中，同构和同胚是图之间重要的关系。
邻接矩阵-南京大学
v4
v3
0 0 A(G) 1 1
1 0 0 0 1 1 1 0 1 0 0 0
可推广到简单无向图
举例（邻接矩阵）
v1 v2
v4
v3
0 1 A(G) 1 1
1 0 1 0
1 1 0 1
1 0 1 0
简单无向图的邻接矩阵是对称矩阵
邻接矩阵(adjacency matrix)
简单有向图G = (V, E, ) ，设V＝v1，…，vn，E＝ e1，…，em。
A(G)＝aij称为G的邻接矩阵(n×n 阶矩阵)，其中
1 如果v i邻接到v j a ij 0 否则
eE. (e)=(vi, vj)
举例（邻接矩阵）
邻接矩阵的运算
逆图（转置矩阵）
设Ｇ的邻接矩阵为 A ，则 G 的逆图的邻接矩阵是 A 的转 置矩阵，用AT表示。
０１００ ００１１ A １１０１ １０００
００１１ １０１０ T A ０１００ ０１１０
邻接矩阵的运算
邻接矩阵的运算
顶点的度
行中1的个数就是行中相应结点的出度
列中1的个数就是列中相应结点的入度
v1
v2
v4
v3
Hale Waihona Puke 0 0 A 1 11 0 0 0 1 1 1 0 1 0 0 0
Deg+(1)=1,Deg-(1)=2
Deg+(2)=2,Deg-(2)=2
Deg+(3)=3,Deg-(3)=1 Deg+(4)=1,Deg-(4)=2
邻接表
邻接矩阵-南京大学
Cij表示同时有边指向结点i和结点j的那些结点的个数； 若i＝j，则Cii表示结点i的入度。
邻接矩阵的运算
v1 v2
0 0 A 1 1 1 0 0 0 1 1 1 0 1 0 0 0
v4
v3
１０１０ ０２１０ T A A １１３１ ００１１
邻接矩阵的运算
逆图（转置矩阵）
设Ｇ的邻接矩阵为 A ，则 G 的逆图的邻接矩阵是 A 的转 置矩阵，用AT表示。
０１００ ００１１ A １１０１ １０００
００１１ １０１０ T A ０１００ ０１１０
邻接矩阵的运算
邻接表
是单射
若图G = (V, E, ) 没有多重边，列出这个图的所有 边。对每个顶点，列出与其邻接的顶点。
b
a
c
e
d
顶点 a b c d e
相邻顶点 b, c, e a a, d, e c, e a, c, d
邻接表（有向图）
是单射
若图G = (V, E, ) 没有多重边，列出这个图的所有 边。对每个顶点，列出与其邻接的顶点。
从v2→v1，有二条长度为2的通路；有一条长度为3的通路
邻接矩阵的运算
v1 v2
0 0 A 1 1 1 0 0 0 1 1 1 0 1 0 0 0
v4
v3
３４２３ ５５４６ B4 A1 A2 A3 A4 ７７４７ ３２１２
长度不大于k的通路个数
图的同构
图同构的定义
设G1=(V1, E1, 1)和G2=(V2, E2, 2)是两个简单无向图。
同构图形的由来及表现形式的论文.doc
同构图形的由来及表现形式的论文【摘要】尽管有时新组合成的画面是非现实的、或与现实相悖的，但就是这奇怪的画面会达到一种形有尽而意无穷的效果，从而使信息得到真正充分地表达作品的主题。
同时这种形式给予观者丰富的心理感受，开启他们的好奇心去想象去联想。
这样就使得观众不再是被动地接受，而是积级地参与到作品中来，更好得完成信息的传达。
【关键词】同构来源图形表现“所谓同构图形，指的是两个或两个以上的图形，因为某种联系组合在一起，共同构成一个新图形，传达出新的信息。
这个新图形所传达的意思并不是原图形意思的简单相加，而是一种超越或突变，使人产生联想、记忆、思考。
”[1]因为它的组合突破了人们意识中的常规物象和认知经验的限制，从而形成强烈的视觉冲击力。
尽管有时新组合成的画面是非现实的、或与现实相悖的，但就是这奇怪的画面会达到一种形有尽而意无穷的效果，从而使信息得到真正充分地表达作品的主题。
同时这种形式给予观者丰富的心理感受，开启他们的好奇心去想象去联想。
这样就使得观众不再是被动地接受，而是积级地参与到作品中来，更好得完成信息的传达。
一同构在东西方艺术中的来源“在西方艺术史上，同构最初来源于绘画艺术。
在摄影技术诞生之前，艺术家们通过对图式传承，专注于用各种独特的视觉语言再现和摹写眼前所见的客观世界!不管是风景还是人物都来自现实生活。
二十世纪科学技术对艺术的影响，使得一部分敏感、优秀的艺术家寻找一种新的语言来增加现代艺术的魅力。
同构即是超现实主义的一种表现形式，对现代图形设计产生了深刻的影响，丰富了平面视觉艺术的表现力，它的出现从某种意义上来说是写实主义与现代绘画的一条分水岭。
”[2] 马格里特的代表作《错误的镜子》描绘了一只巨大的眼睛及投射在上面的蓝天白云，但又看似一个“窗子”，透过它能看到蓝天、白云，从形式上给人始料不及的视觉效果，在马格里特看来，眼睛只是一面错误的镜子，它所得到的只是自然的幻影，而不是自然本身。
世界上没有眼睛看得见的“真实”，因此绘画的“真实”只是图解了人眼睛的幻觉而已。
图的连通性
有关割边的四个等价命题
以下四个命题等价：
(1) e是割边。 (2) e不在G的任一简单回路上。(注意：割点没有相应结论) (3) 存在V的分划{V1, V2}, 使得u∈V1, w∈V2, uw-通路均
包含e。 (4) 存在顶点u,w，使得任意的uw-通路均包含e。
17
连通图“连接的牢固度”不一样
图的连通性
离散数学─图论初步 南京大学计算机科学与技术系
内容提要
通路与回路 通路与同构 无向图的连通性
连通度 2-连通图
有向图的连通性
无向图的定向
2
通路的定义
定义：图G中从v0到vn的长度为n的通路是G的n条边 e1,…, en的序列，满足下列性质
存在viV (0in), 使得vi-1和vi是ei的两个端点 (1in)。
同构图的不变量：长度为k的回路的存在性。
7
通路与同构
u1
u6
u2
v1
v6
v2
u5
u3
v5
u4
u2
v3 v4 v2
u1
u3
v1
v3
u5
定义：无向图G称为是连通的，如果G中任意两个不 同顶点之间都有通路。
b
a
c
b
a
c
e
d
G1
e
d
G2
9
连通分支
连通分支
极大连通子图
定义：使非平凡连通图G成为不连通图或者平凡图需要 删除的最少顶点数称为图G的(点)连通度，记为κ(G)。
(注意：这不意味着任意删除κ(G)个点就一定会使该图不连通)
约定：不连通图或平凡图的连通度为0，而κ(Kn)=n-1 若图G的连通度不小于 k, 则称G是k-连通图；
南京艺术学院图形设计同构-替构-解构-重构参考资料
0
0
0
0
0
0
0
0
0
2、异质同构图形
异质同构表现为物质间表面现象的物理性联系， 以及物质间内在的、隐晦的、变异的联系。通过 改变或夸张其表面机理、质感、分量、表情、动 态等因素，使原本平淡的形象因为材质的改变而 变成新异的视觉图形。
图形设计的方法 同构-替构-解构-重构
主讲人：吴爱峰
替代图形是一种特殊的同构现象，以常规图形为依据，
保持其物形的基本特征，将物体中的某部分用其他相似或
不相似物形所替代，并从根本意义上改变了物体原来所赋 予的含义，产生了“意”的转换，使图形传达出更深刻、
更富哲理性的寓意。
替换同构
同构图形
同构图形
同构图形
同构图形
同构图形
同构：异体同构、异质同构
同构图形就是把不同的甚至矛盾的、但相互间在形式上又有联系的元 素，通过周围空间和造型线的相互利用，巧妙地结合在一起。这并不是两 个形象的叠加和并举，而是给人一种亲切、幽默、明了的感觉，同时，也 传达出新的内涵和信息。
• 异体同构：将两个完全不同的物体，通过其造型的相近性， 进行非现实的结合，传达更深刻的含义。（形态相似，有联 系同构的可能） • 异质同构：将不同质地的事物根据其相似性巧妙的结合在一 起，形成新形象、新内涵。
作业数量：拼置同构、置换同构、置入同构、 肖形同构、异影同构每种不少于10个。 提交方式：在课堂上构画方案草图，选择其 中优秀的进行精细描绘。
五、同构图形
同构就是从不同的视点将两个不同的元素与相关 的内容巧妙的组合在一起，产生具有创造意义的 新图形。新图形不再是现实中自然物形的再现， 而是一种富有吸引力、非现实的整合。
求解图同构的判定算法
求解图同构的判定算法
图同构是一个经典而又有趣的数学问题。
可以简单地定义为：若两张图的边和点的对应关系一致，则这两张图即被称为同构。
因此，不管这两张图的形状如何变化，它们的边和点数目以及它们之间的关系完全保持不变，因此这两张图可以被称为同构。
解决图同构问题要求构造出能够判定两张图是否同构的判定算法。
首先，可以使用广义平行算法（GP）来构建这样的一个判定算法，其主要采
用基于矩阵的数据模型。
算法的基本思想是，首先将图的边和点的对应关系建设为矩阵形式，然后使用GP算法对该矩阵进行求解，最后检查给定的矩阵是否为等价的。
若给定的矩阵是等价的，则表明两张图同构；反之，若给定的矩阵不等价，则表明两张图不同构。
此外，可以采用加权矩阵来实现图同构判定。
具体方法是，首先为图中每一条边分配一个权重，然后将边与点之间的对应关系建模为一个加权矩阵，其中对应边的权重值作为该矩阵的元素值。
然后使用约束规划的方法来求解该矩阵，若给定的矩阵的解被唯一确定，则表明两张图同构；反之，若给定的矩阵的解无法唯一确定，则表明两张图不同构。
另外，还可以使用计数器网络（CN）的方法来构建图同构算法。
该方法主要
采用基于状态空间的数据模型，首先将图的边和点建模为一个计数器网络，然后使用CN方法进行求解，最后检查状态空间中是否存在状态完全相同的路径，若存在，则表明两张图同构；反之，若不存在，则表明两张图不同构。
综上所述，求解图同构的判定算法需要使用广义平行算法（GP），加权矩阵
和计数器网络（CN）等技术。
这些技术可以实现以判定两张图是否同构，从而达
到相应的目的。
本科图论-图基本概念6-2
2） 定义2 一个有向图是一个有序的二元组<V，E>，记作D，其中 (1) V ≠ ø 称为顶点集，其元素称为顶点或结点． (2)E为边集，它是笛卡儿积 V & V的多重子集，其元素称为有向边， 简称边(弧)． 有向图D=<V，E> 其中 V＝｛v1,v2,v3 ｝
2、简单通路和初级通路的关系
有向图中的每一条初级通路，也都必定是简单通路。 反之不成立 回路也可分为简单回路和初级回路。 3、通路的表示：可仅用通路中的边序列表示：e1e2…ek 也可仅用通路中所经过的结点的序列表示：v1v2v3…vk
4、性质： 1）定理 在n阶图D中，若从顶点vi到vj(vi≠vj)存在通路，则从vi到vj存在 长度小于或等于(n－1)的通路 若大于n-1，则存在相同节点（有回路），将回路删去可得 2）在n阶图D中，若从顶点vi到vj存在通路，则vi到vj一定存在长度小于或等 于n－1的初级通路(路径) 3）定理 在一个n阶图D中，若存在vi到自身的回路，则一定存在vi到自身长 度小于或等于n的回路． 4）在一个n阶图D中，若存在vi到自身的简单回路，则一定存在长度小于或等 于n的初级回路．
有环的结点提供的度为2（有向图的环提供入度1和出度1）
3）定义：ᅀ(G)=max{d(v)|v∈V(G)} 为图G中结点最大的度 δ(G)=min{d(v)|v∈V(G)} 为图G中结点最小的度 简记为ᅀ、 δ 定义：ᅀ＋(D)=max{d(v)|v∈V(D)} 为图D中结点最大的出度 ᅀ－(D)=max{d(v)|v∈V(D)} 为图D中结点最大的入度 δ＋(D)=min{d(v)|v∈V(D)} 为图D中结点最小的出度 δ-(D)=min{d(v)|v∈V(D)} 为图D中结点最小的入度 5、握手定理（欧拉） 1)定理1 设G＝<V,E>为任意无向图,V＝{v1，v2，…，vn},｜E｜ = m， 则 ∑d(vi) ＝ 2 m (所有结点的度数值和为边数的2倍) 证: G中每条边(包括环)均有两个端点，所以在计算G中各顶点度数 之和时，每条边均提供2度，当然，m条边共提供2m度 2) 定理2 设D＝<V,E>为任意有向图,V＝{v1，v2，…，vn},|E| = m ， 则 ∑d+(vi) ＝ ∑ d-(vi) = m． 且∑d(vi)＝2 m 任何图(无向的或有向的)中，奇度顶点的个数是偶数
第3章同构图
3.1 同构的定义
• 更精确的描述: 定义2 若两个图仅仅区别在画法与(或顶点)的标号方式上, 则称 它们为同构的.
• 正式地说: 定义3 两个(标号)图G1和G2称为同构的( isomorphic ) (或者,有
相同结构),如果存在一个从V(G1)到V(G2)的一一对应 ,使得：
u1v1 EG1 当且仅当u1 v1 EG2 .
≤k)是邻接的 (定义4).
若y是H中的一个顶点, 满足 y vy1, y2,yk, 则在G中存在顶 点x使得x y, 其中 xu Nu. 因为x和u在G中是不邻接的,
所以y和v在H中是不邻接的 (定义4). 因此degHv=k. (证毕)
3.1 同构的定义
定理 3.5 设G和H为同构图, 则
(a) G是二部的当且仅当H是二部的, (b) G是连通的当且仅当H是连通的.
主要内容
• 3.1 同构的定义 • 3.2 同构关系 • 3.4 延伸阅读: 重构与可解性
3.1 同构的定义
• 回顾: 两个图G和H称为相同的, 若V(G)=V(H)且E(G)=E(H). 两个图G和H是“同构的”, 若它们有相同的结构，并记之为 G≌H.
• 换句话说： 定义1 如果G和H的顶点可以通过标号(或重新标号)而形成两个 相同的图, 那么G≌H.
n i 1
m中i ,
每一条
边被计数了 n - 2 次, 即
n
mi mn 2,
i 1
m
m n
i1 i
.
n2
3.4 重构与可解性
定理 3.13 每个阶至少为 3 的图G 的度序列都是可识别的.
定义6 一个阶为n ≥ 2的图G 称为是可重构的, 如果G可由它 的子图 G-vi ( 1≤ i ≤n ) 唯一确定(在同构的意义下).
53图的表示和同构
例10 判断图7-34所示所示的图是否同构。 解 图G和H都具有8个顶点和10条边。它们都具有4个 2度顶点和4个3度顶点。因为这些不变量都相同，所以可 能想到它们是同构的. 然而G和H不是同构的。为了看明白这一点，注意到 因为在G里deg(a)=2，所以a必然对应于H里的t，u，x或y， 这是因为这些顶点是H里的2度顶点。不过， H里的这4个 顶点中每一个都与H里另一个2度顶点相邻，但是在H里a 却不是这样的。 看出G与H不同构的另一种方式是，注意到若这两个 图同构，则由3度顶点和连接它们的边所组成的子图同构 （读者应当验证它）。然而图图所示的这些子图却不是同 构的。
同构的充分条件，可用于判定同构 给出一个顶点的一一对应，按相应的顺序求出邻接矩阵 邻接矩阵相同同构
同构的必要条件，可用于判定不同构 （1）顶点数相同 （2）边数相同 （3）顶点度的升序相同 （4）同度顶点构成的子图都同构
例9 说明图7-33所示的图不同构。
解 G和H都具有5个顶点和6条边。不过，G有1度顶点 e而H没有1度顶点。所以G与H是不同构的。
函数f满足fu1v1fu2v4fu3v3fu4v2它是vu1和u3u2和u4以及u3?同构的充分条件可用于判定同构给出一个顶点的一一对应按相应的顺序求出邻接矩阵邻接矩阵相同?同构?同构的必要条件可用于判定不同构1顶点数相同2边数相同3顶点度的升序相同4同度顶点构成的子图都同构?例9说明图733所示的图不同构
5.3.2图的同构 同构的图：本质上相同的图，表示了类似的集合和关系 定义1 简单图同构 G1，G2，一一对应f：V1→V2，使 (a, b)∈E1(f(a), f(b))∈E2
例8 说明图G=(V, E) 和H=(W, F)同构。
解： 函数f满足f(u1)=v1,f(u2)=v4 ,f(u3)=v3 ,f(u4)=v2 ,它是V 和W之间的一一对应。为了看出这个对应保持相邻关系， 注意G里相邻的顶点是u1和u2， u1和u3，u2和u4，以及u3 和u4，由f(u1)=v1和f(u2)= v4 ，f(u1)=v1 和f(u3)= v3 ，f(u2)= v4和f(u4)= v2 ，以及f(u3)= v3和f(u4)= v2所组成的每一对顶 点都是在H里相邻的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
离散数学─图论初步 南京大学计算机科学与技术系
内容提要
图的表示 邻接矩阵的运算 图的同构
图的表示
关联矩阵 邻接矩阵 邻接表
关联矩阵(incidence matrix)
无向图G = (V, E, ) ，不妨设V＝v1，…，vn，E＝ e1，…，em。
v4
e3
v3
关联矩阵表示法不适合于有向图
邻接矩阵(adjacency matrix)
简单有向图G = (V, E, ) ，设V＝v1，…，vn，E＝ e1，…，em。
A(G)＝aij称为G的邻接矩阵(n×n 阶矩阵)，其中
1 aij 0
如果vi邻接到v j 否则
eE. (e)=(vi, vj)
图同构的例子
图同构的例子
检测两个简单图是否同构
邻接矩阵表示：n！个 现有最好算法在最坏情况下的时间复杂性是指数级。 （在最坏情况下）时间复杂性为多项式的算法？
检测两个简单图是否同构
图同构下保持的性质称为图不变的
顶点数、度序列、…
利用图不变的性质（没有保持）来推断出不同构
邻接矩阵的运算
顶点的度
行中1的个数就是行中相应结点的出度 列中1的个数就是列中相应结点的入度
v1
v2
0 1 0 0
Deg+(1)=1,Deg-(1)=2
A
0 1
0 1
1 0
1 1
Deg+(2)=2,Deg-(2)=2 Deg+(3)=3,Deg-(3)=1
v4
v3
若aik×akj＝1，则表示有i→k→j长度为2的有向边； dij表示i和j之间具有长度为2的通路个数。
邻接矩阵的运算
v1
v2
v4
v3
００１１
A2
A
A
２１０１ １１１１
０１００
0 1 0 0
A
0 1
0 1
1 0
1 1
1 0 0 0
b
b
a
c
a
c
ed
图G
ed
图H
检测两个简单图是否同构
a e h
d
b
s
f
3度顶点的 导出子图不
w
g
同构
z
c
v
u1 u5
u4
u2
u6 u3
v1
v2
v5
t x y
u
v3
v6 v4
作业
教材[9.3]
p. 477： 15, 24, 29, 31, 67
1 0 0 0
Deg+(4)=1,Deg-(4)=2
邻接矩阵的运算
逆图（转置矩阵）
设Ｇ的邻接矩阵为A，则G的逆图的邻接矩阵是A的转 置矩阵，用AT表示。
０１００
A
００１１ １１０１
１０００
００１１
AT
１０１０ ０１００
０１１０
邻接矩阵的运算
举例（邻接矩阵）
v1
v2
0 1 0 0
A(G)
0 1
0 1
1 0
1 1
v4
v3
1 0 0 0
可推广到简单无向图
举例（邻接矩阵）
v1
v2
0 1 1 1
A(G)
1 1
0 1
1 0
0 1Leabharlann v4v31 0 1 0
简单无向图的邻接矩阵是对称矩阵
邻接表
３２１２
长度不大于k的通路个数
图的同构
图同构的定义
设G1=(V1, E1, 1)和G2=(V2, E2, 2)是两个简单无向图。 若存在双射f: V1V2, u和v在G1中相邻当且仅当 f(u)和 f(v)在G2中相邻。此时称f是一个同构函数。
设G1=(V1, E1, 1)和G2=(V2, E2, 2)是两个无向图。若 存在双射f: V1V2, g: E1E2, e∈E1, 1(e)={u, v}, 当 且仅当 g(e)∈E2, 且2(g(e))={f(u), f(v)}。
２１０１
A3
A2
A
１２１１ ２２１２
００１１
从v2→v1，有二条长度为2的通路；有一条长度为3的通路
邻接矩阵的运算
v1
v2
0 1 0 0
A
0 1
0 1
1 0
1 1
v4
v3
1 0 0 0
３４２３
B4
A1
A2
A3
A4
５５４６ ７７４７
n
C ij aki akj a1i a1 j a2i a2 j ani anj k 1
Cij表示同时有边指向结点i和结点j的那些结点的个数； 若i＝j，则Cii表示结点i的入度。
邻接矩阵的运算
v1
v2
v4
v3
１０１０
A
AT
０２１０ １１３１
v4
v3
2 1 2 0
关于邻接矩阵
当有向图中的有向边表示关系时，邻接矩阵就是 关系矩阵。无向图的邻接矩阵是对称的。
图G的邻接矩阵中的元素的次序是无关紧要的， 只要进行和行、列和列的交换，则可得到相同的 矩阵。
若有二个简单有向图，则可得到二个对应的邻接矩阵， 若对某一矩阵进行行和行、列和列之间的交换后得到 和另一矩阵相同的矩阵，则此二图同构。
００１１
0 1 0 0
A
0 1
0 1
1 0
1 1
1 0 0 0
２１０１
AT
A
１２０１ ００１１
１１１２
邻接矩阵的运算
A A A2 D [dij ]
n
dij aik akj ai1 a1 j ain anj k 1
b
a
c
e
d
顶点 a b c d e
相邻顶点 b, c, d, e b, d a, c, e
b, c, d
关于邻接矩阵
通常，邻接矩阵中的元素为0和1，称为布尔矩阵。 邻接矩阵也可表示包含多重边的图，此时的矩阵不
是布尔矩阵。
v1
v2
0 3 0 2
A
3 0
0 1
1 1
1 2
A AT B [bij ]
n
bij aik a jk ai1 a j1 ai2 a j2 ain a jn k 1
bij表示结点i和结点j均有边指向的那些结点的个数； 若i＝j，则bii表示结点i的出度。
邻接矩阵的运算
AT A C [Cij ]
是单射
若图G = (V, E, ) 没有多重边，列出这个图的所有 边。对每个顶点，列出与其邻接的顶点。
b
a
c
e
d
顶点 a b c d e
相邻顶点 b, c, e a a, d, e c, e a, c, d
邻接表（有向图）
是单射
若图G = (V, E, ) 没有多重边，列出这个图的所有 边。对每个顶点，列出与其邻接的顶点。
M(G) ＝mij称为G的关联矩阵(n×m 阶矩阵), 其中
1 mij 0
如果e j关联vi 否则
vi(ej)
无向图G可以是伪图(含自环或多重边)。
举例（关联矩阵）
v1
e1
v2
1 0 0 1 1
e4
e5
e2
M(G)
1 0
1 1
0 1
0 0
0 1
0 0 1 1 0