第1章 流体流动
化工原理课后习题答案第一章流体流动答案

第一章 流体流动习题解答1.解:(1) 1atm=101325 Pa=760 mmHg真空度=大气压力—绝对压力,表压=绝对压力—大气压力 所以出口压差为p =461097.8)10082.0(10132576.00⨯=⨯--⨯N/m 2(2)由真空度、表压、大气压、绝对压之间的关系可知,进出口压差与当地大气压无关,所以出口压力仍为41097.8⨯Pa 2.解: T=470+273=703K ,p=2200kPa混合气体的摩尔质量Mm=28×0.77+32×0.065+28×0.038+44×0.071+18×0.056=28.84 g/mol混合气体在该条件下的密度为:ρm=ρm0×T0T×pp0=28.8422.4×273703×2200101.3=10.858 kg/m33.解:由题意,设高度为H 处的大气压为p ,根据流体静力学基本方程,得 dp=-ρgdH大气的密度根据气体状态方程,得 ρ=pMRT根据题意得,温度随海拔的变化关系为 T=293.15+4.81000H代入上式得ρ=pMR (293.15-4.8×10-3H )=-dpgdh移项整理得dpp=-MgdHR293.15-4.8×10-3H对以上等式两边积分,101325pdpp=-0HMgdHR293.15-4.8×10-3H所以大气压与海拔高度的关系式为 lnp101325=7.13×ln293.15-4.8×10-3H293.15即:lnp=7.13×ln1-1.637×10-5H+11.526(2)已知地平面处的压力为101325 Pa ,则高山顶处的压力为 p 山顶=101325×330763=45431 Pa将p 山顶代入上式ln 45431=7.13×ln1-1.637×10-5H+11.526 解得H =6500 m ,所以此山海拔为6500 m 。
化工原理第一章第二节

第一章流体流动第一章流体流动第三节流体流动的基本方程一、流量与流速二、稳态流动与非稳态流动三、连续性方程式四、柏努利方程式五、柏努利方程式的应用1.3.1 流量与流速1、流量流量: 单位时间内流过管道任一截面的流体量。
体积流量V S:若流量用体积来计量,单位为:m 3/s 质量流量W S:若流量用质量来计量,单位:kg/s 。
体积流量和质量流量的关系是:ρS S V W =2、流速流速u : 单位时间内流体在流动方向上流过的距离,单位为:m/s数学表达式为:AV u S =流量与流速的关系为:uAV S=ρuA W S =对于圆形管道,24dA π=24d V u S π=uV d S π4=——管道直径的计算式质量流速:单位时间内流体流过管道单位面积的质量流量用G 表示,单位为kg/(m 2.s)。
数学表达式为:A W G s =AV S ρ=ρu = 1.3.2 稳态流动与非稳态流动稳定流动:描述流动的物理量与时间无关的流动稳定流动u =f (x ,y ,z )非稳定流动u =f (x ,y ,z ,θ )1.3.2 稳态流动与非稳态流动流动系统稳态流动流动系统中流体的流速、压强、密度等有关物理量仅随位置而改变,而不随时间而改变非稳态流动上述物理量不仅随位置而且随时间变化的流动。
1.3.3 连续性方程在稳定流动系统中,对直径不同的管段做物料衡算衡算范围:取管内壁截面1-1’与截面2-2’间的管段。
衡算基准:1s对于连续稳定系统:21SSWW=ρuAWs=222111ρρAuAu=如果把这一关系推广到管路系统的任一截面,有:常数=====ρρρuAAuAuWS L222111若流体为不可压缩流体常数======uAAuAuWV SS L2211ρ——一维稳定流动的连续性方程对于圆形管道,22221144duduππ=21221⎟⎟⎠⎞⎜⎜⎝⎛=∴dduu表明:当体积流量VS一定时,管内流体的流速与管道直径的平方成反比。
第一章流体流动

1.2 流体的黏度
本节的目的是了解流体流动的内部结构, 以便为阻力损失计算打下基础。 1、牛顿黏定律
流体的粘性 流体在运动的状态下,有一种抗拒 内在的向前运动的特性。粘性是流动性的反面。 流体的内摩擦力 运动着的流体内部相邻两流体 层间的相互作用力。是流体粘性的表现, 又称为 粘滞力或粘性摩擦力。 由于粘性存在,流体在管内流动时,管内任一截 面上各点的速度并不相同,如图1-12所示。
SI制 N/m2或Pa
压力的单位:Pa、Kgf/m2、atm、at、H2O、mmHg、 bar、torr等。
关系:1atm = 1.0336 at = 1.013×105 Pa = 1.0336 Kgf/m2 = 10.336 mH2O
= 760 mmHg = 1.013 bar = 760 torr
μ ── 比例系数,其值随流体的不同而异,流 体的粘性愈大,其值愈大,所以称为粘滞系数或 动力粘度,简称为粘度。 式(1-6)或(1-6a)所显示的关系,称为牛顿粘性定 律。 (2)物理意义 牛顿粘性定律说明流体在流动过程中流体层间所 产生的剪应力与法向速度梯度成正比,与压力无 关。
流体的这一规律与固体表面的摩擦力规律不同。
(2)运动粘度γ (a)定义
v
运动粘度γ 为粘度μ 与密度ρ 的比值
m d u du d u v d m u dy dy dy v dy
即为单位体积流体的动量梯度
2、比重(相对密度)
d
H 2 O
277 K
3、 比容:ν = 1/ρ 即:单位质量流体所占有的体积, m3/Kg 4、重度:r = ρ·g 式中单位:r — kgf/m3 ;(工程制) N/m3 (SI制) ρ — kgf· 2/m4 s kg/m3 g—9.81m/s2 9.81m/s2
第1章流体流动习题解答

第一章 流体流动1-1某敞口容器内盛有水与油。
如图所示。
已知水及油的密度分别为1000和860kg/m 3,解:h 1=600mm ,h 2=800mm ,问H 为多少mm ?习题1-1附图mH H H m kg m kg mm h mm h 32.181.91080.081.91060.081.9860?,/860/10,800,6003333321=∴⨯=⨯⨯+⨯⨯===== 油水,解:ρρ1-2有一幢102层的高楼,每层高度为4m 。
若在高楼范围内气温维持20℃不变。
设大气静止,气体压强为变量。
地平面处大气压强为760mmHg 。
试计算楼顶的大气压强,以mmHg 为单位。
⎰⎰=∴-=⨯⨯⨯-=⨯⨯-=⎩⎨⎧---⨯=⨯⨯=----=---127.724,04763.040810190.181.9)760/(10190.181.910190.1)2.2938314/(29151408055P P p mmHgp p Ln dz p dp p p gdz d ②代入①,得②①解:ρρ1-3某水池,水深4米,水面通大气,水池侧壁是铅垂向的。
问:水池侧壁平面每3米宽度承受水的压力是多少N ?外界大气压为1atm 。
解:N dz gz P F 64023501045.12/481.9103410013.13)(3⨯=⨯⨯⨯+⨯⨯⨯=+=⎰水ρ 1-4外界大气压为1atm ,试按理想气体定律计算0.20at (表压)、20℃干空气的密度。
空气分子量按29计。
543(1.013100.209.8110)291.439/8314293.2PM kg m RT ρ⨯+⨯⨯⨯===⨯解:1-5有个外径为R 2、内径为R 1为的空心球,由密度为ρ’的材料制成。
若将该球完全淹没在某密度为ρ的液体中,若球能在任意位置停留,试求该球的外径与内径之比。
设球内空气重量可略。
3/1'1232'3132)/1(/)3/4())3/4(--=∴=-ρρρπρπR R gR g R R (解:1-6为放大以U 形压差计测气体压强的读数,采用倾斜式U 形压差计。
第一章-流体`流动

⊿ p~ R 一 一 对 应
U型测压管
•指示液与被测流体 物化学反应且不互溶; •密度大于流体密度
pA
A
h R
p1 p A gh p2 pa i gR
1
2
p A pa i gR gh A点的表压 p A pa i gR gh
第 二 节
流 体 静 力 解:(1) pA = p1 + ρH2O g(1.2 - R) 学 p1 = p2 = p3 = pa + ρHg g R 基 pA = pa + ρHg g R + ρH2O g(1.2 - R) 本 方 = pa + ( ρHg - ρH2O) g R + ρH2O g×1.2 程 = 1.279×105N/m2 式 (2) pA = [(1.279×105 ÷ 1.013×105) -1] ×1.033 = 0.271kgf/cm2
— 连续性假定
第 一 节 概 论
从微观上,流体是由大量的彼此之间有一定间隙 的单个分子所组成的,并且各单个分子作着随机的、混 乱的运动,如果以单个分子作为考察对象,那么流体将 是一种不连续的介质,所需处理的运动将是一种随机的 运动,问题将是非常复杂的。 但是,在研究流动规律时,人们感兴趣的不是单 个分子的微观运动,而是流体宏观的机械运动。
内能 流体所含的能量包括 动能
机械能
势能
位能 压能
○压能(静压能、压强能以及弹簧的势能等)
● 流体流动时存在着三种机械能(即动能、 位能和压能)之间的相互转换。
第 一 节 概 论
● 流体粘性所造成的剪力是一种内摩擦力, 它将消耗部分机械能使之转化为热能(即 内能)。输送机械提供能量补偿。 ● 气体在流动过程中因压强的变化而发生 体积变化时,存在着内能与机械能之间的 相互转换。
化工原理第一章 流体流动.ppt
z1 g
1 2
u1
2
p1
We
z2 g
1 2
u
2
2
p2
W f
(1)
式中各项单位为J/kg。
下午5时49分
24喻国华
(2)以单位重量流体为基准
将(1)式各项同除重力加速度g :
z1
1 2g
u12
p1
g
We g
z2
1 2g
u22
p2
g
Wf g
令
He
We g
1~3 m/s 0.5~1 m/s 8~15 m/s 15~25 m/s
下午5时49分
14喻国华
稳定流动与不稳定流动
稳定流动:各截面上的温度、压力、流速等物理量 仅随位置变化,而不随时间变化;
T, p,u f (x, y, z)
不稳定流动:流体在各截面上的有关物理量既随位 置变化,也随时间变化。
(4)各物理量的单位应保持一致,压力表示方法也 应一致,即同为绝压或同为表压。
下午5时49分
35喻国华
例 如附图所示,从高位槽向塔内进料,高位槽中液
位恒定,高位槽和塔内的压力均为大气压。送液
管 为 φ45×2.5mm 的 钢 管 , 要 求
pa
送液量为 3.6m3/h。设料液在管 内的压头损失为1.2m(不包括出 h
下午5时49分
4喻国华
例1-2
如附图所示,蒸汽锅炉上装一复式压力计,指示 液为水银,两U形压差计间充满水。相对于某一基准 面,各指示液界面高度分别为
Z0=2.1m, Z2=0.9m, Z4=2.0m, Z6=0.7m, Z7=2.5m。
南工大化工原理《第一章 流体流动》习题解答
《第一章流体流动》习题解答1某敞口容器内盛有水与油。
如图。
已知水及油的密度分别为1000和860kg/m3,解:h1=600mm,h2=800mm,问H为多少mm?2.有一幢102层的高楼,每层高度为4m。
若在高楼范围内气温维持20℃不变。
设大气静止,气体压强为变量。
地平面处大气压强为760mmHg。
试计算楼顶的大气压强,以mmHg为单位。
3.某水池,水深4米,水面通大气,水池侧壁是铅垂向的。
问:水池侧壁平面每3米宽度承受水的压力是多少N?外界大气压为1atm。
4.外界大气压为1atm,试按理想气体定律计算0.20at(表压)、20℃干空气的密度。
空气分子量按29计。
5.有个外径为R2、内径为R1为的空心球,由密度为ρ’的材料制成。
若将该球完全淹没在某密度为ρ的液体中,若球能在任意位置停留,试求该球的外径与内径之比。
设球内空气重量可略。
6.为放大以U形压差计测气体压强的读数,采用倾斜式U形压差计。
如图。
指示液是ρ=920kg/m3的乙醇水溶液。
气体密度为1.20kg/m3。
读数R=100mm。
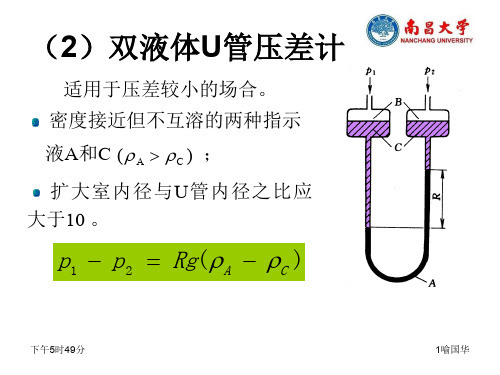
问p1与p2的差值是多少mmHg?采用微差U 形压差计测压差。
如图。
已知U形管内直径d为6mm,两扩大室半径均为80mm,压差计中用水和矿物油作指示液,密度分别为1000及860kg/m3。
当管路内气体压强p与外界大气压p相等时,两扩大室油面齐平,U形管两只管内油、水交界面亦齐平。
现读得读数R=350mm,试计算:(1)气体压强p(表)。
(2)若不计扩大室油面高度差,算得的气体压强p是多少?(3)若压差计内只有水而不倒入矿物油,如一般U形压差计,在该气体压强p值下读数R0为多少?7.某倾斜的等径直管道内有某密度ρ的液体流过。
如图。
在管道的A、B截面设置了两套U形压差计测压差,下测用的是一般U形压差计,上测用的是复式U形压差计,所用的指示液均为密度是ρ1的同一种液体。
复式压差计中两段指示液之间的流体是密度为ρ的流过管道内的液体。
化工原理第一章 流体流动
第一章流体流动二、选择题:1.一个被测量体系外柱按上一个U型压差计,出现如图情况,说明体系与大气压是(A )关系A. 体系>大气压B. 体系<大气压C. 体系=大气压2. 流体在园管内流动时,管中心流速最大,若为湍流时,平均流速与管中心的最大流速的关系为( B )A. Um=1/2UmaxB. Um=0.8UmaxC. Um=3/2Umax3. 从流体静力学基本方程了解到U型管压力计测量其压强差是( A )A. 与指示液密度、液面高度有关,与U形管粗细无关B. 与指示液密度、液面高度无关,与U形管粗细有关C. 与指示液密度、液面高度无关,与U形管粗细无关4. 转子流量计的主要特点是( C )。
A. 恒截面、恒压差;B. 变截面、变压差;C. 恒流速、恒压差;D. 变流速、恒压差。
6. 层流与湍流的本质区别是:( D )。
A. 湍流流速>层流流速;B. 流道截面大的为湍流,截面小的为层流;C. 层流的雷诺数<湍流的雷诺数;D. 层流无径向脉动,而湍流有径向脉动。
7. 在稳定流动系统中,水由粗管连续地流入细管,若粗管直径是细管的2倍,则细管流速是粗管的(C)倍。
A. 2 B. 8 C. 48. 柏努利方程的物理意义可以从题图中得到说明,若忽略A,B间的阻力损失,试判断B 玻璃管水面所处的刻度。
( A )A. a位置B. c位置C. b位置9. 用S I制基本单位表示的压强的单位应该是(C )A. PaB. N.mC. kg.m.sD. mmHg10. 表压与大气压、绝对压的正确关系是(A )。
A. 表压=绝对压-大气压B. 表压=大气压-绝对压C. 表压=绝对压+真空度11. 流体在园管内作滞流流动时,阻力与流速的( C )成比例,作完全湍流时,则呈( A )成比例。
A. 平方B. 五次方C. 一次方12. 流体流动产生阻力的根本原因是,因为流体流动(C )。
A. 遇到了障碍物;B. 与管壁产生摩擦C. 产生了内摩擦切向力13. 在稳定连续流动系统中,单位时间通过任一截面的( B )流量都相等。
第一章流体流动
五、阻力损失的计算
(1)阻力系数法 克服局部阻力所引起的能量损失,可以表示 为动能的倍数,即: Wf ´=0.5ζ u2 式中ζ称为局部阻力系数 突然扩大或突然缩小,式中的流速u应该以 小截面处的流速为准,根据小管与大管的截面 积之比,在图中查取进口与出口,流体从容器 中流出,或流入容器中,可按照大截面积与小 截面积之比为1或为0来计算
五、阻力损失的计算
1、概述 流体在管道中流动,受到阻力的作用,要克 服阻力而做功,即流体有能量损失。根据阻力 产生原因的不同,可以分为直管阻力和局部阻 力。直管阻力是流体流经一定管径的直管时, 由于流体的内摩擦力(即粘性力)而产生的阻 力。局部阻力主要是由于体流经管路中管件、 阀门及管截面形状和尺寸突然扩大和缩小等局 部地方引起流体边界层分离造成的阻力。
第一章 流体流动
主讲:高轶群
本章要点
一、静力学方程 二、连续性方程 三、柏努利方程 四、流体流动现象 五、阻力损失的计算 六、管路计算
一、静力学方程
知识要点:1、基本物理量 2、静力学方程 3、静力学方程的应用
一、静力学方程
1、基本物理量 (1)密度:用表示,属于物性,单位为 kg/m3
影响因素:气体------种类、压力、温度、浓度 液体------ 种类、温度、浓度
五、阻力损失的计算
范宁公式中λ 称为摩擦系数,摩擦应力τ 与流体流动类型有关,因此λ 也因流体不同的 流动类型而变化。 层流时: λ =64/ Re ;λ 只与Re值有关 ,和管壁粗糙度无关; 湍流时的λ 与Re值和相对粗糙度(ε /d) 有关,具体数据在关联图中查取。
五、阻力损失的计算
3、局部阻力损失 流体在管路中流动,在管件处由于流速、方 向的改变,使流体受到的阻力损失,为局部阻 力损失。表示为wf´
化工原理课后习题答案第一章流体流动答案
第一章 流体流动习题解答1.解:(1) 1atm= Pa=760 mmHg真空度=大气压力—绝对压力,表压=绝对压力—大气压力 所以出口压差为p =461097.8)10082.0(10132576.00⨯=⨯--⨯N/m 2(2)由真空度、表压、大气压、绝对压之间的关系可知,进出口压差与当地大气压无关,所以出口压力仍为41097.8⨯Pa 2.解: T=470+273=703K ,p=2200kPa混合气体的摩尔质量Mm=28×0.77+32×0.065+28×0.038+44×0.071+18×0.056=28.84 g/mol混合气体在该条件下的密度为:ρm=ρm0×T0T×pp0=28.8422.4××.3=10.858 kg/m33.解:由题意,设高度为H 处的大气压为p ,根据流体静力学基本方程,得 dp=-ρgdH大气的密度根据气体状态方程,得 ρ=pMRT根据题意得,温度随海拔的变化关系为 T=293.15+4.81000H代入上式得ρ=pMR (293.15-4.8×10-3H )=-dpgdh移项整理得dpp=-MgdHR293.15-4.8×10-3H对以上等式两边积分, pdpp=-0HMgdHR293.15-4.8×10-3H所以大气压与海拔高度的关系式为 lnp=7.13×ln293.15-4.8×10-3H293.15即:lnp=7.13×ln1-1.637×10-5H+11.526(2)已知地平面处的压力为 Pa ,则高山顶处的压力为 p 山顶=×=45431 Pa将p 山顶代入上式ln 45431=7.13×ln1-1.637×10-5H+11.526 解得H =6500 m ,所以此山海拔为6500 m 。
