大学物理 第十四章 电势
大学物理6.3 电势PPT

q0
p εp
UP
v E
电势(电势能)零点的选择 电势能) 任意 视分析问题方便而定
通常: 通常: (1)有限带电体: )有限带电体: (2)无限带电体: )无限带电体:
U∞ = 0 (a ) U∞ ≠ 0 电场中任选一点
r 际应用中或研究电路问题时: )实际应用中或研究电路问题时: 取大地、 取大地、仪器外壳等 3、意义: 描述电场能(电场力作功)方面的性质 意义: 描述电场能(电场力作功)
结论:静电场力做功,与路径无关. 结论:静电场力做功,与路径无关. 静电场的这一特性称为静电场的保守性 相应地,静电力是保守力(像重力一样) 7 相应地,静电力是保守力(像重力一样)
1.单个点电荷产生的电场 1.单个点电荷产生的电场 r r r r Q dW = F ⋅ dl = q0 E ⋅ dl
U
o
Q U 外 (r ) = 4 πε 0 r Q U内 ( r ) = 4 πε 0 R
Q 4 π ε0R
Q 4 π ε 0r
o
R
r
例3 解:
计算电量为 Q 的带电球面球心的电势
dq
o
在球面上任取一电荷元dq
Q R
dq 则电荷元在球心的电势为 dU = 4πε 0 R
由电势叠加原理 球面上电荷在球心的总电势 思考: 思考:
W = q0 ∫
Q P
∞
q0
p εp
v E
r r E ⋅ dl
点为无穷远时, 当Q点为无穷远时,电场力所做的功称为q0 点为无穷远时 在电场中的P点的电势能 点的电势能, 在电场中的 点的电势能,即P点电势能为 点电势能为 r ∞ r ε P = q0 ∫ E ⋅ dl
物理十四章归纳总结

物理十四章归纳总结导言:物理学是一门研究自然界基本规律的学科,包含了十四个重要的章节。
在这篇文章中,我们将对物理学的这十四章进行总结和归纳,希望能够帮助读者对物理学的基础知识有更清晰的理解。
第一章:力及相关概念1.1 力的概念及基本性质1.2 力的分类及力的合成与分解1.3 牛顿第一定律1.4 牛顿第二定律1.5 牛顿第三定律1.6 弹簧力与胡克定律第二章:运动学2.1 位移、速度和加速度2.2 匀速直线运动2.3 加速直线运动2.4 平抛运动2.5 斜抛运动2.6 圆周运动第三章:牛顿运动定律3.1 动量与冲量3.2 力和质量的概念3.3 牛顿第二定律的量和质的关系 3.4 物体的运动状态与力的关系 3.5 牛顿第三定律的应用3.6 质点系的动量第四章:万有引力4.1 引力的概念及性质4.2 引力定律及其应用4.3 行星运动4.4 地球上的物体运动第五章:机械能与能量守恒5.1 动能与动能定理5.2 重力势能与势能的定义5.3 势能和机械能的转化5.4 能量守恒定律及其应用5.5 各种力的非保守性与能量守恒第六章:动量守恒6.1 动量定理6.2 碰撞实验6.3 弹性碰撞6.4 完全非弹性碰撞第七章:静电场7.1 电荷和电场7.2 电场的呈现7.3 电场强度7.4 电场力7.5 电场能第八章:电场8.1 电势能和电势8.2 电势的分布8.3 电场中电势上升和电势差8.4 电势差的计算8.5 电容器的原理和应用第九章:电流和电路9.1 电流的概念9.2 电流的方向与电流强度 9.3 电阻与电压9.4 欧姆定律9.5 串联和并联电路9.6 电功率和电能第十章:磁场10.1 磁场的概念10.2 磁感应强度10.3 磁感应线的性质10.4 安培力定律10.5 楞次定律及其应用10.6 电流感应第十一章:电磁感应和电磁场 11.1 磁生电、电生磁的现象11.2 法拉第电磁感应定律11.3 洛伦兹力和电动势11.4 电磁感应实验的应用11.5 自感和互感第十二章:交流电12.1 交流电的特征12.2 交流电的有效值和频率12.3 交流电的平均值和变化规律12.4 交流电的相量形式12.5 交流电阻、电感和电容的交流特性第十三章:光学13.1 光波的概念及特性13.2 光的反射和折射13.3 光的干涉和衍射13.4 光的偏振和旋光现象13.5 光的光电效应及应用第十四章:相对论14.1 时间、空间和质量的相对性14.2 相对论速度变换14.3 质能关系和能量守恒14.4 狭义相对论的基本概念及应用14.5 引力和广义相对论总结:物理学的十四个章节涵盖了从力学到光学、电磁学和相对论等多个领域,揭示了自然界的基本运行规律。
电势及其梯度

q E= 2 4πε 0 r
1
cosθ dl = dr
q o
r
c
θ
r E
a b rb 1 qq qq0 1 1 0 − ∴W = ∫ dW = ∫ 2 dr = a ra 4πε 4πε 0 ra rb 0 r
温州大学物理与电子信息学院
电势和电势差
结论:在点电荷的电场中, 结论:在点电荷的电场中,电场力对试验电荷所 做的功, 做的功 , 只与试验电荷所带电量以及起点和终点 位置有关,而与所经历的路径无关. 位置有关,而与所经历的路径无关. 问题:任何带电体系产生的电场的结果如何? 问题:任何带电体系产生的电场的结果如何? r r r Q E = E1 + E 2 + L r r r r r r r ∴W = ∫ F ⋅ dl = q0 ∫ E ⋅ dl = q0 ∫ ( E1 + E2 + L) ⋅ dl r r r r = q0 ∫ E1 ⋅ dl + q0 ∫ E2 ⋅ dl + L
ρR 2 r Up = − ln < 0 2εo R
P r o o
温州大学物理与电子信息学院
定义法求电势
R
r ρ r r r < R E= 2ε o
r≥R
r
.
p
ρR 2 r Up = − ln 2εo R < 0
R
r ρR 2 ˆ = λ r E= r ˆ 2πεor 2εor
r<R
r= 0处, U= Umax= ρ R 2 处 2εo ε
温州大学物理与电子信息学院
电势梯度概念 等势面 定义:电势相等的曲面 定义:
U1
+q
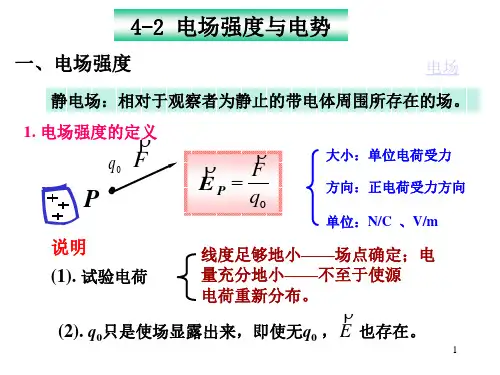
大学物理——电场强度与电势
例题
均匀带电细棒,长 L ,电荷线密度 , 求:中垂面上的场强 。 r dQ
y
dQ dy
解 : dE 4 r 3 0
r1
L0
dE dE x i dE y j E dE i dE x j 0 dE y
L L L
E r
2
3、场强叠加原理
(1)点电荷系的场强 Q2
点电荷的场强
点 电 Q1 荷
试验电荷 F2 Q
0
E
F F
1
Q 4 0 r
2
r0
由定义
F F3 F1 F2 E E1 E2 E3 Q0 Q0 Q0 Q0
L
E E //
x xQ dQ x dQ cos dE 2 L 3 L r 4 r 40 r 0 (1) x 0 xQ i
dE
E
L
dE 0
E0
4 0 x R
2
2
3
2
Q (2)R <<x E 2 4 0 x
dE
P
x
r
R
O
dr
9
讨论 (1) 当R >> x ,圆板可视为无限大薄板
E 2 0
(2)
E1
E1 E2
E1 E2
EI E1 E2 0 EII E1 E2 0 EIII E1 E2 0
E2
(3) 补偿法
10
例 已知圆环带电量为q ,杆的线密度为 ,长为L
qq 0 1 1 A r 4 0 1 r2
《大学物理》第14单元课后答案 高等教育出版社

课后答案网,用心为你服务!
大学答案 --- 中学答案 --- 考研答案 --- 考试答案 最全最多的课后习题参考答案,尽在课后答案网()! Khdaw团队一直秉承用心为大家服务的宗旨,以关注学生的学习生活为出发点, 旨在为广大学生朋友的自主学习提供一个分享和交流的平台。 爱校园() 课后答案网() 淘答案()
Ei N
线圈中感应电动势大小: Ei E1 E 2
0 IvL1 0 IvL1 N 2x 2 ( x L2 )
Ei
N 0 IS v ,其中: S L1 L2 ,动生电动势方向为顺时针。 2 x( x L2 )
(2)如果线圈保持不变,长直导线中通有交变电流 I I 0 sin t 。
kh
da
(D) E L / R
Page84
课
后 答
(B) 21 > 12
(C) 21 = 12
M
N
题 21.图
N
作业登记号
学号
姓名
单元十四
单元十四(二) 自感、互感、磁场能量
一、选择题 1. 自感为 0.25H 的线圈中,当电流在(1/16)秒内由 2A 均匀减小到零时,线圈中自感电动势的大小 为: (A) 7.8 10 V
3
【 C (B) 2.0V (C) 8.0V (D) 3.1 10 V
作业登记号
学号
姓名
单元十四
方向垂直纸面向里。
选顺时针为积分正方向
根据: E i ( v B ) dl
a
b
线段 CA 中产生的动生电动势: E1 N
0 IvL1 2x
方向由 C 到 A。
大学物理静电场2电势

各电势的零点应是同一点)
用“点电荷电势叠加的方法”:
对点电荷系:
对有限的 连续电荷分布:
qi
4 π ori
(选
0)
d q
q 4πor
(选 0)
例. 求半径为 R、带电量为 q 的细圆环 轴线上任意点的电势。
【解】 这是连续带电体, 任取一电荷元dq,
用“点电荷电势叠加法”
dq
R 0
r R2 x2 取轴线上任一点 P,电势:
x
x
P
d q
(q)4 π0r
所以
4π 0
q R2 x2
1/ 2
1
dq
4 π0r (q)
思考: 环上电荷均匀或不均匀结果一样吗?
等势面:
电场中电势相等的点组成的面称为等势面。 等势面是形象描述电场的一种表示方法。 画法:相邻等势面的电势差为常数。
例1. 正点电荷电场的等势面。
等势面有如下特点:
2π0 r
r > r0 的点,电势为负,
r = r0 的点,电势为零,
r < r0 的点,电势为正。
r
可以看到,若选无限远为 电势零点,
会使积分发散。
8.4.5 电势叠加原理
由
po
E
d
l
及
E
p
Ei
得 ( po p
Ei ) d l
po p
i Ei
d
l
i
i
i
i
(注意:用电势叠加原理时,
静电势能是属于电荷 q0 和场源所共有的 (正如重力势能是属于物体和地球),
也叫电荷之间的相互作用能。
例 1. 氢原子中的电子在原子核电场中的 静电势能为
大学物理复习——电势
dq
(1) 球面外: r > R 沿半径方向积分, 沿半径方向积分,则 P 点的电势为
∞ 外 = ∫r E外 dr ∞ = ∫r E外dr
∞
+ + + P ++ + + Ro r + + r ++ + ++ +
q+
4π ε0r (2) 球面内: r < R
r 2
=∫
∞
q
dr =
q 4π ε0 r
环路定理
∫L E dl = 0
2.环路定理的意义 2.环路定理的意义 静电场是保守场 ; 静电场是保守场 静电场力是保守力 作功与路径无关. 保守力, 静电场力是保守力,作功与路径无关. 环路定理表明电场线( 不闭合( 环路定理表明电场线( E线)不闭合( 无旋场 ) . 结论:
E 遵守高斯定理和环路定理说明静电场是 有源保守场. 有源保守场.
E P x
Ey = 0 ,
Ez = 0
∴
qx E= i 2 2 32 4π ε0(R + x )
3.求两个同心均匀带电球面的 E和φ的分布. 3.求两个同心均匀带电球面的 的分布 R 已知内球面: 已知内球面:1, q1;外球面: 2, q2 外球面 R 方法一: 解: 方法一:先用高斯定理求E , q2 q1+ 再用积分关系求φ . 再用积分关系求 + + +R Ⅰ区: r > R2 + 1 + oⅢ + Ⅱ q1 q2 + + E1 dS = E1 4π r2 = , + + ∫S R2 ε0 q1 q2 E1 = 2 4π ε0 r ∞ q1 q2 ∞ q1 q2 dr = , 1 = ∫ E1 dr = ∫ 2 r 4π ε0r 4πε0r r
湖南大学物理(2)第14,15章课后习题参考答案
第14章 稳恒电流的磁场 一、选择题1(B),2(D),3(D),4(B),5(B),6(D),7(B),8(C),9(D),10(A) 二、填空题(1). 最大磁力矩,磁矩 ; (2). πR 2c ; (3). )4/(0a I μ; (4).RIπ40μ ;(5). μ0i ,沿轴线方向朝右. ; (6). )2/(210R rI πμ, 0 ; (7). 4 ; (8). )/(lB mg ; (9). aIB ; (10). 正,负.三 计算题1.一无限长圆柱形铜导体(磁导率μ0),半径为R ,通有均匀分布的电流I .今取一矩形平面S (长为1 m ,宽为2 R ),位置如右图中画斜线部分所示,求通过该矩形平面的磁通量.解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定 律可得:)(220R r r RIB ≤π=μ因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r R I Rd 2020⎰π=μπ=40Iμ 在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r I R Rd 220⎰π=μ2ln 20π=Iμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+Iμ1 m2. 横截面为矩形的环形螺线管,圆环内外半径分别为R 1和R 2,芯子材料的磁导率为μ,导线总匝数为N ,绕得很密,若线圈通电流I ,求.(1) 芯子中的B 值和芯子截面的磁通量. (2) 在r< R 1和r > R 2处的B 值.解:(1) 在环内作半径为r 的圆形回路, 由安培环路定理得NI r B μ=π⋅2, )2/(r NI B π=μ 在r 处取微小截面d S = b d r , 通过此小截面的磁通量r b rNIS B d 2d d π==μΦ穿过截面的磁通量⎰=SS B dΦr b rNId 2π=μ12ln2R R NIbπ=μ (2) 同样在环外( r < R 1 和r > R 2 )作圆形回路, 由于0=∑iI02=π⋅r B ∴ B = 03. 一根很长的圆柱形铜导线均匀载有10 A 电流,在导线内部作一平面S ,S 的一个边是导线的中心轴线,另一边是S 平面与导线表面的交线,如图所示.试计算通过沿导线长度方向长为1m 的一段S 平面的磁通量.(真空的磁导率μ0 =4π×10-7 T ·m/A ,铜的相对磁导率μr ≈1)解:在距离导线中心轴线为x 与x x d +处,作一个单位长窄条, 其面积为 x S d 1d ⋅=.窄条处的磁感强度 202RIxB r π=μμ所以通过d S 的磁通量为 x RIxS B r d 2d d 20π==μμΦ通过1m 长的一段S 平面的磁通量为⎰π=Rr x RIx20d 2μμΦ60104-=π=Ir μμ Wb4. 计算如图所示的平面载流线圈在P 点产生的磁感强度,设线圈中的电流强度为I .解:如图,CD 、AF 在P 点产生的 B = 0x2EF D E BC AB B B B B B+++= )sin (sin 4120ββμ-π=aIB AB , 方向⊗其中 2/1)2/(sin 2==a a β,0sin 1=β∴ a I B AB π=240μ, 同理, a IB BC π=240μ,方向⊗.同样)28/(0a I B B EF D E π==μ,方向⊙.∴ aI B π=2420μaIπ-240μaIπ=820μ 方向⊗.5. 如图所示线框,铜线横截面积S = 2.0 mm 2,其中OA 和DO '两段保持水平不动,ABCD 段是边长为a 的正方形的三边,它可绕OO '轴无摩擦转动.整个导线放在匀强磁场B 中,B 的方向竖直向上.已知铜的密度ρ = 8.9×103 kg/m 3,当铜线中的电流I =10 A 时,导线处于平衡状态,AB 段和CD 段与竖直方向的夹角α =15°.求磁感强度B的大小.解:在平衡的情况下,必须满足线框的重力矩与线框所受的磁力矩平衡(对OO '轴而言).重力矩 αραρsin sin 2121gSa a a gS a M +⋅= αρsin 22g Sa =磁力矩 ααcos )21sin(222B Ia BIa M =-π=平衡时 21M M =所以 αρsin 22g Sa αcos 2B Ia = 31035.9/tg 2-⨯≈=I g S B αρ T6. 如图两共轴线圈,半径分别为R 1、R 2,电流为I 1、I 2.电流的方向相反,求轴线上相距中点O 为x 处的P 点的磁感强度. 解:取x 轴向右,那么有 2/322112101])([2x b R I R B ++=μ 沿x 轴正方向 2/322222202])([2x b R I R B -+=μ 沿x 轴负方向21B B B -=[2μ=2/32211210])([x b R I R ++μ]])([2/32222220x b R I R -+-μ若B > 0,则B 方向为沿x 轴正方向.若B < 0,则B的方向为沿x 轴负方向.P7. 如图所示.一块半导体样品的体积为a ×b ×c .沿c 方向有电流I ,沿厚度a 边方向加有均匀外磁场B (B 的方向和样品中电流密度方向垂直).实验得出的数据为 a =0.10 cm 、b =0.35 cm 、c =1.0 cm 、I =1.0 mA 、B =3.0×10-1 T ,沿b 边两侧的电势差U =6.65 mV ,上表面电势高.(1) 问这半导体是p 型(正电荷导电)还是n 型(负电荷导电)?(2) 求载流子浓度n 0 (即单位体积内参加导电的带电粒子数).解:(1) 根椐洛伦兹力公式:若为正电荷导电,则正电荷堆积在上表面,霍耳电场的方向由上指向下,故上表面电势高,可知是p 型半导体。
大学物理 电势
2、说明:
(1)电势是标量,有正有负; (2)电势具有相对意义,它决定于电势零点的选择。 a 在理论计算中,通常选择无穷远处的电势为零; b 在实际工作中,通常选择地面的电势为零;
c 但是对于“无限大”或“无限长”的带电体,只能
在有限的范围内选取某点为电势的零点。
3、电势差
U AB U A U B
P
U
dq 4 0 r
4、电势的计算方法
(1)利用电势的定义式
Up
U 0 p E dl
步骤: (1)先算场强 (2)选择合适的路径L (3) 积分(计算)
要注意参考点的选择,只有电荷分布在有限的空间时,
才能选无穷远点的电势为零; 积分路径上的电场强度的函数形式要求已知或可求。 (2)利用电势的叠加原理 步骤 (1)把带电体 分为无限多dq (2)由dq d U (3)由d U U = d U
2 2
x2 R2 x
2
把圆盘当作 一个点电荷
当x>>a时
x R x R /(2 x)
R2 q R2 q U 2 0 2 x R 2 2 0 2 x 4 0 x
课堂练习 求均匀带电细杆延长线上一点的电势。已知 q ,L,a
O
x
L
dx
P
a
dU X
dq dU 4 0 ( L a x)
2. 叠加法 思路: dq dU U dU
注意:应用典型带电体的电势公式,选取相同 的零势点。 典型带电体的电势 点电荷: 均匀带电圆环 轴线上: 均匀带电球面:
q U 4 π 0r
q U 2 2 12 4 π 0 (R x )
了解大学物理中的静电学与电势
了解大学物理中的静电学与电势静电学和电势是大学物理课程中的重要内容,它们研究的是与电荷有关的现象和电场的性质。
本文将介绍静电学的基本概念、公式和应用,并探讨电势的概念和计算方法。
一、静电学的基本概念1. 电荷:电荷是物质所具有的一种性质,分为正电荷和负电荷。
同种电荷相互排斥,异种电荷相互吸引。
2. 静电力:静电力是由于电荷之间的相互作用而产生的力,遵循库仑定律。
库仑定律表明,两个点电荷之间的静电力正比于它们之间的距离的平方,并与它们之间的电荷量成正比。
3. 电场:电场是由电荷产生的力场,描述了电荷对周围空间的影响。
电场强度的大小表示单位正电荷在该位置所受的电场力。
4. 高斯定律:高斯定律表明,闭合曲面上的电通量与该曲面内总电荷量成正比。
这个定律可以用于计算电荷在不同几何形状的分布中对电场产生的影响。
二、静电学的公式1. 库仑定律:两个电荷之间的静电力可以通过库仑定律计算。
库仑定律的数学表达式为F = k * q1 * q2 / r^2,其中F是静电力,k是库仑常数,q1和q2是电荷量,r是两个电荷之间的距离。
2. 电场强度公式:电场强度是描述电场的物理量,可以通过公式E= F / q计算,其中E是电场强度,F是电场力,q是电荷量。
3. 高斯定律:高斯定律可以用于计算电荷在闭合曲面内产生的电场。
数学表达式为∮E · dA = Q / ε0,其中∮E · dA表示通过闭合曲面的电场通量,Q是闭合曲面内的总电荷,ε0是真空介电常数。
三、静电学的应用1. 静电除尘:利用静电力可以去除物体表面的粉尘和污垢。
静电除尘器通过产生电场,使带电的粉尘和污垢被吸附到带有相反电荷的电极上,从而实现清洁效果。
2. 静电喷涂:静电喷涂利用静电力将涂料带电,使其在喷涂时更好地附着在物体表面上。
这种喷涂方法可以提高喷涂效率和涂料利用率。
3. 静电除湿:静电除湿器利用静电力去除空气中的湿气。
通过将湿气带电,使其被吸附在带有相反电荷的吸附材料上,从而实现除湿效果。
