电子科大 随机过程第一章作业
清华大学随机过程答案1
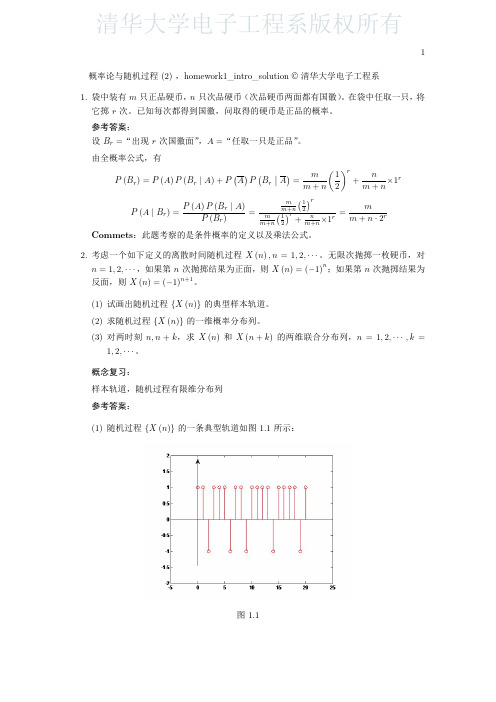
3. 质点在直线上做随机运动,即在 t = 1, 2, 3, · · · 时质点可以在 x 轴上往右或往左做一个 单位距离的随机游动。若往右移动一个单位距离的概率为 p,往左移动一个单位距离的 概率为 q,即 P {ξ (i) = +1} = p,P {ξ (i) = −1} = q,p + q = 1,且各次游动是相互统 ∑n 计独立的。经过 n 次游走,质点所处的位置为 ηn = η (n) = ξi。
参考答案:
(1) V = a 时,一条样本轨道为典型的正弦曲线。 2
(2) ξ (0) = 0,fξ(0)(x) = δ(x);ξ (π/2ω) = V ,其概率密度同 V 一样。
(π) ξ
4ω
=
V
√ 2
,
fξ(
π 4ω
)
(x)
=
√ 2 a
,
0
<
0, 其他
xHale Waihona Puke <√a 2() 5π
ξ 4ω
=
V
−
√ 2
n
pmqn−m = pn − qn。
m=0
m
∑n
解法二:因各次游走是相互统计独立的,则 E [η (n)] = E[ξi] = (p − q)n。
i=1
清华大学电子工程系版权所有
3
(2) 假设 n1 < n2,
Rηη (n1, n2) = E [η (n1) η (n2)] = E {η (n1) [η (n1) + η (n2) − η (n1)]} = E[η (n1)]2 + E [η (n1)] E [η (n2) − η (n1)] = {E [η (n1)]}2 + V ar [η (n1)] + (p − q)2n1 (n2 − n1) = (p − q)2n21 + n1V ar [ξi] + (p − q)2n1 (n2 − n1) = (p − q)2n1n2 + n1[1 − (p − q)2]
电子科技大学随机信号分析CH2习题及答案
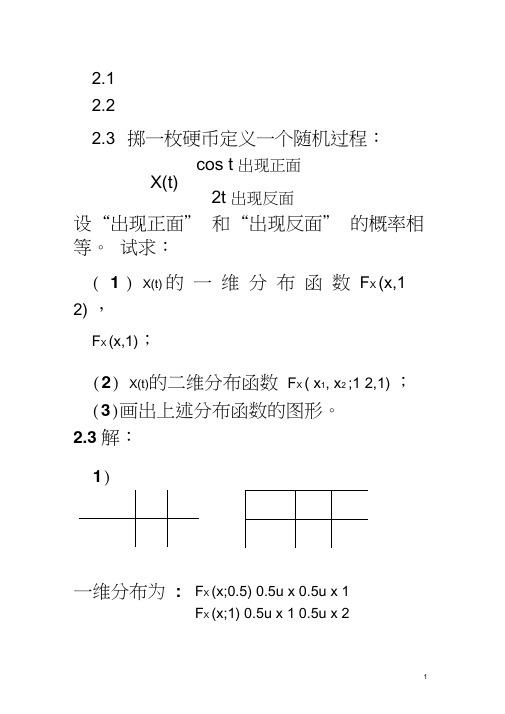
2.12.22.3 掷一枚硬币定义一个随机过程:cos t 出现正面X(t)2t 出现反面设“出现正面” 和“出现反面” 的概率相等。
试求:( 1 ) X(t) 的一维分布函数F X (x,12) ,F X (x,1);(2) X(t)的二维分布函数F X ( x1, x2 ;1 2,1) ;(3)画出上述分布函数的图形。
2.3 解:1)一维分布为:F X (x;0.5) 0.5u x 0.5u x 1F X (x;1) 0.5u x 1 0.5u x 2X (0.5) 0, X (1) 1 , 依概率 0.5发生X (0.5) 1, X (1) 2 ,依概率 0.5发生 二维分布函数为F ( x 1, x 2 ;0.5,1) 0.5u x 1,x 2 1 0.5u x 1 1,x 2 22.4 假定二进制数据序列 {B(n), n=1, 2, 3, , .} 是伯努利随机序列, 其每一位数据对 应随机变量 B(n) ,并有概率 P[B(n)=0]=0.2 和P[B(n)=1]=0.8 。
试问,( 1)连续 4 位构成的串为 {1011}的概率是 多少?(2)连续 4 位构成的串的平均串是什么?( 3)连续 4 位构成的串中,概率最大的 是(2) cos X(t) c 2o t s 出现正面出现反面什么?( 4 )该序列是可预测的吗?如果见到10111后,下一位可能是什么?2.4 解:解:(1)P 1011P B n 1 P B n 1 0 P B n 2 1 P B n 3 10.8 0.2 0.8 0.8 0.10242)设连续 4 位数据构成的串为B(n) ,B(n+1) ,B(n+2) ,B(n+3) ,n=1, 2, 3,⋯.其中B(n) 为离散随机变量,由题意可知,它们是相互独立,而且同分布的。
所以有:3k串(4bit 数据)为:X (n) 2k B(n k),k0其矩特性为:因为随机变量B(n) 的矩为:均值: E[B(n)] 0 0.2 1 0.8 0.802 0.2 12 0.8 0.8220.8 0.82 0.16 所以随机变量 X(n) 的矩为:均值:3E[X(n)] E k0332k E B(n k) 2k 0.8 12k 0 k 0方差:3k D[X(n)] D 2k B(n k) k03 2 3 2k 2 D B(n k) 4k 0.16 13.6k 0 k 0如果将 4bit 串看作是一个随机向量 , 则随机向量的均值和方差为: 串平均 :B n ,B n 1 ,B n 2 ,B n 3 0.8,0.8,0.8,0.8方差:Var B(n) Bn 2Bn 2k B(n k)串方差:Var B n ,B n 1 ,B n 2 ,B n 30.16,0.16,0.16,0.163) 概率达到最大的串为1,1,1,14) 该序列是不可预测的,因为此数据序列各个数据之间相互独立,下一位数据是0 或1,与前面的序列没有任何关系。
(完整版)随机过程题库1

随机过程综合练习题一、填空题(每空3 分)第一章1.X1,X2, X n是独立同分布的随机变量,X i 的特征函数为g(t),则X1 X2 X n 的特征函数是。
2.E E(X Y) 。
3.X 的特征函数为g(t),Y aX b,则Y的特征函数为。
4.条件期望E(X Y)是的函数,(是or不是)随机变量。
5.X1,X2, X n是独立同分布的随机变量,X i 的特征函数为g i(t),则X1 X 2 X n 的特征函数是。
6.n 维正态分布中各分量的相互独立性和不相关性。
第二章7.宽平稳过程是指协方差函数只与有关。
8.在独立重复试验中,若每次试验时事件 A 发生的概率为p(0 p 1),以X(n)记进行到n次试验为止 A 发生的次数,则{X(n),n 0,1,2, }是过程。
9.正交增量过程满足的条件是。
10.正交增量过程的协方差函数C X (s,t) 。
第三章11.{X(t), t ≥0}为具有参数0 的齐次泊松过程,其均值函数为;方差函数为。
12.设到达某路口的绿、黑、灰色的汽车的到达率分别为1, 2 ,3且均为泊松过程,它们相互独立,若把这些汽车合并成单个输出过程(假定无长度、无延时),相邻绿色汽车之间的不同到达时间间隔的概率密度是,汽车之间的不同到达时刻间隔的概率密度是。
13.{X(t), t ≥0}为具有参数0的齐次泊松过程,( t)n e n! 14.n15.240000 16.复合;17.71 4eP X(t s) X(s) n14.设{X(t), t ≥0} 是具有参数0的泊松过程,泊松过程第n 次到达时间W n的数学期望15.在保险的索赔模型中,设索赔要求以平均 2 次/月的速率的泊松过程到达保险公司.若每次赔付金额是均值为10000 元的正态分布,求一年中保险公司的平均赔付金额。
16.到达某汽车总站的客车数是一泊松过程,每辆客车内乘客数是一随机变量.设各客车内乘客数独立同分布,且各辆车乘客数与车辆数N(t) 相互独立,则在[0 ,t]内到达汽车总站的乘客总数是(复合or 非齐次)泊松过程.17.设顾客以每分钟 2 人的速率到达,顾客流为泊松流,求在2min 内到达的顾客不超过 3 人的概率是.第四章18.无限制随机游动各状态的周期是。
电子科大随机信号分析CH1概率论基础

3,4,5,6,1,2,3,4,5, ,2,3,4,5,6,
概率 P A k , k为事件A包含的样本点数
6
2020/11/21
16
2. 条件概率
条件事件: B A 事件A发生条件下的事件B
条件概率(Conditional probability),
PB
A
P AB P A
, P A 0
随机信号分析
2020/11/21
1/92
与同学们共勉
我命在我,不在天地。 天助自助者。 主动还是被动是成功与失败的关键。 梅花香自苦寒来。 听好每堂课,课后研读教材,做好每次作业。 学会读书,读专业书,读文学作品(修身养性, 学会自信)
2020/11/21
2
课程简介
课程性质: 专业基础课 课程基础:《概率论》、《信号与系统》 后续课程:《通信原理》及从事统计信号处理研究 成绩考核:平时作业+期中考试+期末考试
2020/11/21
13
✓ 事件概率的基本性质
1 P = 0 2 0 P A 1 3 如果 A B , P A P B 4 P AB P A P A B
2020/11/21
14
例1.1 分析掷均匀硬币问题。 解: H---正面,T---反面。因此,
(1)样本空间: H ,T
c. 可重复性
✓ 样本点 ( Sample Point )
把随机实验 E 的每一个基本可能结果称为随机实验的 样本点,记为ξ 。
2020/11/21
9
✓ 样本空间 (Sample Space )
随机实验的全部样本点构成的集合,称为随机实验的 样本空间,记为 Ω
✓ 随机事件( Ra HTH , HTT ,THH ,THT ,TTH}
第一章随机过程

12
一维随机变量函数分布(例)
例2 设随机变量X服从正态分布N(0,1),求随机变量 Y=X2的概率密度。 解: Y=X2
Байду номын сангаасX Y
x2 2
dx 1 dy 2 y
y
1 y
1 f X x e 2
y
1 2 1 1 2 1 fY y e e = 2 2 y 2 2 y
9
各阶矩(中心矩、原点矩)
原点矩
E Xk
中心矩
E X E X
k
k=2
x k P( x) x x k f x dx
方差
E X E X
2
《随机信号分析》教学组
10
第二节
随机变量函数分布
《随机信号分析》教学组
e
e
u2 2
《随机信号分析》教学组
特征函数性质
(1) 随机变量X的特征函数CX(u)满足
C X u C X 0 1
(2) 随机变量X的特征函数为CX(u), jub 则 Y=aX+b的特征函数为 CY u e CX au
(3) 独立随机变量X1和X2的特征函数分别为CX1(u) 和CX2(u),则 Z=X1+X2的特征函数为
作业 20% 考试 80%
《随机信号分析》教学组
2
预备知识
概率论
《随机信号分析》教学组
3
主要内容
经典概率问题 一维随机变量 二维随机变量 概率空间、全概率公式和贝叶斯公式 概率分布函数、概率密度函数和一维随机变量函数分布 概率分布函数、概率密度函数和二维随机变量函数分布 数学期望、方差和各阶矩 切比雪夫不等式、弱大数定律、中心极限定理等
【全】电子科大 计算机系统结构第一章作业答案

1.试述Flynn 分类的4 种计算机系统结构有何特点。
参考答案:Flynn按照指令流和数据流两种不同的组合,把计算机系统的结构分为以下4 类:(1)单指令流单数据流SISD(Single Instruction Stream Single Datastream),SISD 是传统的顺序处理计算机;(2)单指令流多数据流SIMD(Single Instruction Stream Multiple Datastream),SIMD 以阵列处理机为代表;(3)多指令流单数据流MISD(Multiple Instruction Stream Single Datastream),MISD 实际代表何种计算机,存在着不同的看法;(4)多指令流多数据流MIMD(Multiple Instruction Stream Multiple Datastream),多处理机与多计算机系统属于MIMD 结构。
单指令流单数据流(Single Instruction Stream Single Data Stream,SISD)SISD其实就是传统的顺序执行的单处理器计算机,其指令部件每次只对一条指令进行译码,并只对一个操作部件分配数据。
单指令流多数据流(SingleInstructionStreamMultipleDataStream,SIMD)SIMD以并行处理机为代表,结构如图,并行处理机包括多个重复的处理单元PU1~PUn,由单一指令部件控制,按照同一指令流的要求为它们分配各自所需的不同的数据。
多指令流单数据流(MultipleInstructionStreamSingleDataStream,MISD)MISD的结构,它具有n个处理单元,按n条不同指令的要求对同一数据流及其中间结果进行不同的处理。
一个处理单元的输出又作为另一个处理单元的输入。
多指令流多数据流(MultipleInstructionStreamMultipleDataStream,MIMD)MIMD的结构,它是指能实现作业、任务、指令等各级全面并行的多机系统,多处理机就属于MIMD。
电子科大随机信号分析CH1概率论基础
2020/10/22
8
✓ 随机试验(Random Experiment): 对随机现象做出的观察与科学实验。 E
随机实验的特点:
a.不唯一性
b.不确定性
c. 可重复性
✓ 样本点 ( Sample Point )
把随机实验 E 的每一个基本可能结果称为随机实验的 样本点,记为ξ 。
2020/10/22
33
u x, y u xu y x, y x y
z u x xi , y y j
y
yj
xi
x
z x xi , y y j
y
yj x
xi
2020/10/22
34
6) 边缘分布
边缘分布函数:
FX ( x) F ( x,) FY ( y) F (, y)
边缘概率密度:
2020/10/22
20
2. 随机变量的概率分布函数(累积分布函数) Probability Distribution Function
✓ 定义 FX (x) F (x) P[ X x]
x
即,F(x) 是R.V.X.落在区间 (, x] 上的概率。
2020/10/22
21
✓ 性质
1) F(x)是x的单调递增函数,即 F ' (x) 0
3,4,5,6,1,2,3,4,5, ,2,3,4,5,6,
概率 P A k , k为事件A包含的样本点数
6
2020/10/22
16
2. 条件概率
条件事件: B A 事件A发生条件下的事件B
条件概率(Conditional probability),
PB
A
P AB P A
随机过程作业
随机过程作业定理、引理及推论部分定理 5.1(Champan-Kolmogorov 方程,简称C-K 方程)对一切n,m ≥0,i,j ∈S 有(1) p ()n m ij+=()()∑∈Sk n kjm ik p p ;(2)()()()nn n n ppp p pp p====-- 21....定理5.2 每个Markov 链}{,2,1,0:=n Yn都具有强的Markov 性;即,对每个停时τ,给定直到时刻τ的过去,之后过程Y }{,1,0:==++n Y n t t在}{∞τ上的分布是P Y .定理5.3 互通是一种等价关系,即满足:(1)自反性i ?i; (2)对称性i ?j,则j ?i ;(3)对称性i ?j ,j ?k,i ?k.定理5.4 若状态i,j 同属一类,则d ()i =d ()j . 定理5.5 状态i 为常返状态当且仅当)(n iin p ∑∞=0=∞;状态i 为非常返态时)(n iin p ∑∞=0=iif-11,因而此时)(.0lim=∞→n iin p引理5.1 对任意状态i,j 及1≤n +∞,有p()()()∑=-=nl l n jj l ij n ijf 1.引理5.2 若i ?j 且i 为常返态,则f .1=ii定理5.6 常返态是一个类性质.定理5.7 任意Markov 链的状态空间S ,可惟一分解为有限个或可列个互不相交的子集D,C 1,C,2之和,使得(1)每一个C n是常返状态组成的不可约闭集;(2) C n中的状态同类,或者全是正常返态,或者全是零常返态。
它们有相同的周期且f.,,1n iiC j i ∈=(3) D 由全体非常返态组成.自C n中状态出发不能到D 达中状态.定理5.8 周期为d 的不可约Markov 链,其状态空间S 可惟一地分解为d 个互不相交的子集之和,即 S=10-=d r S r , S,φ=?s rSr ≠s,且使得自S r中任意状态出发,经1步转移必进入中(其中S=d).定理5.9 若状态i 是周期为d 的常返状态,则∞→n limp (),jndjjdμ=当∞=jμ时,=jdμ.推论5.1 设i 为常返状态,则i 为零常返状态?().0lim =∞→n iin p定理5.10 若j 为非常返状态或零常返状态,则对S i ∈?,().0lim =∞→n ii推论5.2 有限状态Markov 链,不可能全为非常返状态,也不可能有零常返状态,从而不可约的有限Markov 链是正常返的. 推论5.3 若Markov 链有一个零常返状态,则必有无限个零常返状态.定理5.11 若j 为正常返状态且周期为d ,则对i ?及0≤r ≤d-1,有()().lim jii r nd ijn dr f p μ=+∞→推论5.4 设不可约的、正常返的、周期为d 的Markov 链,其状态空间为S,则对任何状态i →j,i,j ,S ∈有,()sj n ijn S j i d p 同属于子集与若其他,,0lim ?=∞→μ引理5.3 设有非负数列{}na 的d 个子列{},1,2,1,0,-=+d s askd 如果对每一个s,存在极限∞→+=n s s kd b a ,lim.1111lims d s k nk n b da n∑∑-==∞→=定理5.12 对于任意状态i,j ,S ∈有()=∑=∞→.,,01lim1为正常返状态状态,为非常返状态或零常返j f j p njijk ijnk n μ推论5.5 如果{}nX 是不可约的、常返的,Markov 链(即每个状态都是常返的),则任意状态i,j ∈S,有().11jk ijnk n p nμ=∑=∞→定理5.13 对于不可约非周期的Markov 链:(1) 若它是遍历的,则()()S j p n ijn j∈=∞→0lim π是不变分布且是惟一的不变分布;(2) 若状态都是顺过的或全为零常返的,则不变分布不存在. 定义部分定义5.1(Markov 链)随机过程}{,2,1,0,=n X n称为Markov 链,若它只取有限或可列个值E ,0E,1(我们已{} ,2,1,0来标记E ,0E,,1它们是过程的状态,{} ,2,1,0或者其子集为S ,成为过程的状态空间).对任意的n ≥0及状态i,j,i,,,,110-n i i有P }{nnn n n i Xi Xi X i Xj X=====--+,.,|11,11001=P {}iXj Xnn ==+|1.定义5.2 (转移概率)称上式中的条件概率=P {}iXj Xnn ==+|1为Markov 链}{,2,1,0,=n Xn的一步转移概率,简称条件概率.定义 5.3 (时齐Markov 链)当Markov 链的转移概率P {}iXj Xnn ==+|1只与状态i,j 有关,而与n 无关时,称Markov链是时齐的,并记p =ijP {}iXj Xnn ==+|1(n 0≥);否则,就称之为非时齐的.定义5.4 (随机矩阵)若一个矩阵具有(1) p;,,0S j i ij∈≥(2)∑∈∈?=Sj ij S i p .,1性质,则称此矩阵为随机矩阵. 定义 5.5 (n 步转移概率)称条件概率p =ijP {}iXj Xnn ==+|1,i,j 1,0,≥≥∈n mS为Markov 链的n 步转移概率,相应的称P ()()()n ij n p =为n 步转移概率矩阵. 定义5.6 令}{,2,1,0:=n Yn是一个定义在概率空间()P Ω,,F 上的具有可数状态空间的随机过程,()P Ω,,F 上的广义随机变量(即可以取值+∞)τ称为一个停时,如果(1)τ只取非负整数值(包含+∞);(2)对每个非负整数m ,事件()}{m ≤ωτω:完全由Y Y,0mY ,1确定.定义5.7 称状态i 可达状态j (),,S j i ∈若存在n 0≥使得()p记为i ?j.若同时有状态j ?i ,则称i 与j 互通,记为i ?j.定义5.8 若Markov 链只存在一个类,就称它是不可约的.否则称为可约的.定义5.9(周期性)若集合()}{0,1: n ijp n n ≥非空,则称它的最大公约数d=d ()i 为状态i 的周期,若d ,1 称i 是周期的;若d=1,称i 是非周期的.并特别规定上述集合为空集时,称i 的周期为无穷大.定义5.10 (常返性)对于任何状态i,j,以f ()n ij记从i 出发经n 步后首次到达j 的概率,则有f (),00=ijf ()}{.1,|1,,2,1,,0≥=-=≠==n iX n k j X j X P k n n ij令f(),1n ij n ijf ∑∞==,1=ij称状态j 为常返状态.若f,1 ij称j 为非常返状态或瞬过状态.定义5.11 对于常返态i,若,+∞ iμ则称i 为正常返态;若,+∞=iμ则称i为零常返状态.特别地,若i 为正常返且是非周期的,则称之为遍历状态.若i 是遍历状态,且f (),11=ii则称i 为吸收状态.此时显然.1=iμ定义5.12 对于Markov 链,概率分布}{Sj j∈,π称为不变的,若.ij i Si j p ππ∑∈=可见若Markov 链的初始分布P {}jp j X==0是不变分布,则X i的分布将是P }}{}{?==?====∑∑∈∈Sk i ij Si p p i X P iX j X P jX.|0011这与X 0的分布是相同的.依次递推,X,3,2,1,0,=n n将有相同的分布,这也是称{}S i p i∈,为不变分布的原因.定义5.13 称Markov 链是遍历的,如果所有状态相通且均是周期为1的正常返状态,对于遍历的Markov 链,极限()Sj p j n ijn ∈=∞→,lim π称为Markov 链的极限分布.。
概率论与随机过程第1章习题
《概率论与随机过程》第1章习题(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《概率论与随机过程》第一章习题1. 写出下列随机试验的样本空间。
(1) 记录一个小班一次数学考试的平均分数(设以百分制记分)。
(2) 同时掷三颗骰子,记录三颗骰子点数之和。
(3) 10只产品中有3只是次品,每次从其中取一只(取出后不放回),直到将3只次品都取出,记录抽取的次数。
(4) 生产产品直到得到10件正品,记录生产产品的总件数。
(5) 一个小组有A ,B ,C ,D ,E5个人,要选正副小组长各一人(一个人不能兼二个职务),观察选举的结果。
(6) 甲乙二人下棋一局,观察棋赛的结果。
(7) 一口袋中有许多红色、白色、蓝色乒乓球,在其中任意取4只,观察它们具有哪几种颜色。
(8) 对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次品就停止检查,或检查4个产品就停止检查,记录检查的结果。
(9) 有A ,B ,C 三只盒子,a ,b ,c 三只球,将三只球装入三只盒子中,使每只盒子装一只球,观察装球的情况。
(10)测量一汽车通过给定点的速度。
(11)将一尺之棰折成三段,观察各段的长度。
2. 设A ,B ,C 为三事件,用A ,B ,C 的运算关系表示下列事件。
(1) A 发生,B 与C 不发生。
(2) A 与B 都发生,而C 不发生。
(3) A ,B ,C 都发生。
(4) A ,B ,C 中至少有一个发生。
(5) A ,B ,C 都不发生。
(6) A ,B ,C 中至多于一个发生。
(7) A ,B ,C 中至多于二个发生。
(8) A ,B ,C 中至少有二个发生。
3. 设{}10,2,1, =S ,{}4,3,2=A ,{}5,4,3=B ,{}7,6,5=C ,具体写出下列各等式 (1)B A 。
(2)B A ⋃。
(3)B A 。
电子科技大学研究生随机过程思考题
电子科技大学研究生随机过程思考题随机过程思考题总结一、第零章(附录):1.如何准确理解“维”的含义?2.如何理解“定义在同一概率空间”?3.定义连续性随机变量的条件分布会遇到什么问题?二、第一章:1.随机过程可以描述哪些工程技术中的随机现象,试举例?来电次数、误码率是泊松过程,机器维修次数等。
天气预报。
2.为什么可以用有限维分布函数族描述随机过程的统计特性?柯尔莫哥洛夫定理可以证明,在一定条件下,随机过程和n维分布函数族是一一对应的,因此可以用有限维分布函数族描述随机过程的统计特性。
3.为什么说随机过程的均值函数和自相关函数在研究过程的概率与统计特性尤其重要?均值函数表征了随机过程在各时间点上的平均特征。
方差函数描述了随机过程在各时点处的波动程度。
刻画两个不同时点随机过程状态之间的线性关联程度,转化为自相关函数的收敛问题。
关于随机过程的均方极限的存在性,均方连续性,可积性和可导性都可转化为自相关函数的性质讨论问题。
4.白噪声过程是否一定是独立过程?不一定。
标准高斯白噪声与[0,1]均匀分布的乘积得到的白噪声过程不独立不相关。
5.独立过程是否是独立增量过程?反之?独立过程是独立增量过程,反之不一定。
三、第二章:1.能否保证Y= CX 服从非退化正态分布?C的行列式不等于0,即C可逆。
2.随机振幅电信号是否是正态过程?可否写出任意n维概率密度?是,知道他的均值函数和协方差函数就可以写出他的任意n维概率密度。
={X(t), t∈T}是正态随机过程?利用正交矩阵变换验3.怎样验证随机过程XT证并写出算法依据?还有其他方法吗?特征函数四、第三章:1.在二阶矩随机变量空间除定义均方极限外,还可以定义其他极限吗?距离定义2.均方极限与普通函数极限有什么相似之处?都用了范数来衡量随机变量或者函数之间的距离,这个距离函数是非随机的普通函数,故二阶矩过程的均方极限实质上是普通函数的极限问题。
3.若,是否有?有施瓦兹不等式及三角不等式可知成立。
