新人教版八年级数学上册“角边角”、“角角边”精选练习2
人教版八年级数学上册角边角、“角角边”1同步练习题

人教版八年级数学试题第3课时 “角边角”、“角角边”一、选择题1. 如图,玻璃三角板摔成三块,现在到玻璃店在配一块同样大小的三角板,最省事的方法( )A. 带①去B. 带②去C. 带③去D.带①②③去 2. 如图,已知∠1=∠2,则不一定能使△A BD ≌△ACD 的条件是( )A. AB=ACB. BD=CDC. ∠B=∠CD.∠BDA=∠CDA3. 如图,给出下列四组条件:①AB DE BC EF AC DF ===,,;②AB DE B E BC EF =∠=∠=,,; ③B E BC EF C F ∠=∠=∠=∠,,;④AB DE AC DF B E ==∠=∠,,. 其中,能使ABC DEF △≌△的条件共有( )A .1组B .2组C .3组D .4组 4.如图,90EF ∠=∠=,B C ∠=∠,AE AF =,结论:①EM FN =; ②CD DN =; ③FAN EAM ∠=∠; ④ACN ABM △≌△. 其中正确的有( )A .1个B .2个C .3个D .4个AEFBCDMN第1题图第2题图第3题图5. 如图,在下列条件中,不能证明△ABD ≌△ACD 的是( )A.BD =DC ,A B =ACB.∠ADB =∠ADC ,BD =DCC.∠B =∠C ,∠BAD =∠CADD.∠B =∠C ,BD =DC6.如图,已知ABC △中,45ABC ∠=, F 是高AD 和BE 的 交点,4CD =,则线段DF 的长度为( ).A .22B . 4C .32D .427. 如图,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边 三角形,则下列结论不一定成立的是( ) A. △ACE ≌△BCD B. △BGC ≌△AFCC. △DCG ≌△ECFD. △ADB ≌△CEA8. 如图,在△ABC 中,AB =AC ,∠ABC .∠ACB 的平分线BD ,CE 相交于O 点,且 BD 交AC 于点D ,CE 交AB 于点E .某同学分析图形后得出以下结论:①△BCD ≌△CBE ;②△BAD ≌△BCD ;③△BDA ≌△CEA ;④△BOE ≌△COD ; ⑤△ACE ≌△BCE ;上述结论一定正确的是( )A .①②③B .②③④C .①③⑤D .①③④第4题图第6题图第5题图第7题图第8题图二、填空题9. 如图,已知△ABC 的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是10.如图,△ABC 中,BD=EC ,∠ADB=∠AEC ,∠B=∠C ,则∠CAE= .11. 如图,点B 、E 、F 、C 在同一直线上,已知∠A =∠D ,∠B =∠C ,要使△ABF ≌△DCE ,(写出一个即可).12.如图,AD=BC ,AC=BD ,则图中全等三角形有 对.13. 如图,已知AB ∥CF, E 为DF 的中点.若AB=9 cm,CF=5 cm,则BD 的长度为 cm.14. 如图,∠A =∠D,OA=OD, ∠DOC=50°,则∠DBC= 度.15.如图,BAC ABD ∠=∠,请你添加一个条件: ,使OC OD =(只DOCBA第15题图第14题图第13题图 E D C B A第9题图第10题图第11题图第12题图CODBAFEDC B AODC B A添一个即可).16. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B ,C 作过点A 的直线的垂线BD ,C E ,垂足分别为点D,E.若BD=2,CE=3,则AE= ,AD= .17. 如图,有一块边长为4的正方形塑料摸板ABCD ,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点F ,与CB 延长线交于点E .则四边形AECF 的面积是 .18.如图,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB =30°.有以下四个结论:①AF 丄BC ;②△ADG ≌△ACF ;③O 为BC 的中点;④AG :DE =错误!未找到引用源。
人教版八年级数学上册角边角、“角角边”1同步练习题

第3课时“角边角”、“角角边”一、选择题1. 如图,玻璃三角板摔成三块,现在到玻璃店在配一块同样大小的三角板,最省事的方法()A. 带①去B. 带②去C. 带③去D.带①②③去2.如图,已知∠1=∠2,则不一定能使△A BD≌△ACD的条件是()A. AB=ACB. BD=CDC. ∠B=∠CD.∠BDA=∠CDA3. 如图,给出下列四组条件:①AB DE BC EF AC DF===,,;②AB DE B E BC EF=∠=∠=,,;③B E BC EF C F∠=∠=∠=∠,,;④AB DE AC DF B E==∠=∠,,.其中,能使ABC DEF△≌△的条件共有()A.1组 B.2组 C.3组 D.4组4.如图,90E F∠=∠=,B C∠=∠,AE AF=,结论:①EM FN=;②CD DN=;③FAN EAM∠=∠;④ACN ABM△≌△.其中正确的有()A.1个B.2个C.3个D.4个AEFBCDMN第1题图第2题图第3题图第4题图5. 如图,在下列条件中,不能证明△ABD ≌△ACD 的是( )A.BD =DC ,A B =ACB.∠ADB =∠ADC ,BD =DCC.∠B =∠C ,∠BAD =∠CADD.∠B =∠C ,BD =DC6.如图,已知ABC △中,45ABC ∠=, F 是高AD 和BE 的 交点,4CD =,则线段DF 的长度为( ).A .22B . 4C .32D .427. 如图,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边 三角形,则下列结论不一定成立的是( ) A. △ACE ≌△BCD B. △BGC ≌△AFCC. △DCG ≌△ECFD. △ADB ≌△CEA8. 如图,在△ABC 中,AB =AC ,∠ABC .∠ACB 的平分线BD ,CE 相交于O 点,且 BD 交AC 于点D ,CE 交AB 于点E .某同学分析图形后得出以下结论:①△BCD ≌△CBE ;②△BAD ≌△BCD ;③△BDA ≌△CEA ;④△BOE ≌△COD ; ⑤△ACE ≌△BCE ;上述结论一定正确的是( )A .①②③B .②③④C .①③⑤D .①③④第6题图第5题图第7题图第8题图二、填空题9. 如图,已知△ABC 的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是10.如图,△ABC 中,BD=EC ,∠ADB=∠AEC ,∠B=∠C ,则∠CAE= .11. 如图,点B 、E 、F 、C 在同一直线上,已知∠A =∠D ,∠B =∠C ,要使△ABF ≌△DCE ,(写出一个即可).12.如图,AD=BC ,AC=BD ,则图中全等三角形有 对.13. 如图,已知AB ∥CF, E 为DF 的中点.若AB=9 cm,CF=5 cm,则BD 的长度为 cm.14. 如图,∠A =∠D,OA=OD, ∠DOC=50°,则∠DBC= 度.15.如图,BAC ABD ∠=∠,请你添加一个条件: ,使OC OD =(只添一个即可).DOCBA第15题图第14题图第13题图 E D C B A第9题图第10题图第11题图第12题图CODBAFEDC B AODC B A16. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B ,C 作过点A 的直线的垂线BD ,C E ,垂足分别为点D,E.若BD=2,CE=3,则AE= ,AD= .17. 如图,有一块边长为4的正方形塑料摸板ABCD ,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点F ,与CB 延长线交于点E .则四边形AECF 的面积是 .18.如图,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB =30°.有以下四个结论:①AF 丄BC ;②△ADG ≌△ACF ;③O 为BC 的中点;④AG :DE =错误!未找到引用源。
数学人教版八年级上册全等三角形边角边判定的基本练习
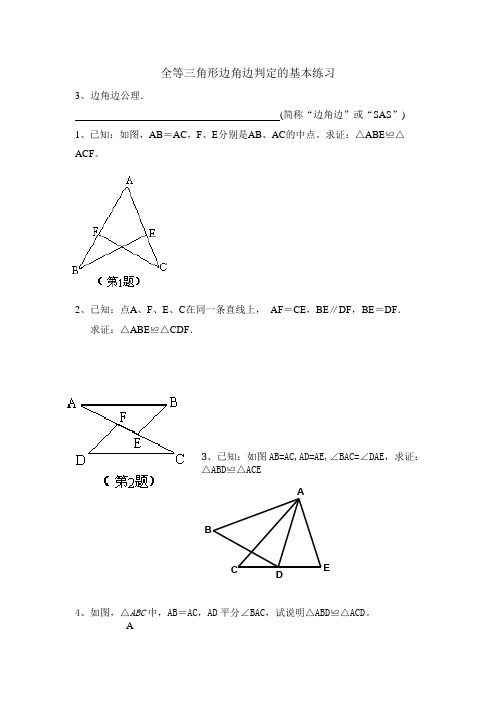
全等三角形边角边判定的基本练习3、边角边公理.(简称“边角边”或“SAS”)1、已知:如图,AB=AC,F、E分别是AB、AC的中点。
求证:△ABE≌△ACF。
2、已知:点A、F、E、C在同一条直线上,AF=CE,BE∥DF,BE=DF.求证:△ABE≌△CDF.3、已知:如图AB=AC,AD=AE,∠BAC=∠DAE,求证:△ABD≌△ACEABC D E4、如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD。
AB D C5、已知:如图,AD ∥BC ,CB AD =。
求证:CBA ADC ∆≅∆。
6、已知:如图,AD ∥BC ,CB AD =,CF AE =。
求证:CEB AFD ∆≅∆。
7、已知:如图,点A 、B 、C 、D 在同一条直线上,DB AC =,DF AE =,AD EA ⊥,AD FD ⊥,垂足分别是A 、D 。
求证:FDC EAB ∆≅∆8、已知:如图,AC AB =,AE AD =,21∠=∠。
求证:ACE ABD ∆≅∆。
9、如图,在ABC ∆中,D 是AB 上一点,DF 交AC 于点E ,FE DE =,CE AE =,AB 与CF 有什么位置关系?说明你判断的理由。
10、已知:如图,DBAAC=。
求证∠C=∠D∠,BDCAB∠=11、已知:如图,AC和BD相交于点O,OCOB=。
OA=,OD求证:DC∥AB。
12、已知:如图,AC和BD相交于点O,DC=∠。
B∠AC=。
求证:CAB=,DB13、已知:如图,D、E分别是△ABC的边AB,AC的中点,点F在DE的延长线上,且EF=DE.求证:(1)BD=FC (2)AB∥CF14、已知: 如图 , AB=AC , EB=EC , AE 的延长线交BC 于D .求证:BD=CD .15、已知:如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:BD=CE16、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD17、如图,已知,AB ∥DE ,AB=DE ,AF=DC 。
最新人教版初中八年级上册数学《角边角、角角边》精品教案

A
几何语言:
在△ABC和△A′ B′ C′中, ∠A=∠A′ (已知),
B
C
A′
AB=A′ B′ (已知),
∠B=∠B′ (已知),
B′
C′
∴ △ABC≌△ A′ B′ C′ (ASA).
典例精析
例1 已知:∠ABC=∠DCB,∠ACB= ∠DBC, 求证:△ABC≌△DCB.
证明:在△ABC和△DCB中,
B
D
2.如图∠ACB=∠DFE,BC=EF,那么应补充一个条
件
,才能使△ABC≌△DEF (写出一个即可).
B A
AB=DE可以吗? ×
C F
D E
AB∥DE
∠B=∠E (ASA) 或∠A=∠D (AAS) 或 AC=DF (SAS)
3.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
第十二章 全等三角形
12.2三角形全等的判定
第3课时 “角边角”、“角角边”
导入新课
讲授新课
当堂练习
课堂小结
学习目标
情境引入
1.探索并正确理解三角形全等的判定方法“ASA”和 “AAS”. 2.会用三角形全等的判定方法“ASA”和“AAS”证明两个 三角形全等.
导入新课
情境引入
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可 以只带其中的一块碎片到商店去,就能配一块与原来一样的 三角形模具吗? 如果可以,带哪块去合适? 你能说明其中理由吗?
A 证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
12
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
八年级数学上册-人教版八年级上册数学 12.2 第3课时 “角边角”、“角角边”精选练习1

第3课时 “角边角”、“角角边”一、选择题1. 如图,玻璃三角板摔成三块,现在到玻璃店在配一块同样大小的三角板,最省事的方法( )A. 带①去B. 带②去C. 带③去D.带①②③去 2. 如图,已知∠1=∠2,则不一定能使△A BD ≌△ACD 的条件是( )A. AB=ACB. BD=CDC. ∠B=∠CD.∠BDA=∠CDA3.如图,给出下列四组条件:①AB DE BC EF AC DF ===,,;②AB DE B E BC EF =∠=∠=,,; ③B E BC EF C F ∠=∠=∠=∠,,;④AB DE AC DF B E ==∠=∠,,. 其中,能使ABC DEF △≌△的条件共有( )A .1组B .2组C .3组D .4组4.如图,90E F ∠=∠=,B C ∠=∠,AE AF =,结论:①EM FN =; ②CD DN =; ③FAN EAM ∠=∠; ④ACN ABM △≌△. 其中正确的有( )A .1个B .2个C .3个D .4个AEFBCDMN第1题图第2题图第3题图第4题图5. 如图,在下列条件中,不能证明△ABD ≌△ACD 的是( )A.BD =DC ,A B =ACB.∠ADB =∠ADC ,BD =DCC.∠B =∠C ,∠BAD =∠CADD.∠B =∠C ,BD =DC6.如图,已知ABC △中,45ABC ∠=, F 是高AD 和BE 的 交点,4CD =,则线段DF 的长度为( ).A.B . 4 C.D.7. 如图,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边 三角形,则下列结论不一定成立的是( ) A. △ACE ≌△BCD B. △BGC ≌△AFCC. △DCG ≌△ECFD. △ADB ≌△CEA8. 如图,在△ABC 中,AB =AC ,∠ABC .∠ACB 的平分线BD ,CE 相交于O 点,且 BD 交AC 于点D ,CE 交AB 于点E .某同学分析图形后得出以下结论:①△BCD ≌△CBE ;②△BAD ≌△BCD ;③△BDA ≌△CEA ;④△BOE ≌△COD ; ⑤△ACE ≌△BCE ;上述结论一定正确的是( )A .①②③B .②③④C .①③⑤D .①③④第6题图第5题图第7题图第8题图二、填空题9. 如图,已知△ABC 的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是10.如图,△ABC 中,BD=EC,∠ADB=∠AEC ,∠B=∠C ,则∠CAE= .11. 如图,点B 、E 、F 、C 在同一直线上,已知∠A =∠D ,∠B =∠C ,要使△ABF ≌△DCE ,(写出一个即可).12.如图,AD=BC ,AC=BD ,则图中全等三角形有 对.13. 如图,已知AB ∥CF, E 为DF 的中点.若AB=9 cm,CF=5 cm,则BD 的长度为 cm.14. 如图,∠A =∠D,OA=OD, ∠DOC=50°,则∠DBC= 度.15.如图,BAC ABD ∠=∠,请你添加一个条件: ,使O C O D =(只添一个即可).DOCBA第15题图第9题图第11题图第12题图16. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B ,C 作过点A 的直线的垂线BD ,C E ,垂足分别为点D,E.若BD=2,CE=3,则AE= ,AD= .17. 如图,有一块边长为4的正方形塑料摸板ABCD ,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点F ,与CB 延长线交于点E .则四边形AECF 的面积是 .18.如图,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB =30°.有以下四个结论:①AF 丄BC ;②△ADG ≌△ACF ;③O 为BC 的中点;④AG :DE =错误!未找到引用源。
新人教版八年级上册数学12.2 第3课时 “角边角”“角角边”2教案

第3课时“角边角”“角角边”教学目标1.三角形全等的条件:角边角、角角边.2.三角形全等条件小结.3.掌握三角形全等的“角边角”“角角边”条件.4.能运用全等三角形的条件,解决简单的推理证明问题.教学重点已知两角一边的三角形全等探究.教学难点灵活运用三角形全等条件证明.教学过程Ⅰ.提出问题,创设情境1.复习:(1)三角形中已知三个元素,包括哪几种情况?三个角、三个边、两边一角、两角一边.(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?三种:①定义;②SSS;③SAS.2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?Ⅱ.导入新课问题1:三角形中已知两角一边有几种可能?1.两角和它们的夹边.2.两角和其中一角的对边.问题2:三角形的两个内角分别是60°和80°,它们的夹边为4cm,•你能画一个三角形同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是不是全等,你能得出什么规律?将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.提炼规律:两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).问题3:我们刚才做的三角形是一个特殊三角形,随意画一个三角形ABC,•能不能作一个△A′B′C′,使∠A=∠A′、∠B=∠B′、AB=A′B′呢?①先用量角器量出∠A与∠B的度数,再用直尺量出AB的边长.②画线段A′B′,使A′B′=AB .③分别以A′、B′为顶点,A′B′为一边作∠DA′B′、∠EB′A ,使∠D′AB=∠CAB ,∠EB′A′=∠CBA .④射线A′D 与B′E 交于一点,记为C′ 即可得到△A′B′C′.将△A′B′C′与△ABC 重叠,发现两三角形全等.C 'A 'B 'DCABE两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”). 思考:在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢? 探究问题4:如图,在△ABC 和△DEF 中,∠A=∠D ,∠B=∠E ,BC=EF ,△ABC 与△DEF 全等吗?能利用角边角条件证明你的结论吗?D ABFE证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180°∠A=∠D ,∠B=∠E ∴∠A+∠B=∠D+∠E ∴∠C=∠F在△ABC 和△DEF 中B EBC EF C F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF (ASA ).两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).[例]如下图,D 在AB 上,E 在AC 上,AB=AC ,∠B=∠C .求证:AD=AE .[分析]AD 和AE 分别在△ADC 和△AEB 中,所以要证AD=AE ,只需证明△ADC ≌△AEB 即可. 证明:在△ADC 和△AEB 中A A AC ABC B ∠=∠⎧⎪=⎨⎪∠=∠⎩所以△ADC ≌△AEB (ASA ) 所以AD=AE . Ⅲ.随堂练习 (一)课本练习. (二)补充练习图中的两个三角形全等吗?请说明理由.50︒50︒45︒45︒DCAB (1)29︒29︒DC A B(2)E答案:图(1)中由“ASA”可证得△ACD ≌△ACB .图(2)由“AAS”可证得△ACE ≌△BDC . Ⅳ.课时小结至此,我们有五种判定三角形全等的方法: 1.全等三角形的定义2.判定定理:边边边(SSS ) 边角边(SAS ) 角边角(ASA ) 角角边(AAS ) 推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径. Ⅴ.作业1.学练优课后练习. 板书设计D CABE。
人教版八年级数学上册三角形边角边判定三角形全等专项小练习(附答案)
《12.2 三角形全等的判定课时2》基础练易错诊断(打“√”或“×”)1.两边和任一角分别相等的两个三角形全等.()2.有两边及其一边的对角分别相等的两个三角形全等.()3.在△ABC和△DEF中,若AB=DE,∠B=∠E,BC=EF,则△ABC≌△DEF.()对点达标知识点一用“SAS”证明三角形全等1.(2021·昆明质检)如图,AB平分∠DAC,要用SAS条件确定△ABC≌△ABD,还需要有条件()A.DB=CBB.AB=ABC.AD=ACD.∠D=∠C2.根据如图所给信息,可得x的长是()A.16B.18C.20D.16或183.(2021·宿州质检)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是()A.∠A=∠CB.∠D=∠BC.AD∥BCD.DF∥BE4.(2020·柳州中考)如图,已知OC平分∠MON,点A,B分别在射线OM,ON上,且OA=OB.求证:△AOC≌△BOC.5.(2020·兰州中考)如图,在△ABC中,AB=AC,点D,E分别是AC和AB的中点求证:BD=CE.知识点二“SAS”的实际应用6.(2021·武汉期中)如图,将两根钢条AA',BB的中点O连在一起,使AA',BB'可以绕着点O自由旋转,就做成了一个测量工件,则A'B′的长等于内槽宽AB,那么判定△OAB≌△OA'B′的理由是.7.如图,一块三角形玻璃碎成了Ⅰ,Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第块玻璃碎片.8.(2021·济南期中)如图,AD,BC表示两根长度相同的木条,若O是AD,BC的中点,经测量AB=9cm,则容器的内径CD为cm.参考答案易错诊断1.×2.×3.√对点达标1.C2.C3.B4.答案:见解析解析:∵OC平分∠MON,∴∠AOC=∠BOC,在△AOC和△BOC中,OA OBAOC BOC OC OC=⎧⎪∠=∠⎨⎪=⎩,,,∴△AOC≌△BOC(SAS).5. 答案:见解析解析:∵AB=AC,D,E分别为AC,AB的中点,∴AD=AE,在△ABD和△ACE中,AB ACA A AD AE=⎧⎪∠=∠⎨⎪=⎩,,,∴△ABD≌△ACE(SAS),∴BD=CE.6.SAS7.I8.9。
人教版八年级数学上册第12章:“角边角”、“角角边”
D
∴ △ABC≌△ADC(AAS),
∴AB=AD.
C
随堂即练
【学以致用】如图,小明不慎将一块三角形模具打 碎为三块,他是否可以只带其中的一块碎片到商店 去,就能配一块与原来一样的三角形模具? 如果 可以,带哪块去合适?你能说明其中理由吗?
答:带1去,因为有两角且 夹边相等的两个三角形全 等.
1 23
因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B',∠ABD=∠A'B'D',AB=AB,
所以△ABD≌△A'B'D'.所以AD=A'D'.
发现:全等三角形对应边上的高也相等.
内容
课堂总结
边角边 角 角 边 应用
为证明线段和角相等 提供了新的证法
A
▼几何语言:
在△ABC和△A′ B′ C′中, ∠A=∠A′ ,
B
C
A′
AB=A′ B′ ,
∠B=∠B′ ,
B′
C′
∴ △ABC≌△ A′ B′ C′ (ASA).
新课讲解
例1 已知:∠ABC=∠DCB,∠ACB= ∠DBC, 求证:△ABC≌△DCB.
证明:在△ABC和△DCB中,
A
D
∠ABC=∠DCB,
能力提升
【拓展】已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′
分别是△ABC 和△A′B′C′的高.试说明AD= A′D′ ,并
用一句话说出你的发现.
人教版初二数学上册边角边练习题
边角边练习题 1、 已知:如图,AC=AD,/ CAB二 / DAB ,
求证:△ ACB^A ADB
2、 已知:AD// BC AD=CB 求证:△ ADC CBA
3、 已知:AD // BC, AD=CB , AE=CF 求证:△ AFD CEB
5、已知:AC=DB , AE=DF , EA 丄 AD , FD 丄
AD ,
求证:△ EAB FDC
4、已知:EA=EC, ED=EB ,
求证:△ AED CEB
A B 6、已知:点C是AB的中点,CD// BE,且CD二BE 7、已知:AB二AC , AD=AE,/ 仁/ 2
8v 已知:如图、AB = AC ・ AD = AE . Zl = Z2 □求iiF: 队如图*在必眈中・DELAfi上一乩 DF交AC于点F • 初与CF有什么位置关系?说明你判斷的理由.
求证:AD=CE 求证:/ B= / C 参考答案: 1 证明: 在厶ACB^n^ ADB中
AC=AD ( 已知
)
I / CAB2 DAB (已知
)
%
AB=AB ( 公共边
)
二△ ACB^A ADB (SAS)
2、证明:T AD // BC (已知
)
•••/ DAC= / BCA (两直线平行,内错角相等
)
在厶ADC和厶CBA中 rAD=CB (已知
)
J / DAC= / BCA (已证
)
AC=CA (公共边
)
•••△ ADC CBA (SAS) 3、证明:T AE=CF (已知
)
••• AE+EF二CF+EF (等式的性质
)
即 AF=CE T AD // BC (已知) •— A= / C (两直线平行,内错角相等
)
在厶AFD和厶CEB中 ^AD=CB (已知) V / A= / C (已证
)
•••△ AFD CEB (SAS) 4、证明:在厶AED和厶CEB中
厂EA=EC (已知) < / AED= / CEB (对顶角相等) -ED=EB (已知
八年级数学人教版(上册)12.2第3课时“角边角”、“角角边”
全等三角形对应边上 的高也相等.
∴△ABD≌△A'B'D'.∴AD=A'D'.
侵权必究
课堂小结
✓ 归纳总结 ✓ 构建脉络
侵权必究
课堂小结
内容
有两角及夹边对应相等的两个三角 形全等(简写成 “ASA”)
边角边 应 用 角角边
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角” 中两角与边的区别
∴BD=AE,AD=CE, ∴DE=DA+AE=BD+CE.
侵权必究
方法总结 判定两三角形全等,先根据已知条件或求证的结论
确定三角形,然后再根据三角形全等的判定方法看缺什 么条件,再去证什么条件,简言之:即综合利用分析法 和综合法寻找证明途径.
利用全等三角形可以解决线段之间的关系,比如线 段的相等关系、和差关系等,解决问题的关键是运用全 等三角形的判定与性质进行线段之间的转化.
∴DF =BE.
侵权必究
当堂练习
变式 若将条件“∠B =∠D”变为“DF∥BE”,那么
原结论还成立吗?若成立,请证明;若不成立,请说明
理由. 成立. 证明:∵AD∥CB∠A =∠C.
E
∵AE =CF , ∴AF =CE.
∵DF∥BE,
∴∠DFE =∠BEF. ∴∠DFA =∠BEC. 在△ADF 和△CBE 中,
B
C
∠A =∠C, AF =CE, ∠DFA =∠BEC, ∴△ADF ≌△CBE(ASA). ∴DF =BE.
侵权必究
当堂练习
6、如图,四边形ABCD中,E点在AD上,其中∠BAE =∠BCE=∠ACD=90°,且BC=CE. 求证:△ABC 与△DEC全等.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
aac丙7250 乙50甲a50
72
50
58
c
b
a
C
B
A
新人教版八年级数学上册“角边角”、“角角边”精选练习2
一、选择题
1.若按给定的三个条件画一个三角形,图形惟一,则所给条件不可能是( )
A.两边一夹角 B.两角一夹边 C.三边 D.三角
2. 在△ABC和△DEF中,已知CD,BE,要判定这两个三角形全等,还
需要条件( )
A.ABED B.ABFD C.ACFD D.AF
3.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A、甲乙 B、甲丙 C、乙丙 D、乙
4.对于下列各组条件,不能判定ABCABC△≌△的一组是( )
A.AA,BB,ABAB
B.AA,ABAB,ACAC
C.AA,ABAB,BCBC
D.ABAB,ACAC,BCBC
5.在ABC△和ABC111△中,已知1AA,11ABAB,在下列说法中,错误的是( )
A.如果增加条件11ACAC,那么111ABCABC△≌△(SAS)
B.如果增加条件11BCBC,那么111ABCABC△≌△(SAS)
C.如果增加条件1BB,那么111ABCABC△≌△(ASA)
D.如果增加条件1CC,那么111ABCABC△≌△(AAS)
二、填空题
6.如图,点B、E、F、C在同一直线上. 已知∠A =∠D,∠B =∠C,要使△ABF≌△DCE,
需要补充的一个条件是 (写出一个即可).
7.如图,直线 L过正方形 ABCD 的顶点 B , 点A、C 到直线 L 的距离分别是AE=1 ,CF=2 ,
则EF长
A B E F C D
三、解答题
8.如图,点DE,分别在ABAC,上,且ADAE,BDCCEB.
求证:BDCE.
9. 如图,已知AC平分∠BAD,∠1=∠2,求证:AB=AD
A
D
E
B
C
参考答案
1.D 2.C 3.C 4.C 5.B
6.AB = DC(填AF=DE或BF=CE或BE=CF也对) 7.3
8.180ADCBDC,180BECAEB,
又BDCCEBADCAEB
()()()AAADCAEBADAEADCAEB
公共角已知已证在△和△中,
(ASA)ADCAEBABAC△≌△
ABADACAE,即BDCE
.
9. 证明:∵AC平分∠BAD ∴∠BAC=∠DAC.∵∠1=∠2∴∠ABC=∠ADC.
在△ABC和△ADC中,,BACDACABCADCACAC
∴△ABC≌△ADC(AAS).∴AB=AD.
