2016-2017年浙江省杭州实验外国语学校高一上学期期中数学试卷带答案
浙江杭州市实验外国语学校2016-2017学年高一英语上学期期中试题

杭州市实验外国语学校高中部2016学年第一学期高一年级英语学科期中考试试题卷满分100分,考试用时90分钟。
第一部分:听力(共两节,满分15分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题纸上。
第一节(共5个小题,每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. How does the woman feel now?A. Angry.B. Surprised.C. sad.2. What is the woman going to do in about 20 minutes?A. Type up some reports.B. Eat together with the man.C. Read a paper in the reading room.3. What are the speakers talking about?A. A repairman.B. The stairs.C. An elevator.4. What are the speakers doing?A. Watching a concert.B. Enjoying a program.C. Waiting for a bus.5. What does Michael do every Friday evening?A. He does a part time job.B. He looks after his children.C. He attends a school activity.第二节(共10个小题,每小题1分,满分10分)听下面3段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
浙江省杭州市实验外国语学校高一英语上学期期中试题

杭州市实验外国语学校高中部2016学年第一学期高一年级英语学科期中考试试题卷满分100分,考试用时90分钟。
第一部分:听力(共两节,满分15分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题纸上。
第一节(共5个小题,每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. How does the woman feel now?A. Angry.B. Surprised.C. sad.2. What is the woman going to do in about 20 minutes?A. Type up some reports.B. Eat together with the man.C. Read a paper in the reading room.3. What are the speakers talking about?A. A repairman.B. The stairs.C. An elevator.4. What are the speakers doing?A. Watching a concert.B. Enjoying a program.C. Waiting for a bus.5. What does Michael do every Friday evening?A. He does a part time job.B. He looks after his children.C. He attends a school activity.第二节(共10个小题,每小题1分,满分10分)听下面3段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
2016-2017年浙江省杭州高中高一上学期数学期中试卷带答案
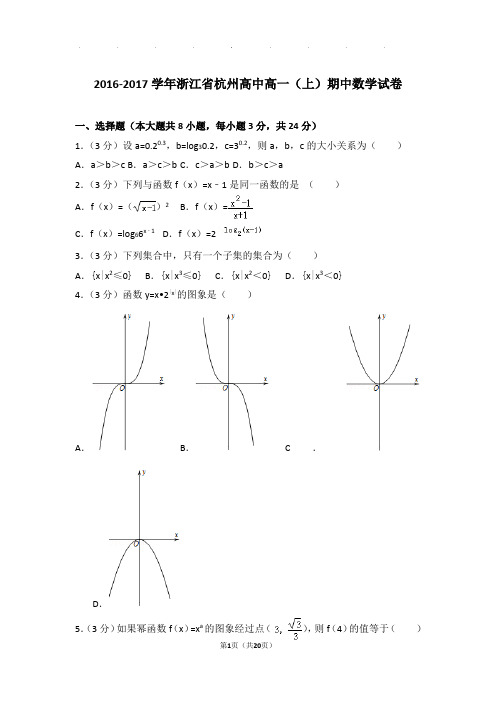
2016-2017学年浙江省杭州高中高一(上)期中数学试卷一、选择题(本大题共8小题,每小题3分,共24分)1.(3分)设a=0.20.3,b=log30.2,c=30.2,则a,b,c的大小关系为()A.a>b>c B.a>c>b C.c>a>b D.b>c>a2.(3分)下列与函数f(x)=x﹣1是同一函数的是()A.f(x)=()2B.f(x)=C.f(x)=log66x﹣1D.f(x)=23.(3分)下列集合中,只有一个子集的集合为()A.{x|x2≤0}B.{x|x3≤0} C.{x|x2<0} D.{x|x3<0}4.(3分)函数y=x•2|x|的图象是()A.B.C.D.5.(3分)如果幂函数f(x)=x a的图象经过点(),则f(4)的值等于()A.B.2 C.16 D.6.(3分)函数f(x)=的定义域是()A.(﹣,0]B.(﹣,0)∪(0,+∞)C.(﹣,+∞)D.(0,+∞)7.(3分)满足下列条件的函数f(x)中,f(x)为偶函数的是()A.f(e x)=|x|B.f(e x)=e2x C.f(lnx)=lnx2D.f(lnx)=x+8.(3分)对于具有相同定义域D的函数f(x)和g(x),若存在函数h(x)=kx+b (k,b为常数),对任给的正数m,存在相应的x0∈D,使得当x∈D且x>x0时,总有,则称l:y=kx+b为曲线y=f(x)和y=g(x)的“分渐近线”.给出定义域为D={x|x>1}的四组函数如下:①f(x)=x2,g(x)=;②f(x)=10﹣x+2,g(x)=;③f(x)=,g(x)=;④f(x)=,g(x)=2(x﹣1﹣e﹣x);则存在“分渐近线”的函数组号是()A.①④B.②③C.②④D.③④二、填空题(本大题共7小题,每小题4分,共28分)9.(4分)若a∈{2,1,a2},则a=.10.(4分)计算:2lg5+lg4+﹣=.11.(4分)已知函数f(x)是奇函数,当x>0时,f(x)=x2﹣+1,则当x<0时,f(x)=.12.(4分)若f(x)=(t2﹣6)•t x﹣1是指数函数,则实数t的值为.13.(4分)函数f(x)=log a x在[2,+∞)上恒有|f(x)|>1,则a取值范围是.14.(4分)已知函数,若∃x1,x2∈R,x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是.15.(4分)已知函数f(x)=(n﹣2m)3x+x2+2nx,方程f(x)=0的解集为A,方程f(f(x))=0的解集为B,若A=B≠∅,则m+n的取值范围为.三、简答题(本题共48分)16.(10分)已知A={x|﹣1<x≤3},B={x|m≤x<1+3m}(1)当m=1时,求A∪B;(2)若B⊆∁R A,求实数m的取值范围.17.(12分)已知函数f(x)=log 2(x2﹣mx+m)(1)若函数f(x)的最小值为1,求实数m的值;(2)若函数f(x)在区间(﹣∞,2)上是减函数,求实数m的取值范围.18.(14分)已知定义域为R的函数f(x)=是奇函数.(1)求a的值;(2)判断并证明函数f(x)的单调性;(3)若对任意的t∈[2,4],不等式f(log2t)+f(k﹣()t)<0有解,求k 的取值范围.19.(12分)已知常数a∈R,函数f(x)=x﹣a,g(x)=,(1)写出函数F(x)=f(x)+g(x)的单调区间;(不需要证明)(2)令h(x)=|f(x)|﹣g(x),求h(x)在[1,2]的最小值.2016-2017学年浙江省杭州高中高一(上)期中数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题3分,共24分)1.(3分)设a=0.20.3,b=log30.2,c=30.2,则a,b,c的大小关系为()A.a>b>c B.a>c>b C.c>a>b D.b>c>a【解答】解:a=0.20.3<0.20=1.b=log30.2<log31=0.c=30.2>30=1.∴b<a<c.故选:C.2.(3分)下列与函数f(x)=x﹣1是同一函数的是()A.f(x)=()2B.f(x)=C.f(x)=log66x﹣1D.f(x)=2【解答】解:A中函数f(x)=()2的定义域为[0,+∞)与函数f(x)=x ﹣1的定义域不同,故与f(x)=x﹣1不是同一函数;B中函数f(x)=的定义域为(﹣∞,﹣1)∪(﹣1,+∞)与函数f(x)=x﹣1的定义域不同,故与f(x)=x﹣1不是同一函数;C中函数f(x)=log66x﹣1=x﹣1的定义域为R,解析式(对应关系)也与f(x)=x ﹣1相同,故与f(x)=x﹣1是同一函数;D中函数f(x)=2的定义域为(1,+∞)与函数f(x)=x﹣1的定义域不同,故与f(x)=x﹣1不是同一函数;故选:C.3.(3分)下列集合中,只有一个子集的集合为()A.{x|x2≤0}B.{x|x3≤0} C.{x|x2<0} D.{x|x3<0}【解答】解:A、由x2≤0,得到x=0,即{0}子集有2个,错误;B、由x3≤0,得到x≤0,即{x|x≤0},子集不只有一个,错误;C、由x2<0,得到集合为∅,即子集只有一个,正确;D、由x3<0,得到x<0,即{x|x<0},子集不只有一个,错误,故选:C.4.(3分)函数y=x•2|x|的图象是()A.B.C.D.【解答】解:设y=f(x)=x•2|x|,则f(﹣x)=﹣x•2|﹣x|=﹣f(x),∴f(x)是奇函数,图象关于原点对称,又当x>0时,f(x)=x•2x>0,故选:A.5.(3分)如果幂函数f(x)=x a的图象经过点(),则f(4)的值等于()A.B.2 C.16 D.【解答】解:幂函数f(x)=x a的图象经过点(),∴3α=,解得α=﹣,∴f(x)=;∴f(4)==.故选:A.6.(3分)函数f(x)=的定义域是()A.(﹣,0]B.(﹣,0)∪(0,+∞)C.(﹣,+∞)D.(0,+∞)【解答】解:要使原函数有意义,则.即2x+1>0且2x+1≠1.解得:且x≠0.所以原函数的定义域为(﹣,0)∪(0,+∞).故选:B.7.(3分)满足下列条件的函数f(x)中,f(x)为偶函数的是()A.f(e x)=|x|B.f(e x)=e2x C.f(lnx)=lnx2D.f(lnx)=x+【解答】解:f(e x)=|x|,f(x)=|lnx|,x>0,函数不是偶函数.f(e x)=e2x,可得f(x)=x2,x>0,函数不是偶函数.f(lnx)=lnx2,f(x)=2x,函数是奇函数;f(lnx)=x+,则f(x)=e x+,函数是偶函数.故选:D.8.(3分)对于具有相同定义域D的函数f(x)和g(x),若存在函数h(x)=kx+b (k,b为常数),对任给的正数m,存在相应的x0∈D,使得当x∈D且x>x0时,总有,则称l:y=kx+b为曲线y=f(x)和y=g(x)的“分渐近线”.给出定义域为D={x|x>1}的四组函数如下:①f(x)=x2,g(x)=;②f(x)=10﹣x+2,g(x)=;③f(x)=,g(x)=;④f(x)=,g(x)=2(x﹣1﹣e﹣x);则存在“分渐近线”的函数组号是()A.①④B.②③C.②④D.③④【解答】解:f(x)和g(x)存在分渐近线的充要条件是x→∞时,f(x)﹣g(x)→0.对于①,f(x)=x2,g(x)=,当x>1时,令F(x)=f(x)﹣g(x)=,由于F′(x)=2x﹣>0,∴h(x)为增函数,不符合x→∞时,f(x)﹣g(x)→0,故①不存在;对于②,f(x)=10﹣x+2,g(x)=,f(x)﹣g(x)=10﹣x+2﹣=()x+,因为当x>1且x→∞时,f(x)﹣g(x)→0,故②存在分渐近线;对于③,f(x)=,g(x)=,f(x)﹣g(x)==x+=,当x>1且x→∞时,与均单调递减,但的递减速度比快,∴当x→∞时f(x)﹣g(x)会越来越小,不会趋近于0,故③不存在分渐近线;对于④,f(x)=,g(x)=2(x﹣1﹣e﹣x),当x→∞时,f(x)﹣g(x)=﹣2x+2+2e﹣x=+2e﹣x=→0,故④存在分渐近线.故存在分渐近线的是②④.故选:C.二、填空题(本大题共7小题,每小题4分,共28分)9.(4分)若a∈{2,1,a2},则a=2或0.【解答】解:∵a∈{2,1,a2},∴a2=a或a=1或a=2,解得a=0或a=1或a=2,验证知当a=1集合中有相同的元素不满足互异性,故a=2或0,故答案为:2或0.10.(4分)计算:2lg5+lg4+﹣=.【解答】解:2lg5+lg4+﹣=(lg25+lg4)+2﹣=4﹣=.故答案为:.11.(4分)已知函数f(x)是奇函数,当x>0时,f(x)=x2﹣+1,则当x<0时,f(x)=﹣x2﹣﹣1.【解答】解:当x<0时,﹣x>0,∵x>0时,f(x)=x2﹣+1,∴f(﹣x)=x2++1,又∵函数f(x)是奇函数,f(x)=﹣f(﹣x)=﹣x2﹣﹣1,故答案为:﹣x2﹣﹣112.(4分)若f(x)=(t2﹣6)•t x﹣1是指数函数,则实数t的值为.【解答】解:由题意,f(x)=(t2﹣6)•t x﹣1是指数函数,∴t2﹣6=1,t>0且t≠1,可得:t=或(舍去).故答案为:13.(4分)函数f(x)=log a x在[2,+∞)上恒有|f(x)|>1,则a取值范围是(,1)∪(1,2).【解答】解:当a>1时,函数f(x)=log a x在[2,+∞)上单调递增,故函数的最小值为f(2)=log a2>0,由|f(x)|>1恒成立可得log a2>1,求得1<a<2.当0<a<1时,函数f(x)=log a x在[2,+∞)上单调递减,故函数的最大值为f(2)=log a2<0,由|f(x)|>1恒成立可得﹣log a2>1,即log a2<﹣1,求得<a<1.综上可得,<a<1或1<a<2,故所求的a的范围是(,1)∪(1,2),故答案为(,1)∪(1,2).14.(4分)已知函数,若∃x1,x2∈R,x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是(﹣∞,2).【解答】解:由题意得,即在定义域内,f(x)不是单调的.分情况讨论:(1)若x≤1时,f(x)=﹣x2+ax不是单调的,即对称轴在x=满足<1,解得:a<2(2)x≤1时,f(x)是单调的,此时a≥2,f(x)为单调递增.最大值为f(1)=a﹣1故当x>1时,f(x)=ax﹣1为单调递增,最小值为f(1)=a﹣1,因此f(x)在R上单调增,不符条件.综合得:a<2故实数a的取值范围是(﹣∞,2)故答案为:(﹣∞,2)15.(4分)已知函数f(x)=(n﹣2m)3x+x2+2nx,方程f(x)=0的解集为A,方程f(f(x))=0的解集为B,若A=B≠∅,则m+n的取值范围为[0,3).【解答】解:根据题意,设x1∈{x|f(x)=0}={x|f(f(x))=0},∴f(x 1)=f(f(x1))=0,∴f(0)=0,即f(0)=n﹣2m=0,解得m=n;故f(x)=x2+2nx,f(f(x))=(x2+2nx)(x2+2nx+2n)=0,当n=0时,满足题意;当n≠0时,0,﹣2n不是x2+2nx+2n=0的根,∴△=4n2﹣8n<0,解得0<n<2;∴m+n=n,则0≤n+m<3;∴m+n的取值范围是[0,3).故答案为:[0,3).三、简答题(本题共48分)16.(10分)已知A={x|﹣1<x≤3},B={x|m≤x<1+3m}(1)当m=1时,求A∪B;(2)若B⊆∁R A,求实数m的取值范围.【解答】解:(1)当m=1时,A={x|﹣1<x≤3},B={x|1≤x<4},则A∪B={x|﹣1<x<4};(2)∵全集为R,A={x|﹣1<x≤3},∴C R A={x|x≤﹣1或x>3},∵B⊆C R A,当B=∅时,m≥1+3m,即m≤﹣;当B≠∅时,m<1+3m,即m>﹣,此时1+3m≤﹣1或m>3,解得:m>3,综上,m的范围为m≤﹣或m>3.17.(12分)已知函数f(x)=log 2(x2﹣mx+m)(1)若函数f(x)的最小值为1,求实数m的值;(2)若函数f(x)在区间(﹣∞,2)上是减函数,求实数m的取值范围.【解答】解:(1)若函数f(x)的最小值为1,则x2﹣mx+m的最小值为2,即=2,解得:m=2,或m=4;(2)若函数f(x)在区间(﹣∞,2)上是减函数,则y=x2﹣mx+m在区间(﹣∞,2)上是减函数且恒大于0,故解得:m∈[4,8].18.(14分)已知定义域为R的函数f(x)=是奇函数.(1)求a的值;(2)判断并证明函数f(x)的单调性;(3)若对任意的t∈[2,4],不等式f(log2t)+f(k﹣()t)<0有解,求k 的取值范围.【解答】解:(1)∵f(x)为奇函数,∴f(0)=0,f(0)==0,解得a=1.经过验证满足条件.(2)由(1)可得:f(x)=,函数f(x)为增函数.证明:任取实数x1<x2,则f(x 1)﹣f(x2)=﹣=,∵x1<x2,∴﹣x2<﹣x1,2﹣x2<2﹣x1,∴2﹣x2﹣2﹣x1<0,又(2﹣x1+1+2)(2﹣x2+1+2)>0,∴f(x1)﹣f(x2)<0,∴函数f(x)为增函数.(3)若对任意的t∈[2,4],不等式f(log2t)+f(k﹣()t)<0有解,由(1),根据函数的奇偶性得f(log2t)<﹣f(k﹣()t)=f(﹣k),由(2),根据函数是增函数得:log2t<﹣k,故对任意的t∈[2,4],k<﹣log2t,令h(t)=﹣log2t,则h(t)在[2,4]递减,故h(t)min=h(4)=﹣,故k<﹣.19.(12分)已知常数a∈R,函数f(x)=x﹣a,g(x)=,(1)写出函数F(x)=f(x)+g(x)的单调区间;(不需要证明)(2)令h(x)=|f(x)|﹣g(x),求h(x)在[1,2]的最小值.【解答】解:(1)F(x)=f(x)+g(x)=x+,该函数的单调增区间为(﹣∞,﹣1),(1,+∞).单调减区间为(﹣1,0),(0,1);(2)h(x)=|f(x)|﹣g(x)=|x﹣a|﹣=,当a≥2时,函数h(x)=﹣()+a,在[1,2]上为减函数,此时;当1<a<2时,h(x)在[1,a]上为减函数,在[a,2]上为增函数,此时;当a≤1时,h(x)=x﹣﹣a在[1,2]上为增函数,此时.∴当a≥2时,函数h(x)在[1,2]上的最小值为a﹣;当a<2时,h(x)在[1,2]上的最小值为.赠送初中数学几何模型【模型一】“一线三等角”模型: 图形特征:60°60°60°45°45°45°运用举例:1.如图,若点B 在x 轴正半轴上,点A (4,4)、C (1,-1),且AB =BC ,AB ⊥BC ,求点B 的坐标;2.如图,在直线l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ,则14S S += .ls 4s 3s 2s 13213. 如图,Rt △ABC 中,∠BAC =90°,AB =AC =2,点D 在BC 上运动(不与点B ,C 重合),过D 作∠ADE =45°,DE 交AC 于E . (1)求证:△ABD ∽△DCE ;(2)设BD =x ,AE =y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)当△ADE 是等腰三角形时,求AE 的长.EB4.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
杭州市高一上学期期中考试数学试卷

高一年级数学学科试卷一、 选择题(本大题共 12 小题,每小题 4 分,共计 48 分. 每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分) 1. 设集合}1|{>∈=x R x A ,则()A.A ⊆2B.A ∈}2{C.A ∈2D.A ∉2 2. 2.设函数x x f 2log )(=,则其定义域为 () A .)1,0(B .),2[+∞C .),0(+∞D .[1, +∞)3. 设全集U 是实数集R ,3|{},2|||{≥=>=x x N x x M 或1<x }都是 U 的子集,则图中阴影部分所表示的集合是( ) A .}2|{<x x B .}22|{≤≤-x x C .}21|{≤<x x D .}12|{<≤-x x4. 给定下列函数,其中在区间)1,0(上单调递增的函数是()A.2x y -=B.|2|2x x y -=C.1)21(+=x yD.xx y 1+=5. 列函数中,与函数x y =相同的函数是 ( )A.xx y 2= B.x e y ln = C.2x y = D.x y 2log 2=6.设函数⎩⎨⎧>-≤-=2),2(2,1)(2x x f x x x f ,则))2((f f 的值为( )A.0B.3C.1-D.27.函数xx y 21-=的图像是( )8. 设11011020172016++=a ,11011020182017++=b ,11011020192018++=c ,则c b a ,,的大小关系( )A .a > c > bB .b > c > aC .a > b > cD .c > b > a9. 函数)3lg()(2x x x f -=的单调递减区间为( )A .),23(+∞B .)23,(-∞ C .),3()0,(+∞-∞Y D .)0,(-∞10.函数)(log )(bx x f a =的图像如图,其中b a ,是常数,下列结论正确是( )A .1,10><<b aB .10,1<<>b aC .1,1>>b aD .10,10<<<<b a11.下列函数中,值域是),0(+∞的是( )A .xy -=13 B .13-=xy C .3217-=x y D .)3(log 2-=x y 12.存在函数)(x f 满足,对于任意的R x ∈都有( )A .|1|)1(2-=-x x fB .|1|)1(2+=-x x fC .|1|)2(2-=-x x x fD .|1|)1(2-=+x x f二、 填空题 (本大题共 5 小题,每空 4 分,共计 20 分)113.已知1)1(2+-=+x x f ,则=)3(f ________14.已知函数⎩⎨⎧≥+<=0,10,)(2x x x x x f ,若2)(=m f ,则实数m 的值为_______15. 若函数)(x f 满足)()(x f x f -=-,并且当0>x 时,32)(2+-=x x x f ,则当0<x 时,=)(x f ________16. 已知函数x x y 22+=在闭区间],[b a 上的值域为]3,1[-,则b a ·的最大值为______17. 已知0,0≥≥y x ,且1=+y x ,则函数)22(log ),(22y x xy x y x f +++=的最大值为______三、解答题(本大题共3个小题,共计32分)18. 已知全集R U =,集合}2|{-==x y x A ,}2|{a x a x B -<<=(1)当1-=a 时,求集合A C B U I(2)若集合A B A =Y ,求实数a 的取值范围19. 已知函数)(,)14(log )(2R k kx x f x ∈++=是偶函数(1)求k 的值(2)求不等式x x f -≥3)(成立时x 的取值范围20. 已知函数xa x f 1)(-=)0,0(>>x a(1)判断函数)(x f 的单调性并利用函数单调性定义加以证明(2)若)(x f 在]3,31[上的值域是]3,31[,求a 的值(3)当),0(,+∞∈n m 时,若)(x f 在],[n m 上的值域是],[n m )(n m <,求实数a 的取值范围。
2016年 浙江省 高一上数学 期中测试卷1

2016年 浙江省 高一上数学 期中测试卷1考生须知:全卷分试卷和答卷.试卷共4页,有3大题,24小题,满分100分,考试时间120分.不得使用计算器.第 Ⅰ 卷一、选择题(本大题有12小题,每小题3分,共36分,请从A ,B ,C ,D 四个选项中,选出一个符合题意的正确选项,填入答题卷,不选,多选,错选均得零分.) 1.已知集合}13|{≤=x x A ,3=a ,那么下列关系正确的是( )(A )A a ⊆ (B )A a ∈ (C )A a ∉ (D )A a ∈}{ 2.函数31)(-=x x f 的定义域是 ( )(A ))3,(-∞ (B )),3(∞+ (C ) )3,(-∞),3(∞+ (D ) )3,(-∞),3(∞+ 3.函数x y =的图像是( )4. 函数()(0)f x kx b k =+>,若[0,1],x ∈ [1,1]y ∈-,则函数()y f x =的解析式是 ()(A )21y x =- (B )1(1)2y x =-(C )21y x =-或21y x =-+ (D )21y x =--5.3.0222,3.0lg ,3.0这三个数的大小顺序是 ( ) (A)3.0lg 23.023.02<<(B)3.02223.0lg 3.0<< (C )3.02223.03.0lg <<(D)23.023.023.0lg <<(A ) (B ) (C ) (D )6.若2log 3()f x x =,则(2)f = ( )(A )3 (B )3- (C )31 (D )31-7.函数x a y =在[0,1]上最大值与最小值的和为3,则a =( )(A )2 (B )21(C )4 (D )418.已知)(x f 是区间(-∝,+∝)上的偶函数,且是[0,+∝)上的减函数,则 ( ) (A))5()3(-<-f f (B))5()3(->-f f (C))5()3(f f <- (D))5()3(-=-f f9. 函数1()4x f x a -=+(0a >,且1a ≠)的图像过一个定点,则这个定点坐标是 ( ) (A )(5,1) (B )(1,5) (C )(1,4) (D )(4,1)10. 若13log <a ,则a 取值范围是 ( ) (A )3>a (B )31<<a (C )10<<a (D )3>a 或10<<a 11.若增函数b ax x f +=)(与x 轴交点是)0,2(,则不等式02>-ax bx 的解集是 ( )(A )),0()21,(+∞--∞ (B ))21,0( (C ))0,21(- (D )),21()0,(+∞-∞12.若]21,0(∈x 时,恒有x a x log 4<,则a 的取值范围是 ( )(A ))22,0( (B ))1,22( (C ))2,1( (D ))2,2 第 Ⅱ 卷二、填空题(本大题有6小题,每小题3分,共18分,请将答案写在答题卷上) 13.函数)(x f 为(-∝,+∝)上的奇函数,则)0(f =_______________.14.计算2327()8= .15.已知函数⎩⎨⎧<->+=0)1(01()(x x x x x x x f ,,).则=-))1((f f _____________.16.函数f (x )=222+-ax x 在(-∞,6)内递减,则a 的取值范围为 .17.已知非空集合}|{22a x R x A <∈=,}31|{<<=x x B ,若}21|{<<=x x B A ,则实数a 的值为____________ .18.已知)(x f 在定义域),0(+∞是单调函数,当),0(+∞∈x 时,都有2]1)([=-x x f f ,则)51(f 的值是___________.三、解答题(本大题有6小题,共46分,请将解答过程写在答题卷上) 19.(本题6分)已知全集R U =,集合}31|{≤≤-=x x A ,}4|{2<=x x B , (1)求A B ; (2)求集合C A U20. (本题6分)计算: 2110025lg 41lg -÷⎪⎭⎫⎝⎛-21.(本题8分)已知函数xx x f 1)(-=, (1)判断函数)(x f 的奇偶性;(2)证明:)(x f 在),0(+∞上为单调增函数;22.(本题8分)已知函数2)1(log )(2-+=x x f .(1)若()0f x >,求x 的取值范围. (2)若]3,1(-∈x ,求)(x f 的值域.23.(本题8分)已知函数222)(a ax x x f --=)(R x ∈.(Ⅰ)关于x 的不等式0)(<x f 的解集为A ,且]2,1[-⊇A ,求a 的取值范围;(Ⅱ)是否存在实数a ,使得当R x ∈时,⎩⎨⎧=-=-0)(|)(|0)(|)(|x f x f x f x f 成立.若存在给出证明,若不存在说明理由.24.(本题10分)已知函数t t t bx x x f +=2)(。
2016-2017年浙江省杭州市五县七校联考高一上学期数学期中试卷带答案

对于 A:元素与集合应该是属于,即 0∈A;
对于 B,集合与集合之间的关系,应该是 { 0} ? A;
对于 C:空集是任何集合的子集,是任何非空集合的真子集,即 ?? A;
对于 D:{ 0} ? A 子集,所以 D 对.
故选: D.
2.(4 分)下列四组函数,两个函数相同的是(
)
A.f (x)= ,g(x)=x B.f(x)=log33x,g(x)=
10.( 4 分)设 f( x) =
﹣ ,若 [ x] 表示不超过 x 的最大整数,则函数 y=[ f
( x)] 的值域是( ) A.{ 0,﹣ 1} B.{ 0,1} C.{ ﹣1,1}
D. { ﹣ 1, 0, 1}
【解答】 解: f(x) =
﹣
=1﹣﹣=﹣ Nhomakorabea,
∵ 3x>0,
∴ 0<
<1,
∴﹣ < ﹣
( x)] 的值域是( ) A.{ 0,﹣ 1} B.{ 0,1} C.{ ﹣1,1}
D. { ﹣ 1, 0, 1}
二、填空题(本大题共 7 个小题,每小题 4 分,共 28 分,请把正确答案填在题
中横线上)
11.( 4 分)已知幂函数 f (x) =k?xa 的图象过点( , )则 k+a=
.
12.( 4 分)设全集 U=R,集合 A={ x| ﹣1<x< 4} ,B={ y| y=x+1,x∈A} ,(?UA)
C.f (x)=( )2, g( x)=| x| D.f( x) =x,g(x)=x0
【解答】 解:对于 A:f (x) = =| x| 的定义域为 R,g(x)=x 的定义域为 R,
它们定义域相同,对应关系不相同,∴不是同一函数; 对于 B:f(x)=log33x=x 与 g(x)= =x 它们的定义域相同,对应关系也相同,
浙江省杭州市实验外国语学校2016-2017学年高一上学期期中考试数学试题解析(解析版)
浙江省杭州市实验外国语学校2016-2017学年高一上学期期中考试数学试题第Ⅰ卷(共40分)一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.已知集合A={1,2,3,4},B={2,4,6},则B A ⋂的元素个数( )A. 0个B.2个C. 3个D.5个试题分析:两集合的交集为两集合相同的元素构成的集合,所以{}2,4A B = ,含有2个元素 考点:交集运算2.下列函数中在区间上为增函数的是( ) A. y=1+x B. y=()21-x C. y=x-2 D. y=-x+1【答案】A【解析】试题分析:A 中函数为增函数;B 中函数有增区间有减区间;C 中函数有增区间有减区间;D 中函数是减函数考点:函数单调性3.若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A B ⋂=( )(A ){}1,2 (B ){}0,1 (C ){}0,3 (D ){}3【答案】C【解析】试题分析:由题意可知{}{}0,3,6,90,3B A B =∴=考点:交集运算4.下列哪组中的两个函数是同一函数( )(A )2y =与y x = (B )3y =与y x =(C)y =2y = (D)y =与2x y x = 【答案】B【解析】试题分析:A 中两函数定义域不同;B 中两函数定义域相同,对应关系相同,所以是同一函数;C 中两函数定义域不同;D 中两函数定义域不同考点:函数概念5.设集合{|12},{|}.A x x B x x a =<<=<若,A B ⊆则a 的范围是( )(A)2a ≥ (B)1a ≤ (C)1a ≥ (D)2a ≤【答案】A【解析】试题分析:由,A B ⊆可知满足12x <<的数x 都在x a <内,所以2a ≥考点:集合的子集关系6.函数()f x =的值域是( )A.]2,(-∞B. ),0(+∞C. ),2[+∞D.]2,0[ 【答案】D【解析】试题分析:()222314x x x --+=--+ ,所以y 的最大值为2,所以值域为]2,0[考点:函数值域 7.设函数()()2,11,1x x f x x x -<⎧⎪=⎨-≥⎪⎩,若()1f α=,则实数α的值为( ) A.1-或0B .2或1-C .0或2D .2【答案】B【解析】试题分析:()1f α=转化为11a a -=⎧⎨<⎩或()2111a a ⎧-=⎪⎨≥⎪⎩,解方程得实数α的值为2或1- 考点:函数求值8.函数f (x )是定义域为R 的奇函数,当x>0时,f (x )=-x+1,则当x<0时,f (x )的 表达式为( )A.1)(+-=x x fB.1)(--=x x fC.1)(+=x x fD.1)(-=x x f【答案】B【解析】试题分析:当0x <时0x ->()()11f x x x ∴-=--+=+()()()1f x f x f x x -=-∴=-- 考点:函数奇偶性求解析式9.若{}21,,0,,b a a a b a ⎧⎫=+⎨⎬⎩⎭,则20052005a b +的值为( )(A )0 (B )1 (C )1- (D )1或1-【答案】C【解析】 试题分析:由两集合相等可知21001b a a b a ⎧=-=⎧⎪∴⎨⎨=⎩⎪=⎩200520051a b ∴+=- 考点:集合相等第Ⅱ卷(共60分)二、填空题(每题4分,满分20分,将答案填在答题纸上)11.函数xx x f -=13)(2的定义域为_______________ 【答案】),(1-∞ 【解析】试题分析:要使函数有意义,需满足101x x ->∴<,所以定义域为),(1-∞ 考点:函数定义域12.若函数x x x f 2)12(2-=+,则)3(f =【答案】-1【解析】试题分析:令213x +=得1x =()23121f ∴=-=- 考点:函数求值13.已知)(x f y =在定义域(-1,1)上是减函数,且)12()1(-<-a f a f ,则a 的取值范围是______________ 【答案】320<<a考点:单调性解不等式14.奇函数()f x 满足:① ()f x 在(0,)+∞内单调递增;② (1)0f =;则不等式(1)()0x f x ->的解集为:【答案】()()U +∞-∞-,11,【解析】试题分析:()f x 在(0,)+∞内单调递增,所以在(),0-∞内递增,由()10f =得()10f -=,所以不等式(1)()0x f x ->转化为()100x f x ->⎧⎨>⎩或()100x f x -<⎧⎨<⎩,所以1x >或1x <-,不等式解集为()()U +∞-∞-,11, 考点:奇偶性单调性解不等式15.已知f (x )=835-++bx ax x,f (-2)=10,则f (2)=____.【答案】-26【解析】试题分析:()21032828108250f a b a b -=∴----=∴+=- ()23282826f a b ∴=++-=- 考点:函数求值 三、解答题 (本大题共4小题,共40分.解答应写出文字说明、证明过程或演算步骤.)16.设{}6|≤∈=x Z x A ,{}{}1,2,3,3,4,5,6B C ==,求:(1)()A B C ⋃⋂;(2)()A A C B C ⋂⋃【答案】(1){}6,5,4,3,2,1,0,1,2,3,4,5,6------(2){}6,5,4,3,2,1,0------【解析】试题分析:两集合的交集为两集合相同的元素构成的集合,并集为两集合所有的元素构成的集合,集合的补集为全集中除去集合中的元素,剩余的元素构成的集合试题解析:{}(1)6,5,4,3,2,1,0,1,2,3,4,5,6A =------.{}{}{}{}'''1,2,3,4,5,6 (2)()6,5,4,3,2,1,0,1,2,3,4,5,6 (2)(2)1,2,3,4,5,6....................................(2)()6,5,4,3,2,1,0.........A B C A B C A B C C B C ⋂=⋃⋂=------=⋃=⋃=------。
浙江省杭州市高一上学期数学期中考试试卷
浙江省杭州市高一上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分) (2017高一上·义乌期末) 已知集合A={x|x2﹣3x+2=0},B={x|3x+1=9},则A∪B=()A . {﹣2,1,2}B . {﹣2,2}C . {1,2}D . {1}2. (2分) (2016高一上·金华期中) 集合M={x|﹣2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是()A .B .C .D .3. (2分)命题且满足.命题且满足.则是的()A . 充分非必要条件B . 必要非充分条件C . 充要条件D . 既不充分也不必要条件4. (2分)(2017·山东) 若a>b>0,且ab=1,则下列不等式成立的是()A . a+ <<log2(a+b))B . <log2(a+b)<a+C . a+ <log2(a+b)<D . log2(a+b))<a+ <5. (2分) (2016高二上·潮阳期中) 已知集合M={x|﹣2<x<2},N={x|x2﹣2x﹣3<0},则集合M∩N=()A . {x|x<﹣2}B . {x|x>3}C . {x|﹣1<x<2}D . {x|2<x<3}6. (2分) (2019高一上·盘山期中) 已知,,,则,,的大小关系正确的是()A .B .C .D .7. (2分)设集合A=[0,1),B=[1,2],函数且则x0的取值范围是()A .B .C .D .8. (2分)下列命题中:①命题“,使得”,则是假命题.②“若,则互为相反数”的逆命题为假命题.③命题“”,则“”.④命题“若,则”的逆否命题是“若,则”.其中正确命题是()A . ②③B . ①②C . ①④D . ②④二、填空题 (共8题;共8分)9. (1分) (2017高一上·丰台期中) 小明需要购买单价为3元的某种笔记本.他现有10元钱,设他购买时所花的钱数为自变量x(单位:元),笔记本的个数为y(单位:个),若y可以表示为x的函数,则这个函数的定义域为________.10. (1分) (2016高三上·沈阳期中) 已知函数f(x)= ,则f(f(﹣1))等于________11. (1分) (2019高一上·兴义期中) 计算: ________.12. (1分) (2016高二下·鹤壁期末) 若f(x)=﹣ x2+bln(x+2)在(﹣1,+∞)上是减函数,则b的取值范围是________.13. (1分)已知全集U=R,集合P={x||x﹣2|≥1},则P=________14. (1分) (2016高一上·如东期中) 已知函数,若f(m)+f(m﹣1)>2,则实数m 的取值范围是________.15. (1分) (2019高一上·昌吉月考) 函数最大值为________.16. (1分)设f(x)是定义在R上的奇函数,且当x>0时,f(x)=x2﹣3,则f(﹣2)=________三、解答题 (共6题;共65分)17. (10分)已知集合A={x|x(x﹣2)≥3},函数f(x)=x2﹣2x﹣1在[﹣1,2]上的值域为集合B.(1)求(∁RA)∩B;(2)若集合D={x|1﹣m<x<2m},且B⊆D,求m的取值范围.18. (10分) (2016高二下·茂名期末) 计算:(1) 0.02 ﹣(﹣)﹣2+25 ﹣3﹣1+(﹣1)0;(2).19. (10分) (2016高一上·徐州期中) 已知二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1,(1)求f(x)的解析式;(2)当x∈[﹣1,1]时,求函数g(x)=f(x)﹣2x的值域.20. (10分) (2017高二下·穆棱期末) 已知函数 .(1)求方程的根;(2)求证:在上是增函数;(3)若对于任意,不等式恒成立,求实数的最小值.21. (10分) (2016高一上·苏州期中) 已知函数y=f(x)满足f(x﹣1)=2x+3a,且f(a)=7.(1)求函数f(x)的解析式;(2)若g(x)=x•f(x)+λf(x)+x在[0,2]上最大值为2,求实数λ的值.22. (15分) (2017高一上·珠海期末) 定义域为R的奇函数f(x)= ,其中h(x)是指数函数,且h(2)=4.(1)求函数f(x)的解析式;(2)求不等式f(2x﹣1)>f(x+1)的解集.参考答案一、单选题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共8题;共8分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共6题;共65分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、。
2016-2017年浙江省杭州实验外国语学校高二上学期期中数学试卷及参考答案
2016-2017学年浙江省杭州实验外国语学校高二(上)期中数学试卷一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个符合题目要求,不选,错选,多选均不得分)1.(4分)有一个几何体的三视图如图所示,这个几何体应是一个()A.棱台B.棱锥C.棱柱D.都不对2.(4分)如图是由哪个平面图形旋转得到的()A.B.C.D.3.(4分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离4.(4分)直线截圆x2+y2=4得到的弦长为()A.1 B.C.D.25.(4分)若,则下列结论不正确的是()A.a2<b2B.ab<b2C.>2 D.|a|﹣|b|=|a﹣b|6.(4分)已知正数x、y满足,则x+2y的最小值是()A.18 B.16 C.8 D.107.(4分)已知直线l过圆x2+(y﹣3)2=4的圆心,且与直线x+y+1=0垂直,则l的方程是()A.x+y﹣2=0 B.x﹣y+2=0 C.x+y﹣3=0 D.x﹣y+3=08.(4分)已知变量,满足,目标函数是z=2x+y,则有()A.z max=5,z min=3 B.z max=5,z无最小值C.z min=3,z无最大值D.z既无最大值,也无最小值9.(4分)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为()A.(﹣1,0)∪(1,+∞) B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞) D.(﹣1,0)∪(0,1)10.(4分)已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A (﹣4,a)作圆C的一条切线,切点为B,则|AB|=()A.2 B.6 C.4 D.2二、填空题(本大题共5小题,每小题4分,共20分)11.(4分)直线(2λ+1)x+(λ﹣1)y+1=0(λ∈R),恒过定点.12.(4分)已知x>0,则函数的最小值为.13.(4分)直线y=3x+3关于点M(3,2)对称的直线l的方程是.14.(4分)若不等式|x﹣3|+|x+1|>a恒成立,则a的取值范围为.15.(4分)直线l1:y=x+a和l2:y=x+b将单位圆C:x2+y2=1分成长度相等的四段弧,则a2+b2=.三、解答题(本大题共4小题,每小题10分,共40分)16.(10分)求经过两条直线l1:x+y﹣4=0和l2:x﹣y+2=0的交点,且分别与直线2x﹣y﹣1=0(1)平行的直线方程;(2)垂直的直线方程.17.(10分)圆心在直线x﹣2y=0上的圆C与y轴的正半轴相切,圆C截x轴所得弦的长为2,则圆C的标准方程为.18.(10分)已知函数f(x)=﹣3x2+a(6﹣a)x+c.(1)当c=19时,解关于a的不等式f(1)>0;(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值.19.(10分)已知圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0.(1)求两圆的公共弦所在的直线方程及公共弦长.(2)求过两圆交点且面积最小的圆的方程.2016-2017学年浙江省杭州实验外国语学校高二(上)期中数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个符合题目要求,不选,错选,多选均不得分)1.(4分)有一个几何体的三视图如图所示,这个几何体应是一个()A.棱台B.棱锥C.棱柱D.都不对【解答】解:由三视图知,从正面和侧面看都是梯形,从上面看为正方形,下面看是正方形,并且可以想象到连接相应顶点的四条线段就是几何体的四条侧棱,故这个三视图是四棱台.故选A.2.(4分)如图是由哪个平面图形旋转得到的()A.B.C.D.【解答】解:图中所给的几何体是由上部的圆锥和下部的圆台组合而成的,故轴截面的上部是直角三角形,下部为直角梯形构成,故选:D.3.(4分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离【解答】解:圆(x+2)2+y2=4的圆心C1(﹣2,0),半径r=2.圆(x﹣2)2+(y﹣1)2=9的圆心C2(2,1),半径R=3,两圆的圆心距d==,R+r=5,R﹣r=1,R+r>d>R﹣r,所以两圆相交,故选:B.4.(4分)直线截圆x2+y2=4得到的弦长为()A.1 B.C.D.2【解答】解:圆的半径为2,圆心(0,0)到直线的距离为d==1,∴弦长为2=2=2,故选:B.5.(4分)若,则下列结论不正确的是()A.a2<b2B.ab<b2C.>2 D.|a|﹣|b|=|a﹣b|【解答】解:由于,不妨令a=﹣1,b=﹣2,可得a2<b2,故A正确;ab=2,b2=4,故B正确;=2+>2,故C正确.|a|﹣|b|=﹣1,|a﹣b|=1,故D不正确.故选:D.6.(4分)已知正数x、y满足,则x+2y的最小值是()A.18 B.16 C.8 D.10【解答】解:∵,∴x+2y=(x+2y)•()=10++≥10+8=18(当且仅当x=4y时等号成立)答案为:18.故选:A.7.(4分)已知直线l过圆x2+(y﹣3)2=4的圆心,且与直线x+y+1=0垂直,则l的方程是()A.x+y﹣2=0 B.x﹣y+2=0 C.x+y﹣3=0 D.x﹣y+3=0【解答】解:由题意可得所求直线l经过点(0,3),斜率为1,故l的方程是y﹣3=x﹣0,即x﹣y+3=0,故选:D.8.(4分)已知变量,满足,目标函数是z=2x+y,则有()A.z max=5,z min=3 B.z max=5,z无最小值C.z min=3,z无最大值D.z既无最大值,也无最小值【解答】解:先根据约束条件画出可行域当直线z=2x+y过点B(2,1)时,z最大是5,当直线z=2x+y过点C(1,1)时,z最小是3,故选:A.9.(4分)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为()A.(﹣1,0)∪(1,+∞) B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞) D.(﹣1,0)∪(0,1)【解答】解:由奇函数f(x)可知,即x与f(x)异号,而f(1)=0,则f(﹣1)=﹣f(1)=0,又f(x)在(0,+∞)上为增函数,则奇函数f(x)在(﹣∞,0)上也为增函数,当0<x<1时,f(x)<f(1)=0,得<0,满足;当x>1时,f(x)>f(1)=0,得>0,不满足,舍去;当﹣1<x<0时,f(x)>f(﹣1)=0,得<0,满足;当x<﹣1时,f(x)<f(﹣1)=0,得>0,不满足,舍去;所以x的取值范围是﹣1<x<0或0<x<1.故选:D.10.(4分)已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A (﹣4,a)作圆C的一条切线,切点为B,则|AB|=()A.2 B.6 C.4 D.2【解答】解:∵圆C:x2+y2﹣4x﹣2y+1=0,即(x﹣2)2+(y﹣1)2 =4,表示以C(2,1)为圆心、半径等于2的圆.由题意可得,直线l:x+ay﹣1=0经过圆C的圆心(2,1),故有2+a﹣1=0,∴a=﹣1,点A(﹣4,﹣1).∵AC==2,CB=R=2,∴切线的长|AB|===6.故选:B.二、填空题(本大题共5小题,每小题4分,共20分)11.(4分)直线(2λ+1)x+(λ﹣1)y+1=0(λ∈R),恒过定点(﹣,).【解答】解:由题意,λ(2x+y)+(x﹣y+1)=0,∵λ∈R,∴∴∴直线恒过定点(﹣,)故答案为:(﹣,)12.(4分)已知x>0,则函数的最小值为5.【解答】解:∵x>0,则函数=2x+﹣3≥﹣3=5,当且仅当x=2时取等号.函数的最小值为5.故答案为:5.13.(4分)直线y=3x+3关于点M(3,2)对称的直线l的方程是y=3x﹣17.【解答】解:设所求直线上的任意点坐标(x,y)关于点M(3,2)对称点(6﹣x、4﹣y),因为对称点在已知直线上,所以将y=3x+3中的x、y分别代以(6﹣x)、(4﹣y),得4﹣y=3(6﹣x)+3,即y=3x﹣17.此为所求直线方程.故答案为:y=3x﹣17.14.(4分)若不等式|x﹣3|+|x+1|>a恒成立,则a的取值范围为(﹣∞,4).【解答】解:(1)∵|x﹣3|+|x+1|≥|(x﹣3)﹣(x+1)|=4,|x﹣3|+|x+1|>a 恒成立,∴4>a恒成立,即a<4,故答案为:(﹣∞,4).15.(4分)直线l1:y=x+a和l2:y=x+b将单位圆C:x2+y2=1分成长度相等的四段弧,则a2+b2=2.【解答】解:由题意可得,圆心(0,0)到两条直线的距离相等,且每段弧长都是圆周的,∴==cos45°=,∴a2+b2=2,故答案为:2.三、解答题(本大题共4小题,每小题10分,共40分)16.(10分)求经过两条直线l1:x+y﹣4=0和l2:x﹣y+2=0的交点,且分别与直线2x﹣y﹣1=0(1)平行的直线方程;(2)垂直的直线方程.【解答】解:联立,解得,(1)由平行关系设所求直线的方程为2x﹣y+c=0代入点(1,3)可得2×1﹣3+c=0,解得c=1故所求直线方程为2x﹣y+1=0(2)由垂直关系设所求直线的方程为x+2y+d=0代入点(1,3)可得1+2×3+d=0,解得d=﹣7故所求直线方程为x+2y﹣7=0.17.(10分)圆心在直线x﹣2y=0上的圆C与y轴的正半轴相切,圆C截x轴所得弦的长为2,则圆C的标准方程为(x﹣2)2+(y﹣1)2=4.【解答】解:设圆心为(2t,t),半径为r=|2t|,∵圆C截x轴所得弦的长为2,∴t2+3=4t2,∴t=±1,∵圆C与y轴的正半轴相切,∴t=﹣1不符合题意,舍去,故t=1,2t=2,∴(x﹣2)2+(y﹣1)2=4.故答案为:(x﹣2)2+(y﹣1)2=4.18.(10分)已知函数f(x)=﹣3x2+a(6﹣a)x+c.(1)当c=19时,解关于a的不等式f(1)>0;(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值.【解答】解:(1)c=19时,f(1)=﹣3+6a﹣a2+19=﹣a2+6a+16>0,化为a2﹣6a﹣16<0,解得﹣2<a<8.∴不等式的解集为(﹣2,8).(2)由已知有﹣1,3是关于x的方程3x2﹣a(6﹣a)x﹣c=0的两个根,则,解得19.(10分)已知圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0.(1)求两圆的公共弦所在的直线方程及公共弦长.(2)求过两圆交点且面积最小的圆的方程.【解答】解:(1)设两圆的交点为A(x1,y1),B(x2,y2),则A、B两点的坐标是圆C1:x2+y2﹣3x﹣3y+3=0,圆C2:x2+y2﹣2x﹣2y=0,联立方程组的解,两方程相减得:x+y﹣3=0,∵A、B两点的坐标都满足该方程,∴x+y﹣3=0为所求.将圆C2的方程化为标准形式,(x﹣1)2+(y﹣1)2=2,∴圆心C2(1,1),半径r=.圆心C2到直线AB的距离d==,|AB|=.即两圆的公共弦长为.(2)C1(,),C2(1,1),直线C1C2方程:x﹣y=0.,交点为,即为圆的圆心,半径r=,所以圆的方程是:.赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD 内接于⊙O ,对角线AC ⊥BD 于P ,设⊙O 的半径是2。
(全优试卷)版高一数学上学期期中试题及答案(人教A版 第148套)
浙江省杭州外国语学校(第一学期)高一期中考试数学试卷一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答卷..相应空格中) 1.已知集合|0,1x M x x R x ⎧⎫=≥∈⎨⎬-⎩⎭,{}2|31,N y y x x R ==+∈,则M N ⋂等于( )A .φB .{}|1x x ≥C .{}|1x x >D .{}|10x x x ≥<或 2.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论用角度制还是用弧度制度量一个角,它们与扇形所在圆的半径的大小无关; ④若sin sin αβ=,则α与β的终边相同; ⑤若cos 0θ<,则θ是第二或第三象限的角. 其中正确..命题的个数是( )A .1B .2C .3D .43.若()f x =,则()f x 的定义域为 ( )A .1,02⎛⎫-⎪⎝⎭ B .1,02⎛⎤- ⎥⎝⎦C .1,2⎛⎫-+∞ ⎪⎝⎭ D .()0,+∞4.下列函数()y f x =中满足“对任意12,(0,)x x ∈+∞,当12x x <时,都有()12()f x f x <”的是 ( ) A .1()f x x= B .()2()1f x x =- C .2()f x e = D .()ln(1)f x x =+ 5.454sincos tan 363πππ⎛⎫⋅⋅- ⎪⎝⎭的值是( )A.4-B.4C.4-D.46.定义在R 上的函数()y f x =是奇函数,且满足(1)(1)f x f x +=-.当[]1,1x ∈-时,3()f x x =,则(2013)f 的值是 ( )A .1B .2C .0D .1-7.若cos2sinαα+=tanα等于 ( ) A.12B.2 C.12-D.2-8.函数x xx xe eye e--+=-的图象大致为 ( ) 9.已知()y f x=为R上的减函数,则满足1(1)f fx⎛⎫<⎪⎝⎭的实数x的取值范围是 ( ) A.()1,1- B.()0,1 C.()()1,00,1-⋃ D.()(),11,-∞-⋃+∞10.已知函数lg,010()13,105x xf xx x⎧<≤⎪=⎨-+>⎪⎩,若,,a b c互不相等,且()()()f a f b f c==,则abc 的取值范围是 ( ) A.()1,10B.()5,10 C.()10,15D.()15,30二、填空题(本大题共7小题,每小题4分,共28分,把答案填在答卷中相应横线上)11.化简1603[(2)](1)---的值为____▲____.12.函数()f x=的单调增区间为____▲____.13.函数()2()log31xf x=+的值域为____▲____.14.已知cos6πα⎛⎫+=⎪⎝⎭,则5cos6πα⎛⎫-⎪⎝⎭的值为____ ▲____.15.已知函数()ln2f x x x=-+有一个零点所在的区间为(),1k k+ (*k N∈),则k的值为____▲____.16.已知函数())f x x=,若实数,a b满足(1)()0f a f b-+=,则a b+等于▲ .17.已知不等式2log 0a x x -<,当10,2x ⎛⎫∈ ⎪⎝⎭时恒成立,则实数a 的取值范围是 ▲ .三、解答题(本大题共4小题,共42分,解答应写出文字说明,证明过程或演算步骤) 18.(本小题满分10分)已知集合2{310}M x x x =-≤,{121}N x a x a =+≤≤+. (Ⅰ)若2a =,求M (R N ð);(Ⅱ)若MN M =,求实数a 的取值范围.19.(本小题满分10分)已知()()sin cos 2ππαπααπ⎛⎫--+=<< ⎪⎝⎭,求下列各式的值: (Ⅰ)sin cos αα-; (Ⅱ) 33sin cos 22ππαα⎛⎫⎛⎫--+⎪ ⎪⎝⎭⎝⎭.20.(本小题满分10分)设a 为实数,函数()2()2f x x x a x a =+--.(Ⅰ)若(0)4f ≥,求a 的取值范围; (Ⅱ)求函数()f x 的最小值.21.(本小题满分12分)已知定义在D 上的函数()f x ,如果满足:对任意D x ∈,存在常数0M >, 使得|()|f x M ≤成立, 则称()f x 是D 上的有界函数, 其中M 称为函数()f x 的上界.下面我们来考虑两个函数:()421xxf x p --=+⋅+, 12()12xxq g x q -⋅=+⋅.(Ⅰ)当1p =时, 求函数()f x 在(),0-∞上的值域, 并判断函数()f x 在(),0-∞上是否为有界函数, 请说明理由;(Ⅱ)若1,22q ⎛∈⎝⎦, 函数()g x 在[]0,1上的上界是()H q , 求()H q 的取值范围;(Ⅲ)若函数()f x 在[)0,+∞上是以3为上界的有界函数, 求实数p 的取值范围.杭州外国语学校2013-1高一年级期中考试数学答题卷一、选择题:(本大题有10小题,每小题3分,共30分)二、填空题:(本大题有7小题,每小题4分,共28分)11. 3 12.[)2,+∞ 13. ()0,+∞14.-1,116⎡⎫⎪⎢⎣⎭三、解答题:(本大题有4小题,共42分,请写出必要的解答过程) 18. (1) 因为a =2,所以N ={x |3≤x ≤5},∁R N ={x |x <3或x >5}. 又M ={x |-2≤x ≤5}, 所以M ∩ (∁R N )={x |x <3或x >5}∩{x |-2≤x ≤5}={x |-2≤x <3}.(2)若M ≠φ,由M N M =,得N ⊆M ,所以⎩⎪⎨⎪⎧a +1≥-22a +1≤52a +1≥a +1.解得0≤a ≤2; 当N =φ,即2a +1<a +1时,a <0,此时有N ⊆M ,所以a <0为所求.综上,实数a 的取值范围是(-∞,2].____________________________________________________________________________________19.(1)sin cos αα+=,所以平方可得:212sin cos 9αα+=,即:7sin cos 18αα=-所以4sin cos 3αα-===(2)原式=3322cos sin (sin cos )(sin sin cos cos )αααααααα+=+-+7(1)31854=+= 班级_______________________ 姓名_____________ 试场号______________ 考号_______________………………………密○………………………………………封○………………………………………○线………………………○20. (1)(0)4f ≥,即:4a a -≥,所以0a <,得到:24a ≤,所以2a ≤-(2)()()22222,()2,x x a x a f x x x a x a⎧+-≥⎪=⎨--<⎪⎩令222212()323,33g x x ax a x a a x a ⎛⎫=-+=-+≥ ⎪⎝⎭;()2222()22,h x x ax a x a a x a =+-=+-<当0a ≥时,2min ()2g g a a ==,2min ()2h h a a =-=-,所以2min 2f a =-当0a <时,2min 1233g g a a ⎛⎫==⎪⎝⎭,2min ()2h h a a ==,所以2min 23f a = 综上:2min22,02,03a a f a a ⎧-≥⎪=⎨<⎪⎩ ____________________________________________________________________________________21. (1)当p=1时,()421xx f x --=++因为)(x f 在(),0-∞上递减,所以()(0)3f x f >=,即)(x f 在(),1-∞的值域为()3,+∞故不存在常数0M >,使|()|f x M ≤成立, 所以函数()f x 在(),1-∞上不是有界函数(2)2()112xg x q =-+⋅,∵ q>0 ,[]1,0∈x ∴ ()g x 在[]0,1上递减,∴)0()()1(g x g g ≤≤ 即121()121q qg x q q--≤≤++∵1(,22q ∈,∴112112q q q q --≥-++,∴1()1q g x q-≤+, ∴1()1q H q q-≥+ ,即 1[,)1qq -+∞+ (3)由题意知,3)(≤x f 在[)1,+∞上恒成立.3)(3≤≤-x f , ∴1142()22()22x x x x p -⋅-≤≤⋅- 在[)0,+∞上恒成立∴ max min 11[42()][22()]22xx x x p -⋅-≤≤⋅-设t x=2,t t t h 14)(--=,tt t p 12)(-=, 由x ∈[)0,+∞得 t ≥1,设121t t ≤<,()()2112121241()()0t t t t h t h t t t ---=>, 所以)(t h 在[)1,+∞上递减,)(t h 在[)1,+∞上的最大值为(1)5h =-, 又()()012)()(21212121<+-=-t t t t t t t p t p ,所以)(t p 在[)1,+∞上递增, )(t p 在[)1,+∞上的最小值为(1)1p =所以实数p 的取值范围为[]5,1-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. (4 分)若 A={0,1,2,3},B={x|x=3a,a∈A},则 A∩B=( A.{1,2} B.{1,0} C.{0,3} D.{3} 4. (4 分)下列哪组中的两个函数是同一函数( A. C. 与 与 y=x B. D. 与 y=x 与 )
5. (4 分)设集合 A={x|1<x<2},B={x|x<a},若 A⊆ B,则 a 的范围是( A.a≥2 6. (4 分) B.a≥1 C.a≤1 D.a≤2 ( )
7. (4 分)设函数 f(x)= A.﹣1 或 0 B.2 或﹣1 C.0 或 2 【解答】解:函数 f(x)= 当 a<1 时,﹣a=1,a=﹣1,成立. 当 a≥1 时, (a﹣1)2=1,解得 a=2,
,若 f(a)=1,则实数 a 的值为( D.2 ,若 f(a)=1,
B.f(x)=﹣x﹣1
9. (4 分)若{1,a, }={0,a2,a+b},则 a2005+b2005 的值为( A.0 B.﹣1 C.1 D.1 或﹣1
第 1 页(共 10 页)
二、填空题(本大题共 5 小题,每小题 5 分,共 25 分) 10. (5 分)已知函数 ,则其定义域为: . .
)
A. C. 与
与 y=x B. D.
与 y=x 与 的定义域不同,故不是同一函数.
【解答】解:A、y=x 与 y= B、 C、f D、 故选:B. 与 与
=x 与 y=x 的对应关系相同,定义域为 R,故是同一函数. 的定义域不同,故不是同一函数. 具的定义域不同,故不是同一函数.
5. (4 分)设集合 A={x|1<x<2},B={x|x<a},若 A⊆ B,则 a 的范围是( A.a≥2 B.a≥1 C.a≤1 D.a≤2
(2)已知 x+x﹣1=3,求
的值.
17. (10 分)已知函数 f(x)=x2+2ax+2,x∈[﹣5,5], (1)当 a=﹣1 时,求函数的最大值和最小值; (2)求实数 a 的取值范围,使 y=f(x)在区间[﹣5,5]上是单调减函数. 18. (10 分)已知函数 f(x)= (1)判断函数 f(x)的奇偶性,并证明. (2)求函数 f(x)的单调性及值域.
2016-2017 学年浙江省杭州实验外国语学校高一(上)期中数学 试卷
一、选择题(本大题共 9 小题,每小题 4 分,共 40 分.在每小题给出的四个选 项中,只有一个符合题目要求,不选,错选,多选均不得分) 1. (4 分)已知集合 A={1,2,3,4},B={2,4,6},则 A∩B 的元素个数( A.0 个 B.2 个 C.3 个 D.5 个 2. (4 分)下列函数中在区间[﹣1,+∞)上为增函数的是( A.y= B.y=(x﹣1)2 C.y=|x﹣2| D.y=﹣x+1 ) ) )
11. (5 分)若函数 f(2x+1)=x2﹣2x,则 f(3)=
12. (4 分)已知 y=f(x)在定义域(﹣1,1)上是减函数,且 f(1﹣a)<f(2a ﹣1) ,则 a 的取值范围是 .
13. (5 分)奇函数 f(x)满足:①f(x)在(0,+∞)内单调递增;②f(1)=0; 则不等式(x﹣1)f(x)>0 的解集为: . .
3. (4 分)若 A={0,1,2,3},B={x|x=3a,a∈A},则 A∩B=( A.{1,2} B.{1,0} C.{0,3} D.{3} 【解答】解;B={x|x=3a,a∈A}={0,3,6,9} 故 A∩B={0,3} 故选:C.
)
4. (4 分)下列哪组中的两个函数是同一函数(
第 3 页(共 10 页)
14. (5 分)已知 f(x)=x5+ax3+bx﹣8,若 f(﹣2)=10,则 f(2)=
三、解答题(本大题共 4 小题,每小题 10 分,共 40 分) 15. (10 分)设 A={x∈Z||x|≤6},B={1,2,3},C={3,4,5,6},求: (1)A∩(B∩C) ; (2)A∩CA(B∪C) . 16. (10 分)计算: (1)
)
【解答】解:∵集合 A={x|1<x<2},B={x|x<a},A⊆ B,∴2≤a, 故选:A.
6. (4 分)
(
)
A. (﹣∞,2] B. (0,+∞) C.[2,+∞) D.[0,2] 【解答】解:∵函数 ≥0, ≤2,
而且﹣x2﹣2x+3=﹣( x2+2x﹣3)=﹣(x+1)2+4≤4,∴ ∴0≤f(x)≤2, 故选:D.
)
A. (﹣∞,2] B. (0,+∞) C.[2,+∞) D.[0,2] 7. (4 分)设函数 f(x)= A.﹣1 或 0 B.2 或﹣1 C.0 或 2 ,若 f(a)=1,则实数 a 的值为( D.2 )
8. (4 分)函数 f(x)是定义域为 R 的奇函数,当 x>0 时 f(x)=﹣x+1,则当 x <0 时,f(x)的表达式为( A.f(x)=﹣x+1 ) C.f(x)=x+1 D.f(x)=x﹣1 )
2. (4 分)下列函数中在区间[﹣1,+∞)上为增函数的是( A.y= B.y=(x﹣1)2 C.y=|x﹣2| D.y=﹣x+1
)
【解答】解:对于 A:y=
,在[﹣1,+∞)上为增函数,
对于 B:y=(x﹣1)2 在[1,+∞)上为增函数,在(﹣∞,1)上为减函数, 对于 C:y=|x﹣2|在[2,+∞)上为增函数,在(﹣∞,2)上为减函数, 对于 D:y=﹣x+1 在 R共 10 页)
2016-2017 学年浙江省杭州实验外国语学校高一(上)期 中数学试卷
参考答案与试题解析
一、选择题(本大题共 9 小题,每小题 4 分,共 40 分.在每小题给出的四个选 项中,只有一个符合题目要求,不选,错选,多选均不得分) 1. (4 分)已知集合 A={1,2,3,4},B={2,4,6},则 A∩B 的元素个数( A.0 个 B.2 个 C.3 个 D.5 个 【解答】解:∵A={1,2,3,4},B={2,4,6}, ∴A∩B={2,4}, 则 A∩B 的元素个数 2 个, 故选:B. )
