2018春北师大版数学九下第三章《圆》单元测试题

合集下载

北师大版九年级数学下第三章圆单元检测试题含答案

第三章圆一、选择题1．如图3－198所示，弦AB的长为6 cm，圆心O到AB的距离为4 cm，则⊙O的半径为( )A．3 cm B．4 cm C．5 cm D．6 cm2．如图3－199所示，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ等于 ( )A．60° B．65° C．72° D．75°3．(2014年广西南宁，第6题3分）在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A． 40cm B． 60cm C． 80cm D． 100cm4．如图3－201所示，AB，AC是⊙O的两条切线，B，C是切点．若∠A＝70°，则∠BOC的度数为A．130° B．120° C．110° D．100°5．如图3－202所示，CD是⊙O的直径，A，B是⊙O上的两点．若∠ABD＝20°，则∠ADC 的度数为 ( )A．40°B．50° C．60°D．70°6．如图3－203所示，在梯形ABCD中，AB∥CD，AB⊥BC，AB＝2 cm，CD＝4 cm，以BC 上一点O为圆心的圆经过A，D两点，且∠AOD＝90°，则圆心O到弦AD的距离是 ( )A．cm B C． D．7．如图3－204所示，∠AOB是⊙O的圆心角，∠AOB＝80°，则弧AB所对圆周角∠ACB 的度数是 ( )A．40° B．45°C．50° D．80°8．如图3－205所示，已知⊙O的半径为5 cm，弦AB的长为8 cm，P是AB延长线上一点，BP＝2 cm，则tan∠OPA等于 ( )A．32B．23C．2 D．129．如图3－206所示，⊙O是△ABC的外接圆，AB是直径，若∠BOC＝80°，则∠A等于( )A．60° B．50°C．40° D．30°10．(2014年贵州安顺，第10题3分)如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为（）A．B． 1 C． 2 D．2二、填空题11．在圆O中，弦AB的长为6，它所对应的弦心距为4，那么半径OA＝．12．直角三角形的斜边长是6，以斜边的中点为圆心，斜边上的中线为半径的圆的面积是．13．（2014•广西来宾，第18题3分）如图，点A、B、C均在⊙O上，∠C=50°，则∠OAB=度．．14．如图3－207所示，AB是⊙O的直径，弦CD∥AB．若∠ABD＝65°，则∠ADC ＝．15．如图3－208所示，在⊙O中，直径MN＝10，正方形AB CD的四个顶点分别在PM以及⊙O的半径OM，OP上，并且∠POM＝45°，则AB的长为．16．如图3－209所示，⊙A，⊙B的圆心A，B在直线l上，两圆的半径都为1 cm，开始时圆心距AB＝4 cm．现⊙A，⊙B同时沿直线l以每秒2 cm的速度相向移动，则当两圆相切时，⊙A运动的时间为秒．17．（2014•黔南州，第19题5分）如图，直径为10的⊙A经过点C（0，6）和点O（0，0），与x轴的正半轴交于点D，B是y轴右侧圆弧上一点，则cos∠OBC的值为．18．如图3－210所示，点A，B是⊙O上两点，AB＝10，点P是⊙O上的动点(P与A，B 不重合)，连接AP，PB，过点O分别作OE⊥AP于E，OF⊥PB于F，则EF＝．19．如图3－211所示，把半径为4 cm的半圆围成一个圆锥的侧面，使半圆圆心为圆锥的顶点，那么这个圆锥的高是 cm．(结果保留根号)20．(2014•陕西,第17题3分)如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是．三、解答题21．如图3－213所示，已知⊙O的直径AB垂直弦CD于点E，连接CO并延长交AD于点F．若CF⊥AD，AB＝2，求CD的长．22．（（2014•黔南州，第24题10分）如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足=，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．（1）求证：△ADF∽△A ED；（2）求FG的长；（3）求证：tan∠E=．23．如图3－215所示，已知△ABC内接于⊙O，点D在OC的延长线上，sin B＝12，∠D＝30°．(1)求证AD是⊙O的切线；(2)若AC＝6，求AD的长．24．如图3－216所示，AB是⊙O的直径，弦BC＝5，∠BOC＝50°，OE⊥AC，垂足为E．(1)求OE的长；(2)求劣弧AC的长．(结果精确到0．1)25．（2014•湖北黄石,第19题7分）如图，A、B是圆O上的两点，∠AOB=120°，C是AB弧的中点．（1）求证：AB平分∠OAC；（2）延长OA至P使得OA=AP，连接PC，若圆O的半径R=1，求PC的长．26．如图3－218(1)所示，圆内接△ABC中，AB＝BC＝CA，OD，OE为⊙O的半径，OD⊥BC 于点F，OE⊥AC于点G．(1)求证阴影部分四边形OFCG的面积是△ABC面积的13；(2)如图3－218(2)所示，若∠DOE保持120°角度不变，求证当∠DOE绕着O点旋转时，由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的13．参考答案1．C 2．D 3．A 4．C 5．D 6．B 7．A 8．D 9．C 10．AB 11．5 12．9π 13．4014．25° 15．16．12或3217． 18．5 19． 20．4．21．解：如图3－219所示，在△AOF 和△COE 中．∠AFO ＝∠CEO ＝90°，∠AOF ＝∠COE ，∴∠A ＝∠C ．连接OD ，则∠A ＝∠ODA ，∠C ＝∠ODC ，∴∠A ＝∠ODA ＝∠ODC ．∵∠A ＋∠ODA ＋∠ODC ＝90°，∴∠ODC ＝30°，∴DE ＝ODcos 30．CD＝2DE ＝22．解：①∵AB 是⊙O 的直径，弦CD⊥AB， ∴DG=CG，∴弧AD=弧AC ，∠ADF=∠AED， ∵∠FAD=∠DAE（公共角）， ∴△ADF∽△AED；②∵=，CF=2，∴FD=6， ∴CD=DF+CF=8， ∴CG=DG=4，∴FG=CG﹣CF=2；③∵AF=3，FG=2，③∵AF=3，FG=2，∴AG=，tan∠E=．23．(1)证明：如图3－221所示，连接OA．∵sin B＝12，∴∠B＝30°，∴∠AOC＝60°．∵∠D＝30°，∴∠OAD＝180°－∠D－∠AOD＝90°．∴AD是⊙O的切线．(2)解：∵OA＝OC，∠AOC＝60°，∴△AOC是等边三角形．∴OA＝AC＝6．∵∠OAD＝90°，∠D＝30°，∴AD＝=24．解：(1)∵OE⊥AC．垂足为E．∴AE＝EC．∵AO＝BO，∴OE＝12BC＝52．(2)∠A＝12∠BOC＝25°，在Rt△AOE中，∵sin A＝OEOA，∴OA＝2.5sin25．∵∠AOC＝180°－50°＝130°，∴劣弧AC的长＝130 2.5180sin25π⨯≈13．4．25．解答：（1）证明：连接OC，∵∠AOB=120°，C是AB弧的中点，∴∠AOC=∠BOC=60°，∵OA=OC，∴△ACO是等边三角形，∴OA=AC，同理OB=BC，∴OA=AC=BC=OB，∴四边形AOBC是菱形，∴AB平分∠OAC；（2）解：连接OC，∵C为弧AB中点，∠AOB=120°，∴∠AOC=60°，∵OA=OC，∴OAC是等边三角形，∵OA=AC，∴AP=AC，∴∠APC=30°，∴△OPC是直角三角形，∴．26．(1)证明：连接OA，OC，∵点O是等边三角形ABC的外心，Rt△OFC≌Rt△OGC≌Rt△OGA，S四边形OFCG ＝2S△OFC＝S△OAC．∵S△OAC＝13S△ABC，∴S四边形OFCG＝13S△ABC． (2)证法1：如图3－223(1)所示，连接OA，OB和OC，则△AOC≌△COB≌△BOA，∠1＝∠2．不妨设OD交BC于点F，OE交AC于点G，∠AOC＝∠3＋∠4＝120°，∠DOE＝∠5＋∠4＝120°，∴∠3＝∠5．在△OAG和△OCF中，21,,35,OA OC∠=∠⎧⎪=⎨⎪∠=∠⎩∴△OAG≌△OCF，∴S四边形OFCG＝S△AOC＝13S△ABC．证法2：如图3－223(2)所示，不妨设OD交BC于点F，OE交AC于点G，作DH⊥BC，OK⊥AC，垂足分别为点H，K．在四边形HOKC中，∠OHC＝∠OKC＝90°，∠C＝60°，∴∠HOK＝360°－90°－90°－60°＝120°，即∠1＋∠2＝120°．又∵∠GOF＝∠2＋∠3＝120°∴∠1＝∠3．∵AC＝BC，∴OH＝OK．又∠OHF＝∠OKG＝90°．∴△OFH≌△OGK，∴S四边形OFCG ＝S四边形OHCK＝13S△ABC．。

北师大版九年级数学下学期第三章《圆》单元测试

北师大版九年级下学期第三章《圆》单元测试姓名:________ 班级:________ 成绩:________一、单选题1 . 如图，射线与相切于点，若，则的值为（）A．B．C．D．2 . 如图，点A，B，C，D，E为⊙O的五等分点，动点M从圆心O出发，沿线段OA→劣弧AC→线段CO的路线做匀速运动，设运动的时间为t，∠DME的度数为y，则下列图象中表示y与t之间函数关系最恰当的是（）A．B．C．D．3 . 如图所示,点M是半径为5的内一点,且OM=3,在过点M的所有的弦中,弦长为整数的弦的条数为（）A．2B．3C．4D．54 . 如图，在⊙O中，弦AC∥半径OB，∠BOC＝48°，则∠OAB的度数为（）A．24°B．30°C．50°D．60°5 . 下列说法：①三点确定一个圆；②任何三角形有且只有一个内切圆；③相等的圆心角所对的弧相等；④正多边形一定是中心对称图形，其中真命题有（）A．1个B．2个C．3个D．4个6 . 如图，直线BC与⊙A相切于点C，过B作CB的垂线交⊙O于D，E两点，已知AC＝，CB＝a，则以BE，BD的长为两根的一元二次方程是（）A．x2+bx+a2＝0B．x2﹣bx+a2＝0C．x2+bx﹣a2＝0D．x2﹣bx﹣a2＝07 . 如图，△ABC内接于⊙O，AB=BC，∠ABC=120°，AD为⊙O的直径，AD=6，那么AB的值为（）A．3B．C．D．28 . 如图，A点是半圆上一个三等分点，B点是弧AN的中点，P点是直径MN上一动点，⊙O的半径为1，则AP ＋BP的最小值为A．1C．D．B．9 . 如图，P为⊙O内的一个定点，A为⊙O上的一个动点，射线AP、AO分别与⊙O交于B、C两点．若⊙O的半径长为3，OP＝，则弦BC的最大值为（）A．2B．3C．D．310 . 如图，AB是⊙O的直径，∠AOC=110°，则∠D=（）A．250B．350C．550D．700二、填空题11 . 如图，为的直径，切于点，交的延长线于，且，则的度数为______．12 . 如图，直径AB为4的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是．13 . 已知扇形的圆心角为120º，半径为6cm，则扇形的弧长为________cm.14 . 如图，在⊙O中，直径AB⊥CD于点M，AM＝18，BM＝8，则CD的长为________．15 . 如图中的同心圆，大的弦切小于，且，则阴影部分即圆环的面积为______.16 . 半径为4的圆中，长为4的弦所对的圆周角的度数是_________．三、解答题17 . 已知是半径为1的圆的一条弦，且,以为一边在圆内作正三角形，点为圆上不同于点的一点，且，的延长线交圆于点，求的长。

北师大版九年级数学下册第三章圆单元检测试卷含答案

北师大版九年级数学下册第三章圆单元检测试卷考试总分： 120 分考试时间： 120 分钟学校：__________ 班级：__________ 姓名：__________ 考号：__________一、选择题（共 10 小题，每小题 3 分，共 30 分）1.有下列四个命题，其中正确的有（）①圆的对称轴是直径；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．A.个B.个C.个D.个2.已知是的直径，，、分别与圆相交于、，那么下列等式中一定成立的是（）A. B.C. D.3.下列说法中正确的是（）A.垂直于半径的直线是圆的切线B.圆的切线垂直于半径C.经过半径的外端的直线是圆的切线D.圆的切线垂直于过切点的半径4.在半径为的圆中，长度等于的弦所对的弧的度数为（）A. B.C. D.或5.如图，为的直径，、为上的点，直线切于点，图中与互余的角有（）A.个B.个C.个D.个6.已知的半径为，为内一点，且，则过点，且长度为整数的弦有（）A.条B.条C.条D.条7.如图内接于，，是的两条切线，已知，，则的弧度数为（）A. B. C. D.8.如图，在中，，，分别与边，相切，切点分别为，，则的半径是（）A. B. C. D.9.如图，是直径，弦于点．若，，则的直径为（）A. B. C. D.10.如图，是的切线，切点为，是的直径，交于点，连接．若，则的大小为（）A. B. C. D.二、填空题（共 10 小题，每小题 3 分，共 30 分）11.在圆内接四边形中，，则________．12.半径为，圆心角为的扇形面积是________（结果保留）．13.如图，已知是外接圆的直径，，则的度数是________．14.如图，在中，弦和相交于点，若，，，则的长为________．15.如图，是的外接圆，于点，为的中点，且的度数为，则________度．16.有一长、宽分别为，的矩形，以为圆心作圆，若、、三点中至少有一点在圆内，且至少有一点在圆外，则的半径的取值范围是________．17.已知在平面内有不重合的四个点，它们一共可以确定________个圆．18.在中，，，，则外接圆半径是________；内切圆半径是________．19.在中，，，，则其外接圆的半径为________．20.如图，四边形是的内接四边形，的半径为，，则的长________．三、解答题（共 8 小题，共 60 分）21.（4分）已知三点、、，用直尺和圆规作，使过点、、．（不写作法，保留痕迹）22.(8分) 如图，是外一点，交于点，切于点，，，求：（1）的半径；阴影部分的面积．23.(8分) 如图，已知是的外接圆，，是劣弧上的点（不与点、重合），延长至．求证：的延长线平分；若，中边上的高为，求的面积．24.(8分) 已知：如图，是的直径，是的切线，切点为．点为射线上一动点（点与不重合），且弦平行于．求证：是的切线；设的半径为．试问：当动点在射线上运动到什么位置时，有？请回答并证明你的结论．25.(8分) 如图，的直径，弦于点，．求的长；延长到，过作的切线，切点为，若，求的长．26.(8分) 为的直径，是外一点，交于点，过点作的切线，交于点，，作于点，交于点．求证：是的切线；求证：．27.(8分) 如图，四边形是平行四边形，以为直径的经过点，是上一点，且，求证：是的切线．若的半径为，，求的正弦值．28.(8分) 如图，是的直径，是上的一点，过点作于点，交于点，且．求证：是的切线；若，，求的长．答案1.C2.C3.D4.D5.C6.C7.A8.A9.D10.A11.12.13.14.15.16.17.或或或18.19.20.21.解：如图所示：即为所求．22.解：根据切割线定理得：，解得；．从图中可以看出阴影部分的面积扇形23.证明：如图，设为延长线上一点，∵ ，，，四点共圆，∴ ，∵ ，∴ ，∵ ，∴ ，∵ ，∴ ，即的延长线平分．设为外接圆圆心，连接比延长交于，交于点，连接，∵ ，∴，∴ ．∴，∴ ，设圆半径为，则，∵ 中边上的高为，∴，解得：，∴ 的外接圆的面积为：．24.证明：连接；∵ ，∴ ，∵ ，∴ ，，∴ ；∵ ，，∴ ，∴ ，∵ 是的半径，∴ 是的切线．解：当时；∵ ，，∴ ，∴ ，∴．25.解： ∵直径，弦于点，∴ ，∴ ，∴ ，∴ ； ∵ 切于点，∴ ，∵，∴ ，或（舍去），∴ ．26.解：连接，∵ ，∴ ，∵ 是的切线，∴ ，∵ 为的直径，∴ ，∴ ，∴ ，∴ ，∴ 是的切线；∵ ，∴ ，∵ ，∴ ，∴ ，，∴，，∴，∵ ，∴ ，∴ ，∴ ，∴ ，∴ ．27.证明：连结，如图，∵ ，∴ ，∵四边形是平行四边形，∴ ，∴ ，∴ 是的切线；解：连结，∵ 为直径，∴ ，根据圆周角定理：，∴．即的正弦值是．28.证明：连接，如图，∵，∴ ，∵ ，∴ ，∴ ，∴ ，∵ ，∴ ，∴ 是的切线；解：连接交于，如图，∵ 是的直径，∴ ，在中，，而，∴ ，∴，∵ ，∴ ，∴，即，解得，∵，即，解得，∵，∴ ，，∴四边形为矩形，∴，∴，∵ 为直径，∴ ，在中，，∴．。

北师大版九年级数学下册第3章圆单元检测试题

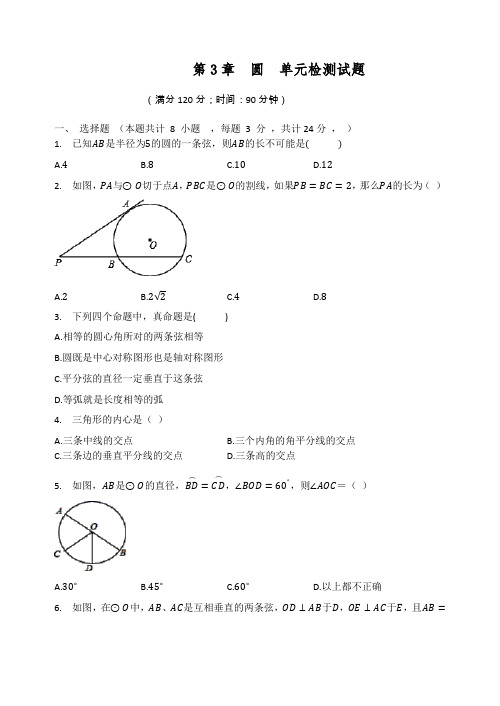
第3章圆单元检测试题（满分120分；时间：90分钟）一、选择题（本题共计 8 小题，每题 3 分，共计24分，）1. 已知AB 是半径为5的圆的一条弦，则AB 的长不可能是( )A.4B.8C.10D.122. 如图，PA 与⊙O 切于点A ，PBC 是⊙O 的割线，如果PB =BC =2，那么PA 的长为（）A.2B.2√2C.4D.83. 下列四个命题中，真命题是( )A.相等的圆心角所对的两条弦相等B.圆既是中心对称图形也是轴对称图形C.平分弦的直径一定垂直于这条弦D.等弧就是长度相等的弧4. 三角形的内心是（）A.三条中线的交点B.三个内角的角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点 5. 如图，AB 是⊙O 的直径，BD ⌢=CD ⌢，∠BOD =60∘，则∠AOC ＝（）A.30∘B.45∘C.60∘D.以上都不正确6. 如图，在⊙O 中，AB 、AC 是互相垂直的两条弦，OD ⊥AB 于D ，OE ⊥AC 于E ，且AB =8cm，AC=6cm，那么⊙O的半径OA长为（）A.4cmB.5cmC.6cmD.8cm7. 如图，⊙O阴影部分为残缺部分，现要在剩下部分裁去一个最大的正方形，若OP=2，⊙O半径为5，则裁去的最大正方形边长为多少？（）A.7B.6C.5D.48. 如图，△ABC是一张周长为17cm的三角形的纸片，BC＝5cm，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（）A.12cmB.7cmC.6cmD.随直线MN的变化而变化二、填空题（本题共计8小题，每题3 分，共计24分，）9. 已知在⊙O中，半径r=2，∠AOB=150∘，则劣弧AB的弧长为________cm．10. 已知扇形的圆心角为120∘，所对的弧长为8π，则此扇形的面积是________．311. 如图：在半径为1的圆中，弦CD垂直平分AB，则CD=________．12. 如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若∠ADB=100∘，则∠ACB的度数为________．13. 如图，弦AB和CD交于内一点P，若AP=3，PB=4，CP=2，则PD=________．14. 如图，直角△ABC的直角顶点C，另一顶点A及斜边AB的中点D都在⊙O上，已知：AC=6，BC=8，则⊙O的半径为________．15. 如图，两边平行的刻度尺在圆上移动，当刻度尺的一边与直径为10cm的圆相切时，另一边与圆两个交点处的读数恰好为“4”和“12”（单位：cm），则刻度尺的宽为________cm．16 如图，点A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为________．三、解答题（本题共计6小题，共计72分，）17 如图所示，CD是△ABC的中线，AB=2CD，∠B=60∘．求证：△ABC的外接圆的半径为CB．18. 已知在四边形ABCD中，∠B+∠D=180∘，能否画出一个圆，使它的四个顶点都在同一个圆上？19 已知：如图，△ABC内接于⊙O，过A点作直线DE，当∠BAE=∠C时，试确定直线DE 与⊙O的位置关系，并证明你的结论．20. 如图，△ABC是⊙O的内接等边三角形，⊙O的半径为r．̂的度数；（1）求BC（2）求证：△ABC的边长为√3r．21. 如图，在梯形ABCD中，AD // BC，∠C=90∘，AD+BC=AB，以AB为直径作⊙O，求证：CD是⊙O的切线．22. 如图所示，点ABD都在⊙O上，BC是⊙O的切线，AD // BC，∠C=30∘，AD=4√3．（1）求∠A的度数；（2）求由线段BC、CD与弧BD所围成的阴影部分的面积．（结果保留π）。

九年级下册数学单元测试卷-第三章圆-北师大版(含答案)

九年级下册数学单元测试卷-第三章圆-北师大版(含答案)一、单选题(共15题，共计45分)1、如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是的中点，则下列结论：①OC∥AE；②EC＝BC；③∠DAE＝∠ABE；④AC⊥OE，其中正确的有( )A.1个B.2个C.3个D.4个2、给出下面四个命题，其中真命题的个数有（）⑴平分弦的直径垂直于这条弦，并且平分这条弦所对的弧；(2)90°的圆周角所对的弦是直径；(3)在同圆或等圆中，圆心角的度数是圆周角的度数的两倍；(4)如下图，顺次连接圆的任意两条直径的端点，所得的四边形一定是矩形．A.1个B.2个C.3个D.4个3、下列命题：①三点确定一个圆；②三角形的外心到三边的距离相等；③相等的圆周角所对的弧相等；④平分弦的直径垂直于弦.其中假命题的个数是（）A.1B.2C.3D.44、如图，与相切于点，若，则的度数为（）A. B. C. D.5、若⊙O的弦AB等于半径，则AB所对的圆心角的度数是（）A.30°B.60°C.90°D.120°6、已知⊙O的半径为10cm，弦AB∥CD，AB=12cm，CD=16cm，则AB和CD的距离为（）A.2cmB.14cmC.2cm或14cmD.10cm或20cm7、如下图：⊙O的直径为10，弦AB的长为8，点P是弦AB上的一个动点，使线段OP的长度为整数的点P有（）A.3 个B.4个C.5个D.6个8、如图所示,直线CD与线段AB为直径的圆相切于点D,并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动．当∠APB的度数最大时,则∠ABP的度数为A.90°B.60°C.45°D.30°9、⊙O的半径是6，点O到直线a的距离为5，则直线a与⊙O的位置关系为（）A.相离B.相切C.相交D.内含10、如图，CD是⊙O的弦，O是圆心，把⊙O的劣弧沿着CD对折，A是对折后劣弧上的一点，∠CAD=110°，则∠B的度数是（）A.110°B.70°C.60°D.55°11、如图，CD为⊙O的弦，直径AB为4，AB⊥CD于E，∠A＝30°，则扇形BOC的面积为（）A. B. C.π D.12、若点A的坐标为（3，4），⊙A的半径5，则点P（6，3）的位置为（）A.P在⊙A内B.P在⊙A上C.P在⊙A外D.无法确定13、下列命题中，正确的是（）A.圆心角相等，所对的弦相等B.三点确定一个圆C.长度相等的弧是等弧D.弦的垂直平分线必经过圆心14、如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD=20°，则下列说法中正确的是（）A.AD=2OBB.CE=EOC.∠OCE=40°D.∠BOC=2∠BAD15、有一个三角形的外接圆的圆心在它的某一边上则这个三角形一定是（）A.等边三角形B.直角三角形C.锐角三角形D.钝角三角形二、填空题(共10题，共计30分)16、如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F.若∠ACF=65°，则∠E=________.17、如图，⊙O的直径为10，弦AB=8，P是弦AB上的一个动点，那么OP的长的范围是________。

北师大版九年级数学下册第三章圆测试题

北师大版九年级数学下册第三章圆测试题1 / 3北师大版九年级数学下册第三章《圆》测试题一、选择题1、如下图， A 、 B 、C 是⊙ O 上的三点，∠ BAC=30 °则∠ BOC 的大小是（）A ．60°B ． 45°C ．30°D ．15°2、已知 AB 、CD 是⊙ O 两条直径，则四边形 ABCD 为（）A 平行四边形；B 菱形；C 矩形；D 正方形。

3、以下命题正确的选项是（）A ．相等的圆心角所对的弦相等B ．等弦所对的弧相等C ．等弧所对的弦相等D ．垂直于弦的直线均分弦1 题图4、如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为 24 米，拱的半径为 13 米，则拱高为 ( )A 5 米 B 8 米 C7 米 D5 3 米5、一个点与定圆近来距离为 4，最远点为 9，则圆的半径为（）A 2.5 或BCD 5或136、如图，⊙ O 的两条弦 AC ，BD 订交于点 E ，∠ A=70 °，∠ C=50 °，那么 sin ∠AEB 的值为 ()A1 B 3 C2 D3 4 题图23227、如图，在 5× 5 正方形网格中，一条圆弧经过 A ，B ，C 三点，那么这条圆弧所在圆的圆心是（）A ．点 P B ．点 Q C ．点 R D ．点 M 8 如图，⊙ O 是△ ABC 的外接圆， AD 是⊙ O 的直径，若⊙ O 的半径为6，sinB=1，则线段3AC 的长是（）9、如图， AB 是⊙ O 的直径，点 D 在 AB 的延伸线上， DC 切⊙ O 于 C 若∠ A=25 °则∠ D等于（）A ．40°B ． 50°C ． 60°D ． 70°10、如图，⊙ O 是△ ABC 的外接圆， AD 是⊙ O 的直径，若⊙ O 的半径为， AC=2 ，则 sinB 的值是（2B ．3 3D ．4） A ．2C ．3346题图7题图 9题图10题图11、如图 1， AB 是⊙ O 的直径， C 是⊙ O 上的一点，若 AC=8 ， AB=10 ，OD ⊥ BC 于点 D ，则 BD 的长为（）A 、B 、3C 、5D 、612、如图，⊙ O 是△ ABC 的外接圆，已知∠ B=60 °，则∠ CAO 的度数是 ()A ． 15°B ．30°C ． 45°D ． 60°13、如图， A 、D 是⊙ O 上的两个点， BC 是直径，若∠ D = 35 °，则∠ OAC 的度数是（）A ．35°B ．55°C ．65°D ．70°11 题图 12 题图 13题图北师大版九年级数学下册第三章圆测试题2 / 3二、填空题14、如图∠ MAB=30 °，P 为 AB 上的点，且 AP=6 ，圆 P 与 AM 相切，则圆 P 的半径为 ________． 15、如图，△ ABC 内接于⊙ O ，AC 是⊙ O 的直径，∠ ACB ＝ 500，点 D 是 BAC 上一点，则 ∠D ＝ _______________16、如图⊙ O 的半径是 6cm ，弦 CB=63 cm ， OD ⊥ BC ，垂足为 D ，则∠ COB=________ ．17、△ ABC 中， AB=10cm ， AC=8cm,BC=6cm, ，以点 B 为圆心、 6cm 为半径作⊙ B ，则边 AC 所在的直线与⊙ B 的地点关系是 _________．18、如图，一个宽为 2 cm 刻度尺在圆形光盘上挪动，当刻度尺的一边与光盘相切时，另一边与光盘边沿两个交点处读数恰巧是“2”和“10（”单位： cm ），那么该光盘的直径是 _____cm.14 题图16 题图题图18 题图1519、如图 AB 为⊙ O 的直径，点 C ， D 在⊙ O 上．若∠ AOD ＝ 30°，则∠ BCD 度数是 _____．20、如图， AB 是⊙ O 的直径，弦 DC 与 AB 订交于点 E ，若∠ ACD=60 °，∠ ADC=50 °，则∠ ABD=________ ，∠ CEB=_________.21、如图，已知 AB 是⊙ O 的直径， PB 是⊙ O 的切线， PA 交⊙ O 于 C ，AB=3cm ，PB=4cm ，则 BC=___________ . 22、如图，点 A 、B 、C 在⊙ O 上，切线 CD 与 OB 的延长线交于点D ，若∠ A=30 °， CD=2 3 ，则⊙ O 的半径长为___________ ．OA19 题图20题图 B21 题三、解答题 16、 CD第19题图如图在⊙ O 中，CD 是直径， AB 是弦，且 CD ⊥ AB ，CD =20，CM=4，求 AB 。

北师大新版九年级下册数学第3章圆单元测试卷及答案解析

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

试卷
·
A
B
C D
O
M
11题

第三章：圆（考查范围：第1-4节小测）
一．选择题
1．与圆心的距离不大于半径的点所组成的图形是（）
A．圆的外部（包括边界） B．圆的内部（不包括边界）
C．圆 D．圆的内部（包括边界）
2．下列说法中，正确的是（）
A．等弦所对的弧相等 B．等弧所对的弦相等
C．圆心角相等，所对的弦相等 D．弦相等，所对的圆心角相等
3．⊙O的半径r=10cm，圆心到直线a的距离OM=8cm，在直线a上有一点P，且PM=6cm，
则点P（）
A．在⊙O内 B．在⊙O 上 C．在⊙O 外 D．可能⊙O内也可能在外
4．若正方形ABCD的边长为1，对角线AC，BD交于点O,现以O为圆心，使点C在⊙O
外，则⊙O的半径可以是（）

A．12 B．32 C．22 D．1
5．如图，A、B、C、D在同一个圆上，则圆中相等的圆周角有（）对
A．1 B．2 C．3 D．4
6. 如图， △ABC 内接于 ⊙O ， ∠B = 45º, AC =4 ，则⊙O的半径为

A ．22 B ．4 C ．23 D ． 5
7. 已知⊙O的半径为5mm，弦mmAB8，则圆心O到AB的距离是
A．1 mm B．2 mm C．3 mm D．4 mm
8.如图，A、B、C是⊙O上的三点，已知60O，则C（）
A．20 B．25 C．30 D．
45

二．填空题
9.如图，在⊙O中，∠ACB＝∠D＝60°，AC＝3，则△ABC的周长为_________.
10
.如图所示，A、B、C、D是圆上的点，∠1＝68°，∠A＝40°．

则∠D＝_______．
11.如图，在直径AB＝12的⊙O中，弦CD⊥AB于M，且M是半径
OB的中点，则弦CD的长是_______（结果保留根号）

C
D

A
B

5题
6题
C
O

O
A
B

8题
A

B D C
9题

O
.

1
D
C
B

10题
试卷
D
C
A
B

12.已知在⊙O中,直径AB垂直弦CD于点M,AM=18,BM=8 ,求CD的
长 .
13.直角三角形的两边长分别为16和12，则此三角形的外接圆半径是 .
三.解答题
14.如图，在三角形ABC中，∠ACB=90°，AC=6，BC=8，以C为圆心，以AC为半径作
圆C，交AB于点D，求BD的长

15.如图，AB是⊙O的直径，C是⊙O上一点，若AC︰BC＝4︰3， AB＝10cm，OD⊥
BC于点D，求BD的长为

16.如图，已知在半圆AOB中，AD＝DC，∠CAB＝30°，AC＝32，求AD的长度．
17.如图，⊙C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第
三象限内OB上一点，BMO120，求⊙C的半径

C
O
A
B

x
y
C
A

O
B

M
试卷

18.如图，在⊙O中，AB为弦，C、D两点在AB上，且AC＝BD．求证：△OCD为等腰三角
形．

19.如图，在⊙O中，点A、B、C、D在⊙O上，若∠ADB=∠ADC=60°，判定△ABC的形
状，并说明理由

20.如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1＝∠C．
（1）求证：CB∥PD；
（2）若BC＝3，sinP＝35，求⊙O的直径．

A
C
O
B