统计学课件第5章概率与概率分布配套讲义
合集下载
统计学课件第5-7章概率分布、抽样分布及参数估计剖析.

第5、6、7章
概率分布、抽样分布及参数估计
Probability Distributions & Sampling Distributions
& Parameter Estimation
Wednesday, January 16, 2019
Statistical Research Office
1
本部分主要研究的问题有:
● 遵循随机性原则 --- 体现在在每一层抽选中;
● 每一层内应包含足够多的个体;
● 在同等条件下,抽样误差要小于简单随机抽 样和系统抽样的抽样误差。
Wednesday, January 16, 2019 Statistical Research Office 12
Wednesday, January 16, 2019
Statistical Research Office
7
●
常用的随机抽样组织方式
► 简单随机抽样(Simple random sampling)
►分层随机抽样(Stratified sampling)
►系统随机抽样(Systematic sampling)
►整群随机抽样 (Cluster sampling) 常用的随机抽样方法: ►重复抽样 (Sampling with replacement) ►不重复抽样(Sampling without replacement)
8
Wednesday, January 16, 2019
Statistical Research Office
★ 简单随机抽样 -定义:从总体中,按照随机的原则,使得总体 中每个个体都有同等被选中的机会,而先后抽 出的n个个体作为一个容量为n的样本。
概率分布、抽样分布及参数估计
Probability Distributions & Sampling Distributions
& Parameter Estimation
Wednesday, January 16, 2019
Statistical Research Office
1
本部分主要研究的问题有:
● 遵循随机性原则 --- 体现在在每一层抽选中;
● 每一层内应包含足够多的个体;
● 在同等条件下,抽样误差要小于简单随机抽 样和系统抽样的抽样误差。
Wednesday, January 16, 2019 Statistical Research Office 12
Wednesday, January 16, 2019
Statistical Research Office
7
●
常用的随机抽样组织方式
► 简单随机抽样(Simple random sampling)
►分层随机抽样(Stratified sampling)
►系统随机抽样(Systematic sampling)
►整群随机抽样 (Cluster sampling) 常用的随机抽样方法: ►重复抽样 (Sampling with replacement) ►不重复抽样(Sampling without replacement)
8
Wednesday, January 16, 2019
Statistical Research Office
★ 简单随机抽样 -定义:从总体中,按照随机的原则,使得总体 中每个个体都有同等被选中的机会,而先后抽 出的n个个体作为一个容量为n的样本。
第五章《概率论与数理统计教程》课件

试决定常数 3.
X ,Y
C
使得随机变量 cY 服从分布
2
分布。
相互独立,都与 N ( 0 , 9 ) 有相同分布, X 分别是来自总体
X ,Y
1
, X 2 , , X 9和
Y1 ,Y 2 , ,Y 9
的样本,
Z
9
X
i
i1
6 - 23
Y
i1
9
则Z 服从—— ,自由度为——。
2 i
4.
X1, X 2, X 3, X 4
是来自总体
X ~ N ( , )
2
的样本,则随机变
量 Y
X3 X4
服从——分布,其自由度为———。
2
(X i )
i1
2
5.
设
X 1 , X 2 , , X 10
是来自总体 X
~ N ( ,4 )
2
的样本, ( S 2 P
a ) 0 .1
一. 单个正态总体的统计量的分布
X 1 , X 2 , X n是来自正态总体 ~ N ( , 2 )的样本, X
X , S 分别是样本均值和样本 方差
2
定理1
X
n
1
n
X i ~ N ( ,
n
2
);
i1
定理2 U
1
X
/
~ N ( 0 ,1 );
n
定理3
6 - 18
定理7
当 1
2
2 2
2 2 时, 令 S w
( n1 1) S 1 ( n 2 1) S 2
2
概率论与数理统计课件第5章-PPT精品文档

PX Q 0 . 5 2
1
第三四分位数Q3: PX Q 0 . 7 5 3
例1
为对某小麦杂交组合F2代的株高X进行研究,抽
取容量为100的样本,测试的原始数据记录如下(单位: 厘米),试根据以上数据,画出它的频率直方图,求随
机变量X的分布状况。
87 99 86 87 84 85 96 90 103 88 91 94 94 91 88 109 83 89 111 98 102 92 82 80 91 84 88 91 110 99 86 94 83 80 91 85 73 98 89 102 99 81 80 87 95 70 97 104 88 102 69 94 95 92 92 90 94 75 91 95 102 76 104 98 83 94 90 96 80 80 90 92 105 92 92 90 94 97 86 91 95 94 88 96 80 94 92 91 77 83
样本方差( X X i n 1i 1
几个常用的统计量
设 (X ,X , 1 2 是总体 X 的一个样本, ,X n) 样本均方差或标准差
2 1 n S X i X n 1i 1
它们的观测值用相应的小写字母表示.反映总 体X取值的平均,或反映总体X取值的离散程度。
几个常用的统计量
设 (X ,X , 1 2 是总体 X 的一个样本, ,X n)
子样的K阶(原点)矩
1 n k Ak X i n i 1
子样的K阶中心矩
1 B k X i X n i1
n
k
数据的简单处理
为了研究随机现象,首要的工作是收集原始数据. 一般通过抽样调查或试验得到的数据往往是杂乱无章
统计学课件 (05)第5章 概率与概率分布

5 - 11
B A
A∩B
统计学
事件的关系和运算 (互斥事件)
事件A与事件B中,若有一个发生,另一个必定不发生, 则称事件A与事件B是互斥的,否则称两个事 件是相容的。显然,事件A与事件B互斥的充分必要条件是事件A与事件B没有公共的样本点
5 - 12
A
B
A 与 B互不相容
统计学
事件的关系和运算 (事件的逆)
5 - 28
统计学
概率的加法法则 (例题分析)
【例】根据钢铁公司职工的例子,随机抽取一名职工,计算该职工为炼钢厂或轧钢厂职工的概率
解:用A表示“抽中的为炼钢厂职工”这一事件;B表示“抽中的为轧钢厂职工”这一事件。随机 抽取一人为炼钢厂或轧钢厂职工的事件为互斥事件A与B 的和,其发生的概率为
P (A B ) P (A ) P (B )48 1 05 0 0 0 .50 04 121 52 05 000
统计学课件 (05)第5 章 概率与概率分布
统计学
第 5 章 概率与概率分布
§5.1 随机事件及其概率 §5.2 概率的性质与运算法则 §5.3 离散型随机变量及其分布 §5.4 连续型随机变量及其分布
5 -2
统计学
学习目标
1.
定义试验、结果、事件、样本空间、概率
2.
描述和使用概率的运算法则
3.
解:设A={读甲报纸},B={读乙报纸},C={至少读一种报纸}。则 P ( C ) =P ( A∪B )
= P ( A ) + P ( B ) - P ( A∩B ) =0.2 + 0.16 - 0.08 = 0.28
5 - 31
统计学
条件概率、乘法公式与独立事件
统计学-概率和分布42页PPT

Thank you
统计学-概率和分布
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
Байду номын сангаас
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
统计学-概率和分布
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
Байду номын сангаас
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
《概率分布》课件
次数分布图与概率密度曲线
(1)
(2)
(3)
(4)
0 .0 0 .1 0 .2 0 .3 0 .4
-2
0
2
f (x)
o
x
要注意的是,密度函数 f (x)在某点处
a的高度,并不反映X取值的概率. 但是,
这个高度越大,则X取a附近的值的概率就
越大. 也可以说,在某点密度曲线的高度
反映了概率集中在该点附近的程度。
学习重点
概率、正态分布、抽样分布
学习难点
正态分布、抽样分布
ቤተ መጻሕፍቲ ባይዱ学方法
讨论
讲授
授课时数: 3学时
基本内容
第一节 概率的一般概念 第二节 二项分布 第三节 正态分布 第四节 抽样分布
刮刮乐、双色球、3D、 地方福彩、七乐彩、 35选7、29选7、25选4
“双色球”就是从33个红色 球号码中选出6个号码,再从 16个蓝色球号码中选出1个号 码,组成乐透式投注。
解:
P 1 1 1 0.04 ( A•B) 5 5 25
答:两个学生同时抽到第1题的概率是0.04。
有限个独立事件积的概率,等于这些事 件概率的乘积。用公式表示为:
P P P P ( A1•A2An )
( A1 )
( A2 )
( An )
如:在学校里,有的老师喜欢用口试,假设 这位老师共编了5个试题,全班每个学生只能抽到 1道题,现在请问五个学生同时抽到第1题的概率 是多少。
有多大?
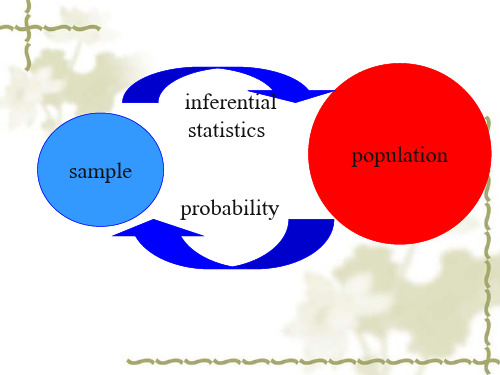
概率 ❖ 如果知道某一样本在总体中出现的概率大,
就可以认为该样本是来自总体,能反映总体 的情况,反之,就不能反映总体的情况。
概率分布
第五章 概率及概率分布
高中数学 第5章 统计与概率 5.4 统计与概率的应用课件 b高一必修第二册数学课件
层
释 疑
就应该派小明参加.]
作 业
难
·
返 首 页
12/12/2021
第八页,共五十页。
情
课
境
2.从某批零件中随机抽出 40 个检查,发现合格产品有 36 个, 堂
导
小
学 则该批产品的合格率为( )
探
·
结 提
新 知
A.36%
B.72%
素 养
·
合
C.90%
D.25%
课
作 探 究
C
[
用
样
本
的
合
格率近
似
代
课
境
堂
导
2.如图所示,A 地到火车站共有两条
小
学
结
·
探 新
路径 L1 和 L2,现随机抽取 100 位从 A 地到
提 素
知
养
达火车站的人进行调查,调查结果如下:
·
合 作
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
课 时
探
究
选择 L1 的人数 6
12
18
12
12
分 层
释
导
小
学
结
·
探 新
提
某市准备实行阶梯电价,要求约 75%的居民用电量在第一阶梯 素
知
养
内,约 20%的居民用电量在第二阶梯内,约 5%的居民用电量在第三
合
作 阶梯内.
课 时
探
究
分
层
释
作
疑
业
难
·
返 首 页
12/12/2021
教育统计学课件-6 概率与概率分布
5. 广义加法公式
对任意两个随机事件A和B,它们和(并)的概率为 两个事件各自概率的和减去两个事件交的概率,即: P(A+B) = P(A) + P(B) - P(AB) 或 P(A∪B) = P(A) + P(B) - P(A∩B)
两个事件的并
两个事件的交
“事件A或事件B发生”的事件,称为事件A与事件B的并。它 是由属于事件 A 或事件 B 的所有基本事件的集合,记为 A∪B 或A+B。
概率的古典定义(先验概率)
若试验由n个有限的基本事件构成,且每个试验中每个基
本事件出现是等可能的,如果事件A发生的次数为m,则 该事件的概率为:
m 事件A包含的基本事件数 P (A) = n 基本事件数
例2:抛掷骰子一次,所得点数小于3的概率。
解:A={1,2}, P(A)=2/6=1/3。
此时,事件A发生的概率就是事件A发生的频率的稳 定值。
概率的统计定义
在大量重复的N次试验中,当N无限增大时,事件 A发生的频率n/N稳定在一个确定的常数附近,我 们就用这个数来表示事件发生的概率,记作: P ( A)
n P (A) = lim N N
例1:一个射手射击500次,有400次中靶,问该射手 的技术水平如何?即中靶概率。
N=50
N=500
n正
1 2 2 3
FN (正)
0.40 0.60
n正
22 25
n正 F(正) N
0.44 0.50 251 249
F(正) N
0.502 0.498
3 4 5
6 7 8 9 10
概率与概率分布PPT课件
结束
2. 计算概率时 ,每一个正态分布都需要有自己的正态概率分布表,这种表格是无穷多的 3. 若能将一般的正态分布转化为标准正态分布,计算概率时只需要查一张表
标准正态分布函数
1. 任何一个一般的正态分布,可通过下面的线性变换转化为标准
正态分布
Z X m ~ N (0,1)
s
2. 标准正态分布的概率密度函数
x x1
1
t2
e 2 dt
2
(b) (a)
式中:a x1 np , b x2 np , q 1 p
npq
npq
为什么概率是近似的
P(x) .3
.2
.1
.0
0
2
二项概率:矩形的面积
正态曲线增加的概率
增加的部分与减少的部分 不一定相等
正态曲线减少的概率
4
6
8
正态概率:曲线下从3.5到 4.5的面积
正态分布
(例题分析)
【例5.22】设X~N(5,32),求以下概率
(1) P(X 10) ; (2) P(2<X <10)
解: (1) (2)
P( X 10) P X 5 10 5
3
3
P X 5 1.67 (1.67) 0.9525
3
P(2 X 10) P 2 5 X 5 10 5
•
比如,标准正态分布变量落在区间(0.51,1.57)中的概率,就是在标准正态密度曲线下面在0.51和1.57之间的面积。
•
很容易得到这个面积等于0.24682;也就是说,标准正态变量在区间(0.51,1.57)中的概率等于0.24682。如果密度
函数为f(x),那么这个面积为积分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 例如:掷一枚骰子出现的点数大于6
事件与样本空间
1. 基本事件(elementary event)
• • 一个不可能再分的随机事件 例如:掷一枚骰子出现的点数 一个试验中所有基本事件的集合,用表示 例如:在掷枚骰子的试验中,{1,2,3,4,5,6} 在投掷硬币的试验中,{正面,反面}
概率的古典定义
(例题分析)
• 解:(1)用A 表示“抽中的职工为男性”这一事件;A 为全公司男职工的集合;基本空间为全公司职工的 集合。则
全公司男性职工人数 8500 P( A) 0.68 全公司职工总人数 12500
(2) 用B 表示“抽中的职工为炼钢厂职工”;B为炼钢 厂 全体职工的集合;基本空间为全体职工的集合。则 炼钢厂职工人数 6200 P( B) 0.496 全公司职工总人数 12500
2. 规范性
• 必然事件的概率为 1;不可能事件的概率为 0。 即P ( ) = 1; P ( ) = 0
若A与B互斥,则P ( A∪B ) = P ( A ) + P ( B ) 推广到多个两两互斥事件 A1, A2, …, An,有 P ( A1∪A2 ∪… ∪An) = P ( A1 ) + P (A2 ) + …+ P (An )
【例】:某工厂为节约用电,规定每天的用电量指 标 为1000度。按照上个月的用电记录,30天中有12天 的 用电量超过规定指标,若第二个月仍没有具体的节 电 措施,试问该厂第一天用电量超过指标的概率。 解:上个月30天的记录可以看作是重复进行了30 次 超过用电指标天数 12 P( A) A 表示用电超过指标出现了 12 0.次。根据 4 试验,试验 试验的天数 30 概 率的统计定义有
(例题分析)
• 【例】 某钢铁公司所属三个工厂的职工人数如下表。
• • •
从 该公司中随机抽取1人,问: (1)该职工为男性的概率 (2)该职工为炼钢厂职工的概率 某钢铁公司所属企业职工人数
工厂 炼钢厂 炼铁厂 轧钢厂 合计 男职工 4400 3200 900 8500 女职工 1800 1600 600 4000 合计 6200 4800 1500 12500
1. 在相同条件下,对事物或现象所进行的观察
• • • • 例如:掷一枚骰子,观察其出现的点数 可以在相同的条件下重复进行 每次试验的可能结果可能不止一个,但试验的所 有可能结果在试验之前是确切知道的 在试验结束之前,不能确定该次试验的确切结果
2. 试验的特点
事件的概念
1. 事件(event):随机试验的每一个可能结果(任何样本点集 合)
i 1
n
全概公式
(例题分析)
【例】某车间用甲、乙、丙三台机床进行生产,各种机床的次品 率分别为5%、4%、2%,它们各自的产品分别占总产量的 25%、 35% 、 40%,将它们的产品组合在一起,求任取一个是次品的概 率。 解:设 A1表示“产品来自甲台机床”, A2表示“产品来自乙台 机床”, A3表示“产品来自丙台机床”, B表示“取到次品”。 根据全概公式有
概率的加法法则
(additive rule)
• • 法则二 对任意两个随机事件A和B,它们和的概率为两个事件分别 概率的和减去两个事件交的概率,即
P ( A∪ B ) = P ( A ) + P ( B ) - P ( A∩B )
概率的加法法则
(例题分析)
【例】设某地有甲、乙两种报纸,该地成年人中 有 20% 读甲报纸, 16% 读乙报纸, 8% 两种报纸 都读。问成年人中有百分之几至少读一种报纸。 解:设A={读甲报纸},B={读乙报纸},C= {至少读一种报纸}。则 P ( C ) =P ( A∪B )
3. 可加性
• •
概率的加法法则
(additive rule)
• 1. 法则一 两个互斥事件之和的概率,等于两个事件概率之和。设A和B为 两个互斥事件,则
P ( A∪B ) = P ( A ) + P ( B )
2. 事件A1,A2,…,An两两互斥,则有
P ( A1∪A2 ∪… ∪An) = P ( A1 ) + P (A2 ) + …+ P (An )
= P ( A ) + P ( B ) - P ( A∩B )
=0.2 + 0.16 - 0.08 = 0.28
条件概率与独立事件
条件概率
(conditional probability)
• 在事件B已经发生的条件下,求事件A发生的概率,称这 种概率为事件B发生条件下事件A发生的条件概率,记为
2.
样本空间(sample spacbability)
1. 2. 3. 4. 事件A的概率是对事件A在试验中出现的可能性大小的一种度量 表示事件A出现可能性大小的数值 事件A的概率表示为P(A) 概率的定义有:古典定义、统计定义和主观概率定义
事件的概率
• 例如:掷一枚骰子出现的点数为3
2.
随机事件 (random event) :每次试验可能出现也可能不 出现的事件
• 例如:掷一枚骰子可能出现的点数
3.
必然事件(certain event):每次试验一定出现的事件,用 表示
• 例如:掷一枚骰子出现的点数小于7
4.
不可能事件 (impossible event):每次试验一定不出现的 事件,用表示
概率的古典定义
• 如果某一随机试验的结果有限,而且各个
结果在每次试验中出现的可能性相同,则事 件 A 发生的概率为该事件所包含的基本事件 个数 m 与样本空间中所包含的基本事件个数 n 的比值,记为
事件A所包含的基本事件个数 P( A) 样本空间所包含的基本事件个数 m = n
概率的古典定义
事件的独立性
(independence)
1. 一个事件的发生与否并不影响另一个事件 发生的概率,则称两个事件独立 2. 若 事 件 A 与 B 独 立 , 则 P(B|A)=P(B) , P(A|B)=P(A) 3. 此时概率的乘法公式可简化为 • P(AB)=P(A)· P(B) 4. 推广到n个独立事件,有 • P(A1 A2 …An)=P(A1)P(A2) … P(An)
P( B) p ( Ai ) P( B | Ai )
i 1
3
0.25 0.05 0.35 0.04 0.40 0.02 0.0345
贝叶斯公式
(逆概公式)
1. 与全概公式解决的问题相反,贝叶斯公式是建立 在条件概率的基础上寻找事件发生的原因 2. 设 n 个 事 件 A1 , A2 , … , An 两 两 互 斥 , A1+A2+…+ An= (满足这两个条件的事件组称为 一个完备事件组),且P(Ai)>0(i=1,2, …,n),则
5. 计算离散型随机变量的概率和概率分布
6. 计算连续型随机变量的概率
7. 用正态分布近似二项分布
8. 用Excel计算分布的概率
5.1 随机事件及其概率
5.1.1 随机事件的几个基本概念
5.1.2 事件的概率 5.1.3 概率计算的几个例子
随机事件的几个基本概念
试 验
(experiment)
概率的统计定义
• 在相同条件下进行n次随机试验,事件A出
现 m 次,则比值 m/n 称为事件A发生的频率。 随着n的增大,该频率围绕某一常数P上下摆 动,且波动的幅度逐渐减小,取向于稳定, 这个频率的稳定值即为事件A的概率,记为
m P ( A) p n
概率的统计定义
(例题分析)
•
• • • • • •
P(AB) P(A|B) = P(B)
概率的乘法公式
(multiplicative rule)
1. 2. 3. 用来计算两事件交的概率 以条件概率的定义为基础 设 A 、 B 为两 个事件 ,若 P(B)>0 ,则 P(AB)=P(B)P(A|B) ,或 P(AB)=P(A)P(B|A)
概率的乘法公式
事件的独立性
(例题分析)
【例】某工人同时看管三台机床,每单位时间 ( 如 30 分钟 ) 内机床 不需要看管的概率:甲机床为0.9,乙机床为0.8,丙机床为0.85。 若机床是自动且独立地工作,求
(1)在30分钟内三台机床都不需要看管的概率
(2)在30分钟内甲、乙机床不需要看管,且丙机床需要看管的 概率
P ( Ai | B )
P ( Ai ) P ( B | Ai )
p( A ) P( B | A )
j 1 j j
n
贝叶斯公式
(例题分析)
【例】某车间用甲、乙、丙三台机床进行生产,各种机床的次品率 分别为5%、4%、2%,它们各自的产品分别占总产量的 25%、35%、 40%,将它们的产品组合在一起,如果取到的一件产品是次品,分 别求这一产品是甲、乙、丙生产的概率
(例题分析)
【例】设有 1000 件产品,其中 850 件是正品, 150 件是次品,从中依次抽取 2 件,两件都是次 品的概率是多少? 解:设 Ai 表示“第 i 次抽到的是次品”(i=1,2), 所求概率为P(A1A2)
P( A1 A2 ) P( A1 ) P( A2 | A1 ) 150 149 0.0224 1000 999
解:设 A1表示“产品来自甲台机床”, A2表示“产品来自乙台机 床”, A3表示“产品来自丙台机床”, B表示“取到次品”。根据 贝叶斯公式有:
0.25 0.05 0.3623 0.0345 0.35 0.04 P ( A2 | B ) 0.406 0.0345 0.4 0.02 P ( A3 | B ) 0.232 0.0345 P ( A1 | B )
事件与样本空间
1. 基本事件(elementary event)
• • 一个不可能再分的随机事件 例如:掷一枚骰子出现的点数 一个试验中所有基本事件的集合,用表示 例如:在掷枚骰子的试验中,{1,2,3,4,5,6} 在投掷硬币的试验中,{正面,反面}
概率的古典定义
(例题分析)
• 解:(1)用A 表示“抽中的职工为男性”这一事件;A 为全公司男职工的集合;基本空间为全公司职工的 集合。则
全公司男性职工人数 8500 P( A) 0.68 全公司职工总人数 12500
(2) 用B 表示“抽中的职工为炼钢厂职工”;B为炼钢 厂 全体职工的集合;基本空间为全体职工的集合。则 炼钢厂职工人数 6200 P( B) 0.496 全公司职工总人数 12500
2. 规范性
• 必然事件的概率为 1;不可能事件的概率为 0。 即P ( ) = 1; P ( ) = 0
若A与B互斥,则P ( A∪B ) = P ( A ) + P ( B ) 推广到多个两两互斥事件 A1, A2, …, An,有 P ( A1∪A2 ∪… ∪An) = P ( A1 ) + P (A2 ) + …+ P (An )
【例】:某工厂为节约用电,规定每天的用电量指 标 为1000度。按照上个月的用电记录,30天中有12天 的 用电量超过规定指标,若第二个月仍没有具体的节 电 措施,试问该厂第一天用电量超过指标的概率。 解:上个月30天的记录可以看作是重复进行了30 次 超过用电指标天数 12 P( A) A 表示用电超过指标出现了 12 0.次。根据 4 试验,试验 试验的天数 30 概 率的统计定义有
(例题分析)
• 【例】 某钢铁公司所属三个工厂的职工人数如下表。
• • •
从 该公司中随机抽取1人,问: (1)该职工为男性的概率 (2)该职工为炼钢厂职工的概率 某钢铁公司所属企业职工人数
工厂 炼钢厂 炼铁厂 轧钢厂 合计 男职工 4400 3200 900 8500 女职工 1800 1600 600 4000 合计 6200 4800 1500 12500
1. 在相同条件下,对事物或现象所进行的观察
• • • • 例如:掷一枚骰子,观察其出现的点数 可以在相同的条件下重复进行 每次试验的可能结果可能不止一个,但试验的所 有可能结果在试验之前是确切知道的 在试验结束之前,不能确定该次试验的确切结果
2. 试验的特点
事件的概念
1. 事件(event):随机试验的每一个可能结果(任何样本点集 合)
i 1
n
全概公式
(例题分析)
【例】某车间用甲、乙、丙三台机床进行生产,各种机床的次品 率分别为5%、4%、2%,它们各自的产品分别占总产量的 25%、 35% 、 40%,将它们的产品组合在一起,求任取一个是次品的概 率。 解:设 A1表示“产品来自甲台机床”, A2表示“产品来自乙台 机床”, A3表示“产品来自丙台机床”, B表示“取到次品”。 根据全概公式有
概率的加法法则
(additive rule)
• • 法则二 对任意两个随机事件A和B,它们和的概率为两个事件分别 概率的和减去两个事件交的概率,即
P ( A∪ B ) = P ( A ) + P ( B ) - P ( A∩B )
概率的加法法则
(例题分析)
【例】设某地有甲、乙两种报纸,该地成年人中 有 20% 读甲报纸, 16% 读乙报纸, 8% 两种报纸 都读。问成年人中有百分之几至少读一种报纸。 解:设A={读甲报纸},B={读乙报纸},C= {至少读一种报纸}。则 P ( C ) =P ( A∪B )
3. 可加性
• •
概率的加法法则
(additive rule)
• 1. 法则一 两个互斥事件之和的概率,等于两个事件概率之和。设A和B为 两个互斥事件,则
P ( A∪B ) = P ( A ) + P ( B )
2. 事件A1,A2,…,An两两互斥,则有
P ( A1∪A2 ∪… ∪An) = P ( A1 ) + P (A2 ) + …+ P (An )
= P ( A ) + P ( B ) - P ( A∩B )
=0.2 + 0.16 - 0.08 = 0.28
条件概率与独立事件
条件概率
(conditional probability)
• 在事件B已经发生的条件下,求事件A发生的概率,称这 种概率为事件B发生条件下事件A发生的条件概率,记为
2.
样本空间(sample spacbability)
1. 2. 3. 4. 事件A的概率是对事件A在试验中出现的可能性大小的一种度量 表示事件A出现可能性大小的数值 事件A的概率表示为P(A) 概率的定义有:古典定义、统计定义和主观概率定义
事件的概率
• 例如:掷一枚骰子出现的点数为3
2.
随机事件 (random event) :每次试验可能出现也可能不 出现的事件
• 例如:掷一枚骰子可能出现的点数
3.
必然事件(certain event):每次试验一定出现的事件,用 表示
• 例如:掷一枚骰子出现的点数小于7
4.
不可能事件 (impossible event):每次试验一定不出现的 事件,用表示
概率的古典定义
• 如果某一随机试验的结果有限,而且各个
结果在每次试验中出现的可能性相同,则事 件 A 发生的概率为该事件所包含的基本事件 个数 m 与样本空间中所包含的基本事件个数 n 的比值,记为
事件A所包含的基本事件个数 P( A) 样本空间所包含的基本事件个数 m = n
概率的古典定义
事件的独立性
(independence)
1. 一个事件的发生与否并不影响另一个事件 发生的概率,则称两个事件独立 2. 若 事 件 A 与 B 独 立 , 则 P(B|A)=P(B) , P(A|B)=P(A) 3. 此时概率的乘法公式可简化为 • P(AB)=P(A)· P(B) 4. 推广到n个独立事件,有 • P(A1 A2 …An)=P(A1)P(A2) … P(An)
P( B) p ( Ai ) P( B | Ai )
i 1
3
0.25 0.05 0.35 0.04 0.40 0.02 0.0345
贝叶斯公式
(逆概公式)
1. 与全概公式解决的问题相反,贝叶斯公式是建立 在条件概率的基础上寻找事件发生的原因 2. 设 n 个 事 件 A1 , A2 , … , An 两 两 互 斥 , A1+A2+…+ An= (满足这两个条件的事件组称为 一个完备事件组),且P(Ai)>0(i=1,2, …,n),则
5. 计算离散型随机变量的概率和概率分布
6. 计算连续型随机变量的概率
7. 用正态分布近似二项分布
8. 用Excel计算分布的概率
5.1 随机事件及其概率
5.1.1 随机事件的几个基本概念
5.1.2 事件的概率 5.1.3 概率计算的几个例子
随机事件的几个基本概念
试 验
(experiment)
概率的统计定义
• 在相同条件下进行n次随机试验,事件A出
现 m 次,则比值 m/n 称为事件A发生的频率。 随着n的增大,该频率围绕某一常数P上下摆 动,且波动的幅度逐渐减小,取向于稳定, 这个频率的稳定值即为事件A的概率,记为
m P ( A) p n
概率的统计定义
(例题分析)
•
• • • • • •
P(AB) P(A|B) = P(B)
概率的乘法公式
(multiplicative rule)
1. 2. 3. 用来计算两事件交的概率 以条件概率的定义为基础 设 A 、 B 为两 个事件 ,若 P(B)>0 ,则 P(AB)=P(B)P(A|B) ,或 P(AB)=P(A)P(B|A)
概率的乘法公式
事件的独立性
(例题分析)
【例】某工人同时看管三台机床,每单位时间 ( 如 30 分钟 ) 内机床 不需要看管的概率:甲机床为0.9,乙机床为0.8,丙机床为0.85。 若机床是自动且独立地工作,求
(1)在30分钟内三台机床都不需要看管的概率
(2)在30分钟内甲、乙机床不需要看管,且丙机床需要看管的 概率
P ( Ai | B )
P ( Ai ) P ( B | Ai )
p( A ) P( B | A )
j 1 j j
n
贝叶斯公式
(例题分析)
【例】某车间用甲、乙、丙三台机床进行生产,各种机床的次品率 分别为5%、4%、2%,它们各自的产品分别占总产量的 25%、35%、 40%,将它们的产品组合在一起,如果取到的一件产品是次品,分 别求这一产品是甲、乙、丙生产的概率
(例题分析)
【例】设有 1000 件产品,其中 850 件是正品, 150 件是次品,从中依次抽取 2 件,两件都是次 品的概率是多少? 解:设 Ai 表示“第 i 次抽到的是次品”(i=1,2), 所求概率为P(A1A2)
P( A1 A2 ) P( A1 ) P( A2 | A1 ) 150 149 0.0224 1000 999
解:设 A1表示“产品来自甲台机床”, A2表示“产品来自乙台机 床”, A3表示“产品来自丙台机床”, B表示“取到次品”。根据 贝叶斯公式有:
0.25 0.05 0.3623 0.0345 0.35 0.04 P ( A2 | B ) 0.406 0.0345 0.4 0.02 P ( A3 | B ) 0.232 0.0345 P ( A1 | B )
