锐角三角函数的真题汇编及答案
锐角三角函数练习题及答案

锐角三角函数练习题及答案锐角三角函数练习题及答案三角函数是数学中的重要概念之一,它们在几何学、物理学和工程学等领域中都有广泛的应用。
其中,锐角三角函数是指角度小于90度的三角函数,包括正弦、余弦和正切。
本文将介绍一些锐角三角函数的练习题及答案,帮助读者加深对这些函数的理解和运用。
1. 练习题:已知一个锐角三角形的一条边长为5,另一条边长为12,求这个三角形的正弦值、余弦值和正切值。
解答:首先,我们可以利用勾股定理求得这个三角形的第三条边长。
根据勾股定理的公式,设第三条边长为c,则有c^2 = 5^2 + 12^2,即c^2 = 25 + 144,解得c ≈ 13。
接下来,我们可以利用三角函数的定义来求解所求的值。
正弦值(sin)定义为对边与斜边的比值,即sinθ = 对边/斜边。
在这个三角形中,对边为5,斜边为13,所以sinθ = 5/13。
余弦值(cos)定义为邻边与斜边的比值,即cosθ = 邻边/斜边。
在这个三角形中,邻边为12,斜边为13,所以cosθ = 12/13。
正切值(tan)定义为对边与邻边的比值,即tanθ = 对边/邻边。
在这个三角形中,对边为5,邻边为12,所以t anθ = 5/12。
因此,这个三角形的正弦值为5/13,余弦值为12/13,正切值为5/12。
2. 练习题:已知一个锐角三角形的两条边长分别为3和4,求这个三角形的角度大小及其正弦值、余弦值和正切值。
解答:根据余弦定理,我们可以求得这个三角形的第三条边长。
设第三条边长为c,则有c^2 = 3^2 + 4^2 - 2 * 3 * 4 * cosθ,即c^2 = 9 + 16 - 24cosθ,解得c ≈ 5。
接下来,我们可以利用三角函数的定义来求解所求的值。
首先,我们可以利用余弦值(cos)的定义来求解角度大小。
由于已知两条边长分别为3和4,我们可以利用余弦定理来求解cosθ。
根据余弦定理的公式,cosθ = (3^2 + 4^2 - 5^2) / (2 * 3 * 4),即cosθ = (9 + 16 - 25) / 24,解得cosθ = 0。
中考数学锐角三角函数(大题培优)含详细答案

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.如图,△ABC 内接于⊙O ,2,BC AB AC ==,点D 为AC 上的动点,且10cos B =. (1)求AB 的长度;(2)在点D 运动的过程中,弦AD 的延长线交BC 的延长线于点E ,问AD•AE 的值是否变化?若不变,请求出AD•AE 的值;若变化,请说明理由.(3)在点D 的运动过程中,过A 点作AH ⊥BD ,求证:BH CD DH =+.【答案】(1) 10AB ;(2) 10AD AE ⋅=;(3)证明见解析.【解析】【分析】(1)过A 作AF ⊥BC ,垂足为F ,交⊙O 于G ,由垂径定理可得BF=1,再根据已知结合RtΔAFB 即可求得AB 长;(2)连接DG ,则可得AG 为⊙O 的直径,继而可证明△DAG ∽△FAE ,根据相似三角形的性质可得AD•AE=AF•AG ,连接BG ,求得AF=3,FG=13,继而即可求得AD•AE 的值; (3)连接CD ,延长BD 至点N ,使DN=CD ,连接AN ,通过证明△ADC ≌△ADN ,可得AC=AN ,继而可得AB=AN ,再根据AH ⊥BN ,即可证得BH=HD+CD. 【详解】(1)过A 作AF ⊥BC ,垂足为F ,交⊙O 于G ,∵AB=AC ,AF ⊥BC ,∴BF=CF=12BC=1, 在RtΔAFB 中,BF=1,∴AB=10cos 10BF B == (2)连接DG ,∵AF ⊥BC ,BF=CF ,∴AG 为⊙O 的直径,∴∠ADG=∠AFE=90°, 又∵∠DAG=∠FAE ,∴△DAG ∽△FAE , ∴AD :AF=AG :AE , ∴AD•AE=AF•AG ,连接BG ,则∠ABG=90°,∵BF ⊥AG ,∴BF 2=AF•FG , ∵22AB BF -=3,∴FG=13,∴AD•AE=AF•AG=AF•(AF+FG)=3×10=10;3(3)连接CD,延长BD至点N,使DN=CD,连接AN,∵∠ADB=∠ACB=∠ABC,∠ADC+∠ABC=180°,∠ADN+∠ADB=180°,∴∠ADC=∠ADN,∵AD=AD,CD=ND,∴△ADC≌△ADN,∴AC=AN,∵AB=AC,∴AB=AN,∵AH⊥BN,∴BH=HN=HD+CD.【点睛】本题考查了垂径定理、三角函数、相似三角形的判定与性质、全等三角形的判定与性质等,综合性较强,正确添加辅助线是解题的关键.2.小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.(1)求∠CAO'的度数.(2)显示屏的顶部B'比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.【解析】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×=12,由C、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,∴sin∠CAO′=,∴∠CAO′=30°;(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×=12,∵O′C⊥OA,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,∴O′B′+O′C﹣BD=24+12﹣12=36﹣12,∴显示屏的顶部B′比原来升高了(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,理由:∵显示屏O′B与水平线的夹角仍保持120°,∴∠EO′F=120°,∴∠FO′A=∠CAO′=30°,∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.3.如图(1),在平面直角坐标系中,点A(0,﹣6),点B(6,0).Rt△CDE中,∠CDE=90°,CD=4,DE=4,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:(1)如图(2),当Rt△CDE运动到点D与点O重合时,设CE交AB于点M,求∠BME的度数.(2)如图(3),在Rt△CDE的运动过程中,当CE经过点B时,求BC的长.(3)在Rt△CDE的运动过程中,设AC=h,△OAB与△CDE的重叠部分的面积为S,请写出S与h之间的函数关系式,并求出面积S的最大值.【答案】(1)∠BME=15°;(2BC=4;(3)h≤2时,S=﹣h2+4h+8,当h≥2时,S=18﹣3h.【解析】试题分析:(1)如图2,由对顶角的定义知,∠BME=∠CMA,要求∠BME的度数,需先求出∠CMA的度数.根据三角形外角的定理进行解答即可;(2)如图3,由已知可知∠OBC=∠DEC=30°,又OB=6,通过解直角△BOC就可求出BC的长度;(3)需要分类讨论:①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,S=S△EDC﹣S△EFM;②当h≥2时,如图3,S=S△OBC.试题解析:解:(1)如图2,∵在平面直角坐标系中,点A(0,﹣6),点B(6,0).∴OA=OB,∴∠OAB=45°,∵∠CDE=90°,CD=4,DE=4,∴∠OCE=60°,∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°,∴∠BME=∠CMA=15°;如图3,∵∠CDE=90°,CD=4,DE=4,∴∠OBC=∠DEC=30°,∵OB=6,∴BC=4;(3)①h≤2时,如图4,作MN⊥y轴交y轴于点N,作MF⊥DE交DE于点F,∵CD=4,DE=4,AC=h,AN=NM,∴CN=4﹣FM,AN=MN=4+h﹣FM,∵△CMN∽△CED,∴,∴,解得FM=4﹣,∴S=S△EDC﹣S△EFM=×4×4﹣(44﹣h)×(4﹣)=﹣h2+4h+8,②如图3,当h≥2时,S=S△OBC=OC×OB=(6﹣h)×6=18﹣3h.考点:1、三角形的外角定理;2、相似;3、解直角三角形4.兰州银滩黄河大桥北起安宁营门滩,南至七里河马滩,是黄河上游的第一座大型现代化斜拉式大桥如图,小明站在桥上测得拉索AB与水平桥面的夹角是31°,拉索AB的长为152米,主塔处桥面距地面7.9米(CD的长),试求出主塔BD的高.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)【答案】主塔BD的高约为86.9米.【解析】【分析】根据直角三角形中由三角函数得出BC相应长度,再由BD=BC+CD可得出.【详解】在Rt△ABC中,∠ACB=90°,sin BCAAB=.∴sin152sin311520.5279.04BC AB A︒=⨯=⨯=⨯=.79.047.986.9486.9BD BC CD=+=+=≈(米)答:主塔BD的高约为86.9米.【点睛】本题考察了直角三角形与三角函数的结合,熟悉掌握是解决本题的关键.5.如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.【答案】(1)见解析;(2)∠FCN=45°,理由见解析;(3)当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=43.理由见解析.【解析】【分析】(1)根据三角形判定方法进行证明即可.(2)作FH ⊥MN 于H .先证△ABE ≌△EHF ,得到对应边相等,从而推出△CHF 是等腰直角三角形,∠FCH 的度数就可以求得了.(3)解法同(2),结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE ,得出EH=AD=BC=8,由三角函数定义即可得出结论. 【详解】(1)证明:∵四边形ABCD 和四边形AEFG 是正方形, ∴AB =AD ,AE =AG =EF ,∠BAD =∠EAG =∠ADC =90°, ∴∠BAE +∠EAD =∠DAG +∠EAD ,∠ADG =90°=∠ABE , ∴∠BAE =∠DAG , 在△ADG 和△ABE 中,ADG ABE DAG BAE AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADG ≌△ABE (AAS ). (2)解:∠FCN =45°,理由如下: 作FH ⊥MN 于H ,如图1所示:则∠EHF =90°=∠ABE , ∵∠AEF =∠ABE =90°,∴∠BAE +∠AEB =90°,∠FEH +∠AEB =90°, ∴∠FEH =∠BAE ,在△EFH 和△ABE 中,EHF ABE FEH BAE AE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△EFH ≌△ABE (AAS ), ∴FH =BE ,EH =AB =BC , ∴CH =BE =FH , ∵∠FHC =90°, ∴∠FCN =45°.(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,理由如下: 作FH ⊥MN 于H ,如图2所示:由已知可得∠EAG=∠BAD=∠AEF=90°,结合(1)(2)得:△EFH≌△GAD,△EFH∽△ABE,∴EH=AD=BC=8,∴CH=BE,∴EH FH FHAB BE CH==;在Rt△FEH中,tan∠FCN=8463 FH EHCH AB===,∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=43.【点睛】本题是四边形综合题目,考查了正方形,矩形的判定及全等三角形的判定方法等知识点的综合运用,其重点是通过证三角形全等或相似来得出线段的相等或成比例.6.如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD=12,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H.(1)求B,D两点的坐标;(2)当点E在线段OB上运动时,求∠HDA的大小;(3)以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.【答案】(1)B(4,4),D(4,2);(2)45°;(3)存在,符合条件的点为(8﹣42,8﹣42)或(8+42,8+42)或42164216,⎛⎫++ ⎪⎪⎝⎭或16421642,77⎛⎫-- ⎪ ⎪⎝⎭,理由见解析 【解析】 【分析】(1)由正方形性质知AB=OA=4,∠OAB=90°,据此得B (4,4),再由tan ∠AOD= 12得AD=12OA=2,据此可得点D 坐标; (2)由1tan 2GF GOF OF ∠==知GF=12OF ,再由∠AOB=∠ABO=45°知OF=EF ,即GF=12EF ,根据GH ∥x 轴知H 为AE 的中点,结合D 为AB 的中点知DH 是△ABE 的中位线,即HD ∥BE ,据此可得答案;(3)分⊙G 与对角线OB 和对角线AC 相切两种情况,设PG=x ,结合题意建立关于x 的方程求解可得. 【详解】解:(1)∵A (4,0), ∴OA =4,∵四边形OABC 为正方形, ∴AB =OA =4,∠OAB =90°, ∴B (4,4),在Rt △OAD 中,∠OAD =90°, ∵tan ∠AOD =12, ∴AD =12OA =12×4=2, ∴D (4,2);(2)如图1,在Rt △OFG 中,∠OFG =90°∴tan∠GOF=GFOF =12,即GF=12OF,∵四边形OABC为正方形,∴∠AOB=∠ABO=45°,∴OF=EF,∴GF=12EF,∴G为EF的中点,∵GH∥x轴交AE于H,∴H为AE的中点,∵B(4,4),D(4,2),∴D为AB的中点,∴DH是△ABE的中位线,∴HD∥BE,∴∠HDA=∠ABO=45°.(3)①若⊙G与对角线OB相切,如图2,当点E在线段OB上时,过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG2x,OF=EF=2x,∵OA=4,∴AF=4﹣2,∵G为EF的中点,H为AE的中点,∴GH为△AFE的中位线,∴GH=12AF=12×(4﹣2)=22,则x=22x,解得:x=22,∴E(8﹣2,8﹣2如图3,当点E在线段OB的延长线上时,x=2x﹣2,解得:x=2+2,∴E(8+42,8+42);②若⊙G与对角线AC相切,如图4,当点E在线段BM上时,对角线AC,OB相交于点M,过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG2,OF=EF=2x,∵OA=4,∴AF=4﹣2,∵G为EF的中点,H为AE的中点,∴GH为△AFE的中位线,∴GH=12AF=12×(4﹣2)=22,过点G作GQ⊥AC于点Q,则GQ=PM=3x﹣2∴3x﹣2=22x,∴227x=,∴42164216,77E⎛⎫⎪ ⎪⎝⎭;如图5,当点E在线段OM上时,GQ=PM=22﹣3x,则22﹣3x=2﹣2x,解得422x-=,∴16421642,77E⎛⎫--⎪ ⎪⎝⎭;如图6,当点E在线段OB的延长线上时,3x﹣22x﹣2,解得:4227x=(舍去);综上所述,符合条件的点为(8﹣2,8﹣2)或(2,2)或42164216++⎝⎭或16421642--⎝⎭.【点睛】本题是圆的综合问题,解题的关键是掌握正方形和直角三角形的性质、正切函数的定义、三角形中位线定理及分类讨论思想的运用.7.超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路(直线AO)的距离为120米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为5秒且∠APO=60°,∠BPO=45°.(1)求A、B之间的路程;(2)请判断此车是否超过了万丰路每小时65千米的限制速度?请说明理由.(参考数≈≈).据:2 1.414,3 1.73【答案】【小题1】73.2【小题2】超过限制速度.【解析】AB=-73.2 (米).…6分解:(1)100(31)(2) 此车制速度v==18.3米/秒8.现有一个“Z“型的工件(工件厚度忽略不计),如图所示,其中AB为20cm,BC为60cm,∠ABC=90,∠BCD=60°,求该工件如图摆放时的高度(即A到CD的距离).(结果精确到0.1m,参考数据:≈1.73)【答案】工件如图摆放时的高度约为61.9cm.【解析】【分析】过点A作AP⊥CD于点P,交BC于点Q,由∠CQP=∠AQB、∠CPQ=∠B=90°知∠A=∠C =60°,在△ABQ中求得分别求得AQ、BQ的长,结合BC知CQ的长,在△CPQ中可得PQ,根据AP=AQ+PQ得出答案.【详解】解:如图,过点A作AP⊥CD于点P,交BC于点Q,∵∠CQP=∠AQB,∠CPQ=∠B=90°,∴∠A=∠C=60°,在△ABQ中,∵AQ=(cm),BQ=AB tan A=20tan60°=20(cm),∴CQ=BC﹣BQ=60﹣20(cm),在△CPQ中,∵PQ=CQ sin C=(60﹣20)sin60°=30(﹣1)cm,∴AP =AQ+PQ=40+30(﹣1)≈61.9(cm),答:工件如图摆放时的高度约为61.9cm.【点睛】本题主要考查解直角三角形的应用,熟练掌握三角函数的定义求得相关线段的长度是解题的关键.9.如图,湿地景区岸边有三个观景台、、.已知米,米,点位于点的南偏西方向,点位于点的南偏东方向.(1)求的面积;(2)景区规划在线段的中点处修建一个湖心亭,并修建观景栈道.试求、间的距离.(结果精确到米)(参考数据:,,,,,,)【答案】(1)560000(2)565.6【解析】试题分析:(1)过点作交的延长线于点,,然后根据直角三角形的内角和求出∠CAE,再根据正弦的性质求出CE的长,从而得到△ABC的面积;(2)连接,过点作,垂足为点,则.然后根据中点的性质和余弦值求出BE、AE的长,再根据勾股定理求解即可.试题解析:(1)过点作交的延长线于点,在中,,所以米.所以(平方米).(2)连接,过点作,垂足为点,则.因为是中点,所以米,且为中点,米,所以米.所以米,由勾股定理得,米.答:、间的距离为米.考点:解直角三角形10.如图,AB 为O 的直径,C 、D 为O 上异于A 、B 的两点,连接CD ,过点C作CE DB ⊥,交CD 的延长线于点E ,垂足为点E ,直径AB 与CE 的延长线相交于点F .(1)连接AC 、AD ,求证:180DAC ACF ∠+∠=︒. (2)若2ABD BDC ∠=∠. ①求证:CF 是O 的切线.②当6BD =,3tan 4F =时,求CF 的长. 【答案】(1)详见解析;(2)①详见解析;② 203CF =. 【解析】 【分析】(1)根据圆周角定理证得∠ADB=90°,即AD ⊥BD ,由CE ⊥DB 证得AD ∥CF ,根据平行线的性质即可证得结论;(2)①连接OC .先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC ∥DB ,再由CE ⊥DB ,得到OC ⊥CF ,根据切线的判定即可证明CF 为⊙O 的切线;②由CF ∥AD ,证出∠BAD=∠F ,得出tan ∠BAD=tan ∠F=BD AD =34,求出AD=43BD=8,利用勾股定理求得AB=10,得出OB=OC=,5,再由tanF=OC CF =34,即可求出CF . 【详解】 解:(1)AB 是O 的直径,且D 为O 上一点,90ADB ∴∠=︒, CE DB ⊥, 90DEC ∴∠=︒, //CF AD ∴,180DAC ACF ∴∠+∠=︒. (2)①如图,连接OC . OA OC =,12∴∠=∠. 312∠=∠+∠, 321∴∠=∠.42BDC ∠=∠,1BDC ∠=∠, 421∴∠=∠, 43∴∠=∠, //OC DB ∴. CE DB ⊥, OC CF ∴⊥.又OC 为O 的半径, CF ∴为O 的切线.②由(1)知//CF AD ,BAD F ∴∠=∠, 3tan tan 4BAD F ∴∠==,34BD AD ∴=. 6BD =483AD BD ∴==,10AB ∴==,5OB OC ==.OC CF ⊥, 90OCF ∴∠=︒,3tan 4OC F CF ∴==,解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果.。
锐角三角函数(附答案)

教材过关二十八 锐角三角函数一、填空题1.在直角三角形中,斜边和一直角边的比是5∶3,最小角为α,则sin α=_______________,cos α=_________________,tan α=__________________. 答案:53 54 43 提示:假如两边长分别为5、3,则另一边为4,且3所对的角最小,由此可得答案. 2.在△ABC 中,若︱sinA-21︱+(23-cosB)2=0, 则∠C=___________________. 答案:120° 提示:由sinA=21,可得∠A=30°, 由cosB=23,得∠B=30°,则∠C=120°. 3.6tan 230°-3sin60°-2cos45°=__________________. 答案:21-2 提示:tan30°=33,sin60°=23,cos45°=22. 4.等腰三角形的两条边长分别是 4 cm ,9 cm ,则等腰三角形的底角的余弦值是________________. 答案:92 提示:三角形三边只能为4,9,9.5.若∠A 为锐角,且tan 2A+2tanA-3=0,则∠A=__________________. 答案:45°提示:解这个一元二次方程,可得tanA 的值,但∠A 为锐角,所以只能取正值. 6.如图9-43,AB 、CD 是两栋楼,且AB=CD=30 m,两楼间距AC=24 m,当太阳光与水平线的夹角为30°时,AB 楼在CD 楼上的影子是m.(精确到0.1 m )图9-43答案:16.2提示:画出图形,解直角三角形. 二、选择题7.在△ABC 中,∠C=90°,下列式子正确的是A.b=atanAB.b=csinAC.a=ccosBD.c=asinA 答案:C 提示:因为cosB=ca,所以a=ccosB. 8.在Rt △ABC 中,各边都扩大四倍,则锐角A 的各三角函数值 A.没有变化 B.分别扩大4倍 C.分别缩小到原来的41D.不能确定 答案:A提示:因为各边都扩大四倍,它们的比值不变,故三角函数值也不变. 9.在Rt △ABC 中, 2sin(α+20°)=3,则锐角α的度数是A.60°B.80°C.40°D.以上结论都不对 答案:C提示:2sin(α+20°)=3,得sin(α+20°)=23, 所以α+20°=60°,α=40°.10.在Rt △ABC 中, ∠C=90°,已知tanB=25,则cosA 等于 A.25 B.35 C.552 D.32答案:B 提示:∵tanB=25,a b =25,可令b=5,a=2,则c=3,cosA=35. 11.有一个角是30°的直角三角形,斜边为1 cm ,则斜边上的高为 A.41 cm B.21cmC.43 cm D.23 cm 答案:C 提示:直角三角形中30°角所对的边等于斜边的一半,求出两直角边再利用面积或射影定理. 三、解答题12.(2010四川泸洲中考)如图9-44,在一次实践活动中,小兵从A 地出发,沿北偏东45°方向行进了53千米到达B 地,然后再沿北偏西45°方向行进了5千米到达目的地点C.图9-44(1)求A 、C 两地之间的距离;(2)试确定目的地C 在点A 的什么方向? 解:根据题意,可知∠ABC=90°,∵AB=53,BC=5, AC 2=AB 2+BC 2 =75+25 =100.∴AC=10千米.(2)在Rt △ABC 中,tan ∠BAC=AB BC =355=33, ∴∠BAC=30°.∴C 在点A 的北偏东15°.提示:根据方向角,先确定出△ABC 是直角三角形,可用勾股定理求AC,再利用三角函数求出CA.13.如图9-45,用测角仪测得铁塔顶点A 的仰角为30°,测角仪离铁塔中心线AB 的距离为40米,测角仪CD 高1.5米,求铁塔的高度.(精确到0.1米)图9-45答案:24.6米.提示:铁塔的高度AB=40tan30°+1.5≈24.6(米). 14.如图9-46,河对岸有铁塔AB ,在C 处测得塔顶A 的仰角为30°,向塔前进14米到达D ,在D 处测得A 的仰角为45°,求铁塔AB 的高.图9-46解:在Rt △ABD 中, ∵tan ∠ADB=BDAB=1,∴BD=AB. 又在Rt △ABC 中,∵tanC=BC AB =33, ∴BC=30tan AB=3AB.又∵BC-BD=14,∴3AB-AB=14. ∴AB=7(3+1)(米).15.如图9-47,水面上有一浮标,在高于水面1米的地方观察,测得浮标顶的仰角30°,同时测得浮标在水中的倒影顶端俯角45°,观察时水面处于平静状态,求水面到浮标顶端的高度.(精确到0.1米)图9-47答案:3.7米.提示:过A 作AD ⊥BC 于D,则∠BAD=30°,∠DAC=45°. 设BD=x,则AD=xcot30°.又AD=DC 且BE=DC,即x+1=xcot30°. 求得x ≈2.73.∴BE=2.73+1≈3.7(米).16.如图9-48,在一次暖气管道的铺设工作中,工程是由A 点出发沿正西方向进行的,在A 点的南偏西60°的方向上有一所学校,学校占地是以B 点为中心方圆100米的圆形,当工程进行了200米时到达C 处,此时B 在C 的南偏西30°的方向上,请根据题中所提供的信息计算、分析一下,工程继续进行下去,是否会穿过学校?图9-48解:过B 作BD ⊥AC 于D,在Rt △BCD 中,∠BCD=60°,∵tan60°=CD BD ,∴CD=︒60tan BD. 同理,在Rt △BAD 中,AD=︒30tan BD,又∵AD-CD=200,∴3BD-33BD=200. ∴BD=1003>100.∴不会穿过学校.。
锐角三角函数练习题及答案
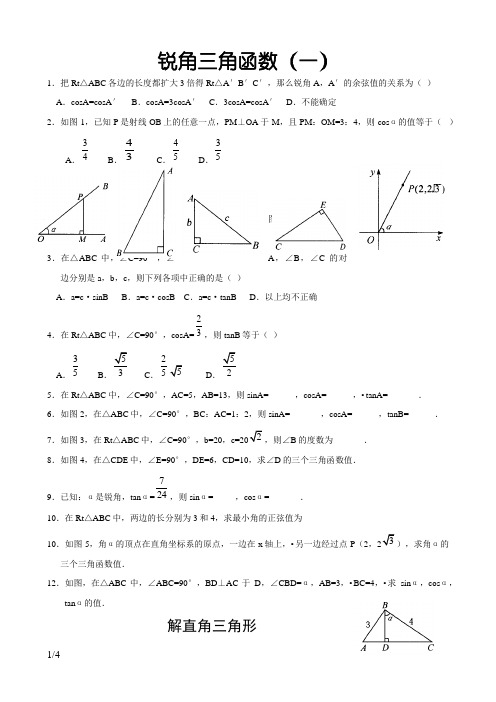
锐角三角函数(一)1.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A,A′的余弦值的关系为()A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定2.如图1,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值等于()A.34 B.43 C.45 D .35图 1 图 2 图3 图4图53.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是()A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确4.在Rt△ABC中,∠C=90°,cosA=23,则tanB等于()A.35 B.53 C.255 D.525.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinA=______,cosA=______,•tanA=_______.6.如图2,在△ABC中,∠C=90°,BC:AC=1:2,则sinA=_______,cosA=______,tanB=______.7.如图3,在Rt△ABC中,∠C=90°,b=20,c=202,则∠B的度数为_______.8.如图4,在△CDE中,∠E=90°,DE=6,CD=10,求∠D的三个三角函数值.9.已知:α是锐角,tanα=724,则sinα=_____,cosα=_______.10.在Rt△ABC中,两边的长分别为3和4,求最小角的正弦值为10.如图5,角α的顶点在直角坐标系的原点,一边在x轴上,•另一边经过点P(2,23),求角α的三个三角函数值.12.如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3,•BC=4,•求sinα,cosα,tanα的值.解直角三角形一、填空题1. 已知cosA=23,且∠B=900-∠A ,则sinB=__________.2. 在Rt △ABC 中,∠C 为直角,cot(900-A)=1.524,则tan(900-B)=_________.3. ∠A 为锐角,已知sinA=135,那么cos (900-A)=___________.4. 已知sinA=21(∠A 为锐角),则∠A=_________,cosA_______,tanA=__________.5. 用不等号连结右面的式子:cos400_______cos200,sin370_______sin420.6. 若cot α=0.3027,cot β=0.3206,则锐角α、β的大小关系是______________. 7. 计算: 2sin450-3tan600=____________. 8. 计算: (sin300+tan450)·cos600=______________.9. 计算: tan450·sin450-4sin300·cos450+6cot600=__________.10. 计算: tan 2300+2sin600-tan450·sin900-tan600+cos 2300=____________. 二、选择题:1. 在Rt △ABC 中,∠C 为直角,AC=4,BC=3,则sinA=( )A . 43;B . 34;C .53;D . 54.2. 在Rt △ABC 中,∠C 为直角,sinA=22,则cosB 的值是( )A .21;B .23;C .1;D .223. 在Rt △ABC 中,∠C 为直角,∠A=300,则sinA+sinB=( )A .1;B .231+;C .221+;D .414. 当锐角A>450时,sinA 的值( )A .小于22; B .大于22; C .小于23; D .大于235. 若∠A 是锐角,且sinA=43,则( )A .00<∠A<300; B .300<∠A<450;C .450<∠A<600;D . 600<∠A<9006. 当∠A 为锐角,且tanA 的值大于33时, ∠A( )A .小于300; B .大于300; C .小于600; D .大于6007. 如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan ∠BCD 等于( )A .43;B .34;C .53;D .548. Rt △ABC 中,∠C 为直角,AC=5,BC=12,那么下列∠A 的四个三角函数中正确的是( )A . sinA=135; B .cosA=1312; C . tanA=1213;D . cotA=1259. 已知α为锐角,且21<cos α<22,则α的取值范围是( )A .00<α<300;B .600<α<900;C .450<α<600;D .300<α<450.三、解答题1、 在△ABC 中,∠C 为直角,已知AB=23,BC=3,求∠B 和AC .2、在△ABC 中,∠C 为直角,直角边a=3cm ,b=4cm ,求sinA+sinB+sinC 的值.3、在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知b=3, c=14. 求∠A 的四个三角函数.4、在△ABC 中,∠C 为直角,不查表解下列问题: (1)已知a=5,∠B=600.求b ; (2)已知a=52,b=56,求∠A .5、在△ABC 中,∠C 为直角, ∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知a=25,b=215,求c 、∠A 、∠B .6、在Rt △ABC 中,∠C =90°,由下列条件解直角三角形: (1) 已知a =156, b =56,求c; (2) 已知a =20, c =220,求∠B ; (3) 已知c =30, ∠A =60°,求a ;(4) 已知b =15, ∠A =30°,求a .7、已知:如图,在ΔABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,若∠B =30°,CD =6,求AB 的长.8、已知:如图,在山脚的C 处测得山顶A 的仰角为︒45,沿着坡度为︒30︒=∠30DCB ,400=CD 米),测得A 的仰角为︒60,求山的高度DCAB9、会堂里竖直挂一条幅AB,如图5,小刚从与B成水平的C点观察,视角∠C=30°,当他沿CB方向前进2米到达到D时,视角∠ADB=45°,求条幅AB的长度。
人教版初中数学锐角三角函数的难题汇编及答案解析

人教版初中数学锐角三角函数的难题汇编及答案解析一、选择题1.如图,在扇形OAB中,120AOB∠=︒,点P是弧AB上的一个动点(不与点A、B重合),C、D分别是弦AP,BP的中点.若33CD=,则扇形AOB的面积为()A.12πB.2πC.4πD.24π【答案】A【解析】【分析】如图,作OH⊥AB于H.利用三角形中位线定理求出AB的长,解直角三角形求出OB即可解决问题.【详解】解:如图作OH⊥AB于H.∵C、D分别是弦AP、BP的中点.∴CD是△APB的中位线,∴AB=2CD=63∵OH⊥AB,∴BH=AH=33∵OA=OB,∠AOB=120°,∴∠AOH=∠BOH=60°,在Rt△AOH中,sin∠AOH=AHAO,∴AO=336sin3AHAOH==∠,∴扇形AOB的面积为:2120612360ππ=g g,故选:A.【点睛】本题考查扇形面积公式,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.2.如图,点E从点A出发沿AB方向运动,点G从点B出发沿BC方向运动,同时出发且速度相同,DE GF AB=<(DE长度不变,F在G上方,D在E左边),当点D到达点B时,点E停止运动.在整个运动过程中,图中阴影部分面积的大小变化情况是()A.一直减小B.一直不变C.先减小后增大D.先增大后减小【答案】B【解析】【分析】连接GE,过点E作EM⊥BC于M,过点G作GN⊥AB于N,设AE=BG=x,然后利用锐角三角函数求出GN和EM,再根据S阴影=S△GDE+S△EGF即可求出结论.【详解】解:连接GE,过点E作EM⊥BC于M,过点G作GN⊥AB于N设AE=BG=x,则BE=AB-AE=AB-x∴GN=BG·sinB=x·sinB,EM=BE·sinB=(AB-x)·sinB∴S阴影=S△GDE+S△EGF=12DE·GN+12GF·EM=12DE·(x·sinB)+12DE·[(AB-x)·sinB]=12DE·[x·sinB+(AB-x)·sinB]=12 DE·AB·sinB∵DE、AB和∠B都为定值∴S阴影也为定值故选B.【点睛】此题考查的是锐角三角函数和求阴影部分的面积,掌握利用锐角三角函数解直角三角形和三角形的面积公式是解决此题的关键.3.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为()A.2+3B.23C.3+3D.33【答案】A【解析】【分析】【详解】设AC=x,在Rt△ABC中,∠ABC=30°,即可得AB=2x,BC=3x,所以BD=BA=2x,即可得CD=3x+2x=(3+2)x,在Rt△ACD中,tan∠DAC=(32)32 CD xAC+==+,故选A.4.直角三角形纸片的两直角边长分别为6,8,现将ABCV如图那样折叠,使点A与点B 重合,折痕为DE,则tan CBE∠的值是()A.247B7C.724D.13【答案】C【解析】试题分析:根据题意,BE=AE.设BE=x,则CE=8-x.在Rt△BCE中,x2=(8-x)2+62,解得x=254,故CE=8-254=74,∴tan∠CBE=724 CECB=.故选C.考点:锐角三角函数.5.如图,为了测量某建筑物MN 的高度,在平地上A 处测得建筑物顶端M 的仰角为30°,向N 点方向前进16m 到达B 处,在B 处测得建筑物顶端M 的仰角为45°,则建筑物MN 的高度等于( )A .8(31)+mB .8(31)-mC .16(31)+mD .16(31)-m 【答案】A【解析】 设MN=xm ,在Rt △BMN 中,∵∠MBN=45∘,∴BN=MN=x ,在Rt △AMN 中,tan ∠MAN=MN AN , ∴tan30∘=16x x+ =3√3, 解得:x=8(3 +1),则建筑物MN 的高度等于8(3 +1)m ;故选A.点睛:本题是解直角三角形的应用,考查了仰角和俯角的问题,要明确哪个角是仰角,哪个角是俯角,知道仰角是向上看的视线与水平线的夹角,俯角是向下看的视线与水平线的夹角,并与三角函数相结合求边的长.6.如图所示,在△ABC 中,∠C =90°,AB =8,CD 是AB 边上的中线,作CD 的中垂线与CD 交于点E ,与BC 交于点F .若CF =x ,tanA =y ,则x 与y 之间满足( )A .2244x y +=B .2244x y -=C .2288x y -=D .2288x y += 【答案】A【解析】【分析】由直角三角形斜边上的中线性质得出CD =12AB =AD =4,由等腰三角形的性质得出∠A =∠ACD ,得出tan ∠ACD =GE CE=tan A =y ,证明△CEG ∽△FEC ,得出GE CE CE FE ,得出y =2FE ,求出y 2=24FE ,得出24y=FE 2,再由勾股定理得出FE 2=CF 2﹣CE 2=x 2﹣4,即可得出答案.【详解】解:如图所示:∵在△ABC 中,∠C =90°,AB =8,CD 是AB 边上的中线,∴CD =12AB =AD =4, ∴∠A =∠ACD ,∵EF 垂直平分CD , ∴CE =12CD =2,∠CEF =∠CEG =90°, ∴tan ∠ACD =GE CE =tanA =y , ∵∠ACD+∠FCE =∠CFE+∠FCE =90°,∴∠ACD =∠FCE ,∴△CEG ∽△FEC , ∴GE CE =CE FE, ∴y =2FE, ∴y 2=24FE , ∴24y=FE 2, ∵FE 2=CF 2﹣CE 2=x 2﹣4, ∴24y=x 2﹣4, ∴24y+4=x 2, 故选:A .【点睛】本题考查了解直角三角形、直角三角形斜边上的中线性质、等腰三角形的性质、相似三角形的判定与性质等知识;熟练掌握直角三角形的性质,证明三角形相似是解题的关键.7.某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为()米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)A.5.6 B.6.9 C.11.4 D.13.9【答案】C【解析】【分析】根据勾股定理,可得CE,BE的长,根据正切函数,可得AE的长,再根据线段的和差,可得答案.【详解】解:如图,延长DC、AB交于点E,,由斜坡轨道BC的坡度(或坡比)为i=1:2,得BE:CE=1:2.设BE=xm,CE=2xm.在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,即x2+(2x)2=(12)2,解得x=12,BE=12m,CE=24m,DE =DC +CE =8+24=32m ,由tan36°≈0.73,得=0.73,解得AB =0.73×32=23.36m .由线段的和差,得AB =AE ﹣BE =23.36﹣12=11.36≈11.4m ,故选:C .【点睛】本题考查解直角三角形的应用,利用勾股定理得出CE ,BE 的长是解题关键,又利用了正切函数,线段的和差.8.如图,一艘轮船位于灯塔P 的北偏东60°方向,与灯塔P 的距离为30海里的A 处,轮船沿正南方向航行一段时间后,到达位于灯塔P 的南偏东30°方向上的B 处,则此时轮船所在位置B 与灯塔P 之间的距离为( )A .60海里B .45海里C .3D .3【答案】D【解析】【分析】 根据题意得出:∠B=30°,AP=30海里,∠APB=90°,再利用勾股定理得出BP 的长,求出答案.【详解】解:由题意可得:∠B=30°,AP=30海里,∠APB=90°,故AB=2AP=60(海里),则此时轮船所在位置B 处与灯塔P 之间的距离为:22303AB AP -=故选:D .【点睛】此题主要考查了勾股定理的应用以及方向角,正确应用勾股定理是解题关键.9.如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在AC 上找一点B ,取145ABD ∠=o ,500BD m =,55D ∠=o ,要使A ,C ,E 成一直线,那么开挖点E 离点D 的距离是( )A .500sin55m oB .500cos55m oC .500tan55m oD .500cos55m o【答案】B【解析】 【分析】根据已知利用∠D 的余弦函数表示即可.【详解】 在Rt △BDE 中,cosD=DE BD, ∴DE=BD •cosD=500cos55°.故选B . 【点睛】 本题主要考查了解直角三角形的应用,正确记忆三角函数的定义是解决本题的关键.10.如图,在Rt ABC V 中,90C ∠︒=,30B ∠=︒,AD 是BAC ∠的角平分线,6AC =,则点D 到AB 的距离为( )A 3B 3C .23D .33【答案】C【解析】【分析】如图,过点D 作DE ⊥AB 于E ,根据直角三角形两锐角互余的性质可得∠BAC=60°,由AD 为∠BAC 的角平分线可得∠DAC=30°,根据角平分线的性质可得DE=CD ,利用∠DAC 的正切求出CD 的值即可得答案.【详解】∵∠B=30°,∠C=90°,∴∠BAC=60°,∵AD 平分∠BAC ,∴∠DAC=30°,DE=CD ,∵AC=6,∴CD=AC·tan ∠DAC=6×33=23,即DE=23, ∴点D 到AB 的距离为23,故选:C .【点睛】本题考查解直角三角形及角平分线的性质,在直角三角形中,锐角的正弦是角的对边比斜边;余弦是邻边比斜边;正切是对边比邻边;余切是邻边比对边;角平分线上的点到角两边的距离相等;熟练掌握三角函数的定义是解题关键.11.如图,在边长为8的菱形ABCD 中,∠DAB =60°,以点D 为圆心,菱形的高DF 为半径画弧,交AD 于点E ,交CD 于点G ,则图中阴影部分的面积是 ( )A .183π-B .183πC .32316πD .1839π-【答案】C【解析】【分析】 由菱形的性质得出AD=AB=8,∠ADC=120°,由三角函数求出菱形的高DF ,图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积,根据面积公式计算即可. 【详解】解:∵四边形ABCD 是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°-60°=120°,∵DF 是菱形的高,∴DF ⊥AB ,∴DF=AD •sin60°=3832⨯= ∴图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积=2120(43)84332316ππ⨯⨯=. 故选:C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.12.在一次数学活动中,嘉淇利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD .如图,嘉淇与假山的水平距离BD 为6m ,他的眼睛距地面的高度为1.6m ,嘉淇的视线经过量角器零刻度线OA 和假山的最高点C ,此时,铅垂线OE 经过量角器的60︒刻度线,则假山的高度CD 为( )A .()23 1.6m +B .()22 1.6m +C .()43 1.6m +D .23m【答案】A【解析】 【分析】 根据已知得出AK=BD=6m ,再利用tan30°= 6CK CK AK =,进而得出CD 的长. 【详解】解:如图,过点A 作AK ⊥CD 于点K∵BD=6米,李明的眼睛高AB=1.6米,∠AOE=60°,∴DB=AK ,AB=KD=1.6米,∠CAK=30°,∴tan30°=6CK CK AK =, 解得:3即3(3+1.6)m .故选:A .【点睛】本题考查的是解直角三角形的应用,根据题意构造直角三角形,解答关键是应用锐角三角函数定义.13.定义:在等腰三角形中,底边与腰的比叫做顶角的正对,顶角A 的正对记作sadA ,即sadA =底边:腰.如图,在ABC ∆中,AB AC =,2A B ∠=∠.则sin B sadA ⋅=( )A .12B .2C .1D .2【答案】C【解析】【分析】证明△ABC 是等腰直角三角形即可解决问题.【详解】解:∵AB=AC ,∴∠B=∠C ,∵∠A=2∠B ,∴∠B=∠C=45°,∠A=90°,∴在Rt △ABC 中,BC=sin AC B ∠=2AC , ∴sin ∠B •sadA=1AC BC BC AC=g , 故选:C .【点睛】本题考查解直角三角形,等腰直角三角形的判定和性质三角函数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.14.如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得60BAC ∠=︒,70DAC ∠=︒,则竹竿AB 与AD 的长度之比为( ).A .2sin70︒B .2cos70︒C .2tan70︒D .2tan 70︒【答案】B【解析】【分析】直接利用锐角三角函数关系分别表示出AB ,AD 的长,即可得出答案.【详解】解:∵∠BAC=60°,∠DAC=70°,∴cos60°=12AC AB =, 则AB=2AC , ∴cos70°=AC AD, ∴AC=AD •cos70°,AD=cos70AC ︒, ∴2cos70AC AC AB AD=︒=2cos70°. 故选:B .【点睛】此题主要考查了解直角三角形的应用,正确表示出各边长是解题关键.15.如图,△ABC 的顶点是正方形网格的格点,则cos A =( )A .12B .22C .32D .5 【答案】B【解析】【分析】构造全等三角形,证明△ABD 是等腰直角三角形,进行作答.【详解】过A 作AE ⊥BE ,连接BD ,过D 作DF ⊥BF 于F.∵AE=BF,∠AEB=∠DFB,BE=DF,∴△AEB≌△BFD,∴AB=DB.∠ABD=90°,∴△ABD是等腰直角三角形,∴cos∠DAB=2 2.答案选B.【点睛】本题考查了不规则图形求余弦函数的方法,熟练掌握不规则图形求余弦函数的方法是本题解题关键.16.如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是()A.AF=12 CFB.∠DCF=∠DFCC.图中与△AEF相似的三角形共有5个D.tan∠CAD3【答案】D【解析】【分析】由AE=12AD=12BC,又AD∥BC,所以12AE AFBC FC==,故A正确,不符合题意;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=12BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故B正确,不符合题意;根据相似三角形的判定即可求解,故C正确,不符合题意;由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D错误,符合题意.【详解】解:A、∵AD∥BC,∴△AEF∽△CBF,∴AE BC =AF FC , ∵AE =12AD =12BC , ∴AF FC =12,故A 正确,不符合题意; B 、过D 作DM ∥BE 交AC 于N ,∵DE ∥BM ,BE ∥DM ,∴四边形BMDE 是平行四边形,∴BM =DE =12BC , ∴BM =CM ,∴CN =NF ,∵BE ⊥AC 于点F ,DM ∥BE ,∴DN ⊥CF ,∴DF =DC ,∴∠DCF =∠DFC ,故B 正确,不符合题意;C 、图中与△AEF 相似的三角形有△ACD ,△BAF ,△CBF ,△CAB ,△ABE 共有5个,故C 正确,不符合题意.D 、设AD =a ,AB =b 由△BAE ∽△ADC ,有b a =2a . ∵tan ∠CAD =CD AD =b a =22,故D 错误,符合题意. 故选:D .【点睛】本题考查了相似三角形的判定和性质,矩形的性质,图形面积的计算,正确的作出辅助线是解题的关键.17.如图,等边ABC V 边长为a ,点O 是ABC V 的内心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①ODE V 形状不变;②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一;③四边形ODBE 的面积始终不变;④BDE V 周长的最小值为1.5a .上述结论中正确的个数是( )A .4B .3C .2D .1【答案】A【解析】【分析】 连接OB 、OC ,利用SAS 证出△ODB ≌△OEC ,从而得出△ODE 是顶角为120°的等腰三角形,即可判断①;过点O 作OH ⊥DE ,则DH=EH ,利用锐角三角函数可得OH=12OE 和3OE ,然后三角形的面积公式可得S △ODE 32,从而得出OE 最小时,S △ODE 最小,根据垂线段最短即可求出S △ODE 的最小值,然后证出S 四边形ODBE =S △OBC 23即可判断②和③;求出BDE V 的周长=a +DE ,求出DE 的最小值即可判断④.【详解】解:连接OB 、OC∵ABC V 是等边三角形,点O 是ABC V 的内心,∴∠ABC=∠ACB=60°,BO=CO ,BO 、CO 平分∠ABC 和∠ACB ∴∠OBA=∠OBC=12∠ABC=30°,∠OCA=∠OCB=12∠ACB=30° ∴∠OBA=∠OCB ,∠BOC=180°-∠OBC -∠OCB=120° ∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG -∠BOE=∠BOC -∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COE BO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形,∴ODE V 形状不变,故①正确;过点O 作OH ⊥DE ,则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12(180°-120°)=30° ∴OH=OE·sin ∠OED=12OE ,EH= OE·cos ∠OED=3OE ∴DE=2EH=3OE ∴S △ODE =12DE·OH=34OE 2 ∴OE 最小时,S △ODE 最小,过点O 作OE′⊥BC 于E′,根据垂线段最短,OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a 33 ∴S △ODE 3223 ∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB +S △OBE = S △OEC +S △OBE =S △OBC =1223 23=1423 ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一,故②正确; ∵S 四边形ODBE 23 ∴四边形ODBE 的面积始终不变,故③正确;∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB +BE +DE= EC +BE +DE=BC +DE=a +DE∴DE 最小时BDE V 的周长最小∵DE=3OE ∴OE 最小时,DE 最小 而OE 的最小值为OE′=3a ∴DE 的最小值为3×3a =12a ∴BDE V 的周长的最小值为a +12a =1.5a ,故④正确; 综上:4个结论都正确,故选A .【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用,掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键.18.已知在 Rt ABC 中, ∠C = 90°,AC = 8, BC = 15 ,那么下列等式正确的是( )A .8sin 17A =B .cosA=815C .tan A =817D .cot A=815 【答案】D【解析】【分析】 根据锐角三角函数的定义进行作答.【详解】 由勾股定理知,AB=17;A.15sin 17BC A AB == ,所以A 错误;B.8cos 17AC A AB ==,所以,B 错误;C.15tan 8BC A AC ==,所以,C 错误;D.cot AC A BC ==815,所以选D. 【点睛】 本题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是本题解题关键.19.如图,正方形ABCD 的边长为4,点E 、F 分别在AB 、BC 上,且AE=BF=1,CE 、DF 交于点O ,下列结论:①∠DOC=90°,②OC=OE ,③CE=DF ,④tan ∠OCD=43,⑤S △DOC =S 四边形EOFB 中,正确的有( )A.1个B.2个C.3个D.4个【答案】D【解析】分析:由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确,③CE=D F正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得④正确;由①易证得⑤正确.详解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.∵AE=BF=1,∴BE=CF=4﹣1=3.在△EBC和△FCD中,BC CDB DCFBE CF=⎧⎪∠=∠⎨⎪=⎩,∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,CE=DF,故③正确,∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;连接DE,如图所示,若OC=OE.∵DF⊥EC,∴CD=DE.∵CD=AD<DE(矛盾),故②错误;∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠DFC=DCFC=43,故④正确;∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故⑤正确;故正确的有:①③④⑤.故选D.点睛:本题考查了正方形的性质、全等三角形的判定与性质、直角三角形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想与转化思想的应用.20.将直尺、有60°角的直角三角板和光盘如图摆放,A为60°角与直尺的交点,B为光盘与直尺的交点,AB=4,则光盘表示的圆的直径是()A.4 B.83C.6 D.43【答案】B【解析】【分析】设三角板与圆的切点为C,连接OA、OB,根据切线长定理可得AB=AC=3,∠OAB=60°,然后根据三角函数,即可得出答案.【详解】设三角板与圆的切点为C,连接OA、OB,由切线长定理知,AB=AC=3,AO平分∠BAC,∴∠OAB=60°,在Rt△ABO中,OB=AB tan∠OAB3∴光盘的直径为3故选:B.【点睛】本题主要考查了切线的性质,解题的关键是熟练应用切线长定理和锐角三角函数.。
备战中考数学综合题专题复习【锐角三角函数】专题解析附答案解析

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B港口之间的距离CB的长为海里.考点:解直角三角形的应用-方向角问题.2.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定3.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(215-+;(3758+【解析】试题分析:(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠CBD=36°, ∵∠CBD=∠A=36°,∠C=∠C , ∴△ABC ∽△BCD ; (2)∵∠A=∠ABD=36°, ∴AD=BD , ∵BD=BC , ∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1, ∵△ABC ∽△BCD ,∴AB BC BD CD =,即111x x +=, 整理得:x 2+x-1=0,解得:x 1=15-+,x 2=15--(负值,舍去),则x=15-+; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=154-+, 在Rt △ABE 中,cosA=cos36°=151514151AE AB -+++==-++ 在Rt △BCE 中,cosC=cos72°=1515414EC BC -+-+==, 则cos36°-cos72°=51+=15-+=12. 【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.4.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.5.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为 cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.【答案】(1);(2)12cm;(3)cm.【解析】试题分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案:∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm.∵∠ACD=30°,∠DAC=90°,AC=12cm,∴(cm).∵点E为CD边上的中点,∴AE=DC=cm.(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,根据轴对称的性质,此时DP+EP值为最小,进而得出答案.(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.试题解析:解:(1).(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE.∴△ADE为等边三角形.∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°.∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′.∴点E,D′关于直线AC对称.如答图1,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′.∵△ADE是等边三角形,AD=AE=,∴,即DP+EP最小值为12cm.(3)如答图2,连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=.在△ABD′和△CBD′中,∵,∴△ABD′≌△CBD′(SSS).∴∠D′BG=∠D′BC=45°.∴D′G=GB.设D′G长为xcm,则CG长为cm,在Rt△GD′C中,由勾股定理得,解得:(不合题意舍去).∴点D′到BC边的距离为cm.考点:1.翻折和单动点问题;2.勾股定理;3.直角三角形斜边上的中线性质;4.等边三角形三角形的判定和性质;5.轴对称的应用(最短线路问题);6.全等三角形的判定和性质;7.方程思想的应用.6.在正方形ABCD中,AC是一条对角线,点E是边BC上的一点(不与点C重合),连接AE,将△ABE沿BC方向平移,使点B与点C重合,得到△DCF,过点E作EG⊥AC于点G,连接DG,FG.(1)如图,①依题意补全图;②判断线段FG与DG之间的数量关系与位置关系,并证明;(2)已知正方形的边长为6,当∠AGD=60°时,求BE的长.BE【答案】(1)①见解析,②FG=DG,FG⊥DG,见解析;(2)3【解析】【分析】(1)①补全图形即可,②连接BG,由SAS证明△BEG≌△GCF得出BG=GF,由正方形的对称性质得出BG=DG,得出FG=DG,在证出∠DGF=90°,得出FG⊥DG即可,(2)过点D作DH⊥AC,交AC于点H.由等腰直角三角形的性质得出DH=AH=2FG=DG=2GH=6,得出DF2DG=3Rt△DCF中,由勾股定理得出CF=3得出结果.【详解】解:(1)①补全图形如图1所示,②FG=DG,FG⊥DG,理由如下,连接BG,如图2所示,∵四边形ABCD是正方形,∴∠ACB=45°,∵EG⊥AC,∴∠EGC =90°,∴△CEG 是等腰直角三角形,EG =GC , ∴∠GEC =∠GCE =45°, ∴∠BEG =∠GCF =135°, 由平移的性质得:BE =CF ,在△BEG 和△GCF 中,BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩,∴△BEG ≌△GCF (SAS ), ∴BG =GF ,∵G 在正方形ABCD 对角线上, ∴BG =DG , ∴FG =DG ,∵∠CGF =∠BGE ,∠BGE+∠AGB =90°, ∴∠CGF+∠AGB =90°, ∴∠AGD+∠CGF =90°, ∴∠DGF =90°, ∴FG ⊥DG.(2)过点D 作DH ⊥AC ,交AC 于点H .如图3所示, 在Rt △ADG 中, ∵∠DAC =45°, ∴DH =AH =2在Rt △DHG 中,∵∠AGD =60°, ∴GH 33236,∴DG =2GH =6, ∴DF 2DG =3 在Rt △DCF 中,CF ()22436-3∴BE =CF =3.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识;本题综合性强,证明三角形全等是解题的关键.7.在Rt△ABC中,∠ACB=90°,AB=7,AC=2,过点B作直线m∥AC,将△ABC绕点C 顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分別交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在C A′,CB′的延长线上时,试探究四边形PA'B′Q的面积是否存在最小值.若存在,求出四边形PA′B′Q的最小面积;若不存在,请说明理由.【答案】(1)60°;(2)PQ=72;(3)存在,S四边形PA'B′Q=33【解析】【分析】(1)由旋转可得:AC=A'C=2,进而得到BC3=∠A'BC=90°,可得cos∠A'CB3'BCA C==∠A'CB=30°,∠ACA'=60°;(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB3=32=,依据tan∠Q=tan∠A32=BQ=BC3=2,进而得出PQ=PB+BQ72=;(3)依据S四边形PA'B'Q=S△PCQ﹣S△A'CB'=S△PCQ3-S四边形PA'B'Q最小,即S△PCQ最小,而S△PCQ12=PQ×BC3=,利用几何法即可得到S△PCQ的最小值=3,即可得到结论.【详解】(1)由旋转可得:AC =A 'C =2.∵∠ACB =90°,AB 7=,AC =2,∴BC 3=. ∵∠ACB =90°,m ∥AC ,∴∠A 'BC =90°,∴cos ∠A 'CB 3'BC A C ==,∴∠A 'CB =30°,∴∠ACA '=60°;(2)∵M 为A 'B '的中点,∴∠A 'CM =∠MA 'C ,由旋转可得:∠MA 'C =∠A ,∴∠A =∠A 'CM ,∴tan ∠PCB =tan ∠A 3=,∴PB 3=BC 32=. ∵∠BQC =∠BCP =∠A ,∴tan ∠BQC =tan ∠A 3=,∴BQ =BC 3⨯=2,∴PQ =PB +BQ 72=; (3)∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ 3-,∴S 四边形PA 'B 'Q 最小,即S △PCQ 最小,∴S △PCQ 12=PQ ×BC 3=PQ , 取PQ 的中点G . ∵∠PCQ =90°,∴CG 12=PQ ,即PQ =2CG ,当CG 最小时,PQ 最小,∴CG ⊥PQ ,即CG 与CB 重合时,CG 最小,∴CG min 3=,PQ min =23,∴S △PCQ 的最小值=3,S 四边形PA 'B 'Q =33-;【点睛】本题属于几何变换综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.8.在Rt △ABC 中,∠ACB =90°,CD 是AB 边的中线,DE ⊥BC 于E ,连结CD ,点P 在射线CB 上(与B ,C 不重合)(1)如果∠A =30°,①如图1,∠DCB 等于多少度;②如图2,点P 在线段CB 上,连结DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连结BF ,补全图2猜想CP 、BF 之间的数量关系,并证明你的结论;(2)如图3,若点P 在线段CB 的延长线上,且∠A =α(0°<α<90°),连结DP ,将线段DP绕点逆时针旋转2α得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系(不需证明)【答案】(1)①∠DCB=60°.②结论:CP=BF.理由见解析;(2)结论:BF﹣BP=2DE•tanα.理由见解析.【解析】【分析】(1)①根据直角三角形斜边中线的性质,结合∠A=30°,只要证明△CDB是等边三角形即可;②根据全等三角形的判定推出△DCP≌△DBF,根据全等的性质得出CP=BF,(2)求出DC=DB=AD,DE∥AC,求出∠FDB=∠CDP=2α+∠PDB,DP=DF,根据全等三角形的判定得出△DCP≌△DBF,求出CP=BF,推出BF﹣BP=BC,解直角三角形求出CE=DEtanα即可.【详解】(1)①∵∠A=30°,∠ACB=90°,∴∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠DCB=60°.②如图1,结论:CP=BF.理由如下:∵∠ACB=90°,D是AB的中点,DE⊥BC,∠DCB=60°,∴△CDB为等边三角形.∴∠CDB=60°∵线段DP绕点D逆时针旋转60°得到线段DF,∵∠PDF=60°,DP=DF,∴∠FDB=∠CDP,在△DCP和△DBF中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF.(2)结论:BF ﹣BP =2DEtanα.理由:∵∠ACB =90°,D 是AB 的中点,DE ⊥BC ,∠A =α,∴DC =DB =AD ,DE ∥AC ,∴∠A =∠ACD =α,∠EDB =∠A =α,BC =2CE ,∴∠BDC =∠A+∠ACD =2α,∵∠PDF =2α,∴∠FDB =∠CDP =2α+∠PDB ,∵线段DP 绕点D 逆时针旋转2α得到线段DF ,∴DP =DF ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF ,而 CP =BC+BP ,∴BF ﹣BP =BC ,在Rt △CDE 中,∠DEC =90°,∴tan ∠CDE =CE DE, ∴CE =DEtanα, ∴BC =2CE =2DEtanα,即BF ﹣BP =2DEtanα.【点睛】本题考查了三角形外角性质,等边三角形的判定和性质,全等三角形的性质和判定,直角三角形的性质,旋转的性质的应用,能推出△DCP ≌△DBF 是解此题的关键,综合性比较强,证明过程类似.9.如图,正方形ABCD+1,对角线AC 、BD 相交于点O ,AE 平分∠BAC 分别交BC 、BD 于E 、F ,(1)求证:△ABF ∽△ACE ;(2)求tan ∠BAE 的值;(3)在线段AC 上找一点P ,使得PE+PF 最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x=1,在Rt△ABE中,∵∠ABE=90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC =22AB BC +=2+2,∴OA =OC =OB =12AC =22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =222+ •(2﹣1)=22, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+..【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.10.小明坐于堤边垂钓,如图①,河堤AC 的坡角为30°,AC 长米,钓竿AO 的倾斜角是60°,其长为3米,若AO 与钓鱼线OB 的夹角为60°,求浮漂B 与河堤下端C 之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
锐角三角函数测试题(含答案)
九年级下册《锐角三角函数》单元测试一、选择题1. 4sin tan 5ααα=若为锐角,且,则为 ( ) 933425543A B C D . . . . 2.在Rt △ABC 中,∠C = 90°,下列式子不一定成立的是( )A .sinA = sinB B .cosA=sinBC .sinA=cosBD .∠A+∠B=90° 3.直角三角形的两边长分别是6,8,则第三边的长为( )A .10B .22C .10或27D .无法确定4.在Rt △ABC 中,∠C=90°,当已知∠A 和a 时,求c ,应选择的关系式是( ) A .c =sin a A B .c =cos a A C .c = a ·tanA D .c = tan aA5、45cos 45sin +的值等于( )A.2B.213+ C.3D. 16.在Rt △ABC 中,∠C=90°,tan A=3,AC 等于10,则S △ABC 等于( )A. 3B. 300C. 503 D. 157.当锐角α>30°时,则cos α的值是( ) A .大于12 B .小于12C .大于32D .小于328.小明沿着坡角为30°的坡面向下走了2米,那么他下降( ) A .1米 B .3米 C .23 D .2339.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=( )(A )4 (B )5 (C )23 (D )83310.已知Rt △ABC 中,∠C=90°,tanA=43,BC=8,则AC 等于( ) A .6 B .323C .10D .12 二、填空题11.计算2sin30°+2cos60°+3tan45°=_______. 12.若sin28°=cos α,则α=________.13.已知△ABC 中,∠C=90°,AB=13,AC=5,则tanA=______. 14.某坡面的坡度为1:3,则坡角是_______度.15.在△ABC 中,∠C =90°,AB =10cm ,sinA =54,则BC 的长为_______cm . 16.如图,在高楼前D 点测得楼顶的仰角为30︒,向高楼前进60米到C 点,又测得仰角为45︒,则该高楼的高度大约为A.82米B.163米C.52米D.70米17.如图,小鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的高度CD =1m ,测得旗杆顶端B 的仰角α=60°,则旗杆AB 的高度为 .(计算结果保留根号)(16题) (17题) 三、解答题18.由下列条件解直角三角形:在Rt △ABC 中,∠C=90°:(1)已知a=4,b=8, (2)已知b=10,∠B=60°.(3)已知c=20,∠A=60°. (4) (2)已知a=5,∠B=35°19.计算下列各题.(1)s in 230°+cos 245°+2sin60°·tan45°; (2)22cos 30cos 60tan 60tan 30︒+︒︒⨯︒+ sin45°(45︒30︒BAD C四、解下列各题20.如图所示,平地上一棵树高为5米,两次观察地面上的影子,•第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长多少米?21.如图,AB是江北岸滨江路一段,长为3千米,C为南岸一渡口,•为了解决两岸交通困难,拟在渡口C 处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸的最短的桥长多少?(精确到0.1)22. 如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通,经测得∠ABC=45o,∠ACB=30o,问此公路是否会穿过该森林公园?请通过计算进行说明。
中考数学—锐角三角函数的综合压轴题专题复习附答案
一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.(1)求∠BPQ的度数;(2)求该电线杆PQ的高度(结果精确到1m).备用数据:,【答案】(1)∠BPQ=30°;(2)该电线杆PQ的高度约为9m.【解析】试题分析:(1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可;(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.试题解析:延长PQ交直线AB于点E,(1)∠BPQ=90°-60°=30°;(2)设PE=x米.在直角△APE中,∠A=45°,则AE=PE=x米;∵∠PBE=60°∴∠BPE=30°在直角△BPE中,BE=33PE=33x米,∵AB=AE-BE=6米,则3,解得:3则BE=(33+3)米.在直角△BEQ中,QE=33BE=33(33+3)=(3+3)米.∴PQ=PE-QE=9+33-(3+3)=6+23≈9(米).答:电线杆PQ的高度约9米.考点:解直角三角形的应用-仰角俯角问题.2.如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;(2)求证:BC2=2CD•OE;(3)若314cos,53BAD BE∠==,求OE的长.【答案】(1)DE为⊙O的切线,理由见解析;(2)证明见解析;(3)OE =356.【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.试题解析:(1)DE为⊙O的切线,理由如下:连接OD,BD,∵AB为⊙O的直径,∴∠ADB=90°,在Rt△BDC中,E为斜边BC的中点,∴CE=DE=BE=BC,∴∠C=∠CDE,∵OA=OD,∴∠A=∠ADO,∵∠ABC=90°,∴∠C+∠A=90°,∴∠ADO+∠CDE=90°,∴∠ODE=90°,∴DE⊥OD,又OD为圆的半径,∴DE为⊙O的切线;(2)∵E是BC的中点,O点是AB的中点,∴OE是△ABC的中位线,∴AC=2OE,∵∠C=∠C,∠ABC=∠BDC,∴△ABC∽△BDC,∴,即BC2=AC•CD.∴BC2=2CD•OE;(3)解:∵cos∠BAD=,∴sin∠BAC=,又∵BE=,E是BC的中点,即BC=,∴AC=.又∵AC=2OE,∴OE=AC=.考点:1、切线的判定;2、相似三角形的判定与性质;3、三角函数3.如图13,矩形的对角线,相交于点,关于的对称图形为.(1)求证:四边形是菱形;(2)连接,若,.①求的值;②若点为线段上一动点(不与点重合),连接,一动点从点出发,以的速度沿线段匀速运动到点,再以的速度沿线段匀速运动到点,到达点后停止运动.当点沿上述路线运动到点所需要的时间最短时,求的长和点走完全程所需的时间.【答案】(1)详见解析;(2)①②和走完全程所需时间为【解析】试题分析:(1)利用四边相等的四边形是菱形;(2)①构造直角三角形求;②先确定点沿上述路线运动到点所需要的时间最短时的位置,再计算运到的时间.试题解析:解:(1)证明:四边形是矩形.与交于点O,且关于对称四边形是菱形.(2)①连接,直线分别交于点,交于点关于的对称图形为在矩形中,为的中点,且O为AC的中点为的中位线同理可得:为的中点,②过点P作交于点由运动到所需的时间为3s由①可得,点O以的速度从P到A所需的时间等于以从M运动到A即:由O运动到P所需的时间就是OP+MA和最小.如下图,当P运动到,即时,所用时间最短.在中,设解得:和走完全程所需时间为考点:菱形的判定方法;构造直角三角形求三角函数值;确定极值时动点的特殊位置4.如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.(1)求tan∠DBC的值;(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.【答案】(1)tan∠DBC=;(2)P(﹣,).【解析】试题分析:(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4,BE=BC﹣DE=.由此可知tan∠DBC=;(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知=,通过解方程求得点P的坐标为(﹣,).试题解析:(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,解得 x1=﹣1,x2=4.∴A(﹣1,0),B(4,0).当x=3时,y=﹣32+3×3+4=4,∴D(3,4).如图,连接CD,过点D作DE⊥BC于点E.∵C(0,4),∴CD//AB,∴∠BCD=∠ABC=45°.在直角△OBC中,∵OC=OB=4,∴BC=4.在直角△CDE中,CD=3.∴CE=ED=,∴BE=BC﹣DE=.∴tan∠DBC=;(2)过点P作PF⊥x轴于点F.∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,∴tan∠PBF=.设P(x,﹣x2+3x+4),则=,解得 x1=﹣,x2=4(舍去),∴P(﹣,).考点:1、二次函数;2、勾股定理;3、三角函数5.如图,矩形OABC中,A(6,0)、C(0,23)、D(0,33),射线l过点D且与x轴平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60º.(1)点B的坐标是,∠CAO= º,当点Q与点A重合时,点P的坐标为;(2)设点P的横坐标为x,△OPQ与矩形OABC重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.【答案】(1)(6,3). 30.(3,3)(2)()()()()243x 430x 3331333x x 3x 5232S {23x 1235x 93543x 9x +≤≤-+-<≤=-+<≤>【解析】解:(1)(6,23). 30.(3,33). (2)当0≤x≤3时, 如图1,OI=x ,IQ=PI•tan60°=3,OQ=OI+IQ=3+x ; 由题意可知直线l ∥BC ∥OA , 可得EF PE DC 31==OQ PO DO 333==,∴EF=13(3+x ), 此时重叠部分是梯形,其面积为:EFQO 14343S S EF OQ OC 3x x 43233==+⋅=+=+梯形()()当3<x≤5时,如图2,)HAQ EFQO EFQO 221S S S S AH AQ243331333 3x 3=∆=-=-⋅⋅=+---梯形梯形当5<x≤9时,如图3,12S BE OAOC 312x 2323 =x 1233=+⋅=--+()()。
历年(2020-2023)全国高考数学真题分类(三角函数)汇编(附答案)
历年(2020‐2023)全国高考数学真题分类(三角函数)汇编【2023年真题】1. (2023ꞏ新课标I 卷 第8题)已知1sin()3αβ-=,1cos sin 6αβ=,则cos(22)αβ+=( ) A.79B.19C. 19-D. 79-2. (2023ꞏ新课标II 卷 第7题) 已知α为锐角,1cos 4α+=,则sin 2α=( )A. 38B. 18-C. 34D. 14-+3. (2023ꞏ新课标I 卷 第15题)已知函数()cos 1(0)f x x ωω=->在区间[0,2]π有且仅有3个零点,则ω的取值范围是__________.4. (2023ꞏ新课标II 卷 第16题)已知函数()sin()f x x ωϕ=+,如图,A ,B 是直线12y =与曲线()y f x =的两个交点,若||6AB π=,则()f π= .【2022年真题】5.(2022·新高考I 卷 第6题)记函数()sin()(0)4f x x b πωω=++>的最小正周期为.T 若23T ππ<<,且()y f x =的图像关于点3(,2)2π中心对称,则(2f π=( ) A. 1B.32C.52D. 36.(2022·新高考II 卷 第6题)若sin()cos()4παβαβαβ+++=+,则( )A. tan()1αβ+=-B. tan()1αβ+=C. tan()1αβ-=-D. tan()1αβ-=7.(2022·新高考II 卷 第9题)(多选)已知函数()sin(2)(0)f x x ϕϕπ=+<<的图象关于点2(,0)3π对称,则( ) A. ()f x 在5(0,)12π单调递减 B. ()f x 在11(,)1212ππ-有两个极值点 C. 直线76x π=是曲线()y f x =的一条对称轴D. 直线2y x =-是曲线()y f x =的一条切线【2021年真题】8.(2021·新高考I 卷 第4题)下列区间中,函数()7sin ()6f x x π=-单调递增的区间是( )A.0,2π⎛⎫⎪⎝⎭B. ,2ππ⎛⎫⎪⎝⎭C. 3,2ππ⎛⎫ ⎪⎝⎭D. 3,22ππ⎛⎫⎪⎝⎭9.(2021·新高考I 卷 第6题)若tan 2θ=-,则sin (1sin 2)sin cos θθθθ+=+( )A. 65-B. 25-C.25 D.65【2020年真题】10.(2020·新高考I 卷 第10题 、II 卷 第11题)(多选)如图是函数()sin y x ωϕ=+的部分图象,则()sin x ωϕ+( )A. sin ()3x π+B. sin (2)3x π- C. cos (2)6x π+D. 5cos (2)6x π- 11.(2020·新高考I 卷 第15题、II 卷 第16题))某中学开展劳动实习,学生加工制作零件,零件的截面如图所示,O 为圆孔及轮廓圆弧AB 所在圆的圆心,A 是圆弧AB 与直线AG 的切点,B 是圆弧AB 与直线BC的切点,四边形DEFG 为矩形,BC DG ⊥,垂足为C ,3tan 5ODC ∠=,//BH DG ,12EF cm =,2DE cm =,A 到直线DE 和EF 的距离均为7cm ,圆孔半径为1cm ,则图中阴影部分的面积为__________2.cm参考答案1. (2023ꞏ新课标I 卷 第8题)解:因为1sin()sin cos cos sin 3αβαβαβ-=-=,1cos sin 6αβ=,则1sin cos .2αβ=故112sin()sin cos cos sin .263αβαβαβ+=+=+= 即2221cos(22)12sin ()12().39αβαβ+=-+=-⨯=故选B.2. (2023ꞏ新课标II 卷 第7题)解:22111cos 36114sin ()sin 222816424ααα+-----=====⇒=故选:.D3. (2023ꞏ新课标I 卷 第15题)解:令()cos 10f x x ω=-=,得cos 1x ω=,又[0,2]x π∈,则[0,2]x ωωπ∈,所以426πωππ<…,得2 3.ω<… 故答案为:[2,3).4. (2023ꞏ新课标II 卷 第16题)解: 设相邻的两个交点A ,B 的横坐标为1 t ,2 t ,则21 - 6t t π=又1sin()2x ωϕ+=,522,.0,66x k k k Z k ππωϕππ+=++∈=或当时 16t πωϕ+=,256t πωϕ+=,212( - )3t t πω=,故 4.ω=函数图象过点2(,0)3π,8sin ()03πϕ+=,故8 ,.3k k Z πϕπ=-∈ 2k =时满足图片条件,故2.3πϕ=-2()sin(4.32f πππ=-=- 5.(2022·新高考I 卷 第6题)解:由题可知:22(,)3T πππω=∈,所以(2,3).ω∈ 又因为()y f x =的图像关于点3(,2)2π中心对称,所以2b =,且33()sin() 2.224f b πππω=⨯++= 所以21(34k ω=-,k Z ∈,所以5.2ω=所以5()sin() 2.24f x x π=++所以() 1.2f π=6.(2022·新高考II 卷 第6题)解:解法一:设0β=则sin cos 0αα+=,取34απ=,排除B ,D 再取0α=则sin cos 2sin βββ+=,取4πβ=,排除;A 选.C解法二:由sin()cos())]44ππαβαβαβαβ+++=++=++)cos 44ππαβαβ=++,cos )sin 44ππαβαβ+=+ 故sin()cos cos(044ππαβαβ+-+=,即sin()04παβ+-=,故sin(sin()cos()0422παβαβαβ-+=-+-=, 故sin()cos()αβαβ-=--,故tan() 1.αβ-=- 7.(2022·新高考II 卷 第9题)(多选) 解:由题意得:24(sin()033f ππϕ=+=, 所以43k πϕπ+=,即43k πϕπ=-+,k Z ∈, 又0ϕπ<<,所以2k =时,23πϕ=,故2()sin(2).3f x x π=+ 选项5:(0,)12A x π∈时,2232(,)332x πππ+∈,由sin y u =图象知()f x 在5(0,)12π单调递减; 选项11:(,1212B x ππ∈-时,252(,)322x πππ+∈,由sin y u =图象知()f x 在11(,1212ππ-有1个极值点; 选项:C 由于,故直线76x π=不是()f x 的对称轴;选项:D 令,得21cos(232x π+=-, 解得222233x k πππ+=+或242233x k πππ+=+,k Z ∈,从而得x k π=或3x k ππ=+,k Z ∈,令0k =,则是斜率为1-的直线与曲线的切点,从而切线方程为(0)2y x -=--,即.2y x =- 8.(2021·新高考I 卷 第4题) 解:由22262k x k πππππ-+-+剟,得222,33k x k k Z ππππ-++∈剟, 所以()7sin ()6f x x π=-的单调递增区间为22,2,33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦, 当0k =时,一个单调递增区间为2,33ππ⎡⎤-⎢⎥⎣⎦,可知20,,233πππ⎛⎫⎡⎤⊆- ⎪⎢⎥⎝⎭⎣⎦, 故选:.A9.(2021·新高考I 卷 第6题)解:原式22sin (sin cos 2sin cos )sin cos θθθθθθθ++=+ 22sin (sin cos )sin sin cos sin cos θθθθθθθθ+==++22222sin sin cos tan tan 422sin cos tan 1415θθθθθθθθ++-====+++, 故选:.C10.(2020·新高考I 卷 第10题 、II 卷 第11题)(多选) 解:由图象可知222()||36T ππππω==-=,故A 错误; 解得2ω=±, 点5(,1)12π-在函数图象上, 当2ω=时,522,k Z 122k ππϕπ⨯+=-+∈, 解得42,k Z 3k πϕπ=-+∈,故44sin 2sin 2sin 2333y x x x ππππ⎛⎫⎛⎫⎛⎫=-=-+-=-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,当2ω=-时,522,k Z 122k ππϕπ-⨯+=-+∈ 解得2,k Z 3k πϕπ=+∈,故函数解析式为sin 23y x π⎛⎫=-+ ⎪⎝⎭,又cos 2sin 2sin 26263x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,故选.BC11.(2020·新高考I 卷 第15题、II 卷 第16题) 解:设上面的大圆弧的半径为x ,连接OA ,过A 作AI BH ⊥交BH 于J ,交DG 于K ,交EF 于I ,过O 作OL DG ⊥于L ,记扇形OAB 的面积为S 扇形,由题中的长度关系易知45AGD ︒∠=,所以45AHO ︒∠=, 又90OAH ︒∠=,可得AOH 为等腰直角三角形,可得2OJ AJ x ==,52OL JK x ==-, 72DL DK LK DK OJ x=-=-=-,3tan 5OL ODC DL ∠==, 5352x-=,解得x =,12AOH O S S S S =+- 阴影圆扇形222131154()24222cm πππ=⨯⨯+⨯-=+,故答案为54.2π+。
2021年全国各省市中考真题分类汇编:锐角三角函数(含答案)
2021年全国各省市数学中考分类汇编锐角三角函数一、选择题1.(2021·山东省淄博市)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为()A. 35B. √55C. 45D. 2√552.(2021·浙江省金华市)如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为()A. 4cosα米B. 4sinα米C. 4tanα米D. 4cosα米3.(2021·山东省泰安市)如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D 处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C 的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:√3≈1.732)()A. 136.6米B. 86.7米C. 186.7米D. 86.6米4.(2021·重庆市)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B ,C ,D ,E 在同一平面内),在点D 处测得建筑物顶A 点的仰角为50°,则建筑物AB 的高度约为( )(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)A. 69.2米B. 73.1米C. 80.0米D. 85.7米5. (2021·广东省)如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P 、Q 两点分别测定对岸一棵树T 的位置,T 在P 的正北方向,且T 在Q 的北偏西70°方向,则河宽(PT 的长)可以表示为( )A. 200tan70°米B. 200tan70∘米C. 200sin 70°米D. 200sin70∘米 6. (2021·湖北省随州市)如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A 处,底端落在水平地面的点B 处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=35,则梯子顶端上升了( ) A. 1米 B. 1.5米 C. 2米 D. 2.5米7. (2021·广西壮族自治区桂林市)如图,在平面直角坐标系内有一点P (3,4),连接OP ,则OP 与x 轴正方向所夹锐角α的正弦值是( )A. 34B. 43 C. 35D. 458.(2021·广东省广州市)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,连结BB′,则sin∠BB′C′的值为()A. 35B. 45C. √55D. 2√559.(2021·贵州省毕节市)如图,拦水坝的横断面为梯形ABCD,其中AD∥BC,∠ABC=45°,∠DCB=30°,斜坡AB长8m,则斜坡CD的长为()A. 6√2mB. 8√2mC. 4√6mD. 8√3m10.(2021·福建省)如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD与⊙O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于()A. 35B. 23C. 34D. 45二、填空题11.(2021·湖北省黄石市)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=5米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为45°,则电线杆AB的高度约为______ 米.(参考数据:√2≈1.414,√3≈1.732,结果按四舍五入保留一位小数)12.(2021·山东省烟台市)如图,在正方形网格中,每个小正方形的边长都是1,⊙O是△ABC的外接圆,点A,B,O在网格线的交点上,则sin∠ACB的值是______ .13.(2021·辽宁省本溪市)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC= ______ .14.(2021·广东省梅州市)如图,在▱ABCD中,AD=5,AB=12,sin A=4.过点D作DE⊥AB,5垂足为E,则sin∠BCE= ______ .15.(2021·浙江省衢州市)图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且OA=OB,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm.(1)椅面CE的长度为______ cm.(2)如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为______ cm (结果精确到0.1cm).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)16.(2021·湖北省荆州市)如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测量知BC=8cm,AB=16cm.当AB,BC转动到∠BAE=60°,∠ABC=50°时,点C到AE的距离为______ cm.(结果保留小数点后一位,参考数据:sin70°≈0.94,√3≈1.73)17.(2021·湖北省黄冈市)如图,建筑物BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为______ m(结果保留小数点后一位).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53≈1.33)18.(2021·浙江省湖州市)如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sin B的值是______ .19.(2021·广东省)如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tan C=______.20.(2021·江苏省常州市)如图,在△ABC中,AC=3,BC=4,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为1的正方形,则sin∠FBA= ______ .三、解答题3-π)0.21.(2021·湖南省岳阳市)计算:(-1)2021+|-2|+4sin30°-(√822.(2021·四川省达州市)计算:-12+(π-2021)0+2sin60°-|1-√3|.23.(2021·湖北省黄冈市)计算:|1−√3|−2sin60°+(π−1)0.)−2+4sin60°−(−1).24.(2021·湖南省怀化市)计算:(3−π)0−√12+(1325.(2021·浙江省金华市)已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=120°,AB=2.(1)求矩形对角线的长.(2)过O作OE⊥AD于点E,连结BE.记∠ABE=α,求tanα的值.26.(2021·湖南省娄底市)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P 处测得B点的仰角∠DPB为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,取√3=1.732,√2=1.414)27.(2021·黑龙江省绥化市)一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为△ABC,点B、C、D在同一条直线上,测得∠ACB=90°,∠ABC=60°,AB=32cm,∠BDE=75°,其中一段支撑杆CD=84cm,另一段支撑杆DE=70cm.求支撑杆上的点E到水平地面的距离EF是多少?(用四舍五入法对结果取整数,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,√3≈1.732)28.(2021·湖北省荆门市)某海域有一小岛P,在以P为圆心,半径r为10(3+√3)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20√2海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.(1)求A,P之间的距离AP;(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?29.(2021·湖南省益阳市)“2021湖南红色文化旅游节--重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A点测得塔底B的仰角∠BAC=13°,塔顶D的仰角∠DAC=38°,斜坡AB=50米,求宝塔BD的高(精确到1米).(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)30.(2021·湖南省湘西土家族苗族自治州)有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30°,在平地上B处观测到楼顶C处的仰角为45°,并测得A、B 两处相距20m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据:√2≈1.41,√3=1.73)参考答案1.A2.A3.A4.D5.B6.C7.D8.C9.B10.D11.10.512.2√5513.14.16.6.317.24.218.1219.1220.√101021.解:原式=-1+2+4×1-1=-1+2+2-1=2.222.解:原式=-1+1+2×√3-(√3-1)2=-1+1+√3-√3+1=1.23.解:原式=√3-1-2×√3+12=√3-1-√3+1=0.24.解:原式=1-2√3+9+4×√3+12=1-2√3+9+2√3+1=11.25.解:(1)∵∠BOC=120°,∴∠AOB=60°,∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,AO=OC,BO=DO,∴△AOB 是等边三角形,∴AB =AO =BO ,∵AB =2,∴BO =2,∴BD =2BO =4,∴矩形对角线的长为4;(2)由勾股定理得:AD =√BD 2−AB 2=√42−22=2√3,∵OA =OD ,OE ⊥AD 于点E ,∴AE =DE =12AD =√3,∴tanα=AE AB =√32.26.解:由题意可得:∠APD =30°,∠BPD =45°,AP =6km ,∠BDP =90°, 在Rt △BPD 中,∵∠APD =30°,AP =6km ,∠ADP =90°,cos ∠APD =cos30°=PDPA , ∴AD =12AP =3km ,PD =PA •cos30°=6×√32=3√3(km ), 在Rt △APD 中,∵∠BPD =45°,PD =3√3km ,∠BDP =90°,tan ∠BPD =tan45°=BDPD , ∴BD =PD tan45°=3√3(km ), 故AB =BD -AD =3√3-3≈5.196-3=2.196(km )=2196m ,则天舟二号从A 处到B 处的平均速度约为:2196÷7.5≈293(m /s ), 答:天舟二号从A 处到B 处的平均速度约为293m /s .27.解:方法一:如图1,过点D 作DM ⊥EF 于M ,过点D 作DN ⊥BA 交BA 延长线于N ,在Rt △ABC 中,∠ABC =60°,AB =32(cm ),∴BC =AB •cos60°=32×12=16(cm ), ∵DC =84(cm ),∴BD =DC +BC =84+16=100(cm ),∵∠F =90°,∠DMF =90°,∴DM ∥FN ,∴∠MDB=∠ABC=60°,,在Rt△BDN中,sin∠DBN=sin60°=DNBD∴DN=√3×100=50√3(cm),2∵∠F=90°,∠N=90°,∠DMF=90°,∴四边形MFND是矩形,∴DN=MF=50√3,∵∠BDE=75°,∠MDB=60°,∴∠EDM=∠BDE-∠MDB=75°-60°=15°,∵DE=70(cm),∴ME=DE•sin∠EDM=70×sin15°≈18.2(cm),∴EF=ME+MF=50√3+18.2≈104.8≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.方法二:如图2,过点D作DH⊥BA交BA延长线于H,过点E作EG⊥HD延长线于G,在Rt△ABC中,∠ABC=60°,AB=32(cm),∴BC=AB•cos60°=32×1=16(cm),2∵DC=84(cm),∴BD=DC+BC=84+16=100(cm),同方法一得,DH=BD•sin60°=50√3,∵在Rt△BDH中,∠DBH=60°,∴∠BDH=30°,∵∠BDE=75°,∴∠EDG=180°-∠BDH-∠BDE=180°-75°-30°=75°,∴∠DEG=90°-75°=15°,∴DG=DE•sin15°≈18.2(cm),∴GH=DG+DH=18.2+50√3≈104.8≈105(cm),∵∠F=90°,∠H=90°,∠G=90°,∴EF=EG≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.28.解:(1)过点P作PC⊥AB,交AB的延长线于点C,由题意得,∠PAC=30°,∠PBC=45°,AB=20√2,设PC=x,则BC=x,在Rt△PAC中,∵tan30°=PCAC =xx+20√2=√33,∴x=10√6+10√2,∴PA=2x=20√6+20√2,答:A,P之间的距离AP为(20√6+20√2)海里;(2)因为PC-10(3+√3)=10√6+10√2-30-10√3=10(√3+1)(√2-√3)<0,所以有触礁的危险;设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,当P到BD的距离PE=10(3+√3)海里时,有sin∠PBE=10(3+√3)√2⋅PC =10(3+√3)20(√3+1)=√32,∴∠PBD=60°,∴∠CBD=60°-45°=15°,90°-15°=75°即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.29.解:在Rt△ABC中,sin∠BAC=BCAB ,cos∠BAC=ACAB,∴BC=AB•sin∠BAC=AB•sin13°≈50×0.22=11(米);AC=AB•cos∠BAC=AB•cos13°≈50×0.97=48.5(米);在Rt△ADC中,tan∠DAC=CDAC,∴CD=AC•tan∠DAC=AC•tan38°≈48.5×0.78-37.83(米);∴BD=CD-BC≈37.83-11=26.83≈27(米),答:宝塔BD的高约为27米.30.解:设CH为x m,由题意得:∠AHC=90°,∠CBH=45°,∠A=30°,∴BH=CH=xm,AH=√3CH=√3x m,∵AH-BH=AB,∴√3x-x=20,解得:x=10(√3+1)≈27.3(m),答:“一心阁”CH的高度约为27.3m.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
故选:A.
【点睛】
本题考查了解直角三角形−仰角俯角问题及解直角三角形−坡度坡脚问题,通过解直角三角形求出BM,AM,CN,DE的长是解题的关键.
8.如图, 是一张顶角是 的三角形纸片, 现将 折叠,使点B与点A重合,折痕DE,则DE的长为()
∴S△ACE:S△BCE= AC·h: BC·h=AC:BC,
又∵S△ACE:S△BCE=AE:BE,
∴AE:BE=AC:BC,
∵在 中, , ,
∴AC:BC=3:4,
∴AE:BE=3:4
∴AE= AB,
∵ 为 边上的中线,
∴AD= AB,
∴ ,
故选:D.
【点睛】
本题主要考查了角平分线定理的应用及三角函数的应用,通过面积比证得AE:BE=AC:BC是解决本题的关键.
在Rt△ABE中,AB=10米,∠BAM=30°,
∴AM=AB•cos30°=5 (米),BM=AB•sin30°=5(米).
在Rt△ACD中,AE=10(米),∠DAE=60°,
∴DE=AE•tan60°=10 (米).
在Rt△BCN中,BN=AE+AM=10+5 (米),∠CBN=45°,
∴CN=BN•tan45°=10+5 (米),
【详解】
解:由题意可得:∠B=30°,AP=30海里,∠APB=90°,
故AB=2AP=60(海里),
则此时轮船所在位置B处与灯塔P之间的距离为:BP= (海里)
故选:D.
【点睛】
此题主要考查了勾股定理的应用以及方向角,正确应用勾股定理是解题关键.
6.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则⊙O的半径为( )
A.1B.2C. D.
【答案】A
【解析】
【分析】
作AH⊥BC于H,根据等腰三角形的性质求出BH,根据翻折变换的性质求出BD,根据正切的定义解答即可.
【详解】
解:作AH⊥BC于H,
∵AB=AC,AH⊥BC,
BH= BC=3,
∵∠BAC=120°,AB=AC,
∴∠B=30°,
∴AB= =2 ,
由翻折变换的性质可知,DB=DA= ,
锐角三角函数的真题汇编及答案
一、选择题
1.如图,在扇形 中, ,点 是弧 上的一个动点(不与点 、 重合), 、 分别是弦 , 的中点.若 ,则扇形 的面积为()
A. B. C. D.
【答案】A
【解析】
【分析】
如图,作OH⊥AB于H.利用三角形中位线定理求出AB的长,解直角三角形求出OB即可解决问题.
∴③ 正确;
∵∠CEP=30°,
∴CP= EP,
∵EP=BP,
∴CP= BP,
∴④PB=2PC正确.
综上所述:正确的共有4个.
故选:A.
【点睛】
此题主要考查了四边形综合,全等三角形的判定与性质,等边三角形的判定与性质,含30度角的直角三角形性质以及三角函数等知识,证明△ABE是等边三角形是解题关键.
A. B. C.8D.
【答案】A
【解析】
【分析】
根据折叠性质可得BE= AB,A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,可得∠EA′B=30°,根据直角三角形两锐角互余可得∠EBA′=60°,进而可得∠ABM=30°,在Rt△ABM中,利用∠ABM的余弦求出BM的长即可.
【详解】
3.如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. B. C. D.
【答案】B
【解析】
【分析】
先根据翻折变换的性质得到 ,再根据等腰三角形的性质及三角形外角的性质可得到 ,设 , ,则 ,再根据勾股定理即可求解.
13.定义:在等腰三角形中,底边与腰的比叫做顶角的正对,顶角 的正对记作 ,即 底边:腰.如图,在 中, , .则 ()
A. B. C. D.
【答案】C
【解析】
【分析】
证明△ABC是等腰直角三角形即可解决问题.
【详解】
解:∵AB=AC,
∴∠B=∠C,
∵∠A=2∠B,
∴∠B=∠C=45°,∠A=90°,
A.4个B.3个C.2个D.1个
【答案】A
【解析】
【分析】
根据矩形的性质结合全等三角形的判定与性质得出△ADE≌△BCE(SAS),进而求出△ABE是等边三角形,再求出△AEP≌△ABP(SSS),进而得出∠EAP=∠PAB=30°,再分别得出AD与AB,PB与PC的数量关系即可.
【详解】
解:∵在矩形ABCD中,点E是CD的中点,
∴∠DEA+∠CEP=90°,
则∠CEP=30°,
故∠PEB=∠EBP=30°,
则EP=BP,
又∵AE=AB,AP=AP,
∴△AEP≌△ABP(SSS),
∴∠EAP=∠PAB=30°,
∴AP⊥BE,故②正确;
∵∠DAE=30°,
∴tan∠DAE= =tan30°= ,
∴AD= DE,即 ,
∵AB=CD,
此题考查相似三角形的判定和性质、锐角三角函数的定义,掌握相似三角形的对应角相等是解题的关键.
12.如图, 中, , 为 中点,且 , , 分别平分 和 ,交于 点,则 的最小值为().
A.1B. C. D.
【答案】D
【解析】
【分析】
根据三角形角平分线的交点是三角形的内心,得到 最小时, 为三角形 内切圆的半径,结合切线长定理得到三角形为等腰直角三角形,从而得到答案.
【详解】
解:如图作OH⊥AB于H.
∵C、D分别是弦AP、BP的中点.
∴CD是△APB的中位线,
∴AB=2CD= ,
∵OH⊥AB,
∴BH=AH= ,
∵OA=OB,∠AOB=120°,
∴∠AOH=∠BOH=60°,
在Rt△AOH中,sin∠AOH= ,
∴AO= ,
∴扇形AOB的面积为: ,
故选:A.
【点睛】
∵对折矩形纸片ABCD,使AD与BC重合,AB=4,
∴BE= AB=2,∠BEF=90°,
∵把纸片展平,再一次折叠纸片,使点A落在EF上的点A’处,并使折痕经过点B,
∴A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,
∴
∴在Rt△ABM中,AB=BM cos∠ABM,即4=BM cos30°,
本题考查扇形面积公式,三角形的中位线定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
2.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()
A. B. C. D.
【答案】D
【解析】
【分析】
根据角平分线定理可得AE:BE=AC:BC=3:4,进而求得AE= AB,再由点D为AB中点得AD= AB,进而可求得 的值.
【详解】
解:∵ 平分 ,
∴点E到 的两边距离相等,
设点E到 的两边距离位h,
则S△ACE= AC·h,S△BCE= BC·h,
解得:BM= ,
故选A.
【点睛】
本题考查了折叠的性质及三角函数的定义,折叠前后,对应边相等,对应角相等;在直角三角形中,锐角的正弦是角的对边比斜边;余弦是角的邻边比斜边;正切是角的对边比邻边;余切是角的邻边比对边;熟练掌握相关知识是解题关键.
10.如图,在 中, , , 为 边上的中线, 平分 ,则 的值()
A.(54 +10)cmB.(54 +10)cmC.64cmD.54cm
【答案】C
【解析】
【分析】
过A作AE⊥CP于E,过B作BF⊥DQ于F,则可得AE和BF的长,依据端点A与B之间的距离为10cm,即可得到可以通过闸机的物体的最大宽度.
【详解】
如图所示,
过A作AE⊥CP于E,过B作BF⊥DQ于F,则
∴DE=CE,
又∵AD=BC,∠D=∠C,
∴△ADE≌△BCE(SAS),
∴AE=BE,∠DEA=∠CEB,
∵EA平分∠BED,
∴∠AED=∠AEB,
∴∠AED=∠AEB=∠CEB=60°,故:①EB平分∠AEC,正确;
∴△ABE是等边三角形,
∴∠DAE=∠EBC=30°,AE=AB,
∵PE⊥AE,
A. B.2 C. D.
【答案】A
【解析】
连接OC,
∵OA=OC,∠A=30°,
∴∠OCA=∠A=30°,
∴∠COB=∠A+∠ACO=60°,
∵PC是⊙O切线,
∴∠PCO=90°,∠P=30°,
∵PC=3,
∴OC=PC•tan30°= ,
故选A
7.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是( )米.
【详解】
解:∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,∠A=∠EDF,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
设CD=1,CF=x,则CA=CB=2,
∴DF=FA=2﹣x,
∴在Rt△CDF中,由勾股定理得,
