2018年博文教育中考圆的证明题专题训练
2018年人教版全国中考数学复习高频集训(八)以圆为背景的综合计算与证明题

[高频集训(八)以圆为背景的综合计算与证明题]类型一圆与切线有关的问题1.[2016·黄石]如图G8-1,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.(1)若BC=3,AB=5,求AC的值;(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.图G8-12.[2017·南充]如图G8-2,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.(1)求证:DE是⊙O的切线;(2)若CF=2,DF=4,求⊙O直径的长.图G8-2类型二圆与平行四边形结合的问题3.[2015·衡阳]如图G8-3,AB是⊙O的直径,点C,D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.(1)求证:CE为⊙O的切线;(2)判断四边形AOCD是否为菱形?并说明理由.图G8-34.[2016·河南]如图G8-4,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.(1)求证:MD=ME;(2)填空:①若AB=6,当AD=2DM时,DE=________;②连接OD,OE,当∠A的度数为________时,四边形ODME是菱形.图G8-4类型三圆与三角函数结合的问题5.[2017·咸宁]如图G8-5,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.(1)求证:DF是⊙O的切线;2(2)若AE=4,cosA=,求DF的长.5图G8-56.[2016·长沙]如图G8-6,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=25DE,求tan∠ABD的值.图G8-6类型四圆与相似三角形结合的问题7.[2017·天门]如图G8-7,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为D,AD 交⊙O于点E,连接CE,CB,AC.(1)求证:CE=CB;(2)若AC=25,CE=5,求AE的长.图G8-78.如图G8-8,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.图G8-8参考答案1.解:(1)∵AB是⊙O的直径,C在⊙O上,∴∠ACB=90°,又∵BC=3,AB=5,∴由勾股定理得AC=4.(2)证明:如图,连接OC,∵AC是∠DAB的平分线,∴∠DAC=∠BAC.又∵AD⊥DC,∴∠ADC=∠ACB=90°,∴∠DCA=∠CBA.又∵OA=OC,∴∠OAC=∠OCA.∵∠OAC+∠OBC=90°,∴∠OCA+∠ACD=∠OCD=90°,∴DC是⊙O的切线.,,2.[解析] (1)连接OD,欲证DE是⊙O的切线,需证OD⊥DE,即需证∠ODE=90°而∠ACB=90°连接CD,根据“等边对等角”可知∠EDC=∠ECD,∠ODC=∠OCD,进而得出∠ODE=90°,从而得证.(2)在Rt△ODF中,利用勾股定理建立关于半径的方程求解.解:(1)证明:连接OD,CD.∵AC是⊙O的直径,∴∠ADC=90°.∴∠BDC=90°.又E为BC的中点,1∴DE=BC=CE.2∴∠EDC=∠ECD.∵OD=OC,∴∠ODC=∠OCD.∴∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°.∴∠ODE=90°.∴DE是⊙O的切线.(2)设⊙O的半径为x.在Rt△ODF中,OD2+DF2=OF2,即x2+42=(x+2)2,解得x=3.∴⊙O的直径为6.3.解:(1)证明:如图,连接OD,∵点C,D为半圆O的三等分点,∴∠AOD=∠COD=∠COB=60°.∵OA=OD,∴△AOD为等边三角形,∴∠DAO=60°,∴AE∥OC.∵CE⊥AD,∴CE⊥OC,∴CE为⊙O的切线.(2)四边形AOCD为菱形.理由:∵OD=OC,∠COD=60°,∴△OCD为等边三角形,∴CD=CO.同理:AD=AO.∵AO=CO,∴AD=AO=CO=DC,∴四边形AOCD为菱形.4.解:(1)证明:在Rt△ABC中,∵点M是AC的中点,∴MA=MB,∴∠A=∠MBA.∵四边形ABED是圆内接四边形,∴∠ADE+∠ABE=180°,又∠ADE+∠MDE=180°,∴∠MDE=∠MBA.同理可证:∠MED =∠A ,∴∠MDE =∠MED ,∴MD =ME.(2)①2[解析]由MD =ME ,MA =MB ,得DE ∥AB ,MD DE ∴=,又AD =2DM ,MA AB MD 1DE 1∴=,∴=,MA 363∴DE =2.②60°[解析]当∠A =60°时,△AOD 是等边三角形,这时易证∠DOE =60°,△ODE 和△MDE 都是等边三角形,且全等,∴四边形ODME 是菱形.5.解:(1)证明:连接OD.∵OB =OD ,∴∠ODB =∠B.又∵AB =AC ,∴∠C =∠B.∴∠ODB =∠C ,∴OD ∥AC.∵DF ⊥AC ,∴∠DFC =90°,∴∠ODF =∠DFC =90°,∴DF 是⊙O 的切线.(2)过点O 作OG ⊥AC ,垂足为G .∴AG =12AE =2.∵cosA =AGOA ,∴OA =AGcosA =5,∴OG =OA 2-AG 2=21.∵∠ODF =∠DFG =∠OGF =90°,∴四边形OGFD 是矩形,∴DF =OG =21.6.解:(1)∵对角线AC 为⊙O 的直径,∴∠ADC =90°,∴∠EDC =90°;(2)证明:连接DO ,∵∠EDC =90°,F 是EC 的中点,∴DF =FC ,∴∠FDC =∠FCD ,∵OD =OC ,∴∠OCD =∠ODC ,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)由图可得∠ABD=∠ACD,∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,∴∠DCA=∠E.又∵∠ADC=∠CDE=90°,∴△CDE∽△ADC,∴DC DE=,AD DC∴DC2=AD·DE.∵AC=25DE,∴设DE=x(x>0),则AC=25x,则AC2-AD2=AD·DE,即(25x)2-AD2=ADx,整理得:AD2+ADx-20x2=0,解得:AD=4x或AD=-5x(负值舍去),则DC=(25x)2-(4x)2=2x,故tan∠ABD=tan∠ACD=AD4x==2. DC2x7.解:(1)证明:连接OC,∵CD为⊙O的切线,∴OC⊥CD.∵AD⊥CD,∴OC∥AD,∴∠1=∠3.又∵OA=OC,∴∠2=∠3,∴∠1=∠2.∴CE=CB.(2)∵AB为⊙O的直径,∴∠ACB=90°.∵AC=25,CB=CE=5,∴AB=AC2+CB2=(25)2+(5)2=5.∵∠ADC=∠ACB=90°,∠1=∠2,∴△ADC∽△ACB.AD AC DC AD25DC∴==,即==,AC AB CB5255∴AD=4,DC=2.在Rt△DCE中,DE=EC2-DC2=(5)2-22=1,∴AE=AD-ED=4-1=3.8.解:(1)证明:∵AB∥CD,∴∠ABC+∠BCD=180°.∵AB,BC,CD分别与⊙O相切于点E,F,G,∴BO平分∠ABC,CO平分∠DCB,11∴∠OBC=∠ABC,∠OCB=∠DCB,2211∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,22∴∠BOC=90°,∴BO⊥CO.(2)如图,连接OF,则OF⊥BC.∴Rt△BOF∽Rt△BCO,∴BF BO=. BO BC∵在Rt△BOC中,BO=6 cm,CO=8 cm,∴BC=62+82=10(cm),BF6∴=,∴BF=3.6 cm.610∵AB,BC,CD分别与⊙O相切,∴BE=BF=3.6 cm,CG=CF.∵CF=BC-BF=10-3.6=6.4(cm),∴CG=CF=6.4 cm.。
2018年中考数学圆的综合题试题

2018年中考数学圆的综合题试题(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆的综合题1.如图,AB是⊙O的弦,AB=4,过圆心O的直线垂直AB于点D,交⊙O于点C和点E,连接AC、BC、OB,cos∠ACB=13,延长OE到点F,使EF=2OE.(1)求证:∠BOE=∠ACB;(2)求⊙O的半径;(3)求证:BF是⊙O的切线.2. 如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且AD DE,过点D作DF⊥BC于点F,连接BD、DE、AE.(1)求证:DF是⊙O的切线;(2)试判断△DEC的形状,并说明理由;(3)若⊙O的半径为5,AC=12,求sin∠EAB的值.3. (2016长沙9分)如图,四边形ABCD内接于⊙O,对角线AC为⊙O 的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=25DE,求tan∠ABD的值.4. (2016德州10分)如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.5. (2015永州)如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC 于点E,F是OE上的一点,使CF∥BD.(1)求证:BE=CE;(2)试判断四边形BFCD的形状,并说明理由;(3)若BC=8,AD=10,求CD的长.6 (2017原创)如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E 为DC的中点,连接OE交CD于点F,连接BE交CD于点G.(1)求证:AB=AG;(2)(2)若DG=DE,求证:GB2=GC·GA;(3)在(2)的条件下,若tan D=34,EG=10,求⊙O的半径.7.(2015达州)在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为AD上一点,且AF BC,连接DF,并延长DF交BA的延长线于点E. (1)判断DB与DA的数量关系,并说明理由;(2)求证:△BCD≌△AFD;(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.8. 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为点D.(1)求证:△ACD∽△ABC;(2)求证:∠PCA=∠ABC;(3)过点A作AE∥PC交⊙O于点E,交CG于点F,连接BE,若sin P=35,CF=5,求BE的长.9、(2016大庆9分)如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB 于点M,若H是AC的中点,连接MH。
中考难点突破圆的证明题练习50道(含详细解析)

中考难点突破——圆的证明题练习50道(含详细解析)一.解答题(共50小题)1.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.2.如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;(2)填空:①当∠B=时,四边形OCAD是菱形;②当∠B=时,AD与⊙O相切.3.如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.(1)求证:PB是⊙O的切线;(2)当OB=3,PA=6时,求MB、MC的长.4.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求证:PA是⊙O的切线;(2)若PD=,求⊙O的直径.5.如图,点B、C、D都在⊙O上,过点C作CA∥BD交OD的延长线于点A,连接BC,且∠B=∠A=30°,BD=2.(1)求证:AC是⊙O的切线;(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.6.如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.(1)求∠ABC的度数;(2)求证:AE是⊙O的切线;(3)当BC=4时,求劣弧AC的长.7.已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D 作DE⊥AC于点E,交BC的延长线于点F.求证:(1)AD=BD;(2)DF是⊙O的切线.8.如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,(1)求∠ABD的度数;(2)若∠CDB=30°,BC=3,求⊙O的半径.9.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,求图中阴影部分的面积.10.如图,已知⊙O中,AB为直径,AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于D,求线段BC,AD,BD的长.11.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.12.如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O 与BC相切于点E,且∠OBA=∠OBC.(1)求证:AB为⊙O的切线;(2)求⊙O的半径;(3)求tan∠BAD.13.如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD=.(1)求∠C的度数;(2)求证:BC是⊙O的切线;(3)求阴影部分面积.14.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线;(2)当BC=4,AC=6时,求⊙O的半径;(3)在(2)的条件下,求线段BG的长.15.如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.(1)求证:AE⊥CD;(2)已知AE=4cm,CD=6cm,求⊙O的半径.16.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.(1)判断直线BC与⊙O的位置关系并证明;(2)若⊙O的半径为2,AC=3,求BD的长度.17.如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)判断直线AC与⊙O的位置关系,并说明理由;(2)当BD=6,AB=10时,求⊙O的半径.18.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求证:PA是⊙O的切线;(2)若AB=4+,BC=2,求⊙O的半径.19.如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.(1)求证:∠DAC=∠DCE;(2)若AB=2,sin∠D=,求AE的长.20.如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;(1)判断AF与⊙O的位置关系并说明理由.(2)若⊙O的半径为4,AF=3,求AC的长.21.已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°.(Ⅰ)如图①,判断CD与⊙O的位置关系,并说明理由;(Ⅱ)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.22.如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B 作BD⊥AE于D.(1)求证:∠DBA=∠ABC;(2)如果BD=1,tan∠BAD=,求⊙O的半径.23.如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.(1)求证:AC是⊙O的切线;(2)若sinC=,AC=6,求⊙O的直径.24.如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.(1)求证:CB平分∠ACE;(2)若BE=3,CE=4,求⊙O的半径.25.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.26.如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD ⊥CD于点D.(1)求证:AE平分∠DAC;(2)若AB=4,∠ABE=60°.①求AD的长;②求出图中阴影部分的面积.27.如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.(1)求证:AC平分∠DAB;(2)探究线段PC,PF之间的大小关系,并加以证明;(3)若tan∠PCB=,BE=,求PF的长.28.在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.29.如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.(1)求证:AD∥OC;(2)若AE=2,CE=2.求⊙O的半径和线段BE的长.30.如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC 的中点,过点D作⊙O的切线交AC边于点E.(1)求证:DE⊥AC;(2)连接OC交DE于点F,若sin∠ABC=,求的值.31.如图,△ABC内接于⊙O,AD是⊙O直径,过点A的切线与CB的延长线交于点E.(1)求证:EA2=EB•EC;(2)若EA=AC,,AE=12,求⊙O的半径.32.如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O 点作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.33.如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.(1)∠ACB=°,理由是:;(2)猜想△EAD的形状,并证明你的猜想;(3)若AB=8,AD=6,求BD.34.如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.(1)判断AE与⊙O的位置关系,并说明理由;(2)当BC=4,AC=3CE时,求⊙O的半径.35.如图,AB是⊙O的直径,点C在⊙O上,CE⊥AB于E,CD平分∠ECB,交过点B的射线于D,交AB于F,且BC=BD.(1)求证:BD是⊙O的切线;(2)若AE=9,CE=12,求BF的长.36.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.(1)求证:AC是⊙O的切线;(2)若BF=6,⊙O的半径为5,求CE的长.37.如图,在平面直角坐标系中,以点M(0,)为圆心,以长为半径作⊙M交x轴于A、B两点,交y轴于C、D两点,连接AM并延长交⊙M于P 点,连接PC交x轴于E.(1)求点C、P的坐标;(2)求证:BE=2OE.38.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E(1)判断直线PD是否为⊙O的切线,并说明理由;(2)如果∠BED=60°,,求PA的长.(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.39.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F(1)求证:FC=FB;(2)若CD=24,BE=8,求⊙O的直径.40.如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.(1)求证:PB是⊙O的切线;(2)若⊙O的半径为2,求弦AB及PA,PB的长.41.如图所示,以Rt△ABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求sin∠CAE的值.42.如图,已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于B.(1)求证:AD是⊙O的切线;(2)若⊙O的半径为3,AB=4,求AD的长.43.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB 上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°,且⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)44.如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.(1)求证:∠ACO=∠BCD.(2)若BE=3,CD=8,求BC的长.45.如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.(1)求证:CE是⊙O的切线;(2)若BF=2,EF=,求⊙O的半径长.46.如图,AB是⊙O的直径,点F,C是⊙O上两点,且==,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.(1)求证:CD是⊙O的切线;(2)若CD=2,∠CAB=30°,求⊙O的半径.47.如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.(1)判断DE与⊙O的位置关系,并说明理由;(2)若⊙O的半径R=5,tanC=,求EF的长.48.如图,AB为⊙O的直径,D为的中点,连接OD交弦AC于点F,过点D 作DE∥AC,交BA的延长线于点E.(1)求证:DE是⊙O的切线;(2)连接CD,若OA=AE=4,求四边形ACDE的面积.49.如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.(1)求证:EF是⊙O的切线;(2)求AE的长.50.如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,(1)求弦AC的长;(2)求证:BC∥PA.圆的证明题练习50道参考答案与试题解析一.解答题(共50小题)1.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.【解答】(1)证明:∵AB是直径,∴∠AEB=90°,∴AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB,∴四边形ABFC是菱形.(2)设CD=x.连接BD.∵AB是直径,∴∠ADB=∠BDC=90°,∴AB2﹣AD2=CB2﹣CD2,∴(7+x)2﹣72=42﹣x2,解得x=1或﹣8(舍弃)∴AC=8,BD==,∴S=8.菱形ABFC∴S=•π•42=8π.半圆2.如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;(2)填空:①当∠B=30°时,四边形OCAD是菱形;②当∠B=45°时,AD与⊙O相切.【解答】解:(1)∵OA=OC,AD=OC,∴OA=AD,∴∠OAC=∠OCA,∠AOD=∠ADO,∵OD∥AC,∴∠OAC=∠AOD,∴∠OAC=∠OCA=∠AOD=∠ADO,∴∠AOC=∠OAD,∴OC∥AD,∴四边形OCAD是平行四边形;(2)①∵四边形OCAD是菱形,∴OC=AC,又∵OC=OA,∴OC=OA=AC,∴∠AOC=60°,∴∠B=∠AOC=30°;故答案为30.②∵AD与⊙O相切,∴∠OAD=90°,∵AD∥OC,∴∠AOC=90°,∴∠B=∠AOC=45°;故答案为:45°3.如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.(1)求证:PB是⊙O的切线;(2)当OB=3,PA=6时,求MB、MC的长.【解答】证明:(1)∵AC是⊙O的直径,PA切⊙O于点A,∴PA⊥OA∴在Rt△MAP中,∠M+∠P=90°,而∠COB=∠APB,∴∠M+∠COB=90°,∴∠OBM=90°,即OB⊥BP,∴PB是⊙O的切线;(2)∵∠COB=∠APB,∠OBM=∠PAM,∴△OBM∽△APM,∴=,设MB=x,则MA=2x,MO=2x﹣3,∴MP=4x﹣6,在Rt△AMP中,(4x﹣6)2﹣(2x)2=62,解得x=4或0(舍去)∴MB=4,MC=2.4.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求证:PA是⊙O的切线;(2)若PD=,求⊙O的直径.【解答】解:(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线.(2)在Rt△OAP中,∵∠P=30°,∴PO=2OA=OD+PD,又∵OA=OD,∴PD=OA,∵PD=,∴2OA=2PD=2.∴⊙O的直径为2.5.如图,点B、C、D都在⊙O上,过点C作CA∥BD交OD的延长线于点A,连接BC,且∠B=∠A=30°,BD=2.(1)求证:AC是⊙O的切线;(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.【解答】(1)证明:连接OC,交BD于E,∵∠B=30°,∠B=∠COD,∴∠COD=60°,∵∠A=30°,∴∠OCA=90°,即OC⊥AC,∴AC是⊙O的切线;(2)解:∵AC∥BD,∠OCA=90°,∴∠OED=∠OCA=90°,∴DE=BD=,∵sin∠COD=,∴OD=2,在Rt△ACO中,tan∠COA=,∴AC=2,∴S=×2×2﹣=2﹣.阴影6.如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.(1)求∠ABC的度数;(2)求证:AE是⊙O的切线;(3)当BC=4时,求劣弧AC的长.【解答】解:(1)∵∠ABC与∠D都是弧AC所对的圆周角,∴∠ABC=∠D=60°;(2)∵AB是⊙O的直径,∴∠ACB=90°.∴∠BAC=30°,∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即BA⊥AE,∴AE是⊙O的切线;(3)如图,连接OC,∵∠ABC=60°,∴∠AOC=120°,∴劣弧AC的长为=.7.已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D 作DE⊥AC于点E,交BC的延长线于点F.求证:(1)AD=BD;(2)DF是⊙O的切线.【解答】证明:(1)连接CD,∵BC为⊙O的直径,∴CD⊥AB.∵AC=BC,∴AD=BD.(2)连接OD;∵AD=BD,OB=OC,∴OD是△BCA的中位线,∴OD∥AC.∵DE⊥AC,∴DF⊥OD.∵OD为半径,∴DF是⊙O的切线.8.如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,(1)求∠ABD的度数;(2)若∠CDB=30°,BC=3,求⊙O的半径.【解答】解:(1)∵∠C=45°,∴∠A=∠C=45°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠ABD=45°;(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠CAB=∠CDB=30°,BC=3,∴AB=6,∴⊙O的半径为3.9.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,求图中阴影部分的面积.【解答】证明:(1)连接OC,∵CD=AC,∴∠CAD=∠D,又∵∠ACD=120°,∴∠CAD=(180°﹣∠ACD)=30°,∵OC=OA,∴∠A=∠1=30°,∴∠COD=60°,又∵∠D=30°,∴∠OCD=180°﹣∠COD﹣∠D=90°,∴CD是⊙O的切线;(2)∵∠A=30°,∴∴∠1=2∠A=60°∠1=2∠A=60°.,∴∴扇形在Rt△OCD中,.∴.∴图中阴影部分的面积为2﹣π.10.如图,已知⊙O中,AB为直径,AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于D,求线段BC,AD,BD的长.【解答】解:∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,∵AB=10cm,AC=6cm,∴BC==8(cm),∵∠ACB的平分线CD交⊙O于点D,∴=,∴AD=BD,∴∠BAD=∠ABD=45°,∴AD=BD=AB•cos45°=10×=5(cm).11.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.【解答】解:(1)∵AB是半圆O的直径,∴∠ACB=90°,又∵OD∥BC,∴∠AEO=90°,即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.∵OA=OD,∴∠DAO=∠ADO=(180°﹣∠AOD)=(180°﹣70°)=55°,∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;(2)在直角△ABC中,BC===.∵OE⊥AC,∴AE=EC,又∵OA=OB,∴OE=BC=.又∵OD=AB=2,∴DE=OD ﹣OE=2﹣. 12.如图,△ABC 中,∠C=90°,AC=3,AB=5,点O 在BC 边的中线AD 上,⊙O与BC 相切于点E ,且∠OBA=∠OBC .(1)求证:AB 为⊙O 的切线;(2)求⊙O 的半径;(3)求tan ∠BAD .【解答】(1)证明:如图,作OF 垂直AB 于点F ,∵⊙O 与BC 相切于点E ,∴OE ⊥BC又∠OBA=∠OBC ,∴OE=OF ,∴AB 为⊙O 的切线(2)解:∵∠C=90°,AC=3,AB=5,∴BC= =4,又D 为BC 的中点,∴CD=DB=2,∵S △ACD +S △COB +S △AOB =S △ABC设⊙O 的半径为r ,即AC•CD + BD•r +∴6+2r +5r=12∴r=∴⊙O 的半径为(3)解:∵∠C=90°,OE⊥BC,∴OE∥AC,∴Rt△ODE∽Rt△ADC,∴,∴DE=,∴BF=BE=,∴AF=AB﹣BF=,∴tan∠BAD==.13.如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD=.(1)求∠C的度数;(2)求证:BC是⊙O的切线;(3)求阴影部分面积.【解答】(1)解:如图,连接BD,∵AD为圆O的直径,∴∠ABD=90°,∴BD=AD=3,∵CD∥AB,∠ABD=90°,∴∠CDB=∠ABD=90°,在Rt△CDB中,tanC===,∴∠C=60°;(2)证明:连接OB,∵OA=OB,∴∠OBA=∠A=30°,∵CD∥AB,∠C=60°,∴∠ABC=180°﹣∠C=120°,∴∠OBC=∠ABC﹣∠ABO=120°﹣30°=90°,∴OB⊥BC,∴BC为圆O的切线;(3)解:过点O作OE⊥AB,则有OE=OA=,∵AB===3,∴S△OAB=AB•OE=×3×=,∵∠AOB=180°﹣2∠A=120°,∴S扇形OAB==3π,则S阴影=S扇形OAB﹣S△AOB=3π﹣.14.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线;(2)当BC=4,AC=6时,求⊙O的半径;(3)在(2)的条件下,求线段BG的长.【解答】(1)证明:连接OM,如图1,∵BM是∠ABC的平分线,∴∠OBM=∠CBM,∵OB=OM,∴∠OBM=∠OMB,∴∠CBM=∠OMB,∴OM∥BC,∵AB=AC,AE是∠BAC的平分线,∴AE⊥BC,∴OM⊥AE,∴AE为⊙O的切线;(2)解:设⊙O的半径为r,∵AB=AC=6,AE是∠BAC的平分线,∴BE=CE=BC=2,∵OM∥BE,∴△AOM∽△ABE,∴=,即=,解得r=,即设⊙O的半径为;(3)解:作OH⊥BE于H,如图,∵OM⊥EM,ME⊥BE,∴四边形OHEM为矩形,∴HE=OM=,∴BH=BE﹣HE=2﹣=,∵OH⊥BG,∴BH=HG=,∴BG=2BH=1.15.如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.(1)求证:AE⊥CD;(2)已知AE=4cm,CD=6cm,求⊙O的半径.【解答】(1)证明:连接OA.∵AE是⊙O切线,∴OA⊥AE,∴∠OAE=90°,∴∠EAD+∠OAD=90°,∵∠ADO=∠ADE,OA=OD,∴∠OAD=∠ODA=∠ADE,∴∠EAD+∠ADE=90°,∴∠AED=90°,∴AE⊥CD;(2)解:过点O作OF⊥CD,垂足为点F.∵∠OAE=∠AED=∠OFD=90°,∴四边形AOFE是矩形.∴OF=AE=4cm.又∵OF⊥CD,∴DF=CD=3cm.在Rt△ODF中,OD==5cm,即⊙O的半径为5cm.16.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.(1)判断直线BC与⊙O的位置关系并证明;(2)若⊙O的半径为2,AC=3,求BD的长度.【解答】解:(1)BC与⊙O相切.证明:连接OD.∵AD是∠BAC的平分线,∴∠BAD=∠CAD.又∵OD=OA,∴∠OAD=∠ODA.∴∠CAD=∠ODA.∴OD∥AC.∴∠ODB=∠C=90°,即OD⊥BC.又∵BC过半径OD的外端点D,∴BC与⊙O相切.(2)由(1)知OD∥AC.∴△BDO∽△BCA.∴=.∵⊙O的半径为2,∴DO=OE=2,AE=4.∴=.∴BE=2.∴BO=4,∴在Rt△BDO中,BD==2.17.如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)判断直线AC与⊙O的位置关系,并说明理由;(2)当BD=6,AB=10时,求⊙O的半径.【解答】解:(1)AC与⊙O相切.理由如下:连结OE,如图,∵BE平分∠ABD,∴∠OBE=∠DBO,∵OE=OB,∴∠OBE=∠OEB,∴∠OBE=∠DBO,∴OE∥BD,∵AB=BC,D是AC中点,∴BD⊥AC,∴OE⊥AC,∴AC与⊙O相切;(2)设⊙O半径为r,则AO=10﹣r,由(1)知,OE∥BD,∴△AOE∽△ABD,∴=,即=,∴r=,即⊙O半径是.18.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求证:PA是⊙O的切线;(2)若AB=4+,BC=2,求⊙O的半径.【解答】(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线;(2)解:过点C作CE⊥AB于点E.在Rt△BCE中,∠B=60°,BC=2,∴BE=BC=,CE=3,∵AB=4+,∴AE=AB﹣BE=4,∴在Rt△ACE中,AC==5,∴AP=AC=5.∴在Rt△PAO中,OA=,∴⊙O的半径为.19.如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.(1)求证:∠DAC=∠DCE;(2)若AB=2,sin∠D=,求AE的长.【解答】解:(1)∵AD是圆O的切线,∴∠DAB=90°.∵AB是圆O的直径,∴∠ACB=90°.∵∠DAC+∠CAB=90°,∠CAB+∠ABC=90°,∴∠DAC=∠B.∵OC=OB,∴∠B=∠OCB.又∵∠DCE=∠OCB.∴∠DAC=∠DCE.(2)∵AB=2,∴AO=1.∵sin∠D=,∴OD=3,DC=2.在Rt△DAO中,由勾股定理得AD==2.∵∠DAC=∠DCE,∠D=∠D,∴△DEC∽△DCA.∴,即.解得:DE=.∴AE=AD﹣DE=.20.如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;(1)判断AF与⊙O的位置关系并说明理由.(2)若⊙O的半径为4,AF=3,求AC的长.【解答】(1)证明:连接OC,如图所示:∵AB是⊙O直径,∴∠BCA=90°,∵OF∥BC,∴∠AEO=90°,∠1=∠2,∠B=∠3,∴OF⊥AC,∵OC=OA,∴∠B=∠1,∴∠3=∠2,在△OAF和△OCF中,,∴△OAF≌△OCF(SAS),∴∠OAF=∠OCF,∵PC是⊙O的切线,∴∠OCF=90°,∴∠OAF=90°,∴FA⊥OA,∴AF是⊙O的切线;(2)∵⊙O的半径为4,AF=3,∠OAF=90°,∴OF===5∵FA⊥OA,OF⊥AC,∴AC=2AE,△OAF的面积=AF•OA=OF•AE,∴3×4=5×AE,解得:AE=,∴AC=2AE=.21.已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°.(Ⅰ)如图①,判断CD与⊙O的位置关系,并说明理由;(Ⅱ)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.【解答】解:(1)CD与圆O相切.证明:如图①,连接OD,则∠AOD=2∠DAB=2×45°=90°,∵四边形ABCD是平行四边形,∴AB∥DC.∴∠CDO=∠AOD=90°.∴OD⊥CD.∴CD与圆O相切.(2)如图②,作EF⊥AB于F,连接BE,∵AB是圆O的直径,∴∠AEB=90°,AB=2×3=6.∵AE=5,∴BE==,∵sin∠BAE==.∴=∴EF=.22.如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B 作BD⊥AE于D.(1)求证:∠DBA=∠ABC;(2)如果BD=1,tan∠BAD=,求⊙O的半径.【解答】(1)证明:如图,连接OA,∵AE为⊙O的切线,BD⊥AE,∴∠DAO=∠EDB=90°,∴∠DBA=∠BAO,又∵OA=OB,∴∠ABC=∠BAO,∴∠DBA=∠ABC;(2)解:∵BD=1,tan∠BAD=,∴AD=2,∴AB==,∴cos∠DBA=;∵∠DBA=∠CBA,∴BC===5.∴⊙O的半径为2.5.23.如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.(1)求证:AC是⊙O的切线;(2)若sinC=,AC=6,求⊙O的直径.【解答】(1)证明:∵AB=AC,AD=DC,∴∠C=∠B,∠1=∠C,又∵∠E=∠B,∴∠1=∠E,∵AE是⊙O的直径,∴∠ADE=90°,∴∠E+∠EAD=90°,∴∠1+∠EAD=90°,即∠EAC=90°,∴AE⊥AC,∴AC是⊙O的切线;(2)解:过点D作DF⊥AC于点F,如图,∵DA=DC,∴CF=AC=3,在Rt△CDF中,∵sinC==,设DF=4x,DC=5x,∴CF==3x,∴3x=3,解得x=1,∴DC=5,∴AD=5,∵∠ADE=∠DFC=90°,∠E=∠C,∴△ADE∽△DFC,∴=,即=,解得AE=,即⊙O的直径为.24.如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.(1)求证:CB平分∠ACE;(2)若BE=3,CE=4,求⊙O的半径.【解答】(1)证明:如图1,连接OB,∵AB是⊙0的切线,∴OB⊥AB,∵CE丄AB,∴OB∥CE,∴∠1=∠3,∵OB=OC,∴∠1=∠2∴∠2=∠3,∴CB平分∠ACE;(2)如图2,连接BD,∵CE丄AB,∴∠E=90°,∴BC===5,∵CD是⊙O的直径,∴∠DBC=90°,∴∠E=∠DBC,∴△DBC∽△CBE,∴,∴BC2=CD•CE,∴CD==,∴OC==,∴⊙O的半径=.25.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.【解答】(1)证明:∵PD切⊙O于点C,∴OC⊥PD,又∵AD⊥PD,∴OC∥AD,∴∠ACO=∠DAC.∵OC=OA,∴∠ACO=∠CAO,∴∠DAC=∠CAO,即AC平分∠DAB;(2)证明:∵AD⊥PD,∴∠DAC+∠ACD=90°.又∵AB为⊙O的直径,∴∠ACB=90°.∴∠PCB+∠ACD=90°,∴∠DAC=∠PCB.又∵∠DAC=∠CAO,∴∠CAO=∠PCB.∵CE平分∠ACB,∴∠ACF=∠BCF,∴∠CAO+∠ACF=∠PCB+∠BCF,∴∠PFC=∠PCF,∴PC=PF;(3)解:∵∠PAC=∠PCB,∠P=∠P,∴△PAC∽△PCB,∴.又∵tan∠ABC=,∴,∴,设PC=4k,PB=3k,则在Rt△POC中,PO=3k+7,OC=7,∵PC2+OC2=OP2,∴(4k)2+72=(3k+7)2,∴k=6 (k=0不合题意,舍去).∴PC=4k=4×6=24.26.如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD ⊥CD于点D.(1)求证:AE平分∠DAC;(2)若AB=4,∠ABE=60°.①求AD的长;②求出图中阴影部分的面积.【解答】(1)证明:连接OE,如图,∵CD与⊙O相切于点E,∴OE⊥CD,∵AD⊥CD,∴OE∥AD,∴∠DAE=∠AEO,∵AO=OE,∴∠AEO=∠OAE,∴∠OAE=∠DAE,∴AE平分∠DAC;(2)解:①∵AB是直径,∴∠AEB=90°,∠ABE=60°.∴∠EAB=30°,在Rt△ABE中,BE=AB=×4=2,AE=BE=2,在Rt△ADE中,∠DAE=∠BAE=30°,∴DE=AE=,∴AD=DE=×=3;②∵OA=OB,∴∠AEO=∠OAE=30°,∴∠AOE=120°,∴阴影部分的面积=S扇形AOE ﹣S△AOE=S扇形AOE﹣S△ABE=﹣••2•2=π﹣.27.如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.(1)求证:AC平分∠DAB;(2)探究线段PC,PF之间的大小关系,并加以证明;(3)若tan∠PCB=,BE=,求PF的长.【解答】解:(1)连接OC.∵OA=OC,∴∠OAC=∠OCA.∵PC是⊙O的切线,AD⊥CD,∴∠OCP=∠D=90°,∴OC∥AD.∴∠CAD=∠OCA=∠OAC.即AC平分∠DAB.(2)PC=PF.证明:∵AB是直径,∴∠ACB=90°,∴∠PCB+∠ACD=90°又∵∠CAD+∠ACD=90°,∴∠CAB=∠CAD=∠PCB.又∵∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE.∴∠PFC=∠PCF.∴PC=PF.(3)连接AE.∵∠ACE=∠BCE,∴=,∴AE=BE.又∵AB是直径,∴∠AEB=90°.AB=,∴OB=OC=5.∵∠PCB=∠PAC,∠P=∠P,∴△PCB∽△PAC.∴.∵tan∠PCB=tan∠CAB=.∴=.设PB=3x,则PC=4x,在Rt△POC中,(3x+5)2=(4x)2+52,解得x1=0,.∵x>0,∴,∴PF=PC=.28.在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.【解答】解:(1)当点O在AC上时,OC为⊙O的半径,∵BC⊥OC,且点C在⊙O上,∴BC与⊙O相切.∵⊙O与AB边相切于点P,∴BC=BP,∴∠BCP=∠BPC=,∵∠ACP+∠BCP=90°,∴∠ACP=90°﹣∠BCP=90°﹣=∠B.′即2∠ACP=∠B;(2)在△ABC中,∠ACB=90°,AB==10,如图,当点O在CB上时,OC为⊙O的半径,∵AC⊥OC,且点C在⊙O上,∴AC与⊙O相切,连接OP、AO,∵⊙O与AB边相切于点P,∴OP⊥AB,设OC=x,则OP=x,OB=BC﹣OC=6﹣x,∵AC=AP,∴BP=AB﹣AP=10﹣8=2,在△OPA中,∠OPA=90°,根据勾股定理得:OP2+BP2=OB2,即x2+22=(6﹣x)2,解得:x=,在△ACO中,∠ACO=90°,AC2+OC2=AO2,∴AO==.∵AC=AP,OC=OP,∴AO垂直平分CP,∴根据面积法得:CP=2×=,则符合条件的CP长大于.由题意可知,当点P与点A重合时,CP最长,综上,当点O在△ABC外时,<CP≤8.。
中考数学专题复习《圆的证明与计算》检测题(含答案)

专题二 圆的证明与计算类型一 圆基本性质的证明与计算1.如图,⊙O 的半径为5,点P 在⊙O 外,PB 交⊙O 于A 、B 两点,PC 交⊙O 于D 、C 两点. (1)求证:P A ·PB =PD ·PC ;(2)若P A =454,AB =194,PD =DC +2,求点O 到PC 的距离.第1题图2. 如图,△ABC 是⊙O 的内接三角形,AB =AC ,点P 是AB ︵的中点,连接P A ,PB ,PC .(1)如图①,若∠BPC =60°,求证:AC =3AP ; (2)如图②,若sin ∠BPC =2425,求tan ∠P AB 的值.第2题图3. 已知⊙O 中弦AB ⊥弦CD 于E ,tan ∠ACD =32. (1)如图①,若AB 为⊙O 的直径,BE =8,求AC 的长;(2)如图②,若AB 不为⊙O 的直径,BE =4,F 为BC ︵上一点,BF ︵=BD ︵,且CF =7,求AC 的长.第3题图4.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O ,交BC 于点D ,交CA 的延长线于点E ,连接AD 、DE .(1)求证:D 是BC 的中点;(2)若 DE =3,BD -AD =2,求⊙O 的半径; (3)在(2)的条件下,求弦AE 的长.第4题图5.如图,⊙O 的半径为1,A ,P ,B ,C 是⊙O 上的四个点, ∠APC =∠CPB =60°.(1)判断△ABC 的形状:________;(2)试探究线段P A ,PB ,PC 之间的数量关系,并证明你的结论; (3)当点P 位于AB ︵的什么位置时,四边形APBC 的面积最大?求出最大面积.第5题图 备用图类型二与切线有关的证明与计算(一、与三角函数结合1.已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD 交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)求证:AC与⊙O相切;(2)当BD=6,sin C=35时,求⊙O的半径.第1题图2.如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:∠PCA=∠ABC;(2)过点A作AE∥PC,交⊙O于点E,交CD于点F,连接BE.若sin ∠P =35,CF =5,求BE 的长.第2题图3. 如图①,在⊙O 中,直径AB ⊥CD 于点E ,点P 在BA 的延长线上,且满足∠PDA =∠ADC .(1)判断直线PD 与⊙O 的位置关系,并说明理由;(2)延长DO 交⊙O 于M (如图②),当M 恰为BC ︵的中点时,试求DE BE 的值;(3)若P A =2,tan ∠PDA =12,求⊙O 的半径.第3题图二、与相似三角形结合1.如图,在Rt △ABC 中,∠ACB =90°,E 是BC 的中点,以AC 为直径的⊙O 与AB 边交于点D ,连接DE . (1)求证:△ABC ∽△CBD ; (2)求证:直线DE 是⊙O 的切线.第1题图2. 如图,⊙O 的圆心在Rt △ABC 的直角边AC 上,⊙O 经过C 、D 两点,与斜边AB 交于点E ,连接BO 、ED ,有BO ∥ED ,作弦EF ⊥AC 于G ,连接DF .(1)求证:CO ·CD =DE ·BO ;(2)若⊙O 的半径为5,sin ∠DFE =35,求EF 的长.第2题图3. 如图,在△ABC 中,AB =AC ,以AB 为直径作半圆⊙O ,交BC 于点D ,连接AD ,过点D 作DE ⊥AC ,垂足为点E ,交AB 的延长线于点F .(1)求证:EF 是⊙O 的切线;(2)若⊙O 的半径为5,sin ∠ADE =45,求BF 的长.第3题图4.如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形;(2)若AC=6,AB=10,连接AD,求⊙O的半径和AD的长.第4题图5.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD =DC,延长CB交⊙O于点E.(1)图①的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图②,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)第5题图6.已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,OF延长线交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH·EA;(3)若⊙O 的半径为5,sin A =35,求BH 的长.第6题图7.如图①,△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交BC 于点E (BE >EC ),且BD =2 3.过点D 作DF ∥BC ,交AB 的延长线于点F .(1)求证:DF 为⊙O 的切线;(2)若∠BAC =60°,DE =7,求图中阴影部分的面积;(3)若AB AC =43,DF +BF =8,如图②,求BF 的长.第7题图三、与全等三角形结合1.如图,已知PC 平分∠MPN ,点O 是PC 上任意一点,PM 与⊙O 相切于点E ,交PC 于A 、B 两点. (1)求证:PN 与⊙O 相切;(2)如果∠MPC =30°,PE =23,求劣弧BE ︵的长.第1题图2.如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M是⊙O上一点,并且∠BMC =60°.(1)求证:AB是⊙O的切线;(2)若E、F分别是边AB、AC上的两个动点,且∠EDF=120°,⊙O 的半径为2.试问BE+CF的值是否为定值,若是,求出这个定值;若不是,请说明理由.第2题图3. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.(1)求证:AE与⊙O相切;(2)连接BD,若ED∶DO=3∶1,OA=9,求AE的长和tan B的值.第3题图4. 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O 交于点C,连接BC,AF.(1)求证:直线P A为⊙O的切线;(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;(3)若BC=6,tan∠F=12,求cos∠ACB的值和线段PE的长.第4题图5. 如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,∠ACB 的平分线CD 交⊙O 于点D ,过点D 作⊙O 的切线PD ,交CA 的延长线于点P ,过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥CD 于点F . (1)求证:PD ∥AB ; (2)求证:DE =BF ;(3)若AC =6,tan ∠CAB =43,求线段PC 的长.第5题图6.如图,点P 是⊙O 外一点,P A 切⊙O 于点A ,AB 是⊙O 的直径,连接OP ,过点B 作BC ∥OP 交⊙O 于点C ,连接AC 交OP 于点D . (1)求证:PC 是⊙O 的切线;(2)若PD =163,AC =8,求图中阴影部分的面积;(3)在(2)的条件下,若点E 是AB ︵的中点,连接CE ,求CE 的长.第6题图7. 如图①,AB是⊙O的直径,OC⊥AB,弦CD与半径OB相交于点F,连接BD,过圆心O作OG∥BD,过点A作⊙O的切线,与OG 相交于点G,连接GD,并延长与AB的延长线交于点E.(1)求证:GD=GA;(2)求证:△DEF是等腰三角形;(3)如图②,连接BC,过点B作BH⊥GE,垂足为点H,若BH=9,⊙O的直径是25,求△CBF的周长.第7题图专题二圆的证明与计算类型一圆基本性质的证明与计算1. (1)证明:如解图,连接AD,BC,∵四边形ABCD内接于⊙O,∴∠P AD=∠PCB,∠PDA=∠PBC,∴△P AD ∽△PCB , ∴P A PD =PC PB , ∴P A ·PB =PD ·PC ;(2)解:如解图,连接OD ,过O 点作OE ⊥DC 于点E , ∵P A =454,AB =194,PD =DC +2,∴PB =P A +AB =16,PC =PD +DC =2DC +2, ∵P A ·PB =PD ·PC ,∴454×16=(DC +2)(2DC +2), 解得DC =8或DC =-11(舍去), ∴DE =12DC =4, ∵OD =5,∴在Rt △ODE 中,OE =OD 2-DE 2=3, 即点O 到PC 的距离为3.2. (1)证明:∵∠BAC 与∠BPC 是同弧所对的圆周角, ∴∠BAC =∠BPC =60°, 又∵AB =AC ,∴△ABC 为等边三角形, ∴∠ACB =60°, ∵点P 是AB ︵的中点, ∴P A ︵=PB ︵,∴∠ACP =∠BCP =12∠ACB =30°,而∠APC =∠ABC =60°, ∴△APC 为直角三角形, ∴tan ∠APC =AC AP , ∴AC =AP tan60°=3AP ;(2)解:连接AO 并延长交PC 于点E ,交BC 于点F ,过点E 作EG ⊥AC 于点G ,连接OC ,BO ,如解图,∵AB =AC , ∴AF ⊥BC , ∴BF =CF , ∵点P 是AB ︵中点, ∴∠ACP =∠PCB , ∴EG =EF .∵∠BPC =∠BAC =12∠BOC =∠FOC , ∴sin ∠FOC =sin ∠BPC =2425, 设FC =24a ,则OC =OA =25a ,∴OF =OC 2-FC 2=7a ,AF =25a +7a =32a , 在Rt △AFC 中,∵AC 2=AF 2+FC 2, ∴AC =(32a )2+(24a )2=40a , ∵∠EAG =∠CAF , ∴△AEG ∽△ACF , ∴EG CF =AE AC ,又∵EG =EF ,AE =AF -EF ,第2题解图∴EG 24a =32a -EG 40a , 解得EG =12a ,在Rt △CEF 中,tan ∠ECF =EF FC =12a 24a =12, ∵∠P AB =∠PCB ,∴tan ∠P AB =tan ∠PCB =tan ∠ECF =12. 3. 解:(1)如解图①,连接BD , ∵直径AB ⊥弦CD 于点E , ∴CE =DE ,∵∠ACD 与∠ABD 是同弧所对的圆周角, ∴∠ACD =∠ABD , ∴tan ∠ABD =tan ∠ACD =32, ∴ED EB =AE CE =32,即ED 8=32, ∴ED =12, ∴CE =ED =12, 又∵AE =32CE =18, ∴AC =AE 2+CE 2=613;(2)连接CB ,过B 作BG ⊥CF 于G ,如解图②, ∵BF ︵=BD ︵, ∴∠BCE =∠BCG , 在△CEB 和△CGB 中第3题解图①⎩⎪⎨⎪⎧∠BCE =∠BCG ∠BEC =∠BGC BC =BC, ∴△CEB ≌△CGB (AAS), ∴BE =BG =4,∵四边形ACFB 内接于⊙O , ∴∠A +∠CFB =180°, 又∵∠CFB +∠BFG =180°, ∴∠BFG =∠A , ∵∠FGB =∠AEC =90°, ∴△BFG ∽△CAE , ∴FG BG =AE CE =32, ∴FG =32BG =6, ∴CE =CG =13, ∴AE =32CE =392,∴AC =AE 2+CE 2=13213. 4. (1)证明:∵AB 是⊙O 的直径, ∴∠ADB =90°, 即AD ⊥BC , ∵AB =AC ,∴等腰△ABC ,AD 为BC 边上的垂线, ∴BD =DC , ∴D 是BC 的中点; (2)解:∵AB =AC ,∴∠ABC =∠C ,∵∠ABC 和∠AED 是同弧所对的圆周角, ∴∠ABC =∠AED , ∴∠AED =∠C , ∴CD =DE =3, ∴BD =CD =3, ∵BD -AD =2, ∴AD =1,在Rt △ABD 中,由勾股定理得AB 2=BD 2+AD 2=32+12=10, ∴AB =10,∴⊙O 的半径=12AB =102; (3)解:如解图,连接BE , ∵AB =10, ∴AC =10,∵∠ADC =∠BEA =90°,∠C =∠C , ∴△CDA ∽△CEB , ∴AC BC =CD CE ,由(2)知BC =2BD =6,CD =3, ∴106=3CE , ∴CE =9510,∴AE =CE -AC =9510-10=4510. 5. 解:(1)等边三角形.第4题解图【解法提示】∵∠APC =∠CPB =60°,又∵∠BAC 和∠CPB 是同弧所对的圆周角,∠ABC 和∠APC 是同弧所对的圆周角,∴∠BAC =∠CPB =60°,∠ABC =∠APC =60°, ∴∠BAC =∠ABC =60°, ∴AC =BC ,又∵有一个角是60°的等腰三角形是等边三角形, ∴△ABC 是等边三角形. (2)P A +PB =PC .证明如下:如解图①,在PC 上截取PD =P A ,连接AD , ∵∠APC =60°, ∴△P AD 是等边三角形, ∴P A =AD =PD ,∠P AD =60°, 又∵∠BAC =60°, ∴∠P AB =∠DAC , 在△P AB 和△DAC 中, ∵⎩⎪⎨⎪⎧AP =AD ∠P AB =∠DAC ,AB =AC ∴△P AB ≌△DAC (SAS), ∴PB =DC , ∵PD +DC =PC , ∴P A +PB =PC ,(3)当点P 为AB ︵的中点时,四边形APBC 的面积最大. 理由如下:如解图②,过点P 作PE ⊥AB ,垂足为E ,第5题解图①第5题解图②过点C 作CF ⊥AB ,垂足为F , ∵S △P AB =12AB ·PE ,S △ABC =12AB ·CF , ∴S 四边形APBC =12AB ·(PE +CF ).当点P 为AB ︵的中点时,PE +CF =PC ,PC 为⊙O 的直径, 此时四边形APBC 的面积最大, 又∵⊙O 的半径为1,∴其内接正三角形的边长AB = 3 , ∴四边形APBC 的最大面积为12×2×3= 3 . 类型二 与切线有关的证明与计算 一、与三角函数结合 针对演练1. (1)证明:连接OE ,如解图, ∵AB =BC 且D 是AC 中点, ∴BD ⊥AC , ∵BE 平分∠ABD , ∴∠ABE =∠DBE , ∵OB =OE , ∴∠OBE =∠OEB , ∴∠OEB =∠DBE , ∴OE ∥BD ,第1题解图∵BD ⊥AC , ∴OE ⊥AC , ∵OE 为⊙O 半径, ∴AC 与⊙O 相切;(2)解:∵BD =6,sin C =35,BD ⊥AC , ∴BC =BDsin C =10, ∴AB =BC =10.设⊙O 的半径为r ,则AO =10-r , ∵AB =BC , ∴∠C =∠A , ∴sin A =sin C =35, ∵AC 与⊙O 相切于点E , ∴OE ⊥AC ,∴sin A =OE OA =r 10-r =35,∴r =154, 即⊙O 的半径是154.2. (1)证明:连接OC ,如解图, ∵PC 切⊙O 于点C , ∴OC ⊥PC , ∴∠PCO =90°, ∴∠PCA +∠OCA =90°, ∵AB 为⊙O 的直径,第2题解图∴∠ACB =90°, ∴∠ABC +∠OAC =90°, ∵OC =OA , ∴∠OCA =∠OAC , ∴∠PCA =∠ABC ; (2)解:∵AE ∥PC , ∴∠PCA =∠CAF , ∵AB ⊥CG , ∴AC ︵=AG ︵, ∴∠ACF =∠ABC , ∵∠PCA =∠ABC , ∴∠ACF =∠CAF , ∴CF =AF , ∵CF =5, ∴AF =5, ∵AE ∥PC , ∴∠F AD =∠P , ∵sin ∠P =35, ∴sin ∠F AD =35,在Rt △AFD 中,AF =5,sin ∠F AD =35, ∴FD =3,AD =4, ∴CD =CF +FD =8, 在Rt △OCD 中,设OC =r , ∴r 2=(r -4)2+82,∴r =10, ∴AB =2r =20, ∵AB 为⊙O 的直径, ∴∠AEB =90°,在Rt △ABE 中,sin ∠EAD =35, ∴BE AB =35, ∵AB =20, ∴BE =12.3. 解:(1)直线PD 与⊙O 相切, 理由如下:如解图①,连接DO ,CO , ∵∠PDA =∠ADC , ∴∠PDC =2∠ADC , ∵∠AOC =2∠ADC , ∴∠PDC =∠AOC , ∵直径AB ⊥CD 于点E , ∴∠AOD =∠AOC , ∴∠PDC =∠AOD , ∵∠AOD +∠ODE =90°, ∴∠PDC +∠ODE =90°, ∴OD ⊥PD , ∵OD 是⊙O 的半径, ∴直线PD 与⊙O 相切; (2)如解图②,连接BD , ∵M 恰为BC ︵的中点,第3题解图①∴∠CDM =∠BDM , ∵OD =OB , ∴∠BDM =∠DBA , ∴∠CDM =∠DBA , ∵直线PD 与⊙O 相切, ∴∠PDA +∠ADO =90°, 又∵AB 是⊙O 的直径,∴∠ADB =90°,即∠ADO +∠BDM =90°, ∴∠PDA =∠BDM , ∴∠PDA =∠DBA =∠CDM , 又∵∠PDA =∠ADC , ∴∠PDM =3∠CDM =90°, ∴∠CDM =30°, ∴∠DBA =30°, ∴DE BE =tan30°=33; (3)如解图③,∵tan ∠PDA =12,∠PDA =∠ADC , ∴AE DE =12,即DE =2AE ,在Rt △DEO 中,设⊙O 的半径为r , DE 2+EO 2=DO 2, ∴(2AE )2+(r -AE )2=r 2, 解得r =52AE ,在Rt △PDE 中,DE 2+PE 2=PD 2,第3题解图②第3题解图③∴(2AE )2+(2+AE )2=PD 2, ∵直线PD 与⊙O 相切,连接BD , 由(2)知∠PDA =∠DBA ,∠P =∠P , ∴△P AD ∽△PDB , ∴PD PB =P A PD ,∴PD 2=P A ·PB ,即PD 2=2×(2+2r ), ∴(2AE )2+(2+AE )2=2×(2+2r ), 化简得5AE 2+4AE =4r , ∵r =52AE , 解得r =3. 即⊙O 的半径为3. 二、与相似三角形结合 针对演练1. 证明:(1)∵AC 为⊙O 的直径, ∴∠ADC =90°, ∴∠CDB =90°, 又∵∠ACB =90°, ∴∠ACB =∠CDB , 又∵∠B =∠B , ∴△ABC ∽△CBD ; (2)连接DO ,如解图,∵∠BDC =90°,E 为BC 的中点, ∴DE =CE =BE , ∴∠EDC =∠ECD ,第1题解图又∵OD =OC , ∴∠ODC =∠OCD ,而∠OCD +∠DCE =∠ACB =90°, ∴∠EDC +∠ODC =90°,即∠EDO =90°, ∴DE ⊥OD , ∵OD 为⊙O 的半径, ∴DE 与⊙O 相切.2. (1)证明:连接CE ,如解图, ∵CD 为⊙O 的直径, ∴∠CED =90°, ∵∠BCA =90°, ∴∠CED =∠BCO , ∵BO ∥DE , ∴∠BOC =∠CDE , ∴△CBO ∽△ECD , ∴CO DE =BO CD , ∴CO ·CD =DE ·BO ;(2)解:∵∠DFE =∠ECO ,CD =2·OC =10,∴在Rt △CDE 中,ED =CD ·sin ∠ECO =CD ·sin ∠DFE = 10×35=6,∴CE =CD 2-ED 2=102-62=8, 在Rt △CEG 中,EG CE =sin ∠ECG =35, ∴EG =35×8=245,第2题解图根据垂径定理得:EF =2EG =485. 3. (1)证明:如解图,连接OD , ∵AB 是⊙O 的直径, ∴∠ADB =90°, ∵AB =AC ,∴AD 垂直平分BC ,即DC =DB , ∴OD 为△BAC 的中位线, ∴OD ∥AC . 而DE ⊥AC , ∴OD ⊥DE , ∵OD 是⊙O 的半径, ∴EF 是⊙O 的切线;(2)解:∵∠DAC =∠DAB ,且∠AED =∠ADB =90°, ∴∠ADE =∠ABD ,在Rt △ADB 中,sin ∠ADE =sin ∠ABD =AD AB =45,而AB =10, ∴AD =8,在Rt △ADE 中,sin ∠ADE =AE AD =45, ∴AE =325, ∵OD ∥AE , ∴△FDO ∽△FEA ,∴OD AE =FO F A ,即5325=BF +5BF +10,第3题解图∴BF =907.4. (1)证明:如解图①,连接OD 、OE 、ED . ∵BC 与⊙O 相切于点D , ∴OD ⊥BC ,∴∠ODB =90°=∠C , ∴OD ∥AC , ∵∠B =30°, ∴∠A =60°, ∵OA =OE ,∴△AOE 是等边三角形, ∴AE =AO =OD ,∴四边形AODE 是平行四边行, ∵OA =OD ,∴平行四边形AODE 是菱形; (2)解:设⊙O 的半径为r . ∵OD ∥AC , ∴△OBD ∽△ABC ,∴OD AC =OBAB ,即10r =6(10-r ). 解得r =154, ∴⊙O 的半径为154.如解图②,连接OD 、DF 、AD . ∵OD ∥AC , ∴∠DAC =∠ADO ,第4题解图①∵OA =OD , ∴∠ADO =∠DAO , ∴∠DAC =∠DAO , ∵AF 是⊙O 的直径, ∴∠ADF =90°=∠C , ∴△ADC ∽△AFD , ∴AD AC =AF AD , ∴AD 2=AC ·AF ,∵AC =6,AF =154×2=152, ∴AD 2=152×6=45,∴AD =45=3 5.(9分) 5. 解:(1)存在,AE =CE . 理由如下:如解图①,连接AE ,ED , ∵AC 是△ABC 的斜边, ∴∠ABC =90°, ∴AE 为⊙O 的直径, ∴∠ADE =90°, 又∵D 是AC 的中点, ∴ED 为AC 的中垂线, ∴AE =CE ;(2)①如解图②,∵EF 是⊙O 的切线, ∴∠AEF =90°.第5题解图①由(1)可知∠ADE=90°,∴∠AED+∠EAD=90°,∵∠AED+∠DEF=90°,∴∠EAD=∠DEF.又∵∠ADE=∠EDF=90°∴△AED∽△EFD,∴ADED=EDFD,∴ED2=AD·FD.又∵AD=DC=CF,∴ED2=2AD·AD=2AD2,在Rt△AED中,∵AE2=AD2+ED2=3AD2,由(1)知∠AED=∠CED,又∵∠CED=∠CAB,∴∠AED=∠CAB,∴sin∠CAB=sin∠AED=ADAE=13=33.②sin∠CAB=a+2 a+2.【解法提示】由(2)中的①知ED2=AD·FD,∵CF=aCD(a>0),∴CF=aCD=aAD,∴ED2=AD·DF=AD(CD+CF)=AD(AD+aAD)=(a+1)AD2,在Rt△AED中,AE2=AD2+ED2=(a+2)AD2,∴sin ∠CAB =sin ∠AED =ADAE =1a +2=a +2a +2. 6. (1)证明:∵∠ODB =∠AEC ,∠AEC =∠ABC , ∴∠ODB =∠ABC , ∵OF ⊥BC , ∴∠BFD =90°,∴∠ODB +∠DBF =90°, ∴∠ABC +∠DBF =90°, 即∠OBD =90°, ∴BD ⊥OB , ∵OB 为⊙O 的半径, ∴BD 是⊙O 的切线;(2)证明:连接AC ,如解图①所示: ∵OF ⊥BC , ∴BE ︵=CE ︵, ∴∠ECH =∠CAE , ∵∠HEC =∠CEA , ∴△CEH ∽△AEC , ∴CE EH =EA CE , ∴CE 2=EH ·EA ;(3)解:连接BE ,如解图②所示: ∵AB 是⊙O 的直径, ∴∠AEB =90°,∵⊙O 的半径为5,sin ∠BAE =35,第6题解图①第6题解图②∴AB =10,BE =AB ·sin ∠BAE =10×35=6, 在Rt △AEB 中,EA =AB 2-BE 2=102-62=8, ∵BE ︵=CE ︵, ∴BE =CE =6, ∵CE 2=EH ·EA , ∴EH =CE 2EA =628=92,在Rt △BEH 中,BH =BE 2+EH 2=62+(92)2=152.7. (1)证明:连接OD ,如解图①, ∵AD 平分∠BAC 交⊙O 于D , ∴∠BAD =∠CAD , ∴BD ︵=CD ︵, ∴OD ⊥BC , ∵BC ∥DF , ∴OD ⊥DF , ∴DF 为⊙O 的切线;(2)解:连接OB ,连接OD 交BC 于P ,作BH ⊥DF 于H ,如解图①,∵∠BAC =60°,AD 平分∠BAC , ∴∠BAD =30°,∴∠BOD =2∠BAD =60°, 又∵OB =OD ,∴△OBD 为等边三角形, ∴∠ODB =60°,OB =BD =23,第7题解图①∴∠BDF =30°, ∵BC ∥DF , ∴∠DBP =30°,在Rt △DBP 中,PD =12BD =3,PB =3PD =3, 在Rt △DEP 中, ∵PD =3,DE =7,∴PE =(7)2-(3)2=2, ∵OP ⊥BC , ∴BP =CP =3,∴CE =CP -PE =3-2=1, 易证得△BDE ∽△ACE , ∴BE AE =DE CE ,即5AE =71, ∴AE =577. ∵BE ∥DF , ∴△ABE ∽△AFD ,∴BE DF =AE AD ,即5DF =5771277,解得DF =12,在Rt △BDH 中,BH =12BD =3, ∴S 阴影=S △BDF -S 弓形BD =S △BDF -(S 扇形BOD -S △BOD )=12·12·3-60·π·(23)2360+34·(23)2=93-2π;(7分)(3)解:连接CD ,如解图②,由AB AC =43可设AB =4x ,AC =3x ,BF =y , ∵BD ︵=CD ︵, ∴CD =BD =23, ∵DF ∥BC ,∴∠F =∠ABC =∠ADC , ∴∠FDB =∠DBC =∠DAC , ∴△BFD ∽△CDA , ∴BD AC =BF CD ,即233x =y 23,∴xy =4,∵∠FDB =∠DBC =∠DAC =∠F AD , 而∠DFB =∠AFD , ∴△FDB ∽△F AD , ∴DF AF =BF DF , ∵DF +BF =8, ∴DF =8-BF =8-y , ∴8-y y +4x =y 8-y , 整理得:16-4y =xy , ∴16-4y =4,解得y =3, 即BF 的长为3.(10分) 三、与全等三角形结合第7题解图②针对演练1. (1)证明:连接OE ,过点O 作OF ⊥PN ,如解图所示, ∵PM 与⊙O 相切, ∴OE ⊥PM ,∴∠OEP =∠OFP =90°, ∵PC 平分∠MPN , ∴∠EPO =∠FPO , 在△PEO 和△PFO 中, ⎩⎪⎨⎪⎧∠EPO =∠FPO ∠OEP =∠OFP OP =OP, ∴△PEO ≌△PFO (AAS), ∴OF =OE ,∴OF 为圆O 的半径且OF ⊥PN, 则PN 与⊙O 相切;(2)解:在Rt △EPO 中,∠MPC =30°,PE =23, ∴∠EOP =60°,OE =PE ·tan30°=2, ∴∠EOB =120°,则劣弧BE ︵的长为120π×2180=4π3.2. (1)证明:如解图①,连接BO 并延长交⊙O 于点N ,连接CN , ∵∠BMC =60°, ∴∠BNC =60°, ∵∠BNC +∠NBC =90°, ∴∠NBC =30°,又∵△ABC 为等边三角形,第1题解图∴∠BAC =∠ABC =∠ACB =60°, ∴∠ABN =30°+60°=90°, ∴AB ⊥BO ,即AB 为⊙O 的切线.(2)解:BE +CF =3,是定值. 理由如下:如解图②,连接D 与AC 的中点P , ∵D 为BC 中点, ∴AD ⊥BC , ∴PD =PC =12AC , 又∵∠ACB =60°,∴PD =PC =CD =BD =12AC , ∴∠DPF =∠PDC =60°, ∴∠PDF +∠FDC =60°, 又∵∠EDF =120°, ∴∠BDE +∠FDC =60°, ∴∠PDF =∠BDE , 在△BDE 和△PDF 中, ⎩⎪⎨⎪⎧∠EBD =∠DPF BD =PD∠BDE =∠PDF, ∴△BDE ≌△PDF (ASA), ∴BE =PF ,∴BE +CF =PF +CF =CP =BD , ∵OB ⊥AB ,∠ABC =60°,第2题解图②∴∠OBC =30°, 又∵OB =2,∴BD =OB ·cos30°=2×32=3, 即BE +CF = 3.3. (1)证明:连接OC ,如解图①, ∵OD ⊥AC ,OC =OA , ∴∠AOD =∠COD . 在△AOE 和△COE 中, ⎩⎪⎨⎪⎧OA =OC ∠AOE =∠COE OE =OE, ∴△AOE ≌△COE (SAS), ∴∠EAO =∠ECO . 又∵EC 是⊙O 的切线, ∴∠ECO =90°, ∴∠EAO =90°. ∴AE 与⊙O 相切;(2)解:设DO =t ,则DE =3t ,EO =4t , 在△EAO 和△ADO 中,⎩⎪⎨⎪⎧∠EOA =∠AOD ∠EAO =∠ADO, ∴△EAO ∽△ADO , ∴AO DO =EO AO ,即9t =4t 9, ∴t =92,即EO =18.第3题解图①∴AE =EO 2-AO 2=182-92=93;延长BD 交AE 于点F ,过O 作OG ∥AE 交BD 于点G , 如解图②, ∵OG ∥AE , ∴∠FED =∠GOD 又∵∠EDF =∠ODG , ∴△EFD ∽△OGD , ∴EF OG =ED OD =31,即EF =3GO . 又∵O 是AB 的中点, ∴AF =2GO ,∴AE =AF +FE =5GO , ∴5GO =93, ∴GO =935, ∴AF =1835, ∴tan B =AF AB =35.4. (1)证明:如解图,连接OB , ∵PB 是⊙O 的切线, ∴∠PBO =90°,∵OA =OB ,BA ⊥PO 于点D , ∴AD =BD ,∠POA =∠POB , 又∵PO =PO ,∴△P AO ≌△PBO (SAS), ∴∠P AO =∠PBO =90°,第3题解图②第4题解图∴OA ⊥P A ,∴直线P A 为⊙O 的切线;(2)解:线段EF 、OD 、OP 之间的等量关系为EF 2=4OD ·OP . 证明:∵∠P AO =∠PDA =90°,∴∠OAD +∠AOD =90°,∠OP A +∠AOP =90°,∴∠OAD =∠OP A ,∴△OAD ∽△OP A ,∴ OD OA =OA OP ,即OA 2=OD ·OP ,又∵EF =2OA ,∴EF 2=4OD ·OP ;(3)解:∵OA =OC ,AD =BD ,BC =6,∴OD =12BC =3,设AD =x ,∵tan ∠F =12,∴FD =2x ,OA =OF =FD -OD =2x -3,在Rt △AOD 中,由勾股定理,得(2x -3)2=x 2+32,解之得,x 1=4,x 2=0(不合题意,舍去),∴AD =4,OA =2x -3=5,∵AC 是⊙O 直径,∴∠ABC =90°,又∵AC =2OA =10,BC =6,∴ cos ∠ACB =610=35.∵OA 2=OD ·OP ,∴3(PE +5)=25,∴PE =103.5. (1)证明:连接OD ,如解图,∵AB 为⊙O 的直径,∴∠ACB =90°,∵∠ACB 的平分线交⊙O 于点D ,∴∠ACD =∠BCD =45°,∴∠DAB =∠ABD =45°,∴△DAB 为等腰直角三角形,∴DO ⊥AB ,∵PD 为⊙O 的切线,∴OD ⊥PD ,∴PD ∥AB ;(2)证明:∵AE ⊥CD 于点E ,BF ⊥CD 于点F ,∴AE ∥BF ,∴∠FBO =∠EAO ,∵△DAB 为等腰直角三角形,∴∠EDA +∠FDB =90°,∵∠FBD +∠FDB =90°,∴∠FBD =∠EDA ,在△FBD 和△EDA 中,⎩⎪⎨⎪⎧∠BFD =∠DEA ∠FBD =∠EDA BD =DA, ∴△FBD ≌△EDA (AAS),∴DE =BF ;第5题解图(3)解:在Rt △ACB 中,∵AC =6,tan ∠CAB =43,∴BC =6×43=8,∴AB =AC 2+BC 2=62+82=10,∵△DAB 为等腰直角三角形,∴AD =AB 2=52, ∵AE ⊥CD ,∴△ACE 为等腰直角三角形,∴AE =CE =AC 2=62=32, 在Rt △AED 中,DE =AD 2-AE 2=(52)2-(32)2=42,∴CD =CE +DE =32+42=72,∵AB ∥PD ,∴∠PDA =∠DAB =45°,∴∠PDA =∠PCD ,又∵∠DP A =∠CPD ,∴△PDA ∽△PCD ,∴PD PC =P A PD =AD DC =5272=57, ∴P A =57PD ,PC =75PD ,又∵PC =P A +AC ,∴57PD +6=75PD ,解得PD =354,∴PC =57PD +6=57×354+6=254+6=494.6. (1)证明:如解图①,连接OC ,∵P A 切⊙O 于点A ,∴∠P AO =90°,∵BC ∥OP ,∴∠AOP =∠OBC ,∠COP =∠OCB ,∵OC =OB ,∴∠OBC =∠OCB ,∴∠AOP =∠COP ,在△P AO 和△PCO 中,⎩⎪⎨⎪⎧OA =OC ∠AOP =∠COP OP =OP, ∴△P AO ≌△PCO (SAS),∴∠PCO =∠P AO =90°,∴OC ⊥PC ,∵OC 为⊙O 的半径,∴PC 是⊙O 的切线;(2)解:由(1)得P A ,PC 都为圆的切线,∴P A =PC ,OP 平分∠APC ,∠ADO =∠P AO =90°, ∴∠P AD +∠DAO =∠DAO +∠AOD ,又∵∠ADP =∠ADO ,∴∠P AD =∠AOD ,∴△ADP ∽△ODA ,∴AD PD =DO AD ,第6题解图①∴AD 2=PD ·DO ,∵AC =8,PD =163, ∴AD =12AC =4,OD =3,在Rt △ADO 中,AO =AD 2+OD 2=5,由题意知OD 为△ABC 的中位线,∴BC =6,AB =BC 2+AC 2=10.∴S 阴影=12S ⊙O -S △ABC =12·π·52-12×6×8=25π2-24;(3)解:如解图②,连接AE 、BE ,作BM ⊥CE 于点M , ∴∠CMB =∠EMB =∠AEB =90°,∵点E 是AB ︵的中点,∴AE =BE ,∠EAB =∠EBA =45°,∴∠ECB =∠CBM =∠ABE =45°,CM =MB =BC ·sin45°=32,BE =AB ·cos45°=52,∴EM =BE 2-BM 2=42,则CE =CM +EM =7 2.7. (1)证明:连接OD ,如解图①所示,∵OB =OD ,∴∠ODB =∠OBD .∵OG ∥BD ,∴∠AOG =∠OBD ,∠GOD =∠ODB ,∴∠DOG =∠AOG ,在△DOG 和△AOG 中,第6题解图②第7题解图①⎩⎪⎨⎪⎧OD =OA ∠DOG =∠AOG OG =OG, ∴△DOG ≌△AOG (SAS),∴GD =GA ;(2)证明:∵AG 切⊙O 于点A ,∴AG ⊥OA ,∴∠OAG =90°,∵△DOG ≌△AOG ,∴∠OAG =∠ODG =90°,∴∠ODE =180°-∠ODG =90°,∴∠ODC +∠FDE =90°,∵OC ⊥AB ,∴∠COB =90°,∴∠OCD +∠OFC =90°,∵OC =OD ,∴∠ODC =∠OCD ,∴∠FDE =∠OFC ,∵∠OFC =∠EFD ,∴∠EFD =∠EDF ,∴EF =ED ,∴△DEF 是等腰三角形;(3)解:过点B 作BK ⊥OD 于点K ,如解图②所示: 则∠OKB =∠BKD =∠ODE =90°,∴BK ∥DE ,∴∠OBK =∠E ,∵BH ⊥GE ,∴∠BHD =∠BHE =90°, ∴四边形KDHB 为矩形, ∴KD =BH =9,∴OK =OD -KD =72,在Rt △OKB 中,∵OK 2+KB 2=OB 2,OB =252, ∴KB =12,∴tan ∠E =tan ∠OBK =OK KB =724,sin ∠E =sin ∠OBK =OK OB =725,∵tan ∠E =OD DE =724,∴DE =3007,∴EF =3007,∵sin ∠E =BH BE =725,∴BE =2257,∴BF =EF -BE =757,∴OF =OB -BF =2514,在Rt △COF 中,∠COB =90°, ∴OC 2+OF 2=FC 2,∴FC =125214,在Rt △COB 中,∵OC 2+OB 2=BC 2,OC =OB =252, ∴BC =2522,∴BC +CF +BF =1502+757, ∴△CBF 的周长=1502+757.。
2018中考专题-圆综合(含答案)
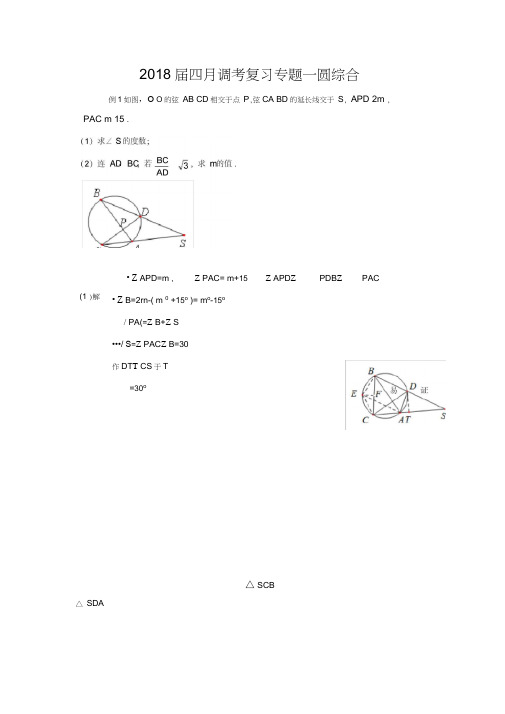
2018届四月调考复习专题一圆综合例1如图,O O 的弦 AB CD 相交于点 P ,弦CA BD 的延长线交于 S , APD 2m ,• Z APD=m ,Z PAC= m+15° Z APD Z PDB Z PAC• Z B=2rn-( m 0 +15o )= m o -15o / PA(=Z B+Z S•••/ S =Z PAC Z B=30作DT T CS 于T=30o△ SCB(1 )解△ SDAPAC m 15 .H=H=、3易证, ST=CT•••/ ACD/ S=30o =Z ABD= rm-15°/• m=45例2.(本题8分)RT^ABC中,/ ACB= 90° , AO是厶ABC的角平分线,以O为圆心,OC为半径作O O.(1)求证:AB为O O的切线;(2)已知AO的延长线交O O于点E,延长AO交O O于D,若tan / D=丄,AC=4,2求O O的半径(1 )过O作OH L AB于H,T AO平分/BAC又ACB=900,•. OH=OC,AB 的切线。
(4分)(2)连接CF, •/ DF O O为直径,•/FCD=90°,易证△ ACF^A ADC,AF AC AC ADCFDC1 AF 4又••• tan / D ,AC=4,「.2 4 AD 1,二AF=2, AD=8,即卩DF=6,2•••OD=3即O O的半径为(8分)例3.在△ PAE中,/ PAE= 90°,点O在边AE上,以OA为半径的O O交AE于B, OP平分/ APEB (1) 求证:PE是O O的切线4M = r, PA 皿一"丁黑h 享•謎财三匚型 EC 4r ・由 RtAFfVt/'RiAFP/i W [ - r_^h J.u - ■4 * 亠•irf 2r s琴齐二t-hZAPfi -乞=?=上a 45 •如图,AC 为O 0的直径,DAB 为O 0的割线,E 为O 0上一点,弧 BE =弧CE DEL AB 于D,交 A0的延长线于F(1) 求证:DF 为O 0的切线5(2) 若 AD= 5,CF= 3,求 tan / CAE 的值例4 •如图,BC 为O O 的直径,AB 为O 0的弦, 丄r1 tanB =-2⑴求证:DE = 2AE (2)求 sin / BFD 勺值D 为弧BC 的中点,CH AD 于 E, AD 交BC 于点F ,11)4;<1> JStA ZW-*■■* E -上收卜■3, il 北丰址科「曲.Vf;£屮ARID *r 轉・” = ■FA AD_ + …厂1 …•旺=用”由1■讶[>E-更.4 46如图,△ ABC内接于O 0, D为直径AC延长线上一点,若/ DCB=Z ABD7 .如图,D为O 0上一点,点C在直径BA的延长线上,且/ CDA M CBD (1)求证:CD是O 0的切线;■j 厶it—M Uy⑴求证:DB为O 0的切线HE t 畑./. w I-:? o于(2)过点B 作。
2018中考专题-圆综合(含答案)

2018届四月调考复习专题—圆综合例1如图,⊙O 的弦AB 、CD 相交于点P ,弦CA 、BD 的延长线交于S ,︒=∠m APD 2,︒+︒=∠15m PAC 。
(1)求∠S 的度数;(2)连AD 、BC ,若3=ADBC,求m 的值.(1)解 ∵∠APD=2m º, ∠P AC= m º+15º ∠APD =∠B +∠PDB =∠B +∠P AC ∴∠B=2m º-( m º+15º)= m º-15º…………2分 ∠P AC =∠B+∠S∴∠S =∠P AC —∠B=30º…………4分 (2) 作DT ⊥CS 于T∵∠S =30º 易证△SDA △SCB ………………………5 分∴ AD BC =SDCS=3易证, ST=CT …………7分∴∠ACD =∠S=30º=∠ABD = m º—15º∴m=45 ………………8分例2. (本题8分)RT △ABC 中,∠ACB =90°, AO 是△ABC 的角平分线,以O 为圆心,OC 为半径作⊙O 。
(1) 求证:AB 为⊙O 的切线;(2) 已知AO 的延长线交⊙O 于点E ,延长AO 交⊙O 于D,若tan ∠D =12,AC=4,求⊙O 的半径(1)过O 作OH ⊥AB 于H ,∵AO 平分∠BAC,又∴∠ACB=090,∴OH=OC , ∴AB 为⊙O 的切线。
——---—-—-——-—-——---—--—---————---——--——---—----—--—(4分)(2)连接CF ,∵DF ⊙O 为直径,∴∠FCD=090,易证△ACF ∽△ADC,∴AF AC CFAC AD DC==E DOCAB又∵tan ∠D 12=,AC=4,∴4142AF AD ==,∴AF=2,AD=8,即DF=6,∴OD=3,即⊙O 的半径为3。
2018圆证明---(-含答案)
圆证明1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)当DF:DE=2:1时,∠BAC的度数为多少?说明理由;2如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.(Ⅰ)求证:直线BF是⊙O的切线;(Ⅱ)若AB=5,sin∠CBF=,求BC和BF的长.3.四边形ABCD是 O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与求则图中阴影部分面积(结果保留π和根号)4.如图,点A、B在⊙O上,直线AC是⊙O的切线,OD⊥OB,连接AB交OC于点D。
(1)求证:AC=CD;(2)若AC=2,AO=,求OD的长度。
CD(1)求证:AD=CD ;(2)若AB=10,cos ∠ABC=53,求tan ∠DBC 的值.. 6如图,OC 平分∠MON ,点A 在射线OC 上,以点A 为圆心,半径为2的⊙A 与OM相切与点B ,连接BA 并延长交⊙A 于点D ,交ON 于点E .(1)求证:ON 是⊙A 的切线;(2)若∠MON=60°,求图中阴影部分的面积.(结果保留π)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.8如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.(1)若∠AOD=52°,求∠DEB的度数;(2)若OC=3,OA=5,求AB的长.已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC=∠DEC,延长BE 依次交AC于G,交⊙O于H。
(1)求证:AC⊥BH;(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长。
2018年最新人教版中考数学 《 圆证明题》 专项复习及答案
2018年中考数学圆证明题专项复习1、如图,点A,B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.求证:AC=CD.2、如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C 作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;(2)若AB=9,BC=6.求PC的长.3、如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.(1)求证:BP平分∠ABC;(2)若PC=1,AP=3,求BC的长.4、已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.(1)求证:PB是⊙O的切线.(2)若OP∥BC,且OP=8,∠C=60°,求⊙O的半径.5、如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N.求证:MN是⊙O的切线.6、如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.(1)求证:∠BDC=∠A;(2)若CE=4,DE=2,求⊙O的直径.7、已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.(1)求证:DC=BD(2)求证:DE为⊙O的切线.8、如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.(1)求证:DC是⊙O的切线;(2)若⊙O的半径为3,sinD=,求线段AF的长.9、如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.(1)求证:NQ⊥PQ;(2)若⊙O的半径R=2,NP=,求NQ的长.10、已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC;连结AC,过点D作DE⊥AC,垂足为E.(1)求证:DC=BD(2)求证:DE为⊙O的切线11、如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F 为BC的中点,连接EF和AD.(1)求证:EF是⊙O的切线;(2)若⊙O的半径为2,∠EAC=60°,求AD的长.12、如图,AB是⊙O的直径,点E是上的一点,∠DBC=∠BED.⑴求证:BC是⊙O的切线;⑵已知AD=3,CD=2,求BC的长.13、如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.(1)求∠ABC的度数;(2)求证:AE是⊙O的切线;(3)当BC=4时,求劣弧AC的长.14、已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;(2)若AB=4,BC=2,求CD的长.15、如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.(1)求证:AC是⊙O的切线;(2)若EF=5,DF=,求⊙O的半径.参考答案1、∵直线AC与⊙O相切,∴OA⊥AC,∴∠OAC=90°,即∠OAB+∠CAB=90°,∵OC⊥OB,∴∠BOC=90°,∴∠B+∠ODB=90°,而∠ODB=∠ADC,∴∠ADC+∠B=90°,∴OA=OB,∴∠OAB=∠B,∴∠ADC=∠CAB,∴AC=CD.2、(1)解:PC与圆O相切,理由为:过C点作直径CE,连接EB,如图,∵CE为直径,∴∠EBC=90°,即∠E+∠BCE=90°,∵AB∥DC,∴∠ACD=∠BAC,∵∠BAC=∠E,∠BCP=∠ACD.∴∠E=∠BCP,∴∠BCP+∠BCE=90°,即∠PCE=90°,∴CE⊥PC,∴PC与圆O相切;(2)解:∵AD是⊙O的切线,切点为A,∴OA⊥AD,∵BC∥AD,∴AM⊥BC,∴BM=CM=BC=3,∴AC=AB=9,在Rt△AMC中,AM= =6,设⊙O的半径为r,则OC=r,OM=AM﹣r=6﹣r,在Rt△OCM中,OM2+CM2=OC2,即32+(6﹣r)2=r2,解得r=,∴CE=2r= ,OM=6 ﹣= ,∴BE=2OM= ,∵∠E=∠MCP,∴Rt△PCM∽Rt△CEB,∴= ,即= ,∴PC= 3、(1)证明:连接OP,∵AC是⊙O的切线,∴OP⊥AC,BC⊥AC,∴OP∥BC,∴∠OPB=∠PBC,∵OP=OB,∴∠OPB=∠OBP,∴∠PBC=∠OBP,∴BP平分∠ABC(2)作PH⊥AB于H.∵PB平分∠ABC,PC⊥BC,PH⊥AB,∴PC=PH=1,在Rt△APH中,AH= =2 ,∵∠A=∠A,∠AHP=∠C=90°,∴△APH∽△ABC,∴= ,∴= ,∴AB=3 ,∴BH=AB﹣AH= ,在Rt△PBC和Rt△PBH中,,∴Rt△PBC≌Rt△PBH,∴BC=BH= .4、(1)证明:连接OB,∵AC是⊙O直径,∴∠ABC=90°,∵OC=OB,∴∠OBC=∠C,∵∠PBA=∠C,∴∠PBA=∠OBC,即∠PBA+∠OBA=∠OBC+∠ABO=∠ABC=90°,∴OB⊥PB,∵OB为半径,∴PB是⊙O的切线;(2)解:∵OC=OB,∠C=60°,∴△OBC为等边三角形,∴BC=OB,∵OP∥BC,∴∠CBO=∠POB,∴∠C=∠POB,在△ABC和△PBO中∵,∴△ABC≌△PBO(ASA),∴AC=OP=8,即⊙O的半径为4.5、证明:连接OM,∵AB=AC,∴∠B=∠C,∵OB=OM,∴∠B=∠OMB,∴∠OMB=∠C,∴OM∥AC,∵MN⊥AC,∴OM⊥MN.∵点M在⊙O上,∴MN是⊙O的切线.6、(1)证明:连接OD,∵CD是⊙O切线,∴∠ODC=90°,即∠ODB+∠BDC=90°,∵AB为⊙O的直径,∴∠ADB=90°,即∠ODB+∠ADO=90°,∴∠BDC=∠ADO,∵OA=OD,∴∠ADO=∠A,∴∠BDC=∠A;(2)∵CE⊥AE,∴∠E=∠ADB=90°,∴DB∥EC,∴∠DCE=∠BDC,∴∠DCE=∠A,∵CE=4,DE=2∴在Rt△ACE中,可得AE=8∴AD=6在在Rt△ADB中可得BD=3∴根据勾股定理可得7、证明:(1)连接AD,∵AB是⊙O的直径,∴∠ADB=90°,又∵AB=AC,∴DC=BD;(2)连接半径OD,∵OA=OB,CD=BD,∴OD∥AC,∴∠ODE=∠CED,又∵DE⊥AC,∴∠CED=90°,∴∠ODE=90°,即OD⊥DE.∴DE是⊙O的切线.8、(1)证明:连接OC,BC,∵AB是⊙O的直径,∴∠ACB=90°,即∠1+∠3=90°.∵OA=OC,∴∠1=∠2.∵∠DCB=∠BAC=∠1.∴∠DCB+∠3=90°.∴OC⊥DF.∴DF是⊙O的切线;(2)解:在Rt△OCD中,OC=3,sinD=.∴OD=5,AD=8.∵=,∴∠2=∠4.∴∠1=∠4.∴OC∥AF.∴△DOC∽△DAF.∴.∴AF=.9、(1)证明:连结OP,如图,∴直线PQ与⊙O相切,∴OP⊥PQ,∵OP=ON,∴∠ONP=∠OPN,∵NP平分∠MNQ,∴∠ONP=∠QNP,∴∠OPN=∠QNP,∴OP∥NQ,∴NQ⊥PQ;(2)解:连结PM,如图,∵MN是⊙O的直径,∴∠MPN=90°,∵NQ⊥PQ,∴∠PQN=90°,而∠MNP=∠QNP,∴Rt△NMP∽Rt△NPQ,∴=,即=,∴NQ=3.10、(1)证明:(1)连接AD;∵AB是⊙O的直径,∴∠ADB=90°.又∵AB=AC∴DC=BD(2)连接半径OD;∵OA=OB,CD=BD,∴OD∥AC.∴∠0DE=∠CED.又∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,即OD⊥DE.∴DE是⊙O的切线.11、(1)证明:连接CE,如图所示:∵AC为⊙O的直径,∴∠AEC=90°.∴∠BEC=90°.∵点F为BC的中点,∴EF=BF=CF.∴∠FEC=∠FCE.∵OE=OC,∴∠OEC=∠OCE.∵∠FCE+∠OCE=∠ACB=90°,∴∠FEC+∠OEC=∠OEF=90°.∴EF是⊙O的切线.(2)解:∵OA=OE,∠EAC=60°,∴△AOE是等边三角形.∴∠AOE=60°.∴∠COD=∠AOE=60°.∵⊙O的半径为2,∴OA=OC=2在Rt△OCD中,∵∠OCD=90°,∠COD=60°,∴∠ODC=30°.∴OD=2OC=4,∴CD=.在Rt△ACD中,∵∠ACD=90°,AC=4,CD=.∴AD==.12、1)AB是⊙O的直径,得∠ADB=90°,从而得出∠BAD=∠DBC,即∠ABC=90°,即可证明BC是⊙O的切线;(2)可证明△ABC∽△BDC,则=,即可得出BC=;13、解:(1)∵∠ABC与∠D都是弧AC所对的圆周角,∴∠ABC=∠D=60°;(2)∵AB是⊙O的直径,∴∠ACB=90°.∴∠BAC=30°,∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即BA⊥AE,∴AE是⊙O的切线;(3)如图,连接OC,∵∠ABC=60°,∴∠AOC=120°,∴劣弧AC的长为.14、(1)证明:∵ED=EC,∴∠EDC=∠C,∵∠EDC=∠B,∴∠B=∠C,∴AB=AC;(2)解:连接AE,∵AB为直径,∴AE⊥BC,由(1)知AB=AC,∴BE=CE=BC=,∵△CDE∽△CBA,∴,∴CE•CB=CD•CA,AC=AB=4,∴•2=4CD,∴CD=.15、(1)证明:连结OD、OC,如图,∵D是弧BE的中点,∴OD⊥BE,∴∠D+∠3=90°,∵∠3=∠2,∴∠D+∠2=90°,∵AF=AC,OD=OC,∴∠1=∠2,∠D=∠4,∴∠1+∠4=90°,∴OC⊥AC,∴AC是⊙O的切线;(2)解:设⊙O的半径为r,则OF=OE﹣EF=r﹣5,在Rt△ODF中,∵OD2+OF2=DF2,∴r2+(r﹣5)2=()2,整理得r2﹣5r﹣6=0,解得r1=6,r2=﹣1,∴,⊙O的半径为6.。
2018全国各地中考数学试题《圆》试题汇编(解答题)
2018全国各地中考数学试题《圆》试题汇编(解答题)2018全国各地中考数学试题《圆》解答题汇编1. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.求证:∠CBP=∠ADB.若OA=2,AB=1,求线段BP的长.2.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O 于点D.已知⊙O的半径为6,∠C=40°.求∠B的度数.求AD的长.3.如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E,点C是BF的中点.求证:AD⊥CD;若∠CAD=30°,⊙O的半径为3,一只蚂蚁从点B出发,沿着BE-EC-CB爬回至点B,求蚂蚁爬过的路程.第 1 页共 27 页4. 如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.求证:OP ⊥CD;连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.5. 如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O 于点F,AC平分∠BAD,连接BF.求证:AD⊥ED;若CD=4,AF=2,求⊙O的半径.6. 如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE 丄AB,交AB的延第 2 页共 27 页长线于点E.求证:CB平分∠ACE;若BE=3,CE=4,求⊙O的半径.7.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB 于点F.求证:BC是⊙O的切线;若⊙O的半径是2cm,E 是AD的中点,求阴影部分的面积8.已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,如图①,若D为AB的中点,求∠ABC和∠ABD的大小;如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,第 3 页共 27 页求∠OCD的大小.9. 如图,D是△ABC外接圆上的动点,且B,D位于AC 的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG ⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.求证:BG∥CD;设△ABC外接圆的圆心为O,若AB=3DH,∠OHD=80°,求∠BDE的大小.10. 如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.求证:AE与⊙O相切于点A;若AE∥BC,BC=27,AC=22,求AD的长.第 4 页共 27 页11.如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC.BC平分∠ABD.求证:CD为⊙O的切线.12.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.求证:DA=DE;若AB=6,CD=43,求图中阴影部分的面积.13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC 于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.求证:DF是⊙O的切线;已知BD=25 第 5 页共27 页25. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.求证:PC是⊙O的切线;若∠ABC=60°,AB=10,求线段CF的长.26. 如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.试判断直线DE与⊙O的位置关系,并说明理;若⊙O的半径为2,∠B=50°,AC=,求图中阴影部分的面积.第 11 页共 27 页27.如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.求证:MD=MC;若⊙O的半径为5,AC=45,求MC的长.27. 如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.判断CM与⊙O的位置关系,并说明理;若∠ECF=2∠A,CM=6,CF=4,求MF的长.第 12 页共 27 页28.如图,在△ABC中,AB=AC,以AB为直径的圆交AC 于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.求证:四边形ABFC是菱形;若AD=7,BE=2,求半圆和菱形ABFC的面积.29.如图,已知A、B、C、D、E是⊙O上五点,⊙O的直径BE=23,∠BCD=120°,A为BE的中点,延长BA到点P,使BA=AP,连接PE.求线段BD的长;求证:直线PE是⊙O的切线.第 13 页共 27 页30.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.求证:EF是⊙O的切线;若AC=4,CE=2,求 BD的长度.31.已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.求扇形OBC的面积;求证:CD是⊙O的切线.32.已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.求证:DF是⊙O的切线;若等边△ABC的边长为8,求第 14 页共 27 页DE、DF、EF围成的阴影部分面积.33.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.求证:AE=ED;若AB=10,∠CBD=36°,求AC的长.34.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.求证:AC是⊙O 的切线;若BD=3,BE=1.求阴影部分的面积.第 15 页共 27 页35.如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.求证:EA是⊙O的切线;求证:BD=CF.36. 如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.若∠ADE=25°,求∠C的度数;若AB=AC,CE=2,求⊙O半径的长.37. 如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,连接OD,过点B作BE∥OD交⊙O于点E,连接DE并延长交BN于点C.求证:DE是⊙O的切线;第 16 页共 27 页若AD=l,BC=4,求直径AB的长.38. 如图所示,PB是⊙O的切线,B为切点,圆心O在PC上,∠P=30°,D为弧BC的中点.求证:PB=BC;试判断四边形BOCD的形状,并说明理.39. 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.40. 如图,AB是⊙O的直径,弦CD⊥AB于点E,过点C 的切线交AB的延长线于点F,连接DF.求证:DF是⊙O的切线;连接BC,若∠BCF=30°,BF=2,求CD的长.第 17 页共 27 页41. 已知,如图AB是⊙O的直径,点P在BA的延长线上,弦BC平分∠PBD,且BD⊥PD于点D.求证:PD是⊙O 的切线.若AB=8cm,BD=6cm,求CD的长.42. 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC 是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.求证:CF是⊙O的切线;若∠F=30°,EB=8,求图中阴影部分的面积.43.如图,已知△ABC内接于⊙O,AB是直径,OD∥AC, AD=OC.求证:四边形OCAD是平行四边形;第 18 页共 27 页探究:①当∠B= °时,四边形OCAD是菱形;②当∠B满足什么条件时,AD与⊙O相切?请说明理.43. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.若∠AOD=52°,求∠DEB的度数;若OC=3,OA=5,求AB的长.44.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.求证:AB=CD;如果⊙O的半径为5,DE=1,求AE的长.第 19 页共 27 页45.如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD. AB,BD,AD围成的阴影部分的面积是;求线段DE的长.46.如图,在△ABC中,AB=AC,O为边AC上一点,以OC 为半径的圆分别交边BC,AC于点D,E,过点D作DF⊥AB于点F.求证:直线DF是⊙O的切线;若∠A=45°,OC=2,求劣弧DE的长.第 20 页共 27 页2018全国各地中考数学试题《圆》解答题汇编1. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.求证:∠CBP=∠ADB.若OA=2,AB=1,求线段BP的长.2.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O 于点D.已知⊙O的半径为6,∠C=40°.求∠B的度数.求AD的长.3.如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E,点C是BF的中点.求证:AD⊥CD;若∠CAD=30°,⊙O的半径为3,一只蚂蚁从点B出发,沿着BE-EC-CB爬回至点B,求蚂蚁爬过的路程.第 1 页共 27 页4. 如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.求证:OP ⊥CD;连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.5. 如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O 于点F,AC平分∠BAD,连接BF.求证:AD⊥ED;若CD=4,AF=2,求⊙O的半径.6. 如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE 丄AB,交AB的延第 2 页共 27 页长线于点E.求证:CB平分∠ACE;若BE=3,CE=4,求⊙O的半径.7.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB 于点F.求证:BC是⊙O的切线;若⊙O的半径是2cm,E是AD的中点,求阴影部分的面积8.已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,如图①,若D为AB的中点,求∠ABC和∠ABD的大小;如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,第 3 页共 27 页求∠OCD的大小.9. 如图,D是△ABC外接圆上的动点,且B,D位于AC 的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG ⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.求证:BG∥CD;设△ABC外接圆的圆心为O,若AB=3DH,∠OHD=80°,求∠BDE的大小.10. 如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.求证:AE与⊙O相切于点A;若AE∥BC,BC=27,AC=22,求AD的长.第 4 页共 27 页11.如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC.BC平分∠ABD.求证:CD为⊙O的切线.12.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.求证:DA=DE;若AB=6,CD=43,求图中阴影部分的面积.13.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC 于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.求证:DF是⊙O的切线;已知BD=25 第 5 页共27 页。
中考专题复习——圆的相关证明(附答案)
中考复习专题——圆的相关证明题1.在⊙O 中,AB 为直径,C 为⊙O 上一点.(Ⅰ)如图①,过点C 作⊙O 的切线,与AB 的延长线相交于点P ,若P ∠︒=42,求∠CAB 的大小; (Ⅱ)如图②,D 为上一点,且OD 经过AC 的中点E ,连接DC 并延长,与AB 的延长线相交于点P , 若∠CAB ︒=10,求∠P 的大小.2.已知AB 是⊙O 的直径,C 是⊙O 上一点,过点C 作⊙O 的切线,交AB 的延长线于点P .(Ⅰ)如图①,连接AC ,BC ,若OB BP =,求A ∠和∠P 的大小;(Ⅱ)如图②,过点P 作⊙O 的切线PD ,切点为D ,连接CD ,BD ,若∠BDC =32°,求BDP ∠的大小.图①图②O B COB D CPE AC3.已知点A ,B ,C 是⊙O 上的三个点,︒=∠120AOB . (Ⅰ)如图①,若AC =BC ,求C ∠和CAO ∠的大小;(Ⅱ)如图②,过点C 作⊙O 的切线,交BA 的延长线于点D ,若AC =AD ,求CAO ∠的大小.4.已知AB 为⊙O 的直径,C 为⊙O 上一点,AD 和过点C 的切线互相垂直,垂足为D ,AD 交⊙O 于点E .(Ⅰ)如图①,求证:AC 平分DAB ∠;(Ⅱ)如图②,过B 作BF AD ∥交⊙O 于点F ,连接CF ,若45AC =4DC =,求CF 和⊙O 半径的长. ABCDEO图①ABCDEO图②F5.已知,△DBC内接于⊙O,DB=DC.(Ⅰ)如图①,过点B作射线BE交⊙O于点A,若∠EAD=75°,求∠BDC的度数.(Ⅱ)如图②,分别过点B、点D作⊙O的切线相交于点E,若∠E=30°,求∠BDC的度数.①②6.已知P A,PB分别与⊙O相切于点A,B,PO交⊙O于点F,且其延长线交⊙O于点C,∠BCP=28°,E为CF上一点,延长BE交⊙O于点D.(Ⅰ)如图1,求∠CDB与∠APB的大小;(Ⅱ)如图2,当BC=CE时,求∠PBE的大小.7.在ABC △中90B ∠=︒D 为AC 上一点,以CD 为直径的⊙O 与AB 相切于点E ,与BC 相交于点F ,连接CE .(Ⅰ)如图①,若27ACE ∠=︒,求A ∠和ECB ∠的大小; (Ⅱ)如图②,连接EF ,若//EF AC ,求A ∠的大小.8. 已知:在⊙O 中OA BC ⊥垂足为E ,点D 在⊙O 上.(Ⅰ)如图①若50AOB ∠=︒,求ADC ∠和∠CAO 的大小;(Ⅱ)如图②CD ∥AO ,过点D 作⊙O 的切线,与BC 的延长线相交于点P ,若26∠=︒ABC 求∠P 的大小.图①图②ABCF OED ABCOED F 图①O EDCBA图②POE DCBA9.如图,在⊙O 中,直径AB 与弦CD 相交于点E ,58ABC ∠=︒. (Ⅰ)如图①若85AEC ∠=︒,求BAD ∠和CDB ∠的大小;(Ⅱ)如图②若CD AB ⊥过点D 作⊙O 的切线DF ,与AB 的延长线相交于点F ,求F ∠的大小.10. 已知AB 是⊙O 的直径,CD 、CB 是⊙O 的弦,且AB CD ∥.(Ⅰ)如图①若25ABC ∠=︒,求BAC ∠和ODC ∠的大小;(Ⅱ)如图②过点C 作⊙O 的切线,与BA 的延长线交于点F 若OD CF ∥求ABC ∠的大小.图①图②EABO DCFE ABO DC图②图①11. 如图,⊙O 是△ABC 的外接圆,AE 切⊙O 于点A ,AE 与直径BD 的延长线相交于点E .(Ⅰ)如图①,若∠C =71°,求∠E 的大小;(Ⅱ)如图②,当AE =AB ,DE =2时,求∠E 的大小和⊙O 的半径.12. 已知DA 、DC 分别与⊙O 相切于点A 点C ,延长DC 交直径AE 的延长线于点P . (Ⅰ)如图①若DC =PC ,求∠P 的度数;(Ⅱ)如图②在⊙O 上取一点B ,连接AB 、BC 、BE ,当四边形ABCD 是平行四边形时,求∠P 及∠AEB 的大小. OEEDCBAD O C BA图①图②DECAPOB图① 图②ECAPOD13.如图①,AB 是⊙O 的弦,OE ⊥AB ,垂足为P ,交AB 于点E ,且OP =3PE ,AB =74.(Ⅰ)求⊙O 的半径;(Ⅱ)如图②过点E 作⊙O 的切线CD ,连接OB 并延长与该切线交于点D ,延长OA 交CD 于C ,求OC 的长. 图②图①EP A BCODP EOBA参考答案1.解:(Ⅰ)如图,连接OC∵ ⊙O 与PC 相切于点C ∴ OC PC ⊥,即90OCP ∠=︒ ∵ 42P ∠=︒∴ 9048COB P ∠=︒-∠=︒ 在Rt OPC △中,48CAB ACO COP ∠+∠=∠=︒ ∵OA =OC ∴∠CAB =∠ACO ∴ 24CAB ∠=︒(Ⅱ)∵ E 为AC 的中点∴ OD AC ⊥,即90AEO ∠=︒在Rt AOE △中,由10EAO ∠=︒得9080AOE EAO ∠=︒-∠=︒ ∴ 1402ACD AOD ∠=∠=︒∵ ACD ∠是ACP △的一个外角∴ 30P ACD CAP ∠=∠-∠=︒2. 解:(Ⅰ)如图①连接OC ∵PC 是⊙O 的切线∴︒=∠90OCP ∵OB BP =∴OB BC =∵OC OB =∴BOC ∆为等边三角形, ∴∠BOC=60° ∴︒=∠=∠3021BOC A ∠P=90°-∠COB =30°(Ⅱ)如图② 连接OC 、OD 设CD 交OP 于点E∵PC ,PD 是⊙O 的切线∴PD PC = ︒=∠=∠90ODP OCP ∵OD OC =∴OP 为CD 的垂直平分线 ∴︒=∠=∠90DEP CEP∵∠BDC =32°∴∠OBD =90°-∠BDC =58° ∵OB OD =∴∠ODB =∠OBD =58° ∴∠BDP =90°-58°=32°3.解: (Ⅰ)∵︒=∠120AOB ∴∠ACB= 12 ∠AOB=60°如图① 连接OC∵AC =BC ∴∠AOC=∠BOC∵∠AOC+∠BOC +∠AOB=360° ∴∠AOC =12 (360°-120°)=120° ∵OA OC ∴∠CAO=∠ACO=12(180°-120°)=30°O AB PCOAB D CPE(Ⅱ)如图② 连接OC设∠ACD= x ∵ACAD ∴∠ACD =∠ADC= x∴∠CAB=2x ∵∠AOB=120°OAOB ∴∠OAB =∠OBA= 12(180°-120°)=30°∵CD 是⊙O 的切线∴∠OCD=90° ∵OAOC ∴∠OCA =∠OAC∴90°-x=2x -30° 解得x=40° ∴∠CAB=80°∴∠CAO=∠CAB -∠OAB =50°4.(Ⅰ)证明:连接OC ∵CD 为⊙的切线∴OC CD ⊥即90OCM OCD ∠=∠=︒ ∵AD CD ⊥垂足为D ∴90ADC ∠=︒ ∵90ADC OCM ∠=∠=︒∴OC AD ∥ ∴DAC ACO ∠=∠∵OC OA =∴CAO ACO ∠=∠∴DAC CAO ∠=∠∴AC 平分DAB ∠ (Ⅱ)解:连接AF 延长CO 交AF 于G ∵AB 为⊙的直径 ∴=90AFB ∠︒ ∵OC AD BF AD ∥,∥ ∴CO BF ∥∴90AFB AGC ∠=∠=︒ ∴OC AF ⊥由垂径定理可得AC=CF∴45AC CF == ∵90ADC ∠=︒22O O ABC DEOF GABCDEOM∴90ADC DCO AGC ∠=∠=∠=︒ ∴四边形ADCG 是矩形∴8AD CG == 4CD AG == 在Rt AGO 中,得222AG OG AO += 设OC x =则,8OA x OG x ==- 可得方程()22248x x +-=解得5x =. ∴⊙半径的长为545CF =.5.(Ⅰ)解:∵四边形ABCD 是⊙O 的内接四边形∴∠DAB +∠C =180° ∵∠EAD +∠DAB =180° ∴∠C =∠EAD ∵∠EAD =75° ∴∠C =75° ∵DB =DC∴∠DBC =∠C =75°∴∠BDC =180°﹣∠C ﹣∠DBC =30°(Ⅱ)解:连结OB OD∵EB ED 与⊙O 相切于点B 点D∴ED OD ⊥⊥,EB OB ∴ ︒=∠︒=∠90ODE 90,OBE∵︒=∠+∠+∠+∠360BOD ODE E OBE ︒=∠30E ∴︒=∠150BOD∴︒=∠=∠7521BOD C ∵DB =DC ,∴∠DBC =∠C =75°,∴∠BDC =180°﹣∠C ﹣∠DBC =30° O6. (I )解:连接OB∵P A 、PB 与圆O 相切于点A 点,B∴PO 平分∠APB 且∠PBO =90° ∵∠BCP =28°∴∠BOP =2∠BCP =28°×2=56° ∴∠BPO =90°-∠BOP =90°-56°=34° ∴∠APB =2∠BPO =2×34°=68°又∠BDC =BOC ∠21=)180(21BOP ∠- ∴∠BDC = 62)56180(21=-∴∠APB =68°∠BDC= 62 (II )连接OB∵BC =CE ∴∠CBE =∠CEB∵∠BCP =28° ∴∠CBE =76228180=-∵OB =OC ∴∠OBC =∠OCB =28° ∴∠EBO =∠CBE -∠OBC =76°-28°=48° ∵P A 与圆O 相切于点A∴OB ⊥PB ∴∠PBO =90°∴∠PBE =90°- ∠EBO =90°-48°=42°7.解:(Ⅰ)如图连接OE .∵ AB 与⊙O 相切∴ OE AB ⊥,即90AEO ∠=︒ ∵ 27ACE ∠=︒∴ 254AOE ACE ∠=∠=︒ ∴ 9036A AOE ∠=︒-∠=︒ ∵ OE OC =∴ OEC OCE ∠=∠∵ 90B ∠=︒∴ //OE BC ∴ ECB OEC ∠=∠ ∴ 27ECB ∠=︒ (Ⅱ)如图,连接OE OF∵ //OE BC //EF AC ∴ 四边形OEFC 为平行四边形 ∴ OE CF = ∴ OC OF CF == ∴ 60ACB ∠=︒∴ 9030A ACB ∠=︒-∠=︒ABCOED F ABCF OED8. 解:(Ⅰ)∵OA BC ⊥ ∴AB AC = 90∠=︒AEC∴∠=∠ACB ADC ∵1252∠=∠=︒ACB AOB∴25∠=∠=︒ADC ACB9065∠=︒-∠=︒CAO ACB(Ⅱ)连接BD . 由OA BC ⊥知,90∠=∠=︒AEB BEO∴ 9064∠=︒-∠=︒OAB ABC ∵AO ∥CD ∴90∠=∠=︒BCD BEO ∴BD 是⊙O 的直径又PD 与⊙O 相切∴⊥BD PD . 即90∠=︒BDP∵=OA OB ∴64∠=∠=︒OBA OAB∴642636∠=∠-∠=︒-︒=︒CBD ABO ABC ∴9052∠=︒-∠=︒P CBD9. (Ⅰ)∵∠AEC 是ΔBEC 的一个外角 58ABC ∠=︒85AEC ∠=︒27C AEC ABC ∴∠=∠-∠=︒∵在⊙O 中BAD C ∠=∠27BAD ∴∠=︒ AB 为⊙O 的直径90ADB ∴∠=︒ ∵在⊙O 中58ADC ABC ∠=∠=︒ 又CDB ADB ADC ∠=∠-∠32CDB ∴∠=︒(Ⅱ)连接OD∵CD ⊥AB 90CEB ∴∠=︒.9032E E CB BC =-∴∠=∠︒︒∴264DOB DCB ∠=∠=︒ ∵DF 是⊙O 的切线∴90ODF ∠=︒90906426F DOB ∴∠=︒-∠=︒-︒=︒图②POE DCBA图①O E DCBA10. 解:(Ⅰ)如图连接OC ∵ AB 是⊙O 的直径 ∴ 90ACB ∠=︒∴ 90BAC ABC ∠+∠=︒由25ABC ∠=︒得65BAC ∠=︒又AB CD ∥得25ABC BCD ∠=∠=︒ ∵ OB OC = ∴ 25OCB ABC ∠==∠=︒ 则50OCD OCB BCD ∠=∠+∠=︒ 由OC OD =得50ODC OCD ∠=∠=︒(Ⅱ)如图,连接OC∵CF 切⊙O 于点C ∴OC FC ⊥则90OCF ∠=︒∵ OD CF ∥ ∴ 90DOC OCF ∠=∠=︒ 又OC OD =则45ODC OCD ∠==∠=︒ 由AB CD ∥得45BOD ODC ∠=∠=︒∴135BOC DOC BOD ∠=∠+∠=︒ ∵ OC OB = ∴22.5ABC OCB ∠=∠=︒11. 解:(Ⅰ)连接OA .∵AE 切⊙O 于点A ∴OA ⊥AE ,∴∠OAE =90° ∵∠C =71° ∴∠AOB =2∠C =2×71°=142° 又∵∠AOB +∠AOE =180° ∴∠AOE =38° ∵∠AOE +∠E =90° ∴∠E =90°﹣38°=52° (Ⅱ)连接OA 设∠E = x .∵AB =AE ∴∠ABE =∠E = x ∵OA =OB ∴∠OAB =∠ABO = x ∴∠AOE =∠ABO +∠BAO =2x∵AE 是⊙O 的切线∴OA ⊥AE ,即∠OAE =90°在△OAE 中∠AOE +∠E =90°即2x +x =90°解得30x =︒∴∠E =30° 在Rt △OAE 中OA =21OE∵OA =OD ∴OA =OD =DE∵DE =2∴OA =2即⊙O 的半径为212.解:(Ⅰ)∵DA 、DC 是⊙O 的切线 ∴DA =DC OA ⊥DA ∴∠DAO =90°∵DC =PC ∴DA =DC =PC ∵∠DAP =90° ∴sin P=DP AD =21∴∠P=30° (Ⅱ)连接OC 、AC∵DA ,DC 是⊙O 的切线 ∴DA =DC∵四边形ABCD 是平行四边形∴□ABCD 是菱形 ∴DA =DC =CB =AB ∠ABC =∠ADC ∵∠AOC =2∠ABC ∴∠AOC =2∠ADC∵DA 、DC 是⊙O 的切线∴OA ⊥AD OC ⊥DC ∴∠DAO =∠DCO =90°∵∠ADC +∠DCO+∠AOC +∠DAO =360° ∴∠ADC +∠AOC =180°∴3∠ADC =180°∴∠ADC =60°∴∠P =90°-∠ADC =30°,∠ABC =60°又AB =BC ∴△ABC 是等边三角形 ∴∠ACB =60° ∴∠AEB =∠ACB=60°13. 解:(Ⅰ)∵OE ⊥AB∴1272APAB 设PE =x 则OP =3x OA =OE =4x在Rt OAP △中222OA OP AP =+即2216928x x =+ 解得x =2(负舍)∴4x =8 ∴半径OA 为8 (Ⅱ)∵ CD 为⊙O 的切线 ∴OE ⊥CD又∵OE ⊥AB ∴AB //CD ∴34OA OP OCOE∴323OCECAPODB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年博文教育中考圆的证明题专题训练一.选择题(共39小题)1.如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.(1)求证:△APE是等腰直角三角形;(2)若⊙O的直径为2,求PC2+PB2的值.2.如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC 的外接圆O于点E,连接AE.(1)求证:四边形AECD为平行四边形;(2)连接CO,求证:CO平分∠BCE.3.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.4.如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.(1)判断直线DE与⊙O的位置关系,并说明理由;(2)若AC=6,BC=8,OA=2,求线段DE的长.5.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.(1)试判断直线BC与⊙O的位置关系,并说明理由;(2)若BD=2,BF=2,求阴影部分的面积(结果保留π).6.如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.(1)若CF交⊙O于点G,⊙O的半径是4,求的长;(2)请判断直线BF与⊙O的位置关系,并说明理由.7.如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.(1)试判断直线EF与⊙O的位置关系,并说明理由;(2)若OA=2,∠A=30°,求图中阴影部分的面积.8.如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.(1)求证:CB平分∠ACE;(2)若BE=3,CE=4,求⊙O的半径.9.已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)如图①,求∠T和∠CDB的大小;(2)如图②,当BE=BC时,求∠CDO的大小.10.如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.(1)求证:∠A=∠ADE;(2)若AD=16,DE=10,求BC的长.11.如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.(1)求证:DF∥AO;(2)若AC=6,AB=10,求CG的长.12.如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO 的延长线交⊙O于点G,EF⊥OG于点F.(1)求证:∠FEB=∠ECF;(2)若BC=6,DE=4,求EF的长.13.如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.(1)求证:PO平分∠APC;(2)连接DB,若∠C=30°,求证:DB∥AC.14.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E 是AB延长线上一点,CE交⊙O于点F,连接OC、AC.(1)求证:AC平分∠DAO.(2)若∠DAO=105°,∠E=30°①求∠OCE的度数;②若⊙O的半径为2,求线段EF的长.15.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.(1)求证:DE⊥AC;(2)若DE+EA=8,⊙O的半径为10,求AF的长度.16.如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.(1)求证:BC是∠ABE的平分线;(2)若DC=8,⊙O的半径OA=6,求CE的长.17.如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.(1)求证:AB平分∠OAD;(2)若点E是优弧上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)18.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.(1)求证:AF⊥EF;(2)若AC=6,CF=2,求⊙O的半径.19.已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.(1)如图1,若DE∥AB,求证:CF=EF;(2)如图2,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.20.如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.(1)求证:DA=DC;(2)求∠P及∠AEB的大小.21.如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为6,BC=8,求弦BD的长.22.如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.23.如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.(1)求证:CE是⊙O的切线;(2)求证:CG=BG;(3)若∠DBA=30°,CG=4,求BE的长.24.如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.(1)求证:CE是⊙O的切线;(2)若BF=2,EF=,求⊙O的半径长.25.如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.(1)求证:DE是⊙O的切线;(2)若CF=2,DF=4,求⊙O直径的长.26.如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.27.如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.(1)求证:AG与⊙O相切;(2)若AC=5,AB=12,BE=,求线段OE的长.28.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.(1)求证:AD=AN;(2)若AB=4,ON=1,求⊙O的半径.29.在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.(1)求证:BF⊥AF;(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.30.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.(1)求证:∠ABD=2∠BDC;(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长31.如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.(1)判断A是否是PB的中点,并说明理由;(2)若⊙O半径为8,试求BC的长.32.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.(1)求证:∠AGD=∠FGC;(2)若AG•AF=48,CD=4,求⊙O的半径.33.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.(Ⅰ)求证:MD=ME;(Ⅱ)如图2,连OD,OE,当∠C=30°时,求证:四边形ODME是菱形.34.如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.(1)请你判断C′D与⊙O的位置关系,并说明理由;(2)过点B作BB′⊥C′D′于B′,交⊙O于E,若CD=,AC=3,求BE的长.35.如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.(1)判断直线BD与⊙O的位置关系,并给出证明;(2)当⊙O的半径是5,BF=2,EF=时,求CE及BH的长.36.如图,在△ABC中,AB=AC.以AC为直径的⊙O交AB于点D,交BC于点E.过E点作⊙O的切线,交AB于点F.(1)求证:EF⊥AB;(2)若BD=2,BE=3,求AC的长.37.如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.(1)求证:AC平分∠DAB;(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长.38.如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.(1)求证:DF垂直平分AC;(2)若弦AD=10,AC=16,求⊙O的半径.39.如图,OA是⊙O的半径,弦CD垂直平分OA于点B,延长CD至点P,过点P作⊙O的切线PE,切点为E,连接AE交CD于点F.(1)若CD=6,求⊙O的半径;(2)若∠A=20°,求∠P的度数.40.如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.(Ⅰ)求∠CPA的度数;(Ⅱ)连接OF,若AC=,∠D=30°,求线段OF的长.。
