渗流理论
渗流理论在地质灾害预警系统

渗流理论在地质灾害预警系统一、渗流理论概述渗流理论是一种研究流体在多孔介质中流动的科学理论,广泛应用于地质学、环境科学、土木工程等领域。
它主要研究流体在岩石、土壤等多孔介质中的渗透、扩散和流动过程。
渗流理论的核心在于理解和预测流体在多孔介质中的运动规律,从而为相关领域的工程实践和科学研究提供理论支持。
1.1 渗流理论的基本原理渗流理论的基本原理包括达西定律和孔隙介质的渗透性。
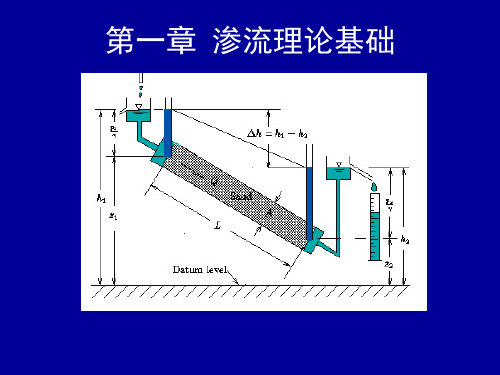
达西定律描述了流体在多孔介质中的线性渗透流动,其基本公式为:\[ Q = k \cdot A \cdot \frac{\Delta h}{L} \]其中,\( Q \) 表示流量,\( k \) 表示渗透系数,\( A \) 表示横截面积,\( \Delta h \) 表示水位差,\( L \) 表示介质长度。
渗透系数是衡量介质渗透性的关键参数,它与介质的孔隙率、孔隙形状和大小等因素有关。
1.2 渗流理论的应用领域渗流理论在多个领域有着广泛的应用,主要包括:- 地下水资源开发:通过渗流理论可以预测地下水的流动路径和速度,为水资源的开发和利用提供科学依据。
- 环境工程:在污染物的迁移和扩散研究中,渗流理论可以帮助预测污染物在土壤和地下水中的传播路径。
- 土木工程:在地基工程、隧道工程等中,渗流理论可以用于评估地基的稳定性和隧道的安全性。
- 地质灾害预警:渗流理论在地质灾害预警系统中,可以预测和评估地质灾害的发生概率和影响范围。
二、地质灾害预警系统中的渗流理论应用地质灾害预警系统是一种用于监测和预测地质灾害的综合性系统,其目的是通过科学的方法和手段,提前发现地质灾害的征兆,减少灾害带来的损失。
渗流理论在地质灾害预警系统中扮演着重要的角色,通过分析和预测流体在多孔介质中的流动,为地质灾害的预警提供理论支持。
2.1 地质灾害预警系统的基本构成地质灾害预警系统一般包括以下几个部分:- 监测设备:用于实时监测地质环境的变化,如地下水位、土壤湿度、地表位移等。
渗流理论基础
岩体的结构分类(GB 50287-1999 )
• Permeability Coefficient— The rate of flow of water through a unit cross-sectional area under a Unit Hydraulic Gradient at the prevailing temperature.
• Hydraulic Conductivity (K)——the volume of water at the existing kinematic viscosity that will move, in unit time, under a unit Hydraulic Gradient through a unit area measured at right angles to the direction of flow, assuming the medium is isotropic and the fluid is homogeneous. In the Standard International System, the units are cubic meters per day per square meter of medium (m3/day/m2) or m/day (for unit measures).
;裂隙介质:
于是有:
或
(1-18)
达西(D)的定义:当液体的动力粘滞度为 0.001Pa·s,压强差为101325Pa的情况下,通过面积 为1cm2、长度为1cm岩样的流量为1cm3/s时岩样的渗 透率,记为D。
尺度效应是指渗透系数与试验范围有关,随着试验 范围的增大而增大的现象,K=K(x)。亦即抽水时间 t长、降深s大的群孔抽水试验所得K较抽水时间t短、 降深s小的抽水试验所得K大。
1渗流基本理论

§1 渗流的基本概念
3、多孔介质中地下水的运动 比较复杂(源于多孔介质的广义性),包括两大类, 运动特点各不相同。 (1)第一类为地下水在孔隙、细小裂隙或发育微弱、 分布均匀的溶隙中运动,具有统一的流场,运动方 向基本一致,符合达西定律,称为达西流。 (2)第二类为地下水沿较大裂隙和溶隙的运动,仍 具有统一的流场,运动方向基本一致,但已不符合 达西定律,流态仍为层流。
§1 渗流的基本概念
根据岩石空隙的性质及其成因,含水介质可划分为: ①孔隙介质:含有孔隙的岩石松散沉积物(黄土:特 殊的孔隙—裂隙介质)。 ②裂隙介质:含有裂隙的坚硬岩石(碎屑岩、火成 岩)。 ③溶隙(岩溶)介质:含有溶隙(穴)的可溶性岩石 (石灰岩、白云岩)。
§1 渗流的基本概念
(3)多孔介质 狭义:孔隙介质 广义:包括孔隙介质、裂隙介质(细小裂隙)和某些 岩溶不十分发育(溶隙分布较均匀)的由石灰岩和 白云岩组成的岩溶介质,都称为多孔介质。 2、多孔介质的特征 (1)空(孔)隙性 ①有效孔隙(Effective pores) 多孔介质中相互连通的,不为结合水所占据的 那部分孔隙。 有效孔隙中存在的是重力水和少量毛细水。
§1 渗流的基本概念 一、地下水在多孔介质中的运动
1、什么是多孔介质? (1)介质 一种物质存在于另一种物质的内部时,后者就 是前者的介质。 《辞海》中的解释:“物体系统在其间存在或物理 过程(力、能量的传递)在其间进行的物质”。 (2)含水介质 地下水存在并运动于岩土空隙中,具有空隙的 岩土称之为含水介质。
§1 渗流的基本概念
4、一点异议 还有一种运动形式:地下水沿大裂隙和发育良好的 岩溶管道的运动,方向没有规律,分属不同的地下 水流动系统,流态为紊流。 属于非多孔介质中地下 水的运动。 地下水在多孔介质和非多孔介质中地下水的运动形 式不同—流态不同(根据雷诺数Re可判断流态)。 @教材上一直将多孔介质中的运动分为: (1)在孔隙和裂隙中运动 (2)大裂隙和管道(岩溶发育好)中运动 我个人认为不妥:多孔介质而非含水介质。
渗流力学知识点总结

渗流力学知识点总结一、渗流基本理论1.渗流的基本概念渗流是指流体在多孔介质中的流动现象。
多孔介质是由孔隙和固体颗粒组成的介质,流体可以通过孔隙和固体颗粒之间的空隙进行流动。
渗流现象在自然界和工程领域都有着广泛的应用,如地下水的运移、石油的开采、地下储层的注水等。
2.渗透性与渗透率渗透性是指单位压力下单位面积介质对流体的渗透能力,通常用渗透率来描述。
渗透率是介质内渗流速度与流体粘滞力之比。
一般来说,渗透性越大,渗透率越高,介质对流体的渗透能力越强。
3.渗透压力与渗透率渗透压力是指多孔介质内部由于孔隙中流体分布不均匀而产生的压力。
渗透压力的大小与介质的孔隙结构、流体的性质、地下水位等因素有关,它是影响渗流速度和方向的重要因素。
4.达西定律达西定律是描述渗透性与渗流速度之间关系的定律,它指出在流体粘滞力不考虑的条件下,渗透速度与渗透压力成正比,与渗透率成反比。
达西定律为渗流理论研究提供了重要的基础。
二、多孔介质渗流规律1.多孔介质的渗流特性多孔介质是由孔隙和固体颗粒组成的介质,它具有复杂的微观结构和介质性质。
渗流在多孔介质中受到许多因素的影响,如介质的孔隙度、渗透率、渗透性等,这些因素决定了渗流规律的复杂性和多样性。
2.渗流方程渗流方程是描述多孔介质中流体运移规律的方程,它通常由渗流方程和质量守恒方程两部分组成。
渗流方程描述了流体在多孔介质中的流动规律,它是渗流力学研究的核心内容。
3.多孔介质的稳定性多孔介质中的渗流现象可能受到介质本身的稳定性限制。
孔隙结构、流体的性质以及渗透压力等因素都会影响介质的稳定性,这对渗流速度和方向产生重要影响。
4.非均质多孔介质中的渗流非均质多孔介质中的渗流现象通常较为复杂,其渗透率、孔隙度、渗透性等参数都可能在空间上呈现非均匀性。
对非均质多孔介质中渗流规律的研究对于实际工程应用具有重要意义。
三、非线性渗流1.非线性渗流模型非线性渗流模型是描述介质非线性渗流现象的数学模型。
渗流立方定律

渗流立方定律渗流立方定律是渗流理论中的一项基本定理,也称为达西定律。
它描述了流体通过孔隙介质的速率与孔隙直径的关系。
渗流立方定律的名称源于其方程的形式,即渗流速率与孔隙直径的立方成正比。
在此文中,我们将详细介绍渗流立方定律及其应用。
1. 渗流立方定律的原理和表达式渗流立方定律反映了渗透流动的速度与介质孔隙结构的特征有关,其数学表达式为:Q=kH^3ΔP/μL其中,Q表示单位时间内通过介质的液体(气体)体积,k表示孔隙介质渗透系数,H表示介质厚度,ΔP表示单位长度介质压力差,μ表示介质的动力黏度,L表示介质中液体(气体)通过的距离。
渗流立方定律反映了孔隙介质中液体渗透速率与渗透孔隙的物理结构性质之间的关系。
具体来说,渗透速率随着孔隙直径的增加而增加,并呈现出孔隙直径的立方次幂关系,即Q∝d^3。
因此,该定理也被称为“孔隙方肆立定律”。
渗流立方定律是地下渗透流动理论的基础,广泛应用于水文地质、土壤力学、石油勘探等领域。
下面列举几个应用:(1) 水文地质学。
渗流立方定律可以用于描述地下水的渗透速率。
在地下水资源开发中,可以根据渗流立方定律确定不同孔隙介质的渗透系数,以评估地下水资源的开采潜力和水文地质条件。
(2) 土壤力学。
渗流立方定律可以用于研究土壤中水分的输运规律和渗透特性,对土壤侵蚀、滑坡和沉降等问题有重要意义。
(3) 石油勘探。
渗流立方定律可以用于预测油气藏中的渗透能力和产能。
通过测量油气藏中不同孔隙介质的孔隙直径和自然渗透试验,可以计算得到渗透系数,从而预测油田的产量和石油资源的分布。
渗流力学基本理论

渗流力学基本理论目录第一章渗流理论基础 ........................................................................... ................................................... 1 1.1 渗流的基本概念 ........................................................................... ................................................... 1 1.2 渗流基本定律 ........................................................................... ....................................................... 7 1.3 岩层透水特征及水流折射定律 ........................................................................... ......................... 11 1.4 流网及其应用 ........................................................................... ..................................................... 14 1.5 渗流连续方程 ........................................................................... ..................................................... 19 1.6 渗流基本微分方程 ........................................................................... ............................................. 24 1.7 数学模型的建立及求解 ........................................................................... . (32)第一章渗流理论基础1.1 渗流的基本概念1.1.1 多孔介质及其特性 1.1.1.1多孔介质的概念多孔介质(Porous medium):地下水动力学中具有空隙的岩石。
【免费下载】渗流力学基本理论

目录第一章渗流理论基础 (1)1.1渗流的基本概念 (1)1.2渗流基本定律 (7)1.3岩层透水特征及水流折射定律 (11)1.4流网及其应用 (14)1.5渗流连续方程 (19)1.6渗流基本微分方程 (24)1.7数学模型的建立及求解 (32)第一章渗流理论基础1.1 渗流的基本概念1.1.1 多孔介质及其特性1.1.1.1多孔介质的概念多孔介质(Porous medium):地下水动力学中具有空隙的岩石。
广义上包括孔隙介质、裂隙介质和岩溶不十分发育的由石灰岩和白云岩组成的介质,统称为多孔介质。
孔隙介质:含有孔隙的岩层,砂层、疏松砂岩等;裂隙介质:含有裂隙的岩层,裂隙发育的花岗岩、石灰岩等。
1.1.1.2 多孔介质的性质(1) 孔隙性:有效孔隙和死端孔隙。
孔隙度(Porosity)是多孔介质中孔隙体积与多孔介质总体积之比(符号为n),可表示为小数或百分数,n=Vv/V。
有效孔隙(Effective pores)是多孔介质中相互连通的、不为结合水所占据的那一部分孔隙。
有效孔隙度(Effective Porosity)是多孔介质中有效孔隙体积与多孔介质总体积之比(符号为n e),可表示为小数或百分数,n e=V e/V。
死端孔隙(Dead-end pores )是多孔介质中一端与其它孔隙连通、另一端是封闭的孔隙。
(2) 连通性:封闭和畅通,有效和无效。
(3) 压缩性:固体颗粒和孔隙的压缩系数推导。
(4) 多相性:固、液、气三相可共存。
其中固相的成为骨架,气相主要分布在非饱和带中,液相的地下水可以吸着水、薄膜水、毛管水和重力水等形式存在。
固相—骨架matrix气相—空气,非饱和带中液相—水:吸着水Hygroscopic water薄膜水pellicular water毛管水capillary water重力水gravitational water1.1.1.3多孔介质中的地下水运动比较复杂,包括两大类,运动特点各不相同,分别满足于孔隙水和裂隙岩溶水的特点。
渗流力学达西定律公式

渗流力学达西定律公式
摘要:
1.渗流力学简介
2.达西定律的概念
3.达西定律的公式
4.达西定律的应用
正文:
1.渗流力学简介
渗流力学是研究流体在多孔介质中渗流规律的学科,它广泛应用于地下水文学、土壤力学、水利工程等领域。
在渗流力学中,达西定律是一个重要的基本定律,对于分析流体在多孔介质中的渗流特性具有重要意义。
2.达西定律的概念
达西定律,又称达西- 威斯巴赫定律,是由法国工程师达西
(C.V.Darcy)和德国工程师威斯巴赫(R.E.Weisbach)分别于19 世纪提出的。
该定律描述了在多孔介质中,流体渗流速度与压力差成正比,即渗流速度等于压力差除以阻力系数。
3.达西定律的公式
达西定律的数学表达式为:
Q = KiA
其中,Q 表示渗流量,K 表示渗透率,i 表示压力差,A 表示渗流面积。
4.达西定律的应用
达西定律在实际工程中有广泛的应用,如计算地下水的渗流速度、分析土壤的渗水性能、设计水利工程等。
通过达西定律,可以更好地了解流体在多孔介质中的渗流规律,从而为相关领域的研究和实践提供理论依据。
总结来说,渗流力学中的达西定律是描述多孔介质中流体渗流规律的一个重要定律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的渗流稳定性,为尾矿库的设计提供科学依据。
5.2 渗流数值模拟方法 5.2.1计算理论简介
采用土木工程数值计算分析软件对石灰窑沟尾矿库进行渗流数值模拟及稳定性分析时,基于如下渗流理论:
①达西定律(线性渗流定律)
假定尾矿库渗透水流在尾矿堆积体内流动时做低雷诺数的层流运动,此时渗透水的运动符合达西线性渗流定律,即水的流速在数值上与其水力坡度成正比,其数学表达式为:
kJ v =
式中:v —(平均)渗流速度(cm/s );
k —介质的渗透系数(cm/s ); J —水力坡度(无量纲)。
在实际的地下水流中,水力坡度往往是各处不同的,此时达西定律的一般性表达式为:
ds
dH
k
v −= 式中:ds
dH
−
—水力坡度(水力比降)。
②饱和-非饱和渗流的基本微分方程
在多孔的岩土介质中,渗流的连续性方程写成张量形式表示为:
()()i w i v S nS x t
ρρ∂∂
−
+=∂∂ i =1,2,3
式中:ρ—水的密度;i v —达西流速;n —岩土介质的孔隙率;S —汇源项。
在非饱和渗流中,非饱和渗流问题的连续性方程如下:
()()()()S nS t
v z v y v x w z y x +∂∂−=∂∂+∂∂+∂∂
ρρρρ 式中:x v 、y v 、z v —非饱和渗流场中达西流速在x 、y 、z 三个方向上的分量;
w S —饱和度,0≤w S ≤1,其它符号意义同前。
饱和土体中水的流动常常用达西定律来表达,达西定律同样也适用于非饱和土体中水的流动,但是,在非饱和土体中渗透系数一般不能假定为常数,相反,渗透系数的变化很大,是非饱和土孔隙比和含水量或基质吸力的函数, 在非饱和渗流中达西定律的表达式为:
()
j
r ij i x H
k k v ∂∂−=θ j i ,=1,2,3 此式即为广义达西定律。
式中:ij k —饱和渗透系数张量;
r k —非饱和渗透系数相对于饱和渗透系数s k 的比值,是饱和度或压力
水头的函数。
在非饱和区,0≤r k <1,在饱和区,r k =1; θ—岩土介质的体积含水量,w S n =θ;
H —总水头,z h H +=,h 为压力水头,z 为位置水头。
非稳定渗流的饱和-非饱和微分方程为:
()()()t h
S C S h k k x h h k k x s
r i j r ij i
∂∂+=+
+∂∂∂∂β3 j i ,=1,2,3 式中:C —容水度,h
C ∂∂=
θ
,在饱和区为0; β—水的体积压缩系数,为水的体积压缩模量w E 的倒数,即w
E 1=
β,在饱和区1=β;
s S —贮水率,对非饱和土体来说,其值为0,对饱和土体其值大小为
一常数,在许多情况下可设s S =0;
其它符号意义同前。
在均质各向同性的情况下,非稳定渗流的饱和-非饱和微分方程为:
()t h
S C S z k z h k z y h k y x h k x s w w w w ∂∂+=+∂∂+ ∂∂∂∂+
∂∂∂∂+ ∂∂∂∂β 式中:w k —非饱和渗透系数,r s w k k k =,s k 为饱和时各向同性的渗透系数;
其它符号意义同前。
稳定渗流的饱和-非饱和微分方程为:
()()03=+
+∂∂∂∂
S h k k x h
h k k x r i j r ij i
j i ,=1,2,3 ③饱和-非饱和渗流场的定解条件
定解条件包括初始条件和边界条件。
对于饱和-非饱和的渗流场来讲,整个渗流区域可以分为饱和区域和非饱和区域;边界条件包括水头边界、已知流量边界和渗出面边界。
因为整体考虑饱和-非饱和的渗流问题,没有必要将自由面作为一种流量补给边界处理。
初始条件是坐标的函数,可以写成:
()()000,,,,,,t z y x h t z y x h =
边界条件包括流量边界和水头边界,可以写成:
()()t z y x h t z y x h ,,,,,,1=, ()∈z y x ,,1S
()()n i r ij j r ij q n h k k x h
h k k = +∂∂−, ()∈z y x ,,2S
()()0≥
+∂∂−i r ij j r ij n h k k x h
h k k 且()0,,,=t z y x h ,()∈z y x ,,3S
式中:1S —水头分布规律已知的边界;
2S —流量情况已知的边界,n q 为法向流量,i n 为边界的单位外法向的
方向余弦; 3S —饱和渗出面边界。
④坝坡发生渗流破坏的判别公式
地下水在土体内流动过程中,作用在土体中的渗流作用力有两种,分为静水压力(浮容重)和动水压力(渗透力),均为体积力。
静水压力(浮容重)γ′按下式计算:
e
w
d +−
=′1γγγ
式中:γ′—静水压力(kN/m 3)
; d γ—土的干容重(kN/m 3
);
w γ—水的容重(kN/m 3
),取10 kN/m 3
;
e —土的孔隙比。
动水压力(渗透力)f 按下式计算:
J dl
dh
f w w
γγ=−= 式中:f —动水压力(kN/m 3),其它符号的意义同前。
以上两种渗流作用力,关系着土体的渗流稳定性,对于土体的渗透变形研究具有重要意义。
虽然静水压力对土体所产生的浮力不会直接破坏土体,但能使土体的有效重量减轻,从而使土体抵抗渗流破坏的能力减弱,因此可将其视为一种消极的破坏力。
地下水在流动过程中,动水压力所产生的渗透力或渗透冲刷力对土体来说是一种积极的破坏力,它与土体发生渗流破坏的程度成直接的比例关系。
对于砂土边坡的渗流破坏,一般是从局部发生渗流破坏开始,进而破坏范围逐渐扩大,严重的将酿成大范围的滑坡。
渗流破坏理论认为,位于自由水面以下坝坡表面层的单位土体,只有当静水压力γ′与动水压力f 的合力克服了土体颗粒对其的摩擦阻力时,土体才可能沿斜坡下滑。
若渗流的流线与
水平面之间的夹角为θ,坝坡坡角为β,则斜坡表面单位土体的力的极限平衡方程式为:
()()sin cos cos sin J J tg C w w c
γβγβθγβγβθϕ
+−=−−+′′ 上式中的c J 即为临界水力坡度。
在坝体的浸润线与坝坡的交点处,由于浸润线与坝坡面相切,此处的流线平行于坝坡面向下,即βθ=,由极限平衡方程式,得临界水力坡度()cos c w
C J tg tg γβϕβγγ
′=−+,因沿坝坡面的水力坡度
βsin =J ,假定w γγ=′,则得ϕβtg tg 2
1=,此即为边坡保持稳定的临界状态数
学表达式,其中ϕ为土体的内摩擦角。
此式可作为判断坝坡在渗流出逸时发生渗流破坏的标准,当ϕβtg <tg 2
1时,坝坡在渗流出逸时将不会发生渗流破
坏;当ϕβtg tg 2
1=时,坝坡处于极限平衡状态;而当ϕβtg >tg 2
1时,则坝坡将
发生渗流破坏。
5.2.2稳定性数值模拟分析方案及模拟分析内容
基于土木工程数值计算分析软件,按以下要求对石灰窑沟尾矿库进行渗流稳定性数值模拟。
(1)建立石灰窑沟尾矿库库区及坝体的二维渗流数值计算模型,对尾矿库堆积标高达到622.0m 、660.0m 及750.0m 时,进行正常运行工况和洪水运行工况下的二维渗流计算及渗流稳定性分析。
模拟尾矿库在上述两种工况下尾矿堆积体内渗透水流的运移规律,包括库区及坝体内渗透水的总压力、孔隙水压力和流速场的分布规律以及浸润线的分布形态和水力比降的分布特征。
(2)建立石灰窑沟尾矿库库区及坝体的三维渗流数值计算模型,对尾。
