第一章 渗流理论基础
地下水动力学(第一章 渗流理论基础-2-专)
∂2H ∂2ψ ∂2H ∂2ψ −K = ; −K =− 2 ∂x∂y ∂y2 ∂y∂x ∂x
二、流网及其性质
流网：在渗流场内，取一组流线和一组等势线 组成的网格。 流网的性质： 流网的性质： 1. 在各向同性介质中，流线与等势线处处垂直， 故流网为正交网格。 证明：等水头线和流线的梯度为：
gradH = ∇H = ∂H ∂H i+ j ∂x ∂y
一般地下水流都为Darcy流。 思考题
§1—3 岩层透水特征分类和渗透系数张量 一、岩层透水特征分类 据岩层透水性随空间坐标的变化情况，将岩层 分为均质的和非均质的两类。 均质岩层：在渗流场中，所有点都具有相同的 渗透系数。 非均质岩层：在渗流场中，不同点具有不同的 渗透系数。 非均质岩层有两种类型：一类透水性是渐变的， 另一类透水性是突变的。 均质、非均质:指 与空间坐标的关系 与空间坐标的关系， 均质、非均质 指K与空间坐标的关系，即不同位 是否相同； 置K是否相同； 是否相同
K1M1 + K2M2 M1 + M2 Kp − Kv = − M1 M2 M1 + M2 + K1 K2 M1M2 = >0 (K1M1 + K2M2 )(M1 + M2 )
(K1 − K2 )
2
渗流理论基础
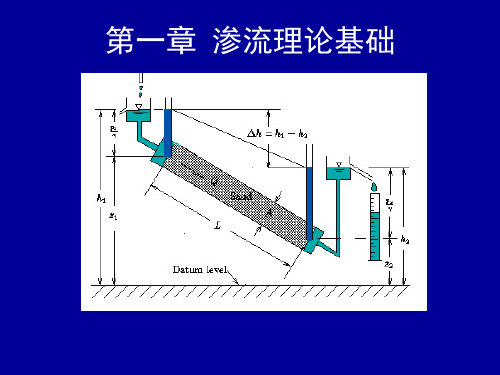
岩体的结构分类（GB 50287-1999 ）
• Permeability Coefficient— The rate of flow of water through a unit cross-sectional area under a Unit Hydraulic Gradient at the prevailing temperature.
• Hydraulic Conductivity (K)——the volume of water at the existing kinematic viscosity that will move, in unit time, under a unit Hydraulic Gradient through a unit area measured at right angles to the direction of flow, assuming the medium is isotropic and the fluid is homogeneous. In the Standard International System, the units are cubic meters per day per square meter of medium (m3/day/m2) or m/day (for unit measures).
；裂隙介质：
于是有：
或
（1-18）
达西（D）的定义：当液体的动力粘滞度为 0.001Pa·s，压强差为101325Pa的情况下，通过面积 为1cm2、长度为1cm岩样的流量为1cm3/s时岩样的渗 透率，记为D。
尺度效应是指渗透系数与试验范围有关，随着试验 范围的增大而增大的现象，K=K(x)。亦即抽水时间 t长、降深s大的群孔抽水试验所得K较抽水时间t短、 降深s小的抽水试验所得K大。
【免费下载】渗流力学基本理论
目录第一章渗流理论基础 (1)1.1渗流的基本概念 (1)1.2渗流基本定律 (7)1.3岩层透水特征及水流折射定律 (11)1.4流网及其应用 (14)1.5渗流连续方程 (19)1.6渗流基本微分方程 (24)1.7数学模型的建立及求解 (32)第一章渗流理论基础1.1 渗流的基本概念1.1.1 多孔介质及其特性1.1.1.1多孔介质的概念多孔介质(Porous medium)：地下水动力学中具有空隙的岩石。
广义上包括孔隙介质、裂隙介质和岩溶不十分发育的由石灰岩和白云岩组成的介质，统称为多孔介质。
孔隙介质：含有孔隙的岩层，砂层、疏松砂岩等；裂隙介质：含有裂隙的岩层，裂隙发育的花岗岩、石灰岩等。
1.1.1.2 多孔介质的性质(1) 孔隙性：有效孔隙和死端孔隙。
孔隙度（Porosity）是多孔介质中孔隙体积与多孔介质总体积之比（符号为n），可表示为小数或百分数，n=Vv/V。
有效孔隙（Effective pores）是多孔介质中相互连通的、不为结合水所占据的那一部分孔隙。
有效孔隙度（Effective Porosity）是多孔介质中有效孔隙体积与多孔介质总体积之比（符号为n e），可表示为小数或百分数，n e=V e/V。
死端孔隙（Dead-end pores ）是多孔介质中一端与其它孔隙连通、另一端是封闭的孔隙。
(2) 连通性：封闭和畅通，有效和无效。
(3) 压缩性：固体颗粒和孔隙的压缩系数推导。
(4) 多相性：固、液、气三相可共存。
其中固相的成为骨架，气相主要分布在非饱和带中，液相的地下水可以吸着水、薄膜水、毛管水和重力水等形式存在。
固相—骨架matrix气相—空气，非饱和带中液相—水：吸着水Hygroscopic water薄膜水pellicular water毛管水capillary water重力水gravitational water1.1.1.3多孔介质中的地下水运动比较复杂，包括两大类，运动特点各不相同，分别满足于孔隙水和裂隙岩溶水的特点。
康-第一章 渗流基本理论
河间地块流网的应用
比较： HA与HB？ JA与JB？ VA与 VB？
A
B
河间地块流网图
层状非均质介质中的流网
典型流网特征
各向异性介质中的流网
1.1.3
渗流分类
1. 按运动要素(v,p,H)是否随时间变化，分：稳定流与非稳定流 2. 按地下水质点运动状态的混杂程度，分： 层流、紊流与过渡区流态 3. 按地下水有无自由表面，分为： 承压流、无压流、承压—无压流
z 4.按渗流速度在空间上变化的特点，分 一维流、二维流、三维流 a. 一维流：仅沿一个方向存在流速 b. 二维流：沿两个方向存在分流速 分：平面二维流、剖面二维流）
图1-2-8a 一维流
y
x
c. 三维流： 三个方向均存在分流速
图1-2-8b1 平面二维流
图1-2-8b2 剖面二维流
三维流图示
图1-2-8c 三维流
同一点各方向上渗透性相同的介质称为各向同性介质； 同一点各方向上渗透性不同的介质称为各向异性介质 。 均质、非均质:指K于空间坐标的关系，即不同位置K是否相同； 各向同性、各向异性: 指同一点不同方向的K是否相同。
这两对概念可任意组合
z
四种介质
均质各向同性 均质各向异性 非均质各向同性 非均质各向异性
V——I 曲线
V
1
砂样
2
O
I
V = K · I ——（3）
达西定律讨论
1 渗流速度（V）与过水断面（ω） Q = K ω I = ω V
过水断面与水力学中的水流过断面是否一致？否 过水断面——ω，假想的断面
实际孔隙断面——ω n
实际水流断面——ω n 有效孔隙度 过水断面比较 Q/ω =V 比照水力学，实际流速 Q/ω’= u
地下水动力学简介
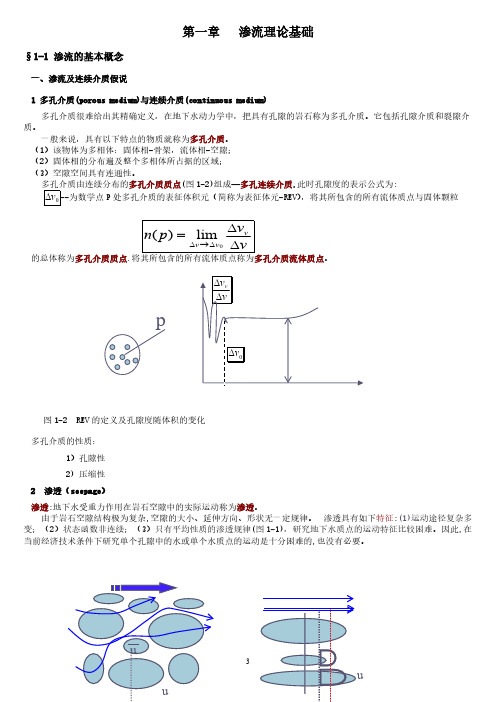
第一章 渗流理论基础§1-1 渗流的基本概念一、渗流及连续介质假说1 多孔介质(porous medium)与连续介质(continuous medium)多孔介质很难给出其精确定义，在地下水动力学中，把具有孔隙的岩石称为多孔介质。
它包括孔隙介质和裂隙介质。
一般来说，具有以下特点的物质就称为多孔介质。
（1）该物体为多相体：固体相-骨架，流体相-空隙；（2）固体相的分布遍及整个多相体所占据的区域；（3）空隙空间具有连通性。
多孔介质由连续分布的多孔介质质点(图1-2)组成—多孔连续介质.此时孔隙度的表示公式为:--为数学点P 处多孔介质的表征体积元（简称为表征体元-REV ），将其所包含的所有流体质点与固体颗粒0v ∆的总体称为多孔介质质点.将其所包含的所有流体质点称为多孔介质流体质点。
图1-2 REV 的定义及孔隙度随体积的变化多孔介质的性质：1）孔隙性2) 压缩性2 渗透（seepage ）渗透:地下水受重力作用在岩石空隙中的实际运动称为渗透。
由于岩石空隙结构极为复杂,空隙的大小、延伸方向、形状无一定规律。
渗透具有如下特征:(1)运动途径复杂多变；（2）状态函数非连续；（3）只有平均性质的渗透规律(图1-1)，研究地下水质点的运动特征比较困难。
因此,在当前经济技术条件下研究单个孔隙中的水或单个水质点的运动是十分困难的,也没有必要。
vv p n v v v ∆∆=∆→∆0lim)(图1-2岩石中地下水的渗透针对这种极为复杂的地下水运功，在地下水动力学中一般可采用两种研究方法。
1) 研究微观情况下的运动，即研究地下水在以孔隙介质中的骨架为边界孔隙或裂隙中的运动。
由于空隙介质的结构具有随机性，所以用统计平均方法来确定地下水运动的宏观规律性；2) 从宏观角度出发，采用试验及数学分析方法，对大量微观运动进行宏观研究得出各种运动条件下地下水运动的基本规律。
3 渗流(seepage flow)前面已经提到,要研究实际的渗透十分困难,因此,我们用一种假想水流来代替真实水流,这种假想水流是在连续介质的基础上通过概化得出的:(1)假定水流充满整个含水层空间(既包括空隙所占据的空间,也包括颗粒/骨架所占据的空间);(2)只考虑水流运动的总体方向,不考虑水流实际运动途径的复杂变化.将通过上述概化后所得到的假想水流—渗流。
第一章 渗流理论基础
第一章渗流理论基础一、名词解释1. 渗透速度：表示水流在过水断面上的平均流速，不能代表任何真实水流的速度。
2. 实际速度：表示地下水在孔隙中的真实速度。
3. 水力坡度：把大小等于梯度值，方向沿着等水头面的法线，指向水头降低方向的矢量称为水力坡度。
4. 贮水系数：当水头变化1m时，从单位水平面积，高度为承压含水层厚度的柱体中释放或贮存的水量。
5. 贮水率：当水头下降1m时，单位体积承压含水层释放出来的水量。
6. 渗透系数：也称水力传导系数，当水力坡度J=1时，渗透系数在数值上等于渗透速度。
7. 渗透率：表示多孔介质能使气体或液体通过介质本身的能力，只与岩石性质有关，与液体性质无关。
8. 导水系数：T=KM，是一个水文地质参数，即水力坡度J=1时，通过整个含水层厚度上的单宽流量。
二、填空题1．地下水动力学是研究地下水在、、和中运动规律的科学。
（孔隙岩石、裂隙岩石、岩溶岩石）2.通常把具有连通性的孔隙岩石称为多孔介质，而其中的岩石颗粒称为。
（骨架）3.地下水在多孔介质中存在的主要形式有、薄膜水、毛管水和重力水，而地下水动力学主要研究的运动规律。
（吸着水、重力水）4.在多孔介质中，不连通的或一端封闭的孔隙对地下水运动来说是，但对贮水来说却是。
（无效、有效）5.地下水的过水断面包括空隙和固体颗粒所占据的面积，渗透流速是上的平均速度，而实际速度是的平均速度。
（过水断面、空隙面积）6.在渗流场中，把大小等于，方向沿着的法线，并指向水头降低方向的矢量，称为水力坡度。
（梯度值、等水头面）7.渗流运动要素包括流量Q、、压强p和等。
（渗流速度v、水头H）8.根据地下水与的关系，将地下水运动分为一维、二维和三维运动。
（运动方向、空间坐标轴）9.渗透率是表征的参数，而渗透系数是表征岩层的参数。
（岩层渗透性能、透水能力）10.影响渗透系数大小的主要因素是以及。
（岩石性质、渗透液体的物理性质）11.导水系数是描述含水层的参数，它是定义维流中的水文地质参数。
岩层透水特征及水流折射定律
（2）各向同性与各向异性
根据岩层透水性与渗流方向的关系划分，若渗流 场中，某一点的K与渗流方向无关，则该岩层是各向 同性的，反之则为各向异性。 各向同性岩层（isotropic strata /aquifer）：渗流 场中某一点的渗透系数不取决于方向，即不管渗流方 向如何都具有相同渗透系数的岩层。 各向异性岩层（anisotropic strata /aquifer）：渗 流场中某一点的渗透系数取决于方向，渗透系数随渗 流方向不同而不同的岩层。
图1-16水流折射
（1-29）
(2)水流垂直层面
特点：水流垂直层面运动，每段水流具有相同的单宽 流量，且每段水力坡度不同。 由 ，由此推导出，
依次类推，有
（1-30）
可见，取决于Ki最小的分层（阻 力最大），Ki=0，则 Kv =0。 另外，总是有 。
图1-15 层状岩层中垂直于层面的渗流
1.3.4 突变界面的水流折射定律 根据水流连续性条件，当水流斜向由一种介质进入另一 种介质时，会发生折射。 如图所示：水流由K1介质进入 K2介质中，二者交界面 上某一点的渗流速度和水头在两介质中的值依次为V1、V2 和H1、H2。对于界面上的任一点应满足以下条件：
(1)水流平行层面 特点：水流为稳定流，岩 层水平分布，各段流量之和 等于各部分流量之和，且各 段具有统一的水头，各段具 有相同的水力坡度。
图1-14 层状岩层中平行于层面的渗流
根据达西定律有： 若把其视为整体时，有 故
水平岩层的等效渗透系数为：
（1-27）
等效导水系数为
（1-28）
垂直方向岩性渐变时，有
• Isotropy — That condition in which a medium has the same properties in all directions. • Anisotropy — • (1) The condition of having different properties in different directions. • (2) The condition under which one or more of the hydraulic properties of an aquifer vary according to the direction of the flow.
地下水动力学习题及答案
《地下水动力学》习題集第一章渗流理论基础二、填空題1. 地下水动力学是研究地下水在孔隙岩石、裂晾岩石和岩溶岩石中运动规律的科学。
通常把具有连通性的孔隙岩石称为多孔介质,而其中的岩石颗粒称为骨架。
名孔介质舸特点是％相性、孔隙性、MUfnftOo2. 地下水在多孔介质中存在的主要形式有吸着水、薄除水、毛管水和重力A，而地下水动办学主要研究重力水的运动规律。
3. 在多孔介质巾，不连通的或一端封冈的孔晾对地下水运动来说是无如, 但对贮水来说却是有效的。
4. 地下水ii水斷面包括一空隙_和=a掘业所占据的面枳•渗透渣速是_过水断肚_上的平沟速度,而实际速度是空輕上—的平均速度。
在渗浦中，水头一股是指测圧管水头，不同数值的等水头面（线）永近不会相交。
5. 在渗流场中，把大小等于方向沿着/水头血_的法线，并指向水头_降低_方向的矢量，称为水力ffiHo水力玻度在空同直角坐标系中的三⑷心羞、6. 渗流运动要素包括』量Q_、_iJOJLv_.」十'强p一和—水头也等等。
7. 根据地下水渗透速度〜矢量方向—弓—空间坐标龜—的关系，将地下水运动分为一绒、二绒和三绒运动。
&达西定律反映了渗流场中的「龍量守与转换_定律。
9. 渗诱率只取决干名孔介质的性质，而与液休的111贯无关，渗透率的单位为cm'或da o10. 渗诱率是表征岩石渗透性能舸参数,而渗诱系数是表征岩层透水能力的参数，影响渗透系数大小的主要是岩层m小以及水的物理性质,随着地下水温度的开高，渗透系数增大。
11. 导水系数是描述含水层岀水能力的参数,它是定义在平面一、二绒流中的水文地质参数。
12. 血质与非血质岩层是根据_蚩石透水性与空间坐札_的关系则分的，各向同性和各向异性岩层是根据—蚩石透水性与水流方闻—关系划分的。
13. 渗透系数在各向同性岩层中是一标量在各向异性岩层是—壘，在三维空间中它由丿f分豊组戒,在二维流中则由_心迅一组成。
地下水动力学习地的题目答案详解
《地下水动力学》习题集第一章渗流理论基础一、解释术语1. 渗透速度2. 实际速度3. 水力坡度4. 贮水系数5. 贮水率6. 渗透系数7. 渗透率8. 尺度效应9. 导水系数二、填空题1．地下水动力学是研究地下水在孔隙岩石、裂隙岩石和岩溶岩石中运动规律的科学。
通常把具有连通性的孔隙岩石称为多孔介质，而其中的岩石颗粒称为骨架。
多孔介质的特点是多相性、孔隙性、连通性和压缩性。
2．地下水在多孔介质中存在的主要形式有吸着水、薄膜水、毛管水和重力水，而地下水动力学主要研究重力水的运动规律。
3．在多孔介质中，不连通的或一端封闭的孔隙对地下水运动来说是无效的，但对贮水来说却是有效的。
4. 地下水过水断面包括_空隙_和_固体颗粒_所占据的面积.渗透流速是_过水断面_上的平均速度，而实际速度是_空隙面积上__的平均速度。
在渗流中，水头一般是指测压管水头，不同数值的等水头面(线)永远不会相交。
5. 在渗流场中，把大小等于_水头梯度值_，方向沿着_等水头面_的法线，并指向水头_降低_方向的矢量，称为水力坡度。
水力坡度在空间直角坐标系中的三个分量分别为_Hx∂-∂_、Hy∂-∂_和_Hz∂-∂_。
6. 渗流运动要素包括_流量Q_、_渗流速度v_、_压强p_和_水头H_等等。
7. 根据地下水渗透速度_矢量方向_与_空间坐标轴__的关系，将地下水运动分为一维、二维和三维运动。
8. 达西定律反映了渗流场中的_能量守恒与转换_定律。
9. 渗透率只取决于多孔介质的性质，而与液体的性质无关，渗透率的单位为cm2或da。
10. 渗透率是表征岩石渗透性能的参数，而渗透系数是表征岩层透水能力的参数，影响渗透系数大小的主要是岩层颗粒大小以及水的物理性质，随着地下水温度的升高，渗透系数增大。
11. 导水系数是描述含水层出水能力的参数，它是定义在平面一、二维流中的水文地质参数。
12. 均质与非均质岩层是根据_岩石透水性与空间坐标_的关系划分的，各向同性和各向异性岩层是根据__岩石透水性与水流方向__关系划分的。
第1章渗流理论基础
25
1.1 渗流的基本概念
1.1.5 渗流速度
渗流是充满整个岩石截面的假想水流。在垂直于 渗流方向取的一个岩石截面，称为过水断面。 地下水的过水断面是整个岩石截面，既包括空隙 面积也包括固体颗粒所占据的面积。
当渗流平行流动时，过水断面为平面，弯曲流动
时则为曲面（图1-6 ）。
26
1.1 渗流的基本概念
22
1.1 渗流的基本概念
实际的地下水流仅存在于空隙空间。为了便于研
究，用一种假想水流来代替真实的地下水流。这 种假想水流的性质（如密度、粘滞性等）和真实 地下水相同；但它充满了既包括含水层空隙的空 间，也包括岩石颗粒所占据的空间。
23
1.1 渗流的基本概念
假想水流运动时，满足以下条件：
3
1.1 渗流的基本概念
1.1.1 地下水在含水岩石中的运动
在地下水动力学中，把具有孔隙的岩石称为多孔介质。 含有孔隙水的岩层，如砂层或疏松砂岩等称为孔隙介质， 也称多孔介质。 含裂隙水的岩石，如裂隙发育的石英岩、花岗岩等称为裂 隙介质。 广义地说，可以把孔隙介质、裂隙介质和某些岩溶不十分 发育的由石灰岩和白云岩组成的介质都称为多孔介质。
渗透速度，比流量）为：
Q A
渗流速度代表渗流在过水断面上的平均流速。它不代表任 何真实水流的速度，只是一种假想速度。假设整个过水断
面都被水充满时，地下水就以这种速度流动。
28
1.1 渗流的基本概念
实际上，地下水仅仅在空隙中流动。在空隙中的不
同地点，地下水运动的方向和速度都可能不同，平 均速度 称为实际平均流速。速度v 和地下水的实际
1）地下水的状态方程 在等温条件下，水的压缩系数为：
1-1渗流基本概念
2020/7/6
13
为了便于研究地下水，采用统计方法将地下水在 多孔介质的运动用一种假想的水流代替，如果满足以 下6个条件：
假想水流连续充满整个介质空间
假想水流的性质和真实水流相同(密度、粘滞性)
不考虑地下水实际运动途径的迂回曲折及方向多变， 只考虑运动的总体方向
任一过水断面的流量Q与真实水流相同
一般地，含水层和隔水层的划分是相对的。例 如，某种岩层的渗透性比较低，从供水角度其可能被 看做隔水层，但从水库渗漏的角度来说，由于水库的 周界长，渗漏时间长，其渗漏量不可忽视，这时就必 须将该岩层看做含水层。
2020/7/6
4
3.地下水(groundwater)
结合水 毛细水 重力水
➢ 广义：指埋藏在地面以下岩石空隙中的水,
v dv
p
dp
v v0
p0
v e ( p p0 ) v0
V V0e ( p p0 )
2020/7/6
同理
e ( p p0 ) 0
11
Ex的Taylor级数展开式为：
ex 1 x x2 ... xn ...
2!
n!
当压强变化不大时，可取其前两项：
V V0[1 ( p p0 )]
2020/7/6
7
➢重力水（gravitational water）
距离土粒固体表面更远的那部分水分子，重 力对它的影响大于固体表面对它的吸引力，能够 在自身重力作用下运动，这部分水就是重力水。
上层滞水(有关详细信息)
指包气带局部隔水层上积聚的具有自由水面的重 力水。
潜水（phreatic water）
包括土壤水(非饱和带地下水)和重力水。
强结合水(吸湿水) 弱结合水(薄膜水)
第一章 渗流理论基础-2-专
H H vx K ; vy K x y
由达西定律知：
v ; v y 流函数满足的条件： x y x H H 有 K ; K x y y x
(2)平行层面的等效渗透系数总是大于垂直 层面的等效渗透系数。 证明：（以二层为例）
K1M 1 K 2 M 2 M 1 M 2 K p Kv M1 M 2 M1 M 2 K1 K 2 M 1M 2 0 K1M 1 K 2 M 2 M 1 M 2
K1 K 2
n
取等效渗透系数Kv，那么单宽流量为：
二式相等得：
因此，
Mq q n M i K vb b i 1 K i
M Kv n Mi i 1 K i
Kv
M
i 1 n
n
i
Mi i 1 K i
此式为层状岩层垂直于层面的等效渗透系数。 说明：(1)当某一层的Ki较小时，Mi/Ki较大，Kv变小； 当Ki→0时， Mi/Ki→∞，Kv→0，也就是说，垂直于层 面的等效渗透系数主要取决于渗透系数最小的分层。
1.2.3非线性运动方程 Re小于1—10时，地下水流为线性流，用 Darcy定律描述； Re大于1—10时，地下水 流为非线性流，用下列定律描述： Forchheimer公式： 1901年福希海默提出Re>10时： J=av+bv2 Chezy公式 1912年克拉斯诺波里斯基提出紊流公式： 1
vK J2
dq=vxac+vybc 因，ac=dy，bc=-dx 所以，dq= vxdy-vydx 把 v ; v
x
渗流理论基础
A 1 4 9 16 25 36 49 64 81 100
Number 6 15 31 51 82 135 193 264 343 399
Dense 6.00 3.75 3.44 3.19 3.28 3.75 3.94 4.13 4.23 3.99
Density
4 3 2 1 0 0 20 40 A 60 80 100
1) 渗透:地下水在岩石空隙或多孔介质中的运动， 这种运动是在弯曲的通道中，运动轨迹在各点处 不等。为了研究地下水的整体运动特征，引入渗 流的概念。
图1-2 岩石中的渗流 （a）实际渗透 (b)假想渗流
2) 渗流（seepage flow）：具有实际水流的运动特 点（流量、水头、压力、渗透阻力），并连续充 满整个含水层空间的一种虚拟水流；是用以代替 真实地下水流的一种假想水流。其特点是： （1）假想水流的性质与真实地下水流相同； （2）充满含水层空隙空间和岩石颗粒所占据的空 间； （3）运动时所受的阻力与实际水流所受阻力相 等； （4）通过任一断面的流量及任一点的压力或水头 与实际水流相同。 渗流场（flow domain）：假想水流所占据的空间 区域，包括空隙和岩石颗粒所占的全部空间。
（1-61）
图1—1 一个可压缩的承压含水层（J. Bear）
在水位下降为H时，有 。 即作用于固体骨架上的力增加了H。 • 作用于骨架上力的增加会引起含水层的压缩，而水压 力的减少将导致水的膨胀。 • 含水层本来就充满了水，骨架的压缩和水的膨胀都会 引起水从含水层中释出，前者就象用手挤压充满了水 的海绵会挤出水一样。
承压含水层抽水时，水的释放是由于压力减少造 成的，这一过程是瞬时完成的。只要水头下降不低到 隔水顶板以下，水头降低只引起含水层的弹性释水， 可用贮水系数*表示这种释水的能力。
渗流理论基础.
体，是渗流场中其物理量的平均值能够近似代替整个渗流 场的特征值的代表性单元体积。 REV具备两个性质：
(1) 其体积和面积，大于个别空隙而小于渗流场，其中的渗流可以从 一点连续运动到另一点； (2) 通过单元体的运动要素（流量Q、水头h、压力p、实际水头受到 的阻力R）与真实水流相等，运动要素是连续变化的。
因Vs=constant，故
故
只在垂直方向上有压缩，
（1-62） （1-63）
上两式表示垂直厚度变化、孔隙度变化与水的压强变化的关 系。 • 水头降低时含水层释出水的特征，取面积为1m2、厚度为l m (即体积为l m3)的含水层，考察当水头下降1m时释放的 水量。此时，有效应力增加了H＝g×1=g。 • 介质压缩体积减少所释放出的水量（dVb）为 • 与水体积膨胀所释放出的水量（dV）之和
REV的作用：
(1) 把物理性质看作是坐标的函数，孔隙度n、导水系数T、给水度 和渗透系数均连续。 (2) 渗流的要素可以微分、积分，可以用微分方程来描述渗流要素。
10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
dL 1 2 3 4 5 6 7 8 9 10
2) 多孔介质的性质
Porosity —the property of containing openings or interstices. In rock or soil, it is the ratio of the volume of openings in the material to the bulk volume of the material. Porosity, Effective — The amount of interconnected pore space in a material available for fluid transmission; expressed as a percentage of the total volume occupied by the interconnecting interstices. Porosity may be primary, formed during deposition or cementation of the material, or secondary, formed after deposition or cementation, such as fractures.
第一章 渗流理论基础-3-专
承压水二维稳定流
非均质各向同性： 非均质各向异性： 均质各向同性：
H H T W 0 T x x y y
H H T T W 0 xx yy x x y y
因为水的压缩性很小， βp忽略不计， t
g
t
代入前式，得
vx v y vz H 2 xyz xyz g n y z t x
vx v y vz vx x v y y vz z xyz x y z H 2 g n xyz t
第二项ρ非常小，忽略不计，于是上式变为：
vx v y vz H 2 x y z xyz g n t xyz
vx v y vz H x y z xyz g n t xyz
根据Darcy定律： (1) 在各向同性介质中，有：
H H H vx K ; vy K ; vz K x y z
代入上式，得
H H H H K xyz K xyz g n K t x x y y z z
因为Ss=ρg（α+nβ） 所以上式变为：
H H H H K K K x y z S xyz s t x x y y z z
两边消去单元体体积Δx ΔyΔz，得：
所以，dρ=ρβdp 前面给出了含水层厚度Δz和孔隙度n随压力p的变 化关系： d(Δz)= Δzαdp ；dn=(1-n) αdp 式中：α为多孔介质压缩系数。 将三式代入连续方程右端项得：
第1章 渗流的基础知识和基本定律
纯溶洞结构简化模型
16
第一节 油气储集层
二、外部几何形状及其简化
以背斜构造为例，对其外部几何形状进行简化。对实际油藏进行水平投影，如 下图所示。 油水分界面(油水接触面)->油水边界(内含油边界、外含油边界) 油气分界面(油气接触面)->油气边界 如果有露头->供给边界(有水源供应) 封闭边界(边界是封闭的)
油藏外部形状及其简化示意图
17
第一节 油气储集层
三、油气储集层的特点
1.储容性 油气储集层具有储存和容纳流体的能力，即储容性。 绝对孔隙度：岩石内总的孔隙体积占岩石体积的百分数。 公式：φt=Vt/V×100% 用途：计算油气藏的绝对储量。 有效孔隙度：岩石中有效孔隙体积占岩石体积的百分数。 公式：φ=Ve/V×100% 用途：计算油气藏的可采储量。
20
第一章 渗流的基础知识和基本定律
第一节 油气储集层 第二节 渗流的基本概念 第三节 力学分析及油藏驱动方式 第四节 线性渗流与非线性渗流
21
第二节 渗流的基本概念
一、渗流的三种基本几何形式 1.平面单向流 流体质点沿同一方向运动。 特点：流线相互平行，垂直于流动方向的截面上各点 的渗流速度相等；如果流动是稳定渗流，那么流动方 向上任一点的压力只是沿程位移x的线性函数。
折算压力计算示意图
30
第一章 渗流的基础知识和基本定律
第一节 油气储集层 第二节 渗流的基本概念 第三节 力学分析及油藏驱动方式 第四节 线性渗流与非线性渗流
31
第三节 渗流过程中的力学分析及油藏的驱动方 式
一、力学分析
油气水在岩石孔道中流动，受到各种力的作用。 1.流体的重力 地球对流体的吸引力称为流体的重力。 重力有时是动力，有时是阻力。
第一章 渗流理论基础
由水的压缩性得: dV V dp n g ng
二者之和表示面积为1个单位、厚度为1个单位的含水层，当 水 头降低1个单位时所释出的水量，用符号 s 表示，即：
s dVb dV g ng g n
称为贮水率或释水率。其量纲为(L-1)。
东北大学资土学院孙宝亮11渗流的基本概念孔隙多孔隙少砂颗粒具规则形状的砂岩具不规则形状的砂岩且分选差粉砂颗粒粘土很小数量的粘土和粉沙颗粒间孔隙空间小数量的裂隙孔隙空间破裂的页岩没破裂的页岩不渗透的岩石没胶结的砂岩胶结的砂岩胶结物孔隙空间孔隙度和渗透性多孔的并可渗透的孔隙度和渗透性降低多孔的并不可渗透的砂颗粒孔隙空间多孔的砂岩胶结的砂岩细粒砂岩有不规则形状的砂岩破裂的页岩没破裂的页岩很小数量的粘土和粉砂颗粒间孔隙空间粉砂颗粒不渗透的岩石胶结物小数量的裂隙孔隙空间孔隙度孔隙度原生孔隙原生孔隙次生孔隙次生孔隙沉积物或沉积岩岩浆岩和变质岩孔隙颗粒花岗岩破裂破裂可渗透的砂岩断裂的花不同的土和岩石供水渗透的孔隙大小是不同的
次生孔隙
岩浆岩和变质岩
好井
差井
井
可渗透的 砂岩
干井
好井
好井
断裂的花 岗岩
不同的土和岩石供水渗透的孔隙大小是不同的。水在大的孔隙 运动更容易。砾石的孔隙大，水渗透的快；粘土的孔隙太小， 水几乎不能渗透。 一些岩层太坚固，能隔水。其它易碎有很多裂隙，如果裂隙连 通，水就可通过。
§1.1 渗流的基本概念
'
σ′ 为作用于多孔介质表面的应力 Vb 为多孔介质的体积 α 为多孔介质的压缩系数
Vb=Vs+Vv，Vs为固体骨架体积，而Vv为其中的孔隙体积。 n=VV/Vb
1 dVb 1 dVs 1 dVV ' ' Vb d Vb d Vb d '
渗流力学第一章笔记
1. 渗流：流体在多孔介质中流动叫做渗流。
渗透率为床力梯度为1时，动力黏滞系数为I的液体在介质中的渗透速度。
是表征土或岩石本身传导液体能力的参数。
其大小与孔隙度、液体渗透方向上空隙的几何形状、颗粒大小以及排列方向等因素有关，而与在介质中运动的液体性质无关。
渗透率（k）用来表示渗透性的大小。
在一定床差下，岩石允许流体通过的性质称为渗透性；在一定压差下, 岩石允许流体通过的能力叫渗透率。
2•开敞式油藏：如果油气藏外币与天然水源相连通，可向汕气藏供液就是开敞式油气藏。
如果外伟1封闭且边缘高程与油水界而高程一致则称为封闭式油藏。
3. 原始地层压力：油气藏开发以前，一般处F平衡状态，此时油层的流体所承受的压力叫原始地层压力。
4. 供给压力：汕气藏中存在液源供给区时，在供给边缘上的压力称为供给压力。
5. 驱动方式可分为：水床驱动，弹性驱动，溶解气驱动和重力驱动。
6. 在渗流过程中，如果运动的备主要元素只随位置变化而与时间没有关系，则称为稳定流，反之，若各主要元素之一与吋间有关，则称为非定常渗流或者不稳定渗流，7•渗流的基本方式：半面一维渗流，平面径向渗流，和球面渗流。
时规定这样的原则：任何相邻两条等床线Z间的床差必须相等，同8.绘制渗流时，任何两条流线之间的流量必须相等。
9•井底结构和井底附近地区油层性质发生变化的井称为渗流不完善井。
不完善井可以分为打开程度不完善，打开性质不完善，双重不完善井。
10.试井：直接从实测的产量圧力数据反求地层参数，然后用求得的地层参数來预测新的工作制度下的产量。
11•井间干扰：油水井工作制度的变化以及新井的投产会使原來的圧力分布状态遭受到破坏引起整个渗流场发生变化，白然会影响到邻井的产量，这种井间柑互影响的现象称为井间干扰。
12•压降叠加原理：多井同时工作时，地层中任一点外的压降等于各井以各〔I不变的产量单•独工作时在该点处造成的压降代数和。
13•势的叠加原理：如果均质等厚不可床缩无限大底层上有许多点源，点汇同时匸作，我们自然会想到地层上任一点的势应该等于每个点源点汇单独工作时在该点所引起的势的代数和，这就是势的叠加原理。
第一章渗流理论基础
地下水动力学：是研究地下水在孔隙岩石、裂隙岩石和岩溶岩石中运动规律的科学。
它是模拟地下水流基本状态和地下水中溶质运移过程，对地下水从数量上和质量上进 行定量评价和合理开发利用，以及兴利防害的理论基础。
第一章渗流理论基础§—1渗流的基本概念、地下水在含水岩石中的运动1多孔介质：具有孔隙的岩石。
含水介质一般分为三类： 孔隙介质：含有孔隙水的岩层。
裂隙介质：含裂隙水的岩层。
岩溶(Karst )介质：含岩溶水的岩层。
、地下水和多孔介质的性质1地下水的状态方程地下水的状态方程：实际上是地下水的体积和密度随压力变化的方程。
：_ 1dVV dp等温条件下，水的压缩系数为： 设初始压强p o 时，水的体积为V o ,当压强变到p 时，体积变为V ，由上式得: V 二V o V =V 0e 七p T )用Taylor 级数展开，舍去高次项，得到如下的状态方程：V = V o [1- 3 ( P-P 0)] p = po [1- 3 ( p-p o )] 2多孔介质的某些性质 (1) 多孔介质的孔隙性孔隙度：指孔隙体积和多孔介质总体积之比。
有效孔隙：互相连通的、不为结合水所占据的那一部分孔隙。
有效孔隙度：指有效孔隙体积和多孔介质总体积之比。
死端孔隙：一端与其它孔隙连通，另一端是封闭的，其中的地下水是相对停滞的。
(2) 多孔介质的压缩性天然条件下，一定深度处的多孔介质，要受到上覆岩层荷重的压力。
荷重增加，将引起 多孔介质的压缩。
多孔介质的压缩系数：VdV V 。
V1 dV b dV 』W 觀厂 dd d 乂 趙忆d VunV L多孔介质的压缩包括固体 上式令V b d V b d 、上式变为：a = (1-n )固体骨架的压缩性比孔隙的压缩性小的多，上式变为:a =n a p三、贮水率和贮水系数1.水位变化对含水层厚度的影响有效应力 地下水位下降，水压力减小，有效应力增大，多孔介质被压缩。
多孔介质的压缩包括固体颗粒的压缩和孔隙的压缩。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
地下水流方向
渗流
实际的地下水流仅存在于孔隙空间。 我们用一种假想水流来代替真实的地下水流。 假想水流的性质(如密度、粘滞性等)和真实地下水相同，但 它充满了整个多孔介质空间。
假设这种假想水流运动时，在任意岩石体积内所受的阻力等 于真实水流所受阻力；通过任一断面的流量Q及任一点的压 力p或水头H均和实际水流相同。
表示，一般为0.05-0.25 ；
来表示，10-3到10-5 。
下部饱水部分弹性释水，用贮水系数
重力释水量 要比弹性释水量 大几个数量级，可忽略弹性 释水量。
承压含水层，是由减压造成的弹性释水， 一般假设弹性释放是在瞬时完成的，并假设贮水系数 不随 时间变化。
潜水含水层，重力疏干存在着滞后疏干现象，
1 dVV dn ' Vb d d ' 1 dVV n n p ' VV d
p为孔隙压缩系数
三、贮水率和贮水系数
下面考虑一下实际承压含水层的受力情况。
承压井模型
没有水流出的承压井 自流的承压井 承压面
隔水层 含水层 隔水层 没有水流出 的承压井 承压面
测流计 水管的 进口 测水深的井
过水断面的大小 影响水流速度
五、渗流速度
设通过过水断面A有一个渗流量Q，则渗流速度为：v
Q A
渗流速度代表渗流在过水断面上的平均流速。它不代表任何 真实水流的速度，只是一种假想速度。
实际地下水仅在孔隙中流动。渗流速度 v 和地下水的实际平 均流速 u 之间有下列关系：
由水的压缩性得: dV V dp n g ng
二者之和表示面积为1个单位、厚度为1个单位的含水层，当 水 头降低1个单位时所释出的水量，用符号 s 表示，即：
s dVb dV g ng g n
称为贮水率或释水率。其量纲为(L-1)。
地下水是沿着一些形状不一、大小各异、弯弯曲曲的通道流 动的。
研究这个微观水平上的个别孔隙或裂隙中地下水的运动很困 难，实际上也无此必要。
因此，人们不去直接研究单个地下水质点的运动特征，而从 宏观角度来研究具有平均性质的渗透规律。
在孔隙中的实 际流动路径
平均线状流 动路径
水分子的实际流经 路径。
土壤颗 粒
现以孔隙度n作为例子来说明典型单元体概念。设p为多孔介 质中的一个数学点，它可能落在孔隙中，也可能落在固体骨 架上。以p为中心，任取一体积Vi，求出其孔隙度ni，
P
五、渗流速度 Q = v
流量 (m3/s)
×
平均速度 (m/s)
过水断面的面积 (A = 宽* 深) (m2)
A
测流量
河道测流量站
0e
p p0
指数相用麦克劳林公式展开：
e
p p0
1 2 1 3 2 3 1 p p0 p p0 p p0 ... 2! 3!
由于β 值很小，在压力变化不大的条件下，上式可近 似取头两相，因此可改写为：
V V0 1 p p0
0 1 p p0
地质物质的压缩系数 (m2 N-1)
粘土 砂 砾 页岩 砂岩 石灰岩 岩浆岩变质岩 水 (B) 10-6 to 10-8 10-7 to 10-9 10-8 to 10-10 10-9 to 10-10 10-10 to 10-11 10-10 to 10-11 10-11 4.4 x 10-10
等水头面和水力坡度
地下水具有粘滞性，在运动过程中能量不断消耗，反映为水头 沿流程不断减小。 我们把渗流场内水头值相同的各点连成一个面，称为等水头面。 等水头面(线)在渗流场中是连续的。 渗流场中各点的水头可表示为H＝H(x,y,z,t)，它构成一个标量 场。由场论可知，标量场可构成一个梯度场。
dH 梯度的大小为 dn ，方向为沿着等水头面的法线，正向为指
七、地下水运动特征的分类
表征渗流运动特征的物理量称为渗流的运动要素。主要有渗流 量Q，渗流速度v，压强p，水头H等。 按照这些运动要素和时间的关系，可把地下水的运动分为稳定 运动和非稳定运动。严格地说来，运动都是非稳定的。稳定运动只是一种暂
(1-λ)p≈p。所以上式变为：
p
'
在承压含水层中抽水，水头下降，它将引起下列作用：
1. 水压降低，但上覆荷重不变，作用于固体骨架上的有效应 力增大。从而压缩多孔介质，使其厚度变薄和孔隙度变小。 释放出部分水。 2. 水压降低，水体积膨胀，从而释放出部分水。 如在承压含水层中注水，水头上升，则发生相反的过程。
向水头增高的方向。
在几何上 z f ( x , y ) 表示一个曲面
曲面被平面 z
c
z f ( x, y) , 所截得 z c
所得曲线在xoy面上投影如图
y f ( x, y) c2
P
f ( x, y) c1
gradf ( x , y )
梯度为等高线上的法向量
f ( x, y ) c
二、多孔介质的压缩性
土的压缩系数（土力学）
n0
dn / dp
n n1 n2 p p2 p1
n 为孔隙度， P 为压力。 n n1 n2 △n
n n1 n2 p p2 p1
二、多孔介质的压缩性
同样，假定多孔介质变形符合弹性定律，按虎克定律，有：
1 dVb d Vb
P（105pa）对方程积分： 来自 dp p0p
v
v0
dV V
V p p0 ln V0
e
p p0
V V0
V V0 e
p p0
水压p的变化引起水体积V的变化,但水的质量m是不变的。由 Vρ=m的关系，体积变化，则密度相应变化。同理可得ρ和p关 系：
潜水含水层 给水度 =
? v H
=V/Ah = s b
s=贮水率
承压含水层 贮水系数 =
v? v H
地面沉降
水使颗粒分开并使 孔隙开放
水
地面裂缝；悬崖和 裂隙发展
过度灌溉
含水层变薄。 空气充填的孔隙空 间变小；颗粒更紧 密堆积一起
空气
四、渗流和典型单元体
次生孔隙
岩浆岩和变质岩
好井
差井
井
可渗透的 砂岩
干井
好井
好井
断裂的花 岗岩
不同的土和岩石供水渗透的孔隙大小是不同的。水在大的孔隙 运动更容易。砾石的孔隙大，水渗透的快；粘土的孔隙太小， 水几乎不能渗透。 一些岩层太坚固，能隔水。其它易碎有很多裂隙，如果裂隙连 通，水就可通过。
§1.1 渗流的基本概念
一、水的压缩性
液体的体积随压力的增加而减少，这种性质称为压缩性。 根据胡克定律，有： dV 1 dV dp E 或 V V dp E 称为体积弹性系数（弹性模量elastic(ity) modulus）
N m
2
或Pa
β 称为体积压缩系数
1 E
E愈大，愈不易变形。 β与E 值也随温度而变化，但变化 不大，一般可视为常数。当改变一个大气压时，水的体积只 改变大约十万分之5。
v nu
我们还要知道某一点p的渗流速度。某一点p的渗流速度就是 以p点为中心的典型单元体积的平均渗流速度矢量。设REV 的体积为ΔV0，其中的空隙体积为(ΔV0)V
1 渗流速度v u V0 V dVV V0 1 因为实际平均流速为 u u V0 vdVV V0 V 所以v
'
σ′ 为作用于多孔介质表面的应力 Vb 为多孔介质的体积 α 为多孔介质的压缩系数
Vb=Vs+Vv，Vs为固体骨架体积，而Vv为其中的孔隙体积。 n=VV/Vb
1 dVb 1 dVs 1 dVV ' ' Vb d Vb d Vb d '
固体骨架本身的压缩性要比孔隙的压缩性小得多，近似认 为固体骨架部分是不可压缩的。
由于水头降低引起的含水层释水现象称为弹性释水．相反， 当水头升高时，会发生弹性贮存过程。
把贮水率 s 乘上含水层厚度M，称为贮水系数或释水系数， 即 s M 。它表示在面积为1个单位、厚度为含水层全厚 度M的含水层柱体中，当水头改变一个单位时弹性释放或贮存 的水量，无量纲。
潜水含水层，当水头下降时，可引起二部分水的排出。 上部潜水面处重力排水，用给水度
V0 V
V0
1 u V0 V dVv nu V0 V
六、水头和水力坡度
测压管水头为：
Hn z
p
总水头是测压管水头与流速水头之和：
u2 H z 2g p
因自然界中地下水的运动很缓慢，流速水头很小，可以忽略 不计。
例如：当地下水流速 u=lcm/s=864 m/d 时(这对地下水来说已经是很快的运 动速度了)，流速水头仅仅为 0.0005cm左右，比测压管水头少几个数量级， 显然可以忽略不计。因此，在地下水运动计算中，可以认为总水头H等于 测压管水头Hn，不再对二者加以区别，统称水头，用H表示。
(3)饱和土体渗流固结过程（土力学）
p
p
p0
作用在该平面上的上覆荷重分别由颗粒(固体骨架)和水承担， 即：
s 1 p 为颗粒与颗粒接触的面 积；为上覆荷重引起的总应 力； s为固体颗粒上的粒间应 力；p为水的压强
令λσs=σ’，σ’称为有效应力。因为λ值非常小，
这种假想水流称为渗流。假想水流所占据的空间区称为渗流 区或渗流场。
典型单元体
对于一个真实的连续水流，如河水，某一点的孔隙度n、压力 p、水头H、速度u等的物理含义很明确。