不动点理论,吸引
不动点原理

不动点原理不动点原理不动点原理是现代数学中的一个基本概念,也是函数式编程语言中的重要概念。
它的核心思想是找到一个函数,使得对于某个输入值,该函数的输出值等于输入值本身。
这个输入值就被称为该函数的不动点。
一、定义在数学中,给定一个函数f,如果存在一个实数x使得f(x)=x,则称x 为f的不动点。
二、举例说明以求平方根为例,假设我们要求一个数的平方根,可以使用牛顿迭代法来实现。
具体过程如下:1. 选取初始值x0;2. 计算f(x0)=x1=x0/2+a/(2*x0),其中a为要求平方根的数;3. 如果|f(x1)-x1|<ε,则停止计算,并将结果输出;否则返回第二步。
通过牛顿迭代法可以求出一个数a的平方根sqrt(a)。
但是我们发现,在计算过程中出现了不动点:当x=sqrt(a)时,有f(x)=sqrt(a)。
因此,sqrt(a)就是函数f(x)=x/2+a/(2*x)的不动点。
三、应用领域1. 函数式编程语言在函数式编程语言中,不动点常用于定义递归函数或实现高阶函数。
例如,在Haskell语言中,可以使用不动点来定义递归函数,如下所示:fix :: (a -> a) -> afix f = let x = f x in x这个函数的作用是寻找一个不动点,使得f(x)=x。
通过这个不动点,可以实现递归。
2. 计算机科学在计算机科学中,不动点理论被广泛应用于程序分析、程序验证和编译器优化等领域。
例如,在静态分析中,可以使用不动点来求解程序的不变量;在编译器优化中,可以使用不动点来实现常量传播、死代码删除等优化技术。
3. 经济学在经济学中,不动点理论被应用于博弈论和均衡分析等领域。
例如,在博弈论中,可以使用不动点来求解纳什均衡;在均衡分析中,可以使用不动点来求解市场均衡等问题。
四、总结总之,不动点原理是一种基本的数学概念,在函数式编程语言、计算机科学和经济学等领域都有广泛的应用。
通过寻找函数的不动点,我们可以实现递归、求解程序的不变量、实现编译器优化、求解均衡分析等问题。
【国家自然科学基金】_不动点指数理论_基金支持热词逐年推荐_【万方软件创新助手】_20140801
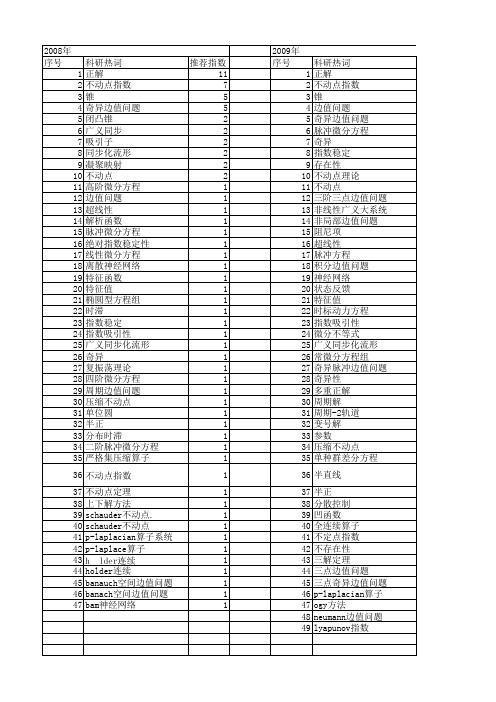
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 正解 不动点指数 锥 边值问题 奇异边值问题 脉冲微分方程 奇异 指数稳定 存在性 不动点理论 不动点 三阶三点边值问题 非线性广义大系统 非局部边值问题 阻尼项 超线性 脉冲方程 积分边值问题 神经网络 状态反馈 特征值 时标动力方程 指数吸引性 微分不等式 广义同步化流形 常微分方程组 奇异脉冲边值问题 奇异性 多重正解 周期解 周期-2轨道 变号解 参数 压缩不动点 单种群差分方程 半直线 半正 分散控制 凹函数 全连续算子 不定点指数 不存在性 三解定理 三点边值问题 三点奇异边值问题 p-laplacian算子 ogy方法 neumann边值问题 lyapunov指数
科研热词 推荐指数 不动点指数 10 正解 9 锥 3 对称正解 2 半正 2 不动点指数理论 2 jensen不等式 2 随机解 1 随机算子方程 1 随机不动点指数 1 闭凸锥 1 超线性 1 脉冲周期边值问题 1 第一特征值 1 稳定性 1 神经网络 1 特征值 1 时滞 1 无穷多点边值问题 1 捕食模型 1 平衡解 1 存在性 1 奇异边值问题 1 奇异s-l边值问题 1 周期解 1 变号解 1 反对称延拓法 1 凹函数 1 凝聚映射 1 全局指数稳定性 1 不动点指教 1 不动点 1 三点边值问题 1 三点奇异边值问题 1 一致持续 1 sturm-liouville 边值问题 1 p-laplace算子 1 n阶常微分方程组 1 m-点边值问题 1 lyapunov泛函 1 holling-ⅳ型函数 1 dirichlet问题 1 banach空间常微分方程 1 2m阶边值问题 1
lefschetz不动点定理

lefschetz不动点定理摘要:一、Lefschetz不动点定理简介二、Lefschetz不动点定理的证明三、Lefschetz不动点定理的应用四、Lefschetz不动点定理的扩展正文:**一、Lefschetz不动点定理简介**Lefschetz不动点定理是拓扑学中的一个重要定理,由美国数学家Lefschetz于1934年首次提出。
该定理主要研究的是流形上的不动点问题,即寻找连续映射下的不变点。
不动点在数学、物理、经济学等领域具有广泛的应用,代表着稳定和均衡的状态。
**二、Lefschetz不动点定理的证明**Lefschetz不动点定理的证明主要基于代数拓扑的方法。
首先,我们需要知道流形上的切向量场和法向量场的概念。
切向量场在流形上的每一点都有一个切向量,而法向量场在流形上的每一点都有一个法向量。
Lefschetz不动点定理的证明过程涉及到计算流形上的切向量场和法向量场之间的内积,并通过分析内积的性质得出不动点存在性。
**三、Lefschetz不动点定理的应用**Lefschetz不动点定理在数学和实际应用领域具有广泛的应用,例如:在控制论中,它被用来研究系统的稳定性;在多元函数论中,它被用来解决非线性方程组的问题;在物理学中,它被用来分析力学系统的平衡状态;在经济学中,它被用来研究市场均衡等。
**四、Lefschetz不动点定理的扩展**Lefschetz不动点定理的研究对象主要是流形上的连续映射。
在此基础上,学者们对其进行了许多扩展,如:Knaster-Tarski不动点定理、Schauder 不动点定理等。
这些扩展不仅丰富了不动点理论,还为各个领域的问题提供了更多的解决方法。
总之,Lefschetz不动点定理是拓扑学领域的一个重要定理,其证明和应用在数学和实际领域具有深远的影响。
(2021年整理)不动点定理及其应用-西安交通大学苏州附属中学

不动点定理及其应用-西安交通大学苏州附属中学(推荐完整)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(不动点定理及其应用-西安交通大学苏州附属中学(推荐完整))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为不动点定理及其应用-西安交通大学苏州附属中学(推荐完整)的全部内容。
不动点定理及其应用—西安交通大学苏州附属中学(推荐完整)编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望不动点定理及其应用—西安交通大学苏州附属中学(推荐完整) 这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力.本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈不动点定理及其应用-西安交通大学苏州附属中学(推荐完整)〉这篇文档的全部内容。
不动点定理及其应用215021 西安交通大学苏州附属中学蒋亚军摘要:本文研究了不动点定理的一些典型问题的经典解法,并对不动点理论在高中数学中的应用作了一些探究。
关键词:不动点;函数1 引言1912年,荷兰数学家布劳维证明,任意一个把n维球体映入自己的连续映象(即拓扑变换)至少有一个不动点。
这就是著名的拓扑不动点定理.我们知道,直线是一维空间,平面是二维空间,普通空间是三维空间,四维、五维以上至n维空间就很抽象了,下面对一维球体做出一个有趣的例子。
某学生进城早晨六点从家里出发,下午六点到达。
将混沌吸引子说清楚来,太精彩了

将混沌吸引子说清楚来,太精彩了"吸引子分为三类:第一类是最简单的吸引子,可以称为定点吸引子或不动点吸引子。
海纳百川,大海就是百川的定点吸引子;落叶归根,树根是一个定点吸引子;热力学系统的平衡态是该系统的定点吸引子。
在相空间中,定点吸引子是一个点,它将周围的轨道全部吸引过来。
第二类是所谓极限环吸引子。
这是比较高级的吸引子。
系统在远离平衡态时,经过若干分叉点之后,由于自组织作用,系统可以进入一个规则而又稳定的周期震荡状态。
极限环吸引子在相空间中是一个封闭的环,它将周围的轨道吸引到这个周期性的循环之中。
这两类吸引子分别描述了系统的两类不同的长期行为:周期性的重复某种运动系列。
其中第二类吸引子正是普里戈金的耗散结构模型所致力于描述的。
它揭示了在非线性系统中,自组织如何从无序中创造出有序结构。
但是,如果系统进一步分叉,更加远离平衡态,有可能达到一种新的稳定态,即第三类吸引子,即各种环面的吸引子。
这种吸引子被称为奇异吸引子或混沌吸引子。
奇异吸引子就是混沌,混沌就是奇异吸引子。
它仍然表征着系统的稳定定态。
它们并不与周期变化相对应,但是,系统从任一初始状态出发,最终都会演化到"相空间"的某一局域上。
混沌吸引子与一般吸引子不同,混沌现象的轨线进入吸引子后,两条距离非常近的轨线将发生指数分离,而两个状态点也迅速分开,此时,吸引子外的所有运动轨线都将进入吸引子之内,而内部的轨线又迅速分开。
从吸引子外部看,是聚集的过程;从吸引子内部看,是分散的过程。
系统在宏观演化上是有规律可循的,而从微观上看,我们又无法指出系统具体的演化轨道。
系统对初始条件依赖的敏感性,使系统运动出现随机偶然性的特点。
"上述整段话,就是从数学语言翻译出来的日常语言同,这个日常语言讲清楚了混沌吸引子吗?所谓"道理是什么"就是指这个道理对应什么现实情况,道理本质是什么,就是更深刻地谈道理,谈出道理的为什么来。
关于实函数不动点的原理及应用

V 13 SiN . ,0 2 o , c. o 3 2 1 .
关 于实 函数不动点 的原理及应用
The The r nd App i a i n ft x d i n Re lVa i bl o ya lc to o he Fi e Po nto a ra e Func i n tO
王国贤 , 罗
鑫
(. 1黑河学 院 数学系 , 黑龙江 黑河 14 0 2 黑河市逸夫中学 , 6 30;. 黑龙江 黑河 1 30) 4 6 0 W ANG Guo in a -x a nd LUO n Xi
(. te ais e at n, eh ol e H ie1 4 0 , hn ; 1 hmt pr Ma cD metH ieC l g, eh 6 3 0 C ia e 2 Heh MideS ho, i 6 3 o C i . iey d l c olHeh 14 o, hn e a)
p n il a e n e poe n u i r cpe h sb e x lrd a d s mmaie nt efn t n o n a a l. ers lsso h ttefx d p itt e r a e i it n d a g f r d i h u ci fo e v r be Th eut h w t a h e on h oyh saf xbly a d wier eo z o i i l i n
.
) 动点 。 的不
不动 点原理
定 理 【 : 如 果 厂是 n l维 实 心 球 体 B 。 】 + = 存 在一个 不动点 EB 。 即满 足 (
0 ) )
{∈ I I 到 自身的连续 映射 (=, …)则. R ≤1) nl, , 厂 2
数学中的拓扑动力系统研究
数学中的拓扑动力系统研究数学中的拓扑动力系统研究是一门研究动力学系统中拓扑结构的学科。
拓扑动力系统的研究领域非常广泛,涉及到了多个数学分支,如拓扑学、动力系统理论、微分方程等。
本文将从拓扑动力系统的定义、研究方法以及实际应用等多个方面对该领域进行探讨。
一、拓扑动力系统的定义拓扑动力系统是指在拓扑空间上定义的时间演化系统。
它由两部分组成,一部分是拓扑空间,另一部分是演化规律。
具体地说,拓扑空间可以是欧几里得空间、流形或者更一般的拓扑空间,演化规律则可以用函数、映射或者微分方程等方式来描述。
拓扑动力系统研究的重点是系统的稳定性、周期性以及混沌性质等。
二、拓扑动力系统的研究方法1. 相空间方法:相空间是拓扑动力系统研究中一个重要的概念。
相空间可以看作是系统可能状态的集合,其中每一个点对应着系统的一个状态。
通过研究相空间中的轨迹,可以揭示系统的运动规律。
相空间方法在研究拓扑动力系统的轨道、吸引子等性质时具有重要作用。
2. 不动点理论:不动点是指在动力系统中不受演化规律影响的点。
不动点理论通常用来研究系统的稳定性。
通过分析不动点的性质,可以得到系统在不同参数下的稳定解。
不动点理论在拓扑动力系统的平衡态分析中起到了关键作用。
3. 分岔理论:分岔是指在动力系统中参数变化时出现解的突变现象。
分岔理论的研究可以帮助我们理解系统在不同参数下的行为,在系统发生分岔时,解的性质发生了显著变化,从而使我们可以探索系统的多样性。
三、拓扑动力系统的实际应用拓扑动力系统的研究不仅仅是理论性的,它也有着广泛的实际应用。
以下是一些典型的应用领域:1. 生物科学:拓扑动力系统可用于描述生物种群的迁移、扩散等动态过程。
通过研究系统的稳定解和周期解,可以揭示种群演化规律,对生态系统的保护和管理起到指导作用。
2. 经济学:拓扑动力系统可以用来描述经济系统的动态行为。
通过建立合适的模型,可以研究经济系统中的不稳定现象和周期性波动,为政策制定者提供决策依据。
knaster-tarski 不动点定理
knaster-tarski 不动点定理Knaster-Tarski不动点定理是数学中的一个重要定理,它确立了在一定条件下,关于一个完备格上的连续递增函数,存在一个不动点的事实。
具体来说,考虑一个完备格(也称为lattice),即一个偏序集$(L,\leq)$,其中对于任意两个元素$a$和$b$,存在最大下界$\inf(a,b)$和最小上界$\sup(a,b)$。
函数$f:L→L$被称作递增的,如果对于任意的$a≤b$,都有$f(a)≤f (b)$。
此外,如果一个元素$a$满足$f(a)=a$,则称$a$是函数$f$的一个不动点。
Knaster-Tarski不动点定理指出:对于一个完备格上的连续递增函数$f:L→L$,存在一个不动点$a$使得$f(a)=a$。
我们可以按照以下步骤来证明这个定理:1. 首先考虑函数$f$的所有下界的集合$X=\{x∈L∣x≤f(x)\}$。
这个集合是非空的,因为$L$是完备格。
同时,$X$也是一个偏序集,因为对于任意的$x$和$y$,如果$x≤y$,则由$f$的递增性可知$f(x)≤f(y)$,进而$x≤f(x)≤f(y)$,所以$x∈X$。
因此,我们可以考虑$X$中所有元素的上界的集合$U=\{u∈L∣∀x∈X,x≤u\}$。
由于$L$是完备格,$U$中存在最小上界$a=\sup U$。
2. 接下来,我们需要证明$a$是$f$的一个不动点。
首先注意到对于任意的$x∈X$,由定义可知$x≤a$,进而$f(x)≤f(a)$。
另一方面,根据$U$的定义,我们知道对于任意的$x∈X$,有$x≤f(x)≤a$,所以$f(a)$也是$x$的上界。
因此,$a≤f(a)$,即$a∈X$,所以根据$X$的定义,$a≤f(a)$。
综上,我们得到了$a≤f(a)≤a$,即$a=f(a)$,证明了$a$是$f$的一个不动点。
综上,Knaster-Tarski不动点定理确立了在完备格上的连续递增函数存在不动点的事实。
角谷不动点定理kakutani's fixed point theorem
角谷不动点定理kakutani's fixed point theorem角谷不动点定理(Kakutani"s Fixed Point Theorem)是数学领域中一个著名的定理,由日本数学家角谷浩吾于1938年提出。
该定理主要研究了凸函数和下半连续函数的不动点问题,对于函数的性质及应用具有重要的理论意义。
一、角谷不动点定理简介1.定理来源及命名角谷不动点定理源于日本数学家角谷浩吾在研究凸函数和下半连续函数的过程中,对不动点问题的深入研究。
该定理在一定程度上解决了凸函数和下半连续函数的不动点问题,因此在数学领域具有较高的地位。
2.定理表述角谷不动点定理表述如下:设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)内单调,那么f(x)在区间[a, b]上至少有一个不动点。
二、不动点及其相关概念1.不动点的定义不动点是指函数在某个区间上取到的值等于该区间内某个点的值,即f(x) = x。
2.不动点的类型根据不动点出现的位置,可以将不动点分为两类:一类是在定义域内的不动点,另一类是在值域内的不动点。
3.不动点与函数性质的关系不动点的存在性与函数的连续性、单调性等性质密切相关。
例如,角谷不动点定理就是研究了凸函数和下半连续函数的不动点问题。
三、角谷不动点定理的证明与应用1.定理的证明思路角谷不动点定理的证明主要依据了函数的连续性、单调性和不动点的定义。
证明过程中,角谷浩吾采用了反证法,首先假设函数f(x)在区间[a, b]上没有不动点,然后通过推导得出矛盾,从而证明了定理的正确性。
2.定理的推广与变形式角谷不动点定理后来被广泛推广,包括布雷尔不动点定理(Brela"s Fixed Point Theorem)等。
这些定理在数学领域有着广泛的应用。
3.定理在实际问题中的应用实例角谷不动点定理在实际问题中具有广泛的应用,如在经济模型、生态模型、物理系统等领域。
以经济模型为例,商品价格的调整过程可以看作是一个动态系统,通过角谷不动点定理可以研究价格调整的稳定状态。
2020高考数学专题复习不动点在数列中的应用
不动点在数列中的应用在高考试题中,数列向所对应函数的不动点收敛的问题,常可以用单调性结合数学归纳法的方法来解决.“不动点”问题虽不是高考大纲的要求,但在函数迭代、力程、数列、解析几何中都有重要的价值和应用,在历年的高考中也经常看到“不动点”的影子。
用“不动点”的方法在学生平时解题中主要是求数列的通项公式、数列的单调性、有界性及收敛性等.1求数列的通项公式定理1 已知数列{}n x 满足()()dcx bax x f x f x n n ++==-,1 ,其中0,0≠-≠bc ad c ,设p 是()x f 唯一的不动点,则数列⎭⎬⎫⎩⎨⎧-p x n 1是一个等差数列. 证明 因为p 是()x f 唯一的不动点,所以p 是方程dcx bax x ++=,亦即p 是一元二次方程()02=--+b x a d cx 的唯一解.得ap cp pd b cda p -=--=2,2 所以()()()()dcx p x pc a dcx apcp x pc a d cx pd b x pc a p d cx b ax p x n n n n n n n n n +--=+-+-=+-+-=-++=---------111211111()()()()px cp a cp d pc a c px cp d p x c pc a p x pc a d cx p x n n n n n n --++-=-++--=--+=------11111111把 cda p 2-=代入上式,得: px d a c p x n n -++=--1121令 d a ck +=2,可得数列⎭⎬⎫⎩⎨⎧-p x n 1是一个等差数列. 在初等数学中经常会遇到求这类问题,已知数列{}n x 的首项,数列的递推关系,求数列的通项,这类问题往往难度很大,通过不定点定理,大大降低了此类问题的难度.例1 若1121,1--=-=n n a a a (*N n ∈,且2≥n )求数列{}n a 的通项公式.解 根据迭代数列121--=n n a a ,构造函数()x x f -=21,易知()x f 有唯一的不动点1=p ,根据定理 可知2,1,1,0=-===d c b a , 则111111-+-=--n n a a 即数列⎭⎬⎫⎩⎨⎧-11n a 是以首项21-,公差为1-的等差数列.则对应的通项公式为()()n n a n -=--+-=-21112111 解得nna n 2123--=又11-=a 也满足上式.所以{}n a 的通项公式为nna n 2123--=. 对于此类形式的数列,已知数列{}n x 满足()()dcx bax x f x f x n n ++==-,1 ,其中0,0≠-≠bc ad c ,求其通项.运用不动点定理,可以简单快捷地解答.即数列⎭⎬⎫⎩⎨⎧-11n a 是以首项1a ,公差为da c+2的等差数列.推论 已知数列{}n x 满足()()b ax x f x f x n n +==-,1 ,其中0≠a ,设p 是()x f 唯一的不动点,则数列{}p x n -是一个公比为a 等比数列例2 若32,111+=-=-n n a a a ,(*N n ∈,且2≥n ),求数列{}n a 的通项公式.解 根据迭代数列321+=-n n a a ,构造函数()32+=x x f ,易知()x f 有唯一的不动点3-=p ,根据推论 可知3,2==b a , 则()()()3231--=---n n a a所以()3231+=+-n n a a所以{}3+n a 是以231=+a 为首项,2为公比的等比数列, 则当2≥n 时,有n n a 23=+, 故32-=n n a 又11-=a 也满足上式.所以{}n a 的通项公式为32-=n n a .在高中阶段,学生在学习了数列之后,经常会遇到已知1a 及递推公式,求数列()n n a f a =+1的通项公式的问题,很多的题目令人感到非常棘手.而不动点定理给出了一个“公式”性的方法——不动点法,应用此法可巧妙地处理此类问题.2 数列的有界性在高考中会经常出现证明数列有界性的问题,不等式问题是高考中的一个难点,数列与不等式结合,使得这类问题更加的棘手了,而不动点定理却给了我们思想上的一个指导,即解决这类问题,我们可以先求出不动点,然后用数学归纳法证明.例3 函数()x x x x f ln -=.数列{}n a 满足()n n a f a a =<<+11,10.证明:11<<+n n a a .分析 函数()x x x x f ln -=的不动点是1=x 显然此题就是要证明数列向不动点1=x 收敛证明 当()1,0∈x 时,()0ln '>-=x x f ,所以()x f 在区间()1,0内是增函数;又101<<a ,所以()()11ln 111121=<-==<f a a a a f a a ;假设k n =时有11<<+k k a a ,因为()x f 是增函数()1,0∈x ,所以()()()111=<<+f a f a f k k ,即121<<++k k a a ,当1+=k n 时结论也成立.故原不等式成立这类问题可以以各种类型的函数与数列为载体.考查导数、单调性、方程的根等问题.对学生综合能力有较高的要求,在2010年的高考中此类问题进一步拓展,又有了一些新变化:利用数列的有界性求含参数列中参数的取值范围.例4 已知数列{}n a 中,nn a c a a 1,111-==+,求使不等式31<<+n n a a 成立的c 的取值范围.解:该数列应该是向其某个不动点收敛.不妨设该不动点为0x ,则有310≤<x ,即方程()x x f =在(]3,1有一个实根.我们继续用不动点的思路方法解决该问题.因为31<<+n n a a 对任意自然数都成立,所以首先应有321<<a a ,可得42<<c . 设()xc x f 1-=,则()x f 是增函数,()+∞∈,0x . 令()x x f =,即01,12=+-=-cx x x xc .当2>c 时,该方程有2个不等的实数根.设为2121,,x x x x <,由韦达定理121=x x ,可知211x x <<只要让32≤x 即可.令()()31003,12≤⇒≥+-=c g cx x x g . 即当310≤c 时,()x f 在(]3,1上存在不动点0x (0x 就是2x )所以c 的取取范围是⎥⎦⎤ ⎝⎛310,2.再用数学归纳法证明结论的正确性:因为310≤<x 且()x c x f 1-=在()+∞,0是增函数,所以当3102≤<c 时, 有()()002111x f x f a a =<=<=.假设k n =时,有301≤<<+x a a k k .因为()x f 是增函数,故()()()01x f a f a f k k <<+,即021x a a k k <<++,当1+=k n 时结论也成立,所以当c 的取值范围是⎥⎦⎤⎝⎛310,2时, ()xc x f 1-=有在区间(]3,1内的不动点0x ,数列{}n a 单调递增向该不动点收敛. 3 数列的单调性及收敛性近几年一些地区高考试题对利用不动点解决递推数列的问题比较青睐,如求数列的通项公式,利用不动点研究数列的单调性等等.下文利用不动点及特征函数的性质研究数列的单调性及收敛性,并借此解决一些高考题.3.1 关于数列单调性、收敛性的重要结论定义1 设R I f →:,其中I 是R 的一个区间,数列{}n x 由a a =1和递推关系()n n x f x =+1来定义.则数列{}n x 称为递推数列.()x f 称为数列{}n x 的特征函数,()x f x =称为数列{}n x 的特征方程,a x =1称为初始值.若设f 是连续的,若{}n x 收敛而且有极限0x ,()()010lim lim x f x f x x n n ===+.因此问题就变为寻找方程 ()x f x =解(即f 的不动点),并验证数列是不是收敛于数 0x .定理 2设f 是定义在I 上的一个压缩映射,则由任何初始值[]b a x ,1∈和递推数列。
