2015年高考数学一轮复习课时训练第1节 直线与方程
2015高考数学一轮配套课件:8-1 第1课时 直线的方程
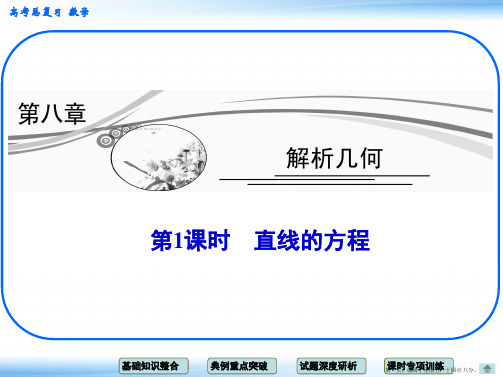
公式.
基础知识整合
典例重点突破
试题深度研析
课时专项训练
第十四页,编辑于星期五:十四点 八分。
高考总复习 数学
直线的倾斜角与斜率的关系 (1)斜率k是一个实数,当倾斜角α≠90°时,k=tan α.直线都有 倾斜角,但并不是每条直线都存在斜率,倾斜角为90°的直线 无斜率. (2)①求直线方程时,若不能断定直线是否具有斜率时,应对 斜率存在与不存在加以讨论.②在用截距式时,应先判断截距 是否为0,若不确定,则需分类讨论.
高考总复习 数学
则 B 点坐标为kk+ +72,4kk+-22. 由已知kk+ +72-12+4kk+-22+12=52, 解得 k=-34,∴y+1=-34(x-1), 即 3x+4y+1=0. 综上可知,所求直线的方程为 x=1 或 3x+4y+1=0.
基础知识整合
典例重点突破
试题深度研析
课时专项训练
高考总复习 数学
第1课时 直线的方程
基础知识整合
典例重点突破
试题深度研析
课时专项训练
第一页,编辑于星期五:十四点 八分。
高考总复习 数学
(一)考纲点击 1.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率
的计算公式. 2.掌握确定直线位置的几何要素,掌握直线方程的三种形式
(点斜式、两点式及一般式),了解斜截式与一次函数的关 系.
基础知识整合
典例重点突破
试题深度研析
课时专项训练
第二十二页,编辑于星期五:十四点 八分。
高考总复习 数学
(2)设所求直线的斜率为 k,依题意 k=-14×3=-34. 又直线经过点 A(-1,-3), 因此所求直线方程为 y+3=-34(x+1), 即 3x+4y+15=0.
2015高考数学一轮课件:第 8篇 第1节 直线与方程

(3)线线距离 两平行直线Ax+By+C1=0与Ax+By+C2=0间的距离 d= |CA1-2+CB22| .
数学 人教A版 ·文科 第十四页,编辑于星期五:十三点 三十四分。
基础梳理
课 时 训考练点 突 破
1.直线y=-x+1的倾斜角等于( )
数学 人教A版 ·文科 第二十七页,编辑于星期五:十三点 三十四分。
基础梳理
课 时 训考练点 突 破
[解析] 法一 设直线l在x轴、y轴上的截距均为a, 由题意得M(3,2). ①若a=0,即l过点(0,0)和(3,2), ∴直线l的方程为y=23x, 即2x-3y=0.
数学 人教A版 ·文科 第二十八页,编辑于星期五:十三点 三十四分。
课 时 训考练点 突 破
2.直线方程的五种形式
名称 点斜式 斜截式
两点式
截距式 一般式
已知条件 斜率k与点(x0, y0)
斜率k与截距b
两点(x1,y1)、 (x2,y2) (其中 x1≠x2、y1≠y2)
截距a与b
方程 y-y0=k(x-x0)
y=kx+b yy2--yy11=xx2--xx11
ax+by=1 ___A_x_+__B_y_+_C_=__0__ (A、B不同时为0)
1.直线的倾斜角与斜率 (1)直线的倾斜角 ①定义.当直线l与x轴相交时,我们取x轴作为基准,x 轴__正__向_与直线l _向__上__方向之间所成的角α叫做直线l的倾斜 角.当直线l与x轴平行或重合时,规定它的倾斜角为0°. ②范围:倾斜角α的范围为____[0_°__,__1_8_0°_ .)
第八篇 平面解析几何
第一页,编辑于星期五:十三点 三十四分。
高三理科数学(重点班)一轮复习课时训练:第九篇第1节 直线与方程Word版含解析

基础对点练(时间:30分钟)1.直线l:xsin 30°+ycos 150°+1=0的斜率是( A )(A)(B)(C)-(D)-解析:设直线l的斜率为k,则k=-=.2.直线x+a2y+6=0和(a-2)x+3ay+2a=0无公共点,则a的值为( C )(A)3或-1 (B)0或3(C)0或-1 (D)-1或0或3解析:两直线无公共点,即两直线平行,所以解得a=0或a=-1.故选C.3.(2015新泰模拟)已知直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0.若l1⊥l2,则实数a的值是( C )(A)0 (B)2或-1 (C)0或-3 (D)-3解析:因为l1⊥l2,所以a+a(a+2)=0,则a=0或a=-3,故选C.4.(2016枣庄模拟)将直线l沿y轴的负方向平移a(a>0)个单位,再沿x轴正方向平移a+1个单位得直线l′,此时直线l′与l重合,则直线l′的斜率为( B )(A)(B)-(C)(D)-解析:设直线l:y=kx+b,l沿y轴负方向平移a个单位得l1:y=kx+b-a,再沿x轴正方向平移a+1个单位得l′:y=k(x-a-1)+b-a,即y=kx+b-ka-k-a,由l′与l重合得-a-ka-k=0,k=-.5.若直线l1:y=k(x-4)与直线l2关于点(2,1)对称,则直线l2经过定点( B )(A)(0,4) (B)(0,2) (C)(-2,4) (D)(4,-2)解析:直线l1:y=k(x-4)经过定点(4,0),其关于点(2,1)对称的点为(0,2),又直线l1与直线l2关于点(2,1)对称,故直线l2经过定点(0,2).故选B.6.不论m为何值时,直线l:(m-1)x+(2m-1)y=m-5恒过定点( D )(A) (1,- ) (B)(-2,0) (C)(2,3) (D)(9,-4)解析:直线(m-1)x+(2m-1)y=m-5,化为(mx+2my-m)+(-x-y+5)=0,即直线l过x+2y-1=0与-x-y+5=0的交点,解方程组得7.(2015合肥一模)已知直线l:x-y-1=0,l1:2x-y-2=0.若直线l2与l1关于l对称,则l2的方程是( B )(A)x-2y+1=0 (B)x-2y-1=0(C)x+y-1=0 (D)x+2y-1=0解析:因为l1与l2关于l对称,所以l1上任一点关于l的对称点都在l2上,故l与l1的交点(1,0)在l2上.又易知(0,-2)为l1上一点,设它关于l的对称点为(x,y),则解得即(1,0),(-1,-1)为l2上两点,可得l2的方程为x-2y-1=0.8.经过点P(1,4)的直线在两坐标轴上的截距都是正值,且截距之和最小,则直线的方程为( B )(A)x+2y-6=0 (B)2x+y-6=0(C)x-2y+7=0 (D)x-2y-7=0解析:直线过P(1,4),代入后舍去选项A,D;又在两坐标轴上的截距均为正值,舍去选项C.故选B.9.已知平面内两点A(1,2),B(3,1)到直线l的距离分别是,-,则满足条件的直线l的条数为( C )(A)1 (B)2 (C)3 (D)4解析:由题知满足题意的直线l在线段AB两侧各有1条;又因为|AB|=,所以还有1条为过线段AB 上的一点且与AB垂直的直线,故共3条.故选C.10.(2016哈尔滨模拟)经过点(-2,2),且与两坐标轴所围成的三角形面积为1的直线l的方程为.解析:设所求直线方程为+=1,由已知得解得或所以2x+y+2=0或x+2y-2=0为所求.答案:2x+y+2=0或x+2y-2=011.已知两直线l1:ax-by+4=0和l2:(a-1)x+y+b=0,求满足下列条件的a,b的值.(1)l1⊥l2,且直线l1过点(-3,-1);(2)l1∥l2,且坐标原点到这两条直线的距离相等.解:(1)因为l1⊥l2,所以a(a-1)-b=0.又因为直线l1过点(-3,-1),所以-3a+b+4=0.故a=2,b=2.(2)因为直线l2的斜率存在,l1∥l2,所以直线l1的斜率存在,k1=k2,即=1-a.又因为坐标原点到这两条直线的距离相等,所以l1、l2在y轴上的截距互为相反数,即=b.故a=2,b=-2或a=,b=2.能力提升练(时间:15分钟)12.(2016哈尔滨模拟)函数y=asin x-bcos x的一条对称轴为x=,则直线l:ax-by+c=0的倾斜角为( D )(A)45°(B)60° (C)120°(D)135°解析:由函数y=f(x)=asin x-bcos x的一条对称轴为x=知,f(0)=f(),即-b=a,所以直线l的斜率为-1,所以倾斜角为135°.13.若m>0,n>0,点(-m,n)关于直线x+y-1=0的对称点在直线x-y+2=0上,那么+的最小值等于.解析:设点(-m,n)关于直线x+y-1=0的对称点为(x0,y0),则有解得x0=1-n,y0=1+m,又点(x0,y0)在直线x-y+2=0上,所以1-n-1-m+2=0,所以m+n=2,所以+=(+) (m+n)=++≥.答案:14.(2015淮安一调)已知入射光线经过点M(-3,4),被直线l:x-y+3=0反射,反射光线经过点N(2,6),则反射光线所在直线的方程为.解析:设点M(-3,4)关于直线l:x-y+3=0的对称点为M′(a,b),则反射光线所在直线过点M′,解得a=1,b=0.又反射光线经过点N(2,6),所以所求直线的方程为=,即6x-y-6=0.答案:6x-y-6=015.已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点,求:(1)当|OA|+|OB|取得最小值时,直线l的方程;(2)当|MA|2+|MB|2取得最小值时,直线l的方程.解:(1)设A(a,0),B(0,b)(a>0,b>0).则直线l的方程为+=1,则+=1,所以|OA|+|OB|=a+b=(a+b) (+)=2++≥2+2=4,当且仅当“a=b=2”时取等号,此时直线l的方程为x+y-2=0.(2)设直线l的斜率为k,则k<0,直线l的方程为y-1=k(x-1),则A(1-,0),B(0,1-k),所以|MA|2+|MB|2=(1-1+)2+12+12+(1-1+k)2=2+k2+≥2+2=4,则当且仅当k2=,即k=-1时等号成立,则直线l的方程为y=-x+2.16. (2015东营模拟)设直线l的方程为(a+1)x+y-2-a=0(a∈R).(1)若直线l在两坐标轴上的截距相等,求直线l的方程;(2)若a>-1,直线l与x,y轴分别交于M,N两点,O为坐标原点,求△OMN面积取最小值时,直线l的方程.解:(1)当直线l经过坐标原点时,设直线在两坐标轴上的截距都为0,此时a+2=0,解得a=-2,此时直线l的方程为-x+y=0,即x-y=0;当直线l不经过坐标原点,即a≠-2且a≠-1时,由直线在两坐标轴上的截距相等可得=2+a,解得a=0,此时直线l的方程为x+y-2=0.所以直线l的方程为x-y=0或x+y-2=0.(2)由直线方程可得M(,0),N(0,2+a),因为a>-1,所以S△OMN=××(2+a)=×=[(a+1)++2]≥×[2+2]=2,当且仅当a+1=,即a=0时等号成立,此时直线l的方程为x+y-2=0.精彩5分钟1.(2014高考四川卷)设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|·|PB|的最大值是.解题关键:两直线过定点,且两直线互相垂直.解析:易求定点A(0,0),B(1,3).当P与A和B均不重合时,不难验证PA⊥PB,所以|PA|2+|PB|2=|AB|2=10,所以|PA|·|PB|≤=5(当且仅当|PA|=|PB|=时,等号成立),当P 与A或B重合时,|PA|·|PB|=0,故|PA|·|PB|的最大值是5.答案:52.(2015黄山一模)已知点A在直线x+2y-1=0上,点B在直线x+2y+3=0上,线段AB的中点为P(x0,y0),且满足y0>x0+2,则的取值范围为.解题关键:利用点到直线的距离,确定x0,y0的关系,求的范围转化为关于x0的函数,求其范围.解析:因为直线x+2y-1=0与直线x+2y+3=0平行,所以=,可得x0+2y0+1=0,因为y0>x0+2,所以-(1+x0)>x0+2,解得x0<-.设=k,所以k==--,因为x0<-,所以0<-<,所以-<<-.答案:(-,-)。
高考数学全程一轮复习第八章解析几何第一节直线的方程课件

5 . ( 易 错 ) 过 点 P(2 , 3) 且 在 两 坐 标 轴 上 截 距 相 等 的 直 线 方 程 为 __x_+__y_-_5_=__0_或_3_x_-__2_y=__0_.
解析:当截距为0时,直线方程为3x-2y=0; 当截距不为0时,设直线方程为xa + ya=1, 则2a + 3a=1,解得a=5.所以直线方程为x+y-5=0.
平面内所有直线
【常用结论】 1.直线的倾斜角α和斜率k之间的对应关系:
α
0°
0°<α<90°
90°
k
0
k>0
不存在
2.特殊位置的直线方程
(1)与x轴重合的直线方程为y=0;
(2)与y轴重合的直线方程为x=0;
(3)经过点(a,b)且平行于x轴的直线方程为y=b;
(4)经过点(a,b)且平行于y轴的直线方程为x=a;
公共点,则直线l斜率的取值范围为__[13_,___3_]_.
解析:∵P(-1,0),A(2,1),B(0, 3), ∴kPA=2−1−−01 =13,kPB=0−3−−01 = 3. 由图可知,直线l的斜率k的取值范围为[13 , 3].
【变式练习】 若本例(2)中“P(-1,0)”改为“P(1,0)”,其他 条件不变,则直线l的斜率的取值范围为__(-__∞__,_-___3_]_∪__1_,__+__∞__.
解析:如图所示:
当直线l过B时设直线l的斜率为k1,
则k1=
3−0=-
0−1
3,
当直线l过A时设直线l的斜率为k2, 则k2=12−−01=1,
∴要使直线l与线段AB有公共点,则直线l的斜率的取值范围是(-∞,- 3] ∪
2015年高考数学理一轮复习精品资料 专题9.1 直线的方程含解析

2015年高考数学理一轮复习精品资料【新课标版】预测卷第九章 解析几何 第一节 直线的方程一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的。
)1.【2014年高考数学全程总复习】过点M (,N (的直线的倾斜角是( )(A)34π (B) 4π (C) 6π (D)3π【答案】B【解析】由斜率公式得k==1.又倾斜角范围为[0,)π,∴倾斜角为4π. 2. 【2013-2014学年福建省清流一中高一下学期第一阶段】直线10x y --=不经过的象限是( )A .第四象限B .第三象限C .第二象限D .第一象限3. 【2013-2014学年四川省资阳市高一下学期期末】直线134x y+=与两坐标轴围成的三角形的周长为( )A .6B .7C .12D .1412434322=+++.4.【2013-2014学年福建省清流一中高一下学期第一阶段】过点P 且倾斜角为45°的直线方程为( )A .3y x +=B .y x =C .y x =-.y = 【答案】C【解析】斜率145tan ==k ,由直线的点斜式方程可得⇒-=+)3(13x y y x =- C.5.【2013-2014学年湖南省安乡一中高二下学期期末】与直线0543=+-y x 关于x 轴对称的直线方程为( )A 、0543=++y xB 、0543=-+y xC 、0543=-+-y xD 、0543=++-y x6.【2013-2014学年福建省三明一中高一下学期期中】下列说法的正确的是 ( )A .经过定点),(00y x 的直线都可以用方程)(00x x k y y -=-表示B .经过定点)0A b ,(的直线都可以用方程b kx y +=表示C .经过任意两个不同的点),(111y x P ,),(222y x P 的直线都可以用方程()()()()y y x x x x y y --=--121121表示D .不经过原点的直线都可以用方程1=+bya x 表示7. 【2014年高考数学全程总复习】直线xcos140°+ysin140°=0的倾斜角是( )(A)40° (B)50° (C)130° (D)140°8. 【2013-2014学年辽宁省铁岭高中高一下学期期初】直线1l :0ax y b -+=,2l :0bx y a -+=(0ab ≠,a b ≠)在同一坐标系中的图形大致是( )9.【2014届陕西省高考前30天】点P (a ,b )关于l :x+y+1=0对称的点仍在l 上,则a+b=( )A .﹣1B .1C .2D .010. 【2014高考名师推荐】设点A(-2,3),B(3,2),若直线ax +y +2=0与线段AB 没有交点,则a 的取值范围是( ) A.B.C.D.【答案】B 【解析】11.【改编自2014届高考数学总复习考点引领】2014届高考数学总复习考点引领直线l 经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,则直线l 的方程为( ). A .8x -5y +20=0 或 2x -5y+10=0 B .2x -5y -10=0 C .8x -5y +20=0或2x -5y -10=0 D .8x -5y +20=012.【改编自2005·全国卷3文理】已知在△ABC 中,∠ACB=90°,BC=3,AC=4,P 是AB 上的点,则点P到AC 、BC 的距离乘积的最大值是( ). A .9 B .4 C .3 D .2 【答案】C【解析】以C 为原点,CA CB 分别为x 轴、y 轴建立直角坐标系如图所示,则直线AB 的方程为143x y+=.由重要不等式得:43x y +≥13xy ≥≤.点P 到AC 、BC 的距离乘积即xy ,所以点P到AC 、BC 的距离乘积的最大值是3,选C .二、填空题(本大题共4小题,每小题5分,共20分。
高三数学一轮复习课时作业5:直线的方程

第1讲 直线的方程基础巩固题组(建议用时:40分钟)一、选择题1.如图中的直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则( )A .k 1<k 2<k 3B .k 3<k 1<k 2C .k 3<k 2<k 1D .k 1<k 3<k 2解析 直线l 1的倾斜角α1是钝角,故k 1<0,直线l 2与l 3的倾斜角α2与α3均为锐角,且α2>α3,所以0<k 3<k 2,因此k 1<k 3<k 2,故选D. 答案 D2.(2015·太原质检)若直线l 与直线y =1,x =7分别交于点P ,Q ,且线段PQ 的中点坐标为(1,-1),则直线l 的斜率为( )A.13B .-13C .-32D.23解析 依题意,设点P (a ,1),Q (7,b ),则有⎩⎪⎨⎪⎧a +7=2,b +1=-2,解得a =-5,b=-3,从而可知直线l 的斜率为-3-17+5=-13.答案 B3.两条直线l 1:x a -y b =1和l 2:x b -ya=1在同一直角坐标系中的图象可以是( )答案 A4.(2014·郑州模拟)直线l 经过点A (1,2),在x 轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( )A.⎝ ⎛⎭⎪⎫-1,15 B.⎝ ⎛⎭⎪⎫-∞,12∪()1,+∞ C .(-∞,1)∪⎝ ⎛⎭⎪⎫15,+∞D .(-∞,-1)∪⎝ ⎛⎭⎪⎫12,+∞解析 设直线的斜率为k ,如图,过定点A 的直线经过点B 时,直线l 在x 轴上的截距为3,此时k =-1;过定点A 的直线经过点C 时,直线l 在x 轴上的截距为-3,此时k=12,满足条件的直线l 的斜率范围是(-∞,-1)∪⎝ ⎛⎭⎪⎫12,+∞.答案 D5.设直线ax +by +c =0的倾斜角为α,且sin α+cos α=0,则a ,b 满足( ) A .a +b =1 B .a -b =1 C .a +b =0D .a -b =0解析 由sin α+cos α=0,得sin αcos α=-1,即tan α=-1.又因为tan α=-a b ,所以-ab =-1.即a =b ,故应选D. 答案 D 二、填空题6.若点A (4,3),B (5,a ),C (6,5)三点共线,则a 的值为________. 解析 ∵k AC =5-36-4=1,k AB =a -35-4=a -3.由于A ,B ,C 三点共线,所以a -3=1,即a =4. 答案 47.(2015·烟台模拟)直线3x -4y +k =0在两坐标轴上的截距之和为2,则实数k =________.解析 令x =0,得y =k 4;令y =0,得x =-k3, 则有k 4-k3=2,所以k =-24. 答案 -248.一条直线经过点A (-2,2),并且与两坐标轴围成的三角形的面积为1,则此直线的方程为________.解析 设所求直线的方程为x a +yb =1. ∵A (-2,2)在此直线上, ∴-2a +2b =1.①又因直线与坐标轴围成的三角形面积为1, ∴12|a |·|b |=1.② 由①②可得(1)⎩⎪⎨⎪⎧a -b =1,ab =2或(2)⎩⎪⎨⎪⎧a -b =-1,ab =-2.由(1)解得⎩⎪⎨⎪⎧a =2,b =1或⎩⎪⎨⎪⎧a =-1,b =-2,方程组(2)无解.故所求的直线方程为x 2+y 1=1或x -1+y-2=1,即x +2y -2=0或2x +y +2=0为所求直线的方程. 答案 x +2y -2=0或2x +y +2=0 三、解答题9.已知直线l 与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l 的方程:(1)过定点A (-3,4); (2)斜率为16.解 (1)设直线l 的方程是y =k (x +3)+4,它在x 轴,y 轴上的截距分别是-4k-3,3k +4,由已知,得(3k +4)⎝ ⎛⎭⎪⎫-4k -3=±6,解得k 1=-23或k 2=-83.故直线l 的方程为2x +3y -6=0或8x +3y +12=0. (2)设直线l 在y 轴上的截距为b ,则直线l 的方程是 y =16x +b ,它在x 轴上的截距是-6b , 由已知,得|-6b ·b |=6,∴b =±1.∴直线l 的方程为x -6y +6=0或x -6y -6=0. 10.设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ). (1)若l 在两坐标轴上的截距相等,求l 的方程; (2)若l 不经过第二象限,求实数a 的取值范围.解 (1)当直线过原点时,该直线在x 轴和y 轴上的截距为0,显然相等. ∴a =2,方程即为3x +y =0.当直线不过原点时,由截距存在且均不为0, 得a -2a +1=a -2,即a +1=1, ∴a =0,方程即为x +y +2=0.综上,l 的方程为3x +y =0或x +y +2=0. (2)将l 的方程化为y =-(a +1)x +a -2,由题意得⎩⎨⎧-(a +1)>0,a -2≤0或⎩⎨⎧-(a +1)=0,a -2≤0,∴a ≤-1.综上可知a 的取值范围是(-∞,-1』.能力提升题组 (建议用时:25分钟)11.(2015·长春三校调研)一次函数y =-m n x +1n 的图象同时经过第一、三、四象限的必要不充分条件是( )A .m >1,且n <1B .mn <0C .m >0,且n <0D .m <0,且n <0解析 因为y =-m n x +1n 经过第一、三、四象限,故-m n >0,1n <0,即m >0,n <0,但此为充要条件,因此,其必要不充分条件为mn <0. 答案 B12.已知直线x +2y =2分别与x 轴、y 轴相交于A ,B 两点,若动点P (a ,b )在线段AB 上,则ab 的最大值为________.解析 直线方程可化为x2+y =1,故直线与x 轴的交点为A (2,0),与y 轴的交点为B (0,1),由动点P (a ,b )在线段AB 上,可知0≤b ≤1,且a +2b =2,从而a =2-2b ,故ab =(2-2b )b =-2b 2+2b =-2⎝ ⎛⎭⎪⎫b -122+12,由于0≤b ≤1,故当b =12时,ab 取得最大值12. 答案 1213.如图,射线OA ,OB 分别与x 轴正半轴成45°和30°角,过点P (1,0)作直线AB 分别交OA ,OB 于A ,B 两点,当AB 的中点C 恰好落在直线y =12x 上时,则直线AB 的方程为________. 解析 由题意可得k OA =tan 45°=1,k OB =tan(180°-30°)=-33,所以直线l OA 和直线l OB 的方程分别为y =x ,y =-33x ,设A (m ,m ),B (-3n ,n ), 所以AB 的中点C ⎝ ⎛⎭⎪⎫m -3n 2,m +n 2,由点C 在y =12x 上,且A ,P ,B 三点共线得⎩⎪⎨⎪⎧m +n 2=12·m -3n 2,m -0m -1=n -0-3n -1,解得m =3,所以A (3,3).又P (1,0),所以k AB =k AP =33-1=3+32,所以l AB :y =3+32(x -1),即直线AB 的方程为(3+3)x -2y -3-3=0. 答案 (3+3)x -2y -3-3=014.直线l 过点P (1,4),分别交x 轴的正方向和y 轴的正方向于A ,B 两点. (1)当|P A |·|PB |最小时,求l 的方程; (2)当|OA |+|OB |最小时,求l 的方程. 解 依题意,l 的斜率存在,且斜率为负. 设l :y -4=k (x -1)(k <0). 令y =0,可得A ⎝ ⎛⎭⎪⎫1-4k ,0; 令x =0,可得B (0,4-k ). (1)|P A |·|PB |=⎝ ⎛⎭⎪⎫4k 2+16·1+k 2 =-4k (1+k 2)=-4⎝ ⎛⎭⎪⎫1k +k ≥8(注意k <0).∴当且仅当1k =k 且k <0即k =-1时,|P A |·|PB |取最小值.这时l 的方程为x +y -5=0.(2)|OA |+|OB |=⎝ ⎛⎭⎪⎫1-4k +(4-k )=5-⎝ ⎛⎭⎪⎫k +4k ≥9.∴当且仅当k =4k 且k <0,即k =-2时,|OA |+|OB |取最小值.这时l 的方程为2x +y -6=0.。
2015年高考数学第一轮复习课件:8.1直线与方程
一个关系
三个防范
直线的倾斜角 与斜率的关系:斜 率 k 是一个实数, 当 倾 斜 角 α≠90° 时,k=tan α.直线 都有斜倾角,但并 不是每条直线都存 在斜率,倾斜角为 90°的直线无斜率, 如(1)错.
一是根据斜率求倾斜角,要 注意倾斜角的范围,如(2);
轴_正__向_与直线 l_向__上_方向之间所成的角α叫做直线 l 的倾斜角;
②规定:当直线 l 与 x 轴平行或重合时,规定它的倾斜角为_0_; ③范围:直线的倾斜角α的取值范围是__[0_,_π_) ___. (2)直线的斜率 ①定义:当直线 l 的倾斜角α≠π2时,其倾斜角α的正切值 tan α 叫做这条斜线的斜率,斜率通常用小写字母 k 表示,即 k=__ta_n_α_; ②斜率公式:经过两点 P1(x1,y1),P2(x2,y2)(x1≠x2)的直线
第十七页,编辑于星期五:十一点 五十分。
经典题目再现
► (2012·湖北)过点 P(1,1)的直线,将圆形区域 【教你审题 】
{(x,y)|x2+y2≤4}分为两部分,使得这两部分的 弄 清 楚过 圆内 一点 截
面积之差最大,则该直线的方程为( ). 得的弦长最短、最长时
A.x+y-2=0 B.y-1=0
的斜率
k2=2,
由点斜式得直线 DE 的方程为 y-2=2(x-0),即 2x-y+2=0.
第十三页,编辑于星期五:十一点 五十分。
直线方程的综合应用
考 点
例 3 已知直线 l 过点 P(3,2),且与 x 轴、y 轴的正半 轴分别交于 A、B 两点,如右图所示,求△ABO 的 面积的最小值及此时直线 l 的方程.
∴l 若
a的≠方0,程则为设y=l 的23x方,程即为2xxa-+3ayy==10,.
直线的方程同步训练(有解析2015数学高考一轮)
直线的方程同步训练(有解析2015数学高考一轮)直线的方程同步训练(有解析2015数学高考一轮)A组基础演练1.过点(-1,2)且倾斜角为30°的直线方程为()A.3x-3y+6+3=0B.3x-3y-6+3=0C.3x+3y+6+3D.3x+3y-6+3=0答案:A2.过两点(-1,1)和(0,3)的直线在x轴上的截距为()A.-32B.32C.3D.-3解析:过两点(-1,1)和(0,3)的直线方程为y-13-1=x----,即y=2x+3,令y=0得x=-32,即为所求.答案:A3.(2014•北京丰台质检)直线x-2y+b=0与两坐标轴所围成的三角形的面积不大于1,那么b的取值范围是()A.-2,2]B.(-∞,-2]∪2,+∞)C.-2,0)∪(0,2]D.(-∞,+∞)解析:令x=0,得y=b2,令y=0,得x=-b,所以所求三角形面积为12b2|-b|=14b2,且b≠0,14b2≤1,所以b2≤4,所以b∈-2,0)∪(0,2].答案:C4.已知直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则a的值是()A.1B.-1C.-2或-1D.-2或1解析:由题意得a+2=a+2a,∴a=-2或a=1.答案:D5.若直线斜率的绝对值等于1,则直线的倾斜角为________.答案:45°或135°6.直线l与两直线y=1,x-y-7=0分别交于P、Q两点,线段PQ 中点是(1,-1),则l的斜率是________.解析:设P(m,1),则Q(2-m,-3),∴(2-m)+3-7=0,∴m=-2,∴P(-2,1),∴k=1+1-2-1=-23.答案:-237.已知A(3,0),B(0,4),直线AB上一动点P(x,y),则xy的最大值是________.解析:直线AB的方程为x3+y4=1,设P(x,y),则x=3-34y,∴xy=3y-34y2=34(-y2+4y)=34--+4≤3.即当P点坐标为32,2时,xy取最大值3.答案:38.已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:(1)过定点A(-3,4);(2)斜率为16.解:(1)设直线l的方程是y=k(x+3)+4,它在x轴,y轴上的截距分别是-4k-3,3k+4,由已知,得(3k+4)4k+3=±6,解得k1=-23或k2=-83.故直线l的方程为2x+3y-6=0或8x+3y+12=0.(2)设直线l在y轴上的截距为b,则直线l的方程是y=16x+b,它在x轴上的截距是-6b,由已知,得|-6b•b|=6,∴b=±1.∴直线l的方程为x-6y+6=0或x-6y-6=0.9.经过P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,求直线l的倾斜角α与斜率k的范围.解:法一:如图所示,kPA=-2---0=-1,kPB=1---0=1,由图可观察出:直线l倾斜角α的范围是135°,180°)∪0°,45°];直线l的斜率k的范围是-1,1].法二:设直线l的斜率为k,则直线l的方程为y+1=kx,即kx-y-1=0.∵A、B两点在直线的两侧或其中一点在直线l上.∴(k+2-1)(2k-1-1)≤0,即2(k+1)(k-1)≤0.∴-1≤k≤1.∴直线l的倾斜角α的范围是135°,180°)∪0°,45°];直线l的斜率k的范围是-1,1].B组能力突破1.(2014•山东济宁二模)直线l经过A(2,1),B(1,m2)(m∈R)两点,那么直线l的倾斜角α的取值范围是()A.0≤α<πB.0≤α≤π4或π2<α<πC.0≤α≤π4D.π4≤α<π2或π2<α<π解析:直线l的斜率为k=m2-11-2=1-m2≤1,又直线l的倾斜角为α,则有tanα≤1,即tanα<0或0≤tanα≤1,所以π2<α<π或0≤α≤π4,故选B.答案:B2.在同一平面直角坐标系中,直线l1:ax+y+b=0和直线l2:bx+y+a=0有可能是()解析:l1:y=-ax-b,l2:y=-bx-a.于是可知,l1的斜率是l2的纵截距,l1的纵截距是l2的斜率.在选项A中,l1的纵截距为正,而l2的斜率为负,不合题意,排除A.同样可排除选项C、D,故选B.答案:B3.经过点P(2,-1),且在y轴上的截距等于它在x轴上的截距的2倍的直线l的方程是________.解析:当截距不等于零时,设l的方程为xa+y2a=1,又点P在l上,∴2a-12a=1,则a=32,∴l的方程为2x+y=3.当截距等于零时,设l的方程为y=kx,又点P在l上,∴k=-12,∴x+2y=0.答案:2x+y=3或x+2y=04.已知直线l过点P(0,1),且与直线l1:x-3y+10=0和l2:2x+y-8=0分别交于点A,B(如图).若线段AB被点P平分,求直线l的方程.解:∵点B在直线l2:2x+y-8=0上,故可设点B的坐标为(a,8-2a).∵P(0,1)是线段AB的中点,得点A的坐标为(-a,2a-6).又∵点A在直线l1:x-3y+10=0上,故将A(-a,2a-6)代入直线l1的方程,得-a-3(3a-6)+10=0,解得a=4.∴点B的坐标是(4,0).因此,过P(0,1),B(4,0)的直线l的方程为x4+y1=1,即x+4y-4=0.。
2015届高三数学(文)湘教版一轮复习配套课件:第8章 第1节 直线的倾斜角与斜率、直线的方程
数学
首页
上一页
下一页
末页
第八页,编辑于星期五:九点 四十三分。
结束
第一节 直线的倾斜角与斜率、直线的方程
(2)待定系数法,具体步骤为: ①设所求直线方程的某种形式; ②由条件建立所求参数的方程(组); ③解这个方程(组)求出参数; ④把参数的值代入所设直线方程.
数学
首页
上一页
下一页
末页
第九页,编辑于星期五:九点 四十三分。
数学
首页
上一页
下一页
末页
第十页,编辑于星期五:九点 四十三分。
结束
第一节 直线的倾斜角与斜率、直线的方程
2.过点(5,10)且到原点的距离是5的直线的方程为________. 解析:当斜率不存在时,所求直线方程为x-5=0; 当斜率存在时,设其为k,则所求直线方程为y-10=k(x-5), 即kx-y+(10-5k)=0. 由点到直线的距离公式,得|10k-2+5k1|=5, 解得k=34.故所求直线方程为3x-4y+25=0. 综上知,所求直线方程为x-5=0或3x-4y+25=0. 答案:x-5=0或3x-4y+25=0
数学
首页
上一页
下一页
末页
第七页,编辑于星期五:九点 四十三分。
结束
第一节 直线的倾斜角与斜率、直线的方程
1.求斜率可用 k=tan α(α≠90°),其中 α 为倾斜角,由此 可见倾斜角与斜率相互联系不可分割,牢记:“斜率变化分两 段,90°是分界线,遇到斜率要谨记,存在与否需讨论”.
2.求直线方程的一般方法 (1)直接法:根据已知条件,选择适当的直线方程形式, 直接写出直线方程,选择时,应注意各种形式的方程的适用范 围,必要时要分类讨论.
高三数学一轮复习 第8篇 第1节 直线与方程课时训练 理
第八篇平面解析几何(必修2、选修21)第1节直线与方程课时训练理【选题明细表】知识点、方法题号直线的倾斜角与斜率1、4、7直线方程3、5、9、11、12两条直线的位置关系2、8、10、16 点到直线的距离、两条平行线之间的距离6、14直线方程的综合应用9、13、15、16一、选择题1.(2014北京朝阳模拟)直线x+错误!未找到引用源。
y+1=0的倾斜角是( D )(A)错误!未找到引用源。
(B)错误!未找到引用源。
(C)错误!未找到引用源。
(D)错误!未找到引用源。
解析:由直线的方程得直线的斜率为k=-错误!未找到引用源。
,设倾斜角为α,则tan α=-错误!未找到引用源。
,又α∈[0,π),所以α=错误!未找到引用源。
.2.直线3ax-y-1=0与直线(a-错误!未找到引用源。
)x+y+1=0垂直,则a的值是( D )(A)-1或错误!未找到引用源。
(B)1或错误!未找到引用源。
(C)-1或-错误!未找到引用源。
(D)1或-错误!未找到引用源。
解析:由题意得,3a(a-错误!未找到引用源。
)-1=0,解得a=1或a=-错误!未找到引用源。
.3.(2014深圳模拟)已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是( B )(A)4x+2y-5=0(B)4x-2y-5=0(C)x+2y-5=0(D)x-2y-5=0解析:线段AB的中点为(2,错误!未找到引用源。
),又因为线段AB的斜率为错误!未找到引用源。
=-错误!未找到引用源。
,所以线段AB的垂直平分线的斜率为k=2,所以线段AB的垂直平分线的方程是y-错误!未找到引用源。
=2(x-2),即4x-2y-5=0.4.(2014山东省泰安模拟)直线x+(a2+1)y+1=0的倾斜角的取值范围是( B )(A)错误!未找到引用源。
(B)[错误!未找到引用源。
,π)(C)错误!未找到引用源。
∪(错误!未找到引用源。
,π) (D)错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必考部分
第八篇平面解析几何(必修2、选修11)
第1节直线与方程
课时训练练题感提知能
【选题明细表】
A组
一、选择题
1.已知两点A(-3,),B(,-1),则直线AB的斜率是( D )
(A) (B)-(C)(D)-
解析:斜率k==-,故选D.
2.已知直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则a的值是( D )
(A)1 (B)-1
(C)-2或-1 (D)-2或1
解析:①当a=0时,y=2不合题意.
②a≠0,
x=0时,y=2+a.
y=0时,x=,
则=a+2,得a=1或a=-2.故选D.
3.两直线3x+y-3=0与6x+my+1=0平行,则它们之间的距离为( D )
(A)4 (B)(C)(D)
解析:把3x+y-3=0转化为6x+2y-6=0,
由两直线平行知m=2,
则d==.
故选D.
4.(2013惠州二调)已知点A(1,-2),B(5,6)到直线l:ax+y+1=0的距离相等,则实数a的值等于( C )
(A)-2或1 (B)2或1
(C)-2或-1 (D)2或-1
解析:法一由=得a2+3a+2=0,
∴a=-1或-2,故选C.
法二由题意知AB∥l或AB的中点在直线l上.
若AB∥l,则k AB==2=-a,
∴a=-2.
若直线l经过AB的中点(3,2),则3a+2+1=0,
∴a=-1,故选C.
5.(2014皖南八校联考)直线2x-y+1=0关于直线x=1对称的直线方程是( C )
(A)x+2y-1=0 (B)2x+y-1=0
(C)2x+y-5=0 (D)x+2y-5=0
解析:由题意可知,直线2x-y+1=0与直线x=1的交点为(1,3),直线
2x-y+1=0的倾斜角与所求直线的倾斜角互补,因此它们的斜率互为相反数,直线2x-y+1=0的斜率为2,故所求直线的斜率为-2,所以所求直线的方程是y-3=-2(x-1),即2x+y-5=0.故选C.
6.(2013泰安一模)过点A(2,3)且垂直于直线2x+y-5=0的直线方程为( A )
(A)x-2y+4=0 (B)2x+y-7=0
(C)x-2y+3=0 (D)x-2y+5=0
解析:直线2x+y-5=0的斜率为k=-2,
∴所求直线的斜率为k'=,
∴方程为y-3=(x-2),即x-2y+4=0.
二、填空题
7.(2013湘潭质检)若过点A(-2,m),B(m,4)的直线与直线2x+y+2=0平行,则m的值为.
解析:∵过点A,B的直线平行于直线2x+y+2=0,
∴k AB==-2,解得m=-8.
答案:-8
8.若过点P(1-a,1+a)与Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是.
解析:由直线PQ的倾斜角为钝角,可知其斜率k<0,
即<0,化简得<0,∴-2<a<1.
答案:(-2,1)
9.已知k∈R,则直线kx+(1-k)y+3=0经过的定点坐标是. 解析:令k=0,得y+3=0,令k=1,得x+3=0.
解方程组得
所以定点坐标为(-3,-3).
答案:(-3,-3)
10.(2013成都模拟)分别过点A(1,3)和点B(2,4)的直线l1和l2互相平行且有最大距离,则l1的方程是.
解析:由题意,l1,l2需与直线AB垂直才能符合题意,
而k AB==1,
∴=-1,
∴直线l1的方程为y-3=-(x-1),即x+y-4=0.
答案:x+y-4=0
三、解答题
11.(2013哈尔滨模拟)经过点(-2,2),且与两坐标轴所围成的三角形面积为1.求直线l的方程.
解:法一由题知直线在两坐标轴上的截距不为0,
设直线方程为+=1,
由题意有
解得或
∴直线方程为+y=1或+=1,
即x+2y-2=0或2x+y+2=0.
法二由题知直线l斜率存在且不为0,
设直线l:y-2=k(x+2).
当x=0时,y=2k+2,当y=0时,x=--2.
则|(2k+2)(--2)|=1,
解得k=-或k=-2.
即直线l方程为2x+y+2=0或x+2y-2=0.
12.已知两直线l1:x+ysin α-1=0和l2:2xsin α+y+1=0,试求α的值,使(1)l1∥l2;(2)l1⊥l2.
解:(1)法一当sin α=0时,直线l1的斜率不存在,
l2的斜率为0,显然l1不平行于l2.
当sin α≠0时,=-,=-2sin α.
要使l1∥l2,需-=-2sin α,
即sin α=±,∴α=kπ±,k∈Z.
故当α=kπ±,k∈Z时,l 1∥l2.
法二由l1∥l2,得∴sin α=±,
∴α=kπ±,k∈Z.
故当α=kπ±,k∈Z时,l 1∥l2.
(2)∵l1⊥l2,∴2sin α+sin α=0,即sin α=0.
∴α=kπ,k∈Z.
故当α=kπ,k∈Z时, l1⊥l2.
13.设直线l1:y=k1x+1,l2:y=k2x-1,其中实数k1,k2满足k1k2+2=0.
(1)证明l1与l2相交;
(2)证明l1与l2的交点在椭圆2x2+y2=1上.
证明:(1)假设l1与l2不相交,则l1∥l2即k1=k2,代入k1k2+2=0,得
+2=0,这与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交.
(2)法一由方程组解得交点P的坐标为(,),
而2x2+y2=2()2+()2
=
=
=1.
即P(x,y)在椭圆2x2+y2=1上.
即l1与l2的交点在椭圆2x2+y2=1上.
法二交点P的坐标(x,y)满足故知x≠0.
从而
代入k1k2+2=0,得·+2=0,
整理后,
得2x2+y2=1.
所以交点P在椭圆2x2+y2=1上.
B组
14.若直线l:y=kx-与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( B )
(A)[,) (B)(,)
(C)(,) (D)[,]
解析:由题意,可作直线2x+3y-6=0的图象,如图所示,则直线与x轴、
y轴交点分别为A(3,0),B(0,2),又直线l过定点
(0,-),由题知直线l与线段AB相交(交点不含
端点),从图中可以看出,直线l的倾斜角的取值范围为(,).故选B.
15.如图所示,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线
AB反射后再射到直线OB上,最后经直线OB反射后又
回到P点,则光线所经过的路程是( A )
(A)2(B)6 (C)3(D)2
解析:由题意知点P关于直线AB的对称点为D(4,2),关于y轴的对称点为C(-2,0),
则光线所经过的路程为|CD|=2.故选A.
16.过点(2,1)且在x轴上截距与在y轴上截距之和为6的直线方程为.
解析:由题意知截距均不为零.
设直线方程为+=1,
由解得或
故所求直线方程为x+y-3=0或x+2y-4=0.
答案:x+y-3=0或x+2y-4=0。
