山东省烟台市2016-2017学年高二(上)期末数学试卷(理科)(解析版)
【全国百强校】2016-2017学年山东省胶州市普通高中高二上学期期末考试数学(理)试卷(带解析)
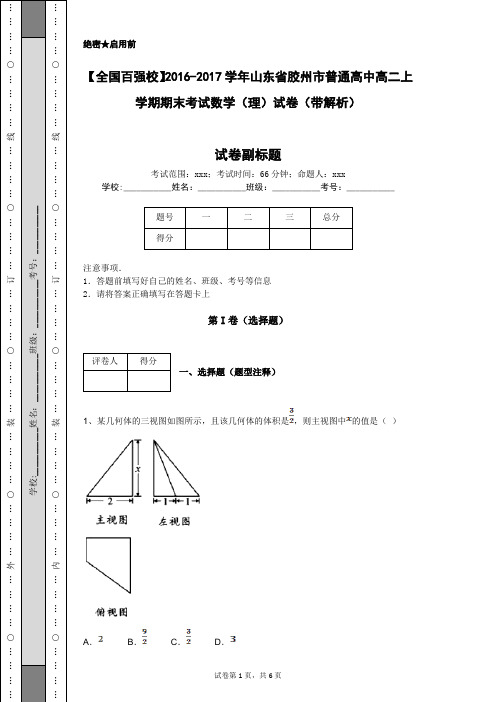
绝密★启用前【全国百强校】2016-2017学年山东省胶州市普通高中高二上学期期末考试数学(理)试卷(带解析)试卷副标题考试范围:xxx ;考试时间:66分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、某几何体的三视图如图所示,且该几何体的体积是,则主视图中的值是( )A .B .C .D .2、已知,分别是双曲线:的左,右焦点,若向关于渐近线的对称点恰好落在以为圆心,为半径的圆上,则双曲线的离心率为( )A .B .3C .D .23、在空间中,给出下面四个命题,则其中正确命题的个数为( ) ①过平面外的两点,有且只有一个平面与平面垂直; ②若平面内有不共线三点到平面的距离都相等,则∥; ③若直线与平面内的无数条直线垂直,则;④两条异面直线在同一平面内的射影一定是两平行线; A .3 B .2 C .1 D .04、那个数学归纳法证明不等式""时,由不等式成立,推证时,左边应增加的项数时( )A .B .C .D .5、设,则“”是“”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .即非充分也非必要条件6、已知平,,,面,直线,,,则下列命题正确的是( ) A .若,,则∥; B .若,,则∥;C .若,,则∥ ; D .若∥,∥,则∥7、已知实数,满足,则的最大值为( )A .5B .6C .7D .8周长为8,则椭圆方程为()A. B. C. D.9、抛物线的焦点坐标是( )A. B. C. D.10、设命题,,则为( )A. B.C. D.11、圆与圆的位置关系是( )A.相离 B.相切 C.相交 D.内含12、复数( )A. B. C.1 D.第II 卷(非选择题)二、填空题(题型注释)13、如图,在四棱锥中,分别是的中点,动点的线段上运动时,下列四个结论:①; ②∥; ③∥平面; ④平面恒成立的是__________.(把正确的序号都填上)14、已知为抛物线上的点,若点到直线:的距离最小,则点的坐标为_________15、方程表示椭圆,则的取值范围是__________.16、过点且和直线垂直的直线方程是__________.三、解答题(题型注释)17、如图,在斜三棱柱中,侧面与侧面都是棱形,.求证:(Ⅰ);(Ⅱ)若,求二面角的余弦值.18、如图,在四棱锥中,底面为平行四边形,为侧棱的中点.(Ⅰ)求证:∥平面(Ⅱ)若,,求证:平面平面19、已知中心在坐标原点的椭圆经过,且点的其右点焦点.(Ⅰ)求椭圆的方程. (Ⅱ)是否存在平行于的直线,使得直线与椭圆有公共点,且直线与的距离等于4 ?若存在,求出直线的方程;若不存在,说明理由.20、已知圆的方程:,(Ⅰ)求的取值范围; (Ⅱ)当圆与圆:相外切时,求直线:被圆,所截得的弦的长.21、(本小题满分16分)已知椭圆的左、右焦点分别为、,短轴两个端点为、,且四边形是边长为2的正方形.(1)求椭圆的方程;(2)若、分别是椭圆长轴的左、右端点,动点满足,连接,交椭圆于点.证明:为定值.(3)在(2)的条件下,试问轴上是否存异于点的定点,使得以为直径的圆恒过直线、的交点,若存在,求出点的坐标;若不存在,请说明理由.22、已知椭圆,过点作直线交椭圆于两点, 是坐标原点;(Ⅰ)求中点的轨迹方程;(Ⅱ)求的面积的最大值,并求此时直线的方程.参考答案1、C2、D3、D4、C5、A6、B7、C8、A9、C10、B11、B12、A13、①③14、15、且;16、17、(1)证明详见解析;(2).18、(1)(2)均见解析.19、(Ⅰ);(Ⅱ)直线不存在.20、(Ⅰ);(Ⅱ).21、,定值为4,存在Q(0,0)满足条件22、(Ⅰ);(Ⅱ)此时,.【解析】1、由三视图可知该几何体为四棱锥,体积为.2、试题分析:如图,又分别为的中点,,故选D.考点:双曲线的性质.3、对于①,过平面外的两点,有可能有无数个平面与平面垂直,故错误;对于②,若平面内有不共线三点到平面的距离都相等,可能,故错误;对于③,若直线与平面内的无数条直线垂直,不能得出,故错误;对于④,两条异面直线在同一平面内的射影一定是两条相交直线,故错误.综上正确命题的个数为 ,故选D.考点:点线面的位置关系4、解:因为用数学归纳法证明:“”时,由不等式成立,等式左边有,因此推证时,左边应,因此应该增加的项数是,选C5、若,则有;充分性成立;若,则或,必要性不成立,故则“”是“”的充分不必要条件,故选A.点睛:充分不必要条件、必要不充分条件、既不充分也不必要条件的判断的一般方法:①充分不必要条件:如果,且,则说是的充分不必要条件;②必要不充分条件:如果,且,则说是的必要不充分条件;③既不充分也不必要条件:如果,且,则说是的既不充分也不必要条件.6、A. 若,则∥或相交,因此不正确;B. 由利用线面垂直的性质定理可得:,正确;C. 若则、相交或异面直线,因此不正确;D. 若则、相交或异面直线,因此不正确。
2016-2017学年山东省菏泽市高二上学期期末考试数学(理)试卷-Word版含答案

2016—2017学年度上学期期末检测高二数学理科试题第Ⅰ卷 选择题(共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)2. 已知向量a=(2,3,5),向量b=(3,x,y),若a ∥b 则( )A.215,29==y x B.15,29==y x C.15,9==y x D.15,9-=-=y x 3. 已知各项不为的等差数列,满足2a 2-a 62+2a 10=0,数列是等比数列,且a 6=b 6,则b 5b 7=( )A. 2B.C.D.4. 已知命题p: “1,b ,4”成等比数列”,命题q :“b=2”,那么p 成立是q 成立的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件5. 已知ABC ∆的顶点,B C 在椭圆191622=+y x 上,顶点A 是椭圆的一个焦点,且椭圆的另一个焦点在BC 上,则ABC ∆的周长是( )A.8B.83C.16D.246. 中心在原点,焦点在x 轴上的双曲线的一条渐近线经过点(2,-1),则此双曲线的离心率为( ) A. 6 B. 5 C.62 D.527. 双曲线2288kx ky -=的一个焦点(0,3),那么k 的值是( ) A.1 B.1- C.1或8. 下列四个命题中,其中是真命题是( )A.“若xy =1,则lg x +lg y =0”的逆命题;B.设,x y R ∈,命题“若022=+y x 则0=xy ”的否命题 C.若p∧q 为假命题,则p 、q 均为假命题D.“若b ≤1,则方程x 2-2bx +b 2+b =0有实根”的逆否命题;9. 某人向正西方向走x 千米后,他向左转150°,然后朝新方向走3千米,结果他离出发点恰好为3千米,则x 的值是( )A .3B . 3C .3或2 3D . 23或310. 已知a >b >0,e 1与e 2分别为圆锥曲线x 2a 2+y 2b 2=1和x 2a 2-y 2b2=1的离心率,则lg e 1+lg e 2的值( )00000000001.,20.,20.,20.,20.,20x x x x x x R A x R B x R C x R D x R ∃∈<∈>∃∈≥∀∈>∀∈≥命题“”的否定是()不存在A .一定是正值B .一定是零C .一定是负值D .符号不确定11. 设x ,y 满足约束条件23-1+1x x y y x ≥⎧⎪≥⎨⎪≥⎩,若目标函数=+(>0,>0)z ax by a b 的最小值为2,则4a 2+9b 2的最小值为( )A .2B .4C .6D .812. 已知椭圆C:)0(12222>>=+b a by a x 的左、右焦点分别为F 1,F 2,若椭圆C 上恰有6个不同的点使得P F F 21∆为等腰三角形,则椭圆的离心率e 的取值范围是( )A.)32,31(B.)1,21(C.)1,32(D.)21,31( )1,21( 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分)13. 点M (5,3)到抛物线x 2=ay (a >0)的准线的距离为6,那么抛物线的方程是______.14. 在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯”。
2016-2017学年山东省烟台市高二(下)期中数学试卷(理科)解析

2016-2017学年山东省烟台市高二(下)期中数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 因为i是虚数单位,复数20171ii z =+则z 的共轭复数是A.1+22iB.122i -C.122i -+D.122i --【答案】B 【解析】()50420174iii i =⋅=,复数()()()2017111111122i i i i z i i i i i -====++++-,则z 的共轭复数122i z =-2.用数学归纳法证明()221*11...1,1n n a a aaa n N a++-++++=≠∈-在验证1n =成立时,左边的项是 A.1 B. 1a + C. 21a a ++ D. 241a a a +++【答案】C【解析】用数学归纳法证明()221*11...1,1n n a a a a a n N a++-++++=≠∈-,把1n =代入,左端为21a a ++3.下列推理过程属于演绎推理的为A.老鼠、猴子与人在身体结构上有相似之处,某医药先在猴子身上试验,试验成功后再用于人体试验B.由22211,132,1353,...=+=++=得出()2135...21n n ++++-=C.由三角形的三条中线交于一点联想到四面体四条中线(四面体每一个顶点与对面重心的连线)交于一点D.通项公式形如()0n n a cq cq =≠的数列{}n a 为等比数列,则数列{}2n -为等比数列 【答案】D【解析】∵老鼠、猴子与人在身体结构上有相似之处, 故A 中推理为类比推理;∵由22211,132,1353,...=+=++=得出()2135...21n n ++++-= 是由特殊到一般故B 中推理为归纳推理;∵由三角形性质得到四面体的性质有相似之处, 故C 中推理为类比推理;∵由通项公式形如()0n n a cq cq =≠的数列{}n a 为等比数列(大前提),数列{}2n -满足这种形式(小前提),则数列{}2n -为等比数列(结论) 可得D 中推理为演绎推理. 4.极坐标方程2cos210ρθ+=表示的曲线A.圆B.椭圆C.双曲线D.抛物线【答案】C【解析】由2cos210ρθ+=, 可得: ()222cos 11ρθ-=-, 得:2222cos 1ρθρ=-22221x x y =+-,即221y x -=,∴极坐标方程2cos210ρθ+=表示的曲线是等轴双曲线. 5.已知()()2'21f x x x f =+⋅,则()'0f 等于A.2-B. 2C.1D.4-【答案】D【解析】因为()()2'21f x x x f =+⋅, 令1x =,可得()()''1221f f =+,∴()'12f =-,∴()()''22124f x x f x =+=-, 6. 直线00cos sin x x t y y t αα=+⎧⎨=+⎩(t 为参数,α是直线的倾斜角)上有两点12,P P ,它们所对应的参数值分别是12,t t ,则12PP 等于A. 12t t +B. 12t t +C.12t t +D.12t t -【答案】D【解析】设()00,P x y ,则知直线经过定点()00,P x y ,直线的倾斜角为θ.不妨规定直线12P P 等于向上的方向为正方向,参数1t 的几何意义为01P P 的数量,2t 的几何意义为02P P 的数量, ∴1212PP t t =-.7.已知函数()()22x f x x x e =-,给以下四个结论:①()0f x >的解集为{}02x x <<;②(f 是极小值,f 是极大值;③()f x 有极小值,但无最小值;④()f x )有极小值,也有最小值.其中正确的是A. ①②B. ①②③C.①②④D. ②④【答案】B【解析】由()0f x >可得()220x x x e -> ∵0x e >,∴220x x ->,∴02x <<,故①正确;()()'2x f x e x =-,由()'0f x =得x =由()'0f x <得x >x <()'0f x >得x∴()f x 的单调减区间为(),,-∞+∞;单调增区间为(.∴()f x 的极大值为f,极小值为(f ,故②正确.∵x <()0f x <恒成立.∴()f x 无最小值,但有极大值. ∴③正确,④错误.8.如图,在平面直角坐标系xoy 中,将直线2x y =与直线1x =及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥,圆锥的体积23110021212x V dx x πππ⎛⎫=== ⎪⎝⎭⎰,以此类比:将曲线()20y x x =≥与直线2y =及y 轴所围成A.πB. 2πC. 3πD.4π 【答案】B【解析】根据类比推理得体积22222120002V dy ydy y ππππ====⎰⎰,9.若函数()()2=f x x x c -在3x =处有极大值,则c =A. 9B. 3C.39或D.以上都不对【答案】A【解析】函数()()2=f x x x c -的导数为()()()()()2'=23f x x x c x x c x c x c -+-=--,由()f x 在3x =处有极大值,即有()'3=0f , 解得9c =或3,若9c =时,()'=0f x ,解得9x =或3x =, 由()f x 在3x =处导数左正右负,取得极大值, 若3c =,()'=0f x ,可得3x =或1由()f x 在3x =处导数左负右正,取得极小值. 综上可得9c =.10.若函数()()()2ln f x x x b b R =+-∈在区间1,22⎡⎤⎢⎥⎣⎦上存在单调递增区间,则实数b 的取值范围是A.3,2⎛⎫-∞ ⎪⎝⎭ B.9,4⎛⎫-∞ ⎪⎝⎭ C.39,24⎛⎫- ⎪⎝⎭D.3,2⎛⎫+∞ ⎪⎝⎭【答案】D【解析】∵函数()f x 在区间1,22⎡⎤⎢⎥⎣⎦上存在单调增区间,∴函数()f x 在区间1,22⎡⎤⎢⎥⎣⎦上存在子区间使得不等式()'0f x >成立.()()2'1122122x bx f x x b x x -+⎡⎤=+-=⎢⎥⎣⎦, 设()2221h x x bx =-+,则()20h >或102h ⎛⎫> ⎪⎝⎭,即8410b -+>或1102b -+>,得94b <。
数学---山东省济南一中2016-2017学年高二(上)期末试卷(理)(解析版)

2016-2017学年山东省济南一中高二(上)期末数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.)1.(5分)在锐角△ABC中,角A,B,C所对的边分别为a,b,c.若a=2b,sin B=,则()A.A=B.A=C.sin A=D.sin A=2.(5分)如果a>b,给出下列不等式:(1)<;(2)a3>b3;(3)a2+1>b2+1;(4)2a>2b.其中成立的不等式有()A.(3)(4)B.(2)(3)C.(2)(4)D.(1)(3)3.(5分)已知数列{a n}中,若a1=,a n=(n≥2,n∈N+),则a2017等于()A.1 B.﹣1 C.D.24.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为()A.2+2 B.C.2﹣2 D.﹣15.(5分)“4<k<6”是“方程表示椭圆”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件6.(5分)设各项均为实数的等比数列{a n}的前n项和为S n,若S10=10,S30=70,则S40等于()A.150 B.﹣200C.150或﹣200 D.400或﹣507.(5分)△ABC中,,则△ABC形状是()A.正三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形8.(5分)已知双曲线﹣=1 (a>0,b>0)的一条渐近线过点(2,),且双曲线的一个焦点在抛物线y2=4x的准线上,则双曲线的方程为()A.﹣=1 B.﹣=1C.﹣=1 D.﹣=19.(5分)变量x,y满足约束条件,若z=2x﹣y的最大值为2,则实数m等于()A.﹣2 B.﹣1 C.1 D.210.(5分)已知,则的最小值是()A.B.C.D.11.(5分)设a>0,b>1,若a+b=2,且不等式+>m2+8m恒成立,则m的取值范围是()A.m>9或m<﹣1 B.m>1或m<﹣9C.﹣9<m<1 D.﹣1<m<912.(5分)已知a>0,则x0满足关于x的方程ax=b的充要条件是()A.B.C.D.二、填空题(本大题共6小题,每小题5分,共30分)13.(5分)命题“∀x∈R,x2+2x+2>0”的否定为.14.(5分)在△ABC中,若sin A+sin B=sin C(cos A+cos B),此三角形的形状是三角形.15.(5分)函数(0<x<1)的最大值为.16.(5分)在数列{a n}中,a1=1,a2=2,且a n+2﹣a n=1+(﹣1)n(n∈N*),则S100=.17.(5分)已知如图,P A、PB、PC互相垂直,且长度相等,E为AB中点,则直线CE与平面P AC所成角的正弦值为.18.(5分)已知O为坐标原点,F是椭圆C:=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为.三、解答题(本大题共5小题,共60分,解答应写出文字说明,证明过程或推演步骤)19.(10分)解关于x的不等式:x2﹣(a2+a)x+a3≥0.20.(12分)在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2a sin B=b.(Ⅰ)求角A的大小;(Ⅱ)若a=6,b+c=8,求△ABC的面积.21.(12分)设递增等比数列{a n}的前n项和为S n,且a2=3,S3=13,数列{b n}满足b1=a1,点P(b n,b n+1)在直线x﹣y+2=0上,n∈N*.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)设c n=,数列{c n}的前n项和T n,若T n>2a﹣1恒成立(n∈N*),求实数a的取值范围.22.(12分)如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(Ⅰ)证明:EF∥B1C;(Ⅱ)求二面角E﹣A1D﹣B1的余弦值.23.(14分)已知椭圆+=1(a>b>0)上的一动点P到左、右两焦点F1,F2的距离之和为2,点P到椭圆一个焦点的最远距离为+1.(Ⅰ)求椭圆的方程;(Ⅱ)过右焦点F2的直线l交椭圆于A,B两点.①若y轴上存在一点M(0,)满足|MA|=|MB|,求直线l斜率k的值;②是否存在这样的直线l,使S△ABO的最大值为(其中O为坐标原点)?若存在,求直线l方程;若不存在,说明理由.参考答案一、选择题1.A【解析】把a=2b,利用正弦定理化简得:sin A=2sin B,将sin B=代入得:sin A=,∵A为锐角,∴A=.故选:A.2.C【解析】(1)取a=2,b=﹣1,满足a>b,但是<不成立;(2)利用函数f(x)=x3在R上单调递增可得:a3>b3;(3)取a=1,b=﹣2,满足a>b,但是a2+1>b2+1不成立;(4)利用指数函数f(x)=2x在R上单调递增可得:2a>2b.其中成立的不等式有(2)(4).故选:C.3.C【解析】∵a1=,a n=(n≥2,n∈N+),∴a2==2,同理可得:a3=﹣1,a4=,…,则a n+3=a n,则a2017=a3×605+1=a1=,故选:C.4.B【解析】∵b=2,B=,C=,∴由正弦定理=得:c===2,A=,∴sin A=sin(+)=cos=,则S△ABC=bc sin A=×2×2×=+1.故选B5.C【解析】若方程表示椭圆则6﹣k>0,且k﹣4>0,且6﹣k≠k﹣4解得4<k<5或5<k<6故“4<k<6”是“方程表示椭圆”的必要不充分条件故选C6.A【解析】根据等比数列的前n项和的公式化简S10=10,S30=70得:S10==10,S30==70,则===7,得到1+q10+q20=7,即(q10)2+q10﹣6=0,解得q10=﹣3(舍去),q10=2,则====15,所以S40=15S10=150.故选A7.B【解析】∵cos2=,∴=,∴cos A=,又根据余弦定理得:cos A=,∴=,∴b2+c2﹣a2=2b2,即a2+b2=c2,∴△ABC为直角三角形.故选B8.D【解析】由题意,=,∵抛物线y2=4x的准线方程为x=﹣,双曲线的一个焦点在抛物线y2=4x的准线上,∴c=,∴a2+b2=c2=7,∴a=2,b=,∴双曲线的方程为.故选:D.9.C【解析】由约束条件作出可行域如图,联立,解得A(),化目标函数z=2x﹣y为y=2x﹣z,由图可知,当直线过A时,直线在y轴上的截距最小,z有最大值为,解得:m=1.故选:C.10.C【解析】=(1﹣t﹣2,1﹣t﹣t,t﹣t)=(﹣t﹣1,1﹣2t,0)==(﹣t﹣1)2+(1﹣2t)2=5t2﹣2t+2∴当t=时,有最小值∴的最小值是故选项为C11.C【解析】∵a+b=2,∴a+b﹣1=1,∴(+)(a+b﹣1)=4+4•++1≥5+2•2=9(当且仅当4•=时取“=”),∴+的最小值为9,则由不等式+>m2+8m恒成立,得:m2+8m<9,即(m+9)(m﹣1)<0,解得:﹣9<m<1.故选:C.12.C【解析】由于a>0,令函数,此时函数对应的开口向上,当x=时,取得最小值,而x0满足关于x的方程ax=b,那么x0═,y min=,那么对于任意的x∈R,都有≥=故选C.二、填空题13.∃x∈R,x2+2x+2≤0【解析】因为全称命题的否定是特称命题,所以,命题“∀x∈R,x2+2x+2>0”的否定为:命题“∃x∈R,x2+2x+2≤0”.故答案为:∃x∈R,x2+2x+2≤0.14.直角【解析】根据正弦定理,原式可变形为:c(cos A+cos B)=a+b…①∵a=b•cos C+c•cos B,b=c•cos A+a•cos C,∴a+b=c(cos A+cos B)+cos C(a+b)…②由于a+b≠0,故由①式、②式得:cos C=0,∴在△ABC中,∠C=90°.故答案为:直角.15.﹣1【解析】由0<x<1,得到lg x<0,∴≤=﹣1,当且仅当lg x=,x=时取等号,则函数(0<x<1)的最大值为﹣1,故答案为:﹣1.16.2600【解析】奇数项:a2k+1=1+(﹣1)2k﹣1+a2k﹣1=a2k﹣1,偶数项:a2k+2=1+(﹣1)2k+a2k=2+a2k所以奇数项相等,偶数项为等差数列,公差为2a100=a2+49×2=100S100=50×a1+50×(a1+a100)×=50+50(2+100)×=2600.故答案为:2600.17.【解析】P A、PB、PC互相垂直,以P为坐标原点,P A、PB、PC分别为x,y,z轴,设P A=2,则平面P AC的法向量可以为=(2,0,0),E(1,0,1),C(0,2,0),=(1,﹣2,1),直线CE与平面P AC所成角的正弦值为:==.故答案为:.18.【解析】由题意可设F(﹣c,0),A(﹣a,0),B(a,0),令x=﹣c,代入椭圆方程可得y=±,可得P(﹣c,±).设直线AE的方程为y=k(x+a),令x=﹣c,可得M(﹣c,k(a﹣c)),令x=0,可得E(0,ka),设OE的中点为H,可得H(0,),由B,H,M三点共线,可得k BH=k BM,即=,即为a=3c,可得e==,故答案为:.三、解答题19.解:不等式x2﹣(a2+a)x+a3≥0化为(x﹣a)(x﹣a2)≥0,①当a>1或a<0时,a2﹣a>0即a2>a,则不等式的解集为(﹣∞,a]∪[a2,+∞);②当a=1或a=0时,a2﹣a=0即a2=a,则不等式的解集为R;③当0<a<1时,a2﹣a<0即a2<a,则不等式的解集为(﹣∞,a2]∪[a,+∞),综上所述,a>1或a<0时,不等式的解集为(﹣∞,a]∪[a2,+∞);a=1或a=0时,不等式的解集为R;0<a<1时,不等式的解集为(﹣∞,a2]∪[a,+∞).20.解:(Ⅰ)由2a sin B=b,利用正弦定理得:2sin A sin B=sin B,∵sin B≠0,∴sin A=,又A为锐角,则A=;(Ⅱ)由余弦定理得:a2=b2+c2﹣2bc•cos A,即36=b2+c2﹣bc=(b+c)2﹣3bc=64﹣3bc,∴bc=,又sin A=,则S△ABC=bc sin A=.21.解:(Ⅰ)∵递增等比数列{a n}的前n项和为S n,且a2=3,S3=13,∴,解得q=3或q=,∵数列{a n}为递增等比数列,所以q=3,a1=1.∴{a n}是首项为1,公比为3的等比数列.∴.∵点P(b n,b n+1)在直线x﹣y+2=0上,∴b n+1﹣b n=2.∴数列{b n}是首项为1,公差为2的等差数列.∴b n=1+(n﹣1)•2=2n﹣1.(Ⅱ)∵,∴.,两式相减得:﹣=1+2×﹣=2﹣()n﹣1﹣.所以=.∵,∴T n≥T1=1.若T n>2a﹣1恒成立,则1>2a﹣1,解得a<1.∴实数a的取值范围{a|a<1}.22.(Ⅰ)证明:∵B1C=A1D且A1B1=CD,∴四边形A1B1CD为平行四边形,∴B1C∥A1D,又∵B1C⊄平面A1EFD,∴B1C∥平面A1EFD,又∵平面A1EFD∩平面B1CD1=EF,∴EF∥B1C;(Ⅱ)解:以A为坐标原点,以AB、AD、AA1所在直线分别为x、y、z轴建立空间直角坐标系A﹣xyz如图,设边长为2,∵AD1⊥平面A1B1CD,∴=(0,2,2)为平面A1B1CD的一个法向量,设平面A1EFD的一个法向量为=(x,y,z),又∵=(0,2,﹣2),=(1,1,0),∴,,取y=1,得=(﹣1,1,1),∴cos<,>==,∴二面角E﹣A1D﹣B1的余弦值为.23.解:(I)由题意可得:2a=2,a+c=+1,及其a2=b2+c2,解得a=,c=1=b,∴椭圆的方程为:=1.(II)①设直线l的方程为:y=k(x﹣1),A(x1,y1),B(x2,y2).联立,化为:(1+2k2)x2﹣4k2x+2k2﹣2=0,∴x1+x2=,x1•x2=,y1+y2=k(x1+x2﹣2)=.∴线段AB的中点G.①k=0时满足条件.k≠0时,∵满足|MA|=|MB|,∴k MG•k=•k=﹣1,化为2k2﹣3k+1=0,解得k=1或.综上可得:满足条件的k的值为0,1,.②当x⊥x轴时,直线l的方程为x=1.代入椭圆方程解得y=,可得S△ABO=,此时直线l的方程为:x=1.当k=0时,△ABO不存在,舍去.当k≠0时,可得S△ABO=====•==<.∴S△ABO<,因此k≠0时,不存在符合条件的直线l.综上所述:当且仅当直线l的方程为x=1时,S△ABO的最大值为.。
【数学】山东省烟台市2016-2017学年高二上学期期末考试试题(文)

山东省烟台市2016-2017学年上学期高二期末自主练习文科数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列四个命题中,真命题的是()A .空间中两组对边分别相等的四边形为平行四边形B .所有梯形都有外接圆C .所有的质数的平方都不是偶数D .不存在一个奇数,它的立方是偶数2.若命题p :α是第一象限角;命题q :α是锐角,则p 是q 的() A .充分不必要条件 B .必要不充分条件 C.充要条件D .既不充分也不必要条件3.命题p :若y x >,则y x tan tan >;命题q :xy y x 222≥+.下列命题为假命题的是() A .q p ∨ B .q p ∧ C .p ⌝ D .q4.命题“x ∃∈0R ,01020<++x x ”的否定是() A .不存在x ∈0R ,01020≥++x xB .x ∃∈0R ,01020≥++x xC .x ∀∈R ,012<++x xD .x ∀∈R ,012≥++x x5.平面内有两定点B A ,及动点P ,设命题甲:“PA 与B P 是定值”,命题乙:“点P 的轨迹是以B A ,为焦点的椭圆”,那么命题甲是命题乙的() A .充分不必要条件 B .必要不充分条件 C.充要条件D .既不充分也不必要条件6.已知点P 是椭圆1422=+y x 上的一点,且以点P 及焦点21,F F 为顶点的三角形的面积等于3,则这样的点P 的个数为()A .1B .2 C.3 D .4 7.在极坐标系中,圆cos ()ρθρ=∈4R 的圆心到直线θπ=3的距离是() A .3B .32C.1D .28.与x 轴相切且和半圆)20(422≤≤=+y y x 内切的动圆圆心的轨迹方程是() A .)10)(1(42≤<--=y y x B .)10)(1(42≤<-=y y x C.)10)(1(42≤<+=y y xD .)10)(1(22≤<--=y y x9.已知椭圆)0(12222>>=+b a by a x ,F 是椭圆的右焦点,A 为左顶点,点P 在椭圆上,x PF ⊥轴,若AF PF 41=,则椭圆的离心率为() A .43 B .21C. 23 D .2210.已知抛物线的参数方程为⎩⎨⎧==ty t x 442,若斜率为1的直线经过抛物线的焦点,且与抛物线相交于B A ,两点,则线段AB 的长为()A .22B .24 C.8 D .411.设点B A ,的坐标分别为)0,4(),0,4(-,直线BP AP ,相交于点P ,且它们的斜率之积为实数m ,关于点P 的轨迹下列说法正确的是()A .当1-<m 时,轨迹为焦点在x 轴上的椭圆(除与x 轴的两个交点)B .当01<<-m 时,轨迹为焦点在y 轴上的椭圆(除与y 轴的两个交点) C. 当0>m 时,轨迹为焦点在x 轴上的双曲线(除与x 轴的两个交点) D .当10<<m 时,轨迹为焦点在y 轴上的双曲线(除与y 轴的两个交点)12.已知双曲线C 的方程为15422=-y x ,其左、右焦点分别是21,F F .若点M 坐标为)1,2(,过双曲线左焦点且斜率为125的直线与双曲线右支交于点P ,则=-∆∆21PMF PMF S S () A .1- B .1 C. 2 D .4二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若命题“,x x x a ∃∈-++<13R ”是真命题,则实数a 的取值范围是.14.已知命题p :方程1422=-+my m x 表示焦点在x 轴上的椭圆,命题q :1)3()1(22=-+-y m x m 表示双曲线.若q p ∨为真命题,则实数m 的取值范围是.15.如图,圆4)2(22=++y x 的圆心为点B ,)0,2(A ,P 是圆上任意一点,线段AP 的垂直平分线l 和直线BP 相交于点Q ,当点P 在圆上运动时,点Q 的轨迹方程为.16.下列三个命题:①“022=+b a ,则b a ,全为0”的逆否命题是“若b a ,全不为0”,则022≠+b a ”; ②“21=m ”是“直线013)2(=+++my x m 与直线03)2()2(=-++-y m x m 相互垂直”的充分不必要条件;③已知双曲线)0,0(12222>>=-b a by a x 的一条渐近线经过点)2,1(,则该双曲线的离心率的值为5.上述命题中真命题的序号为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知实数0>c ,设命题p :函数xc y )12(-=在R 上单调递减;命题q :不等式12>-+c x x 的解集为R ,如果q p ∨为真,q p ∧为假,求c 的取值范围.18. 已知命题p :02082≥++-x x ;命题q :041222≤-++m x x . (1)当m ∈R 时,解不等式041222≤-++m x x ;(2)当0>m 时,若p ⌝是q ⌝的必要不充分条件,求实数m 的取值范围.19. (1)求与双曲线14922=-y x 共渐近线,且过点)4,3(的双曲线的标准方程;(2)过椭圆)0(1:2222>>=+b a by a x M 右焦点的直线03=-+y x 交M 于B A ,两点,O 为坐标原点,P 为AB 的中点,且OP 的斜率为21,求椭圆M 的方程.20. 在直角坐标xOy 平面内,已知点)0,2(F ,直线2:-=x l ,P 为平面上的动点,过P 作直线l 的垂线,垂足为点Q ,且⋅=⋅. (1)求动点P 的轨迹C 的方程;(2)过点F 的直线交轨迹C 于B A ,两点,交直线l 于点M ,已知μλ==,,试判断μλ+是否为定值?若是,求出该定值;若不是,请说明理由.21. 已知点N M ,分别是椭圆)0(1:2222>>=+b a by a x C 的左右顶点,F 为其右焦点,MF与FN 的等比中项是3,椭圆的离心率为21. (1)求椭圆C 的方程;(2)设不过原点O 的直线l 与该轨迹交于B A ,两点,若直线OB AB OA ,,的斜率依次成等比数列,求OAB ∆面积的取值范围.22.已知曲线1C 的参数方程是θθθ(sin ,cos 2⎩⎨⎧==y x 为参数),曲线2C 的参数方程是t t y t x (433,3⎪⎩⎪⎨⎧+=+-=为参数).(1)将曲线1C ,2C 的参数方程化为普通方程;(2)求曲线1C 上的点到曲线2C 的距离的最大值和最小值.参考答案一、选择题1-5:D BB D B 6-10: B AAAC 11、12:CC 二、填空题13.42-<<a 14.14m << 15.2213y x -=16.②③三、解答题17.解:由函数(21)xy c =-在R 上单调递减可得,0211c <-<,解得112c <<. 设函数22,2()|2|2,x c x cf x x x c c x c -≥⎧=+-=⎨<⎩,可知()f x 的最小值为2c , 要使不等式|2|1x x c +->的解集为R ,只需121,2c c >>, 因为p 或q 为真,p 且q 为假,所以,p q 只能一真一假,当p 真q 假时,有11212c c ⎧<<⎪⎪⎨⎪≤⎪⎩,无解;当p 假q 真时,有10,1212c c c ⎧≤≤≥⎪⎪⎨⎪>⎪⎩,可得1c ≥,综上,c 的取值范围为1c ≥.18.解:(1)22+214(12)(12)0+-=+-++=x x m x m x m , 所以22+2140x x m +-=对应的两根为12,12-+--m m ,当0m >时,1212m m -+>--,不等式的解集为{|1212}x m x m --≤≤-+, 当0m =时,12121m m -+=--=-,不等式的解集为{|1}x x =-,当0m <时,1212m m -+<--,不等式的解集为{|1212}-+≤≤--x m x m ; (2)由28+200x x -+≥可得,(10)(2)0x x -+≤, 所以210x -≤≤,即:210p x -≤≤由(1)知,当0m >时,不等式的解集为{|1212}x m x m --≤≤-+, 所以:1212q m x m --≤≤-+,∵p ⌝是q ⌝的必要不充分条件,∴q 是p 的必要不充分条件.即12212100m m m --≤-⎧⎪-+≥⎨⎪>⎩,且等号不能同时取, 解得112m ≥.故实数m 的取值范围为112m ≥. 19.解:(1)设与22194x y -=共渐近线的双曲线的方程为2294x y λ-=,将点(3,4)代入双曲线中,可得91694λ-=,即3λ=-,代入2294x y λ-=可得,双曲线的方程为2211227y x -=.(2)设112200(,),(,),(,)A x y B x y P x y ,将,A B 坐标代入椭圆可得,2211222222221(1)1(2)⎧+=⎪⎪⎨⎪+=⎪⎩x y a b x y a b ,(1)(2)-可得,20212210x y y b x x a y -=-⋅-, 由直线AB 的斜率为1-可得,20201x b a y -⋅=-,而OP 的斜率为0012y x =,所以222a b =,直线0x y +=过椭圆的右焦点,可得c =由222a b c =+,得到226,3a b ==,所以椭圆的标准方程为22163x y +=.20.解:(1)设(,)P x y ,则(2,)Q y -,所以(2,0),(4,),(2,),(4,)QP x QF y FP x y FQ y =+=-=-=-uu u r uuu r uu r uu u r, 由QP QF FP FQ =uu u r uuu r uu r uu u r g g 可得,24(2)4(2)x x y +=--+,整理可得:28y x =.(2)由题意可知,直线AB 的斜率存在且不为0,可设直线方程为2x ty =+,()()1122,,,A x y B x y ,4(2,)M t--联立228x ty y x=+⎧⎨=⎩,消x 可得28160y ty --=,所以128y y t +=,1216y y =-.又1λ=,即1114(2,)(2,)x y x y t λ++=--,114y y tλ+=-, 得141ty λ=--,同理可得241ty μ=--, 所以12121241144822216λμ⎛⎫⎛⎫++=--+=--=--⋅ ⎪ ⎪-⎝⎭⎝⎭y y tt y y t y y t 0=. 21.解:(1)解: |MF |=a c +,|BN |=a c -|MF |与|FN |的等比中项. ∴()()3a c a c +-=, ∴b 2=a 2﹣c 2=3.又12c e a ==,解得2,1a c ==, ∴椭圆C 的方程为22143x y +=.(2)由题意可知,直线l 的斜率存在且不为0.故可设直线l :(0)y kx m m =+≠,1122(,),(,)A x y B x y ,联立直线和椭圆2234120x x m y y k ⎧+-==+⎨⎩,消去y 可得, 222(34)84120k x kmx m +++-=,由题意可知,2222644(43)(412)48(43)0∆=-+-=-+>km k m k m , 即2243k m +>,且21212228412,3434km m x x x x k k-+=-=++, 又直线,,OA AB OB 的斜率依次成等比数列,所以21212y y k x x ⋅=, 将12,y y 代入并整理得22(43)0m k -=, 因为0m ≠,k =±,206m <<,且23m ≠, 设d 为点O 到直线l的距离,则有d =12||||AB x x =-=所以1||2OAB S AB d ∆==<,所以三角形面积的取值范围为.22.解:(1)曲线的普通方程为2214x y +=,曲线2C 的普通方程为34120x y -+=;(2)设点(2cos ,sin )P θθ为曲线上任意一点,则点P 到直线34120x y -+=的距离d 为:|6cos 4sin 12|5d θθ-+==因为cos()[1,1]θϕ+∈-,所以d ∈, 即曲线上的点到曲线2C 的距离的最大值为122135+,最小值为122135-.。
2016_2017学年度高二第二学期期末考试理科数学试题与答案

试卷类型:A高二数学(理科)试题2017.7 注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共5页。
2.答题前,考生务必在答题卡上用直径0.5毫米的黑色字迹签字笔将自己的、号填写清楚,并粘好条形码。
请认真核准条形码上的号、和科目。
3.答第Ⅰ卷时,选出每题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在本试卷上无效。
4.答第Ⅱ卷时,请用直径0.5毫米的黑色字迹签字笔在答题卡上各题的答题区域作答。
答在本试卷上无效。
5.第(22)、(23)小题为选考题,请按题目要求从中任选一题作答,并用2B 铅笔在答题卡上把所选题目题号后的方框涂黑。
6.考试结束后,将本试卷和答题卡一并收回。
附:回归方程ˆˆˆybx a =+中斜率与截距的最小二乘估计公式分别为: ∑∑∑∑====--=---=ni ini ii ni ini iixn xy x n yx x x y yx x b1221121)())((ˆ,x b y aˆˆ-= 第Ⅰ卷一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合 题目要求的。
(1)已知复数iiz +-=122,其中i 是虚数单位,则z 的模等于 (A )2- (B) 3 (C) 4 (D) 2(2)用反证法证明某命题时,对结论:“自然数c b a ,,中恰有一个偶数”正确的反设为 (A) c b a ,,中至少有两个偶数 (B)c b a ,,中至少有两个偶数或都是奇数 (C) c b a ,,都是奇数 (D) c b a ,,都是偶数 (3)用数学归纳法证明:对任意正偶数n ,均有41212111 (41)31211+++=--++-+-n n n n ( )21...n++,在验证2=n 正确后,归纳假设应写成 (A )假设)(*N k k n ∈=时命题成立 (B )假设)(*N k k n ∈≥时命题成立 (C )假设)(2*N k k n ∈=时命题成立 (D )假设))(1(2*N k k n ∈+=时命题成立(4)从3男4女共7人中选出3人,且所选3人有男有女,则不同的选法种数有 (A )30种 (B) 32 种 (C) 34种 (D) 35种 (5)曲线xe y =在点()22e ,处的切线与坐标轴所围三角形的面积为(A)22e (B)2e (C) 22e (D) 492e(6)已知随机变量X 服从正态分布()2,3σN ,且)3(41)1(>=<X P X P ,则)5(<X P 等于(A)81 (B) 85 (C) 43 (D) 87(7)已知⎰≥3sin 2πxdx a ,曲线)1ln(1)(++=ax aax x f 在点())1(,1f 处的切线的斜率为k ,则k 的最小值为 (A)1 (B)23(C)2 (D) 3 (8)甲、乙、丙三人独立参加体育达标测试,已知甲、乙、丙各自通过测试的概率分别为p ,4332,,且他们是否通过测试互不影响.若三人中只有甲通过的概率为161,则甲、丙二人中至少有一人通过测试的概率为 (A)87 (B) 43 (C) 85 (D) 76(9)函数)1(2)(3-'+=f x x x f ,则函数)(x f 在区间[]3,2-上的值域是 (A) ]9,24[- (B) ]24,24[- (C) ]24,4[ (D)[]9,4 (10)设()()5522105)1(...1)1(1x a x a x a a x +++++++=-,则420a a a ++等于(A) 242 (B) 121 (C) 244 (D)122(11)已知函数)()()(2R b x bx x e x f x ∈-=.若存在⎥⎦⎤⎢⎣⎡∈2,21x ,使得0)()(>'+x f x x f ,则实数b 的取值围是(A) ⎪⎭⎫ ⎝⎛∞-65, (B) ⎪⎭⎫ ⎝⎛∞-38, (C) ⎪⎭⎫⎝⎛-65,23 (D) ⎪⎭⎫⎝⎛∞+,38 (12)中国南北朝时期的著作《子算经》中,对同余除法有较深的研究.设)0(,,>m m b a 为整数,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为)(mod m b a =.如9和21被6除得的余数都是3,则记)6(mod 219=.若20202022201200202...22⋅++⋅+⋅+=C C C C a ,)10(mod b a =,则b 的值可以是(A) 2011 (B) 2012 (C) 2013 (D) 2014第II 卷本卷包括必考题和选考题两部分。
山东省烟台市2016-2017学年高二上学期期末考试数学(文)试题含答案
2016—2017学年度第一学期高二期末自主练习文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1。
下列四个命题中,真命题的是( )A .空间中两组对边分别相等的四边形为平行四边形B .所有梯形都有外接圆C .所有的质数的平方都不是偶数D .不存在一个奇数,它的立方是偶数2.若命题p :α是第一象限角;命题q :α是锐角,则p 是q 的( )A .充分不必要条件B .必要不充分条件 C.充要条件 D .既不充分也不必要条件3。
命题p :若y x >,则y x tan tan >;命题q :xy y x 222≥+.下列命题为假命题的是( )A .q p ∨B .q p ∧C .p ⌝D .q4.命题“R x ∈∃0,01020<++x x ”的否定是( )A .不存在R x ∈0,01020≥++x xB .R x ∈∃0,01020≥++x xC .R x ∈∀,012<++x xD .R x ∈∀,012≥++x x5.平面内有两定点B A ,及动点P ,设命题甲:“PA 与B P 是定值”,命题乙:“点P 的轨迹是以B A ,为焦点的椭圆",那么命题甲是命题乙的( )A .充分不必要条件B .必要不充分条件C 。
充要条件D .既不充分也不必要条件6.已知点P 是椭圆1422=+y x 上的一点,且以点P 及焦点21,F F 为顶点的三角形的面积等于3,则这样的点P 的个数为( )A .1B .2C 。
3D .47.在极坐标系中,圆)(cos 4R ∈=ρθρ的圆心到直线3πθ=的距离是( )A .3B .32 C.1 D .28。
与x 轴相切且和半圆)20(422≤≤=+y y x 内切的动圆圆心的轨迹方程是( )A .)10)(1(42≤<--=y y xB .)10)(1(42≤<-=y y xC 。
2016-2017潍坊高二上学期期末考试数学试题(理科)
高二上学期期末数学测试题(三)一、选择题(5分*10 =50分).1.椭圆221259x y +=的离心率为( ) A .35B .45 C .34D .532.命题“x R ∀∈,()0f x >”的否定为( ) A .0x R∃∈,()0f x >B .x R ∀∈,()0f x <C .0x R∃∈,()0f x ≤ D .x R ∀∈,()0f x ≤3.在数列{an}中,a1=2,2an+1=2an+1,n ∈N*,则99a 的值为( )A .49B .50C .51D .524.若抛物线y2=2px (p >0)的焦点与双曲线221124x y -=的右焦点重合,则p=( )A .2B .4C .8D.5.已知a ,b >0,且a ≠1,b ≠1,若log 1b a >,则( )A.(1)(1)0a b --<B. (1)()0a a b -->C. (1)()0b b a --<D. (1)()0b b a -->6.若变量x ,y 满足2,239,0,x y x y x +≤⎧⎪-≤⎨⎪≥⎩则22x y +的最大值是( )(A )4 (B )9 (C )10 (D )127.在ABC ∆中,若222b c a bc +-=,则角A 的值为( ) A .30︒B .60︒C .120︒D .150︒8.已知集合{}{}|(3)0,|1|2,A x x x B x x =-<=-<则“A x ∈”是“B x ∈”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 9.已知数列{}n a 满足3211n a n =-,前n 项的和为n S ,关于n a ,n S 叙述正确的是( ) A .n a ,n S 都有最小值 B .n a ,n S 都没有最小值 C .n a ,n S 都有最大值 D .n a ,n S 都没有最大值 10.下列命题错误的是( )A .命题“∃x ∈R 使得x2+x+1<0”的否定是:“∀x ∈R 均有x2+x+1≥0”B .若p ∧q 为假命题,则p ,q 均为假命题C .若a ,b 满足a+b=1,则不等式a 2+b 2>14成立D .“平面向量a 与b 的夹角是钝角”的必要不充分条件是“.a b <0”11.方程2212sin 3sin 2x y θθ+=+-所表示的曲线是( ) A .焦点在x 轴上的椭圆 B .焦点在y 轴上的椭圆C .焦点在x 轴上的双曲线D .焦点在y 轴上的双曲线12.△ABC 各角的对应边分别为a , b , c , 满足1b ca c a b+≥++,则角A 的范围是( ) A .(0,]6πB .(0,]3πC .[,)3ππD .[,)6ππ二、填空题(5分*4=20分).13. 若锐角三角形ABC的面积为,2AB =,3AC =,则cosA=________.14.数列 131, 391, 5271, 7811, 92431, …, 的前n 项之和等于 _____.15.若命题“∃x ∈R ,使x2+(a ﹣1)x+1<0”是假命题,则实数a 的取值范围为 16.下列四个关于圆锥曲线的命题:①已知M (﹣2,0)、N (2,0),|PM|+|PN|=3,则动点P 的轨迹是一条线段; ②从双曲线的一个焦点到一条渐近线的距离等于它的虚半轴长;③双曲线221169x y -=与椭圆221169x y +=有相同的焦点; ④关于x 的方程x 2﹣mx+1=0(m >2)的两根可分别作为椭圆和双曲线的离心率. 其中正确的命题是 .(填上你认为正确的所有命题序号)三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)17.已知{}n a 是公差为3的等差数列,数列{}n b 满足12111==3n n n n b b a b b nb +++=1,,.(I )求{}n a 的通项公式; (II )求{}n b 的前n 项和.18.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知2,5a c ==,3cos 5B =. (Ⅰ)求b 的值; (Ⅱ)求sinC 的值.19.设命题p :方程22113x y m m +=-+表示的图形是双曲线;命题q :∃x ∈R ,3x 2+2mx+(m+6)<0. 求使“p 且q ”为真命题时,实数m 的取值范围.20.2222C 1x y a b+=椭圆:(a >b >0)的两个焦点为F 1,F 2,点P 在椭圆C 上,且PF 1⊥PF 2,|PF 1|=6,|PF 2|=8, (Ⅰ)求椭圆的方程(Ⅱ)若直线l 过圆 x 2+y 2+4x ﹣2y=0的圆心M ,交椭圆C 于A ,B 两点,且A ,B 关于点M 对称,求直线l 的方程.21(理).如图,在斜三棱柱ABC ﹣A 1B 1C 1中,点O 、E 分别是A 1C 1、AA 1的中点,AO ⊥平面A 1B 1C 1.已知∠BCA=90°,AA 1=AC=BC=2.(Ⅰ)证明:OE ∥平面AB 1C 1;(Ⅱ)求异面直线AB 1与A 1C 所成的角; (Ⅲ)求A 1C 1与平面AA 1B 1所成角的正弦值.21(文).设数列{n a }的前n 项和为n S .已知2S =4,1n a +=2n S +1,*N n ∈. (I )求通项公式n a ; (II )求数列{}2n a n --的前n 项和.22.设函数2()22f x x tx =-+,其中()0+t ∈∞,.(Ⅰ)若1t =,且对任意的[],2x a a ∈+,都有()5f x ≤,求实数a 的取值范围; (Ⅱ)若对任意的1x ,[]20,4x ∈,都有12|()()|8f x f x -≤,求t 的取值范围.高二上学期期末数学测试题(三)参考答案一、选择题 BCCCDCBAAB CB二、填空题 12 211123nn ⎡⎤⎛⎫+-⎢⎥⎪⎝⎭⎢⎥⎣⎦﹣1≤a ≤3. ②④ 三、解答题17.解:(I )由已知,1221121,1,,3a b b b b b +===得1221121,1,,3a b b b b b +===得12a =,所以数列{}n a 是首项为2,公差为3的等差数列,通项公式为31n a n =-.(II )由(I )和11n n n n a b b nb +++= ,得13n n b b +=,因此{}n b 是首项为1,公比为13的等比数列.记{}n b 的前n 项和为n S ,则111()313.122313nn n S --==-⨯- 18.解:(Ⅰ)由余弦定理2222cos b a c ac B =+-,得23425225175b =+-⨯⨯⨯=,∴b =6分(Ⅱ)∵3cos 5B =∴4sin 5B =,由正弦定理sin sin b cB C =,54sin 5C =,sin C =12分 19.解:∵“p 且q ”为真命题,∴命题p 和命题q 都是真命题……………………………2分∵命题p :方程22113x y m m +=-+表示的图象是双曲线,p 是真命题∴(1﹣m )(m+3)<0,解之得m <﹣3或m >1…………………………………………6分 又∵命题q :∃x ∈R ,3x 2+2mx+(m+6)<0,q 是真命题∴△=4m 2﹣12(m+6)>0,解之得m <﹣3或m >6………………………………………10分 因此,使“p 且q ”为真命题时的m 的取值范围为(﹣∞,﹣3)∪(6,+∞).……………12分 20.解 (1)∵PF 1⊥PF 2,|PF 1|=6,|PF 2|=8,∴2a=|PF 1|+|PF 2|=6+8=14, 即a=7,且4c 2═|PF 1|2+|PF 2|2=62+82=100解得c 2=25,∴b 2=49﹣25=24,故椭圆的方程为2214924x y +=,………………………………………………………6分(2)设A (m ,n ),B (x ,y ),圆的标准方程为(x+2)2+(y ﹣1)2=5,圆心M (﹣2,1),∵A ,B 关于M 对称,∴ 42m x n y +=-⎧⎨+=⎩,即2212m xn y +⎧=-⎪⎪⎨+⎪=⎪⎩,∵A ,B 都在椭圆上,∴22221492414924x y m n ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得()()()(04924x+m x -m y+n y -n)+=,即42(04924()y -n)+x -m --=,即直线AB 的斜率k=4849-,∴直线方程为y ﹣1=4849-(x+2),即48x+49y+47=0.……………………………12分21(理).解法一:(Ⅰ)证明:∵点O 、E 分别是A 1C 1、AA 1的中点,∴OE ∥AC 1,又∵EO ⊄平面AB 1C 1,AC 1⊂平面AB 1C 1, ∴OE ∥平面AB 1C 1.(4分)(Ⅱ)∵AO ⊥平面A 1B 1C 1,∴AO ⊥B 1C 1,又∵A 1C 1⊥B 1C 1,且A 1C 1∩AO=O B 1C 1⊥平面A 1C 1CA ,∴A 1C ⊥B 1C 1.(6分)又∵AA 1=AC ,∴四边形A 1C 1CA 为菱形,∴A 1C ⊥AC 1,且B 1C 1∩AC 1=C 1∴A 1C ⊥平面AB 1C 1,∴AB 1⊥A 1C ,即异面直线AB 1与A 1C 所成的角为90°.(8分)(Ⅲ) 设点C 1到平面AA 1B 1的距离为d ,∵,即d .(10分) 又∵在△AA 1B 1中,,∴S △AA 1B 1=.∴,∴A 1C 1与平面AA 1B 1所成角的正弦值.(12分)解法二:如图建系O ﹣xyz ,,,C 1(0,1,0),B 1(2,1,0),.(2分)(Ⅰ)∵=,,∴,即OE ∥AC 1, 又∵EO ⊄平面AB 1C 1,AC 1⊂平面AB 1C 1,∴OE ∥平面AB 1C 1.(6分)(Ⅱ)∵,,∴,即∴AB 1⊥A 1C ,∴异面直线AB 1与A 1C 所成的角为90°.(8分)(Ⅲ)设A 1C 1与平面AA 1B 1所成角为θ,∵,设平面AA 1B 1的一个法向量是则即不妨令x=1,可得,(10分)∴,∴A 1C 1与平面AA 1B 1所成角的正弦值.(12分)21(文)解:(1)由题意得:1221421a a a a +=⎧⎨=+⎩,则1213a a =⎧⎨=⎩,又当2n ≥时,由11(21)(21)2n n n n n a a S S a +--=+-+=,得13n n a a +=,所以,数列{}n a 的通项公式为1*3,n n a n N -=∈.(2)设1|32|n n b n -=--,*n N ∈,122,1b b ==.当3n ≥时,由于132n n ->+,故132,3n n b n n -=--≥.设数列{}n b 的前n 项和为n T ,则122,3T T ==.当3n ≥时,229(13)(7)(2)351131322n n n n n n n T --+---+=+-=-, 所以,2*2,13511,2,2nn n T n n n n N =⎧⎪=⎨--+≥∈⎪⎩. 22.解:∵222()22()2f x x tx x t t =-+=-+-, ∴()f x 在区间(,]t -∞上单调递减,在区间[,)t +∞上 单调递增,且对任意的x R ∈,都有()()f t x f t x +=-.(1)“对任意的[],2x a a ∈+,都有()5f x ≤”等价于“在区间[],2a a +上,max ()5f x ≤”.若1t =,则2()(1)1f x x =-+,所以()f x 在区间(,1]-∞上单调递减,在区间[1,)+∞上单调递增.当11a ≤+,即0a ≥时,由2max ()(2)(1)15f x f a a =+=++≤,得31a -≤≤,从而01a ≤≤;当11a >+,即0a <时,由2max ()()(1)15f x f a a ==-+≤,得13a -≤≤,从而10a -≤<.综上,a 的取值范围为[]1,1-.(2)设函数()f x 在区间[]0,4上的最大值为M ,最小值为m ,所以“对任意的1x ,[]20,4x ∈,都有12|()()|8f x f x -≤”等价于“8M m -≤”. ① 当02t <≤时,(4)188M f t ==-,2()2m f t t ==-,由222188(2)816(4)8M m t t t t t -=---=-+=-≤,44t -≤≤+,从而42t -≤≤;② 当24t <≤时,(0)2M f ==,2()2m f t t ==-,由222(2)8M m t t -=--=≤,得t -≤≤2t <≤③当4t >时,(0)2M f ==,(4)188m f t ==-,由2(188)8168M m t t -=--=-≤,得3t ≤,从而t ∈∅.综上,t的取值范围为4⎡-⎣.。
山东省青岛市胶州市2016-2017学年高二上学期期末数学试卷(理科)Word版含解析
2016-2017学年山东省青岛市胶州市高二(上)期末数学试卷(理科)一、选择题:本大题共12个小题.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数=()A.1﹣2i B.C.1 D.1+2i2.圆x2+y2﹣4=0与圆x2+y2+2x=0的位置关系是()A.相离B.相切C.相交D.内含3.设命题p:∀x∈R,x2+1>0,则¬p为()A. B.C. D.4.抛物线的焦点坐标是()A.(1,0) B.(﹣1,0)C.(0,1) D.(0,﹣1)5.F1(﹣1,0)、F2(1,0)是椭圆的两焦点,过F1的直线l交椭圆于M、N,若△MF2N的周长为8,则椭圆方程为()A.B.C.D.6.某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x的值是()A.2 B.C.D.37.已知实数x,y满足,则z=3x+y的最大值为()A.5 B.6 C.7 D.88.已知平面α,β,γ,直线a,b,c,则下列命题正确的是()A.若α⊥γ,β⊥γ,则α∥βB.若a⊥c,b⊥c,则a∥bC.若a⊥α,b⊥α,则a∥b D.若a∥α,b∥α,则a∥b9.设a∈R,则“a>1”是“a2>1”的()A.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分也非必要条件10.用数学归纳法证明不等式“1+++…+<n(n∈N*,n≥2)”时,由n=k (k≥2)不等式成立,推证n=k+1时,左边应增加的项数是()A.2k﹣1 B.2k﹣1 C.2k D.2k+111.在空间中,给出下面四个命题,则其中正确命题的个数为()①过平面α外的两点,有且只有一个平面与平面α垂直;②若平面β内有不共线三点到平面α的距离都相等,则α∥β;③若直线l与平面α内的无数条直线垂直,则l⊥α;④两条异面直线在同一平面内的射影一定是两条平行线.A.0 B.1 C.2 D.312.已知F1、F2分别是双曲线C:﹣=1的左、右焦点,若F2关于渐近线的对称点恰落在以F1为圆心,|OF1|为半径的圆上,则双曲线C的离心率为()A.B.3 C.D.2二、填空题13.过点(﹣1,2)且和直线3x+2y﹣7=0垂直的直线方程是.14.方程表示椭圆,则k的取值范围是.15.已知P为抛物线y=2x2上的点,若点P到直线l:4x﹣y﹣6=0的距离最小,则点P的坐标为.16.如图,在正四棱锥S﹣ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC恒成立的是.(把正确的序号都填上)三、解答题(本大题共6小题,解答应写出文字说明、证明过程或演算步骤.)17.已知圆C的方程:x2+y2﹣2x﹣4y+m=0.(Ⅰ)求m的取值范围;(Ⅱ)当圆C与圆D:(x+3)2+(y+1)2=16相外切时,求直线l:x+2y﹣4=0被圆C所截得的弦MN的长.18.已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.(1)求椭圆C的方程;(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA 与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.19.如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,E为侧棱PA的中点.(1)求证:PC∥平面BDE;(2)若PC⊥PA,PD=AD,求证:平面BDE⊥平面PAB.20.如图,在斜三棱柱ABC﹣A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.(Ⅰ)求证:AB1⊥CC1;(Ⅱ)若AB1=,求二面角C﹣AB1﹣A1的余弦值.21.已知椭圆,过点M(﹣1,0)作直线l交椭圆于A,B两点,O是坐标原点.(1)求AB中点P的轨迹方程;(2)求△OAB面积的最大值,并求此时直线l的方程.22.已知椭圆的左、右焦点分别为F1、F2,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.(1)求椭圆的方程;(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明:为定值.(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由.2016-2017学年山东省青岛市胶州市高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数=()A.1﹣2i B.C.1 D.1+2i【考点】复数代数形式的乘除运算.【分析】利用复数的除法运算把化简后进行复数的加减运算即可得到结果.【解答】解:=.故选A.2.圆x2+y2﹣4=0与圆x2+y2+2x=0的位置关系是()A.相离B.相切C.相交D.内含【考点】圆与圆的位置关系及其判定.【分析】把圆的方程化为标准形式,求出圆心坐标和圆的半径,再根据这两个圆的圆心距为d=R﹣r,可得两圆相内切.【解答】解:圆x2+y2﹣4=0即x2+y2=4,表示以原点O为圆心、半径等于2的圆,圆x2+y2+2x=0,即(x+1)2+y2 =1,表示以C(﹣1,0)为圆心、半径等于1的圆.由于这两个圆的圆心距为d=OC==2﹣1=R﹣r,故两圆相内切,故选:B.3.设命题p:∀x∈R,x2+1>0,则¬p为()A. B.C. D.【考点】命题的否定.【分析】本题中的命题是一个全称命题,其否定是特称命题,依据全称命题的否定书写形式写出命题的否定即可【解答】解:∵p:∀x∈R,x2+1>0,则¬p为∃x0∈R,x02+1≤0,故选:B4.抛物线的焦点坐标是()A.(1,0) B.(﹣1,0)C.(0,1) D.(0,﹣1)【考点】抛物线的简单性质.【分析】根据题意,将抛物线的方程变形可得其标准方程为x2=4y,分析可得其焦点在y轴正半轴上,且p=2,由抛物线的焦点坐标公式计算可得答案.【解答】解:根据题意,抛物线的方程为:,变形可得x2=4y,其焦点在y轴正半轴上,且p=2,则其焦点坐标为:(0,1);故选:C.5.F1(﹣1,0)、F2(1,0)是椭圆的两焦点,过F1的直线l交椭圆于M、N,若△MF2N的周长为8,则椭圆方程为()A.B.C.D.【考点】椭圆的标准方程.【分析】由题意可知△MF2N的周长为4a,从而可求a的值,进一步可求b的值,故方程可求.【解答】解:由题意,4a=8,∴a=2,∵F1(﹣1,0)、F2(1,0)是椭圆的两焦点,∴b2=3,∴椭圆方程为,故选A.6.某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x的值是()A.2 B.C.D.3【考点】由三视图求面积、体积.【分析】由三视图可知:原几何体是一个四棱锥,其中底面是一个上、下、高分别为1、2、2的直角梯形,一条长为x的侧棱垂直于底面.据此可求出原几何体的体积.【解答】解:由三视图可知:原几何体是一个四棱锥,其中底面是一个上、下、高分别为1、2、2的直角梯形,一条长为x的侧棱垂直于底面.则体积为=,解得x=.故选:C.7.已知实数x,y满足,则z=3x+y的最大值为()A.5 B.6 C.7 D.8【考点】简单线性规划.【分析】先画出约束条件的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数3x+y的最大值.【解答】解:由约束条件,画出如图所示的三角形区域,令z=0得x+2y=0,显然当平行直线x+2y=0过点A(2,1)时,z取得最大值为:7;故选:C.8.已知平面α,β,γ,直线a,b,c,则下列命题正确的是()A.若α⊥γ,β⊥γ,则α∥βB.若a⊥c,b⊥c,则a∥bC.若a⊥α,b⊥α,则a∥b D.若a∥α,b∥α,则a∥b【考点】命题的真假判断与应用.【分析】A.由已知可得α∥β或相交,即可判断出正误;B.由已知可得a∥b、相交或异面直线,即可判断出正误;C.利用线面垂直的性质定理可得:a∥b,即可判断出正误;D.由已知可得:a∥b、相交或异面直线,即可判断出正误.【解答】解:A.若α⊥γ,β⊥γ,则α∥β或相交,因此不正确;B.若a⊥c,b⊥c,则a∥b、相交或异面直线,因此不正确;C.由a⊥α,b⊥α,利用线面垂直的性质定理可得:a∥b,正确;D.若a∥α,b∥α,则a∥b、相交或异面直线,因此不正确.综上:只有C正确.故选:C.9.设a∈R,则“a>1”是“a2>1”的()A.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分也非必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据不等式的关系,结合充分条件和必要条件的定义进行判断即可.【解答】解:由a2>1得a>1或a<﹣1,即“a>1”是“a2>1”的充分不必要条件,故选:A.10.用数学归纳法证明不等式“1+++…+<n(n∈N*,n≥2)”时,由n=k (k≥2)不等式成立,推证n=k+1时,左边应增加的项数是()A.2k﹣1 B.2k﹣1 C.2k D.2k+1【考点】数学归纳法.【分析】分别写出n=k和n=k+1时,不等式左边的所有项,根据分母特点计算多出的项数.【解答】解:n=k时,左边=1+++…+,当n=k+1时,左边=1+++…++++…+.∴左边增加的项数为2k+1﹣1﹣(2k﹣1)=2k+1﹣2k=2k.故选:C.11.在空间中,给出下面四个命题,则其中正确命题的个数为()①过平面α外的两点,有且只有一个平面与平面α垂直;②若平面β内有不共线三点到平面α的距离都相等,则α∥β;③若直线l与平面α内的无数条直线垂直,则l⊥α;④两条异面直线在同一平面内的射影一定是两条平行线.A.0 B.1 C.2 D.3【考点】命题的真假判断与应用.【分析】通过列举反例,判断出各个命题的真假.【解答】解:当过平面α外的两点在垂直于平面α的直线上时,命题①不成立;不共线三点在平面α,β的两侧时,②不成立;无数条直线平行时,③不成立;在正方体中ABCD﹣A1B1C1D1中,AA1与B1C1是异面直线,AA1在面ABCD中的射影是点,故④错.故选A.12.已知F1、F2分别是双曲线C:﹣=1的左、右焦点,若F2关于渐近线的对称点恰落在以F1为圆心,|OF1|为半径的圆上,则双曲线C的离心率为()A.B.3 C.D.2【考点】双曲线的简单性质.【分析】求出F2到渐近线的距离,利用F2关于渐近线的对称点恰落在以F1为圆心,|OF1|为半径的圆上,可得直角三角形,即可求出双曲线的离心率.【解答】解:由题意,F1(﹣c,0),F2(c,0),一条渐近线方程为,则F2到渐近线的距离为=b.设F2关于渐近线的对称点为M,F2M与渐近线交于A,∴|MF2|=2b,A为F2M 的中点又0是F1F2的中点,∴OA∥F1M,∴∠F1MF2为直角,∴△MF1F2为直角三角形,∴由勾股定理得4c2=c2+4b2∴3c2=4(c2﹣a2),∴c2=4a2,∴c=2a,∴e=2.故选D.二、填空题13.过点(﹣1,2)且和直线3x+2y﹣7=0垂直的直线方程是2x﹣3y+8=0.【考点】直线的一般式方程与直线的垂直关系.【分析】设与直线3x+2y﹣7=0垂直的直线方程为2x﹣3y+c=0,把点(﹣1,2)代入能求出直线方程.【解答】解:设与直线3x+2y﹣7=0垂直的直线方程为:2x﹣3y+c=0,把点(﹣1,2)代入,得:c=8.∴过点(﹣1,2),且与直线3x+2y﹣7=0垂直的直线方程是2x﹣3y+8=0.故答案为:2x﹣3y+8=0.14.方程表示椭圆,则k的取值范围是{k|﹣3<k<3且k≠0} .【考点】椭圆的简单性质.【分析】根据题意,由椭圆的标准方程的形式可得,解可得k的取值范围,即可得答案.【解答】解:根据题意,表示椭圆,必有,解可得:﹣3<k<3且k≠0,即k的取值范围是:{k|﹣3<k<3且k≠0};故答案为:{k|﹣3<k<3且k≠0}.15.已知P为抛物线y=2x2上的点,若点P到直线l:4x﹣y﹣6=0的距离最小,则点P的坐标为(1,2).【考点】直线与抛物线的位置关系.【分析】设抛物线y=2x2上一点为A(x0,2x02),求出点A(x0,2x02)到直线l:4x﹣y﹣6=0的距离,利用配方法,由此能求出抛物线y=2x2上一点到直线l:4x ﹣y﹣6=0的距离最短的点的坐标.【解答】解:设抛物线y=2x2上一点为P(x0,2x02),点A (x 0,2x 02)到直线l :4x ﹣y ﹣6=0的距离d==|2(x 0﹣1)2﹣8|,∴当x 0=1时,即当A (1,2)时,抛物线y=2x 2上一点到直线l :4x ﹣y ﹣6=0的距离最短.故答案为:(1,2).16.如图,在正四棱锥S ﹣ABCD 中,E .M .N 分别是BC .CD .SC 的中点,动点P 的线段MN 上运动时,下列四个结论:①EP ⊥AC ; ②EP ∥BD ;③EP ∥平面SBD ; ④EP ⊥平面SAC 恒成立的是 ①③ .(把正确的序号都填上)【考点】命题的真假判断与应用.【分析】在①中:由已知得SO ⊥AC .,AC ⊥平面SBD ,从而平面EMN ∥平面SBD ,由此得到AC ⊥EP ;在②中:由异面直线的定义可知:EP 与BD 是异面直线;在③中:由平面EMN ∥平面SBD ,从而得到EP ∥平面SBD ;在④中:由已知得EM ⊥平面SAC ,从而得到EP 与平面SAC 不垂直.【解答】解:解:如图所示,连接AC 、BD 相交于点O ,连接EM ,EN . 在①中:由正四棱锥S ﹣ABCD ,可得SO ⊥底面ABCD ,AC ⊥BD , ∴SO ⊥AC .∵SO ∩BD=O ,∴AC ⊥平面SBD ,∵E ,M ,N 分别是BC ,CD ,SC 的中点, ∴EM ∥BD ,MN ∥SD ,而EM ∩MN=N ,∴平面EMN ∥平面SBD ,∴AC ⊥平面EMN ,∴AC ⊥EP .故正确. 在②中:由异面直线的定义可知:EP 与BD 是异面直线, 不可能EP ∥BD ,因此不正确;在③中:由①可知平面EMN∥平面SBD,∴EP∥平面SBD,因此正确.在④中:由①同理可得:EM⊥平面SAC,若EP⊥平面SAC,则EP∥EM,与EP∩EM=E相矛盾,因此当P与M不重合时,EP与平面SAC不垂直.即不正确.∴恒成立的结论是:①③.故答案为:①③.三、解答题(本大题共6小题,解答应写出文字说明、证明过程或演算步骤.)17.已知圆C的方程:x2+y2﹣2x﹣4y+m=0.(Ⅰ)求m的取值范围;(Ⅱ)当圆C与圆D:(x+3)2+(y+1)2=16相外切时,求直线l:x+2y﹣4=0被圆C所截得的弦MN的长.【考点】直线与圆相交的性质;圆的一般方程.【分析】(Ⅰ)根据圆的一般方程表示圆的条件即可求m的取值范围;(Ⅱ)根据圆与圆相切的等价条件求出m的值,结合直线的弦长公式进行求解即可.【解答】解:(Ⅰ)圆C的方程可化为(x﹣1)2+(y﹣2)2=5﹣m …令5﹣m>0,得m<5.…(Ⅱ)圆C:(x﹣1)2+(y﹣2)2=5﹣m,圆心C(1,2),半径r=圆D:(x+3)2+(y+1)2=16,圆心D(﹣3,﹣1),半径R=4…∵圆C与圆D相外切∴,解得m=4 …圆心C(1,2)到直线l:x+2y﹣4=0的距离为d=…∴|MN|=…18.已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.(1)求椭圆C的方程;(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA 与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.【考点】椭圆的标准方程;直线与圆锥曲线的综合问题.【分析】(1)先设出椭圆C的标准方程,进而根据焦点和椭圆的定义求得c和a,进而求得b,则椭圆的方程可得.(2)先假设直线存在,设出直线方程与椭圆方程联立消去y,进而根据判别式大于0求得t的范围,进而根据直线OA与l的距离求得t,最后验证t不符合题意,则结论可得.【解答】解:(1)依题意,可设椭圆C的方程为(a>0,b>0),且可知左焦点为F(﹣2,0),从而有,解得c=2,a=4,又a2=b2+c2,所以b2=12,故椭圆C的方程为.(2)假设存在符合题意的直线l,其方程为y=x+t,由得3x2+3tx+t2﹣12=0,因为直线l与椭圆有公共点,所以有△=(3t)2﹣4×3(t2﹣12)≥0,解得﹣4≤t≤4,另一方面,由直线OA与l的距离4=,从而t=±2,由于±2∉[﹣4,4],所以符合题意的直线l不存在.19.如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,E为侧棱PA的中点.(1)求证:PC∥平面BDE;(2)若PC⊥PA,PD=AD,求证:平面BDE⊥平面PAB.【考点】平面与平面垂直的判定;直线与平面平行的判定.【分析】(1)连结AC,交BD于O,连结OE,E为PA的中点,利用三角形中位线的性质,可知OE∥PC,利用线面平行的判定定理,即可得出结论;(2)先证明PA⊥DE,再证明PA⊥OE,可得PA⊥平面BDE,从而可得平面BDE ⊥平面PAB.【解答】证明:(1)连结AC,交BD于O,连结OE.因为ABCD是平行四边形,所以OA=OC.…因为E为侧棱PA的中点,所以OE∥PC.…因为PC⊂平面BDE,OE⊂平面BDE,所以PC∥平面BDE.…(2)因为E为PA中点,PD=AD,所以PA⊥DE.…因为PC⊥PA,OE∥PC,所以PA⊥OE.因为OE⊂平面BDE,DE⊂平面BDE,OE∩DE=E,所以PA⊥平面BDE.…因为PA⊂平面PAB,所以平面BDE⊥平面PAB.…20.如图,在斜三棱柱ABC﹣A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.(Ⅰ)求证:AB1⊥CC1;(Ⅱ)若AB1=,求二面角C﹣AB1﹣A1的余弦值.【考点】用空间向量求平面间的夹角;直线与平面垂直的性质;二面角的平面角及求法.【分析】(Ⅰ)证明:连AC1,CB1,证明CC1⊥OA,CC1⊥OB1,得到CC1⊥平面OAB1,即可证明CC1⊥AB1.(Ⅱ)以OB1,OC1,OA为正方向建立空间直角坐标系,求出C,B1,A,求出平面CAB1的法向量,平面A1AB1的法向量,通过向量的数量积求解二面角C﹣AB1﹣A1的余弦值.【解答】解:(Ⅰ)证明:连AC1,CB1,则△ACC1和△B1CC1皆为正三角形.取CC1中点O,连OA,OB1,则CC1⊥OA,CC1⊥OB1,则CC1⊥平面OAB1,则CC1⊥AB1.…(Ⅱ)解:由(Ⅰ)知,OA=OB1=,又AB1=,所以OA⊥OB1.如图所示,分别以OB1,OC1,OA为正方向建立空间直角坐标系,则C(0,﹣1,0),B1(,0,0),A(0,0,),…设平面CAB1的法向量为=(x1,y1,z1),因为=(,0,﹣),=(0,﹣1,﹣),所以取=(1,﹣,1).…设平面A1AB1的法向量为=(x2,y2,z2),因为=(,0,﹣),=(0,2,0),所以取=(1,0,1).…则cos<>===,因为二面角C﹣AB1﹣A1为钝角,所以二面角C﹣AB1﹣A1的余弦值为﹣.…21.已知椭圆,过点M(﹣1,0)作直线l交椭圆于A,B两点,O是坐标原点.(1)求AB中点P的轨迹方程;(2)求△OAB面积的最大值,并求此时直线l的方程.【考点】直线与圆锥曲线的综合问题;椭圆的应用.【分析】(1)利用点差法,结合中点坐标公式,即可求AB中点P的轨迹方程;(2)令l:x=hy﹣1代入x2+4y2=4,利用韦达定理,表示出△OAB面积,利用函数的单调性,即可求△OAB面积的最大值,及此时直线l的方程.【解答】解:(1)设A(x1,y1),B(x2,y2),P(x,y),则(1)﹣(2),得,∴,即x2+x+4y2=0(2)设A(x1,y1),B(x2,y2),则令l:x=hy﹣1代入x2+4y2=4,得(4+h2)y2﹣2hy﹣3=0,△=16(h2+3)>0,y1+y2=,y1y2=﹣∴,令,则在上单调递减,∴,即h=0时,,此时l:x=﹣1.22.已知椭圆的左、右焦点分别为F1、F2,短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.(1)求椭圆的方程;(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明:为定值.(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由.【考点】椭圆的标准方程;直线与圆锥曲线的综合问题.【分析】(1)由题意知a=2,b=c,b2=2,由此可知椭圆方程为.(2)设M(2,y0),P(x1,y1),,直线CM:,代入椭圆方程x2+2y2=4,得,然后利用根与系数的关系能够推导出为定值.(3)设存在Q(m,0)满足条件,则MQ⊥DP.,再由,由此可知存在Q(0,0)满足条件.【解答】解:(1)a=2,b=c,a2=b2+c2,∴b2=2;∴椭圆方程为(2)C(﹣2,0),D(2,0),设M(2,y0),P(x1,y1),直线CM:,代入椭圆方程x2+2y2=4,得∵x1=﹣,∴,∴,∴∴(定值)(3)设存在Q(m,0)满足条件,则MQ⊥DP则由,从而得m=0∴存在Q(0,0)满足条件2017年3月18日。
易错汇总2016-2017年山东省临沂市高二上学期期末数学试卷(理科)与解析
A.
B.
C.
D.
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.( 5 分)在△ ABC中,边 a, b,c 分别是角 A,B,C 的对边, cosA= ,b=2,
△ABC的面积 S=3,则边 a 的值为
.
14.(5 分)已知等差数列 { an} 的前 n 项和 Sn 满足 S3=0,S5=﹣5,数列 {
2016-2017 学年山东省临沂市高二(上)期末数学试卷(理科)
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分)
1.(5 分)在△ ABC中,若 a=2,b=2 ,A=30°,则 B 为( )
A.60°
B.60°或 120° C.30°
D.30°或 150°
2.(5 分)已知等差数列 { an} 中, a2=7,a4=15,则前 10 项的和 S10=( )
}
的前 2016 项的和为
.
15.( 5 分)已知命题 p:? x∈[ 1,2] , x2﹣a≥0;命题 q:? x0∈ R,使得 +
(a﹣1)x0+1<0.若 “p或 q”为真,“p且 q”为假,则实数 a 的取值范围
.
16.( 5 分)已知 m,n, s,t ∈R+,m+n=2, + =9,其中 m,n 是常数,当 s+t
8.( 5 分)已知正项等比数列 { an} 满足: a3=a2+2a1,若存在两项 am, an,使得
,则
的最小值为(
)
A.
B.
C.
【解答】 解:∵正项等比数列 { an} 满足: a3=a2+2a1,
∴
,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年山东省烟台市高二(上)期末数学试卷(理科)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.命题“∀x∈R,都有x2≥0”的否定为( )
A.不存在x0∈R,使得 B.∀x∈R,都有x2<0 C.∃x0∈R,使得 D.∃x0∈R,使得
2.给出命题:若方程mx2+ny2=1(m,n∈R)表示椭圆,则mn>0.在它的逆命题、否命题、逆否命
题三个命题中,真命题的个数是( ) A.3 B.2 C.1 D.0 3.命题p:若a>b,则ac2>bc2;命题q:∃x0>0,使得x0﹣1+lnx0=0,则下列命题为真命题的是( )
A.p∧q B.(¬p)∧q C.p∨(¬q) D.(¬p)∧(¬q)
4.已知=(2,﹣1,2),=(﹣1,3,﹣3),=(13,6,λ),若向量,,共面,则λ=( )
A.2 B.3 C.4 D.6 5.平面内有两定点A,B及动点P,设命题甲:“|PA|与|PB|之差的绝对值是定值”,命题乙:“点P的轨迹是以A,B为焦点的双曲线”,那么命题甲是命题乙的( ) A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=11,则线段AB的中点到y轴的距离为( ) A.3 B.4 C.5 D.7 7.已知命题p:|x﹣a|<4,命题q:(x﹣2)(3﹣x)>0.若¬p是¬q的充分不必要条件,则实数
a的取值范围是( )
A.[﹣1,6] B.(﹣∞,﹣1) C.(6,+∞) D.(﹣∞,﹣1)∪(6,+∞)
8.已知空间向量=(1,n,2),=(﹣2,1,2),若2﹣与垂直,则||等于( )
A. B. C. D.
9.与x轴相切且和半圆x2+y2=4(0≤y≤2)内切的动圆圆心的轨迹方程是( )
A.x2=﹣4(y﹣1)(0<y≤1) B.x2=4(y﹣1)(0<y≤1)
C.x2=4(y+1)(0<y≤1) D.x2=﹣2(y﹣1)(0<y≤1) 10.在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,
CC1上的点,且,则异面直线A1E与AF所成角的余弦值为( )
A. B. C. D.
11.设点A,B的坐标分别为(4,0),(﹣4,0),直线AP,BP相交于点P,且它们的斜率之积为实
数m,关于点P的轨迹下列说法正确的是( ) A.当m<﹣1时,轨迹为焦点在x轴上的椭圆(除与x轴的两个交点)
B.当﹣1<m<0时,轨迹为焦点在y轴上的椭圆(除与y轴的两个交点)
C.当m>0时,轨迹为焦点在x轴上的双曲线(除与x轴的两个交点)
D.当0<m<1时,轨迹为焦点在y轴上的双曲线(除与y轴的两个交点)
12.已知点F1、F2分别是双曲线C:﹣=1(a>0,b>0)的左右焦点,过F1的直线l与双曲线
C的左、右两支分别交于A、B两点,若|AB|:|BF2|:|AF2|=3:4:5,则双曲线的离心率为( )
A.2 B.4 C. D.
二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.抛物线y=x2的焦点坐标是 .
14.已知在空间四边形OABC中,,点M在OA上,且OM=3MA,N为BC中点,
用表示,则等于 .
15.过椭圆右焦点的直线交M于A,B两点,P为AB的中点,且
OP的斜率为,则椭圆M的方程为 .
16.下列四个命题:
①“a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0”,则a2+b2≠0”; ②已知曲线C的方程是kx2+(4﹣k)y2=1(k∈R),曲线C是椭圆的充要条件是0<k<4; ③“”是“直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0相互垂直”的充分不必要条件;
④已知双曲线的一条渐近线经过点(1,2),则该双曲线的离心率的值为. 上述命题中真命题的序号为 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.已知实数c>0,设命题p:函数y=(2c﹣1)x在R上单调递减;命题q:不等式x+|x﹣2c|>1的解集为R,如果p∨q为真,p∧q为假,求c的取值范围. 18.已知抛物线y2=4x截直线y=2x+m所得弦长.
(1)求m的值; (2)设P是x轴上的点,且△ABP的面积为,求点P的坐标. 19.如图所示,在四棱锥P﹣ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC的中点. (Ⅰ)求证:EF∥平面PAB; (Ⅱ)求直线EF与平面ABE所成角的大小.
20.已知抛物线的焦点F也是椭圆的一个焦点,C1与C2的公共
弦的长为. (1)求椭圆C2的方程; (2)经过点(﹣1,0)作斜率为k的直线l与曲线C2交于A,B两点,O是坐标原点,是否存在实数k,使O在以AB为直径的圆外?若存在,求k的取值范围;若不存在,请说明理由.
21.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥
AD且BC=4,点M为PC中点.
(1)求证:DM⊥平面PBC; (2)若点E为BC边上的动点,且,是否存在实数λ,使得二面角P﹣DE﹣B的余弦值为?若存在,求出实数λ的值;若不存在,请说明理由.
22.设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若=,
则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E: +y2=1,其左顶点为A、右顶点为B. (1)设椭圆E与椭圆F: +=1是“相似椭圆”,求常数s的值; (2)设椭圆G: +y2=λ(0<λ<1),过A作斜率为k1的直线l1与椭圆G仅有一个公共点,过椭圆E的上顶点为D作斜率为k2的直线l2与椭圆G仅有一个公共点,当λ为何值时|k1|+|k2|取得最小值,
并求其最小值;
(3)已知椭圆E与椭圆H: +=1(t>2)是相似椭圆.椭圆H上异于A、B的任意一点C(x0,y0),求证:△ABC的垂心M在椭圆E上. 2016-2017学年山东省烟台市高二(上)期末数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.命题“∀x∈R,都有x2≥0”的否定为( )
A.不存在x0∈R,使得 B.∀x∈R,都有x2<0 C.∃x0∈R,使得 D.∃x0∈R,使得
【考点】命题的否定. 【分析】直接由特称命题与全称命题的否定关系得答案. 【解答】解:命题“∀x∈R,都有x2≥0”为全程命题,其否定为特称命题“∃x0∈R,使得”. 故选:D.
2.给出命题:若方程mx2+ny2=1(m,n∈R)表示椭圆,则mn>0.在它的逆命题、否命题、逆否命
题三个命题中,真命题的个数是( ) A.3 B.2 C.1 D.0 【考点】四种命题. 【分析】根据椭圆的定义判断原命题的真假,从而求出逆否命题的真假,求出逆命题的真假,从而判断出否命题的真假即可. 【解答】解:若方程mx2+ny2=1(m,n∈R)表示椭圆,则m>0,n>0,故mn>0, 故原命题是真命题,逆否命题是真命题, 若mn>0,则方程mx2+ny2=1(m,n∈R)表示椭圆,是假命题, 故否命题是假命题, 故选:B.
3.命题p:若a>b,则ac2>bc2;命题q:∃x0>0,使得x0﹣1+lnx0=0,则下列命题为真命题的是( )
A.p∧q B.(¬p)∧q C.p∨(¬q) D.(¬p)∧(¬q)
【考点】复合命题的真假. 【分析】分别判断出命题p,q的真假,从而判断出符合命题的真假即可. 【解答】解:若a>b,则推不出ac2>bc2,c=0时,不成立, 故命题p是假命题; 显然∃x0=1>0,使得x0﹣1+lnx0=0, 故命题q是真命题; 故(¬p)∧q是真命题, 故选:B.
4.已知=(2,﹣1,2),=(﹣1,3,﹣3),=(13,6,λ),若向量,,共面,则λ=( )
A.2 B.3 C.4 D.6 【考点】共线向量与共面向量. 【分析】根据所给的三个向量的坐标,写出三个向量共面的条件,点的关于要求的两个方程组,解方程组即可. 【解答】解:∵=(2,﹣1,2),=(﹣1,3,﹣3),=(13,6,λ),三个向量共面, ∴, ∴(2,﹣1,2)=x(﹣1,3,﹣3)+y(13,6,λ)
∴
解得: 故选:B. 5.平面内有两定点A,B及动点P,设命题甲:“|PA|与|PB|之差的绝对值是定值”,命题乙:“点P的轨迹是以A,B为焦点的双曲线”,那么命题甲是命题乙的( ) A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断. 【分析】根据双曲线的定义得到:若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离,从而判断出结论即可.
