第八章组合变形案例
《材料力学》课程讲解课件第八章组合变形

强度条件(简单应力状态)——
max
对有棱角的截面,最大的正应力发生在棱角点处,且处于单向应力状态。
max
N A
M zmax Wz
M ymax Wy
x
对于无棱角的截面如何进行强度计算——
1、确定中性轴的位置;
y
F z
M z F ey M y F ez
ez F ey z
y
zk yk z
y
x
1、荷载的分解
F
Fy F cos
Fz F sin
z
2、任意横截面任意点的“σ”
x
F
y
(1)内力: M z (x) Fy x F cos x
M y (x) Fz x F sin x
(2)应力:
Mz k
M z yk Iz
My k
M y zk Iy
(应力的 “+”、“-” 由变形判断)
F
1, 首先将斜弯曲分解
为两个平面弯曲的叠加 Fy F cos
z
L2
L2
Fz F sin
z
2, 确定两个平面弯曲的最大弯矩
y
Mz
Fy L 4
M
y
Fz L 4
3, 计算最大正应力并校核强度
max
My Wy
Mz Wz
217.8MPa
查表: Wy 692.2cm3
4, 讨论 0
y
Wz 70.758cm3
的直径为d3,用第四强度理论设计的直径为d4,则d3 ___=__ d4。
(填“>”、“<”或“=”)
因受拉弯组合变形的杆件,危险点上只有正应力,而无切应力,
r3 1 3 2 4 2
r4
第八章 组合变形的强度计算

FAx A FAy FN
l/2
F2
C
B F1
b
cmax
σcmax
l/2
FB F1
h
z
y
+
z
=
z
M
M max F2 l 4
tmax
Mmax max Wz
σtmax
5.强度计算 (脆性材料)
F M max 1 max t t max A Wz F M c max max 1 max c A Wz
y My M y max Wy
z
My
讨论:无棱角的截面如何确定危险点
b
h
z
y
z
z
Mz
My
y
z
F
y
F
y
t max
Mz M y Wz Wy
Mz M y c max Wz Wy
此时,应先找出组合变形的 中性轴,距中性轴最远的点有最 大的正应力。
F
l
Mz Fy x Fx cos
M y Fz x Fx sin
3.应力计算 (计算A(y,z)点的正应力)
Mz A Mz y Iz
A A A
Mz y M y z A Iz Iy
M y A
M yz Iy
§8-3
概述 两相互垂直平面内的弯曲
拉伸(压缩)与弯曲
§8-4
扭转与弯曲
§8-1 概述
组合变形:由两种或两种以上基本变形组合形成的变形。 工程实例:
第八章 组合变形(修)

E、F点的正应力为零,EF线即是中性轴。
可见B、D点就是危险点,离中性轴最远
强度条件:B、D角点处的切应力为零,按单向应力
状态来建立强度条件。设材料的抗拉和抗压强度相 同,则斜弯曲时的强度条件为
max [ ]
中性轴:正应力为零处,即求得中性轴方程
My z Mz y 0
Iy
Iz
上式可见,中性轴是一条通过横截面
成弯矩所在的平面内,即是斜弯曲。
对圆形、正方形等Iy=Iz的截面,得= ,即是平
面弯曲
例8-1 图示悬臂梁,承受载荷F1与F2作用,已知
F1=800N,F2=1.6kN,l=1m,许用应力[σ]=160MPa。
试分别按下列要求确定截面尺寸:(1) 截面为矩形,
h=2b;(2) 截面为圆形。
解:(1) 矩形截面:
(4) max
M zmax Wz
M ymax Wy
59.77 106 692.2 103
5.23106 70.758103
86.35 73.91 160.3MPa [ ]
例8-3 20a号工字钢悬臂梁承受均布荷载 q 和集中力
F=qa/2 如图。已知钢的许用弯曲正应力[]=160MPa,
a=1m。试求梁的许可荷载集度[q]
Fz F sin 40o 0.321qa
在xoz主轴平面内的 弯矩图(y轴为中性轴)
在xoy主轴平面内的 弯矩图 (z轴为中性轴)
危险截面:由弯矩图 ,可确定A、D两截面为危险截面
A、D截面在xoz、 xoy平面的弯曲截面系数,
可查表得
Wz 237106 m3, Wy 31.5106 m3
q F 40°
z
O
解:作计算简图,将自由
结构力学 组合变形

中性轴位置: 设其上任一点的坐标为( y0,z0)故有中性 y 轴的方程: k M y z0 M y
z 0
Iz
Iy
0
z
中性轴与y轴的夹角θ:
θ
z0 M z I y I y tan tan y0 M y I z I z
2 其中 角为合成弯矩 M M y M z2
与y的夹角。
z
wz
w
wy
例 :矩形截面木檩条如图,跨长L=3.3m,受集度为 q=800N/m 的均布力作用, []=12MPa,容许挠度为:L/200 ,E=9GPa, 试校核此梁的强度和刚度。 解:1、外力分解 qz q sin 800 0.447 358N / m
qy q cos 800 0.894 714N / m
Fy
令 z0、y0 代表中性轴上任意点的坐标
M z y0 M y z0 0 Iz Iy
——中性轴方程 (过截面形心的一条斜直线)
2、找出危险点的位置(离中性轴最远的点); 3、最后进行强度计算。
例题: 图示外伸梁, 许用应力 [σ ]=160MPa (1)当横截面为矩形,校核此梁的强度; (2)若为圆截面,试设计截面尺寸。
3
tan
z 11.99 y 10.63
48.44o
2 2 2 max wz2max wy max 11.99 10.63 16.02(mm)
max
3.3 103 16.02(mm) w 16.5(mm) 200
例: 图示悬臂梁,承受载荷F1与F2作用,已知F1=800N,F2=1.6kN, l=1m,许用应力[σ ]=160MPa。试分别按下列要求确定截面尺寸: (1) 截面为矩形,h=2b;(2) 截面为圆形。
《组合变形》PPT课件

0.266q (12 ) 237 106
(21.5103) q
( max )D
M yD Wy
M zD Wz
0.444q (12 ) 31.5 106
0.456q (12 ) 237 106
(16.02 103) q
危险点在A截面上的外棱角D1和D2处
z
MyA
y
z
MzA
y
D1 z D2
y
32
l 几何参数
A 15103 m2 , zo 7.5 cm, I y 5310 cm4
l 求内力(作用于截面形心)
取研究对象如图
FN P kN,
M y 42.5 102 P kN.m
l 危险截面
各截面相同
l 应力分布
350
FN
33
l 危险截面
各截面相同
l 应力分布
l FN引起的应力
FN P MPa
u 拉伸、压缩
l 组合变形 有两种或两种以上的 基本变形同时发生。
u 剪切
l 求解组合变形的方法
将载荷分为几组分别产生 基本变形的载荷,然后应 用叠加原理。
u 扭转
u 弯曲
3
2 叠加原理 如果内力、应力、变形等与外力成线性关系, 则复杂受力情况下组合变形构件的内力、应 力、变形等可以由几组产生基本变形的载荷 单独作用下的内力、应力、变形等的叠加而 得到,且与各组载荷的加载次序无关。
'' My z Mz y
Iy
Iz
中性轴的方程:
My F1l
F2 (l a)
Mz
My Iy
z0
Mz Iz
y0
0
5
中性轴的方程:
第八章 组合变形5、6
A jy d t
jy P jy 141MPa [ jy] A jy
P4 P4 P4 P4
P
3P 4 P 4
p
+
1
P4 P4 P4 P4
P
1
(3) 钢板的拉伸强度
P 107 MPa [] 11 (b d )t
2
P4 P4 P4
1
P4
P
2
1
3P 4 99.3MPa [] 2 2 (b 2d )t
51.8MPa
§8-6
铆钉连接的主要方式
铆钉连接的计算
P
搭接 P
P P
一个受剪面
单盖板对接
P
P
P
P
一 个受剪面
(b)
双盖板对接
P
铆钉双剪切
P
P
P
两个受剪面
(c)
图 8-6
I、 铆钉组承受横向荷载
P
P
P
P
图 8-7
在铆钉组连接中, 为了简化计算, 假设: 不论铆接的方式如何, 均不考虑弯曲的影响。
T ' 2Q'
Q'
T ' T1 T
s
假想钢轨在接触面上处处传 递剪应力 τ ' ,接触面的宽 度为 b 。 T
S
T1
T ' τ ' bs
τ ' Q S* max z
T ' 2Q'
Q'
bI z
S
为一根钢轨的横截面 面积对中性轴的静矩
* z max
S
* z max
A.c 6406 m4
材料力学第八章组合变形的计算ppt文档
第八章 组合变形及连接部分的计算
故有中性轴的方程:
My Iy
z0
Mz Iz
y0 0
中性轴与y轴的夹角q(图a)为
taqnz0 Mz Iy Iy tan
y0 My Iz Iz
其中 角为合成弯矩 M My2 Mz2
与y的夹角。
第八章 组合变形及连接部分的计算
tanq Iy tan
Iz
这就表明,只要 Iy≠Iz ,中性轴的方向 就不与合成弯矩M的矢量重合,亦即合 成弯矩M 所在的纵向面不与中性轴垂直, 或者说,梁的弯曲方向不与合成弯矩M 所在的纵向面重合。正因为这样,通常 把这类弯曲称为斜弯曲。
强度条件为 r3 [] 或 r4 []
第八章 组合变形及连接部分的计算
注意到发生扭-弯变形的圆截面杆,其危险截面上危险点处:
M W
T T
Wp 2W
为便于工程应用,将上式代入式(a),(b)可得:
r3
M24T2 W 2W
M2T2 W
r4W M 232T W 2
M 20.7T 52 W
式中,M和T分别为危险截面上的弯矩和扭矩,W为圆截面的 弯曲截面系数。
在具体计算中,究竟先按内力叠加(按矢量法则叠加) 再计算应力和位移,还是先计算各基本形式变形下的应力 或位移然后叠加,须视情况而定。
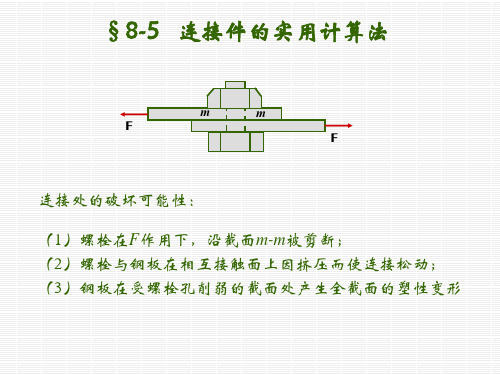
Ⅱ.连接件的实用计算
第八章 组合变形及连接部分的计算
连接件(螺栓、铆钉、键等)以及构件在与它们连接
处实际变形情况复杂。
螺栓连接(图a)中,螺栓主要受剪切及挤压(局部压 缩)。
应该注意,挤压应力是连接件与被连接件之间的相互作 用,因而当两者的材料不同时,应校核许用挤压应力较低的 连接件或被连接件。工程上为便于维修,常采用挤压强度较 低的材料制作连接件。
第八章组合变形完整版-精选
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
课件:材料-08组合变形_1_
F2z= F2cos80o=141N
FAz F1
A
B FAy
150
FCz Mx
z Mx F200
y
T
120 Nm
x
Mx=120Nm F2y= 800N F2z= 141N
②内力分析: 外力分量对应的内力
My (x) ; Mz (x) ;T(x)
内力图
FAz F1
A
B FAy
x
Mymax Fz L FLcosj
3. 应力分析 L
x
My
z
y
Fz Fy
Mz
F
M z引起的应力:
σMz
Mz y Iz
FLcosj
Iz
y
My引起的应力:
σM y
Myz Iy
FLcosj
Iy
z
t max
D
Mz Wz
My Wy
c max
B
Mz Wz
My Wy
任一点的应力:
FL co sj
内的绝对值最大正应力。
解:两柱均为压应力
F
F
d
F
1max
FN A1
M Wz1
200
300
200
图(1)
图(2)
350000 0.2 0.3
350 50 6 0.2 0.32
11.7MPa
2max
FN A
F M
350000 8.75MPa 0.2 0.2
§8–4 弯曲与扭转 弯扭组合变形工程实例
向力)不共面。
斜 弯 曲 的 工 程 实 例
二、斜弯曲的研究方法 :
1.外力分解:将外载沿横截面的两个坐标轴分解,于是得到 两个正交的平面弯曲。
8-第八章组合变形时的强度资料
第八章组合变形8.1 组合变形和叠加原理一、组合变形的概念1. 简单基本变形:拉、压、剪、弯、扭。
2. 组合变形:由两种或两种基本变形的组合而成的变形。
例如:烟囱、传动轴、吊车梁的立柱等。
烟囱:自重引起轴向压缩+ 水平方向的风力而引起弯曲;传动轴:在齿轮啮合力的作用下,发生弯曲+ 扭转立柱:荷载不过轴线,为压缩= 轴向压缩+ 纯弯曲Ph g水坝qPh g二、组合变形的计算方法1. 由于应力及变形均是荷载的一次函数,所以采用叠加法计算组合变形的应力和变形。
2. 求解步骤①外力分解和简化②内力分析——确定危险面。
③应力分析:确定危险面上的应力分布,建立危险点的强度条件。
§8.2 斜弯曲一、 斜弯曲的概念1. 平面弯曲:横向力通过弯曲中心,与一个形心主惯性轴方向平行,挠曲线在纵向对称面内。
2. 斜弯曲:横向力通过弯曲中心,但不与形心主惯性轴平行挠曲线不位于外力所在的纵向平面内。
二、斜弯曲的应力计算 1. 外力的分解对于任意分布横向力作用下的梁,先将任意分布的横向力向梁的两相互垂直的形心主惯性矩平面分解,得到位于两形心主惯性矩平面内的两组力。
位于形心主惯性平面内的每组外力都使梁发生平面弯曲。
如上所示简支梁。
2. 内力计算形心主惯性平面xOy 内所有平行于y 轴的外力将引起横截面上的弯矩z M ,按弯曲内力的计算方法可以列出弯矩方程z M 或画出z M 的弯矩图。
同样,形心主惯性平面xOz 内所有平行于z M 矩方程y M 或画出其弯矩图。
合成弯矩:2Z 2y M M M +=合成弯矩矢量M 与y 轴的夹角为:y z M Mtan =ϕ以上弯矩z M 和y M 均取绝对值计算,由力偶的矢量表示法可知,合成弯矩M 3. 计算xyz I zI y yz M M +=''+'=σσσ4. 轴的位置两平面弯曲组合成斜弯曲,只在横截面上正应力为零的点的连线才是斜弯曲的中性轴。
设中性轴上任一点的坐标)(00,y z ,将0y ,0z 代入应力计算公式,并令σ等于方程:零,得中性轴: 0M M 0y 0z =+yz I z I y中性轴与y 轴的夹角α,ϕαtan tan z z 00I I M M I I y z y y z y =⋅==5. 最大正压力中性轴把横截面分为两个区域,一个受拉区,另一个受压区,离中性轴最远的点,正应力最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N -
F A
在外力偶My、Mz作用下,横截面上任一点(y,z)的弯曲正 应力: Mz y Myz M Iz Iy
根据叠加原理得,偏心受压时,横截面上任一点(y,z)处 的正应力为:
F Mz y Myz - A Iz Iy
四、截面核心 当外力作用点位于横截形心附近的一个区域内时, 就可以保证中性轴不与横截面相交,这个区域称为截面 核心。此时,横截面上仅出现单一的拉应力或是压应力。 外力作用点离形心越近,中性轴距离形心就越远。
FN M max FN 6M max 73.3MPa 2 A Wy bh bh
最小正应力为
min
FN M max FN 6M max 6.7 MPa 2 A Wy bh bh
跨中截面上正应力分布图如图所示,假设中性轴离上边缘的
距离为z1,可求得
z1 1.26cm
bh2 4 82 128 3 Wy cm 6 6 3 hb2 8 42 64 3 Wz cm 6 6 3
B max
M yB Wy
M zB 93.75MPa Wz
在C截面: M yC 1kN m M zC 2kN m
C max
M y M cos j
m
x z z y L F x m Fz Fz
j
Fy
F y
Fy
②应力 My引起的应力: M z引起的应力:
Myz Iy
Mz cosj Iy
Mzy M y sin j Iz Iz
Myz Iy Mz y Iz
合应力:
m
FN M max A Wz
最大拉应力发生在危险截面的下边缘各点处,由于危险
点处于单向受力状态,其强度条件为:
max
三、偏心压缩(拉伸)
将偏心力F平移到顶截面的形心C处,得到轴向压力F, 以及力矩M y=FzF、Mz=FyF,如图所示。
在轴向压力F作用下,任一横截面上的正应力均匀分布:
max
M Wz
在扭矩T作用下引起的切应力为:
T IP
其分布如图(c)示,在边缘处各点切应力最大, T max WP
从图(b)(c)可见,上下边缘的点K1、K2即有最大正应力又有
最大切应力,是截面的危险点。图(d)所示为K1的应力单元
体,K1、K2两点均属平面应力状态,且两点的正应力和切应 力都是相等的,所以可以任意取一点研究。 为建立强度条件,需先算出危险点的主应力:
T F A T F
F 4 50 3 10 6.37 MPa 2 A 0.1
A
T 167000 35.7MPa 3 Wn 0.1
r 3 2 4 2
6.372 435.7 2 71.7MPa
安全。
28
作业: P41 49; P43 60; P77 6
1
第八章 组合变形
§8-1 概述
§8-2 两相互垂直平面内弯曲的组合 §8-3 拉伸(压缩)与弯曲的组合
§8-4 弯曲与扭转的组合
1
§8-1 概述
一、组合变形 :在复杂外载作用下,构件的变形会包含几种简
单变形,当几种变形所对应的应力属同一量级时,不能忽略
之,这类构件的变形称为组合变形。
F z x y F F
例题1:矩形截面简支梁,q=30kN/m,F=500kN, 求梁内最 大正应力及跨中截面上中性轴位置。
解:梁内最大正应力发生在跨中截面的下边缘处,该截面上 弯矩最大,其值为
1 M max ql 2 15 kN m 8
该截面上轴力为 FN F 500kN
故最大正应力为
max
面弯曲。
Fz z
x
j
Fy
F y z y Fz
Fy
F
2.叠加:对两个平面弯曲进行研究;然后将计算结果叠加起来。
x z z y
Fz
j
Fy
F y
Fz F
Fy
解:1.将外载沿横截面的形心主轴分解 Fy F sin j Fz F cosj 2.研究两个平面弯曲 ①内力
M z Fy (L x) F (L x) sin j M sin j
危险截面在A截面,危险点
在其上下边缘 。
3ql2 在A截面上: M 2 ql2 T 2
q
C
l
按第三强度理论:
r 3
1 Wz M 2 T 2
安全
例题: 直径为 d=0.1m的圆杆受力如图,T=7kNm,F=50kN, []=100MPa,试按第三强度理论校核此杆的强度。 解:拉扭组合,危险点应力状态如图
例题2:求图示杆在力F作用下的最大拉应力,并指明所在 位置。
100
200
F=100kN
t max
F A hb2 6
F
b 2
----发生在后铅垂面各点上。
§ 8–4
弯曲与扭转的组合
如图所示,圆轴在某一截面上即有弯矩M又有扭矩T。
在弯矩M作用下引起的正应力为:
My Iz
其分布如图(b)示,在上下边缘处正应力最大,
r 3
1 Wz 1 Wz M 2 T 2 M 2 0.75T 2
r 4
例题:图示水平放置的圆截面直角刚折杆,直径d=100mm, l=2m,q=1kN/m,[σ]=160MPa 。校核该杆的强度。
l q
解:1.荷载简化 2 .内力图(M图、T图)
B
A
在中性轴两侧,距中性轴最远的点为拉压最大正应力点。 ⑤强度条件 危险点一般处于单向应力状态,故: max
说明:
1.中性轴是一条通过截面形心的直线,一般情况下 I I y z
所以中性轴与外力所在的平面不垂直。而梁弯曲变形时的 位移总是垂直于中性轴,因此梁变形后的轴线(即挠曲线) 不在外力所在的平面内,这种弯曲就是斜弯曲。 2.对于有棱角的对称截面(矩形、工字型、箱型),其最
1 1 ( 2 4 2) 2
2 0
3 ( - 2 4 2)
1 2
若采用第三强度理论,将主应力代入得:
r 3 2 4 2
若采用第四强度理论,将主应力代入得:
r 4 2 3 2
对于实心或是空心圆轴,WP=2Wz,所以:
x z
Fz
j
Fy F y
z
y
x
m
L
Fz F
Fy
Myz Iy
Mz y Iz
应力符号规定
M y z0 Iy M z y0 0 Iz
中性轴
③中性轴方程
z
D1
D2
中性轴与z轴夹角 tan y0 I z ctan j
z0 Iy
Fz
j
Fy F y
④最大正应力
大正应力的位置可直接平判别出来。
3.对于圆形、正方形截面 I y I z ,正应力可直接用合成 弯矩进行计算。
例1:简支梁受力如图示,已知材料的许用应力 120MPa 试对(1)矩形截面b=40mm ,h=80mm (2)圆截面,直 径d=65mm,分别校核梁正应力强度。
解:作梁的弯矩图。 (1)矩形截面:可能的危险截面为B,C截面 在B截面: M yB 2kN m M zB 1kN m
T
二、组合变形的研究方法 —— 叠加原理 ①外力分析:外力向形心(或弯曲中心)简化并沿主惯性轴分 解。 ②内力分析:求每个外力分量对应的内力方程和内力图,确
定危险面。
③应力分析:画危险面应力分布图,叠加,建立危险点的强 度条件。
§12–2
一、研究方法 :
两相互垂直平面内弯曲的组合
1.分解:将外载沿横截面的两个形心主轴分解,得到两个正交的平
30
29
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
max
所以,圆截面梁的正应力强度也满足要求。
§ 8– 3
拉伸(压缩)与弯曲的组合
生的变形。
一、拉(压)弯组合变形:杆件同时受横向力和轴向力的作用而产
二、应力分析: 在轴向拉力F1 作用下,各截面上有相同的轴力FN=F1, 而在横向力F2作用下,固定端截面上弯矩最大,Mmax=F2L。 因此固定端截面为杆的危险截面。
N 危险截面上,与轴力对应的正应力为: N A
F
与弯矩对应的正应力为: M M max y Iz 叠加得,危险截面上任一点y处的正应力为:
FN M max y A Iz
FN M max y A Iz
上式表明,正应力沿截面高度呈线性分布,中性轴不通 过截面形心。
max
M yC Wy
M zC 117.2MPa Wz
所以,矩形截面梁的正应力强度满足要求。 (2)圆截面:危险截面为B或C截面,二者同等危险。
2 其合成弯曲为: M M y M z2 2.236kN m
W
d 3
32
26.96cm3
M W 82.94MPa
