第六章习题答案数值分析
钢结构习题答案第6章

钢结构习题答案第6章第6章钢结构习题答案钢结构是一种广泛应用于建筑和工程领域的结构材料。
它具有高强度、耐腐蚀、抗震等优点,因此被广泛应用于大型建筑、桥梁、塔楼等工程中。
然而,钢结构的设计和施工并不简单,需要经过严格的计算和分析。
本文将针对钢结构的第6章习题提供详细的解答,帮助读者更好地理解和掌握钢结构的相关知识。
1. 问题:一根长度为10m的钢梁,截面为矩形,宽度为200mm,高度为400mm。
如果梁的材料为Q345B,弹性模量为200GPa,计算梁的弯矩和最大应力。
解答:首先计算梁的惯性矩I,根据矩形截面的公式I=(1/12)bh^3,代入宽度和高度的数值,得到I=(1/12)×0.2×0.4^3=0.00533m^4。
然后计算梁的弯矩M,根据梁的长度和材料的弹性模量,使用弯矩公式M=EI/R,其中E为弹性模量,I为惯性矩,R为曲率半径。
曲率半径可以通过梁的长度和挠度计算得到,挠度可以通过梁的受力和材料的弹性模量计算得到。
假设梁的受力为F,根据受力平衡,可以得到F=mg,其中m为梁的质量,g为重力加速度。
将质量和重力加速度的数值代入,得到F=780N。
根据梁的受力和挠度的关系,可以得到挠度δ=F×L^3/(48EI),将受力、长度、弹性模量和惯性矩的数值代入,得到挠度δ=0.00026m。
最后,根据挠度和曲率半径的关系,可以得到曲率半径R=δ/(2L^2),将挠度和长度的数值代入,得到曲率半径R=0.0000013m。
将弹性模量、惯性矩和曲率半径的数值代入弯矩公式,可以得到弯矩M=200GPa×0.00533m^4/0.0000013m=820000N·m。
最大应力可以通过弯矩和截面惯性矩的关系计算得到,最大应力σ=M×h/2I,将弯矩、高度和惯性矩的数值代入,得到最大应力σ=820000N·m×0.4m/(2×0.00533m^4)=307MPa。
微积分第六章习题解答

2
3、利用定积分的几何意义,说明下列等式: 利用定积分的几何意义,说明下列等式: 1 1 π 2
(1)
∫ 0 2 x dx = 1 ;
y
y = 2x
(2)∫
0
1 − x dx =
y
4
;
2
x2 + y2 = 1
o
1 x
o
(3) ∫
π
−π
sin x dx = 0 ;
( 4)
∫
π
1
x
2 π − 2
cos x dx = 2∫ 2 cos x dx .
1 1 e−x 0 1 dx + ∫ dx = − ln(1 + e − x ) + ln(1 + x ) =∫ 01+ x −1 1 + e − x 0 −1
e ⋅ y ′ + cos x = 0 ,
y′ = −
cos x e
y
.
11
4、求下列极限: 求下列极限: (2) lim
∫ 0 arctan t dt
x2
x
0 " "型 0
arctan x 1 = lim = . x →0 2x 2
x →0
sin 2 t dt ∫π
x
(3) lim π
x→ 2
2
F ′( x ) = f ( x ) + x f ′( x ) ,
∃c ∈ (ξ ,1) ⊂ (0,1) , 使 F ′( c ) = 0 ,即 f (c) + c f ′(c) = 0 ,
f (c ) 而 c > 0 , 即有 f ′(c ) = − . c
数学分析课本(华师大三版)-习题及答案第六章(20200511214800)

第六章 微分中值定理及其应用2•若 lim1 acosx -bsin ^1,则 a = X T 0 x 23.曲线y = e x在x = 0点处的曲率半径 R = _______ 4•设y =4x J —2,则曲线在拐点处的切线方程为 ___________________x6•设f(x) =x(x 2 —1)(x —4),则f (x) = 0有 ______________ 个根,它们分别位于 __________区间;7.函数f (x) =xln x 在1,2 ]上满足拉格朗日定理条件的© = _________________8•函数f(x)=x 3与g(x)=1+x 2在区间b,2】上满足柯西定理条件的 E = ____________9.函数y =sinx 在0,2】上满足拉格朗日中值定理条件的©= ______ ;xe 10. _________________________________________ 函数f(x) 2的单调减区间是 ;x311. ________________________________ 函数y = x -3x 的极大值点是 ,极大值是 。
12. _________________________________________ 设f(x)=xe x ,则函数f (n)(x)在X 二 处取得极小值 ________________________________________ 。
3 213. 已知f(x)二x ax bx ,在x =1处取得极小值- 2,则a = _________________ , b = _____2 2一、填空题1若a 0,b0均为常数,贝U5. lim(1 x )x -ex —.Qx2XaH XX14. 曲线y =k(x -3)在拐点处的法线通过原点,则k= _______ 。
15 •设 f (x)二 n (1 - x)n(n =1,2 ) , M n 是 f (x)在〔0,1 上的最大值,则lim M n = ________ 。
第六章习题解答(精品)

第六章习题解答6.1 指出下列平衡系统中的组分数C,相数P,及自由度数F。
(1) I2(S)与其蒸气成平衡;(2)CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡;(3) NH4HS(s)放入一抽空的容器中,并与其分解产物NH3(g)和H2S(g)成平衡;(4)取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡;(5) I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡(凝聚系统)。
解:(1)C=1;P=2;F=1-2+2=1(2)C=2;(∵S=3;R=1,∴C=3-1=2);P=3;F=2-3+2=1(3)C=S-R-R'=3-1-1=1(浓度限制条件,产物成NH3(g):H2S(g)=1:1);P=2; F =1(4)C=3-1=2;P=2;F=2(5)C=3;P=2;F=C-P+1=3-2+1=2(凝聚相可以不考虑压力的影响)6.2 已知液体甲苯(A)和液体(B)在90℃时的饱和蒸气压分别为P A=54.22kPa和P B=136.12kPa。
两者可形成理想液态混合物。
今有系统组成为x B,0=0.3的甲苯-苯混合物5mol,在90℃下成气-液两相平衡,若气相组成为y B=0.4556求:(1)平衡时液相组成x B及系统的压力P;(2)平衡时气、液两相的物质的量n(g),n(l)。
解:(1)y A=1-0.4556=0.5444P A=P A*·x A=P A*(1-x B)=P·y AP B=P B*·x B=P·y B∴(2)n(l)+n(g)=5moln(l)·(x B.0-x B)=n(g)·(y B- x B.0)n(l)·(0.3-0.2500)=[5mol-n(l)](0.4556-0.3)n(l)=3.784moln(g)=(5-3.784)mol=1.216mol6.3 单组分系统硫的相图如下图。
数值分析习题(含答案)

第一章 绪论姓名 学号 班级习题主要考察点:有效数字的计算、计算方法的比较选择、误差和误差限的计算。
1 若误差限为5105.0-⨯,那么近似数0.003400有几位有效数字?(有效数字的计算) 解:2*103400.0-⨯=x ,325*10211021---⨯=⨯≤-x x 故具有3位有效数字。
2 14159.3=π具有4位有效数字的近似值是多少?(有效数字的计算) 解:10314159.0⨯= π,欲使其近似值*π具有4位有效数字,必需41*1021-⨯≤-ππ,3*310211021--⨯+≤≤⨯-πππ,即14209.314109.3*≤≤π即取(3.14109 , 3.14209)之间的任意数,都具有4位有效数字。
3 已知2031.1=a ,978.0=b 是经过四舍五入后得到的近似值,问b a +,b a ⨯有几位有效数字?(有效数字的计算)解:3*1021-⨯≤-aa ,2*1021-⨯≤-b b ,而1811.2=+b a ,1766.1=⨯b a 2123****102110211021)()(---⨯≤⨯+⨯≤-+-≤+-+b b a a b a b a故b a +至少具有2位有效数字。
2123*****10210065.01022031.1102978.0)()(---⨯≤=⨯+⨯≤-+-≤-b b a a a b b a ab 故b a ⨯至少具有2位有效数字。
4 设0>x ,x 的相对误差为δ,求x ln 的误差和相对误差?(误差的计算) 解:已知δ=-**xx x ,则误差为 δ=-=-***ln ln xx x x x则相对误差为******ln ln 1ln ln ln xxx x xxx x δ=-=-5测得某圆柱体高度h 的值为cm h 20*=,底面半径r 的值为cm r 5*=,已知cm h h 2.0||*≤-,cm r r 1.0||*≤-,求圆柱体体积h r v2π=的绝对误差限与相对误差限。
材料力学课后习题答案6章
由切应力互等定理可知,纵截面上的切应力 τ x 与 τ 2max 一样大。 左、右端面上弯曲正应力构成的轴向合力分别为
Fx1 =
bh Fa 1 σ1max ( ) = 2 2 2h bh Fa 1 Fx 2 = σ 2max ( ) = h 2 2
左、右端面上弯曲切应力构成的竖向合力大小相等,其值为
(也可用左侧题号书签直接查找题目与解)
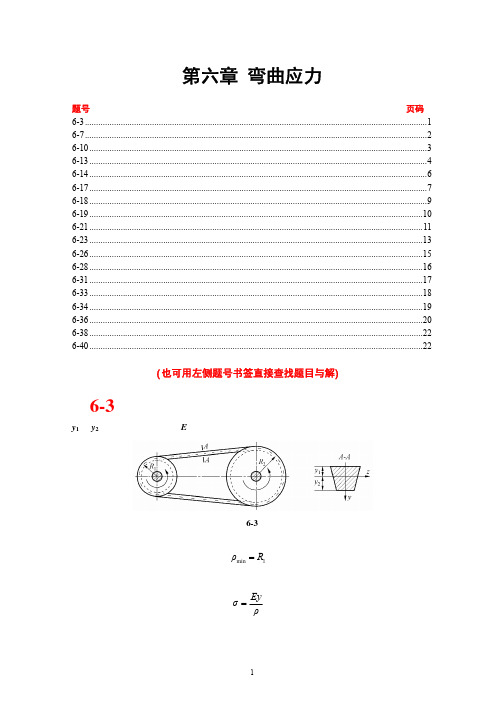
6-3
图示带传动装置,胶带的横截面为梯形,截面形心至上、下边缘的距离分别为
y1 与 y2,材料的弹性模量为 E。试求胶带内的最大弯曲拉应力与最大弯曲压应力。
题 6-3 图 解:由题图可见,胶带中性层的最小曲率半径为
ρmin = R1
依据
σ=
Ey ρ
可得胶带内的最大弯曲拉应力和最大弯曲压应力分别为
Fy 1 = F y 2 =
1ห้องสมุดไป่ตู้F 6
Fa 2h
顺便指出,纵截面上弯曲切应力构成的轴向合力为
FSx = τ x ( ab) =
3.检查单元体的平衡方程是否满足
∑F ∑F
x
= 0,Fx 2 − Fx1 − FSx = = 0,Fy1 − Fy 2
y
Fa Fa Fa − − =0 h 2 h 2h F F = − =0 6 6
题 6-10 图 解:1.查№18 工字钢的有关数据 工字钢截面大致形状及尺寸符号示如图 6-10。
图 6-10 由附录 F 表 4 查得
h = 180mm,b = 94mm t = 10.7mm,I z = 1660cm 4,Wz = 185cm 3
2.计算顶边 AB 的长度改变量 顶边处有
3
σ max =
计算中用到 h1 = h / 2 − t = 79.3mm。
第六章_常微分方程初值问题的数值解法_习题课
h2 h3 y ( x n ) y ( x n ) O(h 4 ) 2 6 而且 y ( x n ) f ( x n , y ( x n )) , y ( x n 1 ) f ( x n 1 , y ( x n 1 )) ,对 y ( x n 1 ) 也在 x n 处作 Talor 展开, y ( x n 1 ) y ( x n ) hy ( x n )
湖北民族学院理学院《数值计算方法》教学辅导材料
陈以平编写
h2 h3 y ( x n ) y ( x n ) O(h 4 ) 2 6 h h h2 h3 y ( x n ) y ( x n ) y ( x n ) y ( x n ) y ( x n ) O(h 4 ) 2 2 2 12 h3 y ( x n ) O(h 4 ) O(h 3 ) 12 h3 所以,梯形公式是 2 阶方法,其截断误差的主项是 y ( x n ) 。 12 y ( x n ) hy ( x n )
y k (0.9 0.1y k sin x k ) 0.1( y k 1 y k 1 sin x k 1 )
2
当 k=0,x0=1, y0=1 时,x1=1.2,有 y y (. . y sin x ) (. sin ) .
y f ( x, y ) 3.求解初值问题 欧拉法的局部截断误差是( y ( x ) y 改进欧拉法的局部截断误差是( ); 四阶龙格-库塔法的局部截断误差是( ). (A)O(h2) (B)O(h3) (C)O(h4) (D)O(h5)
4. 改进欧拉法的平均形式公式是( ) y p y k hf ( x k , y k ) y p y k hf ( x k , y k ) (B) y c y k hf ( x k , y p ) .(A) y c y k hf ( x k , y p ) y k ( y p y c ) y k ( y p y c ) y p y k hf ( x k , y k ) y p y k hf ( x k , y k ) (C) y c y k hf ( x k , y p ) (D) y c y k hf ( x k , y p ) y k h ( y p y c ) y k ( y p y c ) (D) 答案:
建筑结构第六章习题讲解
第六章习题参考答案6—1 某刚性方案房屋砖柱截面为490mm ×370mm ,用MU10烧结普通砖和M2.5混合砂浆砌筑,计算高度为4.5m 。
试验算该柱的高厚比。
〖解〗已知:[β]=15,H o =4500mm ,h = 370 mm15][16.12mm370mm 4500h H 0=<===ββ 该柱满足高厚比要求。
6—2 某刚性方案房屋带壁柱,用MU10烧结普通砖和M5混合砂浆砌筑,计算高度6.7m 。
壁柱间距3.6m ,窗间墙宽1.8m 。
带壁柱墙截面面积5.726×105mm 2,惯性矩1.396×1010mm 4。
试验算墙的高厚比。
〖解〗已知:[β]=24,H o =6700mm 带壁柱墙折算厚度mm mmmm A I h T 5.54610726.510396.15.35.325410=⨯⨯== 承重墙 μ1=1; 有窗洞 μ2=1-0.4b s /s =1-0.4×1.8/3.6=0.8β= H o / h T = 6700/546.5 = 12.26<μ1μ2 [β]=1.0×0.8×24 = 19.2该窗间墙满足高厚比要求。
6—3 某办公楼门厅砖柱计算高度5.1m ,柱顶处由荷载设计值产生的轴心压力为215kN 。
可能供应MU10烧结普通砖,试设计该柱截面(要考虑砖柱自重。
提示:要设定截面尺寸和砂浆强度等级后验算,但承载力不宜过大)。
〖解〗假定采用MU10烧结普通砖、M5混合砂浆砌筑490m m ×490mm 砖柱, a = 0.0015 则砖柱自重设计值为 G=1.2×0.49×0.49×5.1×19=27.9kN该柱所承受轴心压力设计值为 N=215+27.9 = 242.9 kN由于柱截面面积A=0.49×0.49=0.2401m 2<0.3m 2,则γa =0.7+A=0.94该柱高厚比为24240.10.1][4.104905100H 210=⨯⨯=<===βμμβmmmm h 影响系数为86.04.100015.01111220=⨯+=+==αβϕϕ 故N u = γa φf A =0.94×0.86×1.5×4902=291145N=291.1kN >N=242.9kN所以,采用MU10烧结普通砖、M5混合砂浆砌筑490m m ×490mm 砖柱能够满足承载力要求。
(完整版)数值分析部分课后答案第二版朱晓临
数值分析第二版 朱晓临第一章 习题3.324.045≈324.0 60.0876≈60.090.00035167≈0.0003517 2.00043≈2.000 6.①**x x x-≤51441111111010100.005%222a a -+--⨯=⨯⨯≤⨯=(1≤1a ≤9) 故它的相对误差限为0.005%②∵*12120....100....10n n n n x a a a a a a =±⨯=⨯<()10.110na +⨯相对误差限=0.03%***3311*n n n x x x x x x----=⨯⨯⨯⨯⨯⨯<0.03%0.(a +1)10=0.3(0.a +1)10<0.510 ∴至少有3位有效数字。
7.6*1), 1.4,0.004096A A =≈=则1.4≈时,⑴()610.005232781≈⑵(330.008-≈⑶()310.0051252613≈+⑷991-≈所以利用第三个得到的计算结果的绝对误差最小。
8.由函数的绝对误差公式:***(())'()()e f x f x e x ≈ ① 令2**2*(),()(),100f x x f x x x ===cm由题目得,*(())1e f x =,**'()2f x x = ②把②代入①,得: 1≈**2()x e x ⋅ 1≈*2100()e x ⨯⋅ *()e x 0.005cm ≈边长的测量误差不超过0.005cm 时,才能使其面积的误差不超过12cm 。
11.**()ln ,()ln f x x f x x ==令则由公式***(())'()()e f x f x e x ≈,得: ***1(())0.510e f x x x l x≈-<⨯- 又***()r x x x xε-≤, 由此可知,*()0.510l r x ε-=⨯所以*x 的相对误差限为0.510l -⨯,有l 位有效数字。
化工问题的建模与数学分析方法 第6章 习题及答案
第六章习题1. 用摄动法求解以下三次代数方程3(1)x x a证明其三个根的渐进展开式为...)3(5231+++=a a a x εε...])2(1[12+-+=ax εε...])2(1[13+-+-=ax εε将以上解与数值解或准确解比较,取01.0=ε和0.1,讨论其结果。
解:a x x -=3ε,1<<ε (1) ① 证明:(A )设解具有如下形式的渐进展开式+++=2210x x x x εε(2)将其代入(1)式,可得)/31(01302210 +++=+++x x x a x x x εεεε(3)比较两边ε的同幂次项系数,得到)1(O : a x =0)(εO : 331a x x == )(2εO : 501233a x x x ==所求摄动解为: +++=)3()1(522a a a x εε由于方程(1)有三个根,用上述摄动法只能求得一个根,即接近退化解a x =0的那个根。
(B) 做变换ε/u x =,代入方程(1),可得,a u u ε-=3(4)此时,小参数ε不在最高次幂项上。
设此时解u 具有如下形式的渐进展开式,++=10u u u ε(5)将其代入(4)式,可得)/31(013010 +++=++u u u a u u εεε(6)比较两边ε的同幂次项系数,得到10=u 或 10-=u21a u -=所以,可得方程(1)的另外两个解,⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛-+=211)2(a x εε ⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛-+-=211)3(a x εε 至此,方程(1)三个根的渐进展开式为:+++=)3()1(522a a a x εε⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛-+=211)2(a x εε ⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-+-=211)3(a x εε② 上述三个渐进解分别与准确解和数值解的比较分析。
(1)采用Matlab 的符号工具箱,求得方程(1)的三个准确解分别为(其中epsilon 表示ε): x(1) =1/6/epsilon*((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)+2/((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3) x(2) =-1/12/epsilon*((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)-1/((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)+1/2*i*3^(1/2)*(1/6/epsilon*((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)-2/((-108*a+12*3^(1/2)*((-4+27*a^2*epsi lon)/epsilon)^(1/2))*epsilon^2)^(1/3)) x(3)=-1/12/epsilon*((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)-1/((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)-1/2*i*3^(1/2)*(1/6/epsilon*((-108*a+12*3^(1/2)*((-4+27*a^2*epsilon)/epsilon)^(1/2))*epsilon^2)^(1/3)-2/((-108*a+12*3^(1/2)*((-4+27*a^2*epsil on)/epsilon)^(1/2))*epsilon^2)^(1/3))当1.0=ε时,x(1) = 1/3*(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)+10/(-135*a+15*(-120+81*a^2)^(1/2))^(1/3) x(2) =-1/6*(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)-5/(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)+1/2*i*3^(1/2)*(1/3*(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)-10/(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)) x(3) =-1/6*(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)-5/(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)-1/2*i*3^(1/2)*(1/3*(-135*a+15*(-120+81*a^2)^(1/2))^(1/3)-10/(-135*a+15*(-120+81*a^2)^(1/2))^(1/3))当01.0=ε时,x(1) = 1/3*(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)+100/(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3) x(2) =-1/6*(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)-50/(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)+1/2*i*3^(1/2)*(1/3*(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)-100/(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)) x(3) =-1/6*(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)-50/(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)-1/2*i*3^(1/2)*(1/3*(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3)-100/(-1350*a+150*(-1200+81*a^2)^(1/2))^(1/3))(2)为了清楚地比较渐进解与数值解的偏离程度,在本题中选取了10,9,,0,,9,10 --=a ,分别求得了渐进解和数值解,如表1和表2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章习题解答 2、利用梯形公式和Simpson公式求积分21lnxdx的近似值,并估计两种方法计算值的最大误差限。 解:①由梯形公式: 21ln2()[()()][ln1ln2]0.3466222baTffafb
最大误差限 3''
2
()111()()0.083312121212TbaRff
其中,(1,2) ②由梯形公式: 13()[()4()()][ln14ln()ln2]0.38586262babaSffaffb
最大误差限 5(4)
4
()66()()0.0021288028802880SbaRff,
其中,(1,2)。 4、推导中点求积公式 3''()()()()()()224baabbafxdxbaffab
证明:构造一次函数P(x),使'''',()(),()02222ababababPfPfPx 则,易求得'()()()()222abababPxfxf 且'()()()()222bbaaabababPxdxfxfdx 0()()()22baababfdxbaf,令()()baPxdxIf
现分析截断误差:令'()()()()()()()222abababrxfxPxfxfxf 由'''()()()2abrxfxf易知2abx为()rx的二重零点, 所以可令2()()()2abrxxx, 构造辅助函数()()()()()2abKtftPtxt,则易知: ()02abKxK
其中2abt为二重根()Kt有三个零点
由罗尔定理,存在''''''()(,)()0()2()0()2fabKfKxKx使即
从而可知''2()()()()()22fabrxfxPxx 截断误差
''2()()()()()()()()22bbbbaaaafabRffxdxIffxPxdxrxdxxdx
2()2abx
在(a,b)区间上不变号,且连续可积,由第二积分中值定理
''''322''()()()()()()()(,)222224bbaafabfabbaRfxdxxdxfab
综上所述3''()()()()()()()224baabbafxdxIfRfbaff 证毕 6、计算积分10xedx,若分别用复化梯形公式和复化Simpson公式,问应将积分区间至少剖分多少等分才能保证有六位有效数字? 解:①由复化梯形公式的误差限
32''522()1()()101212122TbabaeRfhfenn
可解得:212.85n 即至少剖分213等分。 ②由复化梯形公式的误差限
4(4)5411()()10288028802SbaRfhfen
可解得:3.707n 即至少剖分4等分。
7、以0,1,2为求积节点,建立求积分30()Ifxdx的一个插值型求积公式,并推导此求积公式的截断误差。 解:在0,1,2节点构造lagrange插值多项式,则有
2012()()(0)()(1)()(2)Pxlxflxflxf (1)(2)(2)(1)(0)(1)(2)(01)(02)(10)(12)(20)(21)xxxxxxfff
则(3)233()()()()()(1)(2)3!ffxPxxxxxx 对上式在[0,3]上求积分,则有 (3)333
23000
()()()()3!ffxdxPxdxxdx
其中 3333222
20000
32332333000
(0)(2)()(32)((1))(2)()22(0)131(2)11[2](1)[][]2323232(0)3(2)9222239(0)(2)44ffPxdxxxdxfxxdxxxdxffxxxfxxxxffff
再分析截断误差 3(3)
0
1()()(1)(2)3!Rffxxxdx 此处分段处理
即23(3)(3)120211()()(1)(2)()(1)(2)()()3!3!RffxxxdxfxxxdxRfRf 1)其中,对于2(3)101()()(1)(2)3!Rffxxxdx 由于(1)(2)xxx在[0,2]上不保持常号 故考虑构造一个三次多项式()Fx满足下列插值条件: ''''(0)(0)(1)(1)(2)(2)(1)(1)(2)(2)FfFfFfFfFf
由Hermite插值方法,有 (4)21()()()(0)(1)(2)4!fxFxfxxxdx
则22(4)21001()[()()]()(1)(2)4!RffxFxdxfxxxdx 显然此时2(1)(2)xxx在[0,2]上恒小于等于0.于是由第二积分中值定理 2(4)2
110
2(4)432
10
(4)54322(4)101
1()()(1)(2)4!1()(452)4!1151()[]()4!5390Rffxxxdxfxxxxdxfxxxxf
2)其中3(3)221()()(1)(2)3!Rffxxxdx 显然(1)(2)xxx在[2,3]上恒正.于是由第二积分中值定理 3(3)
222
3(3)32(3)
222
1()()(1)(2)3!13()(32)()3!8Rffxxxdxfxxxdxf
综上,截断误差(3)(4)122131()()()()()890RfRfRfff 所以 3(3)(4)2103931()(0)(2)()(()()())44890IfxdxffRfRfff 8、(1)试确定下列求积公式中的待定系数,指出其所具有的代数精度。 )](')0('[)]()0([2)(20hffhhffhdxxfh
解:分别将1)(xf,x代入求积公式,易知求积公式精确成立。 代入2)(xxf,令求积公式精确成立,于是有:
333
23,3hhh右左
可解得:121 代入3)(xxf,于是有
442,44444hhhh右左
左=右,求积公式成立。 代入4)(xxf,于是有 632,54455hhhh右左 右左,求积公式不精确成立。
综上可知,该求积公式具有三次代数精度。
9、对积分dxxxf102)1)((,求构造两点Gauss求积公式,要求:
(1)在[0,1]上构造带权21)(xx的二次正交多项式; (2)用所构造的正交多项式导出求积公式。 解:(1)构造在[0,1]上构造带权函数21)(xx的正交多项式)(0xQ、)(1xQ、)(2xQ,
取1)(0xQ、)()()(011xQxxQ ,
其中83)1()1()](),([)](),([10210200001dxxdxxxxQxQxQxxQ, 则83)(1xxQ。 同理,95111916)(22xxxQ,求)(2xQ的零点得: 17306907.00x,66903619.01x
求积系数: 39523617.0)(1000dxxlA
27143053.0)(1011dxxlA (2)求(1)可导出求积公式: )()()1)((1100102xfAxfAdxxxf
)66903619.0(27143053.0)17306907.0(39523617.0ff 11、试用三点Gauss-Legendre公式计算dxx311并与精确值比较。 解:设三点Gauss-Legendre求积节点为:
5150t,01t,5152t
相应求积系数为:
