七年级数学整式的乘法3
七年级数学下册整式的乘法整式的乘法多项式的乘法多项式乘多项式

次二项式的乘法
5. 已知(x+3)(x-2)=x2+ax+b,则 a,b 的值分别
是( B )
A.a=-1,b=-6 B.a=1,b=-6
C.a=-1,b=6
D.a=1,b=6
2019年6月9日
你是眼中最美的风景
6
6. 下 列 多 项 式 相 乘 的 结 果 为 x2 + 3x - 18 的 是
(D )
A.x2+3x+2
B.3(x-1)(x-2)
C.x2-3x+2
D.x3-3x2+2x
2019年6月9日
你是眼中最美的风景
9
11. 计算:(a-b)(a+2b)=_a_2_+__a_b_-__2_b_2_; (x+5y)(2x-y)=_2_x_2_+__9_x_y-__5_y_2__.
12. 定义ac db为二阶行列式,规定它的运算法则为
2019年6月9日
你是眼中最美的风景
2
知识点 多项式乘多项式
1. (2018·武汉)计算(a-2)(a+3)的结果是( B )
A.a2-6
B.a2+a-6
C.a2+6
D.a2-a+6
2. 下面的计算结果为 3x2+13x-10 的是( C )
A.(3x+2)(x+5)
B.(3x-2)(x-5)
C.(3x-2)(x+5)
2019年6月9日
你是眼中最美的风景
8
9. 若(x+2)(x-1)=x2+mx+n,则 m+n=( C )
A.1
B.-2
C.-1
D.2
10. (2018·镇江模拟)学校买来钢笔若干支,可以平均
分给(x-1)名同学,也可分给(x-2)名同学(x 为正整
数).用代数式表示钢笔的数量不可能的是( A )
七年级下册数学整式的乘除

七年级下册数学整式的乘除
在七年级下册数学中,学习了一些关于整式的乘除运算。
下面是一些相关的知识点:
1. 整式的乘法:整式的乘法是指将两个或多个整式相乘的运算。
乘法的运算法则包括:同底数幂相乘、同底数幂相除、乘法分配律等。
例如,(2x + 3)(4x - 5) = 8x^2 - 10x + 12x - 15 = 8x^2 + 2x - 15。
2. 整式的除法:整式的除法是指将一个整式除以另一个整式
的运算。
在整式除法中,除数不能为零。
除法的运算法则包括:整式除整式、整式除单项式、整式除多项式等。
例如,(6x^2 + 3x) ÷ 3x = 2x + 1。
3. 整式的约分:整式的约分是指将一个整式的各项的公因式
提取出来并约去的运算。
约分可以简化整式的形式,使其更简洁。
例如,6x^2 + 9x可以约分为3x(2x + 3)。
这些是七年级下册数学中关于整式的乘除运算的一些基本知识点。
希望对你有帮助!。
11.1整式的乘法 课件 七年级数学上册(沪教版2024)

=a²+3+a¹+4 =2a⁵
十观察
(23)²=2³×2³=2³+3=2³×2
(a³)²=a³·a³=a³+3=a³×2
(am)²=am·am=am+m=a²m(m是正整数)
一般地,设m 、n是正整数,如何计算(am)n?
(am)n=am.am..... ·am =amn
(乘方的意义) (同底数幂的乘法性质)
(4)-x·x²·x4;
(5)(x+y)³×(x+y)⁵;
(6)(-a³)·(-a²)·a⁴.
解:(1)84×8³=84+3=87
(4)-x·x²·x⁴;=(-1)·x·x²·x⁴=-x¹+2+4=-x⁷
(2)(-10)⁴×(-10)³=(-10)4+3=(-10)⁷
(5)(x+y)³×(x+y)⁵=(x+y)³+5=(x+y)⁸
)
(乘方的意义
同底数幂的乘法性质:
alm.a=am+n(m、n是正整数) 同底数幂相乘,底数不变,指数相加。
同底数幂的乘法运算
指数的加法运算
例1计算下列各式,结果用幂的形式表示:
(1)10² ×103;
(3)aห้องสมุดไป่ตู้·a⁴;
解:(1)10²×10³=102+3=105
(4)(a-b)·(a-b)³; (5)y·y²·y³.
3.随着科技的发展,纳米技术的运用越来越广泛。1米=109纳米,那 么1米²=1018_纳米2.
解: 1米=109纳米
1米²=(109)2纳米²=1018纳米2
第4讲整式的乘法(3个知识点+3种题型+过关检测)(教师版) 24-25学年七年级数学上册(沪教版)
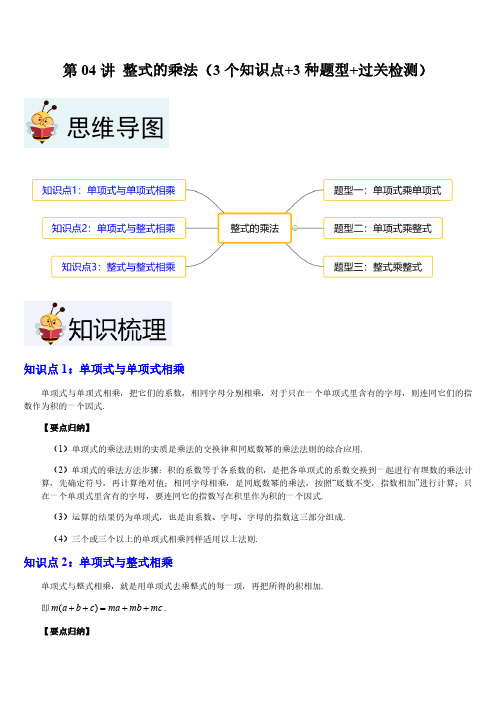
第04讲 整式的乘法(3个知识点+3种题型+过关检测)知识点1:单项式与单项式相乘单项式与单项式相乘,把它们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它们的指数作为积的一个因式.【要点归纳】(1)单项式的乘法法则的实质是乘法的交换律和同底数幂的乘法法则的综合应用.(2)单项式的乘法方法步骤:积的系数等于各系数的积,是把各单项式的系数交换到一起进行有理数的乘法计算,先确定符号,再计算绝对值;相同字母相乘,是同底数幂的乘法,按照“底数不变,指数相加”进行计算;只在一个单项式里含有的字母,要连同它的指数写在积里作为积的一个因式.(3)运算的结果仍为单项式,也是由系数、字母、字母的指数这三部分组成.(4)三个或三个以上的单项式相乘同样适用以上法则.知识点2:单项式与整式相乘单项式与整式相乘,就是用单项式去乘整式的每一项,再把所得的积相加.即()m a b c ma mb mc ++=++.【要点归纳】(1)单项式与整式相乘的计算方法,实质是利用乘法的分配律将其转化为多个单项式乘单项式的问题.(2)单项式与整式的乘积仍是一个整式,项数与原整式的项数相同.(3)计算的过程中要注意符号问题,整式中的每一项包括它前面的符号,同时还要注意单项式的符号.(4)对混合运算,应注意运算顺序,最后有同类项时,必须合并,从而得到最简的结果.知识点3:整式与整式相乘整式与整式相乘,先用一个整式的每一项乘另一个整式的每一项,再把所得的积相加.即()()a b m n am an bm bn ++=+++.【要点归纳】整式与整式相乘,仍得整式.在合并同类项之前,积的项数应该等于两个整式的项数之积.整式与整式相乘的最后结果需化简,有同类项的要合并.特殊的二项式相乘:()()()2x a x b x a b x ab ++=+++.题型一:单项式乘单项式(共9小题)1.(2022秋•嘉定区校级期末)计算221(6)3a b ab ×-= 332a b - .【分析】根据单项式乘单项式的运算法则计算.【解答】解:221(6)3a b ab ×-221(6)())3a ab b =-´××××332a b =-,故答案为:332a b -.【点评】本题考查的是单项式乘单项式,单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.2.(2023秋•静安区校级月考)计算,结果用科学记数法表示:53(310)(510)-´´´= 91.510-´ .【分析】运用整式乘法的运算法则和科学记数法知识进行运算.【解答】解:53(310)(510)-´´´53[(3)5](1010)=-´´´81510=-´91.510=-´故答案为:91.510-´.【点评】此题考查了整式乘法和科学记数法的混合运算能力,关键是能准确确定运算方法,并能进行正确的计算.3.(2023秋•闵行区校级月考)674(310)(510)(410)´´´= 18610´ .【分析】根据单项式乘单项式法则计算后利用科学记数法表示出结果即可.【解答】解:原式1735410=´´´176010=´18610=´,故答案为:18610´.【点评】本题考查单项式乘单项式及科学记数法表示较大的数,熟练掌握相关运算法则是解题的关键.4.(2022秋•杨浦区期中)计算:32347(2)()x x x x x -×-×+-.【分析】直接利用积的乘方运算法则、单项式乘单项式分别化简,进而合并同类项得出答案.【解答】解:原式6774x x x x =×--7774x x x =--72x =.【点评】此题主要考查了积的乘方运算、单项式乘单项式,正确掌握相关运算法则是解题关键.5.(2023秋•闵行区期中)计算:522312()(2)()2x x x x ×---×-.【分析】直接利用积的乘方运算法则化简,再利用单项式乘单项式运算法则计算得出答案.【解答】解:原式526128()2x x x x =×-×7724x x =-72x =-.【点评】此题主要考查了积的乘方运算、单项式乘单项式,正确掌握相关运算法则是解题关键.6.(2023秋•奉贤区期中)计算:37423256(2)5()x x x x x ×-×--.【分析】先根据同底数幂相乘,积的乘方,幂的乘方进行化简,再运用同类项法则进行合并,即可作答.【解答】解:原式3742325685x x x ++´´=+-101010685x x x =+-109x =.【点评】本题考查了同底数幂相乘,积的乘方,幂的乘方,难度较小,正确掌握相关性质内容是解题的关键.7.(2023秋•奉贤区期中)计算:423223()()(3)2a a a a a a -×---××.【分析】根据积的乘方法则、单项式乘单项式的运算法则、合并同类项法则计算即可.【解答】解:原式4266()92a a a a =×---66692a a a =---612a =-.【点评】本题考查的是单项式乘单项式、积的乘方、合并同类项,掌握它们的运算法则是解题的关键.8.(2023秋•浦东新区校级期中)计算:2232(3)(2)a b ab ab ×-+.【分析】利用单项式乘单项式的法则,积的乘方的法则进行运算即可.【解答】解:2232(3)(2)a b ab ab ×-+333368a b a b =-+332a b =.【点评】本题主要考查单项式乘单项式,积的乘方,解答的关键是对相应的运算法则的掌握.9.(2023秋•闵行区校级期中)计算:37423253(2)3()x x x x x ×-×--.【分析】根据同底数幂的乘法,积的乘方,幂的乘方,进行计算即可求解.【解答】解:37423253(2)3()x x x x x ×-×--1046103(8)3x x x x =-´--101010383x x x =+-108x =.【点评】本题考查了幂的运算,熟练掌握同底数幂的乘法,积的乘方,幂的乘方运算法则是解题的关键.题型二:单项式乘整式(共11小题)10.(2023秋•奉贤区期中)计算:23(2)x x x ---= 32336x x x -++ .【分析】直接利用单项式乘多项式运算法则化简,进而得出答案.【解答】解:23(2)x x x ---23(3)(3)2x x x x x =-×--×--´32336x x x =-++.故答案为:32336x x x -++.【点评】此题主要考查了单项式乘多项式,正确掌握相关运算法则是解题关键.11.(2023秋•松江区期末)计算:2(23)x y -= 46x xy - .【分析】根据单项式乘多项式的法则计算即可.【解答】解:2(23)46x y x xy -=-,故答案为:46x xy -.【点评】本题考查了单项式乘多项式,熟练掌握其运算法则是解题的关键.12.(2023秋•浦东新区期中)计算:21(1)(3)3x x x +-×-= 3233x x x --+ .【分析】直接利用单项式与多项式相乘的运算法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加计算得出答案.【解答】解:原式3233x x x =--+.故答案为:3233x x x --+.【点评】此题主要考查了单项式与多项式相乘的运算,正确掌握相关运算法则是解题关键.13.(2023秋•奉贤区期中)计算:223(2)a a ab b -×-+.【分析】利用单项式乘多项式法则计算即可得到结果.【解答】解:原式322336a a b ab =-+-.【点评】此题考查了单项式乘多项式,熟练掌握运算法则是解本题的关键.14.(2023秋•宝山区校级月考)计算:32212(2)(3)23x x x x --+×-.【分析】先计算积的乘法,再利用单项式乘以多项式的乘法法则计算即可.【解答】解:32212(2)(3)23x x x x --+×-32212(2923x x x x =--+×33292(2)23x x x =--+6539932x x x =-+-.【点评】本题考查单项式的乘法,熟练掌握积的乘方和单项式乘以多项式的乘法法则是解题的关键.15.(2023秋•青浦区校级期中)计算:2221(23)52x x x xy y xy --++.【分析】根据单项式乘多项式的计算方法进行计算即可.【解答】解:原式2222212352x x x y xy xy =-+-+222322x x y xy =-++.【点评】本题考查单项式乘多项式,掌握单项式乘多项式的计算方法以及合并同类项法则是正确解答的前提.16.(2023秋•浦东新区期中)计算:23[2(2)2(2)]2x x x y y x y x -+--+.【分析】直接利用单项式乘多项式运算法则化简,再合并同类项,进而得出答案.【解答】解:原式2223(2442)2x x xy xy y x =-+-++222324422x x xy xy y x =--+-+232x y =-.【点评】此题主要考查了单项式乘多项式运算以及合并同类项,正确掌握相关运算法则是解题关键.17.(2023秋•松江区月考)计算:32222442(3)()3()(3)3xy x y x x y xy x ×-+-×--.【分析】先根据幂的乘方与积的乘方运算法则计算,再合并同类项即可.【解答】解:32222442(3)()3()(3)3xy x y x x y xy x ×-+-×--33244544227()333x y x y x x y x y xy =×-+×++54545441833x y x y x y xy =-+++544143x y xy =-+.【点评】本题主要考查整式的混合运算,解题关键是熟练掌握幂的乘方法则:底数不变,指数相乘[()m n mn a a =,m ,n 为正整数].积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘[()n n n ab a b =,n 为正整数].18.(2023秋•松江区月考)计算:2432216(2)()32xy y xy xy -+-.【分析】先算单项式乘多项式,积的乘方,再合并同类项即可.【解答】解:2432216(2)()32xy y xy xy -+-3262611244xy x y x y =-+32615124xy x y =-.【点评】本题主要考查单项式乘多项式,积的乘方,解答的关键是对相应的运算法则的掌握.19.(2023秋•闵行区校级月考)计算:229(2)()x x xy y xy --+-.【分析】先计算单项式乘单项式,再根据单项式乘多项式运算法则进行运算即可.【解答】解:229(2)()x x xy y xy --+-2229(2)x y x xy y =---+432231899x y x y x y =+-.【点评】本题考查了单项式乘多项式,熟练掌握幂的运算是关键.20.(2022秋•青浦区期中)试用整式的运算说明:当10y z +=时,我们计算xy xz ´可以将十位数字与十位数字加一相乘的结果顺次写在千位和百位,将两个数个位数字的乘积顺次写在十位和个位,如果乘积不足两位数可以用0补齐十位.(例:计算3139´时,可以口算3412´=,199´=,则最终结果为1209)【分析】根据10,10xy x y xz x z =+=+,转换成多项式乘以多项式计算说明即可.【解答】解:因为10xy x y =+,10xz x z =+,10y z +=,所以(10)(10)xy xz x y x z ´=++,22100100101010x x xy xy y y =+-++-100(1)(10)100(1)x x y y x x yz =++-=++.【点评】本题考查了多项式乘以多项式,熟练掌握两位数的表示法,多项式乘以多项式的运算法则是解题的关键.题型三:整式乘整式(共10小题)21.(2023秋•静安区校级月考)如图,正方形卡片A 类、B 类和长方形卡片C 类各若干张,如果要拼一个长为(23)a b +,宽为()a b +的大长方形,则需要C 类卡片( )A .2张B .3张C .4张D .5张【分析】由22(23)()253a b a b a ab b ++=++,得A 类卡片的面积为2a ,B 类卡片的面积为2b ,C 类卡片的面积为ab ,因此需要A 类卡片2张,B 类卡片3张,C 类卡片5张.【解答】解:长为(23)a b +,宽为()a b +的大长方形的面积为:22(23)()253a b a b a ab b ++=++,A Q 类卡片的面积为2a ,B 类卡片的面积为2b ,C 类卡片的面积为ab ,\需要A 类卡片2张,B 类卡片3张,C 类卡片5张.故选:D .【点评】本题考查了多项式乘法,熟练掌握多项式乘以多项式是解题的关键.22.(2022秋•浦东新区校级期中)如图,正方形卡片A 类、B 类和长方形卡片C 类各若干张,如果要拼一个长为(3)a b +,宽为(2)a b +的大长方形,则需要A 类、B 类和C 类卡片的张数分别为( )A .2,5,3B .3,7,2C .2,3,7D .2,5,7【分析】根据多项式乘多项式的运算法则可求出长方形的面积.【解答】解:长方形的面积为22(3)(2)273a b a b a ab b ++=++,A Q 类卡片的面积为2a ,B 类卡片的面积为2b ,C 类卡片的面积为ab ,\需要A 类卡片2张,B 类卡片3张,C 类卡片7张.故选:C .【点评】本题考查多项式乘多项式,解题的关键是正确求出长方形的面积,本题属于基础题型.23.(2023秋•浦东新区期末)若2(2)(3)x x x px q +-=++,则p 的值为( )A .5-B .1-C .5D .1【分析】先根据多项式乘多项式法则,计算出(2)(3)x x +-的结果,然后求出p 的值即可.【解答】解:(2)(3)x x +-Q 2326x x x =-+-26x x =--,2(2)(3)x x x px q +-=++,1p \=-,故选:B .【点评】本题主要考查了多项式乘多项式,解题关键是熟练掌握多项式乘多项式法则.24.(2023秋•浦东新区期末)计算:(21)(32)x x -+= 262x x +- .【分析】直接利用多项式乘法运算法则去括号, 进而合并同类项得出即可 .【解答】解: 原式22643262x x x x x =+--=+-.故答案为:262x x +-.【点评】此题主要考查了多项式乘以多项式, 正确掌握运算法则是解题关键 .25.(2023秋•普陀区校级期末)计算:1(3)(912)2x x +-= 2921362x x +- .【分析】根据多项式乘多项式运算法则,准确计算.【解答】解:1(3)(912)2x x +-1(912)3(912)2x x x =-+-29627362x x x =-+-2921362x x =+-.故答案为:2921362x x +-.【点评】本题主要考查了多项式乘多项式,掌握多项式乘多项式运算法则是关键.26.(2023秋•崇明区期末)计算:(32)(2)a b a b +-= 22344a ab b -- .【分析】利用多项式乘多项式的乘法展开计算,进一步合并即可.【解答】解:原式223624a ab ab b =-+-22344a ab b =--.故答案为:22344a ab b --.【点评】此题考查多项式乘多项式,掌握计算方法是解决问题的关键.27.(2023秋•青浦区期末)如图,现有边长为a 的正方形A 、边长为b 的正方形B 和长为2b 宽为a 的长方形C 的三类纸片(其中)a b >.用这三类纸片拼一个长为26a b +、宽为3a b +的长方形(不重叠且不留缝隙),那么需要C 类纸片 10 张.【分析】根据长方形的面积=长´宽,求出长为26a b +、宽为3a b +的长方形的面积是多少,判断出需要C 类卡片多少张即可.【解答】解:长为26a b +、宽为3a b +的长方形的面积为:22(26)(3)6206a b a b a ab b ++=++,Q 正方形A 的面积为2a ,正方形B 的面积为2b ,长方形C 的面积为2ab ,\需要A 类卡片6张,B 类卡片6张,C 类卡片10张,故答案为:10.【点评】本题考查了多项式乘以多项式的运算方法,解题关键是熟练掌握运算法则.28.(2022秋•青浦区期中)已知222(2)(235)x ax bx x x -++-+的展开式中不含三次项和四次项,则展开式中二次项和一次项的系数之和为 2- .【分析】利用多项式乘多项式法则将原式展开,根据题意展开式中不含三次项和四次项,可得220a -=,3320a b -++=,求解即可得a ,b 的值,然后代入求值可确定展开式中二次项和一次项的系数,求和即可得答案.【解答】解:222(2)(235)x ax bx x x -++-+4324323222352352354610x x x ax ax ax bx bx bx x x =-+-+-+-++-+432(22)(332)(5534)(56)10a x a b x a b x b x =-+-+++--++-+,根据题意,展开式中不含三次项和四次项,220a \-=,3320a b -++=,解得1a =,0b =,55345513044a b \--+=-´-´+=,565066b -=´-=-,即展开式中二次项系数为4,一次项的系数为6-,\展开式中二次项和一次项的系数之和为4(6)2+-=-.【点评】本题主要考查了多项式乘多项式运算、多项式相关概念、代数式求值等知识,熟练掌握多项式乘多项式运算法则,正确展开原式是解题关键.29.(2022秋•青浦区期中)计算:232(1)(1)n n n n x x x x ++-+.【分析】根据多项式乘以多项式的法则,即可得出结论.【解答】解:232(1)(1)n n n n x x x x ++-+54243321n n n n n n n n x x x x x x x x =-++-++-+51n n x x =++.【点评】本题主要考查了多项式乘以多项式,正确运用同底数幂的乘法是解题的关键.30.(2022秋•长宁区校级月考)计算:(2)(31)3(1)(25)x x x x -+-+-.【分析】根据整式的混合运算法则先算乘法,然后计算加减即可求解.【解答】解:(2)(31)3(1)(25)x x x x -+-+-223623(2525)x x x x x x =+----+-223526915x x x x =---++23413x x =-++.【点评】此题考查了整式的混合运算,解题的关键是熟练掌握整式的混合运算法则和顺序.一.选择题(共5小题)1.(2022秋•浦东新区校级期中)下列运算中,正确的是( )A .236()x x -=B .236236m m m ×=C .333()xy x y -=-D .22244(3)6a b a b =【分析】根据单项式乘单项式以及幂的乘方与积的乘方法则分别对每一项进行分析,即可得出答案.【解答】解:A 、236()x x -=-,故本选项错误,不符合题意;B 、235236m m m ×=,故本选项错误,不符合题意;C 、333()xy x y -=-,故本选项正确,符合题意;D 、22244(3)9a b a b =,故本选项错误,不符合题意;故选:C .【点评】此题考查了单项式乘单项式、幂的乘方与积的乘方,熟练掌握单项式乘单项式以及幂的乘方与积的乘方法则是解题的关键.2.(2023秋•浦东新区校级期末)53(410)(2510)´´´的计算结果是( )A .810010´B .17110´C .10110´D .1510010´【分析】运用单项式乘单项式和科学记数法知识进行求解、辨别.【解答】解:53(410)(2510)´´´53(425)(1010)=´´´810010=´10110=´,故选:C .【点评】此题考查了科学记数法的应用能力,关键是能准确理解并运用该知识.3.(2023秋•松江区月考)2123(2)(0.5)()4m n n m x y x y x y --×-×的结果是( )A .2122m n x y +-B .22234m n x y -C .21234m nx y +D .212234m n x y ++【分析】利用单项式乘单项式的法则进行运算即可.【解答】解:2123(2)(0.5)()4m n n m x y x y x y --×-×21232(0.5)4m m n n x y ++-++=-´-´212234m n x y ++=.故选:D .【点评】本题主要考查单项式乘单项式,解答的关键是对相应的运算法则的掌握.4.(2023秋•闵行区校级月考)若m 、n 为整数,且2()()12x m x n x ax ++=++,则a 不可能是( )A .7B .6C .13-D .8-【分析】根据12mn =,m 、n 为整数,可得m 、n 有6组值,分别计算即可得出a 的值,从而作出判断.【解答】解:2()()12x m x n x ax ++=++Q ,22()12x m n x mn x ax \+++=++,即12mn =,m Q 、n 为整数,12112(1)(12)26(2)(6)34(3)(4)=´=-´-=´=-´-=´=-´-,1m \=,12n =或1m =-,12n =-或2m =,6n =或2m =-,6n =-或3m =,4n =或3m =-,4n =-,13m n \+=或13m n +=-或8m n +=或8m n +=-或7m n +=或7m n +=-,即a 的值为13±,8±,7±,不可能为6,故选:B .【点评】本题考查了多项式乘多项式,熟练掌握运算法则是解题的关键,注意不要漏解.5.(2023秋•静安区校级月考)若单项式8a x y -和214b x y 的积为562x y -,则ab 的值为( )A .2B .30C .15-D .15【分析】根据单项式乘单项式的计算法则求出a ,b 即可,【解答】解:2215618224a b a b x y x y x y x y ++-´=-=-,25a \+=,16b +=,解得3a =,5b =,3515ab \=´=,故选:D .【点评】此题考查了单项式乘单项式,关键是求得a ,b 的值.二.填空题(共8小题)6.(2023秋•宝山区期末)计算:223a a ×= 36a .【分析】先把系数相乘,然后利用同底数幂的乘法计算.【解答】解:原式36a =.故答案为:36a .【点评】本题考查了单项式乘单项式,掌握单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式是关键.7.(2023秋•普陀区校级期末)计算:38321()711a a ×-= 11911a - .【分析】根据单项式乘单项式运算法则,准确计算.【解答】解:3838113213219()71171111a a a a a ×-=-´×=-.故答案为:11911a -.【点评】本题主要考查了单项式乘单项式,掌握单项式乘单项式运算法则是关键.8.(2023秋•普陀区期末)计算:(5)(2)x y x y -+= 22295x xy y -- .【分析】多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加,根据多项式乘多项式的法则计算即可.【解答】解:(5)(2)x y x y -+222105x xy xy y =+--22295x xy y =--.故答案为:22295x xy y --.【点评】本题考查了多项式乘多项式,解题的关键是熟记法则,运用法则时应注意以下两点:①相乘时,按一定的顺序进行,必须做到不重不漏;②多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.9.(2023秋•静安区校级月考)若22(8)(3)x ax x x b ++-+的乘积中不含2x 和3x 项,a b += 4 .【分析】由多项式乘以多项式进行化简,然后结合不含2x 和3x 项,求出3a =,1b =,即可求出答案.【解答】解:22(8)(3)x ax x x b ++-+432322338248x x bx ax ax abx x x b=-++-++-+432(3)(38)(24)8x a x b a x ab x b =+-+-++-+,Q 其结果中不含2x 和3x 项,30a \-=,380b a -+=,解得:3a =,1b =,314a b \+=+=.故答案为:4.【点评】本题考查了多项式乘以多项式、代数式求值,解题的关键是掌握运算法则,正确的进行化简.10.(2022春•冷水滩区校级期中)若二项式3x a +与2x +相乘,化简后结果中不出现一次项,则a 的值是 6- .【分析】利用多项式乘以多项式法则计算,由结果不出现一次项确定出a 的值即可.【解答】解:根据题意得:2(3)(2)3(6)2x a x x a x a ++=+++,由结果中不出现一次项,得到60a +=,解得:6a =-,故答案为:6-.【点评】此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.11.(2022秋•杨浦区期末)已知:3a b +=,23ab =,化简(1)(1)a b --的结果是 43- .【分析】原式利用多项式乘多项式法则计算,整理后将已知等式代入计算即可求出值.【解答】解:3a b +=Q ,23ab =,\原式24()13133ab a b =-++=-+=-.故答案为:43-.【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.12.(2022秋•浦东新区校级期中)有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2)a b +,宽为(3)a b +的矩形.则需要A 类卡片 2 张,B 类卡片 张,C 类卡片 张.【分析】首先分别计算大矩形和三类卡片的面积,再进一步根据大矩形的面积应等于三类卡片的面积和进行分析所需三类卡片的数量.【解答】解:长为2a b +,宽为(3)a b +的矩形面积为:22(2)(3)273a b a b a ab b ++=++,A Q 类卡片的面积为2a ,B 类卡片的面积为2b ,C 类卡片的面积为ab ,\需要A 类卡片2张,B 类卡片3张,C 类卡片7张.故答案为:2;3;7.【点评】本题考查了多项式与多项式的乘法运算的应用,正确列出算式是解答本题的关键.多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.13.(2022秋•长宁区校级期中)若p 、q 、r 均为整数(0)p q >>,且2()()15x p x q x rx ++=--,则r 的值为 2或2-或14或14- .【分析】将()()x p x q ++展开,根据结果得到p q r +=-,15pq =-,再结合p ,q 的范围求出具体值,代入计算可得r 值.【解答】解:22()()()15x p x q x p q x pq x rx ++=+++=--,则p q r +=-,15pq =-,p Q 、q 、r 均为整数(0)p q >>,5p \=,3q =-或3p =,5q =-,15p =,1q =-或,1p =,15q =-,()2r p q \=-+=±或()14r p q =-+=±,故答案为:2或2-或14或14-.【点评】本题考查了多项式乘法,解题的关键是根据要求求出具体的p ,q 值.三.解答题(共8小题)14.(2023秋•松江区月考)计算:242345(2)x x x ×+-.【分析】根据幂的乘方与积的乘方运算法则计算,再合并同类项即可.【解答】解:242345(2)x x x ×+-66208x x =-612x =.【点评】本题考查幂的乘方与积的乘方,解题关键是熟练掌握幂的乘方法则:底数不变,指数相乘,即()(m n mn a a m =,n 是正整数).积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘,即()(n n n ab a b n =是正整数).15.(2023秋•闵行区校级月考)计算:(1)(32)(76)m n m n +-;(2)2323()()()[()]b a a b b a a b ---+-.【分析】(1)多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加,由此计算即可;(2)根据同底数幂相乘,底数不变,指数相加;幂的乘方,底数不变,指数相乘分别计算即可.【解答】解:(1)(32)(76)m n m n +-2221181412m mn mn n =-+-2221412m mn n =--;(2)2323()()()[()]b a a b b a a b ---+-236()()()()b a b a b a a b =---+-66()()b a a b =-+-66()()a b a b =-+-62()a b =-.【点评】本题考查了多项式乘多项式,同底数幂的乘法,幂的乘方,合并同类项,熟练掌握运算法则是解题的关键.16.(2023秋•松江区月考)计算:2(35)(23)(41)x x x x ---+.【分析】先算单项式乘多项式,多项式乘多项式,再合并同类项即可.【解答】解:2(35)(23)(41)x x x x ---+2261082123x x x x x =---++223x =-+.【点评】本题主要考查多项式乘多项式,单项式乘多项式,解答的关键是对相应的运算法则的掌握.17.(2023秋•松江区月考)若22(3)(3)x nx x x m -+++的展开式中不含2x 和3x 项,求m 、n 的值.【分析】求多项式乘多项式的展开式为43232233393x x mx nx nx mnx x x m ++---+++,根据题意可得30n -=,330m n -+=,计算求解即可.【解答】解:22(3)(3)x nx x x m -+++43232233393x x mx nx nx mnx x x m=++---+++432(3)(33)93x n x m n x mnx x m =+-+-+-++,Q 展开式中不含2x 和3x 项,30n \-=,330m n -+=,解得:6m =,3n =.【点评】本题考查了多项式乘多项式.解题的关键在于正确的运算.18.(2023秋•武侯区校级期末)若2228()(3)3x px x x q ++-+的展开式中不含2x 和3x 的项.(1)求p ,q 的值;(2)求代数式23120142016(2)(3)p q pq p q --++的值.【分析】(1)把首先利用多项式乘多项式法则进而得出原式的展开式的2x 项和3x 项,进而组成方程组得出p ,q 的值;(2)把p ,q 的值代入代数式即可求得答案.【解答】解:(1)2228(3)3x px x x q ++-+Q 4323222828332833x x qx px px pqx x x q =-++-++-+4322828(3)(3)(28)33x p x q p x pq x q =+-++-++-+,\原式的展开式的2x 项和3x 项分别是28(33q p -+,3(3)p x -+,依据题意得:2830330q p p ì-+=ïíï-+=î,解得:313p q =ìïí=-ïî.故p 的值是3,q 的值是13-;(2)23120142016(2)(3)p q pq p q --++23120142016111[23()][33(3()333-=-´´-+´´-+´-31216(3)(3-=+-+-1121639=-+72159=.【点评】此题主要考查了多项式乘多项式,正确展开多项式是解题关键.19.(2024•灞桥区校级开学)如图,某校园内有一块长为(2)a b m +,宽为(2)a b m -的长方形空地()a b >.为美化环境,计划在这块空地上修建一个长为(2)a b m -,宽为bm 的长方形花圆,并将花圆四周余下的空地修建成通道,请用含有a 、b 的代数式表示通道的面积.【分析】先根据通道的面积=长方形空地的面积-长方形花园的面积列出算式,然后根据平方差公式和单项式乘多项式的运算法则计算即可.【解答】解:根据题意得,通道的面积为(2)(2)(2)a b a b a b b+---2224(2)a b ab b =---22242a b ab b =--+22(42)a ab m =-.【点评】本题考查了多项式乘多项式,单项式乘多项式,解题的关键是理解题意,列出算式.20.(2023秋•静安区校级月考)探究应用:(1)计算:2(1)(1)x x x -++= 31x - ;22(2)(42)x y x xy y -++= .(2)上面的乘法计算结果很简洁,你发现了什么规律(公式)?用含字母a 、b 的等式表示该公式为: .(3)下列各式能用第(2)题的公式计算的是 .A .2(2)(24)m m m +++B .22(2)(22)m n m mn n -++C .2(3)(93)n n n -++D .22()(2)m n m mn n -++(4)设9101A =-,利用上述规律,说明A 能被37整除.【分析】(1)用多项式乘以多项式的法则计算即可;(2)观察第(1)问的计算,找出规律,用字母表示即可;(3)判断各选项是否符合公式的特点;(4)公式的逆用,求得A 中有37的因数即可.【解答】解:(1)2(1)(1)x x x -++3221x x x x x =++---31x =-;22(2)(42)x y x xy y -++32222384242x x y xy x y xy y =++---338x y =-;故答案为:31x -;338x y -;(2)从第(1)问发现的规律是:2233()()a b a ab b a b -++=-,故答案为:2233()()a b a ab b a b -++=-;(3)A .第一个多项式不是减法,不符合题意;B .最后一项应该是24n ,不符合题意;C .符合题意;D .第二个多项式的第二项应该为mn ,不符合题意.故选:C .(4)9101A =-33(10)1=-3632(101)(10101)=-++9991001001=´333371001001=´´´´,A \能被37整除.【点评】本题考查了多项式乘以多项式的法则,考查学生的计算能力,能对公式进行逆用是解题的关键.21.(2023秋•右玉县期末)综合与实践如图1,长方形的两边长分别为1m +,7m +;如图2.长方形的两边长分别为2m +,4m +.(其中m 为正整数)E .(1)图1中长方形的面积1S = 287m m ++ ;图2中长方形的面积2S = ;比较1S 2S (选填“<”、“ =”或“>” );(2)现有一正方形,其周长与图1中的长方形周长相等.①求正方形的边长;(用含m 的代数式表示)②试探究:该正方形的面积S 与图1中长方形的面积1S 的差(即1)S S -是一个常数,并求出这个常数.【分析】(1)根据长方形的面积=长´宽,求出图1和图2中长方形的面积,再求出它们的面积差,通过比较,求出答案即可;(2)①先求出图1中长方形的周长,然后根据正方形的周长与图1中的长方形周长相等,求出正方形周长,从而求出正方形边长即可;②由①中所求正方形的边长,从而求出正方形的面积,再求出该正方形的面积S 与图1中长方形的面积1S 的差即可.【解答】解:(1)由题意可知:1(1)(7)S m m =++277m m m =+++287m m =++,2(2)(4)S m m =++2428m m m =+++268m m =++,12S S \-22(87)(68)m m m m =++-++228768m m m m =++---21m =-,m Q 为正整数,m \最小为1,210m \->,12S S \>,故答案为:287m m ++,268m m ++,>;(2)①图1中长方形的周长为:2(71)m m +++2(28)m =+416m =+,Q 正方形的周长与图1中的长方形周长相等,\正方形的周长为416m +,\正方形的边长为1(416)44m m +=+;②Q 正方形的面积2(4)S m =+,1S S \-22(4)(87)m m m =+-++2281687m m m m =++---2288167m m m m =-+-+-9=,\该正方形的面积S 与图1中长方形的面积1S 的差(即1)S S -是一个常数,这个常数为9.【点评】本题主要考查了多项式乘多项式,解题关键是熟练掌握多项式乘多项式法则、长方形和正方形的面积公式与周长公式.。
专题1.6整式的乘法(3)多项式乘多项式

2020-2021学年七年级数学下册尖子生同步培优题典【北师大版】专题1.6整式的乘法(3)多项式乘多项式姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020秋•南关区校级期中)计算(a+3)(﹣a+1)的结果是()A.﹣a2﹣2a+3B.﹣a2+4a+3C.﹣a2+4a﹣3D.a2﹣2a﹣3【分析】运用多项式乘以多项式法则,直接计算即可.解析(a+3)(﹣a+1)=﹣a2﹣3a+a+3=﹣a2﹣2a+3.故选:A.2.(2020秋•朝阳区期中)若(x﹣3)(2x+1)=2x2+ax﹣3,则a的值为()A.﹣7B.﹣5C.5D.7【分析】将题中所给等式左边利用多项式乘多项式的运算法则进行计算,再与等式右边比较即可得出答案.解析(x﹣3)(2x+1)=2x2+x﹣6x﹣3=2x2﹣5x﹣3,∵(x﹣3)(2x+1)=2x2+ax﹣3,∴a=﹣5.故选:B.3.(2020秋•偃师市期中)若(x2+px+8)(x2﹣3x+1)乘积中不含x2项,则p的值为() A.p=0B.p=3C.p=﹣3D.p=﹣1【分析】先利用多项式乘多项式法则,把(x2+px+8)(x2﹣3x+1)展开合并,根据积不含x2的项,得关于p 的方程,求解即可.解析(x2+px+8)(x2﹣3x+1)=x4+px3+8x2﹣3x3﹣3px2﹣24x+x2+px+8=x4+(p﹣3)x3+(9﹣3p)x2+(p﹣24)x+8.∵(x2+px+8)(x2﹣3x+1)乘积中不含x2项,∴9﹣3p=0.∴p=3.故选:B.4.(2020秋•射洪市期中)如果(x﹣3)(3x+m)的积中不含x的一次项,则m的值为() A.7B.8C.9D.10【分析】先根据多项式乘以多项式法则展开,再合并同类项,根据已知得出m﹣9=0,求出即可.解析(x﹣3)(3x+m)=3x2+mx﹣9x﹣3m=3x2+(m﹣9)x﹣3m,∵(x﹣3)(3x+m)的积中不含x的一次项,∴m﹣9=0,解得:m=9,故选:C.5.(2020秋•房县期中)若x+y=1且xy=﹣2,则代数式(1﹣x)(1﹣y)的值等于() A.﹣2B.0C.1D.2【分析】先根据多项式乘以多项式法则进行计算,再变形,最后求出答案即可.解析∵x+y=1,xy=﹣2,∴(1﹣x)(1﹣y)=1﹣y﹣x+xy=1﹣(x+y)+xy=1﹣1+(﹣2)=﹣2,故选:A.6.(2020秋•西陵区校级期中)以下表示图中阴影部分面积的式子,不正确的是()A.x(x+5)+15B.x2+5(x+3)C.(x+3)(x+5)﹣3x D.x2+8x【分析】根据长方形和正方形的面积公式得出各个部分的面积,再逐个判断即可.解析阴影部分的面积为x(x+5)+3×5=x(x+5)+15或x2+5(x+3)或(x+3)(x+5)﹣3x,即选项A、B、C不符合题意,选项D符合题意,故选:D.7.(2020秋•路南区期中)若关于x的多项式(2x﹣m)与(3x+5)的乘积中,一次项系数为25,则m的值() A.5B.﹣5C.3D.﹣3【分析】先求出两个多项式的积,再根据一次项系数为25,得到关于m的一次方程,求解即可.解析(2x﹣m)(3x+5)=6x2﹣3mx+10x﹣5m=6x2+(10﹣3m)x﹣5m.∵积的一次项系数为25,∴10﹣3m=25.解得m=﹣5.故选:B.8.(2020秋•思明区校级期中)如图是一所楼房的平面图,下列式子中不能表示它的面积的是()A.x2+3x+6B.(x+3)(x+2)﹣2xC.x(x+3)+6D.x(x+2)+x2【分析】把楼房的平面图转化为三个矩形,求出三个矩形的面积和即可.解析S楼房的面积=S矩形ABCD+S矩形DEFC+S矩形CFHG=AD•AB+DC•DE+CF•FH.∵AB=DC=AD=x,DE=CF=3,FH=2,∴S楼房的面积=x2+3x+6.故选:D.9.(2021•宁波模拟)已知a、b、c三个数中有两个奇数,一个偶数,n是整数,如果S=(a+n+1)+(b+2n+2)+(c+3n+3),那么()A.S是偶数B.S是奇数C.S的奇偶性与n的奇偶性相同D.S的奇偶不能确定【分析】弄清a+n+1,b+2n+2,c+3n+3的奇偶性即可.可将3数相加,可知和为偶数,再根据三数和为偶数必有一数为偶数的性质可得积也为偶数.解析(a+n+1)+(b+2n+2)+(c+3n+3)=a+b+c+6(n+1).∵a+b+c为偶数,6(n+1)为偶数,∴a+b+c+6(n+1)为偶数∴S是偶数.故选:A.10.(2020秋•沙河口区期末)若(x+a)(x+b)=x2+4x+3,则a+b的值为()A.3B.﹣3C.4D.﹣4【分析】直接利用多项式乘以多项式运算法则去括号,进而得出a+b的值.解析∵(x+a)(x+b)=x2+4x+3,∴x2+(a+b)x+ab=x2+4x+3,∴a+b=4.故选:C.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2020秋•浦东新区期中)计算:(3x+2)(2x﹣3)=6x2﹣5x﹣6.【分析】运用多项式乘多项式的法则计算即可.解析原式=6x2﹣9x+4x﹣6=6x2﹣5x﹣6.故答案为:6x2﹣5x﹣6.12.(2020秋•香坊区校级期中)已知a﹣b=6,ab=5,则(a+1)(b﹣1)=﹣2.【分析】原式利用多项式乘以多项式法则计算,整理后将已知等式代入计算即可求出值.解析∵a﹣b=6,ab=5,∴(a+1)(b﹣1)=ab﹣a+b﹣1=ab﹣(a﹣b)﹣1=5﹣6﹣1=﹣2;故答案为:﹣2.13.(2020秋•浦东新区期中)将关于x的多项式x2+2x+3与2x+b相乘,若积中不出现一次项,则b=﹣3.【分析】根据题意,利用多项式乘多项式法则计算,确定出b的值即可.解析根据题意得:(x2+2x+3)(2x+b)=2x3+(4+b)x2+(6+2b)x+3b,由积中不出现一次项,得到6+2b=0,解得:b=﹣3.故答案为:﹣3.14.(2020秋•朝阳区期中)如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要7张C类卡片.【分析】用长乘以宽,列出算式,根据多项式乘以多项式的运算法则展开,然后根据A、B、C类卡片的形状可得答案.解析∵(3a+b)(a+2b)=3a2+6ab+ab+2b2=3a2+7ab+2b2,∴若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要A类3张,B类2张,C类7张.故答案为:7.15.(2020秋•沙坪坝区校级期中)已知x﹣y=7,xy=5,则(2﹣x)(y+2)的值为﹣15.【分析】认真观察题目的特点,易发现(2﹣x)(y+2)化简后会出现,x﹣y,xy,可以进行整体代入即可求得答案.解析(2﹣x)(y+2)=2y+4﹣xy﹣2x=﹣xy﹣2(x﹣y)+4,把x﹣y=7,xy=5代入,原式=﹣5﹣2×7+4=﹣15.故答案为:﹣15.16.(2020秋•九龙坡区校级期中)已知(x﹣2)(x2+mx+n)的乘积项中不含x2和x项,则m+n=6.【分析】直接利用多项式乘多项式计算,再得出m,n的值,即可得出答案.解析(x﹣2)(x2+mx+n)=x3+mx2+nx﹣2x2﹣2mx﹣2n=x3+(m﹣2)x2+(n﹣2m)x﹣2n∵(x﹣2)(x2+mx+n)的乘积项中不含x2和x项,∴m﹣2=0,n﹣2m=0,解得:m=2,n=4,∴m+n=6.故答案为:6.17.(2020秋•崇川区校级期中)如果(m2+n2+1)与(m2+n2﹣1)的乘积为15,那么m2+n2的值为4.【分析】根据题意列出等式,再根据平方差公式进行计算,最后求出答案即可.解析解;∵(m2+n2+1)与(m2+n2﹣1)的乘积为15,∴(m2+n2+1)(m2+n2﹣1)=15,∴(m2+n2)2﹣1=15,即(m2+n2)2=16,解得:m2+n2=4(负数舍去),故答案为:4.18.(2020秋•西峰区期末)若(x+m)(x+n)=x2﹣7x+mn,则﹣m﹣n的值为7.【分析】按照多项式的乘法法则展开运算后解析∵(x+m)(x+n)=x2+(m+n)x+mn=x2﹣7x+mn,∴m+n=﹣7,∴﹣m﹣n=7,故答案为:7.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤) 19.(2020秋•南岗区期末)化简:(1)(2x)3(﹣5xy2);(2)(3x+2)(x+2).【分析】(1)先算积的乘方,然后再利用单项式乘以单项式计算法则进行计算即可;(2)根据多项式乘以多项式的计算法则进行计算即可.解析(1)原式=8x3•(﹣5xy2)=﹣8x3•5xy2=﹣40x4y2;(2)原式=3x2+6x+2x+4=3x2+8x+4.20.(2020秋•淅川县期末)已知(x2+mx+n)(x﹣1)的结果中不含x2项和x项,求m、n的值.【分析】把式子展开,合并同类项后找到x2项和x项的系数,令其为0,可求出m和n的值.解析(x2+mx+n)(x﹣1)=x3+(m﹣1)x2+(n﹣m)x﹣n.∵结果中不含x2的项和x项,∴m﹣1=0且n﹣m=0,解得:m=1,n=1.21.计算:(1)(2a﹣1)(a﹣4)﹣(a+3)(a﹣1);(2)t2﹣(t+1)(t﹣5);(3)(x+1)(x2+x+1);(4)(2x+3)(x2﹣x+1).【分析】(1)根据多项式的乘法和合并同类项解答即可;(2)根据多项式的乘法和合并同类项解答即可;(3)根据多项式的乘法和合并同类项解答即可;(4)根据多项式的乘法和合并同类项解答即可.解析(1)(2a﹣1)(a﹣4)﹣(a+3)(a﹣1)=2a2﹣8a﹣a+4﹣a2+a﹣3a+3=a2﹣11a+7;(2)t2﹣(t+1)(t﹣5)=t2﹣t2+5t﹣t+5=4t+5;(3)(x+1)(x2+x+1);=x3+x2+x+x2+x+1=x3+2x2+2x+1;(4)(2x+3)(x2﹣x+1)=2x3﹣2x2+2x+3x2﹣3x+3=2x3+x2﹣x+3.22.(2020秋•新宾县期末)如图,某市有一块长(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间空白处将修建一座雕像.(1)求绿化的面积是多少平方米.(2)当a=2,b=1时求绿化面积.【分析】(1)绿化面积=长方形的面积﹣正方形的面积;(2)把a=2,b=1代入(1)求出绿化面积.解析(1)S绿化面积=(3a+b)(2a+b)﹣(a+b)2=6a2+5ab+b2﹣a2﹣2ab﹣b2=5a2+3ab;答:绿化的面积是(5a2+3ab)平方米;(2)当a=2,b=1时,绿化面积=5×22+3×2×1=20+6=26.答:当a=2,b=1时,绿化面积为26平方米.23.如图1,长方形的两边分别是m+8,m+4.如图2的长方形的两边为m+13,m+3(其中m为正整数).(1)求出两个长方形的面积S1、S2,并比较S1、S2的大小;(2)现有一个正方形,它的周长与图1的长方形的周长相等,试证明该正方形的面积与图1的长方形的面积的差是一个常数,并求出这个常数.【分析】(1)利用长方形的面积=长×宽易得S1,S2的大小,并用作差的方法进行比较;(2)利用正方形的周长与图1中的长方形的周长相等易得正方形的边长,从而得正方形的面积,再作差去解决问题.解析(1)∵S1=(m+8)(m+4)=m2+12m+32,S2=(m+13)(m+3)=m2+16m+39,m为正整数,∴S1﹣S2=m2+12m+32﹣(m2+16m+39)=﹣4m﹣7<0,∴S1<S2;(2)∵一个正方形的周长与图1中的长方形的周长相等,∴正方形的边长为2(m+8+m+4)÷4=m+6,正方形的面积为(m+6)2=m2+12m+36,∴m2+12m+36﹣(m2+12m+32)=m2+12m+36﹣m2﹣12m﹣32=4,∴该正方形的面积与图1的长方形的面积的差是一个常数4.24.(2020秋•岳麓区校级月考)定义:L(A)是多项式A化简后的项数.例如多项式A=x2+2x﹣3,则L(A)=3.一个多项式A乘以多项式B,化简得到多项式C(即C=A×B),如果L(A)≤L(C)≤L(A)+1,则称B是A的“郡园多项式”;如果L(A)=L(C),则称B是A的“郡园志勤多项式”.(1)若A=x﹣2,B=x+3;那么B是不是A的“郡园多项式”,说明理由;(2)若A=x﹣2,B=x2+ax+4是关于x的多项式且B是A的“郡园志勤多项式”,求a的值?(3)若A=x2﹣x+3m,B=x2+x+m是关于x的多项式且B是A的“郡园志勤多项式”,求m的值?【分析】(1)根据多项式乘多项式的法则计算,根据“郡园多项式”的定义判断;(2)根据多项式乘多项式的法则计算,根据“郡园志勤多项式”,得到关于a的方程,解方程即可求解;(3)根据多项式乘多项式的法则计算,根据“郡园志勤多项式”,得到关于m的方程,解方程即可求解.解析(1)B是A的“郡园多项式”,理由如下:(x﹣2)(x+3)=x2﹣2x+3x﹣6=x2+x﹣6,x2+x﹣6的项数比A的项数多1项,则B是A的“郡园多项式”;(2)(x﹣2)(x2+ax+4)=x3+ax2+4x﹣2x2﹣2ax﹣8=x3+(a﹣2)x2+(4﹣2a)x﹣8,∵B是A的“郡园志勤多项式”,∴a﹣2=0且4﹣2a=0,解得a=2.∴a的值是2;(3)(x2﹣x+3m)(x2+x+m)=x4+x3+mx2﹣x3﹣2x2﹣mx+3mx2+3mx+3m2=x4+(4m+1)x2+2mx+3m2,∵B是A的“郡园志勤多项式”,∴4m+1=0或m=0,解得m=−14或0.∴m的值是−14或0.。
第4讲整式的乘法(3个知识点+3种题型+过关检测)(学生版) 24-25学年七年级数学上册(沪教版)
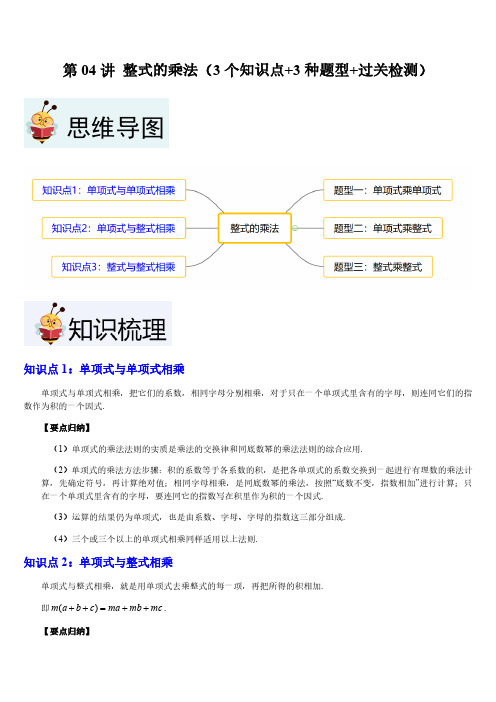
第04讲 整式的乘法(3个知识点+3种题型+过关检测)知识点1:单项式与单项式相乘单项式与单项式相乘,把它们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它们的指数作为积的一个因式.【要点归纳】(1)单项式的乘法法则的实质是乘法的交换律和同底数幂的乘法法则的综合应用.(2)单项式的乘法方法步骤:积的系数等于各系数的积,是把各单项式的系数交换到一起进行有理数的乘法计算,先确定符号,再计算绝对值;相同字母相乘,是同底数幂的乘法,按照“底数不变,指数相加”进行计算;只在一个单项式里含有的字母,要连同它的指数写在积里作为积的一个因式.(3)运算的结果仍为单项式,也是由系数、字母、字母的指数这三部分组成.(4)三个或三个以上的单项式相乘同样适用以上法则.知识点2:单项式与整式相乘单项式与整式相乘,就是用单项式去乘整式的每一项,再把所得的积相加.即()m a b c ma mb mc ++=++.【要点归纳】(1)单项式与整式相乘的计算方法,实质是利用乘法的分配律将其转化为多个单项式乘单项式的问题.(2)单项式与整式的乘积仍是一个整式,项数与原整式的项数相同.(3)计算的过程中要注意符号问题,整式中的每一项包括它前面的符号,同时还要注意单项式的符号.(4)对混合运算,应注意运算顺序,最后有同类项时,必须合并,从而得到最简的结果.知识点3:整式与整式相乘整式与整式相乘,先用一个整式的每一项乘另一个整式的每一项,再把所得的积相加.即()()a b m n am an bm bn ++=+++.【要点归纳】整式与整式相乘,仍得整式.在合并同类项之前,积的项数应该等于两个整式的项数之积.整式与整式相乘的最后结果需化简,有同类项的要合并.特殊的二项式相乘:()()()2x a x b x a b x ab ++=+++.题型一:单项式乘单项式(共9小题)1.(2022秋•嘉定区校级期末)计算221(6)3a b ab ×-= .2.(2023秋•静安区校级月考)计算,结果用科学记数法表示:53(310)(510)-´´´= .3.(2023秋•闵行区校级月考)674(310)(510)(410)´´´= .4.(2022秋•杨浦区期中)计算:32347(2)()x x x x x -×-×+-.5.(2023秋•闵行区期中)计算:522312()(2)()2x x x x ×---×-.6.(2023秋•奉贤区期中)计算:37423256(2)5()x x x x x ×-×--.7.(2023秋•奉贤区期中)计算:423223()()(3)2a a a a a a -×---××.8.(2023秋•浦东新区校级期中)计算:2232(3)(2)a b ab ab ×-+.9.(2023秋•闵行区校级期中)计算:37423253(2)3()x x x x x ×-×--.题型二:单项式乘整式(共11小题)10.(2023秋•奉贤区期中)计算:23(2)x x x ---= .11.(2023秋•松江区期末)计算:2(23)x y -= .12.(2023秋•浦东新区期中)计算:21(1)(3)3x x x +-×-= .13.(2023秋•奉贤区期中)计算:223(2)a a ab b -×-+.14.(2023秋•宝山区校级月考)计算:32212(2)(3)23x x x x --+×-.15.(2023秋•青浦区校级期中)计算:2221(23)52x x x xy y xy --++.16.(2023秋•浦东新区期中)计算:23[2(2)2(2)]2x x x y y x y x -+--+.17.(2023秋•松江区月考)计算:32222442(3)()3()(3)3xy x y x x y xy x ×-+-×--.18.(2023秋•松江区月考)计算:2432216(2)()32xy y xy xy -+-.19.(2023秋•闵行区校级月考)计算:229(2)()x x xy y xy --+-.20.(2022秋•青浦区期中)试用整式的运算说明:当10y z +=时,我们计算xy xz ´可以将十位数字与十位数字加一相乘的结果顺次写在千位和百位,将两个数个位数字的乘积顺次写在十位和个位,如果乘积不足两位数可以用0补齐十位.(例:计算3139´时,可以口算3412´=,199´=,则最终结果为1209)题型三:整式乘整式(共10小题)21.(2023秋•静安区校级月考)如图,正方形卡片A 类、B 类和长方形卡片C 类各若干张,如果要拼一个长为(23)a b +,宽为()a b +的大长方形,则需要C 类卡片( )A .2张B .3张C .4张D .5张22.(2022秋•浦东新区校级期中)如图,正方形卡片A 类、B 类和长方形卡片C 类各若干张,如果要拼一个长为(3)a b +,宽为(2)a b +的大长方形,则需要A 类、B 类和C 类卡片的张数分别为( )A .2,5,3B .3,7,2C .2,3,7D .2,5,723.(2023秋•浦东新区期末)若2(2)(3)x x x px q +-=++,则p 的值为( )A .5-B .1-C .5D .124.(2023秋•浦东新区期末)计算:(21)(32)x x -+= .25.(2023秋•普陀区校级期末)计算:1(3)(912)2x x +-= .26.(2023秋•崇明区期末)计算:(32)(2)a b a b +-= .27.(2023秋•青浦区期末)如图,现有边长为a 的正方形A 、边长为b 的正方形B 和长为2b 宽为a 的长方形C 的三类纸片(其中)a b >.用这三类纸片拼一个长为26a b +、宽为3a b +的长方形(不重叠且不留缝隙),那么需要C 类纸片 张.28.(2022秋•青浦区期中)已知222(2)(235)x ax bx x x -++-+的展开式中不含三次项和四次项,则展开式中二次项和一次项的系数之和为 .29.(2022秋•青浦区期中)计算:232(1)(1)n n n n x x x x ++-+.30.(2022秋•长宁区校级月考)计算:(2)(31)3(1)(25)x x x x -+-+-一.选择题(共5小题)1.(2022秋•浦东新区校级期中)下列运算中,正确的是( )A .236()x x -=B .236236m m m ×=C .333()xy x y -=-D .22244(3)6a b a b =2.(2023秋•浦东新区校级期末)53(410)(2510)´´´的计算结果是( )A .810010´B .17110´C .10110´D .1510010´3.(2023秋•松江区月考)2123(2)(0.5)()4m n n m x y x y x y --×-×的结果是( )A .2122m n x y +-B .22234m n x y -C .21234m nx y +D .212234m n x y ++4.(2023秋•闵行区校级月考)若m 、n 为整数,且2()()12x m x n x ax ++=++,则a 不可能是()A .7B .6C .13-D .8-5.(2023秋•静安区校级月考)若单项式8a x y -和214b x y 的积为562x y -,则ab 的值为( )A .2B .30C .15-D .15二.填空题(共8小题)6.(2023秋•宝山区期末)计算:223a a ×= .7.(2023秋•普陀区校级期末)计算:38321()711a a ×-= .8.(2023秋•普陀区期末)计算:(5)(2)x y x y -+= .9.(2023秋•静安区校级月考)若22(8)(3)x ax x x b ++-+的乘积中不含2x 和3x 项,a b += .10.(2022春•冷水滩区校级期中)若二项式3x a +与2x +相乘,化简后结果中不出现一次项,则a 的值是 .11.(2022秋•杨浦区期末)已知:3a b +=,23ab =,化简(1)(1)a b --的结果是 .12.(2022秋•浦东新区校级期中)有若干张如图所示的正方形和长方形卡片,如果要拼一个长为(2)a b +,宽为(3)a b +的矩形.则需要A 类卡片 张,B 类卡片 张,C 类卡片 张.13.(2022秋•长宁区校级期中)若p 、q 、r 均为整数(0)p q >>,且2()()15x p x q x rx ++=--,则r 的值为 .三.解答题(共8小题)14.(2023秋•松江区月考)计算:242345(2)x x x ×+-.15.(2023秋•闵行区校级月考)计算:(1)(32)(76)m n m n +-; (2)2323()()()[()]b a a b b a a b ---+-.16.(2023秋•松江区月考)计算:2(35)(23)(41)x x x x ---+.17.(2023秋•松江区月考)若22(3)(3)x nx x x m -+++的展开式中不含2x 和3x 项,求m 、n 的值.18.(2023秋•武侯区校级期末)若2228()(3)3x px x x q ++-+的展开式中不含2x 和3x 的项.(1)求p ,q 的值;(2)求代数式23120142016(2)(3)p q pq p q --++的值.19.(2024•灞桥区校级开学)如图,某校园内有一块长为(2)a b m +,宽为(2)a b m -的长方形空地()a b >.为美化环境,计划在这块空地上修建一个长为(2)a b m -,宽为bm 的长方形花圆,并将花圆四周余下的空地修建成通道,请用含有a 、b 的代数式表示通道的面积.20.(2023秋•静安区校级月考)探究应用:(1)计算:2(1)(1)x x x -++= ;22(2)(42)x y x xy y -++= .(2)上面的乘法计算结果很简洁,你发现了什么规律(公式)?用含字母a 、b 的等式表示该公式为: .(3)下列各式能用第(2)题的公式计算的是 .A .2(2)(24)m m m +++B .22(2)(22)m n m mn n -++C .2(3)(93)n n n -++D .22()(2)m n m mn n -++(4)设9101A =-,利用上述规律,说明A 能被37整除.21.(2023秋•右玉县期末)综合与实践如图1,长方形的两边长分别为1m +,7m +;如图2.长方形的两边长分别为2m +,4m +.(其中m 为正整数)E .(1)图1中长方形的面积1S = ;图2中长方形的面积2S = ;比较1S 2S (选填“<”、“ =”或“>” );(2)现有一正方形,其周长与图1中的长方形周长相等.①求正方形的边长;(用含m 的代数式表示)②试探究:该正方形的面积S 与图1中长方形的面积1S 的差(即1)S S -是一个常数,并求出这个常数.。
七年级数学整式的乘法3
澳洲赌场上线了bgm
[单选]在中医脏腑学说中,主藏神志脏器为()。A、脾B、肝C、心D、肾 [单选]以合同的成立是否以标的物的交付为必要条件为标准划分,合同可以分为()。A.双务合同和单务合同B.诺诚合同和实践合同C.主合同和从合同D.有名合同和无名合同 [单选,A2型题,A1/A2型题]带状疱疹病的病因下列哪项是正确的()A.初次或原发感染水痘-带状疱疹病毒引起B.再次或继发感染水痘-带状疱疹病毒引起C.由单纯疱疹病毒Ⅰ型引起D.由腺病毒引起E.由单纯疱疹病毒Ⅱ型引起 [问答题,案例分析题]【病例摘要】某女,30岁,教师。于2011年1月4日就诊。患者于3天前食辛辣肥甘之品后,出现尿频、尿急、尿道灼痛,患者未予重视,又食肥甘厚味之品,今日不适症状加重而来诊治。现症见:尿频、尿急,排尿时自觉尿道灼痛,小腹胀痛,不思饮食,睡眠欠佳,舌质红, [单选]鲁迅在《阿Q正传》中塑造的阿Q形象,是一种()A.再造想象B.创造想象C.幻想D.无意想象 [单选]股骨下端肿痛,局部皮温高,静脉怒张,X线片显示股骨远端有边界不清的骨质破坏区,有三角状骨膜反应。病人可能的诊断是()A.内生骨软骨瘤B.骨肉瘤C.骨巨细胞瘤D.骨软骨瘤E.骨髓瘤 [单选]职业道德是企业文化的重要组成部分,先进的企业文化是把企业职工的思想和()放在首位的。A.安全教育B.品德教育C.职业道德教育D.法律知识的普及 [单选]在研究胃癌与饮食习惯关系的病例对照研究中,不可用作对照的人群是()A.病例的邻居B.慢性萎缩性胃炎患者C.社区中的健康人D.同一医院的其他病例E.胃癌患者的亲属、同事、朋友 [单选]女,35岁,毒性弥漫性甲状腺肿患者,结束抗甲状腺药物疗程已4年,判断是否会复发的最佳指标为()A.血清总T3、T4测定B.血清游离甲状腺激素(FT3,FT4)测定C.血rT3(反T3)测定D.甲状腺吸131I率测定E.TSAb测定 [单选,A2型题,A1/A2型题]一颅脑外伤患者,可正确回答问题,可自动睁眼,右侧肢体偏瘫,刺痛可回缩,左侧肢体可随意运动。GCS评分为()。A.15分B.14分C.13分D.12分E.11分 [单选]微波中继通信中继方式中,适于不需要上下话路的方式是().A.直接中继B.外差中继C.基带中继 [单选]引起艾滋病的病毒是()A.HPVB.HSVC.HIVD.HCV [填空题]我国环境保护的三大政策是预防为()防治()的政策,谁污染谁治理的政策,强化环境,管理的政策。 [单选]钻孔通孔时,要特别注意孔即将钻通时的()。A、主轴转速B、钻头压力C、切削力D、进刀量 [单选,A1型题]泌尿系统结石容易引起的病理生理变化是()A.尿路梗阻和感染B.酸碱平衡失调C.肾功能不全D.诱发癌变E.电解质紊乱 [填空题]一般而言,浓缩浮选的入浮浓度为(),直接浮选的入浮浓度为()。 [名词解释]团体旅客 [单选]V形坡口适用于中低压钢管焊接,坡口的角度为()。A.40°~50°B.50°~60°C.60°~70°D.70°~80° [单选,A2型题,A1/A2型题]以下关于椎骨的描述正确的是()A.一共有25个B.一般由椎体和椎弓组成C.第1颈椎又称枢椎D.胸椎的棘突最短E.椎体和椎弓围成椎间孔 [单选]对于腹股沟综合征的描述中,下列哪项错误()A.常在生殖器初疮发生后2~6周内出现B.多为双侧,亦有单侧的腹股沟淋巴结肿大,逐渐融合成坚实的菱形水肿斑块C.与周围组织分界清楚D.数周后肿大的淋巴结软化,破溃形成多发性瘘管 [单选]相同浓度的下列四种溶液,()溶液的沸点最高。Al2(SO4)3B.CaCl2C.MgSO4D.HAc [单选,A1型题]具有高等学校医学专科学历,参加执业助理医师资格考试者,应在医疗、预防、保健机构中试用期满()A.6个月B.18个月C.1年D.2年E.3年 [填空题]变压器油位下降低于油位计的指示限度时,应()。 [单选,A1型题]右侧同向性偏盲的病损位于()。A.右侧视神经B.视交叉C.左侧视束D.左侧颞叶视辐射E.左侧顶叶视辐射 [判断题]第五套人民币专用纸张在紫外灯下有荧光反应。A.正确B.错误 [填空题]煤气脱硫一般分为两种方法,()和()。 [填空题]媒介组合可有多种方式,最主要的方式有三种:()组合、()组合、自用媒介与租用媒介组合。 [多选]以下选项中,属于行政处分的有()。A.警告B.行政拘留C.剥夺政治权利D.降级E.撤职 [单选]带现金管理员标志的柜员原则上每个网点最多设置()名。A.一B.二C.三D.四 [单选]胡萝卜有“小人参”的美称,它的()含量居蔬菜之首。A、胡萝卜素B、维生素KC、维生素PPD、视紫红质 [单选]关于再保险,下列说法正确的是()。A.再保险双方是通过口头约定来建立再保险关系的B.再保险是一种附属保险业务种类C.再保险是一种风险共担形式D.再保险是一种独立的保险业务种类 [单选]下列不会引起下消化道出血的疾病是()A.急性细菌性痢疾B.缺血性结肠炎C.右膈下脓肿D.结肠息肉E.结肠癌 [单选]船舶防污染的重要法律文件是()。A.油类记录薄B.防污染证书C.轮机日记D.A或B [填空题]浓硫酸为()液体,无(),熔点(℃):10.5,沸点(℃):330.0,相对密度(水=1)()。可以与水()。 [单选]某工商局任意改变了其所分属的营业执照中所确定的营业范围,从行政法理论上说,该工商局违反了行政行为效力的()方面。A.确定力B.拘束力C.执行力D.公定力 [单选]足月妊娠胎盘的特征叙述错误的是().A.胎盘约在孕12周基本形成B.胎盘直径为16-18cm,厚3cmC.胎盘重500~600g,是初生儿体重的1/6D.胎儿面光滑,由羊膜覆盖E.脐带大部分附着在胎盘中央的位置 [判断题]2004年版50美元正面底纹图案采用了彩虹印刷技术,其两边为红色,中间为黄色,色彩过渡自然、渐变。A.正确B.错误 [单选,A型题]膀胱癌多数是()A.透明细胞癌B.移行细胞癌C.腺癌D.未分化癌E.鳞癌 [单选,A2型题,A1/A2型题]关于肝性脑病,正确的是()A.一期脑电图轻度异常B.二期Babinski征阳性C.三期腱反射减弱或消失D.四期有扑翼样震颤E.一期患者出现精神症状 [单选,A2型题,A1/A2型题]基础护理合格率的控制指标属于()A.过程控制B.反馈控制C.同期控制D.环节质量控制E.面向未来控制
七下数学整式的乘法
七下数学整式的乘法
整式的乘法是指两个或多个整式相乘的运算。
在七年级数学中,通常会涉及到单项式与单项式、单项式与多项式、多项式与多项式
的乘法。
下面我将从这几个方面来详细解释整式的乘法。
首先,单项式与单项式的乘法。
单项式是只包含一个字母和一
个数的代数式,例如3x、-2y^2。
当两个单项式相乘时,只需要将
它们的系数相乘,并且将它们的字母部分相乘。
例如,(3x)(-2y^2) = 3 (-2) x y^2 = -6xy^2。
其次,单项式与多项式的乘法。
多项式是由多个单项式相加或
相减而成的代数式,例如2x + 3、-4a^2b + 5ab^2。
当一个单项式
与一个多项式相乘时,需要将单项式中的每一项与多项式中的每一
项分别相乘,然后将所得的乘积再相加。
例如,2x (3x^2 4x + 5) = 2x 3x^2 + 2x (-4x) + 2x 5 = 6x^3 8x^2 + 10x。
最后,多项式与多项式的乘法。
同样需要将一个多项式中的每
一项与另一个多项式中的每一项进行相乘,然后将所得的乘积再相加。
这里需要应用分配律和合并同类项的规则。
例如,(3x 2)(2x + 5) = 3x 2x + 3x 5 2 2x 2 5 = 6x^2 + 15x 4x 10 = 6x^2 +
11x 10。
在进行整式的乘法运算时,需要注意保持代数式的格式,正确地进行系数和字母的相乘,并最终合并同类项。
这样才能得到正确的乘积。
希望这些解释能帮助你更好地理解七年级数学中整式的乘法。
冀教版七年级下册数学《整式的乘法》PPT教学课件
①在直线c的两侧 ②在直线a,b的之间
内错角
c
1 2
a
34
65
b
78
3 5
典例精析 例1 如图,直线DE截直线AB ,AC,构成8个角,指出所有的
同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,
所以8个角中, 同位角:∠2与∠5,∠4与∠7,∠1
D
21 34
B
A
58
67 E C
与∠8, ∠6和∠3;
第八章 整式的乘法
8.4 整式的乘法
学习目标
1.掌握单项式与单项式相乘的运算法则.(重点) 2.能够灵活地进行单项式与单项式相乘的运算.(难点)
复习引入 1.幂的运算性质有哪几条?
同底数幂的乘法法则:am·an=am+n ( m、n都是正整数). 幂的乘方法则:(am)n=amn ( m、n都是正整数).
1 ab2
3a2bc
2
2 1 3 (a a a2 ) (b2 b) c
2
有积的乘方怎么
3a4b3c;
办?运算时应先
(2)(ab2 )2 (5ab)
算什么?
(1)2 a2b4 (5)ab
5(a2 a) (b4 b) 5a3b5.
注意 有乘方运算,先算乘方,再算单项式相乘.
归纳总结
单项式乘以单项式中的“一、二、三” 一个不变:单项式与单项式相乘时,对于只在一个单项 式里含有的字母,连同它的指数不变,作为积的因式. 二个相乘:把各个单项式中的系数、相同字母的幂分别 相乘.
积的乘方法则:(ab)n=anbn ( m、n都是正整数).
2.计算:(1)x2 ·x3 ·x4= x9
; (2)(x3)6=x18
初中七年级数学整式的乘除及乘法公式期末复习
整式的乘法运算:整式的乘法运算是指两个或多个整式相乘的运算。
整式的乘法运算中,我们要注意变量的指数和系数的相乘运算以及同类项的合并运算。
1.变量的指数相乘:当同一个字母的指数相乘时,我们可以将指数相加,然后保留同一个字母,并写上新的指数。
例如:3x²*4x³=12x^(2+3)=12x⁵2.系数的相乘:当整式中的系数相乘时,我们可以直接将系数相乘,然后保留原来的字母和指数。
例如:2x * 3y = 6xy3.同类项的相乘:同类项是指具有相同字母和指数的项。
当整式中的同类项相乘时,我们可以直接将系数相乘,然后保留原来的字母和指数。
例如:3x²*5x²=15x^(2+2)=15x⁴整式的除法运算:整式的除法运算是指一个整式除以另一个整式的运算。
整式的除法运算中,我们要注意变量的指数和系数的相除运算以及整除时的余数。
1.变量的指数相除:当同一个字母的指数相除时,我们可以将指数相减,然后保留同一个字母,并写上新的指数。
例如:10x⁵÷2x²=5x^(5-2)=5x³2.系数的相除:当整式中的系数相除时,我们可以直接将系数相除,然后保留原来的字母和指数。
例如:12xy ÷ 4x = 3y3.整除和余数:当两个整式相除时,如果能整除,则商为一个整式,余数为零。
如果不能整除,余数不为零,我们可以保留余数,但不能继续进行整除运算。
乘法公式的运用:乘法公式是指将一个较为复杂的乘法运算通过一定的方法化简,使运算变得简便的运算法则。
1.二次方差式公式:(a+b)² = a² + 2ab + b²(a-b)² = a² - 2ab + b²例如:(x+2)²=x²+2x*2+2²=x²+4x+42.一次方差式公式:(a+b)(a-b)=a²-b²例如:(x+3)(x-3)=x²-3²=x²-93.三次方差式公式:(a+b)(a²-ab+b²) = a³ + b³例如:(x+2)(x²-2x+4)=x³+2³=x³+8综上所述,整式的乘法运算和除法运算是我们初中七年级数学中的重要内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[单选]甲、乙、丙、丁共有一辆汽车,在营运过程中造成戊的损害。丙对戊的损害进行了全部赔偿。丙赔偿以后,对甲、乙、丁的追偿权,下列表述正确的是:()A.丙可要求甲、乙、丁中的某一人对其所承担的赔偿责任除丙应承担的外予以全部承担B.丙对甲、乙、丁只能要求其承担其按照共有 [单选]集体资产管理的基本任务是()。A.集体资产的保值B.集体资产的增值C.保证集体扩大再生产D.减少集体资金的投入 [单选,A2型题,A1/A2型题]骨髓中嗜碱性粒细胞明显增多,与下列何种疾病的诊断关系不大().A.急性粒细胞性白血病B.慢性粒细胞性白血病C.嗜碱性粒细胞性白血病D.放射线照射反应E.以上都正确 [单选]对无排卵性功血病因的叙述,下列哪项是错误的?()A.青春期功血是由于下丘脑-垂体-卵巢轴调节功能尚未健全而引起B.围绝经期妇女功血是由于垂体功能异常而引起C.育龄期妇女功血可因内、外环境某种刺激(如劳累、应激、手术、流产等)引起D.无排卵性功血时,异常子宫出血还可 [单选]患者,女性,超声见乳房内无回声光团,边清壁薄,CDFI未见血流,如图所示考虑为()。A.乳腺癌B.乳腺腺瘤C.乳腺脓肿D.乳腺囊肿E.以上都不是 [单选]上消化道出血伴休克时首要的治疗是()A.胃管注入止血药B.平卧位,下肢抬高C.积极补充血容量D.胃镜止血E.应用奥美拉唑 [单选]在PFD上,在右下角出现琥珀色的ILS闪亮时,表示:()A、APPR(进近)方式预位而未选择ILS显示。B、ILS信号丢失。C、航向道偏差过大。 [单选,A1型题]既能治疗风寒、风热表证,又能治疗破伤风的药物是()A.蝉衣B.防风C.天麻D.荆芥E.僵蚕 [单选]从企业角度,ERP项目可以分成三个阶段,前期准备阶段、合同项目执行阶段、巩固完善阶段。而其中,在前期准备阶段,软件公司处于什么阶段?()A.售前工作B.项目准备C.蓝图设计D.系统实现 [单选]某一竖直角为17°23,40,化为弧度值为()。A.0.72B.0.304C.0.605 [单选]电子经纬仪区别于光学经纬仪的主要特点是()。A.使用光栅度盘B.使用金属度盘C.没有望远镜D.没有水准器 [单选,A2型题,A1/A2型题]紧急胃镜检查应在上消化道出血后()A.<24小时B.24~48小时C.48~72小时D.>72小时E.出血停止 [单选,A4型题,A3/A4型题]26岁女性,已婚2年,G1P0,婚后一直服用短效口服避孕药避孕,但意外妊娠,于孕50天行人工流产术。患者放置宫内节育器后1个月,月经量增多1倍,且月经间期有点滴出血。B型超声检查提示环位置正常,血Hb:105g/L,对其处理错误的是()A.立即取出宫内节育器 [名词解释]交换 [单选]通风空调系统中单风道集中式系统是指()空调系统。A.全空方式B.空气—水C.全水D.直接蒸发机组 [单选]盐析法分离蛋白质的原理是()A.破坏蛋白质的一级结构B.破坏蛋白质的二级结构C.破坏蛋白质水化膜而改变溶解度D.使蛋白质发生变性沉淀E.使蛋白质电荷发生改变 [单选]下列不属于物权的基本原则的是()。A.一物一权原则B.全面履行原则C.物权公示原则D.物权法定原则 [单选]Allinflatableliferaftshave().A.safetystrapsfromtheoverheadB.builtinseatsC.releasinghooksateachendD.waterstabilizingpocket [单选]能平肝潜阳,重镇降逆,凉血止血的药物是()A.赭石B.蒺藜C.珍珠母D.石决明E.牡蛎 [不定项选择]建设项目清洁生产分析的方法有()。A.指标B.专家判断法C.质量指标法D.分值评定法 [填空题]受拉热轧光圆钢筋(HPB235)的末端应倒做()弯钩,其弯曲直径d不得小于钢筋直径的(),钩端应留有不小于钢筋直径3倍的直线段。 [单选,A1型题]Apgar评分判断新生儿临床恶化的顺序()A.皮肤颜色-呼吸-反射-肌张力-心率B.皮肤颜色-反射-肌张力-呼吸-心率C.皮肤颜色-肌张力-反射-呼吸-心率D.皮肤颜色-呼吸-肌张力-反射-心率E.心率-皮肤颜色-肌张力-反射-呼吸 [单选]关于男扎的节育机制,正确的是()A.抑制雄性激素分泌B.抑制生精能力C.阻止精子输送D.抑制性功能E.阻止精子与卵子结合 [多选]燃气调压站(室)通常由()等组成。A.储气罐B.测量仪表C.过滤器D.调压器 [单选]SPECT脑血流灌注显像表现为局限性放射性分布稀疏或缺损一般不出现在哪项疾病()。A.缺血性脑血管疾病B.偏头痛和脑肿瘤C.脑脓肿D.癫痫的发作间期E.癫痫的发作期 [单选]现场浇注基础的顶面应高于地面(),以防下沉,基础表面水平误差不超过士5mm。A.50一60mmB.60一100mmC.100一200mmD.200一300mm [单选]HIV的免疫缺陷的实验室检查不包括下列哪项()A.外周血淋巴细胞计数B.CD细胞计数C.CD/CD比值D.HIV抗体 [单选]下列选项中哪项不是小肠运动的基本形式?()A、钟摆运动B、集团蠕动C、蠕动和逆蠕动D、分节运动 [单选]制作询问笔录,下列说法错误的是()。A、可以有三名火灾调查人员参加询问B、对于被询问对象的陈述要按照其本人的语气记录,不能作任何修饰、概括和修改。C、被询问对象请求自行书写陈述的,不应准许。D、询问笔录应该按顺序逐页编号,并由被询问对象逐页签名或者捺指印。 [填空题]煤气中硫化氢所含硫约占煤气中硫总量的()以上。 [问答题,简答题]离心泵如何停用? [问答题,简答题]简述汽油机和柴油机的着火和燃烧方式。 [单选]()是招标采购合同规划的根本目的。A.合理确定最小工作单元B.合理确定最小合同单元C.合理确定招标合同单元D.合理确定最小分解单元 [填空题]广告的心理功能有:传播、诱导、教育、()和促销。 [单选]在药品标签上必须印有规定标识的是()A.贵重药品B.自费药品C.处方药D.非处方药品E.内服药品 [名词解释]GPS [单选,A2型题,A1/A2型题]为了区别红白血病与巨幼红细胞性贫血,下列首选试验是().A.PAS染色B.POX染色C.ALP积分测定D.α-NAE染色E.以上都正确 [单选]无线列调地面电台的场强必须覆盖两个相邻地面固定电台之间距离的()以上A.1/3B.1/2C.2/3 [单选]以下不是黄瘤病临床类型的是()A.结节性黄瘤B.扁平黄瘤C.发疹性黄瘤D.重症黄瘤 [单选,A1型题]关于胰岛素的作用下列哪项错误()。A.促进脂肪合成,抑制脂肪分解B.抑制蛋白质合成,抑制氨基酸进入细胞C.促进葡萄糖利用,抑制糖原分解和产生D.促进钾进入细胞,降低血钾E.促进蛋白质
