波动2
专业英语-波动光学 2

Superposition of Waves(波的叠加)
Consider two waves, derived from the same source, but characterized by phase difference Φ. They may be written as
For convenience, we allow them to have the same amplitude. If the waves are superposed, the resultant electric field is
If we multiply both numerator and denominator by b, and define β=kbsinθ/2, we may write
More-proper analysis, based on electromagnetic theory and a twodimensional formulation would include an additional factor of iλ in the expression for E(θ), but the important part is the variable sinβ/β.
The total field at P is the sum of the fields due to individual elements. If the dimension of the slit is b and its center, s=0, this is just the integral where constant terms have been removed from the integral. The integrand is of the form exp(a·s), so the integral is easily evaluated
例析110kV线路TYD二次电压波动问题

例析110kV线路TYD二次电压波动问题TYD是国产电容式电压互感器型号,线路TYD的作用是抽取线路电压,同时还能起到耦合电容的作用,与阻波器和高频滤波器配合,用于载波通讯。
目前国产电容式电压互感器在110kV及以上电压等级的变电站应用相当广泛,几乎代替了电磁式电压互感器在现场的应用。
1 故障概述某110kV变电站某110kV线路CT更换后启动,对侧电源向线路充电时,发现线路保护装置中线路二次电压Ux采样异常,电压值从80V到100V不断波动。
用万用表测量该线路保护屏后线路Ux电压却稳定在103V,在110kV线路备自投装置屏前查看该线路Ux采样电压,发现电压值也是从80V到100V不断波动。
由于保护和备自投装置采样通道同时坏的概率很小,推测该线路TYD二次电压本身含有谐波导致采样波动。
该线路TYD二次电压用万用表测量很稳定,保护装置和备自投装置的采样却不断波动,原因在于保护装置和备自投装置是微机装置,采样速度很快、反应较为灵敏,能反应线路TYD二次电压波动过程;万用表测量交流电压是先把交流信号整流成为直流,所以线路TYD二次电压测量值一直很稳定。
根据推测,用示波器测量该线路TYD二次电压,波形如图1所示。
从图1可以看出,波形还有较大的低频谐波,经现场检查,发现TYD本体旁边的隔离变压器振动响声比较大。
受隔离变压器的有较大低频谐波输入,导致铁心趋于饱和,励磁电流增大,引起较大振动。
图1 线路TYD二次电压波形图2 原因分析由于线路本侧开关处于热备用状态,线路电压由对侧变电站空充至本站,到对侧变电站检查对侧线路TYD二次电压,保护和测控装置中线路TYD二次电压采样均正常。
说明线路一次系统本身并无谐波,谐波来源于本侧线路TYD自身产生的谐波。
根据初步分析,以下四种可能导致谐波存在:(1)TYD二次回路本身存在寄生和某种干扰,导致谐波存在。
(2)隔离变压器本身励磁特性不符合要求,输入未能达到额定电压,铁心就已经饱和了,产生低频谐波。
大学物理习题详解No.2波动方程

《大学物理》作业 No.2波动方程班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题[ F ] 1. 解:电磁波就可以在真空中传播。
[ F ] 2. 解:波动是振动的传播,沿着波的传播方向,振动相位依次落后。
[ F ] 3. 解:质元的振动速度和波速是两个概念,质元的振动速度是质元振动的真实运动速度,而波速是相位的传播速度,其大小取决于介质的性质。
[ F ] 4. 解:振动曲线描述的是一个质点离开平衡位置的位移随时间的变化关系;波形曲线是某一时刻,波线上各个质点离开平衡位置的情况。
[ F ] 5. 解:对于波动的介质元而言,其动能和势能同相变化,它们时时刻刻都有相同的数值。
二、选择题:1. 一平面简谐波表达式为)2(sin 05.0x t y --=π (SI) ,则该波的频率v (Hz)、波速u (m ⋅s -1)及波线上各点振动的振幅A (m)依次为:(A) 2/1,2/1,05.0- (B) 2/1,1,05.0-(C) 2/1,2/1,05.0 (D) 2 ,2,05.0[ C ]解:平面简谐波表达式可改写为(SI))22cos(05.0)2(sin 05.0ππππ+-=--=x t x t y与标准形式的波动方程 ])(2[cos ϕπ+-=u xt v A y 比较,可得 )s (m 21,(Hz)21,(m)05.01-⋅===u v A 。
故选C2. 一平面简谐波的波动方程为)3cos(1.0πππ+-=x t y (SI),t = 0时的波形曲线如图所示。
则:(A) O 点的振幅为-0.1 m(B) 波长为3 m (C) a 、b 两点位相差 π21(D) 波速为9 m ⋅s -1解:由波动方程可知(Hz),23(m),1.0==νA (m)2=λ,)s (m 32231-⋅=⨯==νλua 、b 两点间相位差为:2422πλλπλπϕ===∆ab故选C3. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。
第2节 波动学

第二节 波动学单项选择题(下列选项中,只有一项符合题意)1.在波长为λ的驻波中,两个相邻的波腹之间的距离为( )。
[2010年真题]A .2λB .4λC .34λD .λ 【答案】A【解析】相邻的两个波节(或波腹)之间的距离等于半个波长,即2λ。
2.一平面简谱横波的波动表达式为y=0.05cos(20πt+4πx)(SI),取k=0,±1, ±2,…。
则t=0.5s 时各波峰所在处的位置为( )。
[2008年真题]A .4102-k (m ) B .410+k (m ) C .492-k (m ) D .49+k (m ) 【答案】A【解析】依题意t=0.5s 时,y=0.05cos(20πt+4πx)=0.05,解得X=4102-k =25-k 。
3.一平面简谐横波的波动表达式为y=0.002cos(400πt-20πx)(SI)。
取则t=1s 时各波谷所在处的位置为( )。
[2007年真题]A .B .C .D .【答案】B【解析】平面简谐振动波的波动方程为2cos(2)xy A t πλπυ=-,t=1s 时,波谷位置应满足400π-20πx=k π,解得x=(400-k )/20,k 关于0对称,与B 选项等价。
4.一平面简谱波在弹性媒质中传播时,某一时刻在传播方向上一质元恰好处在负的最大位移处,则它的( )。
[2010年真题]A .动能为零,势能最大B .动能为零,势能为零C .动能最大,势能最大D .动能最大,势能为零 【答案】B【解析】根据机械波能量的公式,质元的总机械能:222K PKPW =W+W =A s i n [()]W =Wxm t uωω∆-且可知,质元中动能与势能同时达到最大值或最小值,故在负的最大位移处K P W =W 0=。
5.一声波波源相对媒质不动,发出的声波频率是0v,设一观察者的运动速度为波速的12,当观察者迎着波源运动时,他接收到的声波频率是( )。
初中八年级下册数学202 数据的波动程度(第2课时)课件q

乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75 样本平均数相同,
解:样本数据的平均数分别是:
估计这批鸡腿的
x甲=
74+74+ +72+73 15
75, x乙=
75+73+ +71+75 15
平均质量相近. 75.
20.2 数据的波动程度/
样本数据的方差分别是:
为应该选甲运动员.
20.2 数据的波动程度/
例2 一次科技知识竞赛,两组学生成绩统计如下:
分数 50 60 70 80 90 100 人数 甲组 2 5 10 13 14 6
乙组 4 4 16 2 12 12
已经算得两个组的人平均分都是80分,请根据你所学过的统 计知识,进一步判断这两个组在这次竞赛中的成绩谁优谁劣, 并说明理由.
6
s2A=1×[(0.2-0.6)2+(0.2-1.9)2+(0.2-0.5)2+(0.2+1.3)2+ (0.2+06.2)2+(0.2+0.3)2]≈0.97(百万元2);
s2B =1×[02+0.82+1.12+0.62+1.12+0.22]≈0.6(百万元2). 这两个6方差的大小反映了A,B两家餐饮店相邻两天的日营业额
, 2
s甲
=(74-75)2 +(74-75)2 +
+(72-75)2 +(73-75)2 15
3
. s乙2 =(75-75)2+(73-75)2+
+(71-75)2 (75-75)2 15
8
由 x甲=x乙可知,两家加工厂的鸡腿质量大致相等;由 s甲2 < s乙2 可知,甲加工厂的鸡腿质量更稳定,大小更均匀.因此,快
波动光学2
QR >> d ∴d ≈ 0
2
r = 2dR = ( ∆ − )R 2
λ
1 r = (k − )Rλ 明环半径 2 r = kRλ 暗环半径
2.讨论 明环半径
0
R r d
1 r = (k − )Rλ (k = 1,2,3,L) 2
暗环半径
r = kRλ (k = 0,1,2,L)
⑴中心点 d = 0 ∆ = λ 2 从反射光中观测是暗点。 从反射光中观测是暗点。 从透射光中观测,中心点是暗点还是亮点? 从透射光中观测,中心点是暗点还是亮点? 干涉条纹是以接触点为中心的同心圆, ⑵干涉条纹是以接触点为中心的同心圆,半径 愈大,条纹级次愈高。 愈大,条纹级次愈高。
n
L
d
b′
∆e
b
λ2
d=
λ L
2n b ⋅
二 牛顿环 牛顿环实验装置 显微镜 T L S M 半透半反镜
R
平凸透镜 平玻璃
r
d
牛顿环干涉图样
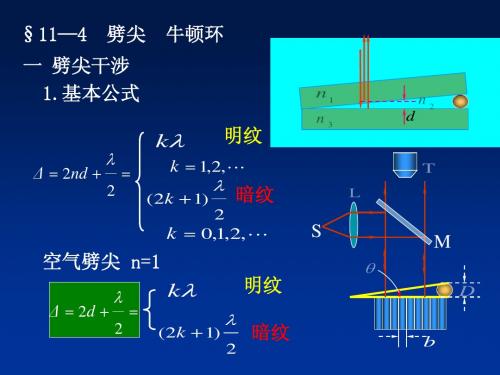
1.基本公式 光程差 ∆ = 2d +
0
λ
2
明纹
R r d
∆=
2
kλ (k = 1,2,L)
1 (k + )λ (k = 0,1,L) 暗纹 2
2 2 2
r = R − (R − d ) = 2dR − d
rk = kRλ
rk +5 = (k + 5)Rλ
5Rλ = r
R= r
2 k +5 2 k
(
2 k +5
−r
2
2 k
)
2
−r (7.96mm) − (5.63mm) = = 10.0m 5λ 5× 633nm
第3讲波动光学(2)反射折射
y z x
qi qr
qt
Bt
Er
ni
Note that Hecht uses a different notation for the reflected field, which is confusing! Ours is better! 钟书上的框架和 我们的有差别!
Et
kt
nt
Note that reflected magnetic field must point into the screen to the achieve E B k . The x means ―into the screen.‖
reflectanceairtoglassinterface空气玻璃界面的反射率noteperpendicularpolarizationincidenceangle306090parallelpolarizationincidenceangle306090垂直偏振平行偏振角度越大反射率越大掠入射brewsteranglereflectanceglasstoairinterface玻璃空气界面的反射率全内反射noteperpendicularpolarizationincidenceangle306090parallelpolarizationincidenceangle306090normalincidence垂直入射的情况whenairglassinterfacesamewhicheverdirectionlighttravelsfromairfromglass4hasbigimplicationsphotographylenses
第三章 波动光学(续)菲涅尔反射和折射公式
Fresnel„s Equations for Reflection and Refraction 参照书上第三章内容
第2课时--1.波动图像与波速公式
-4-
一
二
三
5.描述机械波的物理量 (1)波长 λ:在波动中振动相位总是相同的两个相邻质点间的距离。 (2)频率 f:在波动中,介质中各质点的振动频率都是相同的,都等于波源 的振动频率。 (3)波速 v、波长 λ 和频率 f、周期 T 的关系。 公式 :v= =λf。 机械波的速度大小由 介质决定,与机械波的频率无关。
第二课时
机械波
章节概述
一 二 三
一、机械波
1.定义 机械振动在介质 中传播,形成了机械波。 2.产生条件 一是要有做机械振动的物体作为 波源;二是要有能够传播机械振动的
介质。
3.机械波的分类 (1)质点的振动方向与波的传播方向相互垂直 的波叫作横波。在横波 中凸起的最高处叫作 波峰,凹下的最低处叫作 波谷。 (2)质点的振动方向与波的传播方向在同一直线上 的波叫作纵波。在 纵波中质点分布最密的位置叫作 密部,质点分布最疏的位置叫作疏部。
A.物体做机械振动,一定产生机械波
B.后振动的质点总是跟着先振动的质点重复振动,只是 时间落后一步 C.参与振动的质点群有相同的频率 D.机械波是介质随波迁移,也是振动能量的传递
3.一列简谐横波在x轴上传播,某时刻的波形如图所示,a、b、
c为三个质点,a正向上运动。由此可知( AC ) A.该波沿x轴正方向传播 B.c正向上运动 C.该时刻以后,b比c先到达平衡位置
质点的起振方向与波源的起振方向相同。
【例1 】一列沿x轴正方向传播的简谐机械横波,波速为4 m/s.某时
刻波形如图所示,下列说法正确的是( D ) A.这列波的振幅为4 cm
B.这列波的周期为1 s
C.此时x=4 m处的质点沿y轴负方向运动 D.此时x=4 m处的质点的加速度为0
第2章波动方程
2.齐次方程的初值问题(Cauchy 问题)
考察问题
⎧⎪ ⎨ ⎪⎩
utt
u(
− a2uxx =
x,0) = ϕ (
0,
x)
,
ut
( x,0)
x ∈ \, t > 0,
=ψ ( x), x∈\.
利用齐次波动方程的通解表达式:
(1.1)
u( x, t ) = F ( x − at ) + G ( x + at ) ,
u = F ( x − at ) , a > 0
显然是弦振动方程的解。给 t 以不同的值,就可以看出作一维自由振动的物体在各时刻的相
应位置。在 t = 0 时, u = F ( x ) 对应于初始的振动状态,而 u = F ( x − at ) 作为 ( x, u ) 平
面 上 的 曲 线 是 曲 线 u = F ( x ) 向 右 平 移 了 at 个 单 位 , 所 以 齐 次 弦 振 动 方 程 的 形 如
=
1 2a
⎧∂
⎨ ⎩
∂t
ϕ x+at (ξ )dξ +
x − at
ψ x + at
(ξ
)dξ
⎫ ⎬
.
x − at
⎭
u2 满足非齐次方程的初值问题
4
⎧⎪ ⎨ ⎪⎩
utt
u(
− a2uxx =
x, 0) = 0,
f ut
( (
x, x,
t), 0) =
x∈ 0,
\
, t> x∈
0, \.
为了求解(1.4),首先求解
条件无关。称这个三角形区域为区间 ⎡⎣ x1 , x2 ⎤⎦ 的决定区域。
第12章 波动学基础-2
A2 = A12 + A22 + 2 A1A2 cosϕ12 ⇒ I ∝ A2
波的强度: I = I1 + I2 + 2 I1I2 cos Δϕ
Δϕ =
2kπ k = 0,±1,±2,L
加强
Amax = A1 + A2
Imax = I1 + I2 + 2 I1I2 I1 = I2 = I0 I max = 4I0
(1) t = 0 时 原点处y0=0, v0>0, 求其波函数; (2) 如下图所示,入射波在P点反射,求x 轴上干涉而静止
的点(驻波波节)的位置.
u入
疏密
O
P
x
3λ
4
解:(1) t = 0 时 原点处
y0 = 0,
v0 > 0,
原点初相
ϕ0
=
−
π 2
y0
=
Acos(2 πν
t
−
π) 2
y入
=
Acos[2
两点S1和S2的间距为d = 23m, S1位于原点O. 设波在传播
过程中强度不变, x1=9m和x2=11m处的两点是相邻的两
个因干涉而静止的点. 求 (1) 波长
S1 O
x1 x2 S2
x
(2) S1、S2间的最小相位差
(3) S1、S2连线上, S1、S2外侧合成波的强度
解:设S1和S2的振动初相位分别为 ϕ1, ϕ2
(wavelet)的波源,在其后的任一时刻,这些子波波面
的包迹决定了原波动的新的波前.
子波波源
波前
子波
P.2/30
wzy
二、惠更斯原理的应用
平面波和球面波演示
