6-2平面简谐波的波动方程
合集下载
6.1 平面简谐波的波动方程

杨 鑫
λ
6.1 平面简谐波的波动方程
第6章 机械波
32
2.周期 2.周期
T
一定的振动 位相向前传 播一个波长 所需的时间
纵 波 质点振动方向与 波的传播方向 相互平行的波
6.1 平面简谐波的波动方程
第6章 机械波
30
3.机械波在传播过程中的物理本质 3.机械波在传播过程中的物理本质
波的传播过 程是振动状 态 位相)的 传 (位相) 播 过 程
作者 杨 鑫
沿着 波的 传播 方向
后一质元的 后一质元的 振动总要重 振动总要重 复相邻前一 质元的振动 质元的振动
2.周期 2.周期
T
波的周期
ν
所包含的波长数目
=ν波源
演示: 演示:横波
T
作者
杨
鑫
6.1 平面简谐波的波动方程
第6章 机械波
18
4.波速 单 位 时 间 内 4.波速 某一振动状 态(位相)传 相 速 播 的 距 离
u
波速的大小取决 于介质的性质 波速与介质中质点 波速与介质中质点 的振动速度不同
杨 鑫
6.1 平面简谐波的波动方程
第6章 机械波
5
(2)合 振 幅
A x = Acos(ω t + ϕ) ϕ2 2 A ϕ2 1 ( 1 ) 合振动的频率与 ω ϕ ϕ1 x 分振动的频率相同 o
A=
二、同方向、同频率简谐振动的合成 同方向、 1. 合振动是简谐振动
A
( 3 ) 合振 动初相
作者 杨 鑫
演示: 演示:纵波
6.1 平面简谐波的波动方程
第6章 机械波
12
3. 机械波在传播过程中的物理本质
λ
6.1 平面简谐波的波动方程
第6章 机械波
32
2.周期 2.周期
T
一定的振动 位相向前传 播一个波长 所需的时间
纵 波 质点振动方向与 波的传播方向 相互平行的波
6.1 平面简谐波的波动方程
第6章 机械波
30
3.机械波在传播过程中的物理本质 3.机械波在传播过程中的物理本质
波的传播过 程是振动状 态 位相)的 传 (位相) 播 过 程
作者 杨 鑫
沿着 波的 传播 方向
后一质元的 后一质元的 振动总要重 振动总要重 复相邻前一 质元的振动 质元的振动
2.周期 2.周期
T
波的周期
ν
所包含的波长数目
=ν波源
演示: 演示:横波
T
作者
杨
鑫
6.1 平面简谐波的波动方程
第6章 机械波
18
4.波速 单 位 时 间 内 4.波速 某一振动状 态(位相)传 相 速 播 的 距 离
u
波速的大小取决 于介质的性质 波速与介质中质点 波速与介质中质点 的振动速度不同
杨 鑫
6.1 平面简谐波的波动方程
第6章 机械波
5
(2)合 振 幅
A x = Acos(ω t + ϕ) ϕ2 2 A ϕ2 1 ( 1 ) 合振动的频率与 ω ϕ ϕ1 x 分振动的频率相同 o
A=
二、同方向、同频率简谐振动的合成 同方向、 1. 合振动是简谐振动
A
( 3 ) 合振 动初相
作者 杨 鑫
演示: 演示:纵波
6.1 平面简谐波的波动方程
第6章 机械波
12
3. 机械波在传播过程中的物理本质
第二节 平面简谐波的波动方程

上页 下页 返回 退出
解: 由题意 波长 周期
u 0.40 m
T 1 8105 s
(1)原点处质点的振动表达式
y0 A cost 0.1103 cos(25103 t) m
(2)波函数
y Acos(t x)
u
0.1103
cos
即
y
Acos t
2 x1
上式代表x1处质点在其平衡位置附近以角频率
作简谐运动。
y
A
O
t
上页 下页 返回 退出
t 一定:令t=t1,则质点位移y 仅是x 的函数。
即
y
A
cos
t1
2 x
以y为纵坐标、x 为横坐标,得到一条余弦曲线,
它是t1时刻波线上各个质点偏离各自平衡位置的位移 所构成的波形曲线(波形图)。
y
u
A
x
上页 下页 返回 退出
沿波线方向,任意两点x1、x2的简谐运动相位差为:
2
1
2
x2 x1
2
x
x、t 都变化:
实线:t1 时刻波形;虚线:t2 时刻波形
y
u
o
x
x1 x
上页 下页 返回 退出
y
u
当t=t1时,y
A
cos
t1
0.5
M1
M2
0.4
0.2
a
0
b
0.2 10 20 30 40 50 60 70
解: 由题意 波长 周期
u 0.40 m
T 1 8105 s
(1)原点处质点的振动表达式
y0 A cost 0.1103 cos(25103 t) m
(2)波函数
y Acos(t x)
u
0.1103
cos
即
y
Acos t
2 x1
上式代表x1处质点在其平衡位置附近以角频率
作简谐运动。
y
A
O
t
上页 下页 返回 退出
t 一定:令t=t1,则质点位移y 仅是x 的函数。
即
y
A
cos
t1
2 x
以y为纵坐标、x 为横坐标,得到一条余弦曲线,
它是t1时刻波线上各个质点偏离各自平衡位置的位移 所构成的波形曲线(波形图)。
y
u
A
x
上页 下页 返回 退出
沿波线方向,任意两点x1、x2的简谐运动相位差为:
2
1
2
x2 x1
2
x
x、t 都变化:
实线:t1 时刻波形;虚线:t2 时刻波形
y
u
o
x
x1 x
上页 下页 返回 退出
y
u
当t=t1时,y
A
cos
t1
0.5
M1
M2
0.4
0.2
a
0
b
0.2 10 20 30 40 50 60 70
大学物理平面简谐波的波函数

第六章 机械波
6 – 2 平面简谐波的波函数
各种不同的简谐波
合成 分解
简谐波 1
简谐波 2
合成 复杂波
第六章 机械波
物理学教程 (第二版)
复杂波
6 – 2 平面简谐波的波函数
物理学教程 (第二版)
以速度u 沿
x 轴正向传播的
平面简谐波 . 令
原点O 的初相为
零,其振动方程
yO Acost
时间推 点O 的振动状态
6 – 2 平面简谐波的波函数
物理学教程 (第二版)
一 平面简谐波的波函数
介质中任一质点(坐标为 x)相对其平衡位置的
位移(坐标为 y)随时间的变化关系,即 y(x,t) 称
为波函数.
y y(x,t)
各质点相对平 衡位置的位移
波线上各质点 平衡位置
简谐波:在均匀的、无吸收的介质中,波源作 简谐运动时,在介质中所形成的波. 平面简谐波:波面为平面的简谐波.
第六章 机械波
6 – 2 平面简谐波的波函数
物理学教程 (第二版)
3. 某平面简谐波在t = 0s时波形如图所示,则该波的
波函数为:
(A) y = 0.5cos[4 (t-x/8)-/2] (cm) . (B) y = 0.5cos[4 (t + x/8) + /2] (cm) . (C) y = 0.5cos[4 (t + x/8)-/2] (cm) . (D) y = 0.5cos[4 (t-x/8) + /2] (cm) .
y Acos(Bt
的两点间的相位差.
Cx) y Acos2
π
(
t
x)
T
6 – 2 平面简谐波的波函数
各种不同的简谐波
合成 分解
简谐波 1
简谐波 2
合成 复杂波
第六章 机械波
物理学教程 (第二版)
复杂波
6 – 2 平面简谐波的波函数
物理学教程 (第二版)
以速度u 沿
x 轴正向传播的
平面简谐波 . 令
原点O 的初相为
零,其振动方程
yO Acost
时间推 点O 的振动状态
6 – 2 平面简谐波的波函数
物理学教程 (第二版)
一 平面简谐波的波函数
介质中任一质点(坐标为 x)相对其平衡位置的
位移(坐标为 y)随时间的变化关系,即 y(x,t) 称
为波函数.
y y(x,t)
各质点相对平 衡位置的位移
波线上各质点 平衡位置
简谐波:在均匀的、无吸收的介质中,波源作 简谐运动时,在介质中所形成的波. 平面简谐波:波面为平面的简谐波.
第六章 机械波
6 – 2 平面简谐波的波函数
物理学教程 (第二版)
3. 某平面简谐波在t = 0s时波形如图所示,则该波的
波函数为:
(A) y = 0.5cos[4 (t-x/8)-/2] (cm) . (B) y = 0.5cos[4 (t + x/8) + /2] (cm) . (C) y = 0.5cos[4 (t + x/8)-/2] (cm) . (D) y = 0.5cos[4 (t-x/8) + /2] (cm) .
y Acos(Bt
的两点间的相位差.
Cx) y Acos2
π
(
t
x)
T
6_2 平面简谐波的波函数讲解

波线上各点的简谐运动图
7
6-2 平面简谐波的波函数
该方程表示t 时刻波传播方向上各质点的位移, 即 t 时刻的波形(y — x 的关系) y
2πx y A cos t 2 t 一定 x 变化 (定值) t1 C 令 2πx y A cos 则
解 (1) 写出波动方程的标准式
t x y A cos[ 2π ( ) ] T
11
6-2 平面简谐波的波函数 t x y A cos[ 2π ( ) ] T
在t=0时坐标原点处的质点在平衡 位置沿 oy 轴正向运动.
O
A
y
π t x π y cos[ 2 π ( ) ] (m) 2 2.0 2.0 2
波函数
x y A cos[ (t ) ] u
质点的振动速度,加速度
y x v A sin[ (t ) ] t u 2 y x 2 a 2 A cos[ (t ) ] t u
5
6-2 平面简谐波的波函数
二 1 波函数的物理含义
可得波动方程的几种不同形式:
x y A cos t u t x A cos 2 π T 2 πx A cos t
4
6-2 平面简谐波的波函数
12
6-2 平面简谐波的波函数
(2)求 t 1.0s 波形图
t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2 π y (1.0) cos[ π x] 2 t 1.0 s sin πx (m) 波形方程
y/m
7
6-2 平面简谐波的波函数
该方程表示t 时刻波传播方向上各质点的位移, 即 t 时刻的波形(y — x 的关系) y
2πx y A cos t 2 t 一定 x 变化 (定值) t1 C 令 2πx y A cos 则
解 (1) 写出波动方程的标准式
t x y A cos[ 2π ( ) ] T
11
6-2 平面简谐波的波函数 t x y A cos[ 2π ( ) ] T
在t=0时坐标原点处的质点在平衡 位置沿 oy 轴正向运动.
O
A
y
π t x π y cos[ 2 π ( ) ] (m) 2 2.0 2.0 2
波函数
x y A cos[ (t ) ] u
质点的振动速度,加速度
y x v A sin[ (t ) ] t u 2 y x 2 a 2 A cos[ (t ) ] t u
5
6-2 平面简谐波的波函数
二 1 波函数的物理含义
可得波动方程的几种不同形式:
x y A cos t u t x A cos 2 π T 2 πx A cos t
4
6-2 平面简谐波的波函数
12
6-2 平面简谐波的波函数
(2)求 t 1.0s 波形图
t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2 π y (1.0) cos[ π x] 2 t 1.0 s sin πx (m) 波形方程
y/m
平面简谐波概念
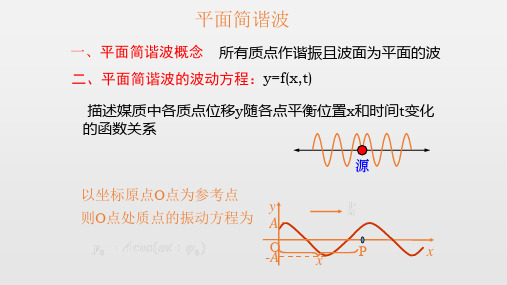
解:
•
(1)T 2, 40,u 20,A 10, 2
T
T
且t 0时:yo 5,vo 0
O
2 3
(2) OB长度
Y(cm)
10 •
u
-5 •
解:O B (O B)2
oB
C
20
-5
x(cm)
•
t 0时:yB 0,vB 0
O
-A
x
P
x
P点比O点超前时间 反向波波函数
y
O
P
x
x
以波线上x0处点为参考点
y
则Q点处质点的振动方程为 A x0 Q
O -A
x
P
x
Q点的任一振动状态传到P点,需要时间
则波动方程:
其中:x xo u
— 表示x处质元的振动落后(或超前)xo处质元
振动的时间
(
x u
xo
)
—
表示x处质元的振动落后(或超前)于xo处质元
(2)同一时刻,沿波线各质元振动状态不同,各质元相位 依次落后
*u
=
T
=
u由介质的性质决定
T T振
振 由振源决定.
得波动方程:
当x确定: y(t)——x处质元的振动方程 当t确定: y(x)——t时刻的波形
二、波的强度
1、能流P : 单位时间通过某一面积的波能 P su
—单位:焦耳/秒米2
波动在无吸收的、均匀无限大介质中传播,
1、平面波:A保持不变。
1
2
2、球面波:A与r成反比。 证明:1、 无吸收, P1 P2
平面简谐波的波函数解读
第十章 波动
5
物理学
第五版
10-2 平面简谐波的波函数二源自波函数的物理含义2π
2πx y A cos t
1 x一定, t 变化 令
x
y
则 y A cost
O
t
表示 x点处质点的振动方程( y — t 的关系)
y( x, t ) y( x, t T ) (波具有时间的周期性)
8m C B
第十章
0
2.0
t 1.0 s
第十章
x/m
-1.0
时刻波形图
波动
14
物理学
第五版
10-2 平面简谐波的波函数
(3) x 0.5m 处质点的振动规律并作图 t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2 x 0.5m 处质点的振动方程
y cos[π t π] (m)
物理学
第五版
10-2 平面简谐波的波函数
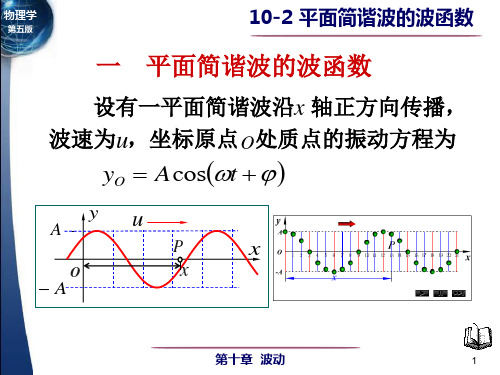
一
平面简谐波的波函数
设有一平面简谐波沿x 轴正方向传播, 波速为u,坐标原点 O 处质点的振动方程为
yO A cost
u
P
A
y
x
A
O
x
第十章
波动
1
物理学
第五版
10-2 平面简谐波的波函数
yO A cost
yO 表示质点O 在 t 时刻离开平衡位置的距离. 考察波线上 P 点(坐标 x ), P 点比 O 点的 x 振动落后 t , P 点在 t 时刻的位移是 O 点
y
o
第十章 波动
x
8
物理学
第五版
5
物理学
第五版
10-2 平面简谐波的波函数二源自波函数的物理含义2π
2πx y A cos t
1 x一定, t 变化 令
x
y
则 y A cost
O
t
表示 x点处质点的振动方程( y — t 的关系)
y( x, t ) y( x, t T ) (波具有时间的周期性)
8m C B
第十章
0
2.0
t 1.0 s
第十章
x/m
-1.0
时刻波形图
波动
14
物理学
第五版
10-2 平面简谐波的波函数
(3) x 0.5m 处质点的振动规律并作图 t x π y 1.0 cos[ 2 π( ) ] 2.0 2.0 2 x 0.5m 处质点的振动方程
y cos[π t π] (m)
物理学
第五版
10-2 平面简谐波的波函数
一
平面简谐波的波函数
设有一平面简谐波沿x 轴正方向传播, 波速为u,坐标原点 O 处质点的振动方程为
yO A cost
u
P
A
y
x
A
O
x
第十章
波动
1
物理学
第五版
10-2 平面简谐波的波函数
yO A cost
yO 表示质点O 在 t 时刻离开平衡位置的距离. 考察波线上 P 点(坐标 x ), P 点比 O 点的 x 振动落后 t , P 点在 t 时刻的位移是 O 点
y
o
第十章 波动
x
8
物理学
第五版
平面简谐波的波动方程

m
0.5 10
yc 3102 c os(4 π t 13 π)
m
5
将点 D 坐标:x=9m代入波动方程
y 3102 cos2π( t x )
m
0.5 10
yD 3102 c os(4πo 9 π)
m
5
4)分别求出 BC ,CD 两点间的相位差
y 3102 cos2π( t x ) 0.5 10
幅 A 1.0m ,T 2.0s , 2.0m . 在 t 0 时坐标
原点处的质点位于平衡位置沿 O y 轴正方向运动 . 求
1)波动方程
解 设原点处振动方程为
y Acos(t )
O
y
t 0
y 0, v 0
y cos(t )
π
2
所以波动方程为
2
y Acos[(t x ) ] Acos[2 ( t x ) ]
T
2π
C
u B 2π d dC
TC
思考:t=T/4时, a,b,c各质点运动方向如何?
3 ) 如图简谐波 以余弦函数表示,
t =0
y t =T/4
A+∆t
u
求 O、a、b、c 各
b
点振动初相位(t=0).
Oa
c
(π ~ π )
A
A
O
A
O
y o π
y
a
π 2
A
O
y
O
y
A
t=T/4
m (以A为 坐标原点)
u
10m
8m 5m 9m
C
B oA
Dx
B点落后C点 :B
C
2 π
平面简谐波的运动方程

y( x,t ) 310-2 cos(4 π t - kx) k 2 5
(310-2 ) cos(4πt - x )
5
u
8m 5m 9m
C
B oA
Dx
20
5-2 平面简谐波的波函数
(2) 以 B 为坐标原点,写出波动方程
yA y(5,t ) (310-2 ) cos(4 π t )
t0 x0
y 0, v y 0 - π
t
2
y cos[2π( t - x ) - π ] (m) 2.0 2.0 2
cos(t - x - )
2
O
y
A
18
5-2 平面简谐波的波函数
例2 一平面简谐波以速度u 20 m s-1
沿直线传播,波线上点 A 的简谐运动方 程
yA 310-2 cos(4 π t); ( y, t单位分别为m,s).
5
yC
y(-13,t )
(310-2 ) cos[4 π t
13 π] 5
yD
y(9,t )
( 3 10-2
)cos[4 π t
-
9 5
π]
u
yA (310 -2 )co1s(04mπ t )
8m 5m 9m
C
B oA
Dx
22
5-2 平面简谐波的波函数
(3) 写出传播方向上点C、D的运动方程
5-2 平面简谐波的波函数
5.2.1 平面简谐波的运动方程--波函数 一、波长 波的周期和频率 波速
1 波长
波传播方向上相邻两振动状态完全相同
的质点间的距离(一完整波的长度).
Ay
u
O
x
-A
(310-2 ) cos(4πt - x )
5
u
8m 5m 9m
C
B oA
Dx
20
5-2 平面简谐波的波函数
(2) 以 B 为坐标原点,写出波动方程
yA y(5,t ) (310-2 ) cos(4 π t )
t0 x0
y 0, v y 0 - π
t
2
y cos[2π( t - x ) - π ] (m) 2.0 2.0 2
cos(t - x - )
2
O
y
A
18
5-2 平面简谐波的波函数
例2 一平面简谐波以速度u 20 m s-1
沿直线传播,波线上点 A 的简谐运动方 程
yA 310-2 cos(4 π t); ( y, t单位分别为m,s).
5
yC
y(-13,t )
(310-2 ) cos[4 π t
13 π] 5
yD
y(9,t )
( 3 10-2
)cos[4 π t
-
9 5
π]
u
yA (310 -2 )co1s(04mπ t )
8m 5m 9m
C
B oA
Dx
22
5-2 平面简谐波的波函数
(3) 写出传播方向上点C、D的运动方程
5-2 平面简谐波的波函数
5.2.1 平面简谐波的运动方程--波函数 一、波长 波的周期和频率 波速
1 波长
波传播方向上相邻两振动状态完全相同
的质点间的距离(一完整波的长度).
Ay
u
O
x
-A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
λ
波动方程的推导
u
y
P
O
x
−x P点在t时刻,将重复原点在(t − 点在t时刻, 时刻的振动状态。 ) 时刻的振动状态。 u 由O点振动方程 yO = A cos(ω t + φ 0 )
可写出P点振动方程为: 可写出P点振动方程为:
x
x y = A cos[ω ( t + ) + φ0 ] u
任意一质点为坐标原点的波动方程
x
T= 2π
u=20m/s,ω=4π, u=20m/s,ω=4π,
λ = uT = 10m
ω
= 0 .5 s
由于波从左向右传播,因此B点振动始终超前于A点,超 由于波从左向右传播,因此B点振动始终超前于A 前时间∆t为 前时间∆t为: ∆x 5
∆t =
u
=
20
= 0.25s
即B点振动方程为: 点振动方程为:
x y ( x) = A cos[ω (t0 − ) + ϕ 0 ] u x y ( x) = A cos[ω (t0 + ∆t − ) + ϕ 0 ] u
行波
6.2
平面简谐波的波动方程
2、波动方程物理意义_行波 波动方程物理意义_
例题
∆x = u∆t
由图可知:x 处 t 时刻振动状态经∆t ,传播到x+∆x 处;即 时刻振动状态经∆ 由图可知:
x 则以B 波动方程一般 形式 y = A cos[ω ( t − ) + ϕ ] ,则以B点坐标原点 u 的波动方程为: 的波动方程为:
y B = 3 cos 4π ( t + 0.25) = 3 cos(4π t + π )
x y = 3 cos[4π ( t − ) + π ] 20
常用的波动方程表达式 (以正方向传播为例)
∆ϕ = −
空间周期性
λ
空间周期性
y x λ
在同一时刻,同一波线上x1、x2处两质点的位相差为: 同一时刻,同一波线上x1、x2处两质点的位相差为 处两质点的位相差为:
∆ϕ = −
2π
λ
( x2 − x1 ) = −
2π
λ
∆x
位移差与位相差
∆x ∆φ
λ -2π
2λ -4π
3λ -6π
4λ -8π
5λ -10π
它表示一条简谐函数曲线,说明它是一列简谐波。 它表示一条简谐函数曲线,说明它是一列简谐波。 对同一质点,相邻两个时刻位相差为: 同一质点,相邻两个时刻位相差为:
2π ∆ϕ = ω (t 2 − t1 ) = ∆t T
时间周期性
时间周期性
y t T
对同一质点,相邻两个时刻位相差为: 对同一质点,相邻两个时刻位相差为:
t x y = A cos[2π ( − ) + φ 0 ] T λ
6.2
平面简谐波的波动方程
2、波动方程物理意义_1 波动方程物理意义_1
x y = A cos[ω ( t − ) + φ0 ] u
(1)若 x = x为给定值,则波动方程蜕化为振动方程。 为给定值,则波动方程蜕化为振动方程。 0
例 一列横波以u=400m/s波速沿x轴正向传播。位于坐标原点 一列横波以u=400m/s波速沿 轴正向传播。 波速沿x O处的质点的振动T= 0.01s,A= 0.1m,取原点处质点经过平 处的质点的振动T 0.01s, 0.1m, 衡位置且向正方向运动时为计时起点。 衡位置且向正方向运动时为计时起点。 (1)O点振动方程 yO = 0.1cos(200π t + 3 π ) 2 x ) + 3 π] 以O点为原点的波动方程 y = 0.1cos[200π ( t − 400 2 画出t=0.005s和t=0.0075s波形 波形。 (3)画出t=0.005s和t=0.0075s波形。 解: 由波动方程可得t=0.005s时刻的波形方程: (3)由波动方程可得 (3)由波动方程可得t=0.005s时刻的波形方程 时刻的波形方程:
6.2
平面简谐波的波动方程_例题 平面简谐波的波动方程_
波动方程可得t=0.005s时刻的波形方程 波动方程可得t=0.005s时刻的波形方程: 时刻的波形方程: y
0.1
0.05
x
2 -0.05 4 6 8 10 12
-0.1
6.2
平面简谐波的波动方程_例题 平面简谐波的波动方程_
1 4
波动方程可得t=0.0075s时刻的波形方程 波动方程可得t=0.0075s时刻的波形方程: 时刻的波形方程: y
2π ∆ϕ = ω (t 2 − t1 ) = ∆t T
位移差与位相差
∆t ∆φ
T 2π
2T 4π
3T 6π
4T 8π
5T 10π
… …
6.2
平面简谐波的波动方程
2、波动方程物理意义_3 波动方程物理意义_3
x y = A cos[ω ( t − ) + φ0 ] u
(3)若t,x 都在变化,则波动方程反映了波形不断 都在变化, 向前推进的波动传播的全过程。 向前推进的波动传播的全过程。 t0时刻波形 t0+∆t时刻波形
t 时刻x 处 振动状态与t +∆t 时刻x+∆x 处振动状态完全相同。 处振动状态完全相同。
y (t + ∆t , x + ∆x) = y (t , x) —— 行波
6.2
平面简谐波的波动方程_例题 平面简谐波的波动方程_
例 一列横波以u=400m/s波速沿x轴正向传播。位于坐标原点 一列横波以u=400m/s波速沿 轴正向传播。 波速沿x O处的质点的振动T= 0.01s,A= 0.1m,取原点处质点经过平 处的质点的振动T 0.01s, 0.1m, 衡位置且向正方向运动时为计时起点。 衡位置且向正方向运动时为计时起点。 写出波动方程; (1)写出波动方程; 写出距原点为2m处的质点 处的质点P (2)写出距原点为2m处的质点P的振动方程及以此点为 原点的波动方程; 原点的波动方程; 画出t=0.005s和t=0.0075s的波形图 的波形图。 (3)画出t=0.005s和t=0.0075s的波形图。 解: 设O处的振动方程为: = A cos[ω t + ϕ 0 ] y (1)设 处的振动方程为: (1) 根据初始条件: 根据初始条件:t = 0, y0 = 0, v0 > 0且v0 = vm 可得O点的振动方程参数: 可得O点的振动方程参数:
T=
2π
y A = 3 cos(4π t )
y B = 3 cos(4π t + π )
ω
= 0 .5 s
λ = uT = 10m
x y = 3 cos[4π ( t − )] 20 x y = 3 cos[4π ( t − ) + π ] 20
B点
任意一质点为坐标原点的波动方程 8m 5m C B A 9m D u
y (t ) = A cos(ωt −
ωx0
u
+ φ0 )
在同一时刻,同一波线上x1、x2处两质点的位相为: 同一时刻,同一波线上x1、x2处两质点的位相为 处两质点的位相为:
ϕ1 = (ωt −
ωx1
u
2π
+ φ 0 ) ϕ 2 = (ωt −
( x2 − x1 )
ωx 2
u
+ φ0 )
则任意两质点间位相差为: 则任意两质点间位相差为:
yO = A cos(ω t + φ0 )
设P为x轴上任一点,坐标为x,用y表示该点偏 轴上任一点,坐标为x 离平衡位置的位移, 点振动方程为: 离平衡位置的位移,则P点振动方程为:
x y = A cos[ω ( t − ) + φ 0 ] u
波动方程的推导
y
u
O
P
x
x
x P点在t时刻,将重复原点在 (t − ) 时刻的振动状态。 点在t时刻, 时刻的振动状态。 u 由O点振动方程 yO = A cos(ω t + φ 0 )
2 yP = 0.1cos[200π ( t − ) + 3 π ] = 0.1cos(200π t + 1 π ) 2 400 2
则以此点为原点的波动方程为: 则以此点为原点的波动方程为:
x y′ = 0.1cos[200π ( t − ) + 1 π] 2 400
6.2
平面简谐波的波动方程_例题 平面简谐波的波动方程_
例 一列横波以u=400m/s波速沿x轴正向传播。位于坐标原点 一列横波以u=400m/s波速沿 轴正向传播。 波速沿x O处的质点的振动T= 0.01s,A= 0.1m,取原点处质点经过平 处的质点的振动T 0.01s, 0.1m, 衡位置且向正方向运动时为计时起点。 衡位置且向正方向运动时为计时起点。 (1)O点振动方程 yO = 0.1cos(200π t + 3 π ) 2 x ) + 3 π] 以O点为原点的波动方程 y = 0.1cos[200π ( t − 400 2 写出距原点为2m处的质点 处的质点P (2)写出距原点为2m处的质点P的振动方程及以此点为 原点的波动方程; 原点的波动方程; 解: 由波动方程可得P (x=2m )处的振动方程: (2)由波动方程可得 (2)由波动方程可得P )处的振动方程 处的振动方程:
§6.2 平面简谐波的波动方程
1、平面简谐波的波动方程 2、波动方程物理意义 3、平面简谐行波的微分方程
6.2
平面简谐波的波动方程
1、平面简谐波的波动方程
设有一平面简谐波,在无吸收的、均匀的、无 设有一平面简谐波,在无吸收的、均匀的、 限大的介质中沿x 正方向传播 速度为 传播。 限大的介质中沿x轴正方向传播。速度为u。 任取一点作坐标原点O 任取一点作坐标原点O,并在原点振动位相为 φ0 时开始计,即O点振动方程为: 时开始计, 点振动方程为:
