力学6-1
结构力学课件6

(b)
P1
YE YE E XE XE E
F
G XG XG G
YG P2 YG D
A YA
B
C
图6-4
YD
(4) 有时同一结构有几种不同的搭法,因此也有几种不 同的拆法。在桁架的结点法中,经常会遇到这样的例子。
6-12
§6-2 几何构造与静力特性的关系
在几何构造分析一章中,已经讨论过一个几何参数:计 算自由度W。 1、计算自由度W的力学含义 (1) 几何含义 W=(各部件的自由度总和)-(全部约束数) (2) 力学含义
6-21
§6-3 零载法
一、零载法
利用结构静力解答的唯一性判定结构的几何构造特性。
前述已知:当W=0时,若平衡方程的解答是唯一的,则 体系几何不变。
零载法要点:当W=0时,若体系几何不变,则是静定结 构,静定结构的解答是唯一的。当采用零载法时,它的全部 内力都为零;反之,若几何可变,必存有多余约束,在零载 下,它的某些内力可不为零。
6-3
但是,用解算联立方程的方法同时求出所有的约束力是 很麻烦、很费事的。所以,实际计算所采用的方法是:按一 定的次序截取单元,对每个单元应用平衡方程,求出部分约 束力,以便收到各个击破的效果。下面是实用分析方法的一 些要点。 1、单元的形式及未知力
从结构中截取的单元可以是结点、杆件或者杆件体系。
搭”的问题;
6-10
(3) 拆和搭是互相联系的,如果拆的次序与搭的次序正 好相反,工作就可以顺利进行;因此,如果截取单元的次序 与结构组成的添加单元的次序相反,结构的受力分析就比较 简便(见图6-4a) 。
(a)
P1 E F G P2
II
A B
I
结构力学——6位移法和力矩分配法

△ △
4、5、6 三个固定端都是不动的点,结点1 、2、3均无竖向位移。又因两根横梁其长 度不变,故三个结点均有相同的水平位移 FP △ 。
1
2
3
4
5
6
(a)
事实上,图(a)所示结构的独立线位移数 将结构的刚结点(包括固定支座)都变成 目,与图(b)所示铰结体系的线位移数目 铰结点(成为铰结体系),则使其成为几何 是相同的。因此,实用上为了能简捷地确 不变添加的最少链杆数,即为原结构的独 定出结构的独立线位移数目,可以 立线位移数目(见图b)。
4
5
6
(a)
共有四个刚结点,结点线位移数目为二 ,基本未知量为六个。基本结构如图所 示。
7
10 返回
5
6
(b)
例:确定图a所示连续梁的基本结构。 D B A C D B A C
(图a)
A A
B B
基本结构 基本结构
C C
D (图b) D
在确定基本结构的同时,也就确定了基本未知量及其数目。
EI
第六章
位移法和力矩分配法
§6—1 位移法的基本概念 §6—2 位移法基本未知量的确定 §6—3 位移法典型方程计算步骤和示例 §6—4 力矩分配法的基本概念 §6—5 用力矩分配法计算连续梁 §6—6 用力矩分配法计算无接点线位移刚架
1
§6—1
位移法的基本概念
一、位移法的提出(Displacement Method)
M
A
B
0
2i
r11 4i 4i 0
8EI r11 8i l
2i
M1
得
15
求自由项R1P,作出基本结构在荷载作用时的弯矩 图(MP图)。 取结点B为隔离体
06-6质心力学定理

V M
C O
的速度) 对 的速度 又 ∵ v ≈ v ′ ( v ′是m对M的速度 1 ∴ m υ ′ 2 + ∆E引 = 0 2 地球参考系不是惯性系⇒ • 地球参考系不是惯性系⇒ 动量守恒不成立 地球参考系仍可正确表示系统的功能 功能关系 • 地球参考系仍可正确表示系统的功能关系
03/2006 S.H.Deng
12
质点组总动能等于质心动能与相对质心动能之和. 质点组总动能等于质心动能与相对质心动能之和. S.H.Deng
理学院 邓胜华
第6章 质心力学定理
二.重力势能与质心势能
定义: 定义:E C = Mgh C
E =
i i i
——质心重力势能 质心重力势能
质点组重力势能 ∑ m gh ——质点组重力势能 M =∑m ∑m h E = ∑ m gh = g ∑ m h = g ∑m ∑m
× m i v iC ) + ∑ (riC × m i v C )
i
S.H.Deng
i
OiBiblioteka C03/200614
理学院 邓胜华
第6章 质心力学定理
L = rC × ∑ m i v C + ∑ (riC × m i v iC ) + rC × ∑ (m i v iC ) i i i + ∑ (m i riC ) × v C
质心动量的改变量等于和外力的冲量. 质心动量的改变量等于和外力的冲量.
dv C = 又:M dt
∑F
i
i
即 M aC =
∑F
i
i
——质心运动定理 质心运动定理
质点组总质量与质心加速度的乘 积等于质点组所受到的合外力. 积等于质点组所受到的合外力. S.H.Deng 03/2006
理论力学第六章 点的合成运动 [同济大学]
![理论力学第六章 点的合成运动 [同济大学]](https://img.taocdn.com/s3/m/63fd0a4dbe1e650e53ea9909.png)
解: 从例6-2已知得: 1 =
vr r 3 , 2
ω 4
O
解: 从上例已知得: 1 =
r
M
ω 4
va
A
aaτ =0 ,
3 , 4
aan=2r aen=
ωr 8
x’
2
ac 21vr 2 r
va
30°
3 1 1/ s2 8
2
动点取A,
va v A
ar
dvr d 2 x ' ' d 2 y ' ' d 2 z ' ' 2 r 2 j 2 k dt dt dt dt
dx ' di ' dy ' dj' dz ' dk ' dt dt dt dt dt dt
ar ω vr
a a ae a r ac; ac= 2vr
ve
a n a ae a rn a rτ
矢量
1.瞬时状态; 2.可解两个未知量 (大小,方向)。
例6-5 曲柄滑道机构,OA=01A=r=10cm, =30°,=4, 求: 转到30°时直杆的加速度a。 va vr 动点取A; 绝对:圆周; ve 解:相对:圆周;牵连:直线。 [速度] =
a a ae a r ac; aa a an ae aen ar arn ac;
例6-8 曲柄绕O转动,並通过滑块M带动滑槽绕O′摆动, ’ y 求摆动到30°时的角加速度1。
例6-9 将例6-8滑槽改变为图示牛头刨床机构,MA=2r, 求:刨床刨刀的速度,加速度。
vr
dv e dω dr r ω dt dt dt α r ω v e ω v r ae ω v r
《材料力学》第6章 简单超静定问题 习题解
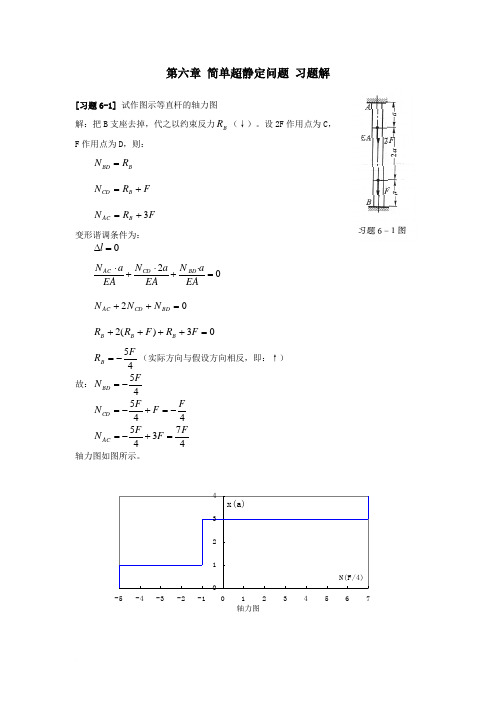
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
工程力学 第6章 弹性静力学基本概念

第6章 弹性静力学的基本概念 刚体静力学研究力系的等效、简化与力系的平衡,并且应用这些基本概念和理论,分析、确定物体的受力。
刚体静力学的模型是质点和质点系以及刚体和刚体系。
弹性静力学则主要研究变形体受力后发生的变形,以及由于变形而产生的附加内力。
分析方法上,弹性静力学与理论力学刚体静力学也不完全相同。
建立在实验基础上的假定、简化计算,是弹性静力学分析方法的主要特点。
本章介绍弹性静力学的基本概念、研究方法以及弹性静力学对于工程设计的重要意义。
§6-1 弹性静力学概述 §6-2 弹性体及其理想化 6-2-1 各向同性与各向异性弹性体 6-2-2 各向同性弹性体的均匀连续性 §6-3 弹性体受力与变形特征 §6-4 应力及其与内力分量之间的关系 6-4-1 分布内力集度-应力 6-4-2 应力与内力分量之间的关系 §6-5 正应变与切应变 §6-6 线弹性材料的物性关系 §6-7工程结构与构件 §6-8 杆件变形的基本形式 §6-9 结论与讨论 6-9-1 关于刚体静力学模型与弹性静力学模型 6-9-2 关于弹性体受力与变形特点 6-9-3 关于刚体静力学概念与原理在弹性静力学中的 可用性与限制性 习 题 本章正文 返回总目录第6章 弹性静力学的基本概念 §6—1 弹性静力学概述 弹性静力学(elastic statics)又称材料力学(strength of materials),其研究内容分属于两个学科。
第一个学科是固体力学(solid mechanics),即研究物体在外力作用下的应力、变形和能量,统称为应力分析(stress analysis)。
但是,弹性静力学所研究的仅限于杆、轴、梁等物体,其几何特征是纵向尺寸远大于横向尺寸,这类物体统称为杆或杆件(bars或rods)。
大多数工程结构的构件或机器的零部件都可以简化为杆件。
6-1核外电子的运动特征
原子由哪些微粒构成?质子中子原子元素的物理化学性质核外电子与宏观物体有何区别?宏观物体核外电子质量很大很小速度较小很大(接近光速)核外电子与宏观物体有何区别?代表性的原子结构模型卢瑟福原子模型:1911年,卢瑟福根据α粒子衍射现象提出了“含核的原子模型”。
玻尔原子模型:1913年波尔提出了核外电子分层排布的波尔理论。
波粒二象性:20世纪30年代,以微观粒子波粒二象性为基础发展起来的量子力学,才建立了比较符合微观世界实际的物质结构近代理论。
代表性的原子结构模型卢瑟福原子模型1911年,卢瑟福根据α粒子衍射现象提出了“含核的原子模型”代表性的原子结构模型玻尔原子模型1913年波尔提出了核外电子分层排布的波尔理论代表性的原子结构模型波粒二象性20世纪30年代,以微观粒子波粒二象性为基础发展起来的量子力学,才建立了比较符合微观世界实际的物质结构近代理论。
卢瑟福原子模型1911年,卢瑟福根据a粒子轰击原子实验,建立了有核原子模型。
卢瑟福原子模型模型要点:原子中央有一个体积非常小的、带正电荷的原子核;在原子核周围很大空间里存在着围绕原子核运动的电子卢瑟福模型的局限An unsatisfactory atomic model 一电子以极大的速度绕核运动,辐射能量(电磁波)则轨道半径越来越小,最后在非常短的时间内掉在原子核上,引起原子毁灭,称为“原子的塌陷”。
卢瑟福模型的局限An unsatisfactory atomic model 二它不能说明元素的线状光谱产生的原因。
据该原子模型,能量的释放应是不间断的,观察到的原子光谱应是连续的带状光谱,这与实验观察到的间隔的线状光谱不符。
玻尔模型1913年,Bohr 在基础上,建立了B ohr 理论爱因斯坦的光子学说普朗克的量子化学说卢瑟福的有核模型氢原子的光谱实验氢放射管狭缝棱镜照相底片线状光谱特点:1 不连续,只是些亮线组成2 不同色,每种颜色对应着一个波长3 不等距,相邻两种光的波长间距不相同玻尔模型玻尔理论要点定态假设电子围绕原子核作圆形轨道运动。
金属的电子论 6-1
经典理论的局限性
★金属中存在着电子,根据自由电子论,
金属的电导率电子密度n,
但为什么电子密度较大的二价金属(如Be、Mg、 Zn、 Cd等)和三价金属(如Al、In等)的电导 率反而低于一价金属(如Cu、Ag、Au等)? ★自由电子论无法解释为什么有些金属的Hall系数 会大于0(如Al、In、Zn、Cd等);
第六章
金属电子论
第一讲
费米统计和电子热容量;
功函数和接触电势。
1
金属(Metal)在固体研究中有特殊的地位。金属是极 好的导电体和导热体(Electrical and heat conductors), 有延展性(Ductile)并有光亮的表面。这些金属性质的 解释极大地推动了现代固体物理的发展。 实际上,从十九世纪末到现在,金属研究一直处 在固体研究的中心。对金属的研究导致了能带论的 提出,最后在能带论的基础上,建立了对包括金属,半 导体,绝缘体的固体电性质的统一的理论.并由此发 展出整个电子工业的理论基础.
11
2. T=0 K 时电子的分布
T=0 K 时,电子的分布函数为 f(E) =
EF
0
f(E) T=0 1
{0
kF 2m
2 2
1
E EF0 E > EF0
0
—— 费米能
0
EF0
E
kF
2mEF
2
—— 费米半径
PF k F m V F —— 费米动量
12
vF
kF m
从量子力学的观点看,电子是费米子(fermion)应服 从Fermi-Dirac统计而不是经典的Maxwell统计。 Fermi-Dirac统计指出,在量子态上的平均占据数为:
结构力学第六章力法
弯矩图可按悬臂梁画出
M X1 M 1 M P
§6-4 力法计算超静定桁架和组合结构
一 超静定桁架
F Ni l ii EA F N i F N jl ij EA F N i FN P l iP EA
2
桁架各杆只产生轴力,系数
典型方程: 11 X 1 1P 0
9 17 FP , X 2 FP 80 40
叠加原理求弯矩: M X 1 M 1 X 2 M 2 M P
3FPL/40 3FPL/40
FP 9FP/80
23FP/40 FNDC
FQDC 3FPL/80 FQBD
FQCD FNDA
FQBD=-9FP/80
FNBD=-23FP/40
FQDC=3FP/40+FP/2=23FP/40
2 P 3P 0
11 X 1 1P 0 22 X 2 23 X 3 0 X X 0 33 3 32 2
11 X 1 1P 0 X 2 X 3 0
反对称荷载作用下, 沿对称轴截面上正对称内力为0 例: FP FP/2 FP/2 FP/2
1)一般任意荷载作用下
11 X 1 12 X 2 13 X 3 1P 0 21 X 1 22 X 2 23 X 3 2 P 0 X X X 0 33 3 3P 31 1 32 2
11 X 1 1P 0 22 X 2 23 X 3 2 P 0 X X 0 33 3 3P 32 2
M FN
超静定结构的内力分布与梁式杆和二力杆的相对刚度有关。 链杆EA大,M图接近与连续梁,链杆EA小,M图接近与简支梁。 例: 中间支杆的刚度系数为k,求结点B的竖向位移?EI=C
6-1平衡态 温度 理想气体状态方程
6–1平衡态 温度 理想气体状态方程 1 2、宏观状态和微观状态 、 (1)宏观描述 )
第六章 气体动理论
宏观状态: 宏观状态:由大量微观粒子所组成的系统整体在 大范围内所体现的状态。 大范围内所体现的状态。 宏观量: 宏观量: 所有可观测的反映了大量分子的集体特 性的物理量, 性的物理量,称之为宏观 量。如:P、 、 V、T。 、 。
热力学
气体动理论
6–1平衡态 温度 理想气体状态方程 1
第六章 气体动理论
教学基本要求
了解气体分子热运动的图像 理解平衡态、 理解平衡态 一 了解气体分子热运动的图像 .理解平衡态、 平衡过程、理想气体等概念. 平衡过程、理想气体等概念 理解理想气体的压强公式和温度公式 理想气体的压强公式和温度公式, 二 理解理想气体的压强公式和温度公式, 通 过推导气体压强公式,了解从提出模型、 过推导气体压强公式,了解从提出模型、进行统计 平均、建立宏观量与微观量的联系, 平均、建立宏观量与微观量的联系,到阐明宏观量 的微观本质的思想和方法 . 能从宏观和微观两方面 理解压强和温度等概念 . 了解系统的宏观性质是微 观运动的统计表现 .
2 体积 V : 气体所能达到的最大空间(几何 气体所能达到的最大空间( 描述) 描述). 3 3 3 3 单位: 单位: 1m = 10 L = 10 dm 3 温度 T : 气体冷热程度的量度(热学描述). 气体冷热程度的量度(热学描述 描述) 单位: 单位:温标 K 开尔文). (开尔文) T = 273 + t
宏观量
实验经验总结, 给出宏观物体热现象的规律, 实验经验总结, 给出宏观物体热现象的规律, 从能量观点出发, 从能量观点出发,分析研究物态变化过程中热功转 换的关系和条件 . 特点 1)具有可靠性; )具有可靠性; 2)知其然而不知其所以然; )知其然而不知其所以然; 3)应用宏观参量 . )
