2019版高中人版B版数学必修4练习:1.1.2弧度制和弧度制与角度制的换算
高中数学新人教B版必修4 弧度制和弧度制与角度制的换算

1.1.2弧度制和弧度制与角度制的换算(1)1弧度的角是如何定义的?(2)如何求角α的弧度数?(3)如何进行弧度与角度的换算?(4)以弧度为单位的扇形弧长、面积公式是什么?[新知初探]1.度量角的两种制度(1)角度制:①定义:用度作单位来度量角的制度.②1度的角:把圆周360等分,则其中1份所对的圆心角是1度.(2)弧度制:①定义:以弧度为单位来度量角的制度.②1弧度的角:长度等于半径长的圆弧所对的圆心角.③弧度数的计算公式:在半径为r的圆中,若弧长为l的弧所对的圆心角为α rad,则α=lr.[点睛]用弧度为单位表示角的大小时,“弧度”两个字可以省略不写,如2 rad的单位“rad”可省略不写,只写2.2.角度与弧度的互化(1)180°=π rad.(2)常用的角度数与弧度数的互化:[点睛](1)在应用扇形面积公式S=12αr2时,要注意α的单位是“弧度”.(2)在运用公式时,根据已知条件,选择合适的公式代入.(3)在弧度制下的扇形面积公式S =12lr ,与三角形面积公式S =12ah (其中h 是三角形底边a 上的高)的形式较相似,可类比记忆.(4)由α,r ,l ,S 中任意的两个量可以求出另外的两个量.[小试身手]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”) (1)1弧度=1°.( )(2)每个弧度制的角,都有唯一的角度制的角与之对应.( ) (3)用弧度制度量角,与圆的半径长短有关.( ) 答案:(1)× (2)√ (3)×2.5弧度的角的终边所在的象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限答案:D3.半径为1,圆心角为2π3的扇形的弧长是( )A.4π3 B .π C.2π3 D.π3答案:C4.(1)2π3=________;(2)-210°=________.答案:(1)120° (2)-7π6[典例] 把下列角度化成弧度或弧度化成角度: (1)72°;(2)-300°;(3)2;(4)-2π9. [解] (1)72°=72×π180=2π5. (2)-300°=-300×π180=-5π3. (3)2=2×⎝⎛⎭⎫180π°=⎝⎛⎭⎫360π°.(4)-2π9=-⎝⎛⎭⎫2π9×180π°=-40°.角度与弧度的互化技巧在进行角度与弧度的换算时,抓住关系式π rad =180°是关键,由它可以得到:度数×π180=弧度数,弧度数×180°π=度数.[活学活用]将下列角度与弧度进行互化: (1)5116π;(2)-7π12;(3)10°;(4)-855°.解:(1)5116π=5116×180°=15 330°.(2)-7π12=-712×180°=-105°. (3)10°=10×π180=π18. (4)-855°=-855×π180=-19π4.用弧度制表示终边相同的角[典例] 已知角α=-2 018°.(1)将α改写成φ+2k π(k ∈Z,0≤φ<2π)的形式,并指出α是第几象限角; (2)在区间[-2π,4π)上找出与α终边相同的角.[解] (1)因为α=-2 018°=-6×360°+142°,且142°=142×π180=71π90, 所以α=-12π+71π90,故α是第二象限角. (2)与α终边相同的角可表示为θ=2k π+71π90,k ∈Z , 又-2π≤θ<4π,所以k =-1,0,1, 将k 的值分别代入θ=2k π+71π90,k ∈Z , 得θ=-109π90,71π90,251π90.用弧度制表示终边相同的角2k π+α(k ∈Z)时,其中2k π是π的偶数倍,而不是整数倍,还要注意角度制与弧度制不能混用.[活学活用]1.将-1 125°表示成2k π+α,0≤α<2π,k ∈Z 的形式为________. 解析:因为-1 125°=-4×360°+315°, 315°=315×π180=7π4, 所以-1 125°=-8π+7π4. 答案:-8π+7π42.用弧度表示终边落在阴影部分内(不包括边界)的角的集合.解:如题图,330°角的终边与-30°角的终边相同,将-30°化为弧度,即-π6,而75°=75×π180=5π12, ∴终边落在阴影部分内(不包括边界)的角的集合为⎩⎨⎧θ⎪⎪⎭⎬⎫2k π-π6<θ<2k π+5π12,k ∈Z .1.已知扇形的圆心角所对的弦长为2,圆心角为2π3.求:(1)这个圆心角所对的弧长; (2)这个扇形的面积.解:(1)因为扇形的圆心角所对的弦长为2,圆心角为2π3,所以半径r =1sin π3=233, 所以这个圆心角所对的弧长l =233×2π3=43π9. (2)由(1)得扇形的面积S =12×233×43π9=4π9.题点二:利用公式求半径和弧度数2.扇形OAB 的面积是4 cm 2,它的周长是8 cm ,求扇形的半径和圆心角. 解:设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l cm ,半径为r cm , 依题意有⎩⎪⎨⎪⎧l +2r =8, ①12l ·r =4, ②由①②,得r =2,∴l =8-2r =4,θ=lr =2.故所求扇形的半径为2、圆心角为2 rad. 题点三:利用公式求扇形面积的最值3.已知扇形的周长是30 cm ,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?解:设扇形的圆心角为α(0<α<2π),半径为r ,面积为S ,弧长为l ,则l +2r =30,故l =30-2r ,从而S =12lr =12(30-2r )r =-r 2+15r =-⎝⎛⎭⎫r -1522+2254⎝⎛⎭⎫15π+1<r <15, 所以,当r =152 cm 时,α=2,扇形面积最大,最大面积为2254cm 2.弧度制下涉及扇形问题的攻略(1)明确弧度制下扇形的面积公式是S =12lr =12|α|r 2(其中l 是扇形的弧长,r 是扇形的半径,α是扇形的圆心角).(2)涉及扇形的周长、弧长、圆心角、面积等的计算,关键是先分析题目已知哪些量求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.[提醒] 运用弧度制下的弧长公式及扇形面积公式的前提是α为弧度.层级一 学业水平达标1.下列说法中,错误的是( )A .“度”与“弧度”是度量角的两种不同的度量单位B .1°的角是周角的1360,1 rad 的角是周角的12πC .1 rad 的角比1°的角要大D .用弧度制度量角时,角的大小与圆的半径有关解析:选D 由角度制和弧度制的定义,知A 、B 、C 说法正确.用弧度制度量角时,角的大小与所对圆弧长与半径的比有关,而与圆的半径无关,故D 说法错误.2.扇形的周长是16,圆心角是2弧度,则扇形的面积是( ) A .16π B .32π C .16D .32解析:选C 弧长l =2r,4r =16,r =4,得l =8, 即S =12lr =16.3.角α的终边落在区间⎝⎛⎭⎫-3π,-5π2内,则角α所在的象限是( ) A .第一象限 B .第二象限 C .第三象限D .第四象限解析:选C -3π的终边在x 轴的非正半轴上,-5π2的终边在y 轴的非正半轴上,故角α为第三象限角.4.时钟的分针在1点到3点20分这段时间里转过的弧度为( ) A.143π B .-143π C.718π D .-718π 解析:选B 显然分针在1点到3点20分这段时间里,顺时针转过了73周,转过的弧度为-73×2π=-143π.5.下列表示中不正确的是( )A .终边在x 轴上的角的集合是{α|α=k π,k ∈Z}B .终边在y 轴上的角的集合是⎩⎨⎧⎭⎬⎫α|α=π2+k π,k ∈ZC .终边在坐标轴上的角的集合是⎩⎨⎧⎭⎬⎫α|α=k ·π2,k ∈Z D .终边在直线y =x 上的角的集合是⎩⎨⎧⎭⎬⎫α|α=π4+2k π,k ∈Z解析:选D 终边在直线y =x 上的角的集合应是⎩⎨⎧⎭⎬⎫α|α=π4+k π,k ∈Z .6.-135°化为弧度为________,11π3化为角度为________. 解析:-135°=-135×π180=-34π,113π=113×180°=660°. 答案:-34π 660°7.扇形的半径是6,圆心角是60°,则该扇形的面积为________. 解析:60°=π3,扇形的面积公式为S 扇形=12αr 2=12×π3×(6)2=π.答案:π8.设集合M =⎩⎨⎧⎭⎬⎫α|α=k π2-π3,k ∈Z ,N ={α|-π<α<π},则M ∩N =________.解析:由-π<k π2-π3<π,得-43<k <83.∵k ∈Z ,∴k =-1,0,1,2, ∴M ∩N =⎩⎨⎧⎭⎬⎫-56π,-π3,π6,23π.答案:⎩⎨⎧⎭⎬⎫-56π,-π3,π6,23π9.一个扇形的面积为1,周长为4,求圆心角的弧度数. 解:设扇形的半径为R ,弧长为l ,则2R +l =4. 根据扇形面积公式S =12lR ,得1=12l ·R .联立⎩⎪⎨⎪⎧2R +l =4,12l ·R =1,解得R =1,l =2,∴α=l R =21=2.10.把下列各角化成2k π+α(0≤α<2π,k ∈Z)的形式,并指出是第几象限角. (1)-1 500°;(2)236π;(3)-4.解:(1)∵-1 500°=-1 800°+300°=-10π+5π3, ∴-1 500°与5π3终边相同,是第四象限角.(2)∵236π=2π+116π,∴236π与116π终边相同,是第四象限角.(3)∵-4=-2π+(2π-4),∴-4与2π-4终边相同,是第二象限角.层级二 应试能力达标1.下列转化结果错误的是( ) A .60°化成弧度是π3B .-103π化成度是-600° C .-150°化成弧度是-76πD.π12化成度是15° 解析:选C 对于A,60°=60×π180=π3;对于B ,-103π=-103×180°=-600°;对于C ,-150°=-150×π180=-56π;对于D ,π12=112×180°=15°.故C 错误.2.集合⎩⎨⎧⎭⎬⎫α|k π+π4≤α≤k π+π2,k ∈Z 中角的终边所在的范围(阴影部分)是( )解析:选C 当k =2m ,m ∈Z 时,2m π+π4≤α≤2m π+π2,m ∈Z ;当k =2m +1,m ∈Z 时,2m π+5π4≤α≤2m π+3π2,m ∈Z ,所以选C.3.若角α与角x +π4有相同的终边,角β与角x -π4有相同的终边,那么α与β间的关系为( )A .α+β=0B .α-β=0C .α+β=2k π(k ∈Z)D .α-β=π2+2k π(k ∈Z)解析:选D ∵α=x +π4+2k 1π(k 1∈Z),β=x -π4+2k 2π(k 2∈Z),∴α-β=π2+2(k 1-k 2)·π(k 1∈Z ,k 2∈Z).∵k 1∈Z ,k 2∈Z ,∴k 1-k 2∈Z. ∴α-β=π2+2k π(k ∈Z).4.已知某机械采用齿轮传动,由主动轮M 带着从动轮N 转动(如图所示),设主动轮M 的直径为150 mm ,从动轮N 的直径为300 mm ,若主动轮M 顺时针旋转π2,则从动轮N 逆时针旋转( )A.π8B.π4C.π2D .π解析:选B 设从动轮N 逆时针旋转θ rad ,由题意,知主动轮M 与从动轮N 转动的弧长相等,所以1502×π2=3002×θ,解得θ=π4,选B.5.若角α的终边与85π角的终边相同,则在[0,2π]上,终边与α4角的终边相同的角是____________.解析:由题意,得α=8π5+2k π(k ∈Z),∴α4=2π5+k π2(k ∈Z).令k =0,1,2,3,得α4=2π5,9π10,7π5,19π10.答案:2π5,9π10,7π5,19π106.圆的半径变为原来的3倍,而所对弧长不变,则该弧所对圆心角是原来圆弧所对圆心角的________.解析:设原来圆的半径为r ,弧长为l ,圆心角为α,则l =αr .设将圆的半径变为原来的3倍后圆心角为α1,则α1=l 3r =αr 3r =α3,故α1α=13.答案:137.已知α=1 690°.(1)把α写成2k π+β(k ∈Z ,β∈[0,2π))的形式; (2)求θ,使θ与α终边相同,且θ∈(-4π,4π). 解:(1)1 690°=4×360°+250°=4×2π+2518π. (2)∵θ与α终边相同,∴θ=2k π+2518π(k ∈Z). 又θ∈(-4π,4π),∴-4π<2k π+2518π<4π(k ∈Z).解得-9736<k <4736(k ∈Z),∴k =-2,-1,0,1.∴θ的值是-4718π,-1118π,2518π,6118π.8.如图,已知在半径为10的圆O 中,弦AB 的长为10. (1)求弦AB 所对的圆心角α的大小; (2)求α所对的弧的长度l 及阴影部分的面积S . 解:(1)由于圆O 的半径为10,弦AB 的长为10, 所以△AOB 为等边三角形,∠AOB =π3,所以α=π3.(2)因为α=π3,所以l =α·r =10π3.S 扇=12lr =12×10π3×10=50π3,又S △AOB =12×10×53=253,所以S =S 扇-S △AOB =50π3-253=50⎝⎛⎭⎫π3-32.。
高一数学人教b版必修4精练:1.1.2 弧度制和弧度制与角度制的换算 含解析

第一章 1.1 1.1.2一、选择题1.已知α=-2,则角α的终边所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限[答案] C[解析] ∵1 rad =(180π)°,∴α=-2 rad =-(360π)°≈-114.6°,故角α的终边所在的象限是第三象限角.2.与-13π3终边相同的角的集合是( )A .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫-π3B .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫5π3 C .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α|α=2k π+π3,k ∈Z D .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α|α=2k π+5π3,k ∈Z[答案] D [解析] 与-13π3终边相同的角α=2k π-13π3,k ∈Z , ∴α=(2k -6)π+6π-13π3=(2k -6)π+5π3,(k ∈Z). 3.扇形周长为6 cm ,面积为2 cm 2,则其圆心角的弧度数是( ) A .1或4 B .1或2 C .2或4 D .1或5[答案] A[解析] 设扇形的半径为r ,圆心角为α,根据题意得⎩⎨⎧2r +r α=612αr 2=2,解得α=1或4.4.已知集合A ={α|2k π≤α≤(2k +1)π,k ∈Z},B ={α|-4≤α≤4},则A ∩B=( )A .∅B .{α|0≤α≤π|C .{α|-4≤α≤4|D .{α|-4≤α≤-π或0≤α≤π} [答案] D[解析] k ≤-2或k ≥1时A ∩B =∅;k =-1时A ∩B =[-4,-π];k =0时,A ∩B =[0,π];故A ∩B =[-4,-π]∪[0,π].故选D .5.一条弧所对的圆心角是2 rad ,它所对的弦长为2,则这条弧的长是( ) A .1sin1 B .1sin2 C .2sin1D .2sin2[答案] C[解析] 所在圆的半径为r =1sin1,弧长为2×1sin1=2sin1.6.如图中,圆的半径为5,圆内阴影部分的面积是( )A .175π36B .125π18C .75π18D .34π9[答案] A [解析] 40°=40×π180=2π9,30°=30×π180=π6, ∴S =12r 2·2π9+12r 2·π6=175π36.二、填空题7.已知一扇形的周长为π3+4,半径r =2,则扇形的圆心角为________.[答案] π6[解析] 设扇形的圆心角为α,则π3+4=2r+2α,又∵r=2,∴α=π6.8.正n边形的一个内角的弧度数等于__________.[答案] (n-2)nπ[解析] ∵正n边形的内角和为(n-2)π,∴一个内角的弧度数是(n-2)πn.三、解答题9.如果角α与x+π4终边相同,角β与x-π4终边相同,试求α-β的表达式.[解析] 由题意知α=2nπ+x+π4(n∈Z),β=2mπ+x-π4(m∈Z),∴α-β=2(n-m)π+π2,即α-β=2kπ+π2(k∈Z).10.设集合A={α|α=32kπ,k∈Z},B={β|β=53kπ,|k|≤10,k∈Z},求与A∩B的角终边相同的角的集合.[解析] 设α0∈A∩B,则α∈A且α∈B,所以α0=32k1π,α=53k2π,所以32k1π=53k2π,即k1=109k2.因为|k2|≤10,k2∈Z,且k1∈Z,所以k1=0,±10.因此A∩B={0,-15π,15π},故与A∩B的角的终边相同的角的集合为{γ|γ=2kπ或γ=(2k+1)π,k∈Z}={γ|γ=nπ,n∈Z}.。
高中数学人教B版必修4 1.1 同步练习 《弧度制和弧度制与角度制的换算》(人教)

《弧度制和弧度制与角度制的换算》同步练习1、若α是第四象限角,则απ-是( )。
A .第一象限角B .第二象限角C .第三象限角D .第四象限角2、若α=-3,则角α的终边在( )。
A .第一象限B .第二象限C .第三象限D .第四象限3、求值:1333-tansin cos πππ·· 等于( )。
A .14 B .34 C .12 D .324、下列各组角中,终边相同的角是( )。
A .π2k 与)(2Z k k ∈+ππ B .)(3k 3Z k k ∈±πππ与 C .ππ)14()12(±+k k 与 )(Z k ∈ D .)(66Z k k k ∈±+ππππ与5、若角α与角β的终边关于y 轴对称,则( )。
A .B .C .D . 6、集合⎭⎬⎫⎩⎨⎧∈==Z k k A ,6παα与⎭⎬⎫⎩⎨⎧∈+==Z n n B ,63ππββ的关系是( )。
A 、B A ⊂ B 、B A ⊃ C 、B A = D 、B A ⊆7、已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是( )。
A .2B .1sin 2C .1sin 2D .2sin8、某扇形的面积为12cm ,它的周长为4cm ,那么该扇形圆心角的度数为( )。
A .2°B .2C .4°D .49、一个半径为R 的扇形,它的周长是4R ,则这个扇形所含弓形的面积是( )。
2222)1cos 1sin D.(1 21.1cos 1sin 21B. )1cos 1sin 2(21A R R C R R -- 10、下列命题中,正确的命题是( )。
A .若两扇形面积的比是1∶4,则两扇形弧长的比是1∶2。
B .若扇形的弧长一定,则面积存在最大值。
C .若扇形的面积一定,则弧长存在最小值。
D .任意角的集合可以与实数集R 之间建立一种一一对应关系。
2018-2019版高中数学人教B版必修四课件:1.1.2 弧度制和弧度制与角度制的换算

28
α+β=1, 则 π α-β=180, 1 π 1 π 解得 α=2+360,β=2-360.
25
1.1.2 弧度制和弧度制与角度制的换算
1 2 3 4
3 11 -4π 4.把- 4 π 表示成 θ+2kπ(k∈Z)的形式, 使|θ|最小的 θ 值是________.
3 11 解析 - 4 π=-2π+-4π 3 =2×(-1)π+-4π.
扇形的弧长及面积公式的应用
例3 一个扇形的面积为1,周长为4,求圆心角的弧度数. 解 设扇形的半径为R,弧长为l,则2R+l=4,
1 ∴l=4-2R,根据扇形面积公式 S=2lR, 1 得 1=2(4-2R)· R, l 2 ∴R=1,∴l=2,∴α=R=1=2,
即扇形的圆心角为2 rad.
1.1.2 弧度制和弧度制与角度制的换算
20
规律方法
1 (1)联系半径、弧长和圆心角的有两个公式:一是 S=2
1 2 lr=2|α|r ,二是 l=|α|r,如果已知其中两个,就可以求出另一个. (2)当扇形周长一定时,其面积有最大值,最大值的求法是把面积 S 转化为半径 r 的函数.
1.1.2 弧度制和弧度制与角度制的换算
21
跟踪演练3 A.40π cm2
l 的弧度数的绝对值是|α|= r .
1.1.2 弧度制和弧度制与角度制的换算
7
2.角度制与弧度制的换算
(1) 角度化弧度 360°= 2π rad 弧度化角度 2π rad= 360°
180°= π rad
π rad= 180°
1 rad=
180 ° π ≈57.30°
π 1°= 180 rad≈0.017 45 rad
人教B版高一数学(必修4)导学案:1.1.2弧度制和弧度制和角度制的换算(无答案)
2.集合 等于()
A.ቤተ መጻሕፍቲ ባይዱB. C. D.
3.已知扇形AOB的面积为4,圆心角的弧度数为2,则该扇形的弧长为()
A. 4 B. 2 C. 1 D. 8
4. 弧度化为角度是,是第象限的角。
B组:
1. 1弧度的圆心角所对的弦长为2,求这个圆心角所对的弧长及圆心角所夹的扇形的面积。
教学反思
落实是成功的保证!
2. 转化为弧度数为()
A. B. C. D.
3.圆的半径是 ,则 的圆心角与圆弧围成的扇形的面积是()
A. B. C. D.
4. 7弧度的角是第象限的角,与7弧度的角的终边相同的最小正角为。
积极思考勤于动手天才来自勤奋!
课后巩固作业
A组:
1.在面积不等的圆内,1弧度的圆心角所对的()
A.弧长相等B.弦长相等
引申(1)把 化成弧度,(2)把 化成度。
探究二把下列各角化成0到 的角加上 的形式,并指出它们是哪个现象的角: 。
引申把下列各角的度数化成弧度数,并写成0到 的角加上 的形式
(1) ;(2) ;(3) 。
认真听讲是学习高效的捷径!
探究三 (1)已知扇形的周长为 ,面积为 ,求扇形圆心角的弧度数;
(2)已知一扇形的圆心角是 ,半径等于 ,求扇形的面积;
2.长度等于的圆弧所对的圆心角叫做1弧度的角,弧度记作。
3.弧度制与角度制的换算
,
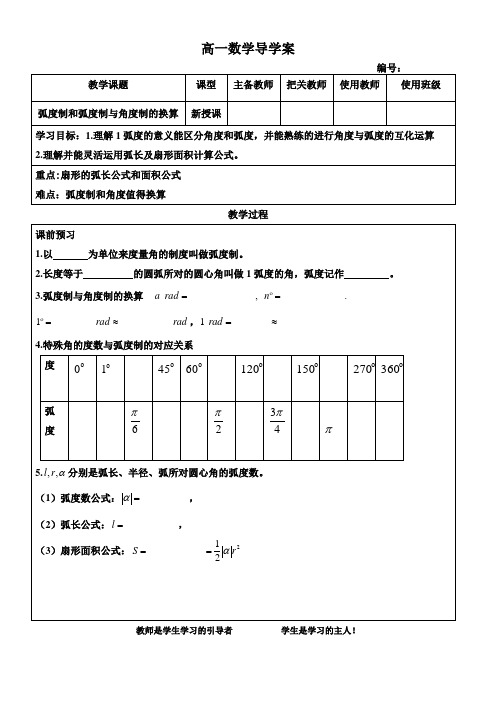
4.特殊角的度数与弧度制的对应关系
度
弧度
5. 分别是弧长、半径、弧所对圆心角的弧度数。
(1)弧度数公式: ,
(2)弧长公式: ,
(3)扇形面积公式:
教师是学生学习的引导者学生是学习的主人!
高一数学人教b版必修4同步训练:1.1.2 弧度制和弧度制与角度制的换算 含解析

1.1.2 弧度制和弧度制与角度制的换算 一、基础过关 1. -300°化为弧度是( )A .-43πB .-53πC .-54πD .-76π2.集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α|α=k π+π2,k ∈Z 与集合B = ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α|α=2k π±π2,k ∈Z 的关系是( ) A .A =B B .A ⊆B C .B ⊆AD .以上都不对3.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长是( )A .2B .sin 2 C.2sin 1D .2sin 14. 已知集合A ={α|2k π≤α≤(2k +1)π,k ∈Z},B ={α|-4≤α≤4},则A ∩B 等于 ( )A .∅B .{α|-4≤α≤π}C .{α|0≤α≤π}D .{α|-4≤α≤-π,或0≤α≤π} 5. 若扇形圆心角为216°,弧长为30π,则扇形半径为________. 6.若2π<α<4π,且α与-7π6角的终边垂直,则α=______. 7. 用弧度制表示顶点在原点,始边重合于x 轴的非负半轴,终边落在阴影部分内的角的集合(包括边界,如图所示).8.用30 cm长的铁丝围成一个扇形,应怎样设计才能使扇形的面积最大?最大面积是多少?二、能力提升9.扇形圆心角为π3,则扇形内切圆的圆面积与扇形面积之比为( )A.1∶3 B.2∶3 C.4∶3 D.4∶910.已知α为第二象限的角,则π-α2所在的象限是( )A.第一或第二象限B.第二或第三象限C.第一或第三象限D.第二或第四象限11.若角α的终边与角π6的终边关于直线y=x对称,且α∈(-4π,4π),则α=____________.12.如图所示,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转,已知P点在1 s内转过的角度为θ (0<θ<π),经过2 s达到第三象限,经过14 s后又回到了出发点A处,求θ.三、探究与拓展13.已知一扇形的中心角是α,所在圆的半径是R.(1)若α=60°,R=10 cm,求扇形的弧长及该弧所在的弓形面积;(2)若扇形的周长是一定值c (c>0),当α为多少弧度时,该扇形有最大面积?答案1.B 2.A 3.C 4.D 5.25 6.7π3或10π37.解(1)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α|2k π-π6≤α≤2k π+5π12,k ∈Z .(2)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α|k π+π6≤α≤k π+π2,k ∈Z . 8. 解 设扇形的圆心角为α,半径为r ,面积为S ,弧长为l ,则有l+2r =30,∴l =30-2r ,从而S =12·l ·r =12(30-2r)·r=-r 2+15r =-⎝ ⎛⎭⎪⎫r -1522+2254.∴当半径r =152 cm 时,l =30-2×152=15 cm , 扇形面积的最大值是2254cm 2, 这时α=lr=2 rad.∴当扇形的圆心角为2 rad ,半径为152 cm 时,面积最大,为2254cm 2. 9.B 10.D 11.-11π3,-5π3,π3,7π312.解 因为0<θ<π,且2k π+π<2θ<2k π+3π2(k ∈Z), 则必有k =0,于是π2<θ<3π4,又14θ=2n π(n ∈Z),所以θ=n π7,从而π2<n π7<3π4,即72<n<214,所以n =4或5,故θ=4π7或5π7.13.解 (1)设弧长为l ,弓形面积为S 弓,。
人教版数学高一B版必修4弧度制和弧度制与角度制的换算
1.1.2 弧度制和弧度制与角度制的换算知识点一:弧度制 1.下列说法正确的是A .一弧度就是一度的圆心角所对的弧B .一弧度是长度为半径的弧C .一弧度是一度的弧与一度的角之和D .一弧度是长度等于半径的弧所对的圆心角,它是角的一种度量单位2.在半径为2的圆内,弧长为4的弧所对的圆心角的弧度数为__________. 知识点二:角度与弧度的换算关系3.把-8π3化成角度是A .-960°B .-480°C .-120°D .-60° 4.把-1 485°化为2kπ+α(k ∈Z,0≤α<2π)的形式为A .-8π+π4B .-8π-7π4C .-10π+π4D .-10π+7π45.下列各角中与7π12终边相同的角为A .435°B .465°C .225°D .-435° 6.填空: (1)-300°=________ rad ,67°30′=________ rad ; (2)8π5=__________°. 7.用弧度表示顶点在原点,始边重合于x 轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如下图所示).知识点三:弧长公式和扇形面积公式8.一条弦的长等于半径,则这条弦所对的圆周角的弧度数为A .1 B.12C.π6或5π6D.π3或5π39.已知弧度数为2的圆心角所对弧长也是2,则这个圆心角所对的弦长是A .2 B.2sin1 C .2sin1 D .sin210.圆的半径为1,所对圆心角为3弧度的弧长为__________.11.已知扇形的圆心角为2π5,半径等于20 cm ,求扇形面积.能力点一:角度与弧度的相互转化 12.下列各式正确的是A .π=180B .π=3.14C .90°=π2rad D .1 rad =π13.时钟的分针在1点到3点20分这段时间里转过的弧度数为 A.14π3 B .-14π3 C.7π18 D .-7π18 14.(1)把202°30′化成弧度;(2)把-5π12化成角度;(3)已知α=15°,β=π10,γ=1,θ=105°,φ=7π12,试比较α、β、γ、θ、φ的大小.能力点二:用弧度制解决与终边相同角有关的问题 15.终边在第二象限和第三象限的角的集合是A .(-π2,π2)B .(π2,3π2)C .(π2+2kπ,3π2+2kπ)(k ∈Z )D .(π2+2kπ,π+2kπ)∪(π+2kπ,3π2+2kπ)(k ∈Z )16.设两个集合M ={x|x =kπ2+π4,k ∈Z },N ={x|x =kπ-π4,k ∈Z },则 A .M =N B .M NC .M ND .M ∩N =17.若角θ的终边与8π5的终边相同,则在[0,2π]内终边与θ4角的终边相同的角是__________.18.已知角θ的终边与-π6的终边共线,且θ∈(0°,360°),求θ的弧度数.能力点三:弧长公式及扇形面积公式的应用19.下列命题正确的是A.若两扇形面积的比为1∶9,则两扇形弧长的比是1∶3B.若扇形的弧长一定,则面积存在最大值C.若扇形的面积一定,则弧长存在最小值D.角的集合与实数集之间可以建立起一一对应20.已知扇形AOB中,所对的圆心角为1 rad,弦AB=2,则该扇形的面积为__________.21.美观的纸扇是一种艺术品,它在设计上符合黄金比例(0.618),即从一圆形(半径为R)的纸片中分割出来的扇形的面积与剩余面积比值为0.618.那么符合黄金比例的纸扇的中心角α大约是__________度(精确到0.1).22.已知一扇形周长为C(C>0),当扇形的圆心角为何值时,它的面积最大?求出面积最大值.23.已知一扇形的中心角为α,所在圆半径为R.(1)若α=60°,R=10,求该扇形的弧长和面积;(2)若该扇形的周长为4R,则扇形中所含弓形的面积是多少?答案与解析基础巩固1.C2.B 由三角函数定义知,x =3,y =4,r =x 2+y 2=5,∴sinα=y r =45,cosα=x r =35,tanα=y x =43,故sinα+cosα+tanα=45+35+43=4115.3.D 由cosα=35,y<0,得y =-4,故tanα=y x =-43.4.2524∵x =7,y =24, ∴r =25,1sinα=1y r =r y =2524.5.B6.A ∵2是第二象限角,3是第二象限角,4是第三角限角, ∴sin2>0,cos3<0,tan4>0,故sin2·cos3·tan4<0. 7.③④8.二、三 由tanα·cscα<0知,tanα与cscα的值异号. ∴α终边位于二、三象限.9.[2kπ+π2,2kπ+π](k ∈Z ) 依题意,得⎩⎨⎧sinx ≥0-cosx ≥0⎩⎪⎨⎪⎧sinx ≥0cosx ≤0⎩⎪⎨⎪⎧2kπ≤x ≤2kπ+π,2kπ+π2≤x ≤2kπ+3π2(k ∈Z ). 故x 的范围是2kπ+π2≤x ≤2kπ+π(k ∈Z ).10.解:由题意得⎩⎨⎧2+log 12x ≥0,x ≠kπ+π2(k ∈Z ),即⎩⎪⎨⎪⎧0<x ≤4,x ≠kπ+π2(k ∈Z ).解得0<x<π2或π2<x ≤4.∴函数的定义域为(0,π2)∪(π2,4].能力提升11.B 由定义知,tan420°=a-4, 又∵tan420°=tan(360°+60°)=tan60°=3, ∴a-4= 3.∴a =-4 3. 12.2 01013.解:在直线y =x 上任取一点P(a ,a)(a ≠0), 则r =a 2+a 2=2|a|.当a>0时,r =2a.sinα=y r =a 2a =22,cosα=x r =a 2a =22,∴sinα+cosα= 2.当a<0时,r =-2a ,sinα=y r =a -2a =-22,cosα=x r =a -2a =-22.∴sinα+cosα=- 2. 综上,sinα+cosα=±2.14.解:由题意得r =(-4a )2+(3a )2=5|a|.当a>0时,r =5a ,α角在第二象限,sinα=y r =3a 5a =35,cosα=x r =-4a 5a =-45,tanα=yx=3a -4a=-34;当a<0时,r =-5a ,α角在第四象限,sinα=-35,cosα=45,tanα=-34.15.解:由r 2=x 2+y 2=3+y 2,得r =3+y 2,由三角函数的定义可得sinα=yr=y 3+y 2=24y , ∴y =±5,r =2 2.∴cosα=x r =-64,tanα=y x =±153.16.C cosα≤0,且sinα>0,则α在第二象限或终边在y 轴的非负半轴上,∴⎩⎪⎨⎪⎧3m -9≤0,m +2>0,即-2<m ≤3. 17.{-1} 由sinαcosα<0,知α在第二象限或第四象限. 当α在第二象限时,sinα>0,cosα<0,tanα<0,则y =-1; 当α在第四象限时,sinα<0,cosα>0,tanα<0,则y =-1. 综上可得,值域为{-1}. 18.(1)> (2)>19.一或三 由(12)sin2θ<1,得sin2θ>0.∴2θ∈(2kπ,2kπ+π),k ∈Z . ∴θ∈(kπ,kπ+π2),k ∈Z .当k =2m 时,m ∈Z ,θ∈(2mπ,2mπ+π2),θ为第一象限角;当k =2m +1时,m ∈Z ,θ∈(2mπ+π,2mπ+3π2),θ为第三象限角. 20.解:所求定义域应满足⎩⎪⎨⎪⎧sinx·tanx ≥0,x ≠kπ+π2(k ∈Z ),即⎩⎪⎨⎪⎧ sinx ≥0,tanx ≥0,x ≠kπ+π2(k ∈Z )或⎩⎪⎨⎪⎧sinx ≤0,tanx ≤0,x ≠kπ+π2(k ∈Z ).根据x 所在象限情况可判断原函数定义域为{x|2kπ-π2<x<2kπ或2kπ<x<2kπ+π2或x =kπ,k ∈Z }.21.解:(1)当角的终边在第一象限时,在角的终边上取点P(1,2), 则r =12+22= 5.∴sinα=y r =25=255.当角的终边在第三象限时,在角的终边上取点Q(-1,-2), 则r =(-1)2+(-2)2=5,∴sinα=y r =-25=-255.(2)依题意,P 到原点O 的距离r =OP =(-3)2+y 2=3+y 2.∴sinα=yr=y 3+y 2=34y. ∵y ≠0,∴9+3y 2=16. ∴y 2=73,y =±213.∴点P 在第二或第三象限,且cosα=-33+y 2=-33+73=-34.拓展探究22.解:(1)由1|sinα|=-1sinα可知sinα<0,∴α是第三或第四象限角或y 轴的负半轴上角. 由lg(cosα)有意义可知cosα>0,∴α是第一或第四象限角或x 轴的正半轴上角. 综上可知角α是第四象限的角. (2)∵点M(35,m)在单位圆上,∴(35)2+m 2=1,解得m =±45. 又α是第四象限角,故m<0, 从而m =-45.由正弦函数的定义可知sinα=-45.23.解:由题意可知P 点坐标为P(a ,-b),Q 点的坐标为Q(b ,a). 根据三角函数定义得:sinα=-ba 2+b2,tanα=-ba ,secα=a 2+b 2a,secβ=a 2+b 2b ,cotβ=ba,cscβ=a 2+b 2a. ∴原式=-b a 2+b2·a 2+b 2b -b a ·b a +a 2+b 2a ·a 2+b 2a=-1-b 2a 2+a 2+b2a2=0.。
数学人教B版必修4课后导练:1.1.2弧度制和弧度制与角
课后导练基础达标1.下列命题中的假命题是( )A.“度”与“弧度”是度量角的两种不同的度量单位B.一度的角是圆周的3601,一弧度的角是圆周的π21 C.根据弧度的定义,180°一定等于π弧度D.不论是用角度制还是弧度制度量角,它们均与圆的半径长短有关解析:根据角度与弧度的定义,可知无论是角度制还是弧度制,角的大小与圆的半径长短无关,而是与弧长和半径的比值有关,应选D. 答案:D2.下列各对角中,终边相同的是( )A.23π和2kπ-23π(k ∈Z )B.5π-和522πC.97π-和911πD.320π和9122π解析:911π=2π97π-.答案:C3.已知两弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长是( ) A.2 B. sin2 C.1sin 2D.2sin1 解析:∵sin1=R1,∴R=1sin 1.又∵l=|α|·R ,∈R ∴l=2·1sin 1=1sin 2. 答案:C 4.扇形圆心角为3π,半径长为a ,则扇形内切圆的面积与扇形面积之比是( ) A.1∶3 B.2∶3 C.4∶3 D.4∶9 解析:S 扇形=21lR=6πa 2. 设内切圆的半径为r,则r=3a. ∴S 圆形=92a π.∴32=扇形圆S S .故选B. 答案:B5.集合A={α|α=kπ+2π,k ∈Z },B={α|α=2kπ±2π,k ∈Z }的关系是( ) A.A=B B.A B C.B A D.以上都不对解析:集合A 中k ∈Z ,分为奇数和偶数表示,即A={α|α=2nπ+2π,n ∈Z }∪{α|α=(2n -1)π+2π,n ∈Z }=B.故选A. 答案:A6.扇形周长为6,面积为2 ,则其圆心角的弧度数是( )A.1或4B.1或2C.2或4D.1或5解析:设此扇形的半径为r ,圆心角的弧度数是α(0<α<2π),则有⎪⎩⎪⎨⎧=∙+=∙)2.(62)1(,2212r r r αα解之,得α=1或α=4.答案:A7.设0≤α<2π,将-1 485°表示成2kπ+α,k ∈Z 的形式是________. 解析:-1 485°=-5×360°+315°=-10π+47π. 答案:-10π+47π 8.如图,阴影部分用弧度制可表示为_______.解析:330°可看成-30°,即6π-,而75°=75×180π=125π,∴{θ|2kπ6π-<θ<2kπ+125π,k ∈Z }.答案:{θ|2kπ6π-<θ<2kπ+125π,k ∈Z }综合运用9.点P 从(1,0)出发,沿单位圆x 2+y 2=1按逆时针方向运动32π弧长到达Q 点,则Q 的坐标为( ) A.(-21,23) B.(23-,-21) C.(-21,23-) D.(23-,21)解析:由弧长公式l=|α|r,l=32π,r=1,得P 点按逆时针方向转过的角度为α=32π,可确定直线OP 的方程为y=3-x(x<0),与圆的方程x 2+y 2=1联立可得P(-21,23). 答案:A10.若一段圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数为( ) A.3π B.32π C.3 D.2 解析:设正三角形ABC 是半径为r 的圆O 的内接三角形. ∵AB=3r, ∴弧长l=3r.∴α=33==rrr l .故选C. 答案:C11.在扇形AOB 中,∠AOB=90°,=l,求此扇形的内切圆的面积.解:如图,∠AOB=90°=2π.设扇形AOB 的半径为R,其内切圆半径为r,由弧长公式有l=2πR, 所以R=πl 2.① 又因为OD=R,HD=r,OH=2r, 所以OD=OH+HD=(1+2)r. 所以r=21+R =(2-1)R.②把①代入②,得r=(2-1)·ππll)12(22-=.所以内切圆的面积S=πr 2=π[πl)12(2-]2=π2)2812(l -.12.设半径为12 cm,长为8π cm 的弧所对圆心角为α,α∈(0,2π),求出与角α终边相同的角的集合A ,并判断A 是否为B={θ|θ=6π+2πk ,k ∈Z }的真子集. 解:由|α|=r l 得α=32π∈(0,2π), ∴与α终边相同的角的集合A={α|α=32π+2kπ,k ∈Z }.在B={θ|θ=6π+2πk ,k ∈Z }中,令k=4m+1,m ∈Z ,则θ=6π+2π+2mπ=32π+2mπ,m ∈Z ,∴A ⊆B. 又∵6π∈B ,而6π∉A, ∴A B,即A 为B 的真子集. 拓展探究13.如图,已知一长为3 cm,宽为1 cm 的长方形木块在桌面上作无滑动的翻滚,翻滚到第三面时,被一小木板挡住,使木块底面与桌面成30°的角.求点A 走过的路程及走过的弧所在的三个扇形的面积的和.解:所对的圆半径是2,圆心角为2π,所对的半径是1,圆心角是2π,所对的圆半径为3,圆心角为3π.所以A 点走过的路程是3段圆弧之和,即2×2π+1×2π+3×3π=6329+π cm.3段弧所在的扇形总面积是21×2×π+21×2π+3214733ππ=⨯ cm 2.。
数学人教B版必修4:1.1.2 弧度制和弧度制与角度制的换算 作业 Word版含解析(数理化网)
双基达标(限时20分钟)1.若α=-3,则角α的终边在().A.第一象限B.第二象限C.第三象限D.第四象限解析∵-π<-3<-π2,∴α是第三象限角.答案 C2.将1 920°转化为弧度数为().A.163 B.323C.16π3 D.32π3解析 1 920°=1 920×π180=32π3.答案 D3.把-114π表示成θ+2kπ(k∈Z)的形式,使|θ|最小的θ值是().A.-3π4B.-π4C.π4 D.3π4解析-11π4=-2π-3π4.∴-11π4与-3π4是终边相同的角,且此时|-3π4|=3π4是最小的.答案 A4.已知扇形的半径是16,圆心角是2弧度,则扇形的弧长是________.解析∵R=16,α=2 rad,∴l=α·R=16×2=32.答案325.已知集合A={x|2kπ≤x≤2kπ+π,k∈Z},集合B={x|-4≤x≤4},则A∩B=________. 解析如图所示,∴A∩B=[-4,-π]∪[0,π].答案[-4,-π]∪[0,π]6.判断下列各角所在的象限:(1)9;(2)-4;(3)-1 999π5.解(1)因为9=2π+(9-2π),而π2<9-2π<π,所以9为第二象限角.(2)因为-4=-2π+(2π-4),而π2<2π-4<π,所以-4为第二象限角.(3)-1 999π5=-200×2π+π5,所以-1 999π5为第一象限角.综合提高(限时25分钟)7.若α是第四象限角,则π-α是().A.第一象限角B.第二象限角C.第三象限角D.第四象限角解析∵α是第四象限角.∴2kπ-π2<α<2kπ(k∈Z),∴-2kπ<-α<-2kπ+π2.∴-2kπ+π<π-α<-2kπ+3π2. ∴π-α是第三象限角.答案 C8.已知半径为1的扇形面积为38π,则扇形的圆心角为().A.316π B.38πC.34π D.32π解析∵S=12rl,∴3π8=12l,∴l=3π4,故选C.答案 C9.已知弧度数为2的圆心角所对的弦长为2,则这扇形圆心角所对的弧长为________.解析设半径为R,则R sin 1=1,∴R=1sin 1,∴弧长l=2sin 1.答案2 sin 110.若α=kπ+π4,k∈Z,则α是第________象限角.解析当k为偶数时,α是第一象限角,当k为奇数时,α是第三象限角.答案一或三11.用弧度表示终边落在图中所示阴影部分内(不包括边界)的角的集合.解以OB为终边的330°角可看成为-30°角,化为弧度为-π6,而75°=75×π180=5π12,∴终边落在阴影部分内的角的集合为{θ|2kπ-π6<θ<2kπ+5π12,k∈Z}.12.(创新拓展)如图,已知一长为 3 dm,宽1 dm 的长方形木块在桌面上作无滑动的翻滚,翻滚到第三面时被一小木板挡住,使木块底面与桌面成30°的角.问点A走过的路程的长及走过的弧度所对扇形的总面积.解 AA 1所对的圆半径是2 dm ,圆心角为π2,A 1A 2所对圆半径是1dm ,圆心角是π2,A 2A 3所对的圆半径是 3 dm ,圆心角是π3,所以走过的路程是3段圆弧之和,即2×π2+1×π2+3×π3=9+236π(dm);3段圆弧所对的扇形的总面积是12×2×π+12×π2+12×3×3π3=7π4(dm 2).。
2019-2020人教B版数学必修4课时分层作业2 弧度制和弧度制与角度制的换算
课时分层作业(二) 弧度制和弧度制与角度制的换算(建议用时:60分钟)[合格基础练]一、选择题1.-25π6的角是( ) A .第一象限的角 B .第二象限的角 C .第三象限的角D .第四象限的角D [因为-25π6=-π6-4π,所以-25π6与-π6的终边相同,为第四象限的角.]2.若2 rad 的圆心角所对的弧长为4 cm ,则这个圆心角所对的扇形面积是( )A .4 cm 2B .2 cm 2C .4π cm 2D .2π cm 2 A [r =l |α|=42=2(cm),S =12lr =12×4×2=4(cm 2).] 3.与30°角终边相同的角的集合是( )A .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=k ·360°+π6,k ∈ZB .{α|α=2k π+30°,k ∈Z }C .{α|α=2k ·360°+30°,k ∈Z }D .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=2k π+π6,k ∈ZD [∵30°=30×π180 rad =π6 rad , ∴与30°终边相同的所有角可表示为 α=2k π+π6,k ∈Z ,故选D.]4.已知扇形的面积为2,扇形圆心角的弧度数是4,则扇形的周长为() A.2 B.4C.6 D.8C[设扇形的半径为r,弧长为l,则由扇形面积公式可得2=12lr=12|α|r2=12×4×r2,解得r=1,l=αr=4,所以所求扇形的周长为2r+l=6.] 5.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数为()A.π3B.2π3C. 3 D.2C[设圆的半径为r,则圆内接正三角形边长为3r,所以圆心角的弧度数为3rr= 3.]二、填空题6.把-570°写成2kπ+α(k∈Z,α∈(0,2π))的形式是________.-4π+56π[-570°=-⎝⎛⎭⎪⎫570×π180rad=-196π rad,∴-196π=-4π+56π.]7.已知一扇形的周长为π3+4,半径r=2,则扇形的圆心角为________.π6[设扇形的圆心角为α,则π3+4=2r+2α.又∵r=2,∴α=π6.]8.经过点P(a,a)(a≠0)的角α的集合是________.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=kπ+π4,k∈Z[当a>0,点P(a,a)在第一象限,此时α=2kπ+π4,k∈Z;a<0,点P(a,a)在第三象限,此时α=2k π+54π,k ∈Z , 故满足条件的角α的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=k π+π4,k ∈Z.] 三、解答题9.已知角α的终边与-253π的终边关于x 轴对称,求角α3在(-π,π)内的值. [解] ∵253π与-253π的终边关于x 轴对称,且253π=8π+π3, ∴α与π3的终边相同.∴α=2k π+π3(k ∈Z ),α3=2k π3+π9(k ∈Z ). ∵-π<α3<π,∴-π<2k π3+π9<π. 当k =-1时,α3=-5π9∈(-π,π); 当k =0时,α3=π9∈(-π,π); 当k =1时,α3=7π9∈(-π,π).∴在(-π,π)内α3的值有三个,它们分别是-5π9,π9和7π9. 10.已知一个扇形的周长是40,(1)若扇形的面积为100,求扇形的圆心角; (2)求扇形面积S 的最大值.[解] (1)设扇形的半径为r ,弧长为l ,圆心角为α, 则由题意得⎩⎪⎨⎪⎧l +2r =40,12lr =100,解得⎩⎨⎧l =20,r =10,则α=lr =2(rad). 故扇形的圆心角为2 rad.(2)由l+2r=40得l=40-2r,故S=12lr=12(40-2r)·r=20r-r2=-(r-10)2+100,故r=10时,扇形面积S取最大值100.[等级过关练]1.如果一个圆的半径变为原来的一半,而弧长变为原来的32倍,则该弧所对的圆心角是原来的()A.12倍B.2倍C.13倍D.3倍D[设圆的半径为r,弧长为l,圆心角的弧度数为lr,将半径变为原来的一半,弧长变为原来的32倍,则弧度数变为32l12r=3·lr,即弧度数变为原来的3倍.]2.若α是第三象限的角,则π-α2是()A.第一或第二象限的角B.第一或第三象限的角C.第二或第三象限的角D.第二或第四象限的角B[因为α为第三象限的角,所以有2kπ+π<α<2kπ+32π,k∈Z,kπ+π2<α2<kπ+34π,k∈Z,-kπ-34π<-α2<-kπ-π2,k∈Z,故-kπ+π4<π-α2<-kπ+π2,k∈Z.当k为偶数时,π-α2在第一象限;当k为奇数时,π-α2在第三象限,故选B.]3.(1)把67°30′化成弧度=________.(2)把35π 化成度=________.(1)38π(2)108°[(1)67°30′=67.5°=67.5×π180=38π.(2)35π=⎝⎛⎭⎪⎫3π5×180π°=108°.]4.一个半径为2的扇形,如果它的周长等于所在的半圆的弧长,那么扇形的圆心角是________弧度,扇形面积是________.π-22(π-2)[由题意知r=2,l+2r=πr,∴l=(π-2)r,∴圆心角α=lr=(π-2)rr=π-2(rad),扇形面积S=12lr=12×(π-2)·r·r=2(π-2).]5.已知半径为10的圆O中,弦AB的长为10.(1)求弦AB所对的圆心角α的大小;(2)求α所在的扇形的弧长l及弧所在的弓形的面积S. [解](1)由⊙O的半径r=10=AB,知△AOB是等边三角形,∴α=∠AOB=60°=π3.(2)由(1)可知α=π3,r=10,∴弧长l=α·r=π3×10=10π3,∴S扇形=12lr=12×10π3×10=50π3,而S△AOB =12·AB·53=12×10×53=5032,∴S=S扇形-S△AOB=50⎝⎛⎭⎪⎫π3-32.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
.203π和
122 9
π
答案 :C
3.已知 2 弧度的圆心角所对的弦长为 2,则这个圆心角所对的弧长是 ( )
2
A.2
B .sin 2
C.
D .2sin 1
sin1
详细分析 :设圆的半径为 R,圆心角为 α,圆心角所对的弧长为 l.
因为
sin1=
1
??,所以
1
R= .
sin1
又因为 l=| α|·R,所以 l= 2× 1 = 2 .
rad,
30
所以秒针端点
A 转过的路程为
d=|
α|·r=
π 6
??
(cm),
2
4
4
π 92 π
28 π
(2)-1104° =- 1104 ×180 =- 15 =- 8π+ 15 .
因为 28 π是第四象限的角 ,所以 -1104 ° 是第四象限的角 .
15
二、 B 组 能力提升
1.已知 θ∈ ?? ??= ??π+ (-1 )??·π4 ,??∈ Z ,则角 θ的终边所在的象限是 (
解得
??= 4, 或 ??= 2 ,
??= ??=
81,(不合题意
,舍去 ).
所以
α=
??
??=
2
4=
1
2.
9.把下列各角化为 2kπ+ α,k∈ Z ,0≤ α< 2π的形式 ,并判断该角是第几象限的角 :
27
(1) 4 π;(2) -1 104° .
解
:(1)274π=
6π+
3π
4.
因为 3π是第二象限的角 ,所以 27 π是第二象限的角 .
=A ,∴A=B. 故选
A.
答案 :A
4.若圆中的一段圆弧长度等于其内接正三角形的边长
,则该圆弧所对圆心角的弧度数为 ( )
A .π
3
B .2π
3
C. 3
D .2
详细分析 :设圆的半径为 R,则圆的内接正三角形的边长为 3R,所以长度为 3 R 的圆弧所对圆心角的
弧度数 α= 3??= 3 .
??
答案 :C
B.扇形的圆心角不变
C.扇形的面积增加到原来的 2 倍
D.扇形的圆心角增加到原来的 2 倍
详细分析 :扇形的圆心角
α=
??
??,l,R
均变为原来的
答案 :B
2 倍 ,故 α不变 .
6.在半径为 2 的圆内 ,长度为 4 的弧所对的圆心角的度数为
.
详细分析 :圆心角
α=4 = 2=
2
180
π ×2
°=
5.若一扇形的弧长变为原来的
的
.
3倍 ,半径变为原来的一半 ,则扇形的面积为原来扇形面积
2
详细分析
:
S=
1
2lr
,l'=
31
2l,r'= 2r,则
1
S'= 2 l'r'=
1 2
× 32l
1
·2 r=
3
4S.
答案 :3
4
6.
73764004 某时钟的秒针端点 A 到中心 O 的距离为 5 cm,秒针均匀地绕点 O 旋转 ,当
3π
10 ,7x=
7π 9π
10 ,9x= 10 .
答案
:π
10
3π 7π 9π
, 10 , 10 , 10
8.
如图 ,扇形 AOB 的面积是 4 cm2,周长是 10 cm,求扇形的圆心角 α的弧度数 . 解 :设弧 AB 长为 lcm,扇形半径为 rcm,
1
则
??+ 2 ??= 10 ,
1
2 ???=? 4,
)
A. 第一象限
B. 第二象限
C.第一或第二象限
D. 第三或第四象限
详细分析 :因为 θ∈ ?? ??= ??π+ (-1 )??·π4 ,??∈ Z , 所以当 k= 2m(m∈ Z )时 ,θ=2mπ+ π4 ,终边在第一象限
象限 .所以 θ终边在第一或第二象限 .
;当 k= 2m+ 1(m∈ Z )时 ,θ= 2mπ+ 34π,终边在第二
答案 :C
2.某扇形的周长为 6,面积为 2,则其圆心角的弧度数是
()
A.1 或 4
B .1 或 2
详细分析 :设此扇形的半径为
答案 :A
C.2 或 4 D .1 或 5
r ,圆心角的弧度数是
α(0<α< 2π),则有
1 2
??·??2
=
2,
解得 α= 1 或 α= 4.
2 ??+ ??·??= 6 .
360 π
°.
答案 :
360 π
°
7.已知四边形四个角的度数的比为 1∶3∶7∶9,用弧度制写出这四个角从小到大的顺序
为
.
详细分析 :因为四边形四个角的度数的比为 1∶3∶7∶9,
所以设这四个角的弧度数分别为 x,3x,7x,9x.
根据题意得 ,x+ 3x+ 7x+ 9x= 2π,
则
x=πΒιβλιοθήκη 10 ,3x=??
3.集合 A= ?? ??= ??π+ 2 ,??∈Z 与集合 B=
α α= 2kπ± π2,k∈ Z
的关系是 (
)
A .A=B
B .A? B
C.B? A
D .以上都不对
详细分析
:∵ B=
?? ??=
2 ??π+
π或 ??=
2
2??π+
3π
2 ,?∈? Z
=
?? ??=
??
π+
π
2 ,?∈? Z
时间 t= 0 时 ,点 A 与钟面上标 12 的点 B 重合 .设秒针端点 A 转过的路程为 d cm,所形成的扇形面积为 S cm2,则当 t∈[0,60] 时 d 与 S 关于时间 t(s)的函数关系式为 .
详细分析 :因为秒针的旋转方向为顺时针 ,
所以 ts后秒针端点
A 转过的角
α=-
π
??
sin1 sin1
答案 :C
29
4.- 12 π的终边所在的象限是 ( )
A .第一象限
B .第二象限 C.第三象限 D .第四象限
详细分析
:
-
29 12
π=-
5
2 π- 12
π,故在第四象限
.
答案 :D
5.若圆的半径变成原来的 2 倍 ,扇形的弧长也变成原来的 2 倍 ,则( )
A .扇形的面积不变
1.1.2 弧度制和弧度制与角度制的换算
课后篇 巩固探究
1.将
7 π化为角度是
5
(
)
A.225 °
B.250 °
答案 :C
一、 A 组 基础巩固
C.252° D.288 °
2.下列各对角中 ,终边相同的是 ( )
A.
3 π和
2
2kπ-32π(k∈ Z )
B
.-
π和
5
22 π 5
C.-79π和
11 π 9
