蚁群算法详细讲解
专题讲座-蚁群算法介绍

城市之间距离
目标函数为
f ( w) d il 1il ,
l 1
n
其中
w (i1 , i2 ,, in )
in 1 i1
。
为பைடு நூலகம்市1,2,…n的
一个排列,
网络路由
对于计算机网络中的路由进行优化,提高路由效率。
聚类
把待聚类的数据随机散布在一个平面上,放置若干只虚拟蚂蚁使其 在平面上随机运动。 当一只蚂蚁遇到一个数据时即拾起并继续行走,在行走过程中,如 果遇到附近的数据与背负的数据相似性高于设置的标准时则将数据 放置在该位置,继续移动。 重复以上过程即可实现数据聚类。
寻食过程
步骤二 本图为从开始算起,经过18个时间单位时的情形:走ABD的蚂 蚁到达终点后得到食物又返回了起点A,而走ACD的蚂蚁刚好走 到D点。
过程分析
假设蚂蚁每经过一处所留下的信息素为一个单位,则经过36个 时间单位后,所有开始一起出发的蚂蚁都经过不同路径从D点 取得了食物,此时ABD的路线往返了2趟,每一处的信息素为4 个单位,而 ACD的路线往返了一趟,每一处的信息素为2个单位, 其比值为2:1。
寻找食物的过程继续进行,则按信息素的指导,蚁群在ABD 路线上增派一只蚂蚁(共2只),而ACD路线上仍然为一只蚂 蚁。再经过36个时间单位后,两条线路上的信息素单位积累 为12和4,比值为3:1。
过程分析
若按以上规则继续,蚁群在ABD路线上再增派一只蚂蚁 (共3只),而ACD路线上仍然为一只蚂蚁。再经过36 个时间单位后,两条线路上的信息素单位积累为24和6, 比值为4:1。
避障规则
如果蚂蚁要移动的方向有障碍物挡住,它会随机的选择另一个 方向,并且有信息素指引的话,它会按照觅食的规则行为。
蚁群算法
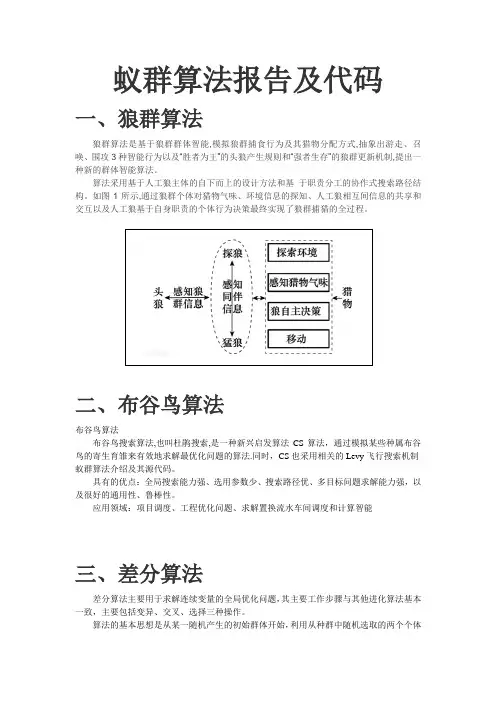
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
简要叙述蚁群算法及其优缺点

简要叙述蚁群算法及其优缺点蚁群算法,说白了,就是从蚂蚁们的“工作方式”中汲取灵感,来解决一些复杂的问题。
你想啊,蚂蚁虽然个头小,脑袋也没啥大智慧,可它们集体合作的时候,可真是让人瞠目结舌。
就拿找食物这事儿来说,蚂蚁们通过一种叫做“信息素”的东西,能把食物的方向告诉其他蚂蚁。
你想,成群结队的蚂蚁在地上爬来爬去,气氛可热闹了。
而这些蚂蚁在寻找最短路径的过程中,就是利用这种“信息素”来引导彼此。
哦对,信息素就是一种化学物质,它能吸引其他蚂蚁走自己走过的路,时间久了,大家都能找到最短最优的路线。
这就是蚁群算法的核心,大家通过简单的规则合作起来,居然能找到很复杂问题的解决方案。
听起来是不是有点神奇?但这就是大自然的魅力,真是让人不得不佩服!蚁群算法的好处,简直是数不胜数。
它特别适合处理那些“大而复杂”的问题。
像是找最短路径、优化调度这些问题,用蚁群算法解决起来特别靠谱。
更妙的是,它不需要预先知道问题的具体情况。
就像蚂蚁不需要知道前方有什么危险,只要它们不断地试探,最终总能找到正确的路。
蚁群算法特别“顽强”,它可以通过不断地调整来适应环境变化。
假设前方的路突然有个障碍,蚂蚁们马上就能改变路线,去找另一条更合适的道路。
这种动态适应能力,在现实世界中有着广泛的应用,像物流配送、网络路由、甚至是金融分析等,蚁群算法都能大显身手。
不过话说回来,世上没有十全十美的事儿,蚁群算法也有它的缺点。
首先吧,虽然它能找到“可行的”解,但并不总能找到“最优”的解。
你要知道,这个算法是基于概率的,蚂蚁们在探索路径时是随机的,所以它有可能会走冤枉路,最终找到一个不错但不是最好的答案。
就像你找餐厅,可能你最后选了个味道还不错的地方,但走了好多冤枉路,吃完饭才发现旁边就有个更好吃的店。
所以,有时候蚁群算法可能不是最理想的选择,特别是当问题特别复杂,解空间又大到让你头晕眼花的时候。
再者呢,蚁群算法的计算量也挺大的。
每次要让大量的“蚂蚁”在问题空间中四处乱窜,寻找最佳路径。
蚁群算法最短路径求解

蚁群算法最短路径求解
蚁群算法是一种模拟蚂蚁寻找食物的行为,通过模拟蚂蚁在路径上的行为来寻找最短路径。
蚂蚁在寻找食物时,会释放一种化学物质,其他蚂蚁会跟随这种化学物质,最终找到食物。
这种化学物质被称为信息素,蚂蚁在路径上释放的信息素越多,其他蚂蚁就越容易跟随这条路径。
蚁群算法最短路径求解的过程可以分为以下几个步骤:
1. 初始化信息素:在开始求解之前,需要将所有路径上的信息素初始化为一个较小的值,通常为1/n(n为路径数量)。
2. 蚂蚁选择路径:每只蚂蚁在选择路径时,会根据信息素浓度和路径长度进行选择。
信息素浓度越高的路径,被选择的概率就越大。
同时,路径长度越短的路径,也被选择的概率就越大。
3. 更新信息素:当所有蚂蚁都选择完路径后,需要根据路径长度更新信息素。
路径长度越短的路径,信息素浓度就越高。
4. 重复执行:重复执行步骤2和步骤3,直到达到最大迭代次数或者找到最短路径为止。
5. 输出结果:输出最短路径和路径长度。
蚁群算法最短路径求解的优点是可以处理大规模的问题,同时也能够处理多目标问题。
但是,蚁群算法也存在一些缺点,例如容易陷入局部最优解、收敛速度较慢等问题。
因此,在实际应用中需要根据具体问题进行调整和优化。
(转载)ACO蚁群算法(算法流程,TSP例子解析)

(转载)ACO蚁群算法(算法流程,TSP例⼦解析)1. 背景——蚁群的⾃组织⾏为特征⾼度结构化的组织——虽然蚂蚁的个体⾏为极其简单,但由个体组成的蚁群却构成⾼度结构化的社会组织,蚂蚁社会的成员有分⼯,有相互的通信和信息传递。
⾃然优化——蚁群在觅⾷过程中,在没有任何提⽰下总能找到从蚁巢到⾷物源之间的最短路径;当经过的路线上出现障碍物时,还能迅速找到新的最优路径。
信息正反馈——蚂蚁在寻找⾷物时,在其经过的路径上释放信息素(外激素)。
蚂蚁基本没有视觉,但能在⼩范围内察觉同类散发的信息素的轨迹,由此来决定何去何从,并倾向于朝着信息素强度⾼的⽅向移动。
⾃催化⾏为——某条路径上⾛过的蚂蚁越多,留下的信息素也越多(随时间蒸发⼀部分),后来蚂蚁选择该路径的概率也越⾼。
2. 算法基本思想:(1)根据具体问题设置多只蚂蚁,分头并⾏搜索。
(2)每只蚂蚁完成⼀次周游后,在⾏进的路上释放信息素,信息素量与解的质量成正⽐。
(3)蚂蚁路径的选择根据信息素强度⼤⼩(初始信息素量设为相等),同时考虑两点之间的距离,采⽤随机的局部搜索策略。
这使得距离较短的边,其上的信息素量较⼤,后来的蚂蚁选择该边的概率也较⼤。
(4)每只蚂蚁只能⾛合法路线(经过每个城市1次且仅1次),为此设置禁忌表来控制。
(5)所有蚂蚁都搜索完⼀次就是迭代⼀次,每迭代⼀次就对所有的边做⼀次信息素更新,原来的蚂蚁死掉,新的蚂蚁进⾏新⼀轮搜索。
(6)更新信息素包括原有信息素的蒸发和经过的路径上信息素的增加。
(7)达到预定的迭代步数,或出现停滞现象(所有蚂蚁都选择同样的路径,解不再变化),则算法结束,以当前最优解作为问题的最优解。
3. 信息素及转移概率的计算:4. 算法步骤算法流程图如下:5. 举例分析我们假设5个城市的TSP问题,然由于某种原因,城市道路均是单⾏道,即A->B和B->A的距离不相同,也就是说这是⼀个不对称的TSP问题。
现在城市距离信息如下表:设置参数:m=5,α=1,β=1,ρ=0.5,τ_ij(0)=2。
蚁群算法概述

蚁群算法概述一、蚁群算法蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来寻找最优解决方案的机率型技术。
它由Marco Dorigo于1992年在他的博士论文中引入,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
蚂蚁在路径上前进时会根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。
其选择一条路径的概率与该路径上分泌物的强度成正比。
因此,由大量蚂蚁组成的群体的集体行为实际上构成一种学习信息的正反馈现象:某一条路径走过的蚂蚁越多,后面的蚂蚁选择该路径的可能性就越大。
蚂蚁的个体间通过这种信息的交流寻求通向食物的最短路径。
蚁群算法就是根据这一特点,通过模仿蚂蚁的行为,从而实现寻优。
这种算法有别于传统编程模式,其优势在于,避免了冗长的编程和筹划,程序本身是基于一定规则的随机运行来寻找最佳配置。
也就是说,当程序最开始找到目标的时候,路径几乎不可能是最优的,甚至可能是包含了无数错误的选择而极度冗长的。
但是,程序可以通过蚂蚁寻找食物的时候的信息素原理,不断地去修正原来的路线,使整个路线越来越短,也就是说,程序执行的时间越长,所获得的路径就越可能接近最优路径。
这看起来很类似与我们所见的由无数例子进行归纳概括形成最佳路径的过程。
实际上好似是程序的一个自我学习的过程。
3、人工蚂蚁和真实蚂蚁的异同ACO是一种基于群体的、用于求解复杂优化问题的通用搜索技术。
与真实蚂蚁通过外激素的留存/跟随行为进行间接通讯相似,ACO中一群简单的人工蚂蚁(主体)通过信息素(一种分布式的数字信息,与真实蚂蚁释放的外激素相对应)进行间接通讯,并利用该信息和与问题相关的启发式信息逐步构造问题的解。
人工蚂蚁具有双重特性:一方面,他们是真实蚂蚁的抽象,具有真实蚂蚁的特性,另一方面,他们还有一些在真实蚂蚁中找不到的特性,这些新的特性,使人工蚂蚁在解决实际优化问题时,具有更好地搜索较好解的能力。
人工蚂蚁与真实蚂蚁的相同点为:1.都是一群相互协作的个体。
蚁群算法(ACO)简要介绍
城市之间距离
目标函数为 其中 w
(d ij ) nn
f ( w) d il 1i, l
l 1 n
(i1 , i2 ,, in )
为城市1,2,…n的一个排列,
in1 i1
算法示例
蚂蚁k(k=1,2,…,m)根据各个城市间连接路径上的信 息素浓度决定其下一个访问城市,设 Pijk (t )表示t时刻蚂蚁k 从城市i转移到城市j的概率,其计算公式为:
is (t )is (t ) , s allowk Pijk (t ) is (t )is (t ) xallowk 0, s allowk
信息更新公式为:
ij (t 1) (1 ) ij (t ) ij n ,0 1 k ij ii k 1
算法原理
算法原理
基于以上蚁群寻找食物时的最优路径选择问题, 可以构造人工蚁群,来解决最优化问题。 人工蚁群中把具有简单功能的工作单元看作蚂蚁。 二者的相似之处在于都是优先选择信息素浓度大的路径。 较短路径的信息素浓度高,所以能够最终被所有蚂蚁选 择,也就是最终的优化结果。 两者的区别在于人工蚁群有一定的记忆能力,能 够记忆已经访问过的节点。同时,人工蚁群再选择下一 条路径的时候是按一定算法规律有意识地寻找最短路径, 而不是盲目的。例如在TSP问题中,可以预先知道当前 城市到下一个目的地的距离。
蚁群算法(ACO)介绍
李杰林
ACO算法起源
20世纪90年代意大利学者M.Dorigo, V.Maniezzo,A.Colorni等从生物进化的机制中 受到启发,通过模拟自然界蚂蚁搜索路径的行为, 提出来一种新型的模拟进化算法——蚁群算法, 是群智能理论研究领域的一种主要算法。用该方 法求解TSP问题、分配问题、job-shop调度问题, 取得了较好的试验结果。虽然研究时间不长,但 是现在的研究显示出,蚁群算法在求解复杂优化 问题(特别是离散优化问题)方面有一定优势, 表明它是一种有发展前景的算法。
昆虫群体行为学中的蚁群算法
昆虫群体行为学中的蚁群算法随着社会的发展和科技的不断进步,人们日常的各种活动都离不开计算机和信息技术的支持,人工智能、机器学习已经成为重要的研究领域。
而昆虫群体行为学中的蚁群算法也成为了这个领域中的热门算法之一。
本文将结合案例深入剖析蚁群算法的工作原理及其应用。
一、蚁群算法概述蚁群算法,又称蚁群优化算法,是一种基于群体智能的优化算法,源于自然界中蚂蚁生活方式的模拟。
自然界中蚂蚁以信息的方式寻找到食物和家,形成了一套完整的优化流程。
在这个过程中,蚂蚁会不断地散发信息素,当有蚂蚁发现了食物或者家后,会回到巢穴,散发出一种信息素,可以引起其他蚂蚁的注意。
一段时间过后,信息素会消失,这样就可以避免信息过时。
蚂蚁就利用这样的方式,在一片茫茫草地中快速找到食物和家。
而蚁群算法就是对这种生物的生命周期进行了模拟。
蚁群算法主要基于以下两大原理:正反馈和负反馈。
正反馈指的是蚂蚁在寻找食物和家的过程中,距离食物和家越近,越有可能被其他蚂蚁选择。
因此,经过一段时间的搜寻,食物或家附近的信息素浓度就会越来越高,吸引越来越多的蚂蚁。
负反馈指的是信息素的挥发时间有限,如果蚂蚁在搜寻过程中进入了死路,无法找到食物或家,很快就会失去它们的踪迹,寻找其它的目标。
二、蚁群算法的原理蚁群算法是一种基于贪心策略和启发式搜索的算法。
贪心策略是指在局部最优解的情况下选择全局最优解。
而启发式搜索则是通过评估函数进行深度优先或广度优先的搜索。
蚁群算法将这两种方法相结合,将其运用到求解优化问题的任务中。
在蚁群算法中,人们把寻优问题抽象成一个图论问题,称之为图。
设有m个蚂蚁在图中寻找最短路径,并假设每个蚂蚁可以移动的来源于强化自身链接的信息素来对图进行搜索,并通过蚁群算法来不断优化搜索的结果。
蚁群算法的核心在于挥发函数(Evaporation Rate)和信息素覆盖(Pheromone Coverage),通过这两个函数控制信息素在搜索过程中的流动和新建,在搜索过程中提高发现最优解的概率。
智能算法之蚁群算法_PPT幻灯片
人工蚁群中把具有简单功能的工作单元看作蚂蚁。二者的 相似之处在于都是优先选择信息素浓度大的路径。较短路径的 信息素浓度高,所以能够最终被所有蚂蚁选择,也就是最终的 优化结果。
两者的区别在于人工蚁群有一定的记忆能力,能够记忆已 经访问过的节点。同时,人工蚁群再选择下一条路径的时候是 按一定算法规律有意识地寻找最短路径,而不是盲目的。例如 在TSP问题中,可以预先知道当前城市到下一个目的地的距离。
13
蚁群算法的计算流程
开始
[ij(t)][ij]
k p (t) ij
jal l o w [iej(dt)][i j]
0
ifjallowed 初始化 otherwise Nc Nc +1
轨迹更新: i( jt n )i( jt) i( jt,t n )
Visi问题
TSP问题的人工蚁群算法中,假设m只蚂蚁 在图的相邻节点间移动,从而协作异步地得到 问题的解。每只蚂蚁的一步转移概率由图中的 每条边上的两类参数决定:1.信息素值,也称 信息素痕迹。2.可见度,即先验值。
信息素的更新方式有2种,一是挥发,也 就是所有路径上的信息素以一定的比率进行减 少,模拟自然蚁群的信息素随时间挥发的过程; 二是增强,给评价值“好”(有蚂蚁走过)的边 增加信息素。
10
蚁群算法与TSP问题
TSP问题表示为一个N个城市的有向图G=(N,A),
其中 N {1n ,A 2 } { ,,j( .|i ) .,ij. N ,}
城市之间距离 目标函数为
(d ij ) nn
n
f (w) d , il1il l1
其中 w (i1,i2, ,in为)城市1,2,…n的一个排列, in1 。i1
浅谈蚁群算法
一、引言蚁群算法(Ant Colony Optimization, ACO),是一种用来在图中寻找优化路径的算法。
它由Marco Dorigo于1992年在他的博士论文中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质。
蚁群算法成功解决了旅行商问题(Traveling Salesman Problem, TSP):一个商人要到若干城市推销物品,从一个城市出发要到达其他各城市一次而且最多一次最后又回到第一个城市。
寻找一条最短路径,使他从起点的城市到达所有城市一遍,最后回到起点的总路程最短。
若把每个城市看成是图上的节点,那么旅行商问题就是在N个节点的完全图上寻找一条花费最少的回路。
最基本的蚁群算法见第二节。
目前典型的蚁群算法有随机蚁群算法、排序蚁群算法和最大最小蚁群算法,其中后两种蚁群算法是对前一种的优化。
本文将终点介绍随机蚁群算法。
二、基本蚁群算法(一)算法思想各个蚂蚁在没有事先告诉他们食物在什么地方的前提下开始寻找食物。
当一只找到食物以后,它会向环境释放一种信息素,信息素多的地方显然经过这里的蚂蚁会多,因而会有更多的蚂蚁聚集过来。
假设有两条路从窝通向食物,开始的时候,走这两条路的蚂蚁数量同样多(或者较长的路上蚂蚁多,这也无关紧要)。
当蚂蚁沿着一条路到达终点以后会马上返回来,这样,短的路蚂蚁来回一次的时间就短,这也意味着重复的频率就快,因而在单位时间里走过的蚂蚁数目就多,洒下的信息素自然也会多,自然会有更多的蚂蚁被吸引过来,从而洒下更多的信息素。
因此,越来越多地蚂蚁聚集到较短的路径上来,最短的路径就找到了。
蚁群算法的基本思想如下图表示:图1 等概率选择图2 最优路径图3 最优比重(二)算法描述基本蚁群算法的算法简单描述如下:1.所有蚂蚁遇到障碍物时按照等概率选择路径,并留下信息素;2.随着时间的推移,较短路径的信息素浓度升高;3.蚂蚁再次遇到障碍物时,会选择信息素浓度高的路径;4.较短路径的信息素浓度继续升高,最终最优路径被选择出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.5 蚁群优化算法应用现状 3/5
基于群智能的聚类算法起源于对蚁群蚁卵的分类研究。 Lumer和Faieta将Deneubourg提出将蚁巢分类模型应 用于数据聚类分析。其基本思想是将待聚类数据随机 地散布到一个二维平面内,然后将虚拟蚂蚁分布到这 个空间内,并以随机方式移动,当一只蚂蚁遇到一个 待聚类数据时即将之拾起并继续随机运动,若运动路 径附近的数据与背负的数据相似性高于设置的标准则 将其放置在该位置,然后继续移动,重复上述数据搬 运过程。按照这样的方法可实现对相似数据的聚类。
17
1.1.5 蚁群优化算法应用现状 2/5
蚁群算法在电信路由优化中已取得了一定的应用成果。HP公 司和英国电信公司在90年代中后期都开展了这方面的研究, 设计了蚁群路由算法(Ant Colony Routing, ACR)。 每只蚂蚁就像蚁群优化算法中一样,根据它在网络上的经验 与性能,动态更新路由表项。如果一只蚂蚁因为经过了网络 中堵塞的路由而导致了比较大的延迟,那么就对该表项做较 大的增强。同时根据信息素挥发机制实现系统的信息更新, 从而抛弃过期的路由信息。这样,在当前最优路由出现拥堵 现象时,ACR算法就能迅速的搜寻另一条可替代的最优路径, 从而提高网络的均衡性、负荷量和利用率。目前这方面的应 用研究仍在升温,因为通信网络的分布式信息结构、非稳定 随机动态特性以及网络状态的异步演化与ACO的算法本质和 特性非常相似。
19
1.1.5 蚁群优化算法应用现状 4/5
ACO还在许多经典组合优化问题中获得了成功的应用, 如二次规划问题(QAP)、机器人路径规划、作业流 程规划、图着色(Graph Coloring)等问题。 经过多年的发展,ACO已成为能够有效解决实际二次 规划问题的几种重要算法之一。AS在作业流程计划 (Job-shop Scheduling)问题中的应用实例已经出现, 这说明了AS在此领域的应用潜力。利用MAX-MIN AS解 决PAQ也取得了比较理想的效果,并通过实验中的计 算数据证明采用该方法处理PAQ比较早的SA算法更好, 且与禁忌搜索算法性能相当。利用ACO实现对生产流 程和特料管理的综合优化,并通过与遗传、模拟退火 和禁忌搜索算法的比较证明了ACO的工程应用价值。
21
1.2 蚁群优化算法概念
1.2.1 蚁群算法原理 1.2.2 简化的蚂蚁寻食过程 1.2.3 自然蚁群与人工蚁群算法 1.2.4 蚁群算法与TSP问题 1.2.5 初始的蚁群优化算法—基于图的
蚁群系统(GBAS) 1.2.6 一般蚁群算法的框架
22
1.2.1 蚁群算法原理
蚁群算法是对自然界蚂蚁的寻径方式进行模似而得出的一种仿 生算法。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称 之为外激素(pheromone)的物质进行信息传递,而且蚂蚁在运动过 程中能够感知这种物质,并以此指导自己的运动方向,因此由大量 蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象:某一路径 上走过的蚂蚁越多,则后来者选择该路径的概率就越大。
为了说明蚁群算法的原理,先简要介绍一下蚂蚁搜寻食物的具 体过程。在蚁群寻找食物时,它们总能找到一条从食物到巢穴之间 的最优路径。这是因为蚂蚁在寻找路径时会在路径上释放出一种特 殊的信息素。当它们碰到一个还没有走过的路口时.就随机地挑选 一条路径前行。与此同时释放出与路径长度有关的信息素。路径越 长,释放的激索浓度越低.当后来的蚂蚁再次碰到这个路口的时 候.选择激素浓度较高路径概率就会相对较大。这样形成一个正反 馈。最优路径上的激索浓度越来越大.而其它的路径上激素浓度却 会随着时间的流逝而消减。最终整个蚁群会找出最优路径。
23
1.2.2 简化的蚂蚁寻食过程 1/3
蚂蚁从A点出发,速度相同,食物在D点,可能随机选择路线ABD 或ACD。假设初始时每条分配路线一只蚂蚁,每个时间单位行走 一步,本图为经过9个时间单位时的情形:走ABD的蚂蚁到达终点, 而走ACD的蚂蚁刚好走到C点,为一半路程。
9
1.1.4 蚁群优化算法研究现状 1/7
90年代Dorigo最早提出了蚁群优化算法---蚂蚁系统 (Ant System, AS)并将其应用于解决计算机算法学 中经典的旅行商问题(TSP)。从蚂蚁系统开始,基本 的蚁群算法得到了不断的发展和完善,并在TSP以及许 多实际优化问题求解中进一步得到了验证。这些AS改 进版本的一个共同点就是增强了蚂蚁搜索过程中对最 优解的探索能力,它们之间的差异仅在于搜索控制策 略方面。而且,取得了最佳结果的ACO是通过引入局 部搜索算法实现的,这实际上是一些结合了标准局域 搜索算法的混合型概率搜索算法,有利于提高蚁群各 级系统在优化问题中的求解质量。
蚁群算法及其应用
1. 蚂蚁觅食行为 与觅食策略
2. 蚂蚁系统—— 蚁群系统的原 型
3. 改进的蚁群优 化算法
4. 蚁群优化算法的仿 真研究
5. 蚁群算法的应用— —对QoS组播路由 问题求解
1
2
3
1.1 蚁群优化算法概述
1.1.1 起源 1.1.2 应用领域 1.1.3 研究背景 1.1.4 研究现状 1.1.5 应用现状
12
1.1.4蚁群优化算法研究现状 4/7
再次,还引入了负反馈机制,每当一只蚂蚁由一 个节点移动到另一个节点时,该路径上的信息素 都按照如下公式被相应的消除一部分,从而实现 一种信息素的局部调整,以减小已选择过的路径 再次被选择的概率。
13
1.1.4蚁群优化算法研究现状 5/7
在对AS进行直接完善的方法中,MAX-MIN Ant System 是一个典型代表。该算法修改了AS的信息素更新方式, 每次迭代之后只有一只蚂蚁能够进行信息素的更新以 获取更好的解。为了避免搜索停滞,路径上的信息素 浓度被限制在[MAX,MIN ]范围内,另外,信息素的 初始值被设为其取值上限,这样有助于增加算法初始 阶段的搜索能力。
8
1.1.3 蚁群优化算法研究背景 3/3
群智能方法易于实现,算法中仅涉及各种基本的数学 操作,其数据处理过程对CPU和内存的要求也不高。而 且,这种方法只需目标函数的输出值,而无需其梯度 信息。已完成的群智能理论和应用方法研究证明群智 能方法是一种能够有效解决大多数全局优化问题的新 方法。更为重要是,群智能潜在的并行性和分布式特 点为处理大量的以数据库形式存在的数据提供了技术 保证。无论是从理论研究还是应用研究的角度分析, 群智能理论及其应用研究都是具有重要学术意义和现 实价值的。
20
1.1.5 蚁群优化算法应用现状 5/5
许多研究者将ACO用于了武器攻击目标分配和 优化问题、车辆运行路径规划、区域性无线电 频率自动分配、Bayesian networks的训练和集 合覆盖等应用优化问题。Costa和Herz还提出 了一种AS在规划问题方面的扩展应用——图着 色问题,并取得了可与其他启发式算法相比的 效果。
6
2.1.3 蚁群优化算法研究背景 1/3
群智能理论研究领域有两种主要的算法:蚁 群算法(Ant Colony Optimization, ACO)和微粒 群算法(Particle Swarm Optimization, PSO)。 前者是对蚂蚁群落食物采集过程的模拟,已成 功应用于许多离散优化问题。微粒群算法也是 起源于对简单社会系统的模拟,最初是模拟鸟 群觅食的过程,但后来发现它是一种很好的优 化工具。
因此,其后的ACO研究工作主要都集中于AS性能的改进方面。较早 的一种改进方法是精英策略(Elitist Strategy),其思想是在算法开始后即 对所有已发现的最好路径给予额外的增强,并将随后与之对应的行程记
为Tgb(全局最优行程),当进行信息素ห้องสมุดไป่ตู้新时,对这些行程予以加权,
同时将经过这些行程的蚂蚁记为“精英”,从而增大较好行程的选择机 会。这种改进型算法能够以更快的速度获得更好的解。但是若选择的精
16
1.1.5 蚁群优化算法应用现状 1/5
随着群智能理论和应用算法研究的不断发展,研究者 已尝试着将其用于各种工程优化问题,并取得了意想不到 的收获。多种研究表明,群智能在离散求解空间和连续求 解空间中均表现出良好的搜索效果,并在组合优化问题中 表现突出。
蚁群优化算法并不是旅行商问题的最佳解决方法,但 是它却为解决组合优化问题提供了新思路,并很快被应用 到其它组合优化问题中。比较典型的应用研究包括:网络 路由优化、数据挖掘以及一些经典的组合优化问题。
14
1.1.4蚁群优化算法研究现状 6/7
另一种对AS改进的算法是Rank-based Version AS。与 “精英策略”相似,在此算法中总是更新更好进程上的 信息素,选择的标准是其行程长度 决定的排序,且每个蚂蚁放置信息素的强度通过下式中 的排序加权处理确定,其中,w为每次迭代后放置信息 素的蚂蚁总数。
10
1.1.4蚁群优化算法研究现状
2/7
最初提出的AS有三种版本:Ant-density、Ant-quantity和Ant-cycle。 在Ant-density和Ant-quantity中蚂蚁在两个位置节点间每移动一次后即 更新信息素,而在Ant-cycle中当所有的蚂蚁都完成了自己的行程后才对 信息素进行更新,而且每个蚂蚁所释放的信息素被表达为反映相应行程 质量的函数。通过与其它各种通用的启发式算法相比,在不大于75城市 的TSP中,这三种基本算法的求解能力还是比较理想的,但是当问题规 模扩展时,AS的解题能力大幅度下降。
5
1.1.2 蚁群优化算法应用领域
这种方法能够被用于解决大多数优化问题或 者能够转化为优化求解的问题。现在其应用领 域已扩展到多目标优化、数据分类、数据聚类、 模式识别、电信QoS管理、生物系统建模、流程 规划、信号处理、机器人控制、决策支持以及 仿真和系统辩识等方面,群智能理论和方法为 解决这类应用问题提供了新的途径。
15
1.1.4蚁群优化算法研究现状 7/7
这种算法求解TSP的能力与AS、精英策略AS、 遗传算法和模拟退火算法进行了比较。在大型 TSP问题中(最多包含132座城市),基于AS 的算法都显示出了优于GA和SA的特性。而且 在Rank-based AS和精英策略AS均优于基本AS 的同时,前者还获得了比精英策略AS更好的解。
