灰色预测GM(1--1)模型实现过程教案资料
灰色系统G(1,1)预测步骤【模板带代码】

=3499.075e -0.1062t
3641.075
编写程序
u=alpha(2)/alpha(1) v=X0(1)-u v=3499.075 u=—3641.075
(5)进行参差检验
1)根据预测公式,计算
v=3499.075 u=—3641.075
Xˆ
1
k
1
X
0
1
for n=0:10
X2(n+1)=v*exp(-alpha(1)*n)+u
end
X2
2.0690
2)累减生成序列
Xˆ X3 =1.0e+003 * (0) 0.1420 0.4079 0.4536
0.5044
0.7713 0.8577 0.9537 1.0605
源程序:X3(1)=X2(1)
for m=1:10
kesi =
4.4388 339.0664 176.2445 203.6132
0 0.1998 1.2682 0.2130 0.8524 0.1330
0.0089
0.3767
0.2203
0.4155
{0%,19.98%,126.82%,0.89%,37.67% ,22.03% ,41.55% ,21.30%,85.24%,13.30%}
e=
179.4592 111.5134 74.1747 175.0204 159.6072 29.2461 215.2168 33.1910
3.2147 24.1540
源程序:S0=0.6745*X0std e=abs(daita0-daita0mean) 对所有的 e 都小于 S0 ,故小参差概率 P(k S0) 1 0.95
Matlab+灰色预测模型模型GM(1,1)
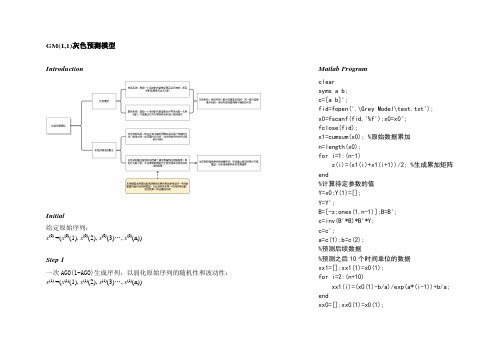
GM(1,1)灰色预测模型IntroductionInitial给定原始序列:x(0) =(x(0)(1), x(0)(2), x(0)(3)…, x(0)(n))Step 1一次AGO(1-AGO)生成序列,以弱化原始序列的随机性和波动性:x(1) =(x(1)(1), x(1)(2), x(1)(3)…, x(1)(n)) Matlab Programclearsyms a b;c=[a b]';fid=fopen('.\Grey Model\test.txt');x0=fscanf(fid,'%f');x0=x0';fclose(fid);x1=cumsum(x0); %原始数据累加n=length(x0);for i=1:(n-1)z(i)=(x1(i)+x1(i+1))/2; %生成累加矩阵end%计算待定参数的值Y=x0;Y(1)=[];Y=Y';B=[-z;ones(1,n-1)];B=B';c=inv(B'*B)*B'*Y;c=c';a=c(1);b=c(2);%预测后续数据%预测之后10个时间单位的数据xx1=[];xx1(1)=x0(1);for i=2:(n+10)xx1(i)=(x0(1)-b/a)/exp(a*(i-1))+b/a; endxx0=[];xx0(1)=x0(1);Step 2(1) dx (1)dt+ax (1)(t )=u ,式中a, u 为待定系数。
灰微分方程模型为:x (0)(k )+az (1)(k )=u ,z 为背景值z (1)(k )=1/2(x (1)(k )+x (1)(k −1))(2) 构造矩阵B 和数据向量Y nY n =Ba ̂Y n =[ x (0)(2)x (0)(3)⋮x (0)(n )] , B =[ −1/2(x (1)(1)+x (1)(2)),−1/2(x (1)(2)+x (1)(3)),⋮−1/2(x (1)(n −1)+x (1)(n )), 1 1 ⋮ 1]a ̂=(au)=(B T B)−1B T Y nStep 3模型响应函数x ̂(1)(k +1)=(x (0)(1)−u a )e −ak +u ax ̂(0)(k +1)=x ̂(1)(k +1)−x ̂(1)(k )Step 4检验和判断GM(1,1)模型的精度 (1) 残差检验for i=2:(n+10)xx0(i)=xx1(i)-xx1(i-1); end%关联度检验 for i=1:ne(i)=abs(x0(i)-xx0(i)); endmmax=max(e); for i=1:nee(i)=0.5*mmax/(e(i)+0.5*mmax); endr=sum(ee)/n; %后验差检验x0bar=sum(x0)/n; s1=0; for i=1:ns1=s1+(x0(i)-x0bar)^2; ends1=sqrt(s1/n); s2=0;ebar=sum(e)/n; for i=1:ns2=s2+(e(i)-ebar)^2; ends2=sqrt(s2/n); C=s2/s1; p=0;for i=1:nif abs(e(i)-ebar)<0.6745*s1绝对误差:ε(k)=|x(0)(k)−x̂(0)(k)|相对误差:Φ(k)=ε(k)x(0)(k)(2) 关联度检验分辨率β一般取0.5,此时若关联度大于0.6则认为模型可接受(3) 后验差检验和小误差概率原始序列标准差:S1=√∑[x(0)(i)−x̅(0)]2n绝对误差序列标准差:S2=√∑[ε(i)−ε̅]2n计算方差比:C=S2S1小误差概率:P=P{|ε(i)−ε̅|<0.6745S1}p=p+1;endendp=p/n;Cpif p>0.95&C<0.35disp('预测精度好');else if p>0.8&C<0.5disp('预测合格');else if p>0.7&C<0.65disp('预测勉强合格'); elsedisp('预测不合格'); endendend%原始数据与预测数据进行比较t1=1:n;t2=1:(n+10);xx0plot(t1,x0,'o',t2,xx0)。
GM(1_1)模型,灰色预测

小额贷款远程智能预警系统 人数预测算法的设计一、灰色系统的引入:灰色系统是指“部分信息已知,部分信息未知”的“小样本”,“贫信息”的不确定性系统,它通过对“部分”已知信息的生成、开发去了解、认识现实世界,实现对系统运行行为和演化规律的正确把握和描述. 灰色系统模型的特点:对试验观测数据及其分布没有特殊的要求和限制,是一种十分简便的新理论,具有十分宽广的应用领域。
目前,灰色系统已经成为社会、经济、科教、技术等很多领域进行预测、决策、评估、规划、控制、系统分析和建模的重要方法之一。
特别是它对时间序列短、统计数据少、信息不完全系统的建模与分析,具有独特的功效。
灰色模型的优点(一) 不需要大量的样本。
(二) 样本不需要有规律性分布。
(三) 计算工作量小。
(四) 定量分析结果与定性分析结果不会不一致。
(五) 可用于近期、短期,和中长期预测。
(六) 灰色预测精准度高。
二、GM (1,1)模型(grey model 一阶一个变量的灰微分方程模型)灰色理论认为系统的行为现象尽管是朦胧的,数据是复杂的,但它毕竟是有序的,是有整体功能的。
灰数的生成,就是从杂乱中寻找出规律。
同时,灰色理论建立的是生成数据模型,不是原始数据模型。
因此,灰色预测的数据是通过生成数据的GM(1,1)模型所得到的预测值的逆处理结果。
GM (1,1)的具体模型计算式设非负原始序列()()(){}n x x x X )0()0()0()0(,...,2,1=对)0(X作一次累加()()∑==ki i x k x1)0()1( ;k=1,2,…,n得到生成数列为()()(){}n x x x X )1()1()1()1(,...,2,1=于是()k x)0(的GM (1,1)白化微分方程为u ax dtdx =+)1()1( (1—1)其中a,u 为待定参数,将上式离散化,即得()()()()u k x az k x =+++∆11)1()1()1((1—2)其中()()1)1()1(+∆k x 为)1(x在(k+1)时刻的累减生成序列,()()()[]()[])1()()1(11)0()1()1()()0()1()0()1()1(+=-+=∆-+∆=+∆k x k x k x k x k x k x r(1—3)()()1)1(+k x z 为在(k+1)时刻的背景值(即该时刻对应的x 的取值)()()()()()k x k x k x z )1()1()1(1211++=+ (1—4)将(1—3)和(1—4)带入(1—2)得()()()()u k x k x a k x +++-=+]121[1)1()1()0( (1—5)将(1—5)式展开得()()()()()()()()()()()()⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+--+-+-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡u a n x n x x x x x n x x x 1:11121:32212121:32)1()1()1()1()1()1()0()0()0( (1—6)令()()()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=n x x x Y )0()0()0(:32,()()()()()()()()()⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+--+-+-=1:11121:32212121)1()1()1()1()1()1(n x n x x x x x B ,[]Tu a =Φ 为待辨识参数向量,则(1—6)可以写成Φ=B Y (1—7)参数向量Φ可用最小二乘法求取,即[]()Y B B B u a T T T 1ˆ,ˆˆ-==Φ(1—8)把求取的参数带入(2—16)式,并求出其离散解为()()a u e a u x k xk a ˆˆˆˆ11ˆ)1()1(+⎥⎦⎤⎢⎣⎡-=+- (1—9)还原到原始数据得()()()()()ka a e a u x e k x k x k x ˆ)1(ˆ)1()1()0(ˆˆ11ˆ1ˆ1ˆ-⎥⎦⎤⎢⎣⎡--=-+=+ (1—10)(1—9)、(1—10)式称为GM (1,1)模型的时间相应函数模型,它是GM (1,1)模型灰色预测的具体计算公式。
高级计算器灰色预测GM(1.1)模型-的计算程序

高级计算器灰色预测GM(1.1 )模型的计算程序毕 永(陕西省子长县疾病预防控制中心 子长 717399)CASIO ƒχ—3800P 计算器,置有4组最大容量135步程序存储器,体积小,价格低,功能多,是基层工作者一种理想的计算工具。
灰色预测GM(1.1 )模型公式冗长,计算过程繁琐复杂,编程运算化繁为简,变难为易,大大提高了工作效率。
在Ⅰ区程序输入x ( t ) 生成u ∧值和a∧值,在Ⅱ区程序输入t 即可得 y ∧( t ) 值。
现介绍操作方法如下:1 公式1.1 ()()1t i y t x t -=∑ 1.2 ()()()11122z t y t y t =+- 1.3 ()()()dy t ay t u d t == 1.4 ()()()1[1]1uu y t x e a t a a +=---+1.5 ()()()()()221/N N N t z t t a N x t z t z t x t D ∧===⎧⎫⎡⎤⎡⎤⎡⎤=--+⎨⎬⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎩⎭∑∑∑1.6 ()()()()()22222/N N Z N t t t t u z t x t z t Z t x t D ∧====⎧⎫⎡⎤⎡⎤⎡⎤⎡⎤=-+⎨⎬⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎩⎭∑∑∑∑1.7 ()()()22221N N t t D N z t z t ==⎡⎤⎡⎤=--⎢⎥⎢⎥⎣⎦⎣⎦∑∑ 2 写入程序2.1 准备MODE EXP (LRN 状态)SHIFT PCL (程序存储器清零)MODE ·(RUN状态)SHIFT KAC (K寄存器清零)令:2 Kin 4 Kin 3 Kin2 SHIFT Min(输入数值给需要使用的寄存器) MODE EXP (LRN状态)2.2 程序Ⅰ(进入程序Ⅰ区)Kin + 3 Kin 6 ÷ 2 + Kout 3 –Kout 6 = Kin + 5 Kin×6 χ2Kin + 2 Kout 6 Kin + 1 1 Kin + 4 Kout 4 SHIFT HLT (显示3)MR Kin-3 Kout 3 SHIFT X←→K 2 Kin×2 SHIFT X←→K 4 Kin×4 SHIFT X←→K 1 Kin×1 SHIFTX←→K 5 Kin×5 Kin×3 χ2Kin-4 Kout 5 Kin-2 Kout 1 Kin-1 Kin-3 Kout 4 Kin÷2 Kin÷3 Kout 3 Kin÷2 Kout 2 SHIFT M-(显示-0.333333333)Ⅱ(进入程序Ⅱ区)- 1 =×Kout 3 =+/- SHIFT e x ×MR + Kout 2 =SHIFT HLT -SHIFT X←→K 1 =(62步显示0.864639944)2.3 退出与运算MODE ·3 运算实例表1:1973~1980年启东县人口恶性肿瘤死亡率(/10万)[1]t 年份死亡率x ( t ) y∧( t ) x∧( t )1 1973 108.462 1974 125.87 240.143 1975 144.08 372.674 1976 127.45 506.045 1977 132.84 640.276 1978 135.55 775.367 1979 139.87 911.328 1980 134.03 1048.149 1981 136.97 1185.84 137.7110 1982 138.14 1324.43 138.5911 1983 142.42 1463.92 139.4812 1984 152.36 1604.29 140.37 3.1 使用Ⅰ区程序生成数据操作:显示:说明:MODE ·RUN状态SHIFT KAC K寄存器清零令:108.46 Kin 3 SHIFT Min 输入变量125.87Ⅰ 1144.08Ⅰ 2::::::134.03 Ⅰ 7RUN - 20427.27008 u∧ / a∧Kout 3 - 0.0063918026 a∧Kout 4 3551879.152 D3.2 使用Ⅱ区程序求出y∧( t ) 值操作:显示:说明:MODE 7 2 设定小数令:2 Ⅱ240.14 y∧(2)3Ⅱ372.67 y∧(3)4Ⅱ506.04 y∧(4)5Ⅱ640.27 y∧(5)6Ⅱ775.36 y∧(6)7Ⅱ911.32 y∧(7)8 Ⅱ1048.15 y∧(8)3.3 模型外推预测时求出y∧( t ) 、x∧( t ) 值操作:显示:说明:令:8 Ⅱ1048.15 y∧(8)RUN 1048.15 存入K1寄存器9 Ⅱ1185.85 y∧(9)RUN 137.71 x∧(9)10 Ⅱ1324.44 y∧(10)RUN 138.59 x∧(10)11 Ⅱ1463.92 y∧(11)RUN 139.48 x∧(11)12 Ⅱ1604.29 y∧(12)RUN 140.37 x∧(12)参考文献[1] 汪爱勤,鱼敏,灰色预测方法在疾病预测中的应用[J],中华流行病学杂志,1988,9(1):49 ̴52[2] 李光,疾病的灰色预测模型(GM)及其电子计算器程序[J],湖北预防医学杂志,1991,2(4):53 ̴55[3] 韩波,林华荣,孙瑞林,用计算器灰色预测环境污染[J],环境监测管理与技术,1994,6(1):44 ̴46。
建立灰色系统GM(1,1)1-AGO模型的步骤

一、建立灰色系统GM (1,1)(即:1-AGO )模型的步骤第一步:累加生成对原始数列中各同类数据依次累加,形成新的序列。
一次累加生成序列为)()}即:(1)(0)(1)(1)x x =,(1)(0)(0)(2)(1)(2)x x x =+,(1)(0)(0)(0)(3)(1)(2)(3)x x x x =++,...第二步:一次拟合参数求解如下G(1,1)模型即微分方程:(1)(1)()()dx t ax t u dt+= (1) 其中:T T T a u B B B Y 1[,]()-=,且()]解方程(1),可得响应函数为:(1)(0)ˆ(1)[(1)]ak u u xk x e a a-+=-+ 第三步:确定预测值预测函数为:(0)(1)(1)(0)ˆˆˆ(1)(1)()(1)[(1)]aa ku xk x k x k ex e a-+=+-=--第四步:精度检验精度检验的方法有三种:相对误差检验法、后验差检验法、关联度检验法1、 相对误差检验法:(仔细辨明(0)(0)ˆ(),()xk x k ) 相对误差为:(0)(0)(0)ˆ()()100%()-⨯x k xk x k 相对误差越小越好。
2、 后验差检验法:计算残差(0)(0)ˆ-X X的方差 2(0)(0)211111[()()]===-∑∑n n k k S x k x k n n2(0)(0)(0)(0)221111ˆˆ()()[()()]==⎡⎤=---⎢⎥⎣⎦∑∑n n k k S x k xk x k x k n n 计算后验差之比: 21/=C S S 计算小概率误差:(0)(0)(0)(0)2111ˆˆ()()[()()]0.6745=⎧⎫=---<⎨⎬⎩⎭∑n k p P x k xk x k x k S n,C p C 指标和是后验差检验的两个重要指标.指标越小越好121.C S S S 越小表示大而越小大表示原始数据方差大,即原始数据离散程度大. 2S C 小表示残方差小,即残差离散程度小.小就表明尽管原始数据很离散,而模型所得计算值与实际值之差并不太离散.1,,0.6745,,,.p p C p 指标越大越好越大表明残差与残差平均值之差小于给定值的点较多即拟合值(或预测值)分布比较均匀.按两个指标可综合评定预测模型的精度模型的精度由后验差和小误差概率共同刻划.一般地,将模型的精度分为四级,见下表精度检验等级参照表{},,=Max p C 模型的精度级别的级别于是的级别如果模型很差,可以考虑进行关联度检验,以便选出更好的模型。
灰色预测GM模型实现过程

灰色预测GM模型实现过程灰色预测GM(1,1)模型是一种基于灰色系统理论的预测模型,广泛应用于各个领域的预测和决策中。
该模型通过对原始序列进行累加、一次指数平滑运算,从而建立灰色微分方程,并利用该方程进行预测。
下面将详细介绍GM(1,1)模型的实现过程。
GM(1,1)模型的基本思想是将原始数据序列进行累加,然后进行一次指数平滑运算,得到一次累加生成序列的差分方程,建立灰色微分方程。
具体实现过程如下:1.数据序列的累加:将原始数据序列进行累加,得到累加序列。
累加操作可以使数据序列趋于线性。
2.累加序列的一次指数平滑:对累加序列进行一次指数平滑运算,得到平滑累加序列。
一次指数平滑可以使得序列的趋势更加明显。
3.灰色微分方程的建立:根据平滑累加序列可以建立灰色微分方程。
假设平滑累加序列为X(0),X(1),...,X(n),则灰色微分方程可以表示为:X(n)+a*X(1)=b其中,a为发展系数,b为灰色作用量。
4.参数估计:通过最小二乘法求解灰色微分方程中的参数a和b。
具体方法是:将方程改为矩阵形式,即[A][X]=[B],其中A为系数矩阵,X为参数向量,B为常数向量。
通过对矩阵A和B进行求逆运算,可以得到参数向量X,进而求得a和b的值。
5.模型检验:通过残差检验、相关系数检验、后验差检验等方法对模型的准确性进行检验。
如果模型通过检验,则认为预测结果可靠;否则,需要进行修正或重新建模。
6.模型预测:利用建立的灰色微分方程进行未来数值的预测。
根据已有的序列,可以求得发展系数a和灰色作用量b的值,从而可以插入到灰色微分方程中,得到未来数值的预测。
总结:GM(1,1)模型是一种简单且有效的预测模型,适用于非线性和不稳定的数据序列。
它基于灰色系统理论,通过累加和一次指数平滑运算建立灰色微分方程,利用最小二乘法估计参数,并进行模型检验和预测。
在实际应用中,可以根据具体情况调整模型中的参数和方法,以提高预测的精度和可靠性。
灰色预测模型GM(1_1)及其应用
灰色预测模型GM(1,1)的应用一、问题背景:蠕变是材料在高温下的一个重要性能。
处于高温状态下的材料长期受到载荷作用时,即使其载荷较低,并且在短时间的高温拉伸试验中材料不发生变形,但在此情况下仍会有微小的蠕变,极端的情况下,甚至会使材料发生破坏。
高温材料多应用于各种车辆的发动机及冶金厂中各种设备上,如果因蠕变引起破坏,可能造成很大的事故。
为了保证设备的安全可靠,在某一使用温度下,预先知道该材料对不同载荷应力下断裂的时间是很重要的。
过去,人们都是通过蠕变试验测量断裂时间。
而做蠕变试验时,需要很长时间才能得到结果,即使通过试验得出的数据,也只是对某几个具体试样而言,存在很大的偶然性,不能代表普遍的规律。
如果将实测的数据用灰色系统理论来处理,可以预测在某一温度下的任何载荷应力的断裂时间。
二、低合金钢铸件蠕变性能的灰色预测下面是对Cr-mo-0.25V 低合金钢铸件高温蠕变情况利用灰色系统理论进行研究。
在500℃的高温下,已测得此铸件在载荷分别为37,36,35,34,33(kg/mm 2)情况下的蠕变断裂时间见下表。
数 列 序 数 K1 2 3 4 5载荷应力(kg/mm 2) 37 36 35 34 33 断裂时间()(100)0(K X ⨯小时)2.38 2.80 4.25 6.85 11.30 一次累加数列)()1(K X 2.38 5.18 9.43 16.28 27.581、建立GM (1,1)模型(1)数据处理:将同一数据列的前k 项元素累加后生成新数据列的第k 项元素。
即根据断裂时间数列)()0(k X 由∑==kn n X k X 1)0()1()()(得到 )()1(k X 。
(2)建立矩阵B,y:根据⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+--+-+-=1)]()1([5.01)]3()2([5.01)]2()1([5.0)1()1()1()1()1()1(N X N X X X X X B 得到 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=19.2118.12130.7178.3B根据 T N N X X X Y )](,),3(),2([)0()0()0( =,得到 T N Y ]3.11,85.6,25.4,80.2[=(3)求出逆矩阵1()T BB - (4)作最小二乘估计,求参数u a ,N T T Y B B B u a 1)(ˆ-=⎪⎪⎭⎫⎝⎛=α 可得,⎪⎪⎭⎫ ⎝⎛-=97.05.0ˆα a = -0.5, u=0.97(5)建立时间响应函数,计算拟合值把a 和u 分别代入au e a u X t X at +-=+-))1(()1(ˆ)0()1(可得到解为2.24.4)1(ˆ5.0)1(-=+t e t X, 取t 为应力序数k 时,即得到时间响应方程为:2.24.4)1(ˆ5.0)1(-=+k e k X即可得到生成累加数列),2,1()1(ˆ)1( =+k k X 。
灰色预测GM(1,1)
南昌市民用汽车保有量灰色GM(1,1)模型预测灰色预测是一种对含有不确定因素的系统进行预测的方法。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
灰色模型适合于小样本情况的预测,当然对于大样本数据,灰色模型也可以做,并且数据个数的选择有很大的灵活性。
原始序列X (0):表1 南昌市民用汽车保有量年份 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 南昌市民用汽车保有量(万辆)24.410926.730730.387836.380741.016143.7348.41615763.1第一步:构造累加生成序列X (1); 第二步:计算系数值;通过灰色关联分析软件GM 进行灰色模型拟合求解,得到:α= -0.101624 , μ=25.290111 , 平均相对误差为4.685749%第三步:得出时间响应预测函数模型为:()()858996.248269896.2731101624.01-=+⋅k e k X第四步:进行灰色关联度检验。
真实值:{24.4109,26.7307,30.3878,36.3807,41.0161,43.7300,48.4100,61.0000,57.0000,63.1000} 预测值:{24.4109,29.2310,32.3578,35.8190,39.6504,43.8917,48.5867,53.7839,59.5371,65.9056}计算得到关联系数为: {1,0.906683,0.444273,0.416579,0.82377,0.357133,0.715694,0.843178,0.333333,0.770986} 于是灰色关联度:r=0.661163关联度r=0.661163满足分辨率ρ=0.5时的检验准则r>0.60,关联性检验通过。
灰色系统预测GM(1,m)
灰色GM (1,1)模型及其原理1灰色GM (1,1)模型的构建GM (1,1)模型是将离散的随机数经过依次累加成算子,削弱其随机性,得到较有规律的生成数,然后建立微分方程、解方程进而建立模型。
设所要预测的某项指标的原始数据序列为:()()()()()()()()(){}n X X X X X 00000,,3,2,1 =对原始数据序列作一次累加生成处理,获得新的数据序列: ()()()()()()(){}n X X X X1111,,2,1 = 式中:()()()()∑==i k k X i X 101 n i 3,2,1=经过累加处理,新生成的数据序列与原始的数据序列相比,具有平稳性增强而波动性减弱的特点。
对生成数列建立GM (1,1)白化形式的微式方程[4]:()()()u aX dt t dX =+11式中:a 称为发展系数,u 称为内控发展灰数。
利用最小二乘法拟合求得估计参数:()n TT X B BB u a 1-=⎥⎦⎤⎢⎣⎡ 式中:()()()()[]()()()()[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-=1121121211111n X n X X X B()()()()()()[]n X X X X n 000,,3,2 =将B 带入公式,最终确定GM (1,1)预测模型()()()()a e a X t X at μμ+⎥⎦⎤⎢⎣⎡-=-∧∧100 n t 2,1,0= 将值代入离散模型公式求()()t X ∧1,预测的累加值还原为预测值:()()()()()()1110--=∧∧∧t X t X t X2模型精度的检验2.1残差检验计算残差()()t 0ε及其相对残差()()t q 0,即:()()()()()()1000--=∧t x t x t ε,()()()()()()%100000⨯=t x t t q ε n t ,,2,1 =相对残差()0q 越小,表示模型精度越高。
灰色GM(1,1)模型预测全国废气中主要污染物排放量趋势(精)
灰色GM(1,1)模型预测全国废气中主要污染物排放量趋势一.实验目的1.掌握GM(1,1)模型的建立方法2.了解灰色系统理论及其在环境预测中的应用3.提升自己查阅资料的能力二.灰色系统理论灰色系统理论是20世纪80年代,由华中理工大学邓聚龙教授首先提出并创立的一门新兴学科。
它是基于数学理论的系统工程学科。
灰色系统法理论就是某一个系统内部各个因素之间的关系不是非常的明确。
例如:在农业生产中,生产作物的生长情况与农药、土壤以及气候等条件之间的关系。
我们对于这一系统内这些因素之间的关系不是非常的了解,所以这就叫作一个灰色系统。
灰色系统理论提出了一种新的分析方法—关联度分析方法,即根据因素之间发展态势的相似或相异程度来衡量因素间关联的程度,它揭示了事物动态关联的特征与程度。
由于以发展态势为立足点,因此对样本量的多少没有过分的要求,也不需要典型的分布规律,计算量少到甚至可用手算,且不致出现关联度的量化结果与定性分析不一致的情况。
用灰色系统理论建立的微分方程模型称为灰色模型,即GM模型。
用于预测的模型主要是GM(1,1)模型,它是一阶单个变量的预测模型,其建模过程中仅利用预测对象本身数据的一个时间数列,而不考虑影响预测对象的其他各种因素。
三.建立GM(1,1)模型设有变量X(0)={X(0)(i),i=1,2,...,n}为某一预测对象的非负单调原始数据列,为建立灰色预测模型:首先对X(0)进行一次累加,生成一次累加序列: X(1)={X(1)(k),k=1,2,…,n}其中X(k)=(1)∑i=1kX(0)(i)=X(1)(k-1)+ X(0)(k) (1) 对X(1)可建立下述白化形式的微分方程:dX(1)(1) 十aX=u (2) dt式(2)即为GM(1,1)模型。
上述白化微分方程的解为(离散响应):X (1)(k+1)=(X(0)(1)-u-aku)e+ (3) aa或X (1)(k)=(X(0)(1)-u-a(k-1)u)e+ (4) aa式中:k为时间序列,取年。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色预测G M(1--1)模型实现过程灰色系统预测模型GM(1,1)实现过程灰色系统预测模型GM(1,1) 1. GM(1,1)的一般形式设有变量X (0)={X (0)(i),i=1,2,...,n}为某一预测对象的非负单调原始数据列,为建立灰色预测模型:首先对X (0)进行一次累加(1—AGO, Acumulated Generating Operator)生成一次累加序列:X (1)={X (1)(k ),k =1,2,…,n}其中X (1)(k )=∑=ki 1X (0)(i)=X (1)(k -1)+ X (0)(k ) (1) 对X (1)可建立下述白化形式的微分方程:dtdX )1(十)1(aX =u (2)即GM(1,1)模型。
上述白化微分方程的解为(离散响应): ∧X (1)(k +1)=(X (0)(1)-a u )ak e -+au(3) 或∧X (1)(k )=(X (0)(1)-a u ))1(--k a e +au (4) 式中:k 为时间序列,可取年、季或月。
2. 辩识算法记参数序列为∧a , ∧a =[a,u]T,∧a 可用下式求解:∧a =(B T B)-1B T Y n (5)式中:B —数据阵;Y n —数据列B =⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+++- 1 (n))X 1)-(n (X 21 ... 1 (3))X (2)X (211 (2))X (1)X (21(1)1(1)(1)(1)(1))(-- (6) Y n =(X (0)(2), X (0)(3),…, X (0)(n))T (7)3. 预测值的还原由于GM 模型得到的是一次累加量,k ∈{n+1,n+2,…}时刻的预测值,必须将GM 模型所得数据∧X (1)(k +1)(或∧X (1)(k ))经过逆生成即累减生成(I —AGO)还原为∧X(0)(k +1)(或∧X (0)(k )),即:∧X(1)(k )=∑=ki 1∧X (0)(i)=∑-=11k i ∧X(0)(i)+∧X (0)(k )∧X(0)(k )=∧X(1)(k )-∑-=11k i ∧X (0)(i)因为∧X(1)(k -1)=∑-=11k i ∧X(0)(i),所以∧X(0)(k )=∧X(1)(k )-∧X (1)(k -1)。
4. 灰色系统模型的检验检验方法一:残差合格(相对误差)定义:设原始序列{})(,),2(),1()0()0()0()0(n x x x X = 相应的模型模拟序列为{})(ˆ,),2(ˆ),1(ˆˆ)0()0()0()0(n x x x X = 残差序列{})(),2(),1()0(n εεεε ={})(ˆ)(,),2(ˆ)2(),1(ˆ)1()0()0()0()0()0()0(n x n x x x xx ---= 相对误差序列⎭⎬⎫⎩⎨⎧=∆)()(,,)2()2(,)1()1()0()0()0(n x n x x εεε{}nk 1∆=1.对于k <n,称)()()0(k x k k ε=∆为k 点模拟相对误差,称)()()0(n x n n ε=∆为滤波相对误差,称∑=∆=∆nk k n 11为平均模拟相对误差;2.称∆-1为平均相对精度,n ∆-1为滤波精度;3.给定α,当α<∆,且α<∆n 成立时,称模型为残差合格模型。
检验方法二:关联合格定义:设)0(X 为原始序列,)0(ˆX为相应的模拟误差序列,ε为)0(X 与)0(ˆX 的绝对关联度,若对于给定的00,0εεε>>,则称模型为关联合格模型。
检验方法三:均方差比合格、小误差概率合格定义:设)0(X 为原始序列,)0(ˆX为相应的模拟误差序列,)0(ε为残差序列。
∑==n k k x n x 1)0()(1为)0(X 的均值,21)0(21))((1x k x n s n k -=∑=为)0(x 的方差,∑==nk k n 1)(1εε为残差均值,∑=-=n k k n s 1222))((1εε为残差方差,1. 称12s sc =为均方差比值;对于给定的00>c ,当0c c <时,称模型为均方差比合格模型。
2. 称()16745.0)(s k P p <-=εε为小误差概率,对于给定的00>p ,当0p p >时,称模型为小误差概率合格模型。
表1 精度检验等级参照表 精度等级相对误差 关联度 均方差比值 小误差概率一级 0.01 0.90 0.35 0.95 二级 0.05 0.80 0.50 0.80 三级 0.10 0.70 0.65 0.70 四级 0.20 0.60 0.800.60一般情况下,最常用的是相对误差检验指标。
5. GM(1,1)预测应用举例设原始时间序列为:{})5(),4(),3(),2(),1()0()0()0()0()0()0(x x x x x X =()679.3,390.3,337.3,278.3,874.2= 建立GM(1,1)模型,并进行检验。
解:1)对)0(X 作1-AGO ,得[D 为)0(X 的一次累加生成算子,记为1-AGO] {})5(),4(),3(),2(),1()1()1()1()1()1()1(x x x x x X =()558.16,579.12,489.9,152.6,874.2=2)对)1(X 作紧邻均值生成,令)1(5.0)(5.0)()1()1()1(-+=k x k x k Z{})5(),4(),3(),2(),1()1()1()1()1()1()1(z z z z z Z =()718.14,84.11,820.7,513.4,874.2=于是,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=1718.14184.111820.71513.41)5(1)4(1)3(1)2()1()1()1()1(z z z z B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=679.3390.3337.3278.3)5()4()3()2()0()0()0()0(x x x x Y ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----•⎥⎦⎤⎢⎣⎡----=T 1718.14184.111820.71513.41111718.14184.11820.7513.4B B ⎥⎦⎤⎢⎣⎡--=4235.38235.38221.423 ⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡--=--T832371.11665542.0165542.0017318.04235.38235.38221.423)(11B B ⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⨯=221.423235.38235.384969.2301221.423235.38235.384235.384221.42312⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎦⎤⎢⎣⎡----•⎥⎦⎤⎢⎣⎡==T -T 679.3390.3337.3278.31111718.14184.11820.7513.4832371.11665542.0165542.0017318.0)(ˆ1Y B B B a⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎦⎤⎢⎣⎡---=679.3390.3337.3278.3604076.10019051.0537833.0085280.1089344.0028143.0030115.0087386.0 ⎥⎦⎤⎢⎣⎡-=065318.3037156.0 3)确定模型065318.3037156.0)1()1(=-x dtdx 及时间响应式abe a b x k xak +-=+-))1(()1(ˆ)0()1( 4986.823728.85037156.0-=k e 4)求)1(X 的模拟值{})5(ˆ),4(ˆ),3(ˆ),2(ˆ),1(ˆˆ)1()1()1()1()1()1(x x x x x X= =(2.8740,6.1058,9.4599,12.9410,16.5538) 5)还原出)0(X 的模拟值,由)(ˆ)1(ˆ)1(ˆ)1()1()0(k x k x k x-+=+ 得 {})5(ˆ),4(ˆ),3(ˆ),2(ˆ),1(ˆˆ)0()0()0()0()0()0(x x x x x X==(2.8740,3.2318,3.3541,3.4811,3.6128)6)误差检验表2 残差与相对误差计算结果 序实际数据 模拟数据 残差 相对误差3 3.337 3.3541 -0.0171 0.51%4 3.390 3.4811 -0.0911 2.69%5 3.679 3.6128 0.0662 1.80%① 平均相对误差%)80.1%69.2%51.0%41.1(414151+++=∆=∆∑=k k=1.0625%…………(参考表1,1级)② 计算X 与Xˆ的灰色关联度 ))1()5((21)1()((42x x x k x S k -+-=∑= =)874.2679.3(21)874.2390.3()874.2337.3()874.2278.3(-+-+-+-0.40250.5160.4630.404+++==1.7855)1(ˆ)5(ˆ(21)1(ˆ)(ˆ(ˆ42x x x k x Sk -+-=∑= )874.26128.3(21)874.24811.3()874.23541.3()874.22318.3(-+-+-+-=3694.06071.04801.03578.0+++= =1.8144[][]∑=---+---=-42))1(ˆ)5(ˆ())1()5((21))1(ˆ)(ˆ())1()((ˆk x x x x x k x x k x S S)4025.03694.0(21)516.06071.0()463.04801.0()404.03578.0(-+-+-+-=01655.0091.00171.00462.0-++-= =0.0453564525.45999.404535.08144.17855.118144.17855.11ˆˆ1ˆ1=+++++=-+++++=S S S S S S ε=0.9902>0.90…………(参考表1,为1级)综合:精度为一级,可以用4986.823728.85)1(ˆ037156.0)1(-=+k e k x其中,)(ˆ)1(ˆ)1(ˆ)1()1()0(k x k x k x-+=+预测。
6. GM(1,1)模型的特点总结GM(1,1)是一种长期预测模型,在没有大的市场波动及政策性变化的前提下,该预测值应是可信的。
在采用灰色系统理论进行定量预测时,如果存在对预测对象影响较大的因素,就要在定性分析的基础上,寻找原始数据信息的突变点的量化值,然后再对预测值进行必要的修正,使预测值更接近实际情况,提高预测值的可信度,为科学决策提供可靠的数据。
