龙格—库塔实验报告
计算方法上机作业——龙格库塔法

计算方法上机作业——龙格库塔法龙格库塔法(Runge-Kutta method)是一种常用于求解常微分方程(Ordinary Differential Equation,ODE)的数值解法。
它是由德国数学家卡尔·龙格(Carl Runge)和马丁·威尔海姆·库塔(Martin Wilhelm Kutta)在20世纪初提出的。
龙格库塔法的基本思想是通过数值逼近来计算微分方程的近似解。
在讲解龙格库塔法之前,我们先来简单回顾一下ODE的一阶常微分方程的基本形式:y′(y)=y(y,y)其中,y(y,y)是已知函数。
龙格库塔法的核心是使用差分逼近计算函数的斜率。
假设我们要求解的方程为:y′(y)=y(y,y),y(y)=y₀所需计算的点为y₀,y₁,...,yy,对应的函数值为y₀,y₁,...,yy,其中y是步长的个数。
龙格库塔法通过递推关系式来计算估计值,并不断更新当前点的函数值。
接下来以龙格库塔法的经典四阶形式为例进行说明。
该方法的基本方程如下:yy+1=yy+(y₁+2y₂+2y₃+y₄)/6y₁=ℎy(yy,yy)y₂=ℎy(yy+ℎ/2,yy+y₁/2)y₃=ℎy(yy+ℎ/2,yy+y₂/2)y₄=ℎy(yy+ℎ,yy+y₃)其中y表示当前步骤,ℎ表示步长,yy表示当前点的函数值,y₁,y₂,y₃和y₄则表示对应的斜率。
使用龙格库塔法,我们可以通过不断递归计算来求得指定区间(例如[y,y])上的函数值。
具体步骤如下:1.确定求解区间[y,y]和初始点(y₀,y₀)以及步长ℎ。
2.初始化:设置yy=y₀,yy=y₀。
3.对所有y=0,...,y−1:计算y₁,y₂,y₃和y₄,根据上述递推关系式。
根据递推关系式计算yy+1更新当前点的函数值,即yy+1=y(yy+1)。
更新当前点的y值,即yy+1=yy+ℎ。
4.返回结果:最终求得的函数值。
需要注意的是,选择适当的步长对最终结果的精度和计算效率都有重要影响。
四阶龙格—库塔法的原理及其应用

《四阶龙格—库塔法的原理及其应用》
龙格—库塔法(又称龙格库塔法)是由一系列有限的、独立的可能解组成的无穷序列,这些解中每个都与原来的数列相差一个常数。
它是20世纪30年代由匈牙利著名数学家龙格和库塔提出的,故得此名。
1.它的基本思想是:在n 阶方阵M 上定义一个函数,使得当n 趋于无穷时,它在m 中所表示的数值为M 的某种特征值,从而构造出一族具有某种特性的可计算函数f (x)= Mx+ C (其中C 为任意正整数)。
例如,若f (x)=(a-1) x+ C,则称之为(a-1) x 的龙格—库塔法。
2.它的应用很广泛,可以求解各类问题,且能将大量的未知数变换成少数几个已知数,因此它是近似计算的一种重要工具。
3.
它的优点主要有:(1)可以将多项式或不等式化成比较简单的形式;(2)对于同一问题可以用不同的方法来解决,并取得同样的结果;(3)适合处理高次多项式或者不等式,尤其适合处理多元函数的二次型。
第三部分龙格-库塔方法

内江师范学院数学与信息科学学院 吴开腾 制作
于是有
其中
y ( xn +1 ) − y ( xn ) = y '(ξ ), ξ ∈ ( xn , xn +1 ) h y ( xn +1 ) = y ( xn ) + hf (ξ , y (ξ ))
k * = f (ξ , y (ξ )) 称作区间 [ xn , xn +1 ] 上的平均斜率。 上的平均斜率 平均斜率。 问题:计算近似值y ( xn +1 ) 的关键是如何选择算法确定平均斜率 k *
(15)
f ( xn +1 , yn + h ( − k1 + 2 k 2 ))
内江师范学院数学与信息科学学院 吴开腾 制作
注释1 可以用Taylor展示证明格式(14) 注释1:可以用Taylor展示证明格式(14)具有三阶精 展示证明格式
度,并且还可以用类似的方法得到四阶及其以上的更高 阶精度的Runge-Kutta格式 阶精度的Runge-Kutta格式。 Runge 格式。
内江师范学院数学与信息科学学院 吴开腾 制作
h yn + ( k1 + 2 k 2 + 2 k3 +k 4) 6 f ( xn , y n ) h f ( x 1 , yn + k1 ) n+ 2 2 h f ( x 1 , yn + k 2 ) n+ 2 2 f ( xn +1 , yn + hk3 ) (16)
四阶龙格- 四阶龙格-库塔格式计算结果
xn
0.1 0.2 0.3 0.4 0.5
yn
欧拉格式计算结果 xn yn y ( xn )
fluent runge-kutta methods

fluent runge-kutta methods
龙格-库塔法(Runge-Kutta methods)是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。
简写做RK法。
对于任意的
Y=f(X),假设某点(Xi,Yi)的斜率为ki,如果有无限小的dX,则有
Yi+1=Yi+ki*dx。
dx就是迭代步长,然而在现实中它不可能是无限小的,我们一般写作h。
将它与上式中的dx替换就是一阶RK法。
一般我们采用四阶RK法,其形式如下:
k1是时间段开始时的斜率;
k2是时间段中点的斜率,通过欧拉法采用斜率k1来决定y在点tn+h/2的值;
k3也是中点的斜率,但是这次采用斜率k2决定y值;
k4是时间段终点的斜率,其y值用k3决定。
通过四阶RK法的迭代可以得到较为精确的数值解。
数值计算方法第3、4次实验--龙贝格--龙格库塔

1.完成复合梯形、复合辛普森求积公式,用变步长、事后误差估计的方法完成P145例题6.3.1对应表6-3的计算,课后作业题7.%复合梯形求积公式的MATLAB实现%姓名:王定%学号:1306034248%中北大学仪器与电子学院function T_n=ComTrapezoidal(a,b,n)%a为积分上限%b为积分下限%n为划分区间的个数h=(b-a)/n;for(k=0:n)x(k+1)=a+k*h;if(x(k+1)==0)x(k+1)=10^(-10);endendI_1=h/2*(f(x(1))+f(x(n+1)));for(i=2:n)F(i)=h*f(x(i));endI_2=sum(F);I_n=I_1+I_2%****************************% %复合辛普森求积公式的MATLAB实现function I=ComSimpson(a,b,n)n=2;h=(b-a)/2;I1=0;I2=(f(a)+f(b))/h;eps=1.0e-4;while(abs(I2-I1)>eps)n=n+1;h=(b-a)/n;I1=I2;I2=0;for(i=0:n-1)x=a+h*i;x1=x+h;I2=I2+h/6*(f(x)+4*f((x+x1)/2)+f(x1));endendI=I2 %变步长梯形求积法的MATLAB实现function AdaptiveTrapezoidal(a,b,eps)m=1t0=0;t2=(f(a)+f(b))/4+f((a+b)/2)while(abs(t2-t0)>eps)m=m+1p=t2;t1=0;n=2^m;h=(b-a)/n;for(k=0:(n-1))t1=t1+h*((f(a+k*h)+f(a+(k+1)*h))/4+f(a+(k+1/2)*h)/2);endt2=t1t0=p;endI=t2%**************************%>>AdaptiveTrapezoidal(1,2,0.000001)m = 1t2 = 3.03948481584447m = 2t2 = 2.02304986763725m = 3t2 = 2.02080858246806m = 4t2 = 2.02024624995310m = 5t2 = 2.02010553934348m = 6t2 = 2.02007035369492m = 7t2 = 2.02006155678257m = 8t2 = 2.02005935752321m = 9t2 = 2.02005880770641I = 2.02005880770641%课后作业题7.>>AdaptiveTrapezoidal(1,3,0.0001)m = 1t2 =7.99930630234471m = 2t2 =10.84204346755743m = 3t2 =10.92309388961378m = 4t2 =10.94339842118680m = 5t2 =10.94847716722413m = 6t2 =10.94974701694155m = 7t2 =10.95006448956964m = 8t2 =10.95014385836406I =10.950143858364062.完成龙贝格积分,计算P150例题6.4.2对应的表6-5,按例题列表格显示数值,完成课后作业题8.%龙贝格求积法的MATLAB实现%姓名:王定%学号:1306034248%中北大学仪器与电子学院function [I,step]=Romberg(f,a,b,eps)f=input('please input f=');a=input('please input a=');b=input('please input b=');eps=input('please input eps=');%I为所求积分值%step为积分划分的子区间次数%f为被积函数%a为积分上限%b为积分下限%eps为积分精度if(nargin==3)eps=1.0e-4;end;M=1;tol=10;k=0;T=zeros(1,1);h=b-a;T(1,1)=(h/2)*(subs(sym(f),findsym(sym(f)),a)+subs(sym(f),findsy m(sym(f)),b));while(tol>eps)k=k+1;h=h/2;Q=0;for(i=1:M)x=a+h*(2*i-1);Q=Q+subs(sym(f),findsym(sym(f)),x);endT(k+1,1)=T(k,1)/2+h*Q;M=2*M;for(j=1:k)T(k+1,j+1)=T(k+1,j)+(T(k+1,j)-T(k,j))/(4^j-1);endtol=abs(T(k+1,j+1)-T(k,j));endI=T(k+1,k+1)step=k %计算P150例题6.4.2对应的表6-5>> [I,step]=Romberg('4/(1+x^2)',0,1); format longI,stepI =3.14159266527772step =4%********************************%%按例题列表格显示数值,完成课后作业题8.>>please input f='(2/sqrt(pi))*exp(-x)'please input a=0please input b=1please input eps=1.0e-5I =0.71327166981418step =31、完成预报校正公式的程序,完成P183例题7.3.2对应表7—6第3列结果的计算,课后作业题3。
机械动力学作业--四阶龙格库塔法
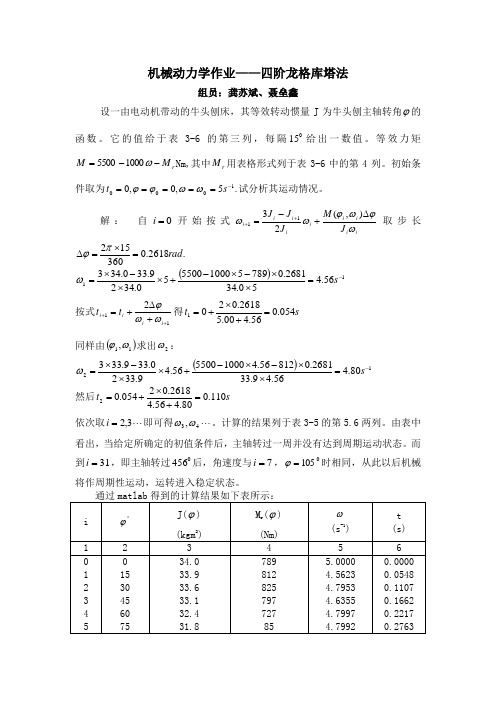
机械动力学作业——四阶龙格库塔法组员:龚苏斌、聂垒鑫设一由电动机带动的牛头刨床,其等效转动惯量J 为牛头刨主轴转角ϕ的函数。
它的值给于表3-6的第三列,每隔015给出一数值。
等效力矩r M M --=ω10005500Nm,其中r M 用表格形式列于表3-6中的第4列。
初始条件取为.5,0,01000-=====s t ωωϕϕ试分析其运动情况。
解: 自0=i 开始按式ii i i i i i i i J M J J J ωϕωϕωω∆+-=++),(2311取步长.2618.0360152rad =⨯=∆πϕ ()1156.450.342681.078951000550050.3429.330.343-=⨯⨯-⨯-+⨯⨯-⨯=s ω 按式112+++∆+=i i i i t t ωωϕ得s t 054.056.400.52618.0201=+⨯+=同样由()11,ωϕ求出2ω:()1280.456.49.332681.081256.41000550056.49.3320.339.333-=⨯⨯-⨯-+⨯⨯-⨯=s ω 然后s t 110.080.456.42618.02054.02=+⨯+=依次取 3,2=i 即可得 43,ωω。
计算的结果列于表3-5的第5.6两列。
由表中看出,当给定所确定的初值条件后,主轴转过一周并没有达到周期运动状态。
而到31=i ,即主轴转过0456后,角速度与7=i ,0105=ϕ时相同,从此以后机械将作周期性运动,运转进入稳定状态。
运用四阶龙格—库塔公式)22(6143211k k k k i i ++++=+ωω其中,),(1i i hf k ωϕ=、)2,2(12k h hf k i i ++=ωϕ、)2,2(23k hhf k i i ++=ωϕ、),(33k h hf k i i ++=ωϕ。
主要函数ωϕωωϕωϕJ d dJM f 2),(),(2-=,其中ϕϕ∆-=+i i i J J d dJ 1)(利用上述的公式在matlab 中编写程序,主要就是编写循环函数。
计算方法实验指导与实验报告
6
实验题目 2 龙贝格(Romberg)积分法
方法概要:利用复化梯形求积公式、复化辛普生求积公式、复化柯特斯求积公式 的误差估计式计算积分 计算公式:
b
a
f ( x)dx 。记 h
ba , xk a k h , k 0,1, n
, n ,其
Tn
1 n h k 1[ f ( xk 1 ) f ( xk )] 2
2
实验题目 1 拉格朗日(Lagrange)插值
方法概要: 给定平面上 n 1 个不同的数据点 ( xk , f ( xk )) , k 0,1, 则满足条件
, n , xi x j , i j ;
Pn ( xk ) f ( xk ) , k 0,1,
的 n 次拉格朗日插值多项式
, n ,构造 Pn ( x ) ,利用拉格朗日插值多项式 Pn ( x ) 作
为 f ( x) 的近似值。分别取 n 5 , n 10 , n 20 ,同时计算 Pn ( x ) 在 x 0.95 ,
x 0.05 , x 0.05 , x 0.95 处的函数值。
(2)设 f ( x) e , x [1,1] ,考虑非等距节点的拉格朗日插值多项式 Pn ( x ) ,
问题 2 插值区间越小越好吗? 考虑下面两个拉格朗日插值问题:
1 , x [1,1] ,考虑等距节点的拉格朗日插值多项式 Pn ( x ) , 1 x2 2.0 xk 1.0 k h , 即将区间 [1,1] 进行 n 等分, 记h , 构造 Pn ( x ) , k 0,1, , n , n
问题 4 考虑拉格朗日插值问题,内插比外推更可靠吗? 考虑下面两个拉格朗日插值问题: (1)设 f ( x)
利用龙格库塔法求解质点运动方程
利用龙格-库塔法求解质点运动常微分方程一、待解问题讨论常微分方程的初值问题,边值问题的数值解法,最常用的基本方法就是龙格-库塔法使一些物理方程的计算简便,所得结果的精确提高。
下面是利用龙格-库塔法求解一个质点运动的常微分方程 以初速s km v /80=自地球表面(半径km R 6000=)竖直向上发射一质量为 m 的火箭,如图所示。
若不计空气阻力,火箭所受引力 F 大小与它到地心距离的平方成反比,求火箭所能到达的最大高度H 。
火箭为我们分析的对象,对其做受力分析,火箭在任意位置 x 处仅受地球引力F 作用。
由题意知,F 的大小与 x 2 成反比,设μ为比例系数,则有:(1)当火箭处于地面时,即R x =时F = m g ,由式(1)可得2mgR =μ,于是火箭在任意位置 x 处所受地球引力 F 的大小为 22xmgR F =由于火箭作直线运动,火箭的直线运动微分方程式为:2x F μ=2222xmgR dt x d m -=分离变量积分22vx gR dx dv -=二、物理机理1.龙格-库塔法的基本思想及一般形式设初值问题],[)(b a x y y ∈=,由微分中值定理可知,必存在],[1+∈n n x x ξ,使设)(n n x y y =,并记))(,(*ξξy f K =,则*1)(hK y x y n n +=+其中*K 称为)(x y 在][1,+n n x x 上的平均斜率,只要对平均斜率*K 提供一种算法,上式就给出了一种数值解公式,例如,用),(1n n y x f K =代替*K ,就得到欧拉公式,用),(112++=n n y x f K 代替*K ,就得到向后欧拉公式,如果用21,K K 的平均值来代替*K ,则可得到二阶精度的梯形公式。
可以设想,如果在],[1+n n x x 上能多预测几个点的斜率值,用它们的加权平均值代替*K ,就有望的到具有较高精度的数值解公式,这就是龙格-库塔(Runge -Kutta )法的基本思想。
龙格库塔法
2020/4/25
10
令 y(xi1) yi1 对应项的系数相等,得到
c1 c2 1 ,
a2c2
1 2
,
b21c2
1 2
这里有 4 个未知 数,3 个方程。
存在无穷多个解。所有满足上式的格式统称为2阶龙格 - 库塔格式。
2020/4/25
• 1.在运动流体的整个空间,可绘出一系列的流线,称为流 线簇。流线簇的疏密程度反映了该时刻流场中速度的不同。 2.当为非定常流时,流线的形状随时间改变:对于定常流, 流线的形状和位置不随时间而变化。 3.定常流的流线和迹线重合。 4.一般情况下,流线不能相交,不能折转,只能是一条光 滑曲线。
龙格库塔法
2020/4/25
5
引入记号
y(xi1) y(xi ) K
K hy(i) hf i, y(i)
yi1 yi K
K可以认为是y y(x)在区间[xi , xi1]上的平均斜率
y
只要使用适当的方法求 出y(x)在区
y y(x)
间[xi , xi1]上平均斜率的近似值 K
K
就可得到相应的Runge-Kutta方法
2!
3!
4!
2020/4/25
20
龙格—库塔方法的推导基于Taylor展开方法,因而它要求所求的解具有
较好的光滑性。如果解的光滑性差,那么,使用四阶龙格—库塔方法求得的数 值解,其精度可能反而不如改进的欧拉方法。在实际计算时,应当针对问题的 具体特点选择合适的算法。对于光滑性不太好的解,最好采用低阶算法而将步 长h 取小。
23 4 5 6
高等流体力学龙格库塔法求解实际问题汇报PPT
结论:水平方向速度u随y的变化曲线,当y很小时速度梯 度很大,随着y的增加速度梯度逐渐减小,水平方向速度 u逐渐趋于主流速度U=25m/s。 对于平板的不同位置(取x=0.01m,x=0.5m,x=2m,x=5m 处),水平方向速度u趋于主流速度U的快慢也不尽相同, 随着X的增加u的变化逐渐减慢。
由Y方向的速度公式 v Ue [ f '() f ()],以及 y 2 x
k2 2
,yn +
l2 2
,zn +
m2 2
,tn +
t ) 2
l4 =tf(2 xn +k3,yn +l3,zn +m3,tn +t)
%求解F得到A x=0;y=0;z=1;h=0.001;t0=0;tn=6;j=1;t=t0:h:tn;N=(tn-t0)/h; x1=zeros(N,1);y1=zeros(N,1);z1=zeros(N,1); for i=1:N+1
引入流函数,将未知 函数的数量降为1个, 并做无因次相似性变 换,变为常微分方程, 定解条件相应变换。
将初边值问题转换为 初值问题
4.通过 编程进行流场分析
我们小组主要对 X Y 方向的速度、边界层厚度、排挤厚度、 以及板面切应力进行了求解分析。
程序实现
f =x,f =y,f =z f =y,f =z,f =-xz f 0 A
%求边界层厚度 板面切应力 排挤厚度 动量切应力 x=0:0.001:5; Ue=25;n=0.00002593; p=1.205; m1=5.138*sqrt(2*n/p/ Ue *x); m2=sqrt(2*n/p/25*x).*(sum(1-y1))*h; m3=sqrt(2*n/p/15*x).*(sum(y1.*(1-y1)))*h m4=0.1656*x.^(-0.5); figure(5);plot(x,m1); title(' 边 界 层 厚 度 δ 随 x 的 变 化 曲 线 '); xlabel('x(m)'); ylabel('y(m)--边界层厚度'); grid on;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
龙格—库塔法解常微分方程实验报告
一、实验题目
求解初值问题
1)0()10(2'y
xyxyy
二、实验引言
1、实验目的
进一步理解龙格—库塔方法的设计思路和算法流程,培养动手实践能力和分
析能力。
2、实验意义
龙格—库塔方法的推导基于泰勒展开方法,因而它要求的解具有较好的光滑
性质。反之,如果解得光滑性差,那么,使用四阶龙格—库塔法方法求得的数值
解,其精度可能反而不如梯形方法。实际计算中,应当针对问题的具体特点选择
合适的算法。
三、算法设计
1. 基本思想
由Lagrange微分中值定理,
11()()'()()()(,())nnnnnyxyxyxxyxhfy
记*(,())khfy,则得到
*
1()()nnyxyxk
这样,给出*k的一种算法,就得到求解微分方程初值问题的一种计算公式。
四阶龙格_库塔法是用1k,2k,3k和4k的加权平均值来近似*k。最经典的四
阶龙格—库塔公式为:
121324311234(,)(,)22(,)22(,)y(22)2nn
nn
nn
nn
nnKfxyhhKfxyKhhKfxyKKfxhyhKhyKKKK
四阶龙格—库塔法的误差估计局部截断误差为5()Oh。
2.算法流程图
计算N=fix((b-x0)/h)
n=1
x0+h=>x1
f(x0,y0)=>K1
f(x0+h/2,y0+h/2*K1)=>K2
f(x0+h/2,y0+h/2*K2)=>K3
f(x0+h,y0+h*K3)=>K4
y0+h/6*(K1+2*K2+2*K3+K4)=>y1
输出x1,y1
n=n+1
x1=>x0
y1=>y0
n=N ?
结束
开始
读入x0,y0,b,h
四、程序设计
program longgekuta
implicit none
real,parameter::b=1
real::h=0.2
integer::n
real::x,K1,K2,K3,K4,y
real,external::f
x=0
y=1
open (unit=10,file='1.txt')
do while(x<=b)
K1=f(x,y)
K2=f(x+h/2,y+K1*h/2)
K3=f(x+h/2,y+K2*h/2)
K4=F(x+h,y+K3*h)
y=y+(k1+2*K2+2*K3+K4)*h/6
x=x+h
write(10,*) x,y
end do
end
function f(x,y)
implicit none
real::f,x,y
f=y-2*x/y
end function
五、结果及讨论
1.实验结果
0.2000000 1.183229
0.4000000 1.341667
0.6000000 1.483281
0.8000000 1.612514
1.000000 1.732142
1.200000 1.844040
六、算法评价
1、本次实验实现了常微分方程初值问题数值解法中的四阶龙格—库塔法
2、对欧拉法和龙格—库塔法进行比较:在相同步长的情况下,欧拉法每步只
计算一个函数值,四阶龙格—库塔法每步需计算四个函数值,就是说,四阶龙格
—库塔法的计算量差不多是欧拉法的四倍,为了比较它们的计算精度,可以将欧
拉法的步长取为h,将四阶龙格—库塔法的步长取为4h。这样,如果用二种方法
求解同一初值问题,则它们的计算量相当。在计算量相当的条件下,比较它们的
计算结果,就能够看出它们的精度差异。
3、比较了其数值解与精确解之间的误差。可以发现四阶龙格—库塔法都非常
接近精确解。
附:
向前欧拉法程序
program xiangqianoula
implicit none
real,parameter::a=0,b=1
integer,parameter::k=10
real::h=0.1,y0=1
integer::n
real::x,y
y=y0
open (unit=10,file='1.txt')
do n=0,k-1
x=a+n*h
y=y+h*(y-2*x/y)
write(10,*) x+h,y
end do
end
运行结果:
0.1000000 1.100000
0.2000000 1.191818
0.3000000 1.277438
0.4000000 1.358213
0.5000000 1.435133
0.6000000 1.508966
0.7000000 1.580338
0.8000000 1.649784
0.9000000 1.717780
1.0000000 1.784771
